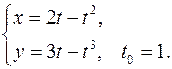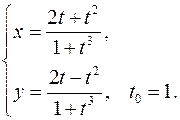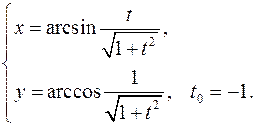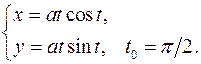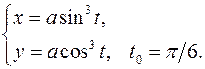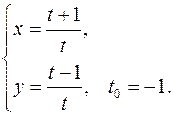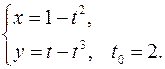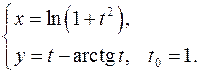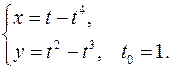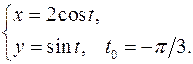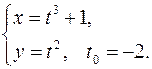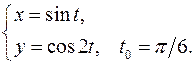Задача 16
. Составить уравнения касательной и нормали к кривой в точке, соответствующей значению параметра  .
16.1. 
x0
= 3a√3/8
y0
= a/8
x'= 3a sin2
tcost
y'= -3a cos2
tsint
y'x
= -tgt
y'x0
= -√3
Касательная
y – a/8= -√3(x-3a√3/8)
y+√3x – 10a/8=0
Нормаль
y – a/8= 1/√3*(x-3a√3/8)
√3y – x +2√3a/8=0
16.2. 
x0
= √3/2
y0
= √3/2
x'= -√3sint
y'= cost
y'x
= -√3/3*ctgt
y'x
0
= -1/3
Касательная
y - √3/2= -1/3*(x-√3/2)
y+1/3*x - 4√3/6=0
Нормаль
y - √3/2= 3*(x-√3/2)
y-3x+√3=0
16.3. 
x0
= a(π/3-√3/2)
y0
= a/2
x'= a(1-cost)
y'= asint
y'x
= sint/(1-cost)
y'x0
= √3
Касательная
y-a/2= √3(x-a(π/3-√3/2))
y-√3x-2a+πa/√3=0
Нормаль
y-a/2= -1/√3(x-a(π/3-√3/2))
y+x/√3-πa/3√3=0
16.4. 
x0
= 1
y0
= 2
x'= 2-2t
y'= 3-3t2
y'x
= 3/2*(1+t)
y'x
0
= 3
Касательная
y-2=3(x-1)
y-3x+1=0
Нормаль
y-2=-1/3(x-1)
y+x/3-7/3=0
16.5. 
x0
= 3/2
y0
= 1/2
x'= (2+2t)(1+t3
)-3t2
(2t+t3
)
= 2+2t-4t3
-t4
(1+t3
)2
(1+t3
)2
y'= (2-2t)(1+t3
)-3t2
(2t-t3
)
= 2-2t-4t3
+t4
(1+t3
)2
(1+t3
)2
y'x
= 2-2t-4t3
+t4
2+2t-4t3
-t4
y'x0
= 3
Касательная
y-1/2=3(x-3/2)
y-3x+4=0
Нормаль
y-1/2=-1/3(x-3/2)
y+x/3-1=0
16.6. 
x0
= 5π/4
y0
= π/4
x'= √(1+t2
)-t2
/√(1+t2
)
= 1/(1+t2
)
√(1-t2
/(1+t2
))(1+t2
)
y'= -t
= -1/(1+t2
)
√(1-1/(1+t2
))√(1+t2
)3
y'x
= -1
y'x0
= -1
Касательная
y-π/4=-(x-5π/4)
y+x-6π/4=0
Нормаль
y-π/4=x-5π/4
y-x+π=0
16.7. 
x0
= π√2(π-8)/32
y0
= π√2(π+8)/32
x'= -2sint-t2
sint
y'= 2cost+t2
cost
y'x
= -ctgt
y'x0
= -1
Касательная
y-π√2(π+8)/32= -(x-π√2(π-8)/32)
y+x-π2
√2/16 = 0
Нормаль
y-π√2(π+8)/32= x-π√2(π-8)/32
y+x+π2
√2/2 = 0
16.8. 
x0
= 6a/5
y0
= 12a/5
x'= 3a-3at2
y'= 6at
y'x
= 2t/(1-t2
)
y'x
0
= -4/3
Касательная
y-12a/5 = -4/3(x-6a/5)
y+4x/3-4a=0
Нормаль
y-12a/5 = 3/4(x-6a/5)
y-0.75x-1.5a=0
16.9. 
x0
= 1
y0
= 2
x'= -(2tgt+1)/sin2
t
y'= 1/cos2
t-1/sin2
t
y'x
= cos2t _
cos2
t(2tgt+1)
y'x0
= 0
Касательная
y=2
Нормаль
x=1
16.10. 
x0
= 0
y0
= 0
x'= t-t3
y'= t+t2
y'x
= 1/(1-t)
y'x
0
= 1
Касательная
y= x
Нормаль
y= -x
16.11. 
x0
= 0
y0
= aπ/2
x'= acost-atsint
y'= asint+atcost
y'x
= sint+tcost
cost-tsint
y'x
0
= -2/π
Касательная
y-aπ/2+2x/π=0
Нормаль
y-aπ/2-πx/2=0
16.12. 
x0
= 1/2
y0
= √3/2
x'= cost
y'= -sint
y'x
= -tgt
y'x0
= -√3/3
Касательная
y-√3/2= -√3/3(x-1/2)
y+x√3/3-2√3/3=0
Нормаль
y-√3/2= √3(x-1/2)
y=x√3
16.13. 
x0
= π/4
y0
= π/4
x'= √(1+t2
)-t2
/√(1+t2
)
= 1/(1+t2
)
√(1-t2
/(1+t2
))(1+t2
)
y'= -t
= -1/(1+t2
)
√(1-1/(1+t2
))√(1+t2
)3
y'x
= -1
y'x0
= -1
Касательная
y-π/4=-(x-π/4)
y+x-π/2=0
Нормаль
y-π/4=x-π/4
y=x
16.14. 
x0
= 1
y0
= 3
x'= (-1-2lnt)/t3
y'= (-1-2lnt)/t2
y'x
= t
y'x0
= 1
Касательная
y-3=x-1
y-x-2=0
Нормаль
y-3=-x+1
y+x-4=0
16.15. 
x0
= 3/4
y0
= 11/8
x'= (-t-2)/t3
y'= (-3-2t)/t3
y'x
= (3+2t)/(t+2)
y'x
0
= 7/4
Касательная
y-11/8=7/4(x-3/4)
y-7/4x-1/16=0
Нормаль
y-11/8= -4/7(x-3/4)
y+4/7x-53/56=0
16.16. 
x0
= a/8
y0
= a3√3/8
x'= 3asin2
tcost
y'= -3acos2
tsint
y'x
= -ctgt
y'x0
= -√3
Касательная
y-a3√3/8= -√3(x-a/8)
y+x√3-a√3/2=0
Нормаль
y-a3√3/8= √3/3(x-a/8)
y-x√3/3-a√3/3=0
16.17. 
x0
= a√2(π+4)/8
y0
= a√2(8-π)/8
x'= atcost
y'= atsint
y'x
= tgt
y'x
0
= 1
Касательная
y-a√2(8-π)/8=x-a√2(π+4)/8
y-x+a√2(π-2)/4=0
Нормаль
y-a√2(8-π)/8= -x+a√2(π+4)/8
y+x+a3√2/2=0
16.18. 
x0
= 0
y0
= 2
x'= -1/t2
y'= 1/t2
y'x
= -1
y'x
0
= -1
Касательная
y+x-2= 0
Нормаль
y-x-2=0
16.19. 
x0
= -3
y0
= -6
x'= -2t
y'= 1-3t2
y'x
= (3t2
-1)/2t
y'x0
= 11/4
Касательная
y+6= 11/4(x+3)
y-11/4x +13/4=0
Нормаль
y+6= -4/11(x+3)
y+4/11x+78/11=0
16.20. 
x0
= ln2
y0
= 1-π/4
x'= 2t/(1+t2
)
y'=1-1/(1+t2
)=t2
/(1+t2
)
y'x
= t/2
y'x
0
= 1/2
Касательная
y-1+π/4= 1/2(x-ln2)
y-1/2x+1/2ln2+π/4=0
Нормаль
y-1+π/4= -2(x-ln2)
y+2x-2ln2+π/4=0
16.21. 
x0
= 0
y0
= 0
x'= 1-sint-tcost
y'= cost-tsint
y'x
= (cost-tsint)/(1-sint-tcost)
y'x0
= 1
Касательная
y=x
Нормаль
y=-x
16.22. 
x0
= 3
y0
= 2/3
x'= t4
-2t2
-2t
(t2
-1)2
y'= (-t2
-1)/(t2
-1)2
y'x
= (-t2
-1)/(t4
-2t2
-2t)
y'x0
= -5/4
Касательная
y-2/3= -5/4(x-3)
y+5/4x-53/12=0
Нормаль
y-2/3= 4/5(x-3)
y-4/5x+26/15=0
16.23. 
x0
= 3√2/2
y0
= 2√2
x'= -3sint
y'= 4cost
y'x
= -4/3*tgt
y'x
0
= -4/3
Касательная
y-2√2= -4/3(x-3√2/2)
y+4/3x-4√2=0
Нормаль
y-2√2= 3/4(x-3√2/2)
y-3/4x-7√2/8=0
16.24. 
x0
= 0
y0
= 0
x'= 1-4t3
y'= 2t-3t2
y'x
= (2t-3t2
)/(1-4t3
)
y'x0
= 1/3
Касательная
y=1/3x
Нормаль
y= -3x
16.25. 
x0
= 2
y0
= 3
x'= 3t2
y'= 2t+1
y'x
= (2t+1)/(3t2
)
y'x
0
= 1
Касательная
y-3=x-2
y-x-1=0
Нормаль
y-3= -x+2
y+x-5=0
16.26. 
x0
= 1
y0
= -√3/2
x'= -2sint
y'= cost
y'x
= -1/2*ctgt
y'x0
= √3/6
Касательная
y+√3/2= √3/6(x-1)
y-x√3/6+2√3/3=0
Нормаль
y+√3/2= -2√3(x-1)
y+2x√3-2√3+√3/2=0
16.27. 
x0
= 2
y0
= 2
x'= 2/cos2
t
y'= 2sin2t+2cos2t
y'x
= (sin2t+cos2t)/cos2
t
y'x
0
= 2
Касательная
y-2= 2(x-2)
y-2x+2=0
Нормаль
y-2= -1/2(x-2)
y+x/2-3=0
16.28. 
x0
= -7
y0
= 4
x'= 3t2
y'= 2t
y'x
= 2/(3t)
y'x0
= -1/3
Касательная
y-4= -1/3(x+7)
y+x/3-5/3=0
Нормаль
y-4= 3(x+7)
y-3x-25=0
16.29. 
x0
= 0
y0
= 1
x'= cost
y'= at
lna
y'x
= at
lna/cost
y'x
0
= lna
Касательная
y-1-xlna=0
Нормаль
y-1+x/lna=0
16.30. 
x0
= 1/2
y0
= 1/2
x'= cost
y'= -2sin2t
y'x
= -4sint
y'x0
= -2
Касательная
y-1/2= -2(x-1/2)
y+2x-3/2=0
Нормаль
y-1/2= 1/2(x-1/2)
y-x/2-1/4=0
16.31. 
x0
= 2
y0
= 2
x'= 2et
y'= -e-t
y'x
= -1/(2e2t
)
y'x0
= -1/2
Касательная
y-2= -1/2(x-2)
y+x/2-3=0
Нормаль
y-2= 2(x-2)
y-2x+2=0
|