Реферат: Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.19

Задача 19 . Найти производную второго порядка от функции, заданной параметрически.

19.1.

x'= -2sin2t= -4sintcost

y'= 4sint/cos³ t

y''_xx = 4sint = -1 _

16sin² tcos⁵ t 4sintcos⁵ t

19.2.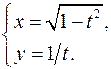

x'= -t/√(1-t² )

y'= -1/t²

y''_xx = (1-t² )² t⁴

19.3.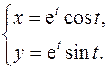

x'= e^t cost-e^t sint= e^t (cost-sint)

y'= e^t sint+e^t cost= e^t (sint+cost)

y''_xx = e^t (sint+cost) = sint+cost

e^2t (cost-sint)² e^t (cost-sint)²

19.4.

x'= 2shtcht

y'= -2sht/ch³ t

y''_xx = -2 sht = -1_

4shtch⁴ t 2ch⁴ t

19.5.

x'= 1+cost

y'= sint

y''_xx = sint/(1+cost)²

19.6.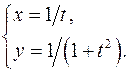

x'= -1/t²

y'= -2t/(1+t² )²

y''_xx = -2t³ _

(1+t² )²

19.7.

x'= 1/2√t

y'= 1/√(1-t)³

y''_xx = 4 t _

√(1-t)³

19.8.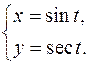

x'= cost

y'= sint/cos² t

y''_xx = sint/cos⁴ t

19.9.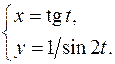

x'= 1/cos² t

y'= -2cos2t/sin² 2t

y''_xx = -2cos2tcos⁴ t

sin² 2t

19.10.

x'= 1/2√(t-1)

y'= (2-t)/(1-t)^3/2

y''_xx = 4( t -1)(2- t ) = 2 t -8

(1-t)^3/2 √(1-t)

19.11.

x'= 1/2√t

y'= 1/³ √(t-1)²

y''_xx = 4t/³ √(t-1)²

19.12.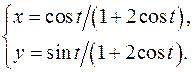

x'= -sint/(1+2cost)²

y'= (cost+2)/(1+2cost)²

y''_xx = ( cost+2)(1+2cost)⁴ = ( cost+2)(1+2cost)²

sin² t(1+2cost)² sin² t

19.13.

x'= 3t² / 2√(t³ -1)

y'= 1/t

y''_xx = 2 ( t ³ -1)

3t⁵

19.14.

x'= cht

y'= 2tht/ch² t

y''_xx = 2tht/ch⁴ t

19.15.

x'= 1/2√(t-1)

y'= -1/2√t³

y''_xx = - 2t + 2

√t³

19.16.

x'= -2cost sint

y'= 2sint/cos³ t

y''_xx = 2sint = 1/2cos⁴ t

4cos⁴ tsint

19.17.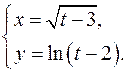

x'= 1/2√(t-3)

y'= 1/(t-2)

y''_xx = 4(t-3)/(t-2)

19.18.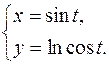

x'= cost

y'= -sint/cost

y''_xx = -sint/cos³ t

19.19.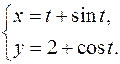

x'= 1+cost

y'= -sint

y''_xx = -sint/(1+cost)²

19.20.

x'= 1-cost

y'= sint

y''_xx = sint/(1-cost)²

19.21.

x'= -sint

y'= cost/sint

y''_xx = -cost/sin³ t

19.22.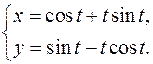

x'= -sint+sint+tcost= tcost

y'= cost-cost+tsint= tsint

y''_xx = sint/cos² t

19.23.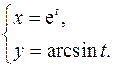

x'= e^t

y'= 1/√(1-t² )

y''_xx = e^t /√(1-t² )

19.24.

x'= -sint

y'= 2sin3(t/2)cos(t/2)

y''_xx = -2sin³ (t/2)cos(t/2)/sint= -sin² (t/2)

19.25.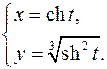

x'= sht

y'= 2cht/3³ √sht

y''_xx = 2cht/3³ √sh⁴ t

19.26.

x'= 1/(1+t² )

y'= t

y''_xx = t(1+t² )²

19.27.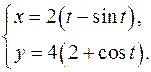

x'= 2-2cost

y'= -4sint

y''_xx = -2sint/(1-cost)

19.28.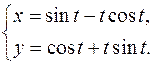

x'= cost-cost+tsint= tsint

y'= -sint+sint+tcost= tcost

y''_xx = cost/sin² t

19.29.

x'= -2/t³

y'= -2t/(t² +1)²

y''_xx = -t⁷ /2(t² +1)²

19.30.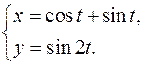

x'= cost-sint

y'= 2cos2t

y''_xx = 2cos2t/( cost-sint)= 2cost+2sint

19.31.

x'= 1/t

y'= 1/(1+t² )

y''_xx = t² /(1+t² )