СОДЕРЖАНИЕ
1. Раскройте содержание многофакторных эконометрических
моделей выпуска продукции. Метод трёх точек. Анализ результатов решения системы и выбор конкретных выводов и рекомендаций
2. Решение задачи
Список использованной литературы
1. Раскройте содержание многофакторных эконометрических моделей выпуска продукции. Метод трёх точек. Анализ результатов решения системы и выбор конкретных выводов и рекомендаций.
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики.
В настоящее время множественная регрессия один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, может привести к нежелательным последствиям. Система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости.
Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель.
Поэтому отбор факторов обычно осуществляется в две стадии:
1) подбираются факторы исходя из сущности проблемы;
2) на основе матрицы показателей корреляции определяют статистики для параметров регрессии.
Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии.
Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам.
Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
1. Метод исключения – отсев факторов из полного его набора.
2. Метод включения – дополнительное введение фактора.
3. Шаговый регрессионный анализ – исключение ранее введенного фактора.
Возможны разные виды уравнений множественной регрессии: линейные и нелинейные.
Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК).
Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации.
Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.
Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции. При правильном включении факторов в регрессионную модель величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках).
При использовании отдельных уравнений регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако, это предположение является очень грубым: практически изменение одной переменной, как правило, не может происходить при абсолютной неизменности других.
Если нет полного ряда данных, в этих обстоятельствах оценки параметров функции, возможно на основе трёх точек.
Пример. Предположим, что требуется провести логическую кривую через три точки: у = 12,9; у1 = 62,1; у2= = 152,7. Причем интервалы у0-у1 и у1-у2 равны 6 единицам времени.
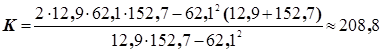
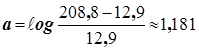

Итак, 
Аналогично: 
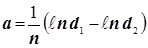
(d1
, d2
- это разность между точками)
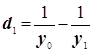

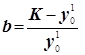
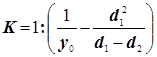
Рассмотренный метод оценки параметров очень чувствителен к величине значений y y y , которые даже если получены усреднённым путём, могут содержать существенный элемент случайности.
Несомненно, что построение любой модели, необходимо для прогнозирования дальнейшего развития событий при изменении одного или нескольких факторов. Выводы и рекомендации будут индивидуальны для каждого конкретного случая. Зависеть они будут от результатов анализа модели, от тенденции изменения факторов, от исходных данных и поставленной задачи.
Проверить качество прогноза можно будет только в будущем, сравнив предсказанное значение с реальностью. Но следует ожидать, что модель, хорошо описывающая существующие данные, будет также давать хороший прогноз.
2. Обоснуйте целесообразность расширения производства, если:
У(спрос) {84,3; 84,9; 85,1; 85,7; 85,9; 86,4 }
Х1 (н. р.) {90,3; 90,4; 90,8; 91,3; 91,7; 91,8}
Х2 (цена) {13,3; 13,7; 13,9; 14,1; 14,3; 14,8}
При этом коэффициент использования производственной мощности не превышает 59 %.
Решение задачи:
| у |
х1 |
х2 |
| 84,3 |
90,3 |
13,3 |
| 84,9 |
90,4 |
13,7 |
| 85,1 |
90,8 |
13,9 |
| 85,7 |
91,3 |
14,1 |
| 85,9 |
91,7 |
14,3 |
| 86,4 |
91,8 |
14,8 |
Рассчитаем коэффициент корреляции между X и Y применяя «Анализ данных»:
Корреляция
| у
|
х1 |
х2 |
| у |
1 |
| х1 |
0,97 |
1 |
| х2 |
0,99 |
0,94 |
1 |
r(y
х
1
)
= 0,97 — связь прямая, сильная - линейная регрессия; r(yx2) =
0,99 - связь прямая, сильная - линейная регрессия, что свидетельствует о существовании линейной зависимости между X и Y.
Линейная функция имеет вид:
у= а + bх1 + сх2
Регрессионную функцию линейной зависимости у= а + bх1 + сх2 найдем с помощью анализа данных в Excel, представленных в Приложении 1. Получим следующие значения:
Уравнение регрессии имеет вид:
у=35,570 + 0,395 х1+0,989 х2
Доверительные интервалы для коэффициентов регрессии:
Выводы: С достоверностью 97% можно утверждать, что при данной цене и росте спроса на 2,5 %, использовании производственной мощности на 59 %, расширение производства считается целесообразным.
Список использованной литературы
1. Практикум по эконометрике: Учебн. пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2006. – 344 с.
2. Н.М. Хубулава. Эконометрика. Учебно-практическое пособие. М., МГТА, 2004.
3. Н.М. Хубулава. Практическое пособие по курсу: "Эконометрика". М., изд. Комплекс. 2005.
4. Эконометрика: Учебно-методическое пособие / Шалабанов А.К., Роганов Д.А. – Казань: ТИСБИ, 2005. – 56 с.
5. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2006. – 576 с.
ПРИЛОЖЕНИЕ 1
| ВЫВОД ИТОГОВ |
| Регрессионная статистика
|
| Множественный R |
0.993027067 |
r(yx2) |
| R-квадрат |
0.986102756 |
коэфф.детерминации 99% - влияние фактора на результат |
| Нормированный R-квадрат |
0.976837926 |
| Стандартная ошибка |
0.115671769 |
стандартная ошибка |
| Наблюдения |
6 |
| Дисперсионный анализ |
ESS<<RSS |
Критерий ФИШЕРА |
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия RSS |
2 |
2.848193459 |
1.42409673 |
106.435067 |
0.001638299 |
<0,05 |
| Остаток ESS |
3 |
0.040139874 |
0.013379958 |
| Итого TSS |
5 |
2.888333333 |
F>F(таб)=7,71 |
кр.Фишера выполнен; модель надежна в целом |
| Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
| Y-пересечение |
35.5701069 |
17.26080824 |
2.060743993 |
0.131402158 |
-19.36148851 |
90.50170232 |
| Переменная X 1 |
0.39484464 |
0.230805521 |
1.710724412 |
0.185658055 |
-0.339681539 |
1.129370819 |
| Переменная X 2 |
0.989009891 |
0.289857587 |
3.412054527 |
0.042087232 |
0.066553685 |
1.911466097 |
| a, b, с - коэффициенты модели: у^(x)=а + bх1 + сх2 |
t(таб)=2,57 |
оба значения должны |
| y увеличится на 0,39% при увеличении х1 (н.р) на 1% |
|t(a)|<2,57 |
быть < 0,05 |
| и на 0,99% при увеличении х2 (спрос) на 1%. |
|t(b)|>2,57 критерий не выполняется |
| параметр а надежен на уровне 17% |
| Так как F > Fтабл., то найденные значения a и b надёжны. |
| При уровне значимости 0,05 имеем: Fрасч = 106,44 |
| ВЫВОД ОСТАТКА |
| Наблюдение
|
Предсказанное Y
|
Остатки
|
| 1 |
84.37840943 |
-0.078409432 |
| 2 |
84.81349785 |
0.086502148 |
| 3 |
85.16923769 |
-0.069237686 |
| 4 |
85.56446198 |
0.135538016 |
| 5 |
85.92020182 |
-0.020201818 |
| 6 |
86.45419123 |
-0.054191228 |
| ВЫВОД ВЕРОЯТНОСТИ |
| Персентиль
|
Y
|
| 8.333333333 |
84.3 |
| 25 |
84.9 |
| 41.66666667 |
85.1 |
| 58.33333333 |
85.7 |
| 75 |
85.9 |
| 91.66666667 |
86.4 |
|