Середні значення
Статистика оперує такими середніми значеннями: середнє арифметичне, середнє квадратичне, середнє геометричне.
Середнє арифметичне.
Нехай ми маємо п
об'єктів, у якихвиміряно деяку характеристику, що має значення x1
,x2
, …, xn
.
Середнім значенням (або середнім арифметичним) називається таке число  , яке дістають діленням суми всіх даних вибірки x1
, x2
, …, xn
на число цих даних n, , яке дістають діленням суми всіх даних вибірки x1
, x2
, …, xn
на число цих даних n,
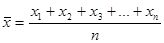
або  ( (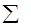 - знак суми – “сигма” велика) - знак суми – “сигма” велика)
Приклади. 1) Протягом перших п’яти днів березнятемпература повітря, вимірювана о 8 год. ранку, становила 3°, 5°, 4°, 1°, 2°. Знайти середню температуру за ці дні.
Маємо: 
2) 3 двох учнів треба вибрати одного в баскетбольну команду. Відомі кількості їхніх влучень м'яча в корзину накожні десять кидків під час тренувань.
Таблиця 1
Номер тренувань
|
1
|
2
|
3
|
4
|
5
|
Перший учень
|
4
|
3
|
5
|
3
|
6
|
Кількість влучень
|
Другий учень
|
5
|
4
|
3
|
6
|
5
|
Розв'язання.
Знаходимо середню кількість влучень.
Для першого учня:

Для другого учня:
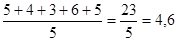
Отже, в команду слід узяти другого учня.
Розглянемо деякі властивості середнього арифметичного.
1) Знайдемо відхилення l
кожного значення xj
від середнього .
Різниця х — .
Різниця х —
 може бути від'ємною або додатною. може бути від'ємною або додатною.
Сума всіх п
відхилень дорівнює нулю. Проілюструємо цю властивість на прикладі. Вихідні дані:. (0; 0; 1; 1; 3;3;3; 5); n= 8;  = 2. = 2.
2) Якщо до кожного результату спостережень додати деяке число с
(константу), то середнє арифметичне  перетвориться в перетвориться в  + с.
Візьмемо, наприклад, попередні 8 значень і додамо до кожного з них по 5. Дістанемо числа 5; 5; 6: 6; 8; 8; 8; 10, середнє арифметичне яких (5 + 5+ 6 + 6 + 8 + 8 + 8+10) : 8 = 7. Середнє на 5 одиниць більше. + с.
Візьмемо, наприклад, попередні 8 значень і додамо до кожного з них по 5. Дістанемо числа 5; 5; 6: 6; 8; 8; 8; 10, середнє арифметичне яких (5 + 5+ 6 + 6 + 8 + 8 + 8+10) : 8 = 7. Середнє на 5 одиниць більше.
Таблиця 2
| Значення |
Середнє арифметичне |
Відхилення |
| 0 |
2 |
-2 |
| 0 |
2 |
-2 |
| 1 |
2 |
-1 |
| 1 |
2 |
-1 |
| 3 |
2 |
1 |
| 3 |
2 |
1 |
| 3 |
2 |
1 |
| 5 |
2 |
3 |
| - |
| 0 |
3) Якщо кожне значення сукупності з середнім  помножити на константу с,
то середнє арифметичне стане с помножити на константу с,
то середнє арифметичне стане с
 .
Перевірте властивість, використовуючи попередні дані. .
Перевірте властивість, використовуючи попередні дані.
Якщо величини деяких даних повторюються, то середнє арифметичне визначають за формулою
 ,де ,де
fi
—
частота повторення результату xi
.
Приклади. 1) Протягом двадцяти днів серпня температура повітря вранці була такою: 17°, 18°, 19°, 20°, 18°, 18°, 18o
, 19o
, 19°, 20°, 20°, 19°, !9°,
19°, 20°, 19o
, 18°, 17°, 16°, 19°.
Знайти середню температуру за цими даними.
Тут окремі значення (17°, 18°, 19°, 20°) повторюються. Середня температура дорівнює:

2) Подаємо запис обчислення середнього арифметичного при повторенні деяких даних у вигляді таблиці.
Таблиця 3
Вихідні
дані
|
xi
|
Частота fi
|
xi
fi
|
Остаточне обчислення
|
| 2 |
6 |
10 |
2 |
2 |
4 |

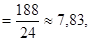
де I=1,2,3,…,11
|
| 2 |
6 |
10 |
3 |
1 |
3 |
| 3 |
6 |
11 |
4 |
3 |
12 |
| 4 |
6 |
12 |
5 |
2 |
10 |
| 4 |
8 |
12 |
6 |
4 |
24 |
| 4 |
9 |
15 |
8 |
1 |
8 |
| 5 |
9 |
15 |
9 |
3 |
27 |
| 5 |
9 |
15 |
10 |
2 |
20 |
| 11 |
1 |
11 |
| 12 |
2 |
24 |
| 15 |
3 |
45 |
 |
3) За контрольну роботу учні одержали такі оцінки
Оцінки (бали) 5 4 3 2
Кількість
учнів 6 7 4 17
Чи достатньо засвоєний матеріал?
Знайдемо середню величину оцінок.

Ця оцінка є задовільною. Але частота оцінки «2» (мода) дуже висока, вона дорівнює 17. Отже, матеріал засвоєний учнями недостатньо.
Середнє квадратичне відхилення
. Ми вже встановили, що сума відхилень даних від середнього значення дорівнює нулю. Тому, якби ми вирішили шукати середній показник відхилень, то він також дорівнював би нулю. В статистиці користуються іншим показником — середнім квадратичним відхиленням, який знаходять так: усі відхилення підносять до квадрата; знаходять середнє арифметичне цих квадратів; із знайденого середнього арифметичного добувають квадратний корінь. Середнє квадратичне відхилення позначають грецькою буквою σ (“сигма” мала):

Знаходження середнього квадратичного відхилення подано в таблиці 4.
Таблиця 4
Значення xi
|
Середнє арифметичне 
|
Відхилення
xi
— 
|
Квадрат відхилення
(xi
-
 )2 )2
|
Квадратичне відхилення σ
|
| 5 |
-
7
|
49 |
| 8 |
- 4 |
16 |
| 10 |
- 2 |
4 |
| 12 |
0 |
0 |
| 17 |
5 |
25 |
| 20 |
8 |
64 |
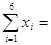 =72 =72 |
 = =
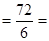 =12 =12
|
  |


|
  |
У статистиці користуються також величиною σ2
(квадрат середнього квадратичного відхилення), яку називають дисперсією.
Середнє геометричне
п
додатних чисел х1,
х2
, х3
, ...,хп
визначається виразом
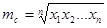 , тобто середнє геометричне х1
х2
х3
...п
є корінь n-го степеня з добутку всіх xi
(і
= 1, 2, ...). , тобто середнє геометричне х1
х2
х3
...п
є корінь n-го степеня з добутку всіх xi
(і
= 1, 2, ...).
У випадку двох чисел а
і b
середнє геометричне називають середнім пропорційним цих чисел. З рівності тс
= аb
випливає, що а : mc
= тс
: b.
На практиці окремим особам, організаціям, керівникам підприємств доводиться розв'язувати різноманітні задачі, пов'язані з використанням поняття моди, медіани, середнього. Наприклад, яких розмірів дитячого взуття слід випускати більше, ніж інших; на якому з
міських маршрутів треба пустити автобусів більше, ніж на решті; якого розміру спортивних костюмів слід виготовити найбільше для учнів 10—11 класів тощо.
Розглянуті моду, медіану і середні значення називають мірами центральної тенденції.
|