Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное общеобразовательное учреждение высшего
профессионального образования
«СИБИРСКАЯ ГОСУДАРСТВЕННАЯ ГЕОДЕЗИЧЕСКАЯ
АКАДЕМИЯ» (ГОУ ВПО «СГГА»)
Кафедра высшей геодезии
Лабораторная работа №2
Решение сфероидических треугольников.
Вариант №28
Выполнил: Проверил:
ст.гр. АГ-41 Телеганов Н.А.
Жулина И.С.
Новосибирск – 2010
Содержание работы
1. Кратко изложить основные положения теории замены сфероидического треугольника сферическим при заданных искажениях элементов треугольника с приведением необходимых чертежей и окончательных формул.
2. Описать последовательность решения сферических треугольников с применением теоремы Лежандра и по способу аддитаментов.
Решить треугольники своей сети по способу аддитаментов, а затем, используя вычисленные стороны, решить эти же треугольники как линейные с применением теоремы Лежандра.
Контрольные вопросы
- Что такое сфероидический треугольник?
- При каких размерах сторон сфероидические треугольники можно решить как сферические, если требуется определить элементы треугольника с точностью 1·10-6
?
- В чем отличие решения сфероидических и сферических треугольников?
- Что такое аддитамент стороны, и как он вычисляется?
- Сформулировать теорему Лежандра и привести формулу перехода от угла сфероидического треугольника к плоскому при больших сторонах.
- Как вычисляется сферический избыток ε при сторонах меньших и больших 90 км?
Каковы возможные теоретические пределы изменения ε?
Решение сфероидических треугольников
Виды геодезических треугольников и условия замены сфероидических треугольников сферическими
Треугольники на любой поверхности, образованные геодезическими линиями называются геодезическими
. Однако, такое общее название треугольников (по виду сторон, образующих их) не всегда является удобным. Так, например, на плоскости треугольник, образованный прямыми линиями, есть геодезический, на сфере, образованный дугами больших кругов, так же является геодезическим и т. д. Гораздо удобнее треугольники, стороны которых есть геодезические линии, называть по принадлежности их к поверхности: на плоскости
- плоские
, на сфере
- сферические
, на эллипсоиде
- сфероидические
.
Для образования сфероидического треугольника на поверхности эллипсоида необходимо в каждое непосредственно измеренное горизонтальное направление ввести поправку за переход от азимута нормального сечения к азимуту геодезической линии. Вводить поправки в измеренные стороны не следует, т.к. сторона после ее редуцирования на эллипсоид будет представлять собой нормальное сечение, длина которого с очень высокой точностью равна длине, соответствующей геодезической линии.
Решение сфероидических треугольников представляет собой сложную задачу. Сложность этой проблемы обусловлена переменной кривизной поверхности эллипсоида.
Так, если взять два сфероидических треугольника с одинаковыми сторонами, но расположенных под разными широтами поверхности эллипсоида, то соответствующие их углы, в общем случае, равны не будут. Аналогично не будут равны и стороны треугольников, расположенных под разными широтами, у которых углы и одна (исходная) сторона соответственно равны.
Поэтому, сфероидические треугольники решать без учета изменения кривизны нельзя. Однако, в теории математики отсутствует специальный математический аппарат, позволяющий решать треугольники в замкнутом виде на любой поверхности, подобно тому, как это сделано для плоскости и сферы.
Поверхность земного эллипсоида по своей форме близка к сфере (α=1:300), и поэтому, можно ожидать, что элементы сфероидического треугольника будут мало отличаться от соответствующих элементов сферического треугольника с надлежаще подобранным радиусом шара. Причем, очевидно, эти различия будут прямо пропорциональны размерам треугольников: чем меньше длины сторон треугольников, тем меньше их искажения и наоборот.
Найдём наибольшие размеры сторон сфероидического треугольника, при которых замена его сферическим будет вызывать ошибки в элементах треугольника, не превышающие наперед заданной величины.
Решение этой задачи выполним с использованием отображения части поверхности эллипсоида на шар, радиус которого примем равным среднему радиусу кривизны эллипсоида
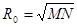 в некоторой точке О
(рис. 1), в некоторой точке О
(рис. 1),

Рис. 1
выбранной в центре отображаемого участка поверхности эллипсоида, ограниченного геодезической окружностью радиуса So
.
Приняв точку О
за полюс системы полярных координат So
и А, отобразим часть поверхности эллипсоида на шар таким образом, чтобы полярные координаты точки Q
1
'
на шаре не изменялись.
Тогда, при таком способе изображения линейные искажения в точке Q
1
'
в направлении Q
1
`
o
`
(дуги большого круга) будут отсутствовать, а в перпендикулярном направлении Q
1
`
Q
2
`
(дуги малого круга) будут наибольшими.
Обозначая длины элементарных дуг Q
1
Q
2
и Q
1
`
Q
2
,
. как этопоказано на рис 1, можно найти наибольшие относительные линейные искажения ΔS:S, как:
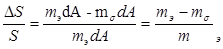 (1) (1)
Здесь m - величины, представляющие собой в общем случае некоторые функции полярных координат. В геодезии эти величины называют приведенной длиной геодезической линии.
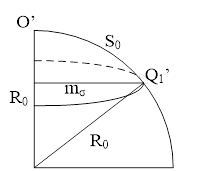
Рис. 2
На шаре (рис. 2) приведенной длине дуги большого круга ( с полюсом в точке О') будет соответствовать радиус кривизны геодезической окружности (малого круга ). Поэтому, для шара, непосредственно из чертежа (рис. 2), можно написать
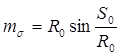 (2) (2)
Для поверхности эллипсоида приведенная длина геодезической линии mэ
не имеет такой простой геометрической интерпретации как для сферы, поэтому, полагая, что mэ
есть функция длины геодезической линии So
, можно написать:
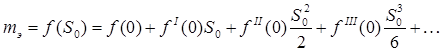
Очевидно f(o) = m0
есть приведенная длина геодезической линии, вычисленная для точки 0 (рис. 1) и, тогда:
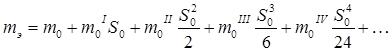 (3) (3)
Для получения производных приведенной длины геодезической линии по длине So
можно воспользоваться формулой (2), в которой для поверхности эллипсоида следует радиус считать величиной переменной.
Дифференцируя выражение (2) по So
последовательно, находим:
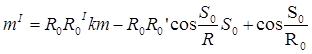
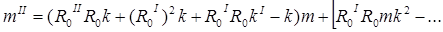 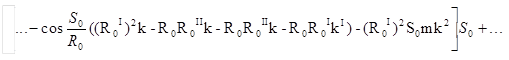 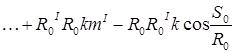
и т.д.
В этих формулах через "к" обозначена полная кривизна поверхности эллипсоида.
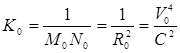 (4) (4)
Приведенная длина геодезической линии и ее производные в формуле (3) должны вычисляться по аргументам точки 0, для которой So
= 0. Но при So
= 0 , m0
как функция расстояния Sо
, очевидно, также должно быть равно нулю, а производные примут следующие значения:
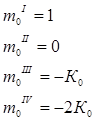
Подставляя производные в формулу приведенной длины (3), находим
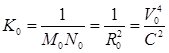 (5) (5)
По этой формуле, вообще говоря, можно вычислять приведенную длину геодезической линии для любой поверхности, а не только поверхности эллипсоида вращения. Для этого достаточно знать только полную кривизну поверхности и ее производные.
Так, например, для плоскости К0
= 0 и, поэтому, приведенная длина для плоскости равна самой длине линии.
Для сферы Ко
= 1 / Ro
2
, а производные полной кривизны будут равны нулю, отсюда для сферы имеем:
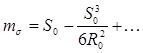 (6) (6)
Если в формуле приведенной длины дуги большого круга (2) синус заменить рядом, то, с точностью до членов пятого порядка малости, получим формулу (6).
Для получения формулы приведенной длины геодезической линии поверхности эллипсоида вначале найдем производную полной кривизны:

Продифференцировав формулу полной кривизны (4) по широте, а затем умножив полученное равенство на выражение производной dB/dS, находим
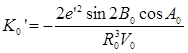
Подставив производную К0
', а также полную кривизну поверхности эллипсоида (4) в выражение (5), получаем окончательно формулу вычисления приведенной длины геодезической линии на поверхности эллипсоида
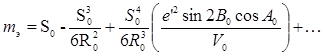 (7) (7)
Имея выражения для приведенных длин геодезических линий сферы и поверхности эллипсоида вращения, нетрудно теперь получить по формуле (1) относительные линейные искажения.
Подставляя в числитель формулы (1) выражения (6) и(7) , а в знаменателе с достаточной точностью можно ограничиться mэ
~ So
, находим
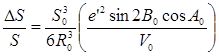
Из этой формулы видно, что наибольшие линейные искажения будут при Во = 45° и Ао = 0°. Следовательно,
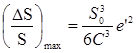
(8)
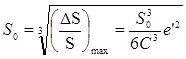
Формула (8) позволяет установить размеры области поверхности эллипсоида, ограниченной геодезической окружностью, в пределах которой линейные искажения при отображении ее на сферу не могут превзойти наперед заданных величин.
Если, ориентируясь на точность первоклассных геодезических построений, принять (ΔS/S)max< 1*10-8
, то по формуле (8) находим радиус геодезической окружности, равный 133 км. А так как вписать в окружность радиуса 133 км можно треугольник со сторонами порядка 250-270 км то, следовательно, сфероидические треугольники со сторонами, не превышающими 270 км, можно решать как сферические, при этом относительные искажения их элементов не будут превышать 1*10-8
. Радиус сферы, при решении таких треугольников, следует принимать равным среднему радиусу кривизны для центра тяжести сфероидического треугольника.
Решение сферических треугольников
Решение сферических треугольников, с точки зрения теории, не вызывает никаких затруднений и может быть выполнено с необходимой степенью точности по различным формулам сферической тригонометрии.
В геодезии, в большинстве случаев, приходится решать треугольники, у которых известны: либо три угла и одна сторона (триангуляция), либо три стороны (триллатерация). Для таких случаев наиболее простым будет применение при решении формул синусов и косинусов сторон сферической тригонометрии.
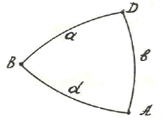
Рис. 3
Выражая стороны сферического треугольника (рис.3) в частях радиуса сферы:
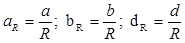
при заданных углах А, В, в и стороне а
, находим:
(9)
или
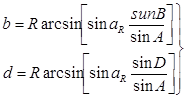 (10) (10)
Если в треугольнике известны все стороны, то на основании теоремы косинуса стороны, будем иметь:
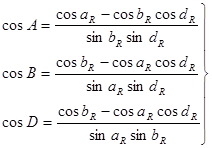 (11) (11)
или
 (12) (12)
Совершенно очевидно, приведенные алгоритмы - это не единственный путь решения сферических треугольников. Возможно использование и других формул сферической тригонометрии при решении тех же треугольников и с теми же самыми исходными данными.
На практике решение треугольников непосредственно по формулам сферической тригонометрии удобно и оправдано в том случае, если это решение выполняется на ЭВМ. Если же оно ведется в ручную - не по программе на ЭВМ, а с использованием настольных средств вычислительной техники, то решение, непосредственно, по формулам сферической тригонометрии становится практически громоздким. Действительно, в этом случае приходится с большой степенью точности вычислять ряд вспомогательных величин (R, a/R, sin (a/R), sin (b/R)), которые в конечном итоге не нужны.
Для решения малых сферических треугольников с использованием настольной вычислительной техники разработаны два способа: способ аддитаментов и способ решения сферических треугольников c применением теоремы Лежандра.
Способ аддитаментов
Суть способа заключается в замене решения сферического треугольника решением плоского с углами, равными углам сферического треугольника, и измененной (на аддитамент) исходной стороной с последующим введением в полученные из решения плоского треугольника стороны поправок (аддитаментов).
Рассмотрим теоретические основы этого способа.
Полагая, что стороны сферического треугольника - малые величины (S < 200 км), по сравнению с радиусом сферы, разложим синусы сторон в выражении (9) в ряд, ограничиваясь членами пятого порядка малости:
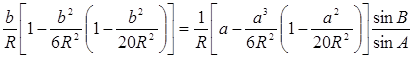
Откуда, с той же степенью точности, .находим
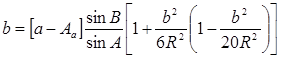 (13) (13)
где
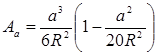
Обозначая:
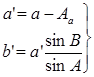 (14) (14)
тогда выражение (13) примет вид:
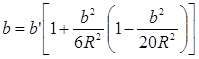 (15) (15)
или 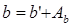
где
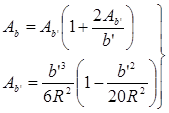 (
16) (
16)
По аналогии, без вывода, можно написать формулы и для вычисления стороны d:
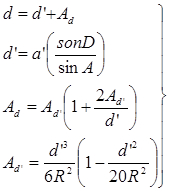 (17) (17)
Формулы (14)-(17) позволяют решать сферические треугольники со сторонами S<
250 км. При этом ошибки вычисления сторон не будут превосходить 0.0005 м.
Если стороны треугольников не превышают 100 км, то, при той же точности вычисления, в формулах (14) - (17) можно отбросить малые поправочные члены и вычисления вести по формулам:
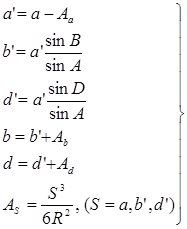 (18) (18)
Рабочие формулы:
R=6371116
м
№
тр.
|
Вер-
шина
|
Углы сфериче-
ского треуго-
льника
|
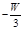 |
Уравненные
углы
|
Синусы углов |
Условные сторы (S') |
AS
|
| I |
D
B
A
|
81°29'09,117"
45°48'31,438"
52°42'23,540"
|
-1,111"
-1,111"
-1,111"
|
81°29'08,006"
45°48'30,327"
52°42'22,429"
|
0,98897857
0,71701311
0,79553937
|
22879,562
16587,767
18404,435
|
0,049
0,019
0,025
|
Σ
ε
W
|
180°00'04,095"
00,762"
03,333"
|
-3,333"
|
180°00'0,762"
|
| II |
D
B
С
|
46°40'25,875"
68°03'27,593"
65°16'06,893"
|
0,091"
0,091"
0,092"
|
46°40'25,966"
68°03'27,684"
65°16'06,985"
|
0,72746003
0,92756057
0,90827908
|
14740,504
18795,136
18404,435
|
0,013
0,027
0,025
|
Σ
ε
W
|
180°00'00,361"
0,635"
-0,274"
|
0,274"
|
180°00'00,635"
|
Решение сферических треугольников с применением теоремы Лежандра
В 1787 г. А. Лежандр доказал теорему, которая в последующем была положена в основу решения сферических треугольников со сторонами, не превышающими 200 - 220 км. Достоинством такого решения является то, что в этом случае решение сферического треугольника заменяется решением плоского треугольника со сторонами, равными соответствующим сторонам сферического треугольника, но измененными углами. Изменения сферических углов при переходе к углам плоского треугольника вычисляются на основании теоремы Лежандра, которая гласит: если сферический треугольник заменить плоским с теми же сторонами, то углы плоского треугольника будут равны соответствующим углам сферического треугольника, уменьшенным, на одну треть сферического избытка.
Доказательство теоремы Лежандра
Пусть дан сферический треугольник ABD (рис. 3) и соответствующий ему плоский треугольник A'B'D' (рис. 4) с теми же сторонами, но отличными углами А', В', D'.
Напишем очевидное соотношение
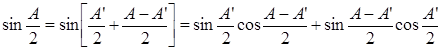 (19) (19)
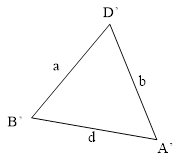
Рис. 4
Если соответствующие стороны сферического и плоского треугольников равны и не превосходят 200 км, то, вероятно, для сферы радиуса R = Rср
= (MN)1/2
углы сферического и плоского треугольников будут отличаться на небольшие величины. Исходя из этого примем с ошибкой на величины второго порядка малости (если за первый порядок принять А - А'):
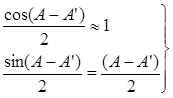 (20) (20)
И тогда из (19) с учетом (20), находим
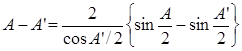
Заменяя синусы и косинусы углов известными соотношениями:
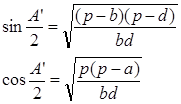

получаем
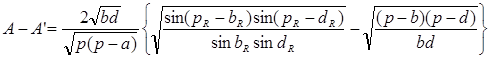
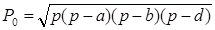 ( формула Герона ) ( формула Герона )
После разложения квадратов разностей и дальнейших простых преобразований, окончательно получаем:
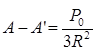 (21) (21)
Можно по аналогии написать формулы для разностей (В - В') и (D-
D'):
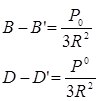 (22) (22)
Суммируя левые и правые части выражений (21) и (22), находим для треугольника:
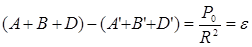 (23) (23)
С учетом равенства (23), формулы (21) и (22) можно представить в следующем виде:
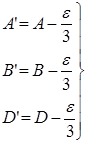 (24) (24)
которые и выражают теорему Лежандра.
Если при разложении синусов в ряд удерживались бы члены пятого порядка малости, то в результате были бы получены более точные формулы:
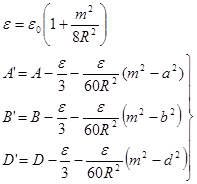 (25) (25)
Где 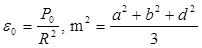
Сравнивая формулы (24) и (25) приходим к выводу, что сферические треугольники со сторонами S < 250 км можно решать по формулам (24), т.к. поправочные члены
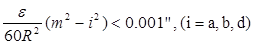
При этом сферический избыток при сторонах 90 км < S < 250 км, следует вычислять по формуле (25), а при сторонах S <90 км -по формуле (23).
Рабочие формулы:
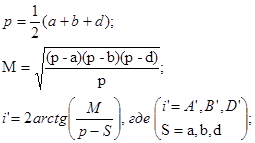 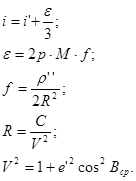
№
тр.
|
Стороны (S) |
P-S
|
Углы (i'
) |
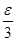 |
Углы (i
) |
| I |
D
B
A
|
22879,6106
16587,785
18404,461
|
6056,318
12348,143
10531,467
|
81°29'07,750"
45°48'30,074"
52°42'22,176"
|
0,254
0,254
0,254
|
81°29'08,004"
45°48'30,328"
52°42'22,430"
|
P
M
ε
|
28935,928
5217,121
0,762
|
180°00'00,00" |
0,762 |
180°00'00,762" |
| II |
D
B
C
|
14740,517
18795,163
18404,461
|
11229,553
7174,907
7565,609
|
46°40'25,756"
68°03'27,472"
65°16'06,772"
|
0,211
0,212
0,212
|
46°40'25,967"
68°03'27,684"
65°16'06,984"
|
P
M
ε
|
25970,07
4844,788
0,635
|
180°00'00,00" |
0,635 |
180°00'00,635" |
|