МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ ГУМАНИТАРНЫЙ ИНСТИТУТ
«Сжижение газов»
Выполнила студентка
физико-математического
факультета
4 курса группы 4-м-2
Афанасьева Анастасия.
Проверила: Волина Е.П.
Орехово-Зуево
2009
Содержание
· Введение……………………………………………………………………..3
· Низкие температуры………………………………………………………..4
· §1. Сжижение газов…………………………………………………………5
· §2. Эффект Джоуля – Томсона…………………………………………….6
· §3. Адиабатное расширение газа с совершением внешней работы……11
· §4. Сжижение газов с использованием эффекта Джоуля – Томсона (метод Линде)………………………………………………………………………..14
· §5. Сжижение газов методом адиабатного расширения в детандерах (метод Клода)………………………………………………………………………..17
· §6. Некоторые свойства сжиженных газов……………………………….19
· §7. Сверхнизкие температуры…………………………………………….20
· §8. Свойства вещества при низких температурах……………………….22
· §9. Жидкий гелий…………………………………………………………...24
· Заключение………………………………………………………………….33
· Список литературы…………………………………………………………34
Введение.
Проблемой изучения свойств веществ при низких температурах занимались многие ученые. Для этого требовались сжиженные газы. Определенных успехов в сжижении газов добился М. Фарадей. Он получил в жидком состоянии все известные газы кроме азота, кислорода, водорода, метана, оксида азота и оксида углерода. До обнаружения критической температуры пытались сжижать и эти газы, главным образом увеличивая давление. Однако после установления критической температуры для каждого вещества стало ясно, что получение жидкого азота, кислорода и т. д. требует охлаждения любого газа ниже его критической температуры, то есть более глубокого охлаждения, чем применявшегося ранее.
Большой вклад в проблему сжижения газов внес Петр Леонидович Капица. В 1934 году он создал необычайно производительную установку для сжижения гелия, который кипит или сжижается при температуре около 4,3 К. В 1938 г. он усовершенствовал небольшую турбину, очень эффективно сжижавшую воздух. Капице удалось обнаружить необычайное уменьшение вязкости гелия при охлаждении температуры ниже 2,17 К, при которой он переходит в форму, называемую гелием-2. Утрата вязкости позволяет ему беспрепятственно вытекать через мельчайшие отверстия и даже взбираться по стенкам контейнера, как бы не чувствуя силы тяжести. Отсутствие вязкости сопровождается также увеличением теплопроводности. Капица назвал открытое им явление сверхтекучестью.
Построенные Капицей уже после войны установки для сжижения газов нашли широкое применение в промышленности. Использование кислорода, извлеченного из жидкого воздуха, для кислородного дутья произвело подлинный переворот в советской сталелитейной промышленности.
Низкие (криогенные) температуры находят все большее применение в биологии и медицине. Так, температуры жидкого азота используют для длительного хранения крови, плазмы, спинного мозга, тканей и отдельных органов человека. С успехом используется криохирургический инструмент, дающий возможность местно замораживать удаляемые участки больных органов. Возникла новая отрасль науки - криобиология, изучающая процессы в клетках и тканях при их глубоком охлаждении.
Низкие температуры.
Непрерывные хаотические тепловые движения, в которых всегда участвуют частицы любого вещества и интенсивность (энергия) которых определяет его температуру, оказывают существенное внимание на все происходящие в веществе явления. Они являются как бы фоном, на котором разыгрываются любые процессы внутри вещества. Именно поэтому почти всякое свойство вещества так или иначе зависит от температуры, т.е. от интенсивности тепловых движений частиц в нем.
Естественно, что изучение свойств вещества при очень низких температурах, когда молекулярные движения в большей или меньшей степени ослаблены, представляют большой интерес. Только при низких температурах можно исследовать те или иные явления в условиях, когда постоянный фон тепловых движений не влияет на них.
При низкотемпературных исследованиях изучаемое тело приводят в контакт с телом достаточно низкой температуры, с так называемым хладогентов. Задачей техники низких температур и является создание таких хладогентов. Ими обычно являются различные сжиженные газы, находящиеся в состоянии кипения. Они особенно удобны тем, что контакт с охлажденным телом не изменяет их температуру, а приводит лишь к более интенсивному испарению. Именно сжижение газов открыло для исследования область низких температур, в том числе и самых низких – близких к абсолютному нулю.
§1. Сжижение газов.
Уравнение состояния идеальных газов Ван-дер-Ваальса показывает, что всякий газ может быть переведен в жидкое состояние, но необходимым условием для этого является предварительное охлаждение газа до температуры ниже критической. Углекислый газ, например, можно сжижить при комнатной температуре, поскольку его критическая температура равна 31,1°C. То же можно сказать и о таких газах, как аммиак и хлор.
Но есть и такие газы, которые при комнатной температуре нельзя перевести в жидкое состояние, какие бы не применять давления и до каких бы плотностей их ни доводить. К таким газам относятся, например, воздух (а так же его составные части – азот, кислород и аргон), водород и гелий, у которых критические температуры значительно ниже комнатной. До открытия критической температуры (Каньяр-де-ла-Тур, 1822 г.) их даже считали постоянными газами, т.е. газами, вообще не способными сжижаться.
Для сжижения таких газов их необходимо предварительно охладить, по крайней мере до температуры несколько ниже критической, после чего повышением давления газ может быть переведен в жидкое состояние. Сжиженные таким образом газы удобнее хранить под атмосферным давлением (в открытом сосуде), но в этом случае их температура должна быть еще более низкой – такой, при которой давление, соответствующее горизонтальному участку изотермы реального газа, равна 1 атм. Для азота такая изотерма соответствует температуре 77,4 К, в то время как критическая температура азота равна 126,1 К. для кислорода эти цифры соответственно равны 90 К и 154,4 К, для водорода 20,5 К и 33 К и, наконец, для гелия 4,4 К и 5,3 К. мы упомянули эти четыре газа потому, что именно они широко используются практически: и как средства получения низких температур (хладоагенты), и для других целей.
Из приведенных цифр как критических температур, так и тех конечных температур, до которых должны быть охлаждены сжижаемые газы, визно ,что охлаждение требуется весьма значительное, какое нигде в природе (в земных условиях) не встречается. Для достижения столь сильного охлаждения обычно используются два метода (по отдельности и комбинированно), которые мы здесь и рассмотрим.
Первый из них связан с использованием, так называемого эффекта Джоуля – Томсона.
§2. Эффект Джоуля – Томсона.
Расширение идеального газа в пустоту не сопровождается изменением его температуры.
Небольшое изменение температуры, наблюдаемое при точных измерениях, объясняется неидеальностью
газа. Следующее видоизменение опыта по расширению газа, предложенное Джоулем и Томсоном, позволяет достичь заметного изменения температуры газа, в частности охлаждения, обусловленного его неидеальностью.
Газ при достаточно большом, но постоянном давлении вынуждают протекать через теплоизолированную пористую перегородку. Это значит, что протекание газа происходит адиабатно
.
Гидродинамическое сопротивление перегородки приводит к тому, что на ней теряется часть давления газа и газ выходит из перегородки при более низком давлении. Газ, следовательно, расширяется или, как говорят в технике, дросселируется
. Дросселем называется любое устройство, представляющее сопротивление для протекания газа. В технических установках для охлаждения газов вместо пористой перегородки часто используется достаточно узкие сопла.
Для того, чтобы давление газа было стационарным
, т.е. происходило при постоянных значениях давлений по обе стороны дросселя, необходим какой – либо насос (компрессор), который поддерживал бы постоянными эти давления. Этот компрессор производит внешнюю работу сжатия газа, которая расходуется на преодоление сопротивления дросселя. Этим процесс дросселирования отличается от расширения газа в пустоту, при котором внешняя работа равна нулю.
Мы покажем, что для неидеального газа
процесс Джоуля – Томсона, т.е. процесс дросселирования, вообще говоря, должен сопровождаться изменением его температуры. Такое же расширение идеального газа
не вызывает никакого изменения температуры.
Явление изменения температуры газа при его адиабатном расширении дросселированием от одного постоянного давления к другому называется эффектом Джоуля – Томсона.
Изменение температуры неидеального газа в процессе Джоуля – Томсона объясняется тем, что при расширении газа увеличивается расстояние между молекулами и, следовательно, совершается внутренняя работа против взаимодействия между молекулами. За счет этой работы изменяется кинетическая энергия молекул, а следовательно, и температура газа. В идеальном газе, где силы взаимодействия молекул равны нулю, эффекта Джоуля – Томсона нет.
Количественно эффект Джоуля – Томсона характеризуется дифференциальным коэффициентом Джоуля – Томсона µ, который определяется отношением изменения температуры газа ΔТ
к вызвавшему его изменение давления Δр
:
µ=ΔТ/
Δр
.
Вычислим коэффициент Джоуля – Томсона, пользуясь выделенными термодинамическими соотношениями. Это вычисление явится полезной иллюстрацией применения термодинамики для решения конкретных задач. Но прежде чем приступить к этим вычислениям, проанализируем детальнее процесс Джоуля – Томсона. Для этой цели несколько схематизируем этот процесс.
Представим себе, что определенная масса, например 1 моль газа, протекает слева направо через пористую перегородку L
(рис. 1), помещенную в теплоизолированный цилиндр.
 рис. 1 рис. 1
Пусть один моль газа занимает объем V
1
между перегородкой L
и точкой М
слева (рис. 1, а), а после прохождения перегородки, т.е. после расширения, - объем V
2
между перегородкой и точкой N
справа (рис. 1, б). Для наглядности поместим мысленно в точке М поршень К1
, перемещение которого вправо называет протекание газ через перегородку пол постоянным давлением р1
. После прохождения через перегородку этот же газ перемещает воображаемый поршень К2
, испытывающий противодавление (тоже постоянное) р2
, до положения N. В действительности роль поршней К1
и К2
выполняет упомянутый выше компрессор.
Вычислим внешнюю работу, совершенную газом. При перемещении поршня К1
от положения М до перегородки Lобъем газа изменяется от значения V1
до нуля. При постоянном давлении совершенная работа равна произведению этого давления на изменение объема, следовательно, работа перемещения моля газа слева от перегородки равна –р1
V1
. По тем же причинам работа, совершенная газом справа от перегородки, равна р2
V2
. Общая работа ΔА расширений газа
ΔA=p2
V2
– p1
V1
.
Согласно первому началу термодинамики, работа, совершенная газом, должна быть равна изменению его внутренней энергии с обратным знаком, поскольку процесс расширения проведен адиабатно, так что ΔQ=
0. Поэтому, если U1
и U2
– внутренняя энергия моля газа до и после его расширения, то
p2
V2
– p1
V1
= U1
– U2
, илиU1
+ p1
V1
=U2
+ p2
V2
.
Функция U +
pV =
I
называется тепловой функцией
или энтальпией
газа. Это функция состояния, которая при изобарическом процессе играет ту же роль, какую при адиабатном процессе играет внутренняя энергия U, а при изотермическом – свободная энергия F. Значит, процесс Джоуля – Томсона происходит так, что тепловая функция газа остается постоянной по обе стороны перегородки (дросселя):
d(U + pV) =
0. (1)
Для идеального газа как внутренняя энергия, так и произведение pV
зависят только от температуры
(они пропорциональны Т
); потому и тепловая функция U +
pV
зависит только от температуры. Равенство тепловых функций идеального газа по обе стороны перегородки одновременно означает и равенство температур. Значит, для идеального газа коэффициент Джоуля – Томсона равен нулю
.
Для неидеального газа, как мы знаем, внутренняя энергия зависит не только от температуры, но и от объема V, занимаемого газом. Поэтому равенство тепловых функций в случае реальных газов еще не свидетельствует о равенстве температур.
Действительно, опыт показывает, что большинство газов (азот, кислород, углекислота и др.) в процессе дросселирования при комнатной температуре охлаждаются
. Но такие газы ,как водород и гелий, при тех же условиях нагреваются
. Это означает, что в первом случае коэффициент Джоуля – Томсона µ=ΔТ/Δр положительный (при Δр<0 и ΔT<0), во втором он отрицательный.
Заметим еще, наконец, что процесс Джоуля – Томсона является существенно необратимым, следовательно, он сопровождается увеличением энтропии, dS>
0.
После приведенных замечаний нетрудно вычислить коэффициент Джоуля – Томсона.
Уравнение (1) может быть переписано в виде:
d
(U + pV
) = dU + p dV + V dp
=0,
но dU +
p
dV =
T
dS
; следовательно,
T dS + V dp =
0. (2)
Теперь необходимо выразить изменение энтропии dS
через изменение температуры dT
и изменение давленияdp.
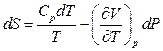 . .
Поставив это значение dS
в (2), получаем:
 , (3) , (3)
Откуда и получается интересующий нас коэффициент Джоуля – Томсона:
 , (4) , (4)
где  - коэффициент расширения газа. - коэффициент расширения газа.
Все величины, входящие в (4), могут быть определены, если известно уравнение состояния газа, и во всяком случае могут быть измерены. Следовательно, коэффициент µ может быть определен.
Из уравнения (4) видно ,что знак коэффициента µ зависит от величины αТ.
При αТ
> 1 коэффициент µ > 0; при αТ
< 1 имеем µ< 0.
Для идеальных газов
 и µ = 0, и µ = 0,
в чем мы убедились выше.
Для реальных газов µ может быть как положительным, так и отрицательным. Больше того, для одного и того же газа в одной области температур µ может быть положительным, а в другой – отрицательным.
Другими словами, существует температура Ti
, характерная для данного газа, при которой коэффициент Джоуля – Томсона меняет свой знак
. Эта температура Ti
называется температурой инверсии
.
Если состояние газа описывается уравнением Ван – дер –Ваальса, то, пользуясь (4), нетрудно найти и численное значение коэффициента Джоуля – Томсона. Для этого нужно вычислить производную  , входящую в (4). , входящую в (4).
Раскрыв скобки в левой части уравнения Ван – дер –Ваальса

получаем:
 . .
Дифференцирование обеих частей по Т
при p
=const дает:
 . .
Поставив вместо р
значение из уравнения Ван – дер –Ваальса  , получаем: , получаем:
 , ,
откуда
 . (5) . (5)
Если давление газа не очень велико (порядка 100 – 200 атм), то
 « 1 и « 1 и  « 1, « 1,
и в (5) ими можно пренебречь; тогда
 . (6) . (6)
Из этой формулы сразу видно, что коэффициент Джоуля – Томсона положителен, пока  > b, или T< > b, или T<
 . При Т> . При Т>
 коэффициент µ< 0, т.е. газ при дросселировании нагревается. коэффициент µ< 0, т.е. газ при дросселировании нагревается.
Очевидно, что температура инверсии определяется равенством:
 (7) (7)
Сопоставив (7) с выражением для критической температуры

получаем следующее простое соотношение между температурой инверсии и критической температурой:
 . .
Это соотношение, полученное в очень грубом приближении, довольно удовлетворительно подтверждается опытом. Во всяком случае, чем ниже критическая температура Тк
, тем ниже и Т
i
. для кислорода, например, температура инверсии равна 893 К (Тк
= 154,36 К). у водорода же и гелия температура инверсии равны соответственно 204,6 и 40 К (критические температуры 33 К и 5,2 К).
Тот факт, что в опыте Джоуля и Томсона, который ставился при комнатной температуре, водород при расширении нагревался, в то время как другие газы охлаждались, не является, конечно, особым свойством водорода. Любой газ обнаружит такое же свойство, если ставить опыт при более высокой, чем температура инверсии. Как мы увидим ниже, эффект Джоуля – Томсона используется именно для охлаждения водорода и гелия при их сжижении.
Рассмотрим теперь второй способ охлаждения газов, также применяемый для их сжижения.
§3. Адиабатное расширение газа с совершением внешней силы.
При дросселировании газа (эффект Джоуля – Томсона) охлаждение достигается за счет внутренней
работы, совершаемой газом против сил притяжения между молекулами. Как известно охлаждение газа происходит и в том случае, когда он адиабатно расширяется, совершая внешнюю
работу (например, поднимая поршень). Это непосредственно следует из первого начала термодинамики
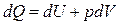 , ,
из которого видно, что при адиабатном  расширении расширении
 . .
Это значит ,что газ, расширяясь и совершая при этом работу, уменьшает свою внутреннюю энергию, а значит, и температуру. Это в данной мере относится и к идеальному, и к реальному газам. Причиной охлаждения газа при совершении им внешней работы является уменьшение скоростей молекул при их ударах об удаляющийся от них поршень, которому они передают часть своей кинетической энергии.
Вообще говоря, охлаждение при адиабатном расширении с совершением внешней работы должно быть более эффективным ,чем при дросселировании, так как адиабатное расширение – процесс обратимый (или, по крайней мере, могущий быть обратимым), в то время как эффект
Джоуля – Томсона – процесс необратимый. Нам уже известно, что обратимость процессов в машине обеспечивает большой коэффициент полезного действия. Правда, этот вывод относился к машине, преобразующей тепло в механическую работу, а не в холодной воде. Но все, что говорилось о к.п.д. тепловой машины, полностью относится и к холодным аппаратам, которые можно считать устройствами, обратными тепловым двигателям.
В холодной машине тепло отбирается от холодного тела и передается более нагретому. При этом затрачивается механическая работа, за счет которой и происходит передача тепла от холодного тела к теплому. Сам собой такой процесс не может идти. «теплым» телом для холодильника служит окружающая среда, которая для теплового двигателя служит холодильником. Ей передается тепло от того тела, которое требуется охладить.
Холодильная машина является ,таким образом, обращенным двигателем. Коэффициентом полезного действия холодильной машины мы должны считать отношение количества теплоты Q
, отнятого от охлаждаемого тела, к затраченной при этом работе А
:
 . .
В применении к холодильным аппаратам он называется холодильным коэффициентом
. Легко показать, что для холодильной машины, работающей по циклу Карно, холодильный коэффициент равен
 , ,
где Т1
– температура охлаждаемого тела и Т2
– температура тела, которому тепло передается. Холодильный коэффициент, разумеется, может быть и больше единицы. Лучшей машиной считается та, которая для отнятия данного количества тепла от охлаждаемого тела тратит наименьшую работу.
Подобно тому, как в тепловом двигателе его цель – совершение работы – достигается при расширении газа, в холодильном аппарате его цель – охлаждение – тоже достигается при расширении (адиабатном) газа. Поэтому самой существенной частью такой машины является та часть ,в которой происходит расширение газа. Она называется детандером
. Устройство его может быть самым разнообразным.
Чтобы газ можно было подвергнуть расширению (в детандере), он должен быть сперва сжат компрессором. Работа, совершаемая компрессором, и есть та работа, за счет которой становится возможной передача тепла от холодного тела к теплому. Но при сжатии газа он нагревается, что, конечно, уменьшает эффективность последующего охлаждения при расширении. Поэтому тепло, выделяемое при сжатии, отводится (например, проточной водой), так что процесс сжатия может считаться изотермическим.
С термодинамической точки зрения сущность работы рассматриваемой нами холодильной машины, использующей адиабатное расширение газа, я яснее всего видна из диаграммы зависимости энтропии от температуры. Такая диаграмма показана нарис.2, на котором изображена зависимость энтропии газа S от температуры Т при постоянном давлении для двух различных давлений – высокого р1
и низкого р2
.
 рис. 2 рис. 2
Легко видеть ,что кривые правильно передают особенности энтропии как меры беспорядка. Ясно, что беспорядок (а значит и энтропия) тем больше, чем выше температура, и тем меньше, чем выше давление. Именно это отражает этот рисунок.
Процесс изотермического сжатия от давления р2
до р1
изображается на этом рисунке вертикальной прямой АВ (энтропия уменьшается). Обратимому адиабатному расширению от давления р1
до р2
соответствует горизонтальная прямая ВС, так как при этом процесс энтропия остается постоянной. Из рисунка видно, что расширенное сопровождается понижением температуры от Т2
до Т1
. Это значит, что рост энтропии, вызванный расширением, как бы компенсируется уменьшением ее, сопровождающим охлаждение.
Рассмотренное только что охлаждение газа его расширением в детандере используется , как и эффект Джоуля – Томсона, для понижения температуры газов с низкими критическими температурами перед их сжатием. Обычно расширение в детандере служит лишь для предварительного охлаждения сжигаемых газов до возможно более низкой температуры (во всяком случае ниже критической). Самое же сжижение осуществляется с помощью дросселирования уже охлажденного газа. Можно, разумеется, добиться сжижения газа в самом детандере, не прибегая к дросселированию, но при очень низких температурах сжижаемых газов это создает очень тяжелые условия для его работы. Поэтому в тех машинах, в которых применяется метод адиабатного расширения в детандерах, он комбинируется с методом дросселирования.
Рассмотрим теперь некоторые примеры машин, в которых используются описанные нами методы охлаждения – метод
Джоуля – Томсона и метод адиабатного расширения с совершением внешней работы.
§4. Сжижение газов с использованием эффекта Джоуля – Томсона (метод Линде)
 В исторически первой машине для сжижения газов (воздуха) в технических масштабах (Линде и Гэмпсон, 1895 г.) для охлаждения газов ниже критической температуры и последующего сжижения использовался метод дросселирования. В настоящее время для этой цели применяются главным образом машины с расширением в детандерах. Но все же приведем здесь схему машины Линде, поскольку в ней наряду с использованием эффекта Джоуля – Томсона был применен важный конструктивный принцип противоточного теплообмена
, в той или иной форме и теперь применяемый во всех ожижительных машинах. В исторически первой машине для сжижения газов (воздуха) в технических масштабах (Линде и Гэмпсон, 1895 г.) для охлаждения газов ниже критической температуры и последующего сжижения использовался метод дросселирования. В настоящее время для этой цели применяются главным образом машины с расширением в детандерах. Но все же приведем здесь схему машины Линде, поскольку в ней наряду с использованием эффекта Джоуля – Томсона был применен важный конструктивный принцип противоточного теплообмена
, в той или иной форме и теперь применяемый во всех ожижительных машинах.
Схема машины Линде представлена на рис. 3.
Воздух поступает в компрессор К
, в котором он сжимается до 200 атм. После этого он проходит в змеевик, охлаждаемый проточной водой, где о отдает тепло, выделившееся при сжатии. Таким образом, в дальнейший путь к сжижению идет сжатый газ с температурой такой же, как и до сжатия. Этот газ проходит затем через змеевик ab
к дроссельному вентилю (крану) V
1
и расширяется через него в приемник f
до давления в 1 атм. При расширении газ несколько охлаждается, но, конечно, не настолько, чтобы превратиться в жидкость.
Охлажденный, но не сжижившийся газ возвращается затем обратно через змеевик cd
. Оба змеевика, ab
и cd
, расположены друг относительно друга так, что между ними, а также между порциями газа, проходящими по ним, существует тепловой контакт. Благодаря этому испытавший расширение и охлаждение газ охлаждает идущую ему навстречу порцию сжатого газа, которой еще предстоит расшириться через вентиль V
1
. В этом и заключается метод противоречивого обмена теплом. Ясно, что рис. 3
вторая порция газа подойдет к расширительному
вентилю V
1
, имея более низкую температуру, чем первая, а после дросселирования она еще более понизится. Проходя в свою очередь через теплообменник, этот уже дважды охлажденный газ снова поглотит тепло от новой встречной порции сжатого газа , и т.д. Таким образом к вентилю будет подходить все более холодный газ. Через некоторое время поле начала работы машины постепенное охлаждение газа холодными встречными потоками приведет к тому, что газ при очередном дросселировании начнет частично сжижаться и накапливаться в приемнике f
, откуда он может быть слит через кран V
2
в сосуд Дьюра.
При установившемся процессе работы машины в разных ее местах наблюдаются приблизительно такие температуры: у входа в змеевик ab
температура 293 К (комнатная); на выходе из этого змеевика 170 К; после дросселирования 80 К; у входа а змеевик cd
(в точке с) 80 К; на выходе из него – комнатная температура. Давление перед вентилем 200 атм, после дросселирования 1 атм.
Устройство, включающее оба змеевика ab
и cd
, в котором происходит охлаждение газа встречным потоком охлажденного газа, называется теплообменником
. В машине Линде теплообменник осуществляется в виде вставленных одна в другую трубок, которым вместе придавалась форма змеевика. Газ высокого давления поступает по внутренней трубке (рис. 4). Встречный поток охлажденного газа низкого давления проходит по внешней трубке, омывая внутреннюю и охлаждая, таким образом, газ в ней.

Рис. 4 рис. 5
Описанный принцип противотока применяется во всех холодильных машинах, хотя конструкции теплообменников подверглись значительным изменениям. В современных установках они обеспечивают лучший теплообмен и, кроме того, делают возможной очистку сжижаемого газа от примесей.
На схемах изображены теплообменники расположенными рядом змеевиками, причем жирными линиями показывают трубки, по которым проходит газ под высоким давлением, тонкими – трубки, в которых проходит газ низкого давления.
В настоящее время машины типа Линде для сжижения воздуха применяются редко. Однако для сжижения водорода и гелия машины этого типа, действие которых основано на использовании эффекта Джоуля – Томсона, применяются и до сих пор. В качестве примера рассмотрим схему одной из машин для сжижения гелия.
Так как температура инверсии эффекта Джоуля – Томсона Ti
для гелия очень низкая (около 50 К), то он должен быть предварительно охлажден до температуры ниже Ti
. в описываемой машине гелий охлаждается жидким водородом до температуры 14,5 К. Работу машины иллюстрирует схема, представленная на рис. 5
Гелий, сжатый компрессором до давления 30 атм, поступает в машину двумя потоками по двум трубкам, соединяющимся вместе в точке О. обе эти трубы являются частями двух теплообменников – І и ІІ. В теплообменнике І гелий охлаждается встречным потоком газообразного гелия, испаряющегося из приемника f
и прошедшего уже через теплообменник ІV. В теплообменнике ІІ вторая часть сжатого газа охлаждается встречным потоком газообразного водорода, испаряющегося из ванны с жидким водородом Н.
Соединившись в точке О, оба потока вместе поступают в змеевик ІІІ, проходящий через жидководородную ванну Н, и принимает ее температуру (14,5 К). пройдя через эту ванну, гелий попадает в теплообменник ІV, где он дополнительно охлаждается испаряющимся из приемника гелием до температуры 5,8 К. При такой температуре гелий подвергается дросселированию через вентиль V и сжижается.
Весь аппарат помещается в вакуумный чехол, обеспечивающий надежную тепловую изоляцию.
Приведенные выше цифры для температур в разных частях установки относятся, конечно, к установившемуся режиму работы. Во время разгона машины температура гелия перед дросселированием выше, чем 5,8 К (но, конечно, не выше 14,5 К), так как в это время в приемнике еще нет жидкого гелия. Машина обладает проводимостью около 10 литров жидкого гелия в час, что является сравнительно высокой цифрой.
§5. Сжижение газов методом адиабатного расширения в детандерах (метод Клода)
Применение детандеров, в которых газ охлаждается при адиабатном расширении с совершением внешней работы, повышает, как мы уже видели, эффективность ожижительных машин. В машинах для сжижения гелия использование расширения в детандерах позволяет, кроме того, отказаться от предварительного охлаждения газа жидким водородом – веществом, легко воспламеняющимся и взрывоопасным. Обе эти причины привели к широкому использованию детандерных машин.
Впервые такая машина была построена Клодом (1902 г.) для сжижения воздуха. Схема машины представлена на рис. 6.
 рис. 6 рис. 6
Газ подвергается изотермическому сжатию в компрессоре К, откуда он поступает в теплообменник Е1
. Здесь он разделяется на два потока (в точке О). первый идет через теплообменник Е2
к дроссельному вентилю и подвергается дросселированию с охлаждением за счет эффекта Джоуля – Томсона; второй поток (на его долю приходится 80 % газа) поступает в детандер, расширяется в нем, совершая работу, и за этот счет охлаждается. Из детандера охлажденный газ возвращается в теплообменник Е1
, охлаждая встречную очередную порцию сжатого газа. К нему в точке О' присоединяется и тот газ, который охладился в результате дросселирования. До этого он, проходя через теплообменник Е2
, тоже охлаждал встречный газовый поток.
Из приведенного краткого описания видно ,что охлаждение в детандере используется для предварительного охлаждения перед дросселированием.
В первой машине Клода детандер представлял собой поршневую машину. Работу, которую в ней совершает сжатый газ, можно использовать для облегчения работы компрессора, для принудительной смазки машины и т.д.
Условия, характерные для машины Клода (ожижающей воздух), примерно таковы: давление на выходе компрессора 40 атм, температура на входе в детандер (т.е. после охлаждения в теплообменник Е1
) 200 К; температура после расширения в детандере 110 К при давлении в 1 атм.
Существует много различных по конструкции машин типа Клода для сжижения воздуха. Одной из самых интересных является машина П. Л. Капицы, в которой поршневой детандер заменен турбиной (турбодетандер). Другой возможностью этой машины является низкое давление, по которым газ поступает в детандер. Оно равно лишь 6,5 атм. Зато в этой машине почти весь газ (а не 80%, как в машине Клода) проходит через детандер. В результате расширения в турбодетандере газ охлаждается до 86 К и сжижает ту часть газа, которая миновала детандер. Получившаяся жидкость находится под повышенным давлением и дросселируется через соответствующий вентиль к боле низкому давлению.
Расширение в детандерах (исключительно поршневых) используется также в машинах для сжижения водорода и гелия. Первая детандерная машина для сжижения гелия также была построена П. Л. Капицей (1934 г). Она была рассчитана на предварительное охлаждение гелия не жидким водородом, а жидким азотом
. Недостающее охлаждение создавалось расширением в детандере. Самое ожижение газа производилось дросселированием.
При использовании детандеров в гелиевых ожижительных машинах возникает острая проблема смазки, так как при тех низких температурах, которые создаются в таких машинах, все смазочные средства твердеют. В детандере П. Л. Капицы смазкой служит сам гелий, для которого между поршнем и цилиндром оставлялся зазор около 0,05 мм. Впоследствии Коллинз (1947 г) построил детандерную машину для сжижения гелия, усовершенствовав детандер П. Л. Капицы (зазор в детандере Коллинза не превышает 10 микрон). Машина Коллинза снабжен двухступенчатым детандером и может работать без предварительного охлаждения гелия. Производительность машины сравнительно велика – до 10 литров в час, а с предварительным охлаждением жидким азотом – до 30 литров в час.
§6. Некоторые свойства сжиженных газов
Сжиженные газы, о которых шла речь выше , - азот, кислород, водород и гелий, - позволяют получить низкие температуры в интервалах температур, простирающихся от температур их кипения под атмосферным давлением до температур их отвердения, до которого их можно довести, откачивая пары над ними (исключение составляет гелий, не твердеющий ни при каком охлаждении). В твердом состоянии эти газы могут служить хладоагентами, так как трудно создать надежный тепловой контакт между ними и охлажденными телами.
| N2
|
O2
|
H2
|
He4
|
| Температура кипения под давлением 1атм, К |
77,32 |
90,12 |
20,39 |
4,21 |
| Температура отвердения, К |
63,14 |
54,36 |
14,04 |
Не твердеет |
| Упругость пара при температуре отвердения, мбар |
129 |
1,50 |
75,8 |
- |
| Плотность при температуре кипения при 1 атм, кг/м3
|
800 |
1150 |
71 |
125 |
| Теплота испарения при температуре кипения при 1 атм, кДж/кг |
200 |
212,8 |
456,2 |
23 |
| Плотность в твердом состоянии, кг/м3
|
1026 |
1425 |
80 |
- |
В таблице приведены данные, показывающие, какие именно интервалы температур перекрываются этими сжиженными газами. Там же приведены и некоторые другие сведения о них.
 Из таблицы видно, что сжиженные газы позволяют непосредственно получать низкие температуры в следующих интервалах: Из таблицы видно, что сжиженные газы позволяют непосредственно получать низкие температуры в следующих интервалах:
63,14 – 77,32 К – жидкий азот,
54,36 – 90,12 К – жидкий водород,
14,04 – 20,39 К – жидкий водород,
0,7 – 4,21 К – жидкий гелий (0,7 К – наинизшая температура, достигаемая откачкой паров жидкого гелия Не4
.)
С помощью этих сжиженных газов могут быть получены и любые промежуточные температуры, хотя это требует применения особых, иногда весьма сложных устройств.
Устройства эти, служащие для проведения исследований как внутри, так и вне приведенных выше температурных интервалов, называются криостатами
. Они позволяют получить не только нужную температуру, но и поддерживать ее во время исследования постоянной. Они снабжаются даже тем или иным термометром для измерения температуры.
На рис. 7 показан простейший криостат для исследований в области гелиевых температур.
Он состоит из двух, помещенных один на другой сосудов Дьюара – внутреннего А и внешнего В. первый из них рис.7
наполняется жидким гелием, второй – жидким азотом. Такое азотное «окружение» необходимо для уменьшения подвода тепла извне, что позволяет замедлить испарение и продлить тем самым «срок службы» налитого жидкого гелия. Внутренний сосуд вакуумно плотно закрывается крышкой (уплотнение обеспечивается резиновой манжетой m, охватывающей крышку и сосуд). Трубка N в крышке служит для откачки паров гелия, что позволяет изменять его температуру. Поддерживая упругость паров постоянной (с помощью особого устройства вне криостата, не показанного на рисунке), можно поддерживать и температуру жидкости постоянной. Манометр (также не показанный на рисунке), присоединенный к криостату через трубку М, служит для измерения упругости паров, а по ней судят о температуре жидкости. Исследуемое тело, помещаемое в жидкий гелий, крепится к крышке тонкостенными трубками из материала ,плохо проводящего тепло.
§8. Сверхнизкие температуры
Данные, приведенные в таблице ,показывают, что сжиженные газы позволяют получить температуры вплоть до 4,21 К (жидкий гелий).
Если заставить жидкий гелий кипеть под пониженным давлением (для этого нужно откачивать пары над ним), то его температуру можно понизить примерно до 1К. Рекордно низкая температура, полученная таким образом, равна 0,69 К. дальнейшее понижение температуры жидкого гелия откачкой его паров оказывается практически невозможным, так как упругость паров гелия в этой области температур становится очень малой. Если при 0,7 К упругость паров гелия равна 2,2*10-3
мм рт. ст., то при 0,5 К она становится равной 1,6*10-5
, а при 0,3 К – 3,2 *10-10
мм рт. ст. Имея в виду легкость, с какой испаряется жидкий гелий (теплота испарения 23 кДж/кг), ясно ,что насосы не могут «успеть» откачивать пары до столь малых давлений.
Поэтому для получения еще более низких температур (их называют сверхнизкими) используется другой способ – так называемый магнитный метод охлаждения
. Сущность его легко понять из второго начала термодинамики.
В качестве хладоагента в этом методе используется особый вид веществ – так называемые парамагнитные соли. Это сложные химические соединения, примером которых может служить соль Fe2
(SO4
)3
(NH4
)2
SO4
· 24H2
O (железоаммониевые квасцы). Вещества эти заманчивы тем, что каждая их молекула обладает магнитным моментом, т.е. ведет себя как постоянный маленький магнит. В обычных условиях, т.е. в отсутствие магнитного поля, эти макроскопические магнитики ориентированы совершенно беспорядочно из-за тепловых движений, в которых участвуют молекулы соли (рис. 8, а) с этим магнитным беспорядком, так же как с беспорядком тепловым, связана определенная энтропия.

Рис. 8
Если поместить парамагнитное вещество в магнитное поле, то магнитные моменты частично повернуться в направлении поля, так что в их расположении появится некоторый порядок (рис8, б). Этом процесс называется намагничиванием. Значит, магнитное поле приводит к тому, что степень беспорядка (магнитного) уменьшается. Уменьшается поэтому и связанная с ним энтропия.
Представим себе теперь, что парамагнитное вещество намагничивается в адиабатных условиях (обратимым образом
). Энтропия в этом случае остается, как мы знаем, постоянной. Но так как магнитная часть энтропии при намагничивании уменьшается, то тепловая часть должна соответственно увеличиваться, т.е. должна повыситься температура. Наоборот, если предварительно намагниченный образец адиабатно
размагнитить, то он должен охладиться: вызванное размагничиванием увеличение магнитного беспорядка, а значит, и связанной с ним энтропии должно скомпенсироваться уменьшением тепловой части энтропии, что и происходит при охлаждении. Размагничивание играет в магнитном методе такую же роль, какую при охлаждении газа играет его расширение.
Опыт с магнитным охлаждением ставится так: сначала парамагнитную соль охлаждают с помощью жидкого гелия до возможно низкой температуры. Затем, не прерывая контакта соли с жидким гелием, ее намагничивают в возможно более сильном магнитном поле. Выделяющееся при этом тепло поглощается жидким гелием, так что намагничивание производится в изотермических условиях. После этого соль изолируют от жидкого гелия и размагничивают ее (адиабатно), удаляя из магнитного поля. В результате соль оказывается охлажденной. Этим способом удается получить рекордно низкие температуры – порядка ста тысячных долей градуса.
Полученная таким образом охлажденная соль используется для охлаждения других исследуемых тел. Существуют различные способы создания теплового контакта между солью и исследуемыми образцами.
§9. Свойства вещества при низких температурах
При низких температурах, когда интенсивность тепловых движений оказывается ослабленной, должны, конечно, наблюдаться существенные изменения свойств вещества. Однако при рассмотрении этих изменений нужно прежде всего установить, какие именно температуры должны считаться низкими. Нетрудно видеть, что по отношению к разным веществам и для различных свойств этих веществ «низкими» должны считаться совершенно различные температуры. Так, например, если речь идет о свойствах жидкостей, то ясно, что для них не имеет смысла говорить о температурах более низких, чем температура их отвердения Тотв
(об исключительной случае жидкого гелия см. ниже). Для воды, например, комнатная температура может считаться весьма низкой, так как отношение ее к Тотв
мало отличаются от единицы.
Нет возможности описать здесь сколько -нибудь подробно все особенности поведения веществ при низких температурах. Поэтому ограничимся лишь некоторыми общими замечаниями о низкотемпературных явлениях и о свойствах различных классов веществ в этих условиях.
При самых низких температурах – тех, которые получаются с помощью жидкого гелия («гелиевые» температуры) и тем более магнитным способом, - тепловые движения оказываются настолько ослабленными, что они во многих случаях не играют большой роли. Благодаря этому как бы вскрываются те сложные взаимодействия между атомами и молекулами, которые обусловлены их строением и которые при более высоких температурах полностью или частично маскируются влиянием тепловых движений. А так как атомы и молекулы состоят из частиц, то при температурах ,близким к абсолютному нулю, квантовые эффекты становятся весьма заметными, некоторые явления имеют чисто квантовый характер. С одним из таких явлений мы познакомимся позже.
Газы при низких температурах.
При обычных температурах и давления газы с большой точностью могут считаться идеальными. Это значит, что молекулы газа ведут себя так, как будто они совершенно не взаимодействуют между собой, и поэтому каждой молекуле приписывается только кинетическая энергия тепловых движений.
В действительности, однако, взаимодействие между частицами существует и молекулы газа на самом деле обладают не только кинетической, но и потенциальной энергией, обусловленной силами взаимодействия и зависящей от их взаимных расстояний. Но при высоких температурах, когда кинетическая энергия молекул велика, потенциальной энергией можно по сравнению с ней пренебречь и считать газ идеальным. При низкой температуре относительная роль потенциальной энергии возрастает, что вызывает отклонение свойств газов идеальности.
Закон соответственных состояний, основанный на приведенном уравнении Ван-дер-Ваальса
 , ,
позволяет сразу определить, является ли данная температура высокой или низкой для того или иного вещества. Низкими, очевидно, должны считаться температуры, при которых θ = Т/Тк
близко к единице или меньше единицы.
Так, например, для паров воды (Тк
= 647,1 К) комнатная температура (Т = 290 К) – это очень низкая температура, потому что
 . .
Ее можно считать низкой и для ксенона (Тк
= 289,1 К):
 . .
Но для кислорода (Тк
= 154,2) комнатная температура должна уже считаться высокой, так как θ значительно больше единицы:
 . .
Сложность сил взаимодействия между молекулами газа приводит к тому, что при низких температурах уравнение Ван-дер-Ваальса оказывается недостаточно точным. При температурах вблизи и ниже критической лучше всего согласуется с опытом уравнения состояния в виде ряда (для 1 моля)
 , (8) , (8)
в котором силы взаимодействия находят свое отражение в зависящих от температуры вириальных коэффициентах
В, С и т. д.
Первый член ряда соответствует отсутствию сил взаимодействия: если ограничиться этим членом, то, как видно из уравнения (8), мы получим уравнение состояния идеального газа. Второй вириальный коэффициент В отражает такие взаимодействия, в которых участвуют две сближающиеся молекулы (парное взаимодействие), третий учитывает взаимодействия, связанные с одновременным сближением трех частиц, и т. д.
Если давление газа не слишком велико, то играет роль только второй член ряда, т.е. второй вириальный коэффициент, так как вероятность встречи (столкновения) трех частиц (тем более четырех и больше) может стать заметной только при больших плотностях газа. Точное вычисление второго вириального коэффициента может быть произведено только с учетом построения атомов и квантовых законов.
При самых низких температурах только два вещества – водород и гелий – могут находиться в газообразном состоянии с заметным давлением. Все прочие газы при более значительных температурах твердеют, а упругости их паров становятся ничтожно малыми. Но в обоих «низкотемпературных» газах обнаруживаются заметные квантовые эффекты. Строго говоря, низкие критические температуры гелия и водорода сами по себе являются квантовыми эффектами.
Жидкости при низких температурах.
Область существования жидкого состояния ограничена критической точкой со стороны высоких и со стороны низких температур (последняя зависит от давления). Изменения свойств жидкостей при переходе к низким температурам (близким к точке отвердения) сводятся к росту коэффициента поверхностного натяжения и к сильному увеличению коэффициента внутреннего трения. У некоторых веществ рост вязкости приводит даже к тому, что жидкость приобретает некоторые признаки твердого тел и прежде всего способность сохранять не только объем, но и форму.
Как уже упоминалось, при самых низких температурах наблюдаются некоторые специфические квантовые явления, которые нельзя считать результатом постепенного изменения свойств вещества с понижением температуры. Явления эти возникают скачком при вполне определенной температуре и не имеют аналогов при высоких температурах. Мы имеем в виду явления сверхпроводимости и сверхтекучести. Первое из них заключается к скачкообразном исчезновении электрического сопротивления в металлах и наблюдаются у довольно большого числа чистых металлов и сплавов. Второе относится к одному единственному в природе веществу – жидкому гелию.
§10. Жидкий гелий
Жидкий гелий замечателен прежде всего тем, что это самая холодная жидкость в природе. Обычный гелий (Не4
), состоящий из атомов с атомным весом 4, имеет критическую температуру 5,25 К. следовательно, в жидком состоянии он может существовать только ниже этой температуры. При давлении в 1 атм он кипит при 4,21 К. еще более низкую критическую температуру имеет редкий изотоп гелия с атомным весом 3 (Не3
). Она равна 3,35 К, а под давлением своих паров, равным 1 атм, жидкий гелий Не3
кипит при 3,195 К.
Все другие вещества уже при более высоких температурах переходят в твердое состояние. Жидкий же гелий не твердеет и при температурах, еще более близких к абсолютному нулю, и все указывает на то, что и при абсолютном нуле нормальным состоянием гелия является жидкое состояние. Это, однако, не значит, что гелий вообще не может быть твердым. Но в твердое состояние он может быть переведен только под повышенным давлением, тем более высоким, чем выше температура. Даже при абсолютном нуле для кристаллизации гелия потребовалось бы давление в 25,27 атмосферы.
Наиболее важной особенностью жидкого гелия является существование двух его модификаций, переходящих одна в другую при 2,186  К (при этой температуре переход происходит при давлении паров в одну атмосферу; под повышенным давлением температура перехода более низкая). Эти две модификации называются Не І и Не ІІ. Точка перехода Не І – Не ІІ обычно называется λ-точкой. Название это принято из-за вида кривой температурной зависимости теплоемкости жидкого гелия, напоминающей букву λ (рис. 9). Скачок теплоемкости в точке перехода является важной чертой этого перехода ,отличающей его от таких, например, превращений, как парообразование или плавление, которые не сопровождаются скачком теплоемкости, но при которых выделяется скрытая теплота. Переход Не І в Не ІІ происходит без выделения или поглощения скрытой теплоты. К (при этой температуре переход происходит при давлении паров в одну атмосферу; под повышенным давлением температура перехода более низкая). Эти две модификации называются Не І и Не ІІ. Точка перехода Не І – Не ІІ обычно называется λ-точкой. Название это принято из-за вида кривой температурной зависимости теплоемкости жидкого гелия, напоминающей букву λ (рис. 9). Скачок теплоемкости в точке перехода является важной чертой этого перехода ,отличающей его от таких, например, превращений, как парообразование или плавление, которые не сопровождаются скачком теплоемкости, но при которых выделяется скрытая теплота. Переход Не І в Не ІІ происходит без выделения или поглощения скрытой теплоты.
Жидкий Не І, т.е. жидкий гелий выше λ-точки, обладает нормальными для сжижения газов свойствами, если не считать его низкой температуры. Внешне это бесцветная жидкость, бурно кипящая с обильным выделением пузырьков. Плотность жидкого гелия около 0,12 г/см3
. Низкотемпературная же модификация жидкого Не ІІ по своим свойствам резко отличается как от Не І, так и от других жидкостей в природе. Даже внешне Не ІІ резко отличается от Не І тем, что тотчас после понижения температуры ниже λ-точки прекращается бурное кипение и образование пузырьков. О причинах этого явления будет сказано ниже.
Жидкий гелий ІІ. Сверхтекучесть.
Самой разительной особенностью жидкого Не ІІ является сверхтекучесть. Это свойство, которым ни одно другое вещество (не исключая и легкого изотопа гелия) не обладает, заключается в том, что жидкий Не ІІ при своем течении через тонкие капилляры, щели и т.д. не испытывает никакого трения. Течение жидкого Не ІІ происходит так, как будто бы вязкость его равна нулю (П. Л. Капица, 1940).
Как известно, вязкость (внутренне трение) связана с переносом количества движения (импульса) от одного слоя движущейся жидкости к другому. Этот процесс происходит при столкновении молекул, совершающих тепловые движения при одновременном упорядоченном движении всей жидкости или как газа целого.
Жидкий Не І, как и всякая другая жидкость, обладает вязкостью, хотя и очень малой, не большей, чем у газообразного гелия (около 2·10-5
пуаз). Течение Не І происходит таким же образом, как и течение обычных жидкостей. Но при переходе через λ-точку вязкость гелия внезапно уменьшается по крайней мене в миллион раз и становится меньше 10-11
пуаз, т.е. практически равно нулю (вязкость воды равна 10-2
пуаз). Это значит ,что жидкий гелий Не ІІ может свободно протекать через самые тонкие капилляры, щели и отверстия, непроницаемые даже для газа. И именно в самых тонких капиллярах течение жидкого Не ІІ характеризуется закономерностями, коренным образом отличающимися от законов течения обычных жидкостей.
У обычных жидкостей скорость течения определяется, как известно, уравнением Пуазейля
 , ,
где V
– объем жидкости ,протекающей за 1 с через сечение трубки, Δp
– перепад давления,l
и r –
длина и радиус трубки, η –
вязкость жидкости. Скорости течения, следовательно, при данной вязкости растет с увеличением Δp
и падает с ростом l.
Скорость же течения жидкого Не ІІ в тонких капиллярах (10-4
– 10-5
см) от разности давлений и от длины капилляра вообще не зависит ,а с увеличением толщины капилляра скорость не растет, а уменьшается. Это показывает ,что движение Не ІІ в таких капиллярах является вполне безвякостным. Существует ,однако, определенная скорость течения, так называемая критическая скорость
, выше которой начинает действовать силы трения и движение становится вязким. Величина критической скорости растет с понижением температуры и только при самых низких температурах становится постоянной величиной.
В широких капиллярах («широким» для жидкого Не ІІ являются капилляры шире 10-3
см) течение жидкого Не ІІ происходит несколько иначе. Здесь нет определенной критической скорости, выше которой появляются силы трения. Скорость течения в широких капиллярах пропорциональна разности давлений. Это означает, что если в узких капиллярах силы трения вплоть до критической скорости вовсе отсутствуют, то в широких такие силы почти при всех скоростях существуют, но они достаточно малы, чтобы не препятствовать росту скорости с увеличением разности давлений. В широких капиллярах ,следовательно, нет вполне безвязкостного течения Не ІІ. Однако и здесь закономерности течения сильно отличаются от обычных.
Удивительное свойство сверхтекучести, наблюдающееся у Не ІІ, нельзя объяснить с помощью обычных представлений и жидком состоянии вещества. Ведь эти представления относятся к обычным молекулярным системам, в которых тепловые движения играют очень большую роль. Жидкий же гелий существует не только при очень низких температурах, когда энергия тепловых движений становится очень малой. Неудивительно, что при таких условиях могут происходить явления, которые при более высоких температурах не наблюдаются. Свойство сверхтекучести, как, впрочем, и все другие явления, происходящие при температурах, близких к абсолютному нулю, оказалось квантовым эффектом, т.е.явлением, которое может быть объяснено только квантовой механикой. Такое объяснение было дано в 1941 г. Л. Д. Ландау.
Сущность теории Л. Д. Ландау заключается в следующем.
При абсолютном нуле жидкий гелий, как и всякое другое вещество, находится в состоянии, в котором энергия (и импульс) его атомов не может измениться. Поэтому при движении относительно какого-нибудь тела, например стенки капилляра (или, что то же, при движении тела относительно жидкости), жидкость не может увеличить свой импульс или энергию (возбудиться), если скорость этого относительного движения меньше некоторой критической. Ясно, что жидкость, частицы которой не могут обмениваться импульсом с другими атомами, не обладает вязкостью, является сверхтекучей.
При температуре же, отличной от абсолютного нуля, жидкий гелий возбуждается, но происходит это так, как будто возбуждается только часть жидкости. Остальная же часть остается невозбужденной, т.е. остается в остается в таком же состоянии, в каком она была бы при абсолютном нуле. Таким образом ,пи всех температурах выше абсолютного нуля и ниже λ-точки жидкий гелий представляет собой как бы смесь двух компонент – возбужденной и невозбужденной. Первая обладает ,а другая не обладает вязкостью. Каждая из компонент обладает своей плотностью, но на опыте измеряется, конечно, полная плотность жидкости. Если обозначить плотность нормальной компоненты ρn
, сверхтекучей ρs
, а суммарную плотность через ρ, то зная температурную зависимость ρ и одной из составляющих ρn
или ρs
, можно определить эти последние.
Опытным путем можно, как оказывается, определить отношение  . Поэтому, зная ρ и ρп
/ρ и полагая, что . Поэтому, зная ρ и ρп
/ρ и полагая, что  , можно вычислить значения , можно вычислить значения  и и  и их зависимость от температуры. Очевидно, что при изменении температуры от абсолютного нуля до λ-точки значение и их зависимость от температуры. Очевидно, что при изменении температуры от абсолютного нуля до λ-точки значение  изменяется от нуля до ρ, а изменяется от нуля до ρ, а  - от ρ до нуля: при абсолютном нуле вся жидкость сверхтекучая, а выше λ-точки вся она нормальная, вязкая. С этой точки зрения переход Не І – Не ІІ состоит в том, что в нормальном жидком гелии появляется сверхтекучая компонента, количество которой с дальнейшим понижением температуры возрастает. Жидкий гелий – вещество, которое фактически можно наблюдать как бы в условиях абсолютного нуля (который, как мы знаем, недостижим). И это – единственное такое вещество в природе. - от ρ до нуля: при абсолютном нуле вся жидкость сверхтекучая, а выше λ-точки вся она нормальная, вязкая. С этой точки зрения переход Не І – Не ІІ состоит в том, что в нормальном жидком гелии появляется сверхтекучая компонента, количество которой с дальнейшим понижением температуры возрастает. Жидкий гелий – вещество, которое фактически можно наблюдать как бы в условиях абсолютного нуля (который, как мы знаем, недостижим). И это – единственное такое вещество в природе.
Описанная только что картина жидкого гелия Не ІІ позволяет понять те особенности течения этой жидкости через капилляры, о которых было рассказано выше.
В самом деле, течение жидкого гелия через капилляры осуществляется, конечно, обеими компонентами жидкости. Но нормальная компонента испытывает при этом действие силы трения, на сверхтекучую же компоненту такая сила не действует. Чем уже капилляр, тем меньше участие нормальной компоненты, испытывающей в таких капиллярах наибольшее трение. В самых узких капиллярах нормальная компонента практически в течении участвовать не может и оно оказывается безвязкостным. В широких же капиллярах роль нормальной компоненты становится более заметной и вполне безвязкостное течение уже не может наблюдаться. Однако благодаря присутствию сверхтекучей компоненты обычные законы гидродинамики все же не выполняются и в этом случае.
Экспериментально установлено, что явление сверхтекучести наблюдается и в жидком Не3
. Но это вещество становится сверхтекучим при температуре в несколько милликельвинов.
Тонкие пленки в жидком гелии ІІ.
В тесной связи с описанным свойством сверхтекучести жидкого гелия находится другое явление – образование тонкой движущейся пленки жидкого гелия Не ІІ на поверхности всякого твердого тела, соприкасающегося с ним.
Явление это заключается в том, что когда какое-нибудь тело частично погружено в жидкий гелий ІІ, причем верхняя часть тела имеет более высокую температуру, чем жидкость, то вдоль непогруженной части поднимается тонкая пленка жидкости и доходит до той части поверхности тела, где температура выше λ-точки. Здесь большая часть пленки испаряется. Разумеется, тонкая пленка образуется и на стенках самого сосуда, в котором хранится Не ІІ, выше его уровня. Заметим, что эта пленка увеличивает площадь поверхности, с которой происходит испарение жидкого гелия, и затрудняет откачку его паров.
Как уже указывалось, пленка жидкого гелия подвижна и двигается она в ту сторону, где температура выше. Если же поверхность тела на всем своем протяжении имеет одинаковую температуру (ниже λ-точки), то непогруженная часть поверхности покрывается неподвижной пленкой.
Интересными примерами образования и движения пленки Не ІІ могут служить опыты, схематически изображенные на рис 10.
 Если погрузить в жидкий Не ІІ пустую пробирку так, как это показано на рис 10,а, то на наружной стенке пробирки образуется пленка жидкости. Двигаясь вверх по стенке, она проникает внутрь пробирки, и в конце концов жидкость наполняет пробирку, так что уровни жидкости в пробирке и в сосуде, в который она погружена, оказывается одинаковыми. Рис. 10 Если погрузить в жидкий Не ІІ пустую пробирку так, как это показано на рис 10,а, то на наружной стенке пробирки образуется пленка жидкости. Двигаясь вверх по стенке, она проникает внутрь пробирки, и в конце концов жидкость наполняет пробирку, так что уровни жидкости в пробирке и в сосуде, в который она погружена, оказывается одинаковыми. Рис. 10
Если, наоборот, в резервуар погружена пробирка, в которой уровень жидкого гелия выше, чем в самом резервуаре, то жидкий гелий, двигаясь по пленке, образующейся на внутренней поверхности пробирки, вытекает из нее, пока не выровняются уровни жидкости в пробирке и вне ее (рис 10,б).
Наконец, если пробирку с жидким гелием подвесить над уровнем жидкости в резервуаре (рис 10, в), то, благодаря пленке, гелий будет переходить по стенкам пробирки и каплями стекать в резервуар, пока весь гелий не вытечет из пробирки. Благодаря пленке, следовательно, жидкий гелий не может храниться в отдельном сосуде, все части которого находятся при температуре ниже λ-точки.
Толщина пленки, как показали измерения, равна приблизительно 2·10-6
см, т. е. около 100 атомных слоев.
Интересно, что зависимость скорости течения жидкого Не ІІ по пленке от температуры имеет такой же вид ,как и для скорости течения в узких капиллярах. Так же, как и для этого последнего, скорость движения в пленке не зависит от разности высот. Наконец, для течения по пленке, так же как для течения через узкие капилляры, существует определенная критическая скорость, выше которой течение перестает быть безвязкостным. Все это позволяет считать, что течение жидкого гелия в узких капиллярах не является объемным, а происходит главным образом в пристенном слое и именно это течение и осуществляется сверхтекучей компонентой жидкого Не ІІ.
Явление образования пленок жидкости само по себе не является исключительным свойством жидкого Не ІІ. Многие другие жидкости также образуют такие пленки (керосин является наиболее известным примером). Причиной их образования являются силы взаимодействия между частицами жидкости и твердого тела. Но в обычных жидкостях вязкость препятствует образованию и движению пленок. В гелии же, благодаря сверхтекучести, пленка легко образуется и беспрепятственно движется. Таким образом, пленочное явление в жидком Не ІІ – это следствие главной его особенности – сверхтекучести.
 Термомеханический эффект и жидком гелии ІІ.
Мы уже отмечали, что движение жидкого гелия в пленке происходит при наличии разности температур и притом в направлении более высокой температуры. Это движение, как оказывается, является частным случаем так называемого термомеханического эффекта
, который состоит в том, что когда в тонком капилляре с жидким гелием существует поток тепла, то в направлении, противоположном этому потоку, возникает поток жидкости. Термомеханический эффект и жидком гелии ІІ.
Мы уже отмечали, что движение жидкого гелия в пленке происходит при наличии разности температур и притом в направлении более высокой температуры. Это движение, как оказывается, является частным случаем так называемого термомеханического эффекта
, который состоит в том, что когда в тонком капилляре с жидким гелием существует поток тепла, то в направлении, противоположном этому потоку, возникает поток жидкости.
Это явление легко наблюдать, например, в простом устройстве, схематически показанном на рис11. Сосуд с нагревателем внутри, снабженный капилляром, погружен в ванну с жидким гелием ( на рис. 11 сосуд изображен закрытым сверху, но он может быть и открытым). При отсутствии тока в нагревателе уровни жидкости в сосуде и вне его одинаковы. Но при включении тока в нагреватель рис. 11
создается поток тепла через гелий в капилляре, направленный к жидкости в ванне. Навстречу его возникает поток жидкого Не ІІ, и в результате уровень жидкости в сосуде повышается.
Особенно ярко термомеханический эффект проявляется в так называемом явлении фонтанирования
. Соответствующее устройство для его  наблюдения изображено на рис12.Оно представляет собой узкую длинную капиллярную трубку, нижняя часть которой расширена и полностью мелким темным порошком (например, наждачным). Трубка погружена в жидкий Не ІІ, как показано на рис. 12. Если направить на нижнюю широкую часть трубки пучок света, так чтобы порошок нагрелся, то тепло через жидкий гелий, заполняющий тончайшие каналы между частицами порошка, передается наружному гелию. Тогда в обратном направлении из ванны в трубку устремляется жидкий гелий и выходит в виде фонтана из ее верхнего открытого конца. Этот своеобразный насос может поднимать жидкость на высоту до 30 см. наблюдения изображено на рис12.Оно представляет собой узкую длинную капиллярную трубку, нижняя часть которой расширена и полностью мелким темным порошком (например, наждачным). Трубка погружена в жидкий Не ІІ, как показано на рис. 12. Если направить на нижнюю широкую часть трубки пучок света, так чтобы порошок нагрелся, то тепло через жидкий гелий, заполняющий тончайшие каналы между частицами порошка, передается наружному гелию. Тогда в обратном направлении из ванны в трубку устремляется жидкий гелий и выходит в виде фонтана из ее верхнего открытого конца. Этот своеобразный насос может поднимать жидкость на высоту до 30 см.
Термомеханический эффект может наблюдаться и в таком устройстве, в котором роль тонкого капилляра играет пленка Не ІІ. Такой прибор показан нарис. 13.
 Открытый цилиндрический сосуд, снабженный электрическим нагревателем, погружается в гелиевую ванну. Благодаря пленке он быстро наполняется жидким гелием, так что уровни жидкости в сосуде и вне его выравниваются. Если теперь пропустить через нагреватель электрический ток, то вдоль по пленке к наружному гелию пойдет поток тепла, а в противоположном Открытый цилиндрический сосуд, снабженный электрическим нагревателем, погружается в гелиевую ванну. Благодаря пленке он быстро наполняется жидким гелием, так что уровни жидкости в сосуде и вне его выравниваются. Если теперь пропустить через нагреватель электрический ток, то вдоль по пленке к наружному гелию пойдет поток тепла, а в противоположном
направлении возникает поток жидкости. Рис. 13
В результате уровень жидкости в сосуде повышается.
Только что описанное удивительное явление также может быть объяснено свойством сверхтекучести жидкого Не ІІ приводит к обеднению нагреваемой части сверхтекучей компонентой. Поэтому по обе стороны капилляра или пленки образуется разность концентраций этой компоненты. Поскольку вязкость ее равна нулю, то через капилляр или пленку происходит выравнивание концентраций.
Термомеханический эффект, таким образом, несколько напоминает явление осмоса, причем капилляр или пленка играют роль полупроницаемой перегородки.
Механотермический эффект.
Наряду с только что описанным термомеханическим эффектом существует и обратный ему эффект, который можно назвать механотермическим эффектом
(или механокалорическим). Он заключается в том, сто если по капилляру или по пленке течет жидкий Не ІІ,то в направлении, обратном этому потоку жидкости
, возникает поток тепла
. Вследствие этого гелий вытекает, и той, куда он втекает. Явление это можно наблюдать, например, в приборе, показанном на рис.14.
 Закрытый (за исключением небольшого отверстия) сосуд, снабженный термометром сопротивления, погружается в резервуар с жидки Не ІІ. Через множество тончайших капилляров в порошке, закрывающем отверстие в нижней части сосуда, жидкий гелий проникает в сосуд и наполняет его до уровня жидкости в резервуаре. Если теперь приподнять сосуд над жидкостью в резервуаре, то жидкий гелий будет вытекать из сосуда через тонкие каналы в порошке. При этом термометр показывает повышение температуры жидкого гелия в верхней части сосуда. Это объясняется тем, что через рис. 14 Закрытый (за исключением небольшого отверстия) сосуд, снабженный термометром сопротивления, погружается в резервуар с жидки Не ІІ. Через множество тончайших капилляров в порошке, закрывающем отверстие в нижней части сосуда, жидкий гелий проникает в сосуд и наполняет его до уровня жидкости в резервуаре. Если теперь приподнять сосуд над жидкостью в резервуаре, то жидкий гелий будет вытекать из сосуда через тонкие каналы в порошке. При этом термометр показывает повышение температуры жидкого гелия в верхней части сосуда. Это объясняется тем, что через рис. 14
тонкие каналы протекает главным образом сверхтекучая компонента, т. е. та часть жидкости, которая не обладает энтропией и, значит, находится в состояниях абсолютного нуля.
Очевидно, что если измерять температуру там, куда попадает вытекающий гелий, то окажется, что в этом месте температура понижается. Таким образом, «процеживание» жидкого гелия через тонкие капилляры может, по крайней мере принципиально, служить методом получения температур более низких, чем температура жидкого гелия.
Механотермический эффект в термодинамическом отношении, очевидно, обратен термомеханическому.
Теплопроводность жидкого гелия ІІ.
Теплопроводность относится к числу тех свойств жидкого гелия, которые в λ-точке претерпевают резкое изменение. Жидкий Не І по своей теплопроводности (как и по вязкости) сходен с газами, и не только по численному значению коэффициента теплопроводности, но и потому, что для жидкого гелия, как и для газов, справедливо соотношение
 , ,
где  - коэффициент теплопроводности, η – коэффициент вязкости и - коэффициент теплопроводности, η – коэффициент вязкости и  - удельная теплоемкость при постоянном объеме. - удельная теплоемкость при постоянном объеме.
Но при переходе через λ-точку теплопроводность жидкого гелия внезапно возрастает приблизительно в 5·106
раз, так что теплопроводность жидкого гелия оказывается в сотни раз больше, чем у лучших металлических проводников тепла. Жидкий Не ІІ, следовательно, не только сверхтекуч, но и «сверхтеплопроводен».
Однако легко видеть, что наблюдаемая теплопроводность вовсе не является теплопроводностью в обычном смысле этого слова и что перенос тепла в жидком Не ІІ осуществляется более сложным, чем теплопроводность, механизмом. В самом деле, для переноса тепла необходима, как мы знаем, разность температур. Но в жидком Не ІІ при наличии разности температур возникает поток сверхтекучей компоненты, направленный против потока тепла (термомеханический эффект). Передача тепла в жидком Не ІІ поэтому непременно сопровождается переносом массы жидкости, чего при обычной теплопроводности, конечно, не происходит. Значит, передача в жидком гелии осуществляется не столько теплопроводностью, сколько своеобразной конвекцией особыми потоками жидкости.
 Существование таких потоков при переносе тепла было очень наглядно показано в опытах П. Л. Капицы (1941 г.). один из таких опытов схематически показан на рис15. Существование таких потоков при переносе тепла было очень наглядно показано в опытах П. Л. Капицы (1941 г.). один из таких опытов схематически показан на рис15.
Небольшой стеклянный сосуд с впаянными нагревателем и термометром заканчивается в нижней своей части тонкой трубкой. Сосуд помещается в сосуд Дьюара с жидким гелием, а напротив конца трубки помещается легкое крылышко на тонком подвесе. На нити подвеса укреплено зеркальце, позволяющее наблюдать за закручиванием нити.
При пропускании тока через нагреватель и нагреве жидкости наблюдается поворот крылышка вместе с нитью подвеса. Это означает, что оно испытывает действие силы, которая может исходить только от струи жидкости, выходящей из трубки. Струя эта состоит, рис. 15
очевидно, из нормальной компоненты жидкого
Не ІІ, так как сверхтекучая компонента, неспособная изменять свой импульс, не может вызывать и силу.
Выходящая из сосуда струя нормальной компоненты должна, конечно, компенсироваться обратной струей компоненты (протекающей, по-видимому, в пристенном слое трубки). Но эта струя, направленная в сторону источника тепла, на крылышко не действует и непосредственно не обнаруживается.
Таким образом, перенос тепла в жидком Не ІІ связан со сложными движениями в жидкости, и именно они обеспечивают необычайно высокую кажущуюся теплопроводность жидкого Не ІІ. Этими движениями, по-видимому, объясняется и прекращение видимого кипения жидкого гелия при переходе через λ-точку.
Естественно, что характер потоков жидкости, а значит и теплопередача в жидком Не ІІ должны зависеть от толщины капилляров, так как в очень тонких трубках возможно течение только сверхтекучей компоненты. Теплопередача должна зависеть также от скорости потоков, так как при скорости выше критической течение перестает быть безвязкостным даже для сверхтекучей компоненты.
Низкие температуры очень важны в нашей жизни. Окружающий нас космос – это природный гигантский холодильник, не дающий нам сгореть от палящих лучей солнца. Но и созданный человеком рукотворный холод нашел не мало применений: это и получение кислорода для современной металлургии, и громадные сверхпроводящие магниты, предназначенные приблизить осуществление управляемого термоядерного синтеза, и целая отрасль медицины – криохирургия, и наиболее чувствительные приборы для обнаружения радиосигналов и измерения магнитных полей, это в перспективе создание машин нового поколения и многое, многое другое.
В результате изучения материалов по рассматриваемому вопросу, были сделаны следующие основные выводы:
1. Вещества при изменении температуры меняют свои свойства. При понижении температуры большинство веществ меняют фазовое состояние. При самых низких температурах только два вещества – водород и гелий – могут находиться в газообразном состоянии с заметным давлением, все прочие газы при значительно более высоких температурах твердеют, а упругости их паров становятся ничтожно малыми.
2. Получение низких температур, от 200 К и ниже, имеет огромное значение для лабораторных исследований свойств веществ и для некоторых промышленных целей.Основными методами получения очень низких температур является магнитный способ и метод с применением жидкого гелия.
3. У всех веществ есть особая точка называемая тройной. В ней граничат сразу 3 фазы: твердая, жидкая и газообразная, и их все три можно наблюдать одновременно. Как выяснил в своих исследованиях Камерлинг-Оннес, у гелия нет тройной точки. Это единственное вещество, обладающее таким свойством.
4. Капица, измеряя вязкость методом перетекания, выяснил, что вязкость гелия II чрезвычайно мала. Он назвал обнаруженное явление сверхтекучестью. Сверхтекучесть – чисто квантовое явление, а жидкий гелий является единственной квантовой жидкостью, в то время как другие жидкости отвердевают при значительно более высоких температурах, при которых описываемый квантовый эффект еще не проявляется.
Список литературы
1. В.С. Эдельман. Вблизи абсолютного нуля. Москва, 1983г.
2. А.К. Кикоин, И.К. Кикоин. Молекулярная физика. Москва, 1976 г.
3. Д.В. Сивухин. Термодинамика и молекулярная физика. Москва, 1990 г
4. И.В. Савельев. т.1. Механика. Молекулярная физика. М.: Наука. Гл. ред. физ.-мат. лит., 1989Г.
|