Реферат: Расчет закрытых передач
|
Название: Расчет закрытых передач Раздел: Промышленность, производство Тип: реферат | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный университет» Кафедра деталей машин и прикладной механики Ю.А.ЧИРКОВ, Р.Н. УЗЯКОВ, Н.Ф. ВАСИЛЬЕВ, В.Г. СТАВИШЕНКО, С.Ю. РЕШЕТОВ РАСЧЕТ ЗАКРЫТЫХ ПЕРЕДАЧ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАСЧЕТУ ПЕРЕДАЧ В КУРСОВЫХ ПРОЕКТАХ Рекомендовано к изданию Редакционно-издательским советом государственного образовательного учреждения высшего профессионального образования «Оренбургский государственный университет» Оренбург 2003 ББК 34.445.72с Ч 65 УДК 621.833(075.8) Рецензент доктор технических наук, профессор В.М. Кушнаренко Чирков Ю.А., Узяков Р.Н., Васильев Н.Ф., СтавишенкоВ.Г., Решетов С.Ю. Ч 65 Расчет закрытых передач: Методические указания по расчету передач в курсовых проектах. - Оренбург: ГОУ ОГУ, 2001- 31 с. Методические указания предназначены для выполнения расчета цилиндрических, конических и червячных передач в курсовых проектах (работах) по дисциплине «Прикладная механика», «Механика», «Техническая механика» для студентов немеханических специальностей. ББК 34.445 Ó Чирков Ю.А. Ó ГОУ ОГУ, 2001 Содержание Введение................................................................................................... 4 1 Расчет закрытых цилиндрических передач......................................... 5 1.1 Выбор материала зубчатых колес, назначение упрочняющей обработки и определение допускаемых напряжений........... 6 1.2 Определение размеров зубчатых колес и параметров зацепления........ 7 1.3 Проверочные расчеты передачи............................................................ 10 1.4 Определение сил, действующих в зацеплении...................................... 11 2 Расчет закрытых конических передач............................................... 13 2.1 Выбор материала конических колес, назначение упрочняющей обработки и определение допускаемых напряжений......... 14 2.2 Определение размеров конических колес и параметров зацепления... 14 2.3 Проверочные расчеты передачи............................................................ 16 2.4 Определение сил, действующих в зацеплении...................................... 17 3 Расчет червячных передач................................................................. 18 3.1 Выбор материала червячной пары. Назначение упрочняющей обработки и определение допускаемых напряжений.................................. 19 3.2 Определение размеров и параметров червячного зацепления............. 20 3.3 Проверочные расчеты передачи............................................................ 22 3.4 Определение сил, действующих в зацеплении, и КПД передачи......... 23 3.5 Тепловой расчет и охлаждение червячных передач............................. 24 Список использованных источников.................................................... 25 Приложение А........................................................................................ 26 ВведениеВ методических указаниях изложена методика расчета закрытых передач, используемых в силовых приводах, изучаемых студентами в курсах «Прикладная механика», «Механика», «Техническая механика». Указания способствуют ускорению и унификации выполнения и оформления расчетов закрытых передач в курсовых проектах и работах. Цель расчета: определение параметров зацепления, геометрических размеров зубчатых колёс и сил, действующих в зацеплении. Для закрытых передач проектный расчет выполняется на выносливость по допускаемым контактным напряжениям, чтобы не допустить усталостного выкрашивания рабочих поверхностей зубьев. Определив на основе этого расчета размеры колес и параметры зацепления, выполняют проверочный расчет на выносливость зубьев по напряжениям изгиба, чтобы установить, не появляется ли опасность усталостного разрушения зубьев – основного вида отказа данного типа передач. Методические указания содержат рекомендации, справочный материал и примеры расчетов цилиндрических, конических и червячных закрытых передач. В методических указаниях принята единая система физических единиц (СИ) со следующими отклонениями, допущенными в стандартах (ИСО и ГОСТ) на расчеты деталей машин: размеры деталей передач выражаются в миллиметрах (мм), силы в ньютонах (Н), и соответственно напряжения в ньютонах, деленных на миллиметры в квадрате (Н/мм2 ), т.е. мегапаскалях (МПа), а моменты в ньютонах, умноженных на миллиметр (Н·мм). У отдельных групп соответствующих формул даны соответствующие примечания. После выполнения расчетов рекомендуется выполнить расчеты на ЭВМ, вызвав необходимую программу указав С:/DMRA/start.bat. В процессе этих расчетов можно варьировать некоторые данные передачи и сделать проверку правильности расчетов. 1 Расчет закрытых цилиндрических передачЗакрытые цилиндрические передачи (прямозубые, косозубые, шевронные, с внешним и внутренним зацеплением) и обозначение их параметров показаны на рисунке 1.
а) б) а – внешнее зацепление; б – внутреннее зацепление Рисунок 1 Исходные данные для расчета передачи выбираются из кинематического расчета силового привода с соответствующих валов и вводятся новые обозначения: параметры для зубчатой шестерни обозначаются с индексом единица, а параметры для зубчатого колеса обозначаются с индексом два. Вращающий момент:
Угловая скорость:
Частота ращения:
Передаточное число:
В редукторостроении экономически целесообразно применять стали с 1.1.1 Материал колеса
выбираем потаблице А.1
приложения – сталь с Твердость Предел прочности Предел текучести Допускаемые контактные напряжения:
где
Допускаемые напряжения изгиба:
где
1.1.2 Материал шестерни должен быть тверже материала колеса, так как зубья шестерни входят в зацепление чаще, чем зубья зубчатого колеса.
По найденной твердости Твердость HB1 = 230, Предел прочности Предел текучести Допускаемые контактные напряжения:
Допускаемые напряжения изгиба:
Расчетное контактное напряжение для прямозубых колес:
Расчетное контактное напряжение для косозубых и шевронных принимаем в соответствии с выполнением неравенства:
Если условие не выполняется, то принимаем:
1.2 Определение размеров зубчатых колес и параметров зацепления 1.2.1 Принимаем расчетные коэффициенты в зависимости от расположения зубчатых колес относительно опор: 1) коэффициент нагрузки Кн : КH =1,1…1,15 – для симметричного расположения; КH =1,15…1,25 – для несимметричного расположения; KH =1,25…1,4 - для консольного расположения колес. 2) коэффициент ширины колеса по межосевому расстоянию:
большее значение принимают для симметричного расположения колес, среднее - несимметричного, меньшее - консольного расположения зубчатых колес относительно опор: ψba ω ≤ 0,2; 0,25; 0,315- для прямозубых колес, ψba ω ≤ 0,315; 0,4; 0,5- для косозубых. 1.2.2 Определяем минимальное межосевое расстояние из условия контактной прочности:
где (u+1) – для передач с внешним зацеплением; (u-1) – для передач с внутренним зацеплением; C=310 – для прямозубых передач; C=270 – для косозубых передач; T2 – момент на колесе в Н·мм. Расчетные значения 1.2.3 Определяем нормальный модуль . Для внешнего зацепления:
Для внутреннего зацепления:
Расчетное значение округляем до стандартного (таблица А.3 приложения). Уменьшение модуля, т.е. увеличение числа зубьев зубчатых колес z1 и z2 увеличивает коэффициент перекрытия εα , т.е. увеличивает плавность зацепления, но уменьшает прочность зуба на изгиб. Поэтому, если передача находится после электродвигателя, то принимаем меньшее значение модуля, а для тихоходной ступени, большее значение модуля. 1.2.4 Для косозубых колес предварительно назначаем угол наклона зубьев.
1.2.5 Определяем число зубьев шестерни и колеса. Суммарное число зубьев косозубых шестерни и колеса:
Суммарное число зубьев прямозубых шестерни и колеса:
Для внешнего зацепления: число зубьев шестерни:
число зубьев колеса: z2 = zC - z1 . Для внутреннего зацепления:
Если z1 окажется меньше 17, то изменяем модуль в меньшую сторону и заново рассчитываем числа зубьев. Значения z1 и z2 округляем до целых чисел. Уточняем передаточное число:
Расхождения с исходным значением
Если 1.2.6 Определяем основные геометрические размеры передачи. Диаметры делительных окружностей, (мм):
Проверяем условие:
Диаметры окружностей выступов (мм):
Диаметры окружностей впадин (мм):
Ширина зубчатых колес (мм):
Значения Проверяем условие
Если условие не выполняется, то принимаем b2 = d1 и b2 = 1,5·d1 соответственно. Определяем коэффициент ширины относительно диаметра:
1.3 Проверочные расчеты передачи 1.3.1 Проверяем условие прочности по контактным напряжениям. Окружная скорость, м/с:
Назначаем степени точности изготовления колес (таблица А.18 приложения). Уточняем коэффициент нагрузки:
где
Проверяем условие прочности:
Допускается недогрузка на 10% и перегрузка на 5%. Если условие прочности не выполняется, то либо увеличивают степень точности, либо увеличивают 1.3.2 Проверяем условие прочности зубьев по напряжениям изгиба. Для косозубых колес определяем приведенное число зубьев шестерни и колеса:
Определяем по ГОСТ 21354-87 коэффициенты формы зуба - Проводим сравнительную оценку прочности на изгиб зубьев шестерни и колеса:
Дальнейший расчет ведем по минимальному значению найденных отношений. Определяем коэффициент нагрузки:
где
Коэффициент, учитывающий наклон зубьев (для косозубых колес),
Проверяем условие прочности по минимальному значению
Возможна большая недогрузка. Если условие прочности не выполняется, то задаются большим значением mn
, не изменяя Если это не дает положительного эффекта, то назначают другие материалы и расчет повторяют. 1.4 Определение сил, действующих в зацеплении В прямозубой передаче сила нормального давления раскладывается на окружную и радиальную составляющие силы (рисунок 2а).
Окружные силы, в ньютонах:
где
Радиальные силы, в ньютонах:
где Силы нормального давления, в ньютонах:
В косозубой передаче появляется осевая составляющая (рисунок 2б). Окружные силы в ньютонах:
Осевые силы в ньютонах:
Радиальные силы в ньютонах:
Силы нормального давления в ньютонах:
где
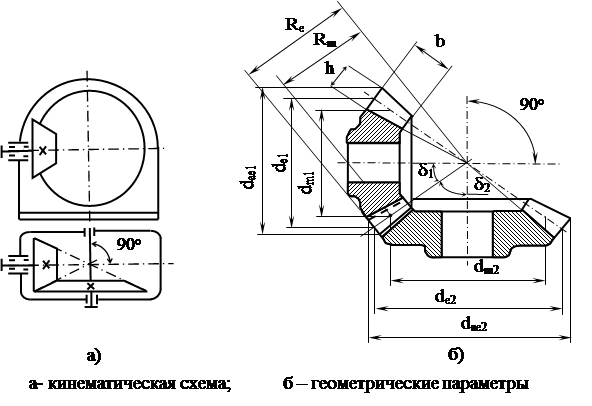
2 Расчет закрытых конических передачКонические зубчатые колеса применяют в передачах между валами, оси которых расположены под углом. Основное применение имеют передачи с пересекающимися под углом 90о осями (рисунок 3).
Рисунок 3 – Прямозубая коническая передача Исходные данные для расчета конической передачи выбираются из кинематического расчета силового привода с соответствующих валов и вводятся новые обозначения: параметры для зубчатой шестерни обозначаются с индексом единица, а параметры для зубчатого конического колеса обозначаются с индексом два. Вращающий момент:
Угловая скорость:
Частота ращения:
Передаточное число:
2.1 Выбор материала конических колес , назначение упрочняющей обработки и определение допускаемых напряжений 2.1.1 Материал колеса (см. расчет закрытых цилиндрических передач п. 1.1.1). 2.1.2 Материал шестерни (см. там же п. 1.1.2 ). Расчетное контактное напряжение для прямозубых колес:
2.2 Определение размеров конических колес и параметров зацепления 2.2.1 Принимаем расчетные коэффициенты: 1) коэффициент нагрузки 2) коэффициент ширины зубчатого венца по конусному расстоянию:
2.2.2 Определяем внешний делительный диаметр колеса из условия контактной прочности, мм:
где T2 – вращающий момент на колесе, Н·мм. Расчетные значения 2.2.3 Определяем внешний окружной модуль , мм:
По таблице А.3 (приложения), рекомендуется принимать такие стандартные значения модуля mte , которому соответствует целое число зубьев колеса:
2.2.4 Число зубьев шестерни:
Значения 2.2.5 Уточняем передаточное число:
Расхождения с исходным значением:
Если условие не соблюдается, тогда увеличивают или уменьшают 2.2.6 Определяем основные геометрические размеры передачи Углы делительного конуса:
Внешние делительные диаметры , мм:
Внешние диаметры окружностей выступов, мм:
Внешние диаметры окружностей впадин, мм:
Внешние конусное расстояние, мм:
Ширина зубчатого венца, мм:
Значение округляем до целого числа. Среднее конусное расстояние, мм:
Средние делительные диаметры, мм:
Средний модуль, мм:
Коэффициент ширины колеса по среднему диаметру: 2.3 Проверочные расчеты передачи 2.3.1 Проверяем условие прочности по контактным напряжениям Средняя окружная скорость, м/с
Назначаем степени точности изготовления колес (таблица А.18 приложения). Уточняем коэффициент нагрузки
где
Проверяем условие прочности, Н/мм2 :
Допускается недогрузка до 10% и перегрузка до 5%. Если условие прочности не выполняется, то можно увеличить de 2 . Если это не дает должного эффекта, то назначают другие материалы и расчет повторяют. 2.3.2 Проверяем условие прочности зубьев по напряжениям изгиба Определяем приведенное число зубьев:
Определяем по ГОСТ 21354-87 коэффициенты формы зуба - Проводим сравнительную оценку прочности на изгиб зубьев шестерни и колеса:
Дальнейший расчет ведем по минимальному значению найденных отношений. Определяем коэффициент нагрузки:
где
Проверяем условие прочности по
Возможна большая недогрузка. Если условие прочности не выполняется, то назначают другие материалы и расчет повторяют. 2.4 Определение сил, действующих в зацеплении В конической передаче сила нормального давления раскладывается на три составляющие: окружную, радиальную и осевую силы (рисунок 4).
Окружные силы, Н:
где Т2 - вращающий момент на шестерне (колесе), Н·м; dm 2 - средний диаметр шестерни (колеса), мм. Осевая сила шестерни, равная радиальной силе колеса, Н:
где Радиальная сила шестерни, равная осевой силе колеса:
Сила нормального давления, Н:
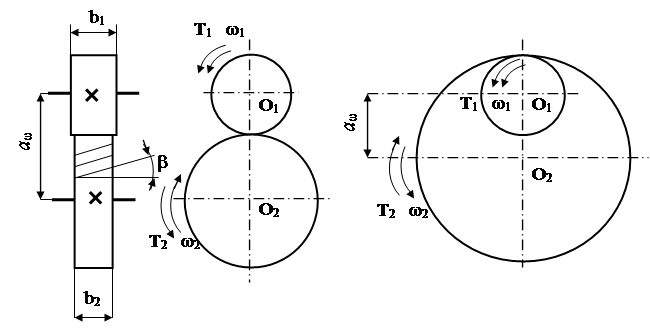
3 Расчет червячных передачЧервячные передачи относятся к числу зубчато-винтовых, имеющих характерные черты зубчатых и винтовых передач. Червячные передачи применяют между перекрещивающимися осями валов для получения большого передаточного числа. Наибольшее распространение получили червячные передачи с цилиндрическими червяками (рисунок 5).
а) б) а- кинематические схемы; б – геометрические параметры Рисунок 5 – Червячная передача Исходные данные для расчета червячной передачи выбираются из кинематического расчета силового привода с соответствующих валов и вводятся новые обозначения: параметры для червяка обозначаются с индексом единица, а параметры для червячного колеса обозначаются с индексом два.
Угловая скорость:
Частота ращения:
Передаточное число:
3.1 Выбор материала червячной пары . Назначение упрочняющей обработки и определение допускаемых напряжений 3.1.1 Материал червячного колеса В большинстве случаев червячные колеса делают составными: зубчатый венец из бронзы, а центр – из чугуна или стали. При скорости скольжения Предварительно скорость скольжения определяем по формуле:
По таблице А.10 приложения принимаем материал для венца червячного колеса. Например, при скорости скольжения 5 м/с принимаем безоловянную бронзу БрАж–9-4л, отливка в землю. Допускаемое контактное напряжение:
Если в таблице А.10 нет значения
где
где
Во всех случаях Допускаемое напряжение изгиба:
где
где
Во всех случаях 3.1.2 Материал червяка Для выбранной бронзы принимаем соответствующий материал червяка: например Сталь 45 с закалкой до твердости HRC ≥ 45 с последующим шлифованием витков (таблица А.10 , А.11 приложения). 3.2 Определение размеров и параметров червячного зацепления 3.2.1 Число заходов червяка и число зубьев колеса Принимаем при u=8…14 Z1 =4; при u=16…30 Z1 =2; при u=30 и выше Z1 =1. Число зубьев червячного колеса составит:
3.2.2 Предварительно принимаем расчетные коэффициенты: 1) коэффициент нагрузки 2) коэффициент диаметра червяка определяем по формуле:
Полученное значение коэффициента диаметра червяка округляем до стандартного значения (таблица А.13 ). 3.2.3 Определяем минимальное межосевое расстояние из условия контактной прочности:
где T2 – вращательный момент на колесе, в Н·мм. Расчетный модуль, мм:
3.2.4 Принимаем основные параметры передачи по ГОСТ 2144-76 (таблица А.12 , А.13 приложения) aω = , m = , q = . Если принятые параметры передачи и u=Z2 /Z1 не совпали со стандартными значениями по таблице А.12 , то передачу следует выполнять со смещением. Коэффициент смещения:
Коэффициент смещения должен быть в пределах -1≤X≤1. Если это условие не выполняется, то либо увеличивают, либо уменьшают параметры передачи не выходя за пределы рекомендуемых. Если это не дает должного эффекта, то назначают другие материалы и расчет повторяют. 3.2.5 Определяем основные геометрические размеры передачи Диаметры делительных окружностей, мм:
Диаметры начальных окружностей, мм:
Диаметры окружностей выступов, мм:
Диаметры окружностей впадин, мм:
Наибольший диаметр червячного колеса, мм:
Длина нарезной части червяка, мм:
Ширина венца червячного колеса, мм: b2 ≤0,75da1 Значения b1 и b2 округляют до целых, принимая из ряда предпочтительных чисел. Угол подъема винтовой линии:
3.3 Проверочные расчеты передачи 3.3.1 Проверяем условие прочности по контактным напряжениям Окружная скорость червяка, м/с:
Скорость скольжения, м/с:
Назначаем степени точности изготовления (таблица А.19 приложения). Уточняем коэффициент нагрузки:
где Кβ - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:
x – коэффициент, зависящий от характера изменений нагрузки, x
=1,0 ( x =0,6 – при переменной нагрузке; Kv - коэффициент динамичности (таблица А.15 приложения). Проверяем условие прочности:
Допускается недогрузка 10% и перегрузка 5%. Если условие прочности не выполняется, то назначают другие параметры или материалы червячной передачи и расчет повторяют. 3.3.2 Проверяем условие прочности зубьев червячного колеса по напряжениям изгиба Приведенное число зубьев червячного колеса:
Определяем коэффициент формы зуба Проверяем условие прочности:
Если условие прочности не выполняется, то назначают другие материалы и расчет повторяют. 3.4 Определение сил, действующих в зацеплении, и КПД передачи В червячной передаче сила нормального давления раскладывается на три составляющие: окружную, радиальную и осевую силы (рисунок 6).
Рисунок 6 Окружная сила на червяке равна осевой силе на колесе:
Окружная сила на червячном колесе равна осевой силе на червяке:
Радиальные силы на червяке и червячном колесе:
где α=200 – угол зацепления. Силы нормального давления:
КПД передачи с учетом потерь на разбрызгивание и перемешивание масла:
где 3.5 Тепловой расчет и охлаждение червячных передач Червячные передачи работают с большим тепловыделением. Тепловой расчет проводят на основе теплового баланса – количество теплоты, выделяющееся в червячной передаче, должно отводится свободной поверхностью корпуса передачи и фланцем крепления к фундаментной плите или раме. По тепловому балансу определяют рабочую температуру масла tм , которая не должна превышать максимально допустимую величину: [tм ] =80…95о С. Температура масла:
где tо =20 о С - температура окружающего воздуха; Р1 – мощность на червяке принимается из кинематического расчета силового привода или определяется как Р1 =Т1 ·ω1 /1000, Вт; η – КПД передачи; А – поверхность теплоотдачи корпуса передачи, в которую включается 50% поверхности ребер, м2 :
а ω - межосевое расстояние, мм; Кт – коэффициент теплоотдачи, равный 11…13 Вт/(м2 ·о С) при отсутствии циркуляции воздуха, 15…18 Вт/(м2 ·о С) при наличии хорошей циркуляции воздуха, 20…30 Вт/(м2 ·о С) при искусственном обдуве стенок редуктора; Ψ – коэффициент, учитывающий теплоотвод в фундаментную плиту или раму, принимается от 0,15…0,25. Список использованных источников1. Дунаев П.Ф., Леликов О.П. Детали машин. Курсовое проектирование. – М.: Высшая школа, 1984. – 336 с. 2. Зубчатые передачи: Справочник. Под. Ред. Е.Г. Гинзбурга. –Л.: Машиностроение, 1980. – 416 с. 3. Курсовое проектирование деталей машин. Под ред. Кудрявцева В.Н. – М.: Машиностроение, 1984. – 400 с. 4. Курсовое проектирование деталей машин. Под ред. Чернавского С.А. – М.: Машиностроение, 1979. – 350 с. 5. Расчет деталей машин на ЭВМ. Под ред. Д.Н. Решетова и С.А. Шувалова. – М.: Высшая школа, 1985. – 368 с. 6. Чернавский С.А., Снесарев Г.А., Козинцев Б.С. и др. Проектирование механических передач. – М.: Машиностроение, 1984 – 560 с. Приложение А(справочное) Таблица А.1 - Механические свойства сталей
Таблица А.2
- Межосевое расстояние (СТ СЭВ 229-75) (мм)
Таблица А.3
- Модуль
Таблица А.4 - Значения коэффициента КНα
Таблица А.5
- Значения коэффициента
Таблица А.6
- Значения коэффициента
Таблица А.7
- Значения коэффициента
Таблица А.8
- Значения коэффициента
Таблица А.9
- Значения коэффициента
Таблица А.10 - Материалы для червяков и червячных колес
Таблица А.11 - Механические характеристики для материалов червячных колес, МПа
Таблица А.12 - Основные параметры червячных передач (ГОСТ 2144-76)
Таблица А.13 - Сочетание m и q (ГОСТ 2144-76)
Таблица А.14
- Коэффициент деформации червяка
Таблица А.15
- Значения коэффициента
Таблица А.16
- Коэффициенты формы зуба
Таблица А.17
- Значения коэффициентов трения
Таблица А.18 - Предельные окружные скорости для силовых передач, м/с
Таблица А.19 - Допустимые скорости и области применения червячных передач
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 .
. ,
, ,
,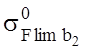 - предел выносливости при базовом числе циклов переменных напряжений
- предел выносливости при базовом числе циклов переменных напряжений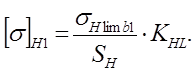


 ,
, мм,
мм,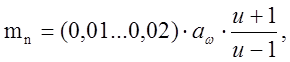


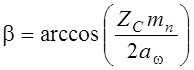 , (вычисляют с точностью до 4 знака).
, (вычисляют с точностью до 4 знака). ,
,

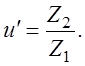
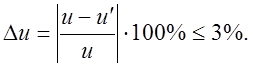

 - для внешнего зацепления;
- для внешнего зацепления; - для внутреннего зацепления.
- для внутреннего зацепления.
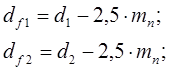
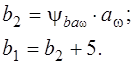




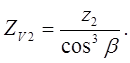


 , подставив параметры шестерни или зубчатого колеса в формулу вычисления напряжений изгиба:
, подставив параметры шестерни или зубчатого колеса в формулу вычисления напряжений изгиба: 



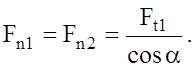

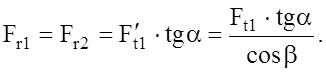


 по ГОСТ 12289 -76.
по ГОСТ 12289 -76.
 .
.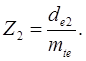









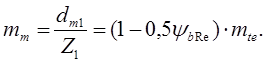


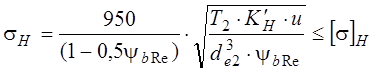 .
.







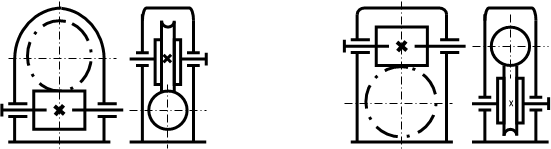

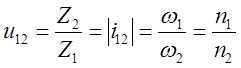
 , м/с.
, м/с.
 ,
,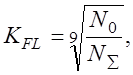
 мм,
мм,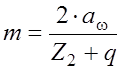 .
. .
.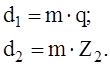


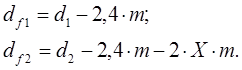
 .
.

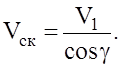
 ,
,
 .
.





 ,
,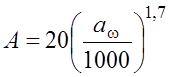 ,
,
