| Симетричні нерозгалужені трифазні кола синусоїдного струму
1.
Трифазний генератор
Трифазний генератор має дві основні частини: статор і ротор. На статорі розміщуються три самостійні обмотки, осі яких зсунуті одна щодо іншої в просторі на 120° (рис.4.1).
Разом з ротором обертається створене його струмом магнітне поле й у кожній обмотці наводиться е.р.с. Оскільки е.р.с. досягає максимального значення, коли осі обмотки і полюсів ротора збігаються, то зсув за фазою між трьома е.р.с. становить 120°. Окремі обмотки генератора одержали назву фаз
, а сам генератор за кількістю фаз називається трифазним
.
Аналітичні вирази миттєвих значень е.р.с.
окремих фаз будуть мати при цьому такий вигляд:
 ; ;
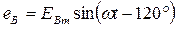 ; ;
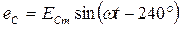 . .
Приклад
Діюче значення фазної е.р.с. дорівнює 220 В
. Записати миттєві значення фазних е.р.с., прийнявши y
еА
= 0
.
Рішення.
1. Максимальне значення фазної е.р.с.:
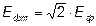 ; ;
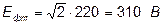 . .
2. Миттєві значення фазних е.р.с.:
еА
= 310 sіnw
t
;
еB
= 310 sіn(w
t
– 120°);
еC
= 310 sіn(w
t
– 240°).
Побудуємо вектори е.р.с. на площині, осі якої зсунемо на 90° проти годинникової стрілки.
Система трьох е.р.с., однакових за величиною і зсунутих за фазою одна щодо іншої на 120°, називається симетричною трифазною системою е.р.с.
Сума миттєвих значень фазних е.р.с. у будь-який момент часу дорівнює нулю, що видно з векторної діаграми (рис.4.3).
2. Трифазні системи
Розрахункова схема окремої фази генератора (наприклад, фази А
) має вигляд, зображений на рис.4.4. Але частіше її показують так, як зображено на рис.4.5. На цих схемах r
, xА
, 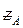 – відповідно активний, реактивний і повний опори обмотки.
– відповідно активний, реактивний і повний опори обмотки.
Кожну фазу (обмотку) трифазного генератора можна з'єднати з окремим споживачем електричної енергії (фазою навантаження), як показано на рис.4.6. У цьому випадку створюється незв'язана трифазна система
з трьома самостійними колами і шістьма проводами. Така система неекономічна і тому не знайшла застосування.
Три фази генератора або три фази навантаження можна з'єднати за схемою зірки
, при цьому однойменні затиски фаз генератора або фаз навантаження поєднуються в один вузол (рис.4.7).
Якщо фази генератора і навантаження, які з'єднані за схемою зірки, поєднати між собою, то створиться зв'язана трифазна чотирипровідна система
(рис.4.8).
Три проводи, що з'єднують початки фаз генератора і навантаження, називаються лінійними
, а четвертий, який з'єднує вузли схеми генератора і схеми навантаження, називається нульовим
(нейтральним
) проводом. Відповідно струм, що проходить по лінійному проводу, називається лінійним
струмом, а по нульовому (нейтральному) проводу – нульовим
(нейтральним
) струмом.
Відповідно до першого закону Кірхгофа
iN
=
iА
+
iB
+
iC
.
Три фази генератора або три фази навантаження можна з'єднати за схемою трикутника
: кінець першої фази з'єднується з початком другої і так далі (рис.4.9).
Якщо фази генератора і навантаження, які з'єднані за схемою трикутника, поєднати між собою, то створиться зв'язана трифазна трипровідна система
(рис.4.10).
Можна також створити зв'язані трифазні трипровідні системи зі схемами з'єднання фаз генератора і навантаження: зірка – зірка
, зірка – трикутник
, трикутник – зірка
.
3. З'єднання фаз генератора зіркою
Складемо розрахункову схему генератора, фази якого з'єднані зіркою, у випадку, коли генератор не навантажений, тобто працює на холостому ході (рис.4.11).
Приймемо, що потенціал точки 0 дорівнює нулю, і знайдемо потенціали точок А
, В
і С
:
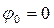 ;
;
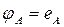 ;
;
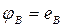 ;
;
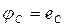 .
.
Різниця потенціалів на затисках фази генератора називається фазною напругою
. Знайдемо миттєві значення фазних напруг генератора:
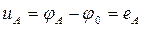 ;
;
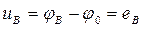 ;
;
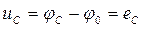 .
.
Різниця потенціалів на вихідних затисках генератора називається лінійною напругою
. Знайдемо миттєві значення лінійних напруг генератора:
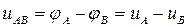 ;
;
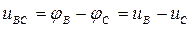 ;
;
 .
.
Побудуємо векторну діаграму фазних і лінійних напруг генератора (для діючих значень) на площині (рис.4.12).
Запишемо миттєві значення фазних і лінійних напруг генератора:
uА
= Uфm
sіnw
t
;
uВ
= Uфт
sіn(w
t
– 120°);
uС
= Uфт
sіn(w
t
– 240°);
uАB
= Uлm
sіn(w
t
+ 30°);
uBC
= Uлт
sіn(w
t
– 90°);
uCA
= Uлт
sіn(w
t
– 210°).
де Uфm
і Uлm
– максимальні (амплітудні) значення відповідно фазних і лінійних напруг генератора, В
.
Встановимо зв'язок між діючими значеннями фазних (Uф
) і лінійних (Uл
) напруг генератора, для чого розглянемо трикутник напруг (рис.4.13), який одержано з векторної діаграми.
З трикутника напруг знаходимо:
Uл
= 2Uф
cos 30° = 2Uф
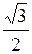 = =  Uф
. Uф
.
Приклад
Записати миттєві значення фазних і лінійних напруг генератора на холостому ході, якщо діюче значення фазної напруги дорівнює 220 В
і y
uА
= 0
.
Рішення.
1. Максимальне значення фазної напруги:
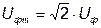 ; ;
 . .
2. Миттєві значення фазних напруг:
uА
=
310 sіnw
t
;
uВ
=
310 sіn(w
t
– 120°) ;
uС
=
310 sіn(w
t
– 240°) .
3. Максимальне значення лінійної напруги:
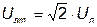 ; ;
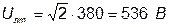 . .
4. Миттєві значення лінійних напруг:
uАB
=
536 sіn(w
t
+ 30°) ;
uBC
=
536 sіn(w
t
– 90°) ;
uCA
=
536 sіn(w
t
– 210°) .
Складемо розрахункову схему генератора, фази якого з'єднані зіркою, у випадку, коли генератор навантажений (рис.4.14).
Введемо поняття фазного струму
, під яким будемо розуміти струм, що проходить по фазі генератора. При з'єднанні обмоток генератора зіркою фазний струм дорівнює лінійному струму, тобто
Iф
= Iл
.
4. З'єднання фаз навантаження трикутником
трифазний генератор коло потужність
Складемо розрахункову схему при з'єднанні навантаження трикутником (рис.4.15). При цьому:
i
А
, iВ
, iС
– лінійні струми навантаження, А
;
iaв
, ibc
, ica
– фазні струми навантаження, А
;
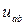 ,
, 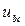 ,
, 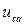 – лінійні (фазні) напруги навантаження, В
.
– лінійні (фазні) напруги навантаження, В
.
Як видно з розрахункової схеми, фазна напруга навантаження дорівнює лінійній напрузі навантаження, тобто
Uф
= Uл
.
За першим законом Кірхгофа знайдемо лінійні струми через фазні:
iА
= iab
– ica
;
iВ
= ibc
– iab
;
iС
= ica
– ibc
.
Встановимо зв'язок між діючими значеннями фазних (Iф
) і лінійних (Iл
) струмів навантаження при з'єднанні його фаз трикутником, для чого розглянемо трикутник струмів (рис.4.17), який одержано з векторної діаграми.
З трикутника струмів знаходимо:
Iл
= 2 Iф
cos 30° = 2 Iф
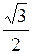 = = 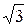 Iф
. Iф
.
5. Потужності трифазного кола
Кожна фаза трифазного навантаження споживає активну, реактивну і повну потужності. При симетричному навантаженні та схемі з'єднання фаз навантаження зіркою ці потужності в кожній фазі можна розрахувати в такий спосіб:
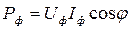 ; ;
 ; ;
 . .
Потужності, які споживають три фази навантаження, можна розрахувати, помноживши на кількість фаз навантаження (тобто на три) потужності, які споживає одна фаза:
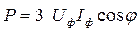 ; ;
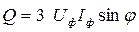 ; ;
 . .
Визначимо ці потужності через лінійні напруги і струми:
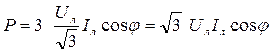 ; ;
 ; ;
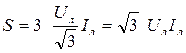 . .
При з'єднанні фаз навантаження трикутником вирази (4.28) і (4.29) справедливі, тільки в цих виразах будуть свої фазні струми і напруги. Визначимо ці потужності через лінійні напруги і струми:
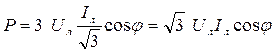 ; ;
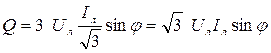 ; ;
 . .
Таким чином, потужності, які споживає трифазне навантаження (незалежно від схеми його з'єднання), можна розрахувати в такий спосіб:
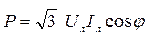 ; ;
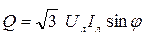 ; ;
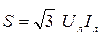 . .
6. Розрахунок нерозгалужених трифазних кіл синусоїдного струму
Розглянемо розрахункову схему трифазного трипровідного електричного кола, яке складається з ідеального генератора, з'єднаного зіркою, ідеальної лінії електропередачі, навантаження, з'єднаного зіркою (рис.4.18).
Нехай задано діюче значення електрорушійної сили Е
в фазі симетричного генератора і повні опори фаз навантаження
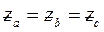 ,
,
а також коефіцієнти потужності фаз навантаження
cos j
а
=
cos j
b
=
cos j
с
=
cos j
.
Потрібно розрахувати діючі значення фазних і лінійних сил струмів генератора і навантаження, фазних і лінійних напруг генератора і навантаження, а також потужності, які віддаються генератором і споживаються навантаженням.
Алгоритм розрахунку наступний:
1.
Складаємо розрахункову схему однієї фази кола
.
Приймаємо, що потенціал точки 0 дорівнює нулю. Можна довести, що при симетричному режимі роботи кола потенціал точки 0’ також дорівнює нулю.
Тому можна з'єднати точки 0 і 0’, від чого режим роботи кола не зміниться.
Виділяємо одну фазу кола (рис.4.19).
2.
Визначаємо діючі значення сил струмів
.
У даному випадку фазний струм генератора дорівнює лінійному струму і дорівнює фазному струму навантаження. Наприклад, для фази А
він дорівнює:
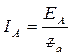 . .
Інші струми Iв
і Iс
дорівнюють струму Iа
.
3.
Визначаємо діючі значення фазних напруг
.
У даному випадку фазні напруги генератора дорівнюють фазним напругам навантаження. Наприклад, для фази а
воно дорівнює:
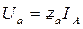 . .
Інші напруги Uа
, Uв
, Uс
, Ub
, Uс
дорівнюють Uа
.
4. Визначаємо діючі значення
лінійних напруг
.
У даному випадку лінійні напруги генератора дорівнюють лінійним напругам навантаження. Наприклад:
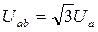 . .
Інші напруги Uав
, Uвс
, Uса
, Ubс
, Uса
дорівнюють Uаb
.
5. Визначаємо активну потужність
.
У даному випадку активна потужність, яка віддається генератором, дорівнює активної потужності, яку споживає навантаження:
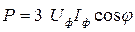
 , ,
де Uф
і Uл
– відповідно фазна і лінійна напруги, В
;
Iф
і Iл
– відповідно фазний і лінійний струми, А
.
6. Визначаємо реактивну потужність
.
У даному випадку реактивна потужність, яка віддається генератором, дорівнює реактивної потужності, яку споживає навантаження:
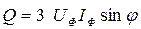
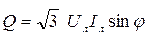 . .
7. Визначаємо повну потужність
.
У даному випадку повна потужність, яка віддається генератором, дорівнює повній потужності, яку споживає навантаження:
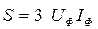
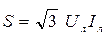 . .
Приклад
Трифазне симетричне навантаження одержує живлення від трифазного симетричного генератора за допомогою ідеальної лінії електропередачі. Генератор з'єднаний зіркою, навантаження з'єднане зіркою, лінія електропередачі трипровідна. Активний опір фази навантаження дорівнює 12 Ом
, індуктивний опір фази навантаження дорівнює 16 Ом
. Діюче значення е.р.с. у фазі генератора дорівнює 300 В
.
Розрахувати дане трифазне електричне коло.
Рішення.
1. Розрахункова схема кола приведена на рис.4.18, а для однієї фази – на рис.4.19.
2. Визначаємо повні опори навантаження:
 . .
3. Визначаємо діючі значення фазних і лінійних сил струмів генератора і навантаження:
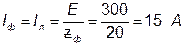 . .
4. Визначаємо діючі значення фазних напруг генератора і навантаження:
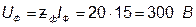 .
.
5. Визначаємо діючі значення лінійних напруг генератора і навантаження:
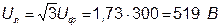 .
.
6. Визначаємо кут зсуву фаз навантаження:
 . .
7. Визначаємо активну потужність, яка віддається генератором і споживається навантаженням:
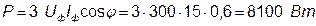 . .
8. Визначаємо реактивну потужність генератора і навантаження:
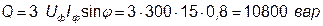 . .
9. Визначаємо повну потужність, яка віддається генератором і споживається навантаженням:
 . .
7. Переключення навантаження із зірки на трикутник
Одержимо основні співвідношення між струмами, а також між потужностями, при переключенні схеми з'єднання фаз навантаження зіркою на схему трикутника (рис.4.20).
При з'єднанні фаз навантаження зіркою лінійний (фазний) струм дорівнює:
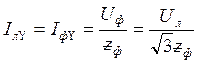 . .
Знаходимо потужності при з'єднанні фаз навантаження зіркою:
P
Y
= 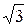 Uл
Iл
cos φ
= Uл
Iл
cos φ
= 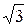 Uл Uл
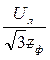 cos φ
= cos φ
=  cos φ
; cos φ
;
Q
Y
=  sin φ
; sin φ
;
S
Y
=  . .
При з'єднанні фаз навантаження трикутником лінійний струм більше фазного в 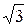 раз: раз:
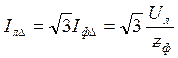 . .
Знаходимо потужності при з'єднанні фаз навантаження трикутником:
P
Δ
= 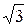 Uл
Iл
cos φ
= Uл
Iл
cos φ
= 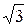 Uл Uл
 cos φ
= 3 cos φ
= 3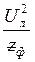 cos φ
; cos φ
;
Q
Δ
= 3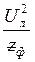 sin φ
; sin φ
;
S
Δ
= 3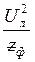 . .
Співвідношення між струмами дорівнює:
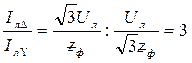 . .
Знайдемо співвідношення між потужностями:
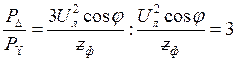 . .
Аналогічно:
 ; ;  . .
Таким чином, при переключенні фаз навантаження зі схеми з'єднання зіркою на схему трикутника лінійні струми і потужності, які споживає навантаження, збільшуються в три
рази.
|