| ГОУ ВПО «Башкирская академия государственной службы и управления при Президенте Республики Башкортостан»
Кафедра экономической теории и экономической политики
Контрольная работа по курсу
СТАТИСТИКА
Тема
1. Средняя величина в статистике, ее сущность и условия применения. Виды и формы средних.
2. Статистическое изучение динамики прибыли и
рентабельности.
Уфа – 2008
Содержание.
|
|
стр.
|
| Введение
|
3
|
| Часть 1.
Средняя величина в статистике, ее сущность и условия применения. Виды и формы средних величин.
1.1. Сущность средней величины.
1.2. Условия применения средних величин.
1.3. Виды средних величин.
|
4
4
5
7
|
| Часть 2.
Статистическое изучение динамики прибыли и рентабельности.
2.1. Анализ динамики прибыли.
2.2. Анализ динамики рентабельности.
|
17
17
23
|
| Заключение
|
31
|
| Список использованной литературы
|
32
|
Введение.
Данная контрольная работа состоит из двух частей – теоретической и практической. В теоретической части будет подробно рассмотрена такая важная статистическая категория как средняя величина с целью выявления её сущности и условий применения, а также выделения видов средних и способов их расчёта.
Практическая часть посвящена анализу динамики важнейших показателей работы любого предприятия – прибыли и рентабельности с целью выделения основных факторов, влияющих на изменение этих показателей.
Прибыль является основным показателем эффективности деятельности предприятия. Полученная прибыль используется на выполнение обязательств перед государством и на ведение производственно-хозяйственной деятельности. Поэтому важно оценить источники ее формирования, резервы роста, влияние различных факторов на ее величину и проводить ее детальный анализ, так как абсолютная величина в недостаточной мере характеризует экономическую эффективность работы предприятия.
Нестабильность рыночных отношений, жесткая кредитная политика, несовершенство налоговой системы, постоянно меняющиеся нормативные акты – те условия, которые в настоящее время характеризуют экономическую ситуацию в стране. И, совершенно очевидно, что эти факторы крайне неблагоприятно влияют на промышленно-производственные предприятия, так как любое предприятие – это долгосрочная программа, рассчитанная на определенные капиталовложения. Все вышеуказанное можно смело отнести и к рентабельности, поскольку прибыль и рентабельность тесно взаимосвязаны, нуждаются в подробном анализе и изучении.
Часть 1. Средняя величина в статистике, ее сущность и условия применения. Виды и формы средних.
Статистика, как известно, изучает массовые социально-экономические явления. Каждое из этих явлений может иметь различное количественное выражение одного и того же признака. Например, заработная плата одной и той же профессии рабочих или цены на рынке на один и тот же товар и т.д. Средние величины характеризуют качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.
Для изучения какой-либо совокупности по варьирующим (количественно изменяющимся) признакам статистика использует средние величины.
1.1. Сущность средней величины.
Средняя величина - это обобщающая количественная характеристика совокупности однотипных явлений по одному варьирующему признаку. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.
Важнейшее свойство средней величины заключается в том, что она представляет значение определенного признака во всей совокупности одним числом, несмотря на количественные различия его у отдельных единиц совокупности, и выражает то общее, что присуще всем единицам изучаемой совокупности. Таким образом, через характеристику единицы совокупности она характеризует всю совокупность в целом.
Средние величины связаны с законом больших чисел. Суть этой связи заключается в том, что при осреднении случайные отклонения индивидуальных величин в силу действия закона больших чисел взаимопогашаются и в средней выявляется основная тенденция развития, необходимость, закономерность. Средние величины позволяют сравнивать показатели, относящиеся к совокупностям с различной численностью единиц.
В современных условиях развития рыночных отношений в экономике средние служат инструментом изучения объективных закономерностей социально-экономических явлений. Однако в экономическом анализе нельзя ограничиваться лишь средними показателями, так как за общими благоприятными средними могут скрываться и крупные серьезные недостатки в деятельности отдельных хозяйствующих субъектов, и ростки нового, прогрессивного. Так,
например, распределение населения по доходу позволяет выявлять формирование новых социальных групп. Поэтому наряду со средними статистическими данными необходимо учитывать особенности отдельных единиц совокупности.
Средняя величина являются равнодействующей всех факторов, оказывающих влияние на изучаемое явление. То есть, при расчете средних величин взаимопогашаются влияние случайных (пертурбационных, индивидуальных) факторов и, таким образом, возможно определение закономерности, присущей исследуемому явлению. Адольф Кетле подчеркивал, что значение метода средних величин состоит в возможности перехода от единичного к общему, от случайного к закономерному, и существование средних величин является категорией объективной действительности.
1.2.Условия применения средних величин.
Важнейшим условием научного использования средних величин в статистическом анализе общественных явлений является однородность совокупности, для которой исчисляется средняя. Качественная однородность совокупности определяется на основе всестороннего теоретического анализа сущности явления. Так, например, при исчислении средней урожайности требуется, чтобы исходные данные относились к одной и той же культуре (средняя урожайность пшеницы) или группе культур (средняя урожайность зерновых). Нельзя вычислять среднюю для разнородных культур. Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления, фальсифицировать его, или будут бессмысленными.
Однако нельзя сводить роль средних только к характеристике типических значений признаков в однородных по данному признаку совокупностях. На практике современная статистика использует так называемые системные средние,
обобщающие неоднородные явления (характеристики государства, единой народнохозяйственной системы: например, средний национальный доход на душу населения, средняя урожайность зерновых по всей стране, средний реальный доход на душу населения, среднее потребление продуктов питания на душу населения, производительность общественного труда).
Если исследуемое явление не является однородным, то его разбивают на группы, содержащие только однородные элементы. Для такого явления рассчитываются сначала средние по группам, которые называются групповые средние, – они будут выражать наиболее типичную величину явления в каждой группе. Затем рассчитывается для всех элементов общая средняя величина, характеризующая явление в целом, – она рассчитывается как средняя из групповых средних, взвешенных по числу элементов совокупности, включенных в каждую группу
Еще одним важным условием применения средних величин в анализе является достаточное количество единиц в совокупности, по которой рассчитывается среднее значение признака. Достаточность анализируемых единиц обеспечивается корректным определением границ исследуемой совокупности, т.е. закладывается еще на начальном этапе статистического исследования. Данное условие становится решающим при применении выборочного наблюдения, когда необходимо обеспечить репрезентативность выборки.
Определение максимального и минимального значения признака в изучаемой совокупности также является условием применения средней величины в анализе. В случае больших отклонений между крайними значениями и средней, необходимо проверить принадлежность экстремумов к исследуемой совокупности. Если сильная изменчивость признака вызвана случайными, кратковременными факторами, то, возможно, крайние значения не характерны для совокупности. Следовательно, их следует исключить из анализа, т.к. они оказывают влияние на размер средней величины.
1.3.Виды средних величин.
В статистике выделяют несколько видов средних величин:
1. По наличию признака-веса:
а) невзвешенная средняя величина;
б) взвешенная средняя величина.
2. По форме расчета:
а) средняя арифметическая величина;
б) средняя гармоническая величина;
в) средняя геометрическая величина;
г) средняя квадратическая, кубическая и т.д. величины.
3. По охвату совокупности:
а) групповая средняя величина;
б) общая средняя величина.
Средние величины различаются в зависимости от учета признаков, влияющих на осредняемую величину:
Если средняя величина рассчитывается для признака, без учета влияния на него каких-либо других признаков, то такая средняя величина называется средней невзвешенной или простой средней.
Если имеются сведения о влиянии на осредняемый признак некоторого признака или нескольких признаков, которые необходимо учесть при расчете для корректного расчета средней величины, то рассчитывается средняя взвешенная.
По форме расчета выделяют несколько видов средних величин, которые образованы из единой степенной средней величины. Степенная средняя величина имеет форму:
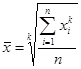 , ,
где 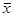 - среднее значение исследуемого явления; - среднее значение исследуемого явления;
k – показатель степени средней;
x – текущее значение (вариант) осредняемого признака;
i –i-тый элемент совокупности;
n – число наблюдений (число единиц совокупности).
При разных показателях степени k получаем, соответственно, различные по форме средние величины. (Табл. 1):
Таблица 1
| Степень
средней величины (k)
|
Название
средней
|
| -1
|
гармоническая
|
| 0
|
геометрическая
|
| 1
|
арифметическая
|
| 2
|
квадратическая
|
| 3
|
кубическая
|
Выбор формы средней обусловлен исходным соотношением, суть которого приводилась выше. Существует порядок расчета средней величины:
1. Определение исходного соотношения для исследуемого показателя.
2. Определение недостающих данных для расчета исходного соотношения.
3. Расчет средней величины.
Рассмотрим некоторые виды средних, которые наиболее часто используются в статистике. Для этого введем следующие понятия и обозначения:
Признак, по которому находится средняя, называемый осредняемым признаком, обозначим буквой "х"
Значения признака, которые встречаются у группы единиц или отдельных единиц совокупности (не повторяясь) называются вариантами признака и обозначаются через x1
, x2
, x3
и т.д. Средняя величина этих значений обозначается через " " .
Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.
Отдельные значения признака называют вариантами и обозначают через х (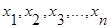 ); число единиц совокупности обозначают через n, среднее значение признака - через ); число единиц совокупности обозначают через n, среднее значение признака - через 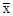 . Следовательно, средняя арифметическая простая равна: . Следовательно, средняя арифметическая простая равна:
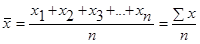
Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.
Средняя арифметическая взвешенная вычисляется по формуле 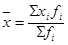 , где fi
- частота повторения i-ых вариантов признака, называемая весом. Таким образом, средняя арифметическая взвешенная равна сумме взвешенных вариантов признака, деленная на сумму весов. , где fi
- частота повторения i-ых вариантов признака, называемая весом. Таким образом, средняя арифметическая взвешенная равна сумме взвешенных вариантов признака, деленная на сумму весов. 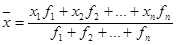 Она применяется в тех случаях, когда каждая варианта признака встречается несколько (неравное) число раз. Она применяется в тех случаях, когда каждая варианта признака встречается несколько (неравное) число раз.
Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами. В таких рядах условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы - величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше.
При расчете средней по интервальному вариационному ряду
необходимо сначала найти середину интервалов.
В практике экономической статистики иногда приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним). В таких случаях за варианты (х) принимаются групповые или частные средние, на основании которых исчисляется общая средняя как обычная средняя арифметическая взвешенная.
Средняя арифметическая обладает рядом свойств:
1. От уменьшения или увеличения частот каждого значения признака х в п раз величина средней арифметической не изменится.
Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.
2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:
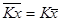
3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:
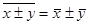
4. Если х = с, где с - постоянная величина, то 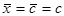 . .
5. Сумма отклонений значений признака Х от средней арифметической х равна нулю:
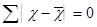
Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной. Применяется она тогда, когда необходимые веса (fi
) в исходных данных не заданы непосредственно, а входят сомножителем в одни из имеющихся показателей.
Средняя гармоническая простая рассчитывается по формуле 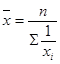 , ,
т.е. это обратная величина средней арифметической простой из обратных значений признака.
Например, бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.
На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:
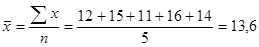
Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением:
все затраченное время
Среднее время, затраченное = --------------------------------------
на одну деталь число деталей
Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:
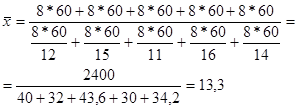
Это же решение можно представить иначе:
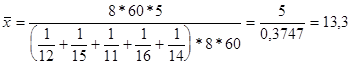
Таким образом, формула для расчета средней гармонической простой будет иметь вид:
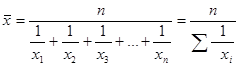
Средняя гармоническая взвешенная:
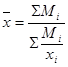 , где Mi
=xi
*fi
(по содержанию). , где Mi
=xi
*fi
(по содержанию).
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к
предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическая исчисляется извлечением корня степени и из произведений отдельных значений — вариантов признака х:
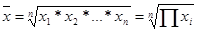
где n — число вариантов; П — знак произведения.
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.
В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая (например, для вычисления средней величины стороны и квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны и кубов).
Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
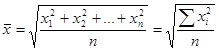 , ,
где x1
,x2
,…xn
- значения признака, n- их число.
Средняя квадратическая взвешенная:
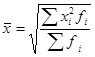 , ,
где f-веса.
Средняя кубическая простая является кубическим корнем из частного от деления суммы кубов отдельных значений признака на их число:
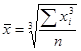 , ,
где x1
,x2
,…xn
- значения признака, n- их число.
Средняя кубическая взвешенная:
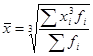 , ,
где f-веса.
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов x,
и из их отклонений от средней (х — 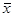 ) при расчете показателей вариации. ) при расчете показателей вариации.
Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней может быть средняя прогрессивная как одна из частных средних, вычисляемая не для всех, а только для "лучших" (например, для показателей выше или ниже сред- них индивидуальных).
Для характеристики структуры вариационных рядов применяются так называемые структурные средние. Наиболее часто используются в экономической практике мода и медиана.
Мода
– значение случайной величины встречающейся с наибольшей вероятностью. В дискретном вариационном ряду это вариант имеющий наибольшую частоту.
В дискретных вариационных рядах мода определяется по наибольшей частоте. Предположим товар А реализуют в городе 9 фирм по цене в рублях:
44; 43; 44; 45; 43; 46; 42; 46;43;
Так как чаще всего встречается цена 43 рубля, то она и будет модальной.
В интервальных вариационных рядах моду определяют приближенно по формуле
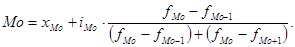 , ,
где 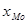 - начальное значение интервала, содержащего моду; - начальное значение интервала, содержащего моду;
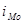 - величина модального интервала; - величина модального интервала;
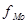 - частота модального интервала; - частота модального интервала;
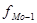 - частота интервала, предшествующего модальному; - частота интервала, предшествующего модальному;
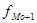 - частота интервала, следующего за модальным. - частота интервала, следующего за модальным.
Место нахождения модального интервала определяют по наибольшей частоте
Мода применяется для решения некоторых практических задач. Так, например, при изучении товарооборота рынка берется модальная цена, для изучения спроса на обувь, одежду используют модальные размеры обуви и одежды и др.
Медиана
- это численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда (построенного в порядке возрастания, либо убывания значения изучаемого признака). Медиану иногда называют серединной вариантой, т.к. она делит совокупность на две равные части.
В дискретных вариационных рядах с нечетным числом единиц совокупности - это конкретное численное значение в середине ряда. Так в группе студентов из 27 человек медианным будет рост у 14-го, если они выстроятся по росту. Если число единиц совокупности четное, то медианой будет средняя арифметическая из значений признака у двух средних членов ряда. Так, если в группе 26 человек, то медианным будет рост средний 13-го и 14-го студентов.
В интервальных вариационных рядах медиана определяется по формуле:
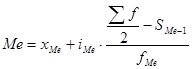 , где , где
x0
- нижняя гранича медианного интервала;
iMe
- величина медианного интервала;
Sme
-1
- сумма накопленных частот до медианного интервала;
fMe
- частота медианного интервала.
Cоотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если M0
<Me<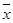 имеет место правосторонняя асимметрия. Если же имеет место правосторонняя асимметрия. Если же 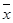 <Me<M0
- левосторонняя асимметрия ряда. Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду. <Me<M0
- левосторонняя асимметрия ряда. Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду.
Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.
Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.
Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части — квартели, на пять равных частей — квинтели, на десять частей — децели, на сто частей — перцентели.
Таковы основные виды средних величин широко применяемых в статистике
2. Статистическое изучение динамики прибыли и рентабельности.
Прибыль и рентабельность относятся к важнейшим показателям, характеризующим эффективность производственно-хозяйственной деятельности предприятия. Проведем анализ прибыли и рентабельности для ОАО «Башмебель»
2.1. Анализ динамики прибыли .
Более чем, какой либо другой показатель прибыль отражает результаты всех сторон деятельности предприятия. На ее величину влияет объем продукции, ее ассортимент, качество, уровень себестоимости, штрафы, неустойки и другие факторы.
Прибыль влияет на такой обобщающий показатель, как рентабельность, состояние собственных оборотных средств, платежеспособность и размеры поощрительных фондов.
Прибыль от реализации товарной продукции является результатом производственной деятельности и процесса обращения и занимает наибольший удельный вес в балансовой прибыли предприятия. Прибыль от реализации продукции состоит из двух частей:
1. Прибыль от реализации товарной продукции
Таблица 3.
Показатели для анализа прибыли от реализации товарной продукции
|
№ п/п
|
Наименование показателей
|
Значение показателей,
в тыс. руб
|
|
2006г.
|
2007г.
|
| По с/с и ценам 2005г.
|
По действ. ценам
|
| 1.
|
Производственная себестоимость
|
97005
|
100843
|
112515
|
| 2.
|
Коммерческие расходы
|
4329
|
4904
|
5885
|
| 3.
|
Полная себестоимость реализованной продукции
|
101334
|
105747
|
118400
|
| 4.
|
Выручка от реализации продукции (без НДС)
|
114761
|
122759
|
140118
|
| 5.
|
Прибыль
|
13427
|
17012
|
21718
|
Рассмотрим влияние каждого из перечисленных факторов.
1. Изменение цен на прибыль
DПцен
= Qр
ф
- Qр
пф
;
DПцен
140118-122759=17359тыс. руб.
За счет роста цен на реализованную продукцию прибыль взросла на 17359тыс. руб.
2. Изменение объема реализации товарной продукции
DПор
= Пп
C (Sр
пф
: Sр
п
) - Пп
;
DПор
= 13427*(105747/101334)-13427=585 тыс. руб.
В связи с ростом объема реализации в отчетном году прибыль увеличилась на 585тыс. руб.
3. Влияние сдвигов в структуре и ассортименте реализованной продукции.
DПстр
= Пп
C (Qр
пф
/ Qр
п
- Sр
пф
/ Sр
п
);
DПстр
= 13427*(122759/114761-105747/101334)=352 тыс. руб.
В связи с ростом в объеме реализации удельного веса более рентабельных изделий прибыль на предприятии возросла на 352тыс. руб.
4. Изменение производственной себестоимости реализованной продукции
DПпс/с
= Sр
ф
- Sр
пф
DПпс/с
= 112515-100843=11672 тыс. руб.
Увеличение производственной себестоимости в отчетном году за счет повышения цен на сырье и материалы привело к снижению прибыли на 11672 тыс. руб.
5. Изменение коммерческих расходов
DПкр
= Sр
ф
- Sр
пф
DПкр
= 5885-4904=981 тыс.руб.
В связи с увеличением коммерческих расходов в отчетном году, по сравнению с предыдущим годом прибыль уменьшилась на 981 тыс. руб.
6. Приращение производственной себестоимости за счет структурных сдвигов.
DПппс
= Sр
п
х Qр
пф
/ Qр
п
- Sр
пф
;
DПппс
= 97005**122759/114761-100843=2923тыс. руб.
Увеличение в объеме реализации удельного веса изделий, по которым производственная себестоимость снизилась, привело к повышению прибыли на 2923 тыс.руб.
7. Приращение коммерческих расходов за счет структурных сдвигов.
DПпкр
= Sр
п
х Qр
пф
/ Qр
п
- Sр
пф
;
DПпкр
= 4329*122759/114761-4904=-273 тыс. руб.
В связи с увеличением в объеме реализованной продукции изделий, по которым коммерческие расходы увеличились, прибыль снизилась на 273тыс.руб.
Суммарное влияние всех факторов, влияющих на изменение прибыли, равно величине отклонения прибыли от реализации товарной продукции двух смежных лет.
DПобщ
= DПцен
+ DПор
+ DПстр
+ DПпс/с
+ DПкр
+ DПппс
+ DПпкр
DПобщ
= 17359+585+352-11672-981+2923-273=8291 тыс.руб.
Балансовая прибыль характеризует конечные результаты всей производственно-хозяйственной деятельности и непромышленных хозяйственных объектов предприятия.
Формула хозяйственной прибыли:
Пбал = П реал + Ппр реал + Посн ф + ВР
ВР – внереализационные результаты – штрафы, пени, неустойки, полученные или уплаченные предприятием в отчетном году.
Анализ балансовой прибыли по сравнению с прошлым годом показывает влияние стоимости сырья, материалов, топлива и др. материально-технических ресурсов, изменение цен на реализацию продукции и методология расчета прибыли. Для того чтобы это влияние исключить, необходимо привести в сопоставимые условия сумму прибыли.
Таблица 4. Динамика роста прибыли.
| Наименование показателей
|
Значение показателей по отчету,
в тыс. руб
|
Темпы роста к предыдущему году
|
| 2006.
В действ. ценах
|
2007г.
|
| В действ. ценах
|
В ценах прошлого года,
|
В фактич. ценах,
%
|
В ценах прошлого года,
%
|
| Балансовая прибыль
|
13756
|
20677
|
16202
|
150
|
118
|
| Прибыль от реализации товарной продукции
|
13427
|
21718
|
17012
|
162
|
127
|
Таблица 5. Прибыли и убытки.
| Прибыль
|
Сумма, тыс.руб.
|
Убыток
|
Сумма, тыс.руб.
|
| 2006 г.
|
2007 г.
|
2006 г.
|
2007 г.
|
| От реализации продукции и услуг
|
13427
|
21718
|
От реализации продукции
|
31
|
84
|
| Пени полученные
|
101
|
19
|
Пени уплаченные
|
17
|
249
|
| От внереализационной деятельности
|
218
|
43
|
Прочие долги от ВД
|
84
|
798
|
| Прочие доходы
|
125
|
28
|
Чрезвычайные расходы
|
-
|
-
|
| Итого:
|
13871
|
21808
|
|
115
|
1131
|
| Балансовая прибыль
|
13756
|
20677
|
|
|
|
Данные таблицы 4 и 5 показывают, что в 2006 году балансовая прибыль превышала прибыль от реализации на 324тыс. руб.; в 2007 году прибыль от реализации была больше балансовой на 1041 тыс.руб. Такие изменения произошли в результате доходов и убытков полученных от внереализационной деятельности. В 2006 году эти доходы составили 4444тыс. руб., а в 2007году 90тыс. руб., в то же время убытки в 2007 году составили 1131тыс. руб., а в предыдущем году 115 тыс. руб.
Прибыль, полученная на предприятии, должна быть распределена по соответствующим направлениям: на уплату в бюджет, выплату налогов и т.д.
Рассмотрим подробно, по каким направлениям была распределена прибыль на предприятии, для этого воспользуемся приложением к балансу и формой «Справка к отчету о финансовых результатах и их использовании» и составим следующую аналитическую таблицу 6.
Таблица 6. Прибыль, остающаяся в распоряжении предприятия, в тыс. руб.
| № п/п
|
Наименование показателей
|
Отчет 2006г.
|
Отчет 2007г.
|
Отклонение (+, -)
|
| 1.
|
Прибыль балансовая
|
13756
|
20677
|
+6921
|
| 2.
|
Налогооблагаемая прибыль
|
11404
|
16899
|
+5495
|
| 3.
|
Налог на прибыль и иные платежи
|
3193
|
4901
|
+1708
|
| 4.
|
Прибыль, остающаяся в распоряжении предприятия
|
10563
|
15776
|
+5213
|
| 5.
|
Прибыль, направленная:
|
|
|
|
| |
а) в фонд накопления
|
5282
|
7888
|
+2603
|
| |
б) в фонд потребл.
|
4225
|
6310
|
+2085
|
| |
в) другие цели
|
1056
|
1578
|
+522
|
Для более полного представления финансового состояния предприятия в 2007 году рассмотрим фактическое использование прибыли в более подробном виде.
Таблица 7. Баланс доходов и расходов за 2007 год
| № п/п
|
Наименование показателей
|
Значение показателей тыс.руб.
|
% к итогу
|
| 1.
|
Прибыль балансовая, всего
|
20677
|
90,6
|
| |
В том числе:
|
|
|
| |
- от реализации продукции
|
21718
|
-
|
| |
- от внереализационной деятельности
|
-1041
|
-
|
| 2.
|
Амортизация
|
2134
|
9,4
|
| 3.
|
Привлеченные средства
|
-
|
-
|
| 4.
|
Итого доходы
|
22811
|
100
|
| 5.
|
Платежи в бюджет
|
4901
|
21,5
|
| 6.
|
Фонды накопления, всего
|
11600
|
50,8
|
| |
В том числе:
|
|
|
| |
- фонд капитальных вложений
|
10022
|
43,9
|
| |
- фонд средств социальной сферы
|
1578
|
6,9
|
| 7.
|
Фонды потребления, всего
|
6310
|
27,7
|
| |
В том числе:
|
|
|
| |
- оплата за лечение
|
798
|
3,5
|
| |
- возмещение стоимости путевок
|
570
|
2,5
|
| |
- материальная помощь
|
1597
|
7,0
|
| |
- содержание профкома
|
91
|
0,4
|
| |
- доплаты командированным
|
228
|
1,0
|
| |
- премии за выполнение особо важных заданий
|
730
|
3,2
|
| |
- ссуды работающим
|
958
|
4,2
|
| |
- штрафные санкции
|
456
|
2,0
|
| |
- расчеты с учредителями (дивиденды)
|
890
|
3,9
|
| |
Итого расходы:
|
22811
|
100
|
2.2. Анализ динамики рентабельности .
Анализ рентабельности предприятия включает:
- анализ рентабельности производства;
- анализ рентабельности реализации;
- анализ рентабельности важнейших видов продукции;
- анализ рентабельности предприятия.
Анализ рентабельности производства продукции дает возможность установить тот уровень рентабельности, с которым работало предприятие в отчетном году по выпуску продукции.
Рентабельность производства продукции (Рпр) определяется по формуле:
Рпр = (Птп/Sтп)х100%, где
Птп – прибыль от производства товарной продукции;
Sтп – себестоимость товарной продукции;
Птп = Qтп – Sтп, где
Qтп – объем товарной продукции в оптовых ценах предприятия.
Для анализа рентабельности производства составим таблицу.
Таблица 8. Динамика рентабельность производства продукции
| № п/п
|
Наименование показателей
|
Ед. изм.
|
Значение показателей
|
Отклонение (+, -)
|
| 2006г.
|
2007г.
|
| 1.
|
Товарная продукция предприятия в оптовых ценах
|
Тыс.руб.
|
115347
|
138962
|
+23615
|
| 2.
|
Полная себестоимость
|
Тыс.руб.
|
101851
|
117423
|
+15572
|
| 3.
|
Прибыль от производства товарной продукции
|
Тыс.руб.
|
13496
|
21539
|
+8043
|
| 4.
|
Рентабельность производства
|
%
|
13,25
|
18,34
|
+5,1
|
Из данных этой таблицы видно, что фактический уровень рентабельности производства в 2007 году выше, чем в 2006 году на 5,1%. Это объясняется тем, что за отчетный период произошло повышение прибыли и снижение затрат на 1 рубль товарной продукции.
По данным отчета о прибылях и убытках можно проанализировать динамику рентабельности продаж, а так же влияние факторов на изменение этого показателя (табл.9).
Таблица 9. Рентабельность продаж, в тыс. руб.
| № п/п
|
Наименование показателей
|
Значение показателей
|
Отклонение (+, -)
|
| 2005г.
|
2006г.
|
| 1.
|
Выручка от реализации за вычетом НДС (В)
|
66415
|
94564
|
+28149
|
| 2.
|
Производственная себестоимость (С)
|
53353
|
74365
|
+21012
|
| 3.
|
Коммерческие расходы (КР)
|
3132
|
3759
|
+627
|
| 4.
|
Управленческие расходы
|
6743
|
8867
|
+2124
|
| 5.
|
Рентабельность продаж
|
4,8%
|
8,0%
|
+3,2%
|
Рентабельность продаж (Рп) – это отношение суммы прибыли от продаж к объему реализованной продукции:
Рп = (В – С – КР – УР)/В*100% = Пр/В*100%
Из этой факторной модели следует, что на рентабельность продаж влияют те же факторы, что и на прибыль от продажи. Чтобы определить, как каждый фактор повлиял на рентабельность продаж, необходимо осуществить следующие расчеты.
В приводимых ниже формулах использованы следующие обозначения:
В1
и Во
– отчетная и базисная выручка;
С1
и Со
– отчетная и базисная себестоимость;
КР и КРо – отчетные и базисные коммерческие расходы;
УР и УРо – управленческие расходы в отчетном и базисном периодах.
1.Влияние изменения выручки от реализации на рентабельность продаж:
DРп
в
= [(В – Со
– КРо – УРо)/В – (Во – Со – КРо – УРо/Во)/Во]*100%
DРп
в
= [(140118-84797-4329-12208)/140118-(114761-84797-4329-12208)/114761]*100% = +16%
В связи с ростом выручки от реализации в отчетном году рентабельность
выросла на 16%.
2.Влияние изменения себестоимости продукции:
DРп
с
= [(В1
– С1
– КРо
– УРо
)/В1
– (В1
– Со
– КРо
– УРо
)/В1
]*100%
DРп
с
= [(140118-94522-4329-12208)/140118-(140118-84797-4329-12208)/140118]*100% = -6,94%
Повышение себестоимости продукции привело к снижению
рентабельности продаж на 6,94%.
3.Влияние изменения коммерческих расходов:
DРп
кр
= [(В1
– С1
– КР1
– УРо
)/В1
– (В1
– С1
– КРо
– УРо
)/В1
]*100%
DРп
кр
= [(140118-94522-5885-12208)/140118-(140118-94522-4329-12208)/140118 ]*100% = -1,11%
За счет роста коммерческих расходов рентабельность продаж снизилась
на 1,11%.
4. Влияние изменения управленческих расходов:
DРп
ур
= [(В1
– С1
– КР1
– УР1
)/В1
– (В1
– С1
– КР1
– УРо
)/В1
]*100%
DРп
ур
= [(140118-94522-5885-17993)/140118-(140118-94522-5885-12208)/140118]*100% = -4,15%
В связи с ростом управленческих расходов рентабельность продаж
снизилась на 4,15%.
Общее влияние всех факторов составит:
DРп
общ
= 16,0-6,94-1,11-4,15=3,8%
Рентабельность изделий, выпускаемых предприятием, оказывает существенное влияние, как на рентабельность производства, так и на рентабельность предприятия в целом.
Так, предприятие выпускает широкий ассортимент продукции, для анализа рентабельности изделий целесообразно рассмотреть основные виды продукции.
Для проведения анализа составим аналитическую таблицу 10.
| Наименование видов продукции
|
По отчету 2006г. и ценам 2007г.
|
По отчету 2007 г.
|
| Кол-во,
шт.
|
Товарная продукция
тыс. руб.
|
Себестоимость
продукции
тыс. руб.
|
Рентабельность продукции, %
|
Кол-во,
шт.
|
Товарная
продукция
тыс. руб.
|
Себестоимость
продукции
тыс. руб.
|
Рентабель
ность
продукции, %
|
| Стенка бытовая
|
1068
|
22437
|
19682
|
14,0
|
1851
|
43384
|
33681
|
19,9
|
| Шкаф – сушка
|
3458
|
10663
|
9395
|
13,5
|
3358
|
11443
|
9976
|
14,7
|
| Колонка
|
4381
|
15884
|
14297
|
11,1
|
3988
|
14575
|
18990
|
12,2
|
| Стол кухонн.
|
4502
|
13351
|
12260
|
8,9
|
4703
|
15221
|
13875
|
9,7
|
| Стол обеден.
|
9860
|
23156
|
19638
|
15,2
|
9902
|
27904
|
23429
|
19,1
|
| Тумба с ящиками
|
2058
|
6134
|
5531
|
10,9
|
2300
|
8281
|
7430
|
11,5
|
| Изделия деревообработки
|
-
|
15953
|
13957
|
14,3
|
-
|
16558
|
13833
|
19,7
|
| Прочая продукция
|
-
|
7769
|
7091
|
9,6
|
-
|
4596
|
4028
|
14,1
|
| Всего
|
25327
|
115347
|
101851
|
13,25
|
26102
|
138962
|
117423
|
18,3
|
Таблица 10. Рентабельность отдельных видов продукции
Уровень рентабельности изделия (Ри) был определен по формуле:
Ри = (Пи / С)*100%,где
Пи – прибыль по изделию, руб.;
Си – себестоимость изделия, руб.
Анализируя данные этой таблицы, приходим к выводу, что наименьшую рентабельность имеет производство столов кухонных (9,7%), а наибольшую – производство бытовых стенок (19,9%)
По рассчитанным выше показателям рентабельности нельзя судить об эффективности использования основных производственных фондов и оборотных средств. Поэтому, наряду с рассмотренными показателями рентабельности необходимо также проанализировать уровень рентабельности в целом, а именно, общей и расчетной.
Показатель общей рентабельности рассчитывается по формуле
РОБЩ.
= ПБАЛ
/ (ФОСН
+ ФОБ
), где
ПБАЛ
- балансовая прибыль по предприятию, тыс. руб.
ФОСН
- среднегодовая стоимость ОФП, тыс. руб.
ФОБ
- среднегодовая стоимость нормируемых оборотных средств, тыс. руб.
Проведя преобразование формулы, можно проанализировать зависимость уровня общей рентабельности от:
- размера прибыли на1 руб. реализованной продукции (ПБАЛ
\QР
)
- фондоемкости (1 / QР
) / ФОСН
- оборачиваемости оборотных средств 1 / QР
/ ФОБ
- РОБЩ.
= ПБАЛ
/ (ФОСН
+ ФОБ
) * 100 = (ПБАЛ
\QР
) / [(ФОСН
/ QР
) + (ФОБ
/ QР
)] * 100 ;
Для анализа влияния отдельных факторов на уровень общей рентабельности необходимо составить следующую таблицу.
Таблица 11. Исходные данные для анализа общей рентабельности.
| №
|
Наименование показателей
|
Един. изм.
|
Условное обозначение
|
Значение показателей
|
| Отчет 2006 г.
|
Отчет 2007 г.
|
| 1
|
Балансовая прибыль
|
Тыс. руб.
|
ПБАЛ
|
13756
|
20677
|
| 2
|
Объем реализованной продукции
|
Тыс. руб.
|
QP
|
114761
|
140118
|
| 3
|
Среднегодовая стоимость основных производственных фондов
|
Тыс. руб.
|
ФОСН
|
36793
|
37047
|
| 4
|
Средние остатки основных оборотных средств
|
Тыс. руб.
|
ФОБ
|
34396
|
39703
|
| 5
|
Фондоотдача основных производственных фондов
|
Руб. / руб.
|
QP
/ ФОСН
|
3,12
|
3,78
|
| 6
|
Фондоемкость
|
Руб. / руб.
|
ФОСН
/ QP
|
0,32
|
0,26
|
| 7
|
Количество оборотов нормируемых оборотных средств
|
Число оборотов
|
QP
/ ФОБ
|
3,34
|
3,53
|
| 8
|
Коэффициент закрепления оборотных средств
|
Доли единиц
|
ФОБ
/ QP
|
0,3
|
0,28
|
| 9
|
Прибыль на 1 руб. реализованной продукции
|
Руб. / руб.
|
ПБАЛ
/ QP
|
0,12
|
0,15
|
| 10
|
Уровень общей рентабельности
|
%
|
ПБАЛ
/ (ФОСН
+ ФОБ
) * 100
|
19,3
|
26,9
|
Для удобства проведения анализа используем следующие обозначения:
Р1
и Р0
– общая рентабельность отчетного и базового периодов
П1
и П0
– прибыль на 1 руб. РП в отчетном и базовом периоде
Е1
и Е0
– фондорентабельность в отчетном и базовом периоде
К1
и К0
– коэффициент закрепления оборотных средств в отчетном и базовом периоде
Данные таблицы показывают, что уровень общей рентабельности изменился на: DРОБЩ
= Р1
– Р0
= 26,9-19,3=7,6%
1.
Определяем влияние прибыльности:
DР1
= П1
/ (Е0
+ К0
)*100 – Р0
;
DР1
= 0,15/(0,32+0,30)*100-19,3=4,9%
В связи с увеличением прибыли на 1 руб. реализованной продукции общая рентабельность возросла на 4,9%
2. Определяем влияние фондорентабельности:
DР2
= П1
/ (Е1
+ К0
)*100 – П1
/ (Е0
+ К0
)*100;
DР2
= 0,15-(0,26+0,30)*100-0,15/(0,32+0,30)*100=2,6 %
Уменьшение фондорентабельности привело к росту общей рентабельности на 2,6 %
3. Определяем влияние коэффициента закрепления оборотных средств:
DР3
= П1
/ (Е1
+ К1
)*100 – П1
/ (Е1
+ К0
)*100;
DР3
=0,15/(0,26+0,28)*100-0,15(0,26+0,30)*100=1,1 %
За счет ускорения оборачиваемости оборотных средств общая рентабельность возросла на 1,1 %
Общее влияние всех факторов составит:
DРОБЩ
= 4,9+2,6+1,1=7,6%
Анализ показал, что наибольшее влияние на изменение прибыли оказывает рост цен как на готовую продукцию, так и на сырьевые и материальные ресурсы. Большое влияние на увеличение прибыли имеет рост объемов производства и выручки от реализации продукции.
На изменение балансовой прибыли существенное влияние оказывают различного рода непроизводственные расходы.
Обновление ассортимента и его расширение при соответствующем качестве позволяет увеличить спрос на продукцию предприятия.
Заключение
В первой части контрольной работы подробно рассмотрена средняя величина, активно использующаяся в статистических исследованиях, описана её сущности и условий применения, представлены виды средних величин, формулы по которым они рассчитываются и примеры их использования на практике.
Во второй части контрольной работы проведен всесторонний анализ динамики прибыли и рентабельности на примере ОАО «Башмебель»
Основными факторами роста прибыли являются здесь увеличение объемов производства и реализации, снижение себестоимости, улучшение качества и увеличение ассортимента выпускаемой продукции, повышение эффективности производственных фондов, внедрение новых технологий, повышение производительности труда и совершенствование системы управления производством. Все эти факторы влияют на размер прибыли и рентабельности исследуемого предприятия.
Список литературы.
1. Бизнес-планирование. Учебник / Под ред. В.М. Попова – М.: ИНФРА, 2004- 625 с.
2. Боярский А.Я., Громыко Г.Л. Общая теория статистики / Боярский А.Я., Громыко Г.Л. - М.: 1995.
3. Гусаров В.М. Теория статистики. – М., 1998.
4. Давыдов Г.Е., Попов Н.И., Химич Е.И. Методы определения экономической эффективности хозяйственных: Учебное пособие / Давыдов Г.Е. и др. - изд. 2-е – М.: МГУЛ. 2005 -137 с.
5. Донцова Л.В., Никифорова Н.А. Анализ бухгалтерской отчетности / Донцова Л.В., Никифорова Н.А. - М.: LВС, 2000 – 384 с.
6. Едронова В. Н., Малафеева М. В. Общая теория статистики: Учебник / Едронова В. Н., Малафеева М. В. – 2-е изд. перераб. и доп. — М.:Магистр, 2007 – 606 с.
7. Савицкая Г.В. Анализ хозяйственной деятельности предприятия / Савицкая Г.В. – Минск.: Новое знание, 2004 – 487с.
|