Контрольная работа: Двокроковий метод найменших квадратів
|
Название: Двокроковий метод найменших квадратів Раздел: Рефераты по математике Тип: контрольная работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Двокроковий метод найменших квадратів Нехай маємо таку модель: функція доходу:
функція пропозиції грошей:
де Змінні Рівняння доходу, яке ми розглядаємо, показує, що доход визначається пропозицією грошей, інвестиційними витратами та витратами уряду. Рівняння пропозиції грошей показує, що запас грошей визначається відповідно до рівня доходів. Очевидно, що ми маємо симультативну модель. Застосовуючи умову порядку для її ототожнення, бачимо, що рівняння доходу неототожнене, тоді як рівняння пропозиції грошей – переототожнене. Переототожнена функція пропозиції грошей не може бути оцінена за допомогою методу ННК, тому що ми отримаємо дві різні оцінки Якщо застосувати метод найменших квадратів для оцінки невідомих параметрів рівняння пропозиції грошей, то отримані оцінки будуть зміщеними через кореляцію між змінною 1. Щоб позбавитись кореляції між
де et є помилками. Невідомі параметри рівняння (3) отримаємо за допомогою МНК:
Рівняння (3) є нічим іншим, як регресією скороченої форми, тому що в правій частині з'являються тільки екзогенні або попередньо визначені змінні. Його ще можна записати у вигляді:
який показує, що змінна 2. Рівняння пропозиції грошей можна записати таким чином:
де Порівнюючи (6) з (2) бачимо, що зовні ці рівняння дуже схожі, єдина відмінність полягає в тому, що Для подальшої ілюстрації методу 2МНК видозмінимо модель доходу та пропозиції грошей:
де додатково
На другому етапі заміщуємо
де Отримані таким чином оцінки будуть спроможними, тобто з розміром вибірки наближатимуться до BLUE-оцінок. Можна виділити такі особливості методу 2МНК. 1. Метод можна застосувати до окремого рівняння в системі без врахування інших. Отже, для економетричних моделей, що складаються з великої кількості рівнянь, метод 2МНК є дуже економним, тому він широко використовується на практиці. 2. На відміну від МНК, який дає декілька різних оцінок параметра у переототожнених рівняннях, 2МНК дає лише одну оцінку параметра. 3. Для застосування методу потрібно знати тільки загальну кількість екзогенних або попередньо визначених змінних у системі. 4. Хоча метод 2МНК був спеціально розроблений для переототожнених рівнянь, його також можна застосовувати до точно ототожнених рівнянь. У цьому разі МНК та 2МНК дадуть ідентичні оцінки. Задача № 1 У таблиці наведені статистичні дані для економічного показника
На основі цих даних: · побудувати діаграму розсіювання; · обчислити числові характеристики показника і фактора: середні значення, дисперсії, середні квадратичні відхилення, кореляційний момент та коефіцієнт кореляції; · записати рівняння лінійної регресії та знайти оцінки параметрів цього рівняння; · побудувати лінію регресії; · використовуючи критерій Фішера, з надійністю Р=0,95 оцінити адекватність прийнятої економетричної моделі статистичним даним; · з надійністю Р=0,95 знайти надійні зони для параметрів регресії та розрахункових значень показника; · для заданого значення · знайти коефіцієнти еластичності для базисних даних та для прогнозного значення; · зробити економічний аналіз. Рішення: Складемо робочу таблицю:
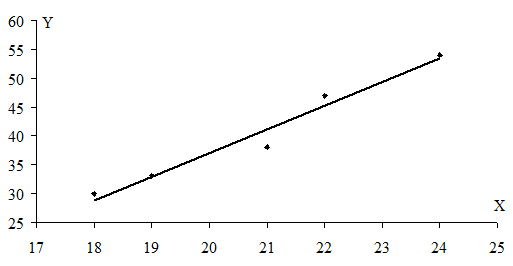
Побудуємо діаграму розсіювання:
Обчислимо числові характеристики показника і фактора: Середні значення
Дисперсії
Середньоквадратичні відхилення
Кореляційний момент (коваріація)
Коефіцієнт кореляції
Висновок: коефіцієнт кореляції дорівнює 0,981, що свідчить про наявність дуже сильного прямого зв’язку між кількістю витрат на капітал і реальним валовим продуктом. Запишемо рівняння лінійної регресії залежності реального валового продукту від кількості витрат на капітал:
Точкові оцінки параметрів
Одержимо рівняння регресії, що визначає залежність показника
Обчислимо значення регресії:
Побудуємо лінію регресії:
Висновок: якщо витрати капіталу зростуть на 1 млн. грн., то за інших рівних умов реальний валовий продукт збільшиться на 4,1 млн. грн. Зробимо оцінку статистичної якості одержаного рівняння регресії. Для цього обчислимо відхилення
Сума відхилень дорівнює нулю, отже, розрахунок виконано правильно. Вибіркова дисперсія характеризує міру розсіювання значень показника
Розрахуємо коефіцієнт детермінації:
Індекс кореляції
Коефіцієнт детермінації дорівнює 0,9633, отже, достовірно 96,33% дисперсії економічного показника Оскільки значення Використовуючи критерій Фішера, з надійністю Р=0,95 оцінимо адекватність прийнятої економетричної моделі статистичним даним. Розрахункове значення F-статистики обчислимо за формулою:
Висновок: за статистичною таблицею F-розподілу Фішера для заданої довірчої ймовірності (надійності)
знаходимо критичне значення F-статистики:
Оскільки Визначимо надійні зони для параметрів регресії:
Для
Визначимо надійні зони розрахункових значень показника за формулою
Розрахунок надійних зон представимо в таблиці:
Прогнозні значення показника обчислимо за формулою
Визначимо довірчі межі прогнозних значень:
Знайдемо коефіцієнти еластичності за формулою:
Висновок: для прогнозного значення Задача № 2 На основі статистичних даних для економічного показника
Розв’язання: Запишемо лінійну функцію попиту:
Для визначення
Всі обчислення представимо в таблиці:
Після підстановки значень сум одержимо систему лінійних рівнянь:
Для її розв’язку використаємо формули Крамера:
Тоді лінійна функція попиту на цукор прийме вигляд
Якість лінійної регресії оцінимо за допомогою коефіцієнта детермінації:
Коефіцієнт детермінації дорівнює 0,9933, отже, достовірно 99,33% дисперсії економічного показника Частинні коефіцієнти еластичності визначимо за формулами (див. два останніх стовпчики розрахункової таблиці):
Висновок: При збільшення ціни на товар першої необхідності на 1% попит зменшується на 0,4-1,2%, а при збільшенні доходу на одиницю населення на 1% попит зростає на 0,6-1,1%. Література 1. Лук'яненко І.М., Краснікова Л.І.. Економетрика: Підручник. - К.: Товариство "Знання", КОО, 1998 - 494с. 2. Наконечний С.І., Терещенко Т.О., Романюк Т.П. Економетрія: Підручник. - Вид.2-ге, допов. та перероб. - К.: КНЕУ, 2000 - 296с. 3. Толбатов Ю.А. Економетрика: Підручник для студентів економічних спеціальностей вищих навчальних закладів. - К.: Четверта хвиля, 1997 - 320с. |
 (6)
(6)
 ;
;  .
. ;
;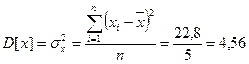 .
. .
.
 .
. ;
;  .
.
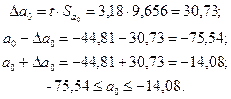
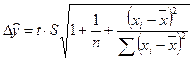 .
.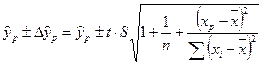 .
.

 ;
; ;
;  ;
;  ;
;  .
.