| СОДЕРЖАНИЕ:
1. Введение ……………………………………………………………………………………………………3
2. Физические величины ………………………………………………………………………………5
3. Понятие о системе физических величин ………………………………………………….7
4. Шкалы величин ………………………………………………………………………………………..10
5. Случайная погрешность …………………………………………………………………………..13
6. Основные понятия об эталонах ………………………………………………………………..18
7. Эталоны основных единиц СИ …………………………………………………………………..20
8. Заключение ……………………………………………………………………………………………….28
ВВЕДЕНИЕ.
Метрология – это наука, об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Наука и промышленность не могут существовать без измерений. Каждую секунду в мире производятся многие миллиарды измерительных операций, результаты которых используются для обеспечения качества и технического уровня выпускаемой продукции, обеспечения безопасной и безаварийной работы транспорта, для медицинских и экологических диагнозов и других важных целей. Практически нет ни одной сферы деятельности, где бы интенсивно не использовались результаты измерений, испытаний и контроля. Для их получения задействованы многие миллионы человек и большие финансовые средства.
Диапазон измеряемых величин и их количество непрерывно растет, что вызывает адекватное возрастание сложности измерений. Измерения, по сути, перестают быть одноактными действиями и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента, обработки и интерпретации полученной информации. Поэтому следует говорить об измерительных технологиях, понимаемых как последовательность действий, направленных на получение измерительной информации требуемого качества.
Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, планирования, контроля и регулирования – достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Современная наука и техника позволяют выполнять многочисленные и точные измерения, однако затраты на них становятся соизмеримыми с затратами на исполнительные операции.
Важной задачей метрологии является создание эталонов физических величин, привязанных к физическим константам и имеющих диапазоны, необходимые для современной науки и техники. Стоимость поддержания мировой системы эталонов весьма велика.
Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого. Таким образом, физические величины – это измеренные свойства физических объектов или процессов, с помощью которых они могут быть изучены. Мы оперируем такими физическими величинами как длина, время, температура, сила, давление, скорость и т.д. Все они определяют общие в качественном отношении физические свойства, количественные же характеристики их могут быть совершенно различными. Получение сведений о количественных отношениях величин и является задачей измерений.
С древних времен люди пользовались различными единицами для количественного оценивания расстояния, массы тел, продолжительности дня и т.д.
Самые древние из единиц относятся к антропометрическим, т.е. те, которые отождествлялись с названиями частей человеческого тела.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ЕДИНИЦЫ ИХ ИЗМЕРЕНИЯ.
Физические величины
.
Технологическая деятельность человека связана с измерением различных физических величин.
Физическая величина
– это характеристика одного из свойств физического объекта (явления или процесса), общая в качественном отношении многим физическим объектам, но в количественном отношении индивидуальная для каждого объекта.
Значение физической величины –
это оценка ее величины в виде некоторого числа принятых для нее единиц или числа по принятой для нее шкале. Например, 120 мм – значение линейной величины; 75 кг – значение массы тела, НВ 190 – число твердости по Бринеллю.
Измерением физической величины
называют совокупность операций, выполняемых с помощью технического средства, хранящего единицу, или воспроизводящую шкалу физической величины, заключающихся в сравнении (в явном или в неявном виде) измеряемой величины с ее единицей или шкалой с целью получения значения этой величины в форме, наиболее удобной для использования.
В теории измерений принято, в основном, пять типов шкал: наименования, порядка, интервалов, отношений и абсолютная.
Практическая реализация шкал конкретных свойств достигается путем стандартизации единиц измерений, шкал и (или) способов и условий их однозначного воспроизведения. Понятие неизменной для любых точек шкалы единиц измерений имеет смысл только для шкал отношений и интервалов (разностей). В шкалах порядка можно говорить только о числах, приписанных конкретным проявлениям свойства. Говорить о том, что такие числа отличаются в такое-то число раз или на столько-то процентов, нельзя. Для шкал отношений и разностей иногда не достаточно установить только единицу измерений. Так, даже для таких величин, как время, температура, сила света (и другие световые величины), которым в Международной системе единиц (SI) соответствуют основные единицы – секунда, Кельвин и кандела
, практические системы измерений опираются так же на специальные шкалы. Кроме того, сами единицы SI в ряде случает базируются на фундаментальных физических константах.
В этой связи можно выделить три вида физических величин, измерение которых осуществляется по различным правилам.
К первому виду физических величин относятся величины, на множестве размеров которых определены лишь отношения порядка и эквивалентности. Это отношение типа «мягче», «тверже», «теплее», «холоднее».
К величинам такого рода относятся, например, твердость, определяемая как способность тела оказывать сопротивление проникновения в него другого тела; температура как степень нагретости тела и т.п.
Существование таких отношений устанавливается теоретически или экспериментально с помощью специальных средств сравнения, а также на основе наблюдений за результатами воздействия физической величины на какие либо объекты.
Для второго вида физических величин отношение порядка и эквивалентности имеет место как между размерами, так и между разностями в парах их размеров. Так, разности интервалов времени считаются равными, если расстояние между соответствующими отметками равны.
Третий вид составляют аддитивные физические величины.
Аддитивными физическими величинами
называются величины, на множестве размеров которых определены не только отношения порядка и эквивалентности, но операции сложения и вычитания. К таким величинам относятся длина, масса, сила тока. Их можно измерять по частям, а также воспроизводить с помощью многозначной меры, основанной на суммировании отдельных мер. Например, сумма масс двух тел – это масса такого тела, которое уравновешивает на равноплечих весах первые два.
Понятие о системе физических величин.
Множество физических величин представляет собой некоторую систему, в которой отдельные величины связаны между собой системой уравнений.
Система физических величин –
это совокупность взаимосвязанных физических величин, образованная в соответствии с принятыми принципами, когда одни величины принимаются за независимые, а другие являются функциями независимых величин. Система физических величин содержит основные физические величины, условно принятые в качестве независимых от других величин этой системы, и производные физические величины, определяемые через основные величины этой системы.
Основная физическая величина –
физическая величина, входящая в систему единиц и условно принятая в качестве независимой от других величин этой системы.
Производная единица системы единиц –
единица производной физической величины системы единиц, образованная в соответствии с уравнением, связывающим ее с основными единицами.
Производная единица называется когерентной,
если в этом уравнении числовой коэффициент принят равным единице. Соответственно, система единиц, состоящая из основных единиц и когерентных производных, называется когерентной системой единиц физических величин.
Для каждой физической величины должна быть установлена единица измерения.
Единица физической величины –
физическая величин фиксированного размера, которой условно присвоено значение, равное единице, и применяемая для количественного выражения однородных физических величин.
Кроме основных и производных физических величин различают кратные, дольные, когерентные, системные и несистемные единицы.
Число независимых установленных величин равно разности числа величин, входящих в систему, и числа независимых уравнений связи между величинами.
Размерность физической величины –
выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях и отражающее связь от данной величины с физическими величинами, принятыми в данной системе величин за основные, и с коэффициентом пропорциональности, равным единице.
Показатель размерности физической величины –
показатель степени, в которую возведена размерность основной физической величины, входящая в размерность производной физической величины.
Размерности широко используют при образовании производных единиц и проверки однородности уравнений. Если все показатели степени размерности равны нулю, то такая физическая величина называется безразмерной. Все относительные величины (отношения одноименных величин) являются безразмерными.
Систему единиц как совокупности основных и производных единиц впервые в 1832г. предложил немецкий ученый К. Гаусс. Он построил систему единиц, где за основу принял единицы длины (миллиметр), массы (миллиграмм) и времени (секунда), и назвал ее абсолютной системой.
Многообразие единиц измерения физических величин и систем единиц осложняло их применение. Одни и те же уравнения между величинами имели различные коэффициенты пропорциональности. Свойства материалов, процессов выражались различными числовыми значениями. Международный комитет по мерам и весам выделил из своего состава комиссию по разработке единой Международной системы единиц. Комиссия разработала проект Международной системы единиц, который был утвержден XI Генеральной конференцией по мерам и весам в 1960 г. Принятая система была названа Международной системой единиц, сокращенно СИ.
Учитывая необходимость охвата Международной системой единиц всех областей науки и техники, в ней в качестве основных выбрать семь единиц. В механике такими являются единицы длины, массы и времени, в электричестве добавляется единица силы электрического тока, в теплоте – единица термодинамической температуры, в оптике – единица силы света, в молекулярной физике, термодинамике и химии – единица количества вещества. Эти семь единиц соответственно: метр, килограмм, секунда, ампер, Кельвин, кандела и моль – и выбраны в качестве основных единиц СИ.
Единица длины (метр)
– длина пути, проходимого светом в вакууме за 1/ 299792458 долю секунды.
Единица массы (килограмм) –
масса, равная массе международного прототипа килограмма.
Единица времени (секунда) –
продолжительность 9192631770 периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
Единица силы электрического тока (ампер) –
сила неизменяющего тока, который, проходя по двум нормальным прямолинейным проводникам бесконечной длины и ничтожно малой площади круглого поперечного сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает между проводниками силу взаимодействия, равную 2*10-7
Н на каждый метр длины.
Единица термодинамической температуры (Кельвин) –
1/273,16 термодинамической температуры тройной точки воды. Допускается использовать также шкалу Цельсия.
Единица силы света (кандела) –
силы света в заданном направлении источника, испускающего монохроматическое излучение частотой 540*1012
Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.
Единица количества вещества (моль) –
количество веществ системы, содержащей столько же структурных элементов, сколько атомов содержится в углероде-12 массой 0, 012 кг.
Международная система единиц содержит также две дополнительные единицы: для плоского угла – радиан и для телесного угла – стерадиан.
Радиан (рад0
– единица плоского угла, равная углу между двумя радиусами окружности, длина дуги между которыми равна радиусу. В градусном исчислении 1 рад = 570
17’44, 8”.
Стерадиан (ср) –
единица, равная телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.
В международной системе единиц, как и в других системах единиц физических единиц, важную роль играет размерность.
Размерностью
называют символическое (буквенное) обозначение зависимости производных величин (или единиц) от основных. Размерность служит качественной характеристикой величины и выражается произведением степеней основных величин, через которые может быть определена.
ШКАЛЫ ВЕЛИЧИН. ШКАЛА НАИМЕНОВАНИЙ (ШКАЛА КЛАССИФИКАЦИЙ).
Исторически измерения возникли как процесс количественного сравнения оцениваемого свойства предмета с установленной мерой данного свойства. Это было естественно, так как количество оцениваемых свойств было невелико, а основные, наиболее практически востребованные из них (длина, масса, объем) допускали изготовление довольно простых, наглядных и практически удобных мер (в России: мера длины – фут, аршин, сажень; мера массы – золотник, фунт, пуд; мера объема – бутылка, ведро, бочка). Однако уже в то время были в ходу меры, не имевшие материального выражения (меры площади, меры длины большого размера – верста).
С развитием производства и товарообмена количество измеряемых свойств расширялось, многие из них не были столь наглядными, как перечисленные выше, к тому же остро стоял вопрос межгосударственной унификации мер. Как следствие, неизбежен был переход от мер к единицам физических величин. Дальнейшее развитие науки и техники поставило вопрос об измерительном контроле свойств, до недавних пор считавшихся неизменяемыми. Прежде всего, следует отметить качественные свойства. К качественным свойствам можно применять признаки дискретности, упорядоченности и др. если мы представим себе такое качественное свойство, как цвет, то вспомним, что в последнее время широко используются цветовые атласы (наборы), сопоставление с которыми позволяет четко идентифицировать и классифицировать тот или иной оттенок. К нему не применимы традиционные понятия измерений, такие, как больше или меньше, однако можно найти порядок расположения цветов (цветовая гамма) и выстроить шкалу наименований. Подобный подход позволяет сделать вывод о наличии еще более общих признаков, чем единицы измерений, - шкал измерений и распространить понятия и подходы метрологии на практически все многообразие предметов, процессов, явлений – на весь окружающий нас мир.
Вообще говоря, теория шкал разрабатывается уже достаточно долго, исходя из потребностей и логики развития физико-математических наук. В соответствии с этим отправной точкой теории шкал является положение о том, что свойство (свойства) объекта образуют дискретное множество, между элементами которого существует любого рода логические взаимосвязи. Тогда под шкалой измерений данного свойства понимают отображение элементов данного множества на систему условных знаков с аналогичными отношениями. Системами условных знаков могут являться множество обозначений (названий), например цветов; совокупность классификационных символов или понятий, баллов оценки состояния объекта, действительные числа. Таким образом, для установления шкалы измерений необходимо, как минимум, две предпосылки – описание дискретного множества и установления логической взаимосвязи между его элементами.
В настоящее время в соответствии с логической структурой проявления свойств в теории измерений принято различать пять типов шкал измерений:
· шкала наименований (классификаций);
· шкала порядков (рангов);
· шкала разностей (интервалов);
· шкала отношений;
· Абсолютная шкала.
Шкала наименований –
шкала, элементы (ступени) которой характеризуются только соотношениями эквивалентности (совпадения, равенства и сходства) конкретных качественных проявлений свойств( например, атлас цветов).
Измерения с помощью шкал наименований представляют собой процесс сравнения исследуемого объекта со шкалой и установления элементов шкалы, совпадающих с объектом. В шкалах наименований принципиально невозможно ввести единицы измерений и нулевой элемент (нулевую точку шкалы). Это чисто качественные шкалы. Они допускают проведение некоторых статистических операций при обработке результатов измерений, полученных с их помощью. Для создания шкалы наименований нет необходимости в эталонах, но если эталон шкалы наименований создан, то он воспроизводит весь применяемый на практике участок шкалы.
Шкала порядка (ранга)
– шкала, элементы которой допускают логическую взаимосвязь элементов не только в виде отношений эквивалентности (как у шкал наименований), но и отношений порядка по возрастанию или убыванию количественного проявления измеряемого свойства (например, шкалы чисел твердости, баллов землетрясений, и силы ветра).
У шкал порядка (ранга) есть предпосылка для введения единицы измерения, но этого не удается сделать ввиду их абсолютной нелинейности. Также, как и для шкал наименований, для шкал порядка наличие эталонов не является необходимым. В них может быть или может отсутствовать нулевой элемент. Внесение любого изменения в шкалы наименований и порядка невозможно, так как это фактически обозначает создание новой шкалы.
Шкалы разностей (интервалов) –
шкала, допускающая дополнительно к соотношениям эквивалентности и порядка суммирования интервалов (разностей) между различными количественными проявлениями свойств (например, шкалы времени, температуры Цельсия).
Шкалы разностей имеют условные (принятые по соглашению) единицы измерений и нулевые элементы, соответствующие характерным (реперным) значениям измеряемой величины. В этих шкалах допустимы линейные преобразования и процедуры статистической обработки результатов измерений.
Шкалы отношений –
шкалы, к множеству количественных проявлений которых применимы соотношения эквивалентности и порядка – операции вычитания и умножения (шкалы отношений первого рода – пропорциональные шкалы) и суммирования (шкалы отношений второго рода – аддитивные шкалы).
В шкалах отношений используются условные (принятые по соглашению) единицы измерений и естественные нули (например, шкала термодинамической температуры (шкала первого рода); шкала массы (шкала второго рода)). Шкалы отношений допускают все арифметические и статистические операции.
Абсолютные шкалы –
шкалы, обладающие всеми признаками шкал отношений, но дополнительно в них существует естественное однозначное определение единицы измерений. Такие шкалы используются для измерений относительных величин, таких, как, например, коэффициент полезного действия. Абсолютные шкалы могут опираться на эталоны, воспроизводящие любые их участки, но могут быть построены и без эталонов.
Практическая реализация шкал измерений достигается посредством стандартизации как самих шкал и единиц измерений, так и способов и условий их воспроизведения.
СЛУЧАЙНАЯ ПОГРЕШНОСТЬ.
О природе случайных погрешностей, их источниках и путях возникновения известно мало, можно лишь сказать, что существует много причин, вызывающих появление эти погрешностей. Каждая из них незаметно воздействует на результат воздействия, но суммарное их воздействие может вызывать заметные погрешности. В каждый данный момент эти причины проявляют себя по-разному, без закономерной связи между собой, независимо друг от друга. Как следствие, заметные погрешности появляются без закономерной связи с предыдущими и последующими погрешностями.
Теория вероятностей разрабатывает математические методы изучения свойств случайных событий в больших совокупностях. Теория погрешностей, использующая математический аппарат теории вероятностей, основывается на аналогии между появлением случайных погрешностей при многократно повторяемых измерениях и совершением случайных событий. Недостаточное значение природы и происхождения случайных погрешностей не в коей мере не ограничивает эффективность применения вероятностных методов.
Случайной
называют такую величину, которая в результате опыта может применять то или иное значение, неизвестно заранее – какое именно. Случайные величины, принимающие только отдельные друг от друга значения, которые можно заранее перечислить, называются прерывными, или дискретными
, случайными величинами. Такими величинами являются, например, возможное число очков при бросании кости, возможное число попаданий при ста выстрелах, возможное число горошин в одном килограмме. Величины, возможные значения которых не отделены друг от друга и непрерывно заполняют некоторый промежуток, называются непрерывными
случайными величинами. Промежуток, который заполняют подобные величины, может иметь как резко выраженные границы, так и границы неопределенные, расплывчатые. Непрерывными случайными величинами являются длина отрезка линии, промежуток времени, интервал температуры.
Факторы, определяющие возникновение случайных погрешностей проявляются нерегулярно, в различных комбинациях и с интенсивностью, которую трудно предвидеть. Случайная погрешность случайно изменяется при повторных измерениях одной и той же физической величины. Однако, если оперировать исправленными результатами измерений, т.е. такими, из которых исключены систематические погрешности, то чисто случайные погрешности будут обладать следующими свойствами:
- Равные по абсолютной величине положительные и отрицательные погрешности равновероятны;
- Большие погрешности наблюдаются реже, чем малые;
- С увеличением числа измерений одной и той же величины среднее арифметическое погрешностей стремится к нулю, и, следовательно, среднее арифметическое результатов измерений стремится к истинному значению измеряемой величины.
Фактическое значение случайной погрешности, полученное при поверки средства измерения, не характеризуют его точности. Для оценки интервалов значений погрешностей и вероятности появления определенных значений необходимы многократные измерения и использование математического аппарата теории вероятностей.
Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения.
Интегральной функцией распределения
F(x) называют функцию, значение которой для каждого х является вероятностью появления значений хi
( в i-м наблюдении), меньших х:
F
(
x
)=
P
{
xi
≤
x
}=
P
{-∞<
xi
≤
x
},
где Р – символ вероятности события, описание которого заключено в фигурных скобках.
Обычно график интегральной функции распределения результатов наблюдений представляет собой непрерывную неубывающую кривую, начинающуюся от нуля на отрицательной бесконечности и асимптотически приближающуюся к единице при увеличении аргумента до плюс бесконечности.
Если интегральная функция имеет точку перегиба при значении х, близком к истинному значению измеряемой величины, и принимает в этой точке значение, равное 0,5, то говорят о симметричности распределения результатов.
Более наглядным является описание свойств результатов наблюдений, содержащих случайные погрешности, с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:
р(х)=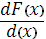
Поскольку F (x = + ∞) =1, то  , то есть площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице. Вероятность попадания случайной величины х в заданный интервал (х1
; х2
) равна площади, заключенной между абсциссами х1
и х2
: , то есть площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице. Вероятность попадания случайной величины х в заданный интервал (х1
; х2
) равна площади, заключенной между абсциссами х1
и х2
:
Р {x1
<x<x2
}=
Отыскание функций распределения требует проведения весьма трудоемких исследований и вычислений. На практике встречаются трапециидальные, уплощенные, экспоненциональные и другие виды распределений. Однако для наибольшего числа встречающихся на практике случайных величин можно ожидать распределение по так называемому закону нормального распределения.
Теоретически доказано, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
Плотность нормального распределения вероятностей для случайной величины описывается уравнением
Р (х)= - -
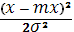 , где , где
mx
и 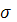 - математическое ожидание и среднее квадратическое отклонение, являющиеся основными параметрами нормального распределения; е – основание натурального логарифма. - математическое ожидание и среднее квадратическое отклонение, являющиеся основными параметрами нормального распределения; е – основание натурального логарифма.
Кривая имеет точки перегиба, соответствующие абсциссам mх
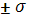 . .
Если данную кривую рассматривают как плотность распределения случайных погрешностей, то начало координат переносят в центр распределения и по оси абсцисс откладывают значения погрешностей  mx
. Уравнение принимает вид mx
. Уравнение принимает вид
Р(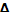 )= )=
Математическое ожидание
случайной величины mx
= 2
P(x)dx представляет собой оценку истинного значения измеряемой величины. Математическое ожидание случайных погрешностей равно нулю. 2
P(x)dx представляет собой оценку истинного значения измеряемой величины. Математическое ожидание случайных погрешностей равно нулю.
Дисперсия
результатов наблюдений является характеристикой их рассеивания:
D(x)=
Она имеет размерность квадрата измеряемой величины и не всегда удобна для использования в качестве характеристики рассеивания.
Среднее квадратическое отклонение
результатов наблюдений  имеет размерность измеряемой величины и наиболее часто используется в качестве основного параметра, характеризующего рассеивание результатов измерений. имеет размерность измеряемой величины и наиболее часто используется в качестве основного параметра, характеризующего рассеивание результатов измерений.
Если абсцисса функций нормального распределения выражается в долях среднего квадратического отклонения
t=
и начало координат находится в центре распределения, то распределение называется нормированным. Уравнения дифференциальной и интегральной функций нормированного нормального распределения принимают следующий вид:
P(t)= F(t)= dt dt
Определенный интеграл
Ф(t)=
Называют функцией Лапласа. Заметим, что F(t)-Ф(t)=0,5.
В производственной практике часто считается необходимым выполнение следующего условия: допустимое предельное отклонение от заданного номинального размера должно быть не меньше интервала 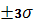 . В этом случае в среднем только одно из 370 изделий будет бракованным. . В этом случае в среднем только одно из 370 изделий будет бракованным.
Область технологического рассеивания какого-либо размера изделия, как правило, подчиняется нормальному закону, и периодически определяемое отклонение является показателем изменений в технологическом цикле.
ЭТОЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН.
Основные понятия об эталонах.
Для обеспечения единства измерений необходима тождественность единиц, в которых проградуированы все средства измерений одной и той же физической величины. Это достигается путем точного воспроизведения и хранения единиц физических величин и передачи их размеров стоящим ниже поверочной схеме средством измерений с помощью эталонов.
Классификация и назначение эталонов, а так же общие требования к их хранению и применению определены в ГОСТ 8.057-80 «ГСИ. Эталоны физических величин. Основные положения».
Перечень эталонов не повторяет перечня физических величин. Некоторые величины воспроизводятся с наивысшей точностью путем косвенных измерений, т.е. путем использования эталонов единиц других величин, связанных с первой определенной зависимостью.
По своему назначению и предъявляемым требованиям различают следующие виды эталонов.
Первичный эталон –
обеспечивает воспроизведение и хранение единицы физической величины с наивысшей в стране (по сравнению с другими эталонами той же величины) точностью. Первичные эталоны – уникальные измерительные комплексы, созданные с учетом новейших достижений науки и техники и обеспечивающие единства измерений в стране.
Специальный эталон -
обеспечивает воспроизведение единицы физической величины в особых условиях, в которых прямая передача размера единицы от первичного эталона с требуемой точностью не осуществима, и служит для этих условий первичным эталоном.
Первичный или специальный эталон, официально утвержденный в качестве исходного для страны, называется государственным. Государственные эталоны утверждаются Госстандартом, и на каждый их них утверждается государственный стандарт. Государственные эталоны создаются, хранятся и применяются центральными научными метрологическими институтами страны.
Вторичный эталон –
хранит размеры единицы физической величины, полученной путем сличения с первичным эталоном соответствующей физической величины. Вторичные эталоны относятся к подчиненным средствам хранения единиц и передачи их размеров при проведении поверочных работ и обеспечивают сохранность и наименьший износ государственных первичных эталонов.
По своему метрологическому назначению вторичные эталоны подразделяются на эталоны-копии, эталоны сравнения, эталоны-свидетели и рабочие эталоны.
Эталон-копия –
предназначен для передачи размера единицы физической величины рабочим эталоном при большом объеме поверочных работ. Он является копией государственного первичного эталона только по метрологическому назначению, но не всегда является физической копией.
Эталон сравнения –
применяется для сличения эталонов, которые по тем или иным причинам не могут непосредственно сличаться друг с другом.
Эталон-свидетель –
предназначен для проверки сохранности и неизменности государственного эталона и замены его в случае порчи или утраты. Поскольку большинство государственных эталонов создано на основе использования наиболее устойчивых физических явлений и являются по этому неразрушаемыми, в настоящее время только эталон килограмма имеет эталон-свидетеля.
Рабочий эталон –
применяется для передачи размера единицы физической величины рабочим средством измерения. Это самый распространенный вид эталонов, которые используются для проведения поверочных работ территориальными и ведомственными метрологическими службами. Рабочие эталоны подразделяются на разряды, определяющие порядок их соподчинения в соответствии с поверочной схемой.
Эталоны основных единиц СИ.
Эталон единицы времени
. Единицу времени – секунду – долгое время определяли как 1/86400 часть средних солнечных суток. Позднее обноружили, что вращение Земли вокруг соей оси происходит неравномерно. Тогда в основу определения единицы времени положили период вращения Земли вокруг Солнца – тропический год, т.е. интервал времени между двумя весенними равноденствиями, следующими одно за другим. Размер секунды был определен как 1/31556925,9747 часть тропического года. Это позволило почти в 1000 раз повысить точность определения единицы времени. Однако в 1967 году 13-я Генеральная конференция по мерам и весам приняла новое определение секунды как интервала времени, в течении которого совершается 9192631770 колебаний, соответствующих резонансной частоте энергетического перехода между уровнями сверхтонкой структуры основного состояния атома цезия-133 при отсутствии возмущения внешними полями. Данное определение реализуется с помощью цезиевых реперов частоты.
В 1972 году осуществлен переход на систему всемирного координированного времени. Начиная с 1997 года, государственный первичный контроль и государственная поверочная схема для средств измерения времени и частоты определяются правилами межгосударственной стандартизации ПМГ18-96 «Межгосударственная поверочная схема для средств измерения времени и частоты».
Государственный первичный эталон единицы времени, состоящий из комплекса измерительных средств, обеспечивает воспроизведение единиц времени со средним квадратическим отклонением результата измерений, не превышающим 1*10-14
за три месяца.
Эталон единицы длины.
В1889 году метр был принят равным расстоянию между двумя штрихами, нанесенными на металлическом стержне Х-образного поперечного сечения. Хотя международный и национальные эталоны метра были изготовлены из сплава платины и иридия, отличающегося значительной твердостью и большим сопротивлением окислению, однако не было полной уверенности в том, что длина эталона с течением времени не изменится. Кроме того, погрешность сличения между собой платино-иридиевых штриховых метров составляет + 1,1*10-7
м (+0,11 мкм), а так как штрихи имеют значительную ширину, существенно повысить точность этого сличения нельзя.
После изучения спектральных линий ряда элементов было найдено, что наибольшую точность воспроизведения единицы длины обеспечивает оранжевая линия изотопа криптона-86. В 1960 году 11-я Генеральная конференция по мерам и весам приняла выражение размера метра в длинах этих волн как наиболее точное его значение.
Криптоновый метр позволил на порядок повысить точность воспроизведения единицы длины. Однако дальнейшее исследование позволило получить более точный эталон метра, основанный на длине волны в вакууме монохроматического излучения, генерируемого стабилизированным лазером. Разработка новых эталонных комплексов по воспроизведению метра привела к определению метра как расстояния, которое проходит свет в вакууме за 1/299792458 долю секунды. Данное определение метра закреплено законодательно в 1985 году.
Новый эталонный комплекс по воспроизведению метра кроме повышения точности измерения в необходимых случаях позволяет так же следить за постоянством платино-иридиевого эталона, ставшего теперь вторичным эталоном, используемым для передачи размера единицы рабочим эталоном.
Эталон единицы массы.
При установлении метрической системы мер в качестве единицы времени приняли массу одного кубического дециметра чистой воды при температуре ее наибольшей плотности (40
С).
В этот период были проведены точные определения массы известного объема воды путем последовательного взвешивания в воздухе и воде пустого бронзового цилиндра, размеры которого были тщательно определены.
Изготовленный на основе этих взвешиваний первый прототип килограмма представлял собой платиновую цилиндрическую гирю высотой 39 мм, равной ее диаметру. Как и прототип метра, он был передан на хранение в Национальный архив Франции. В 19 веке повторно осуществили несколько тщательных измерений массы одного кубического дециметра чистой воды при температуре 40
С. При этом было установлено, что эта масса немного (приблизительно на 0, 028г) меньше прототипа килограмма Архива. Для того, чтобы при дальнейших, более точных, взвешиваниях не менять значение исходной единицы массы, Международной комиссией по прототипам метрической системы в 1872г. было решено за единицу массы принять массу прототипа килограмма Архива.
При изготовлении платино-иридиевых эталонов килограмма за международной прототип был принят тот, масса которого меньше всего отличалась от массы прототипа килограмма Архива.
В связи с принятием условного прототипа единицы массы литр оказался не равным кубическому дециметру. Значение этого отклонения (1л=1, 000028 дм3
) соответствует разности между массой международного прототипа килограмма и массой кубического дециметра воды. В 1964 году 12-я Генеральная конференция по мерам и весам приняла решение о приравнивании объема 1 л к 1дм3
.
Следует отметить, что в момент установления метрической системы мер не было четкого разграничения понятий массы и веса, поэтому международный прототип килограмма считался эталоном единицы веса. Однако уже при утверждении международного прототипа килограмма на 1-й Генеральной конференции по мерам и весам в 1889 году килограмм был утвержден в качестве прототипа массы.
Четкое разграничение килограмма как единицы массы и килограмма как единицы силы было дано в решениях 3-й Генеральной конференции по мерам и весам (1901г).
Государственный первичный эталон и поверочная схема для средств изменения массы определяется ГОСТ 8.021 – 84. Государственный эталон состоит из комплекса мер и измерительных средств:
· национального прототипа килограмма – копии № 12 международного прототипа килограмма, представляющего собой гирю из платино-иридиевого сплава и предназначенного для передачи размера единицы массы гире R1;
· национального прототипа килограмма – копия № 26 международного прототипа килограмма, представляющего собой гирю из платино-иридиевого сплава и предназначенного для проверки неизменности размера единицы массы, воспроизводимый национальным прототипом килограмма – копии № 12, и замены последнего в период его сличений в Международном бюро мер и весов;
· гири R1 и набора гирь, изготовленных из платино-иридиевого сплава и предназначенных для передачи размера единицы массы эталонам – копиям;
· эталонных весов.
Номинальное значение массы, воспроизводимое эталоном, составляет 1кг. Государственный первичный эталон обеспечивает воспроизведение единицы массы со средним квадратическим отклонением результата измерений при сличении с международным прототипом килограмма, не превышающим 2*10-3
мг.
Эталонные весы, с помощью которых производится сличение эталона массы, с диапазоном взвешивания 2*10-3
… 1кг имеют среднее квадратическое отклонение результата наблюдения на весах 5*10-4
… 3*10-2
мг.
Эталоны единицы температуры.
Измерение температуры с момента изобретения термометра Галилеем в 1598 году основывалось на применении того или иного термометрического вещества, изменяющего свой объем или давление при изменении температуры.
В 1715 году Фаренгейт создал ртутный термометр и предложил для построения термометрической шкалы две точки: температура смеси льда с солью и нашатырем, которую он обозначил 0, и температуру тела человека, которую он обозначил числом 96.
В 1736 году Реомюр предложил для термометрической шкалы другие две постоянные точки, более удобные для воспроизведения: точку таяния льда 0 и точку кипения воды 80.
В 1742 году Цельсий предложил термометрическую шкалу, в которой расстояние по шкале между точкой таяния льда и точкой кипения воды делилась на 100 частей. Показания термометров такого типа зависели от рода применяемого термометрического вещества, особенностей и условий его теплового расширения.
В 1848 году Кельвин и независимо от него Д.И.Менделеев предложили построить термодинамическую шкалу температур по одной реперной точке, приняв за нее тройную точку воды (точка равновесия воды, находящейся в специальном герметичном сосуде, в твердой, жидкой и газообразной фазах), которую можно воспроизвести с наименьшей погрешностью (0, 0001 К).
Нижней границей температурного интервала в этом случае служит точка абсолютного нуля. Данное предложение полностью было реализовано только в 18954 году, когда после тщательного анализа результатов, полученных в разных лабораториях, признали значение тройной точки воды, равное 273,16К, и точки таяния льда – 273,15К. Таким образом, термодинамическая температура является основной и обозначается символом Т. ее единицей служит кельвин (К), определенный как 1/273,16 часть термодинамической температуры тройной точки воды. Температура (t) в градусах Цельсия (0
С) определяется по формуле:
t=T-T0
,
где Т0
=273,15К.
Один градус Цельсия равен одному кельвину.
Поскольку воспроизведение термодинамической шкалы по одной реперной точке представляет значительные трудности, в 1968 г ввели Международную практическую температурную шкалу (МПТШ-68). Для ее воспроизведения кроме тройной точки воды использовали еще 10-11 реперных точек, реализуя состояние равновесия между жидкой и газообразной или твердой или жидкой фазами чистых веществ. При воспроизведении шкалы в интервале температур, близких к абсолютному нулю, использовали тройную точку водорода (Т=13,81К). При температурах, близких к 1000К, использовали точки затвердения серебра и золота. Точность воспроизведения кельвина (градуса Цельсия) различна в различных интервалах температур. Наименьшая погрешность (0, 0002К) достигается в тройной точке воды.
В качестве эталонных приборов при воспроизведении шкалы используют платиновый термометр сопротивления (-259,34…+630,740
С) и термопару платинородий-платина (630,74…1064,430
С).
В 1989 году вместо МПТШ-68 была принята новая международная практическая температурная шкала МПТШ-90, позволившая повысить точность воспроизведения кельвина в некоторых интервалах шкалы за счет введения дополнительных реперных точек плавления (точка галлия) и затвердевания (точки индия, алюминия, меди).
Во ВНИИМ им. Д,И.Менделеева созданы два государственных первичных и один специальный эталоны, обеспечивающие единство измерений температуры в диапазоне измерений 273,15…6300К. государственная поверочная схема для средств измерения температуры установлена ГОСТ 8.558-93.
Эталон единицы электрического тока.
Ввиду отсутствия возможности на практике определить размер ампера через количество электричества используются другие физические величины, с которыми электрический ток связан определенными зависимостями. Долгое время за один ампер принимали неизменяющийся ток, который, проходя через водный раствор азотно-кислого серебра, при соблюдении приложенной спецификации выделяет 0,001118г серебра в одну секунду.
С 1948 года в качестве эталона ампера были приняты токовые весы, с помощью которых определяли силу взаимодействия между двумя проводниками (в соответствии с определением единицы ампера). Переход к этому эталону был связан с тем, что силу, с которой один проводник действует на другой, можно измерить более точно, чем количество выделенного вещества на электродах.
В настоящее время в связи с введением в метрологическую практику эталонов ома и вольта назначение токовых весов как средства, необходимого для воспроизведения ампера, утратило смысл, поскольку воспроизведение ампера через единицы сопротивления и напряжения повысило точность на два порядка.
Новый государственный первичный эталон ампера состоит из двух комплексов. В первом из них размер ампера воспроизводится через ом и вольт, а во втором – через фарад, вольт и секунду с использованием методов электрометрии.
Эталон и поверочная схема для средств измерения силы тока в диапазоне 30…110А регламентированы ГОСТ 8.022-91.
Эталон единицы силы света.
С начала ХХ века в качестве эталонов силы света использовали электрические лампы накаливания, позволяющие сохранять световые единицы с погрешностью не более 0,1%. К концу 1930-х гг. были созданы новые световые эталоны, основанные на полном излучателе (абсолютно черном теле). Начиная с 1980 г. кандела воспроизводится путем косвенных измерений. В диапазоне измерений 30…110кд среднее квадратическое отклонение результата измерений составляет 1*10-3
кд. Государственный первичный эталон канделы и поверочная схема для средств измерений световых величин непрерывного и импульсного излучений регламентированы ГОСТ 8.023-90.
Последняя основная единица системы СИ – моль – не имеет эталона, поскольку является расчетной. Однако в области физико-химических измерений зарегистрированы три государственных эталона, воспроизводящих единицы молярной доли компонентов в газовых средах, объемного влагосодержания нефти и нефтепродуктов, относительной влажности газов.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ:
1. «Управление качеством» под общей редакцией В.Е.Сыцко. Мн. «Вышэйшая школа»,2008
2. Сергеев А.Г., Крохин В.В. Метрология: Учебное пособие для вузов. – М.; Логос, 2001
3. Основы метрологии, стандартизации и контроля качества: Учебное пособие. – М.;2000
4. Сыцко В.Е. «Управление качеством»: Учебное пособие для вузов, 2-е издание, 1999
|