|
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
1 Задание №1 4
2 Задание №1 6
Задание №2 11
ЗАКЛЮЧЕНИЕ 13
СПИСОК ЛИТЕРАТУРЫ 14
ВВЕДЕНИЕ
Современное управление сложными социально-экономическими и производственными системами в рамках рыночных отношений требует принятия решений, учитывающих влияние большого числа случайных возмущающих факторов, взаимосвязанных динамических процессов, неполноты исходной информации, множественности стратегий развития, много вариантности путей достижения конечных результатов, разнообразия оценок их эффективности. Все это обусловливает необходимость формирования у современного специалиста в области экономики системных представлений о сфере профессиональной деятельности, глубокого изучения математических методов и вычислительной техники, навыков анализа экономических проблем, постановки задач и оценки последствий альтернативных вариантов принимаемых решений с использованием моделей разных классов и эффективной компьютерной поддержки. Подобные возможности предоставляет специальность "Экономическая кибернетика".
Цель кибернетики – создание принципов, методов и средств для достижения эффективных результатов управления, то есть кибернетика – наука об управлении сложными системами.
В экономической кибернетике объект – экономические системы, предмет – функционирование и развитие экономики как управляемой системы.
Зарубежным аналогом нашего "экономиста-математика» является "системный аналитик", специализирующийся в сфере экономики.
Благодаря кибернетике и созданию ЭВМ одним из основных способов познания, наравне с наблюдением и экспериментом, стал метод моделирования. Применяемые модели становятся все более масштабными: от моделей функционирования предприятия и экономической отрасли до комплексных моделей управления биогеоценозами, эколого-экономических моделей рационального природоиспользования в пределах целых регионов, до глобальных моделей.
1 Задание№ 1(5
;
5
;
5)
Используя линейную модель межотраслевого баланса определить вектор валового выпуска продукции трех отраслей и ее распределение по потребляющим отраслям,если:
a a+c b y1
А= d+0.1 c-d 0 Y= y2
c-0.05 0.1 a y3
Числовые данные для матрицы A и Y берутся из таблицы в соотвецтвии с заданным индивидуальным трехзначным шрифтом.
| a =
|
0,12
|
|
| b =
|
0,06
|
|
| c =
|
0,08
|
|
| d =
|
0,03
|
|
| |
|
|
По формуле вычисляем кофициенты прямых затрат:
т.е матрица прямых затрат А имеет не отрицательные элементы
| |
0,12
|
0,2
|
0,06
|
| A=
|
0,13
|
0,05
|
0
|
| |
0,03
|
0,1
|
0,12
|
и для вектора конечного потребления Y можно найти необходимый обьем валового выпуска.
Вектор валового продукта и межотраслевые потоки определяются экономико- математической маделью задачи планирования производства и распределения продукции
-- вектор конечного продукта на плановый год
Вначале составляется матрица:
| |
0,88
|
-0,2
|
-0,06
|
| ( E -A)=
|
-0,13
|
0,95
|
0
|
| |
-0,03
|
-0,1
|
0,88
|
затем вычисляется определитель этой матрицы
| |
1,176951
|
0,256226
|
0,080247
|
| ( E -A)-1=
|
0,161056
|
1,087694
|
0,010981
|
| |
0,058425
|
0,132337
|
1,140347
|
Тогда вектор валового продукта равен:
| |
49,07153
|
|
| X =
|
80,39926
|
|
| |
51,71826
|
|
| |
|
|
Выводы:
На основе линейной модели Леонтьева для трех базовых отраслей промышленности найден необходимый обьем валового выпуска в каждой отрасли для заданного обьема конечного потребления продукции этих отраслей
2 Задание №1. (3;7;1)
В случае линейной зависимостей спроса и предложения от цены товара, принятые в виде
 , ,
требуется:
1. исследовать динамику цены товара  для пяти временных интервалов для пяти временных интервалов 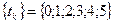 ; ;
2. построить диаграмму, иллюстрирующую изменение цены во времени;
3. по полученным результатам сделать вывод.
Для определения постоянной интегрирования, цену в начальный момент времени принять в виде 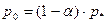 , где , где 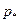 - равновесная цена, найденная из частного решения разностного уравнения. - равновесная цена, найденная из частного решения разностного уравнения.
 0,25 0,25
a
=6,6;
b
=5;
c
=3,4;
d
=5.
Решение.
В реальности часто складывается рыночная ситуация, когда цикл производства продукции отстает от цикла реализации. Рассмотрим паутинообразную модель рыночного равновесия, которая является одной из классических экономико-математических моделей.
Предположим, что предложение товара  на рынке реагирует на изменение цены р
с лагом в один период, в то время как спрос Dt
определяется текущей ценой, и обе эти зависимости линейны: на рынке реагирует на изменение цены р
с лагом в один период, в то время как спрос Dt
определяется текущей ценой, и обе эти зависимости линейны:
 
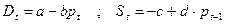
где Dt
– спрос на товар в момент времени t;
St
– предложение товара в момент времени t;
pt
– цена на товар в момент времени t;
a
,
b
,
c
,
d
– коэффициенты, где a
,
b
,
c
,
d
>0.
Предложение ведет себя таким образом, потому как модель относится к продукции, которая не производится мгновенно – требуется определенный промежуток времени. Решающим фактором является то, что производители считают, что цена, установленная в начале периода, не изменяется на его протяжении и является основой для выбора объемов производства в будущем.
В каждом периоде рынок устанавливает такую цену, при которой спрос поглощает в точности весь объем предложения, таким образом:
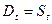
Подставив уравнения имеем:
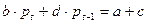
Поделив обе части на _ и, переходя для удобства на шаг вперед по времени, получается линейное неоднородное разностное уравнение первого порялка с постоянными коэффициентами относительно цены р
:

Решение однородного уравнения

ищется в виде 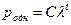 . .
Характеристическое уравнение 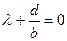 имеет корень имеет корень 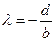 . .
Тогда решение однородного уравнения
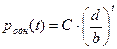 , ,
где С
– произвольная постоянная, определяемая из начального условия.
Частное решение уравнения  ищется по виду правой части в виде ищется по виду правой части в виде 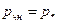 , где , где  - постоянная. - постоянная.
Получаем 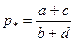 - равновесная цена. - равновесная цена.
Общее решение уравнения  имеет вид: имеет вид:

Для определения постоянной С
рассмотрим задачу Коши: пусть в начальный момент времени 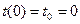 известна цена продукции известна цена продукции  . Тогда из начального условия . Тогда из начального условия

устанавливается значение постоянной, равное: 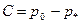
Тогда 
В зависимости от входных параметров задачи, динамика цены во времени может быть разной.
Здесь возможны 3 случая:
a)  >1 – текущая цена >1 – текущая цена 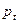 расходится с равновесной. расходится с равновесной.
b) 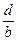 <1 - текущая цена <1 - текущая цена 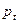 стремится к равновесной с колебаниями около неё (условие стабильности). стремится к равновесной с колебаниями около неё (условие стабильности).
c) 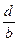 =1 – две точки равновесия: в зависимости от четности t
имеет место колебание от одной точки к другой. =1 – две точки равновесия: в зависимости от четности t
имеет место колебание от одной точки к другой.
Исходные данные:
| Показатель
|
Формула
|
Значение
|
| a
|
|
6,6
|
| b
|
|
5
|
| c
|
|
3,4
|
| d
|
|
5
|
| 
|
|
0,25
|
| P0
(цена в начальный момент времени)
|
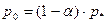
|
(1-0,25)*1=0,75
|
| Р* (равновесная цена)
|
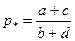
|

|
| P(t)
|

|
|
Исследуем динамику цены товара 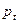 для пяти временных интервалов для пяти временных интервалов  и построим диаграмму, иллюстрирующую изменение цены во времени при помощи Excel. и построим диаграмму, иллюстрирующую изменение цены во времени при помощи Excel.
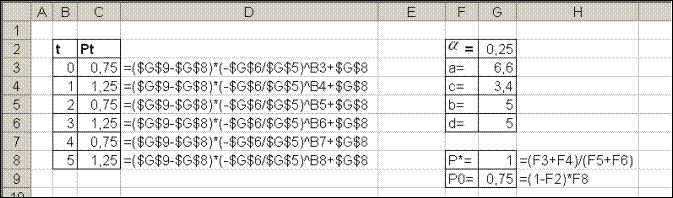
Рис.1 Динамика цены товара 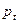 для пяти временных интервалов для пяти временных интервалов
Диаграмма 1. Изменение цены во времени

На диаграмме видно, что цена колеблется вокруг равновесной цены в двух точках.
Т. к. в исходных данных b
=
d
=5,
тогда 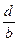 =1 – следовательно, имеется две точки равновесия (на графике значения 0,75 и 1,25): в зависимости от четности t
имеет место колебание от одной точки к другой: =1 – следовательно, имеется две точки равновесия (на графике значения 0,75 и 1,25): в зависимости от четности t
имеет место колебание от одной точки к другой:
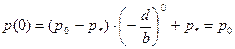 ; ;
 ; ;

Значит, 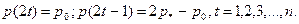
Равновесная цена колеблется в диапазоне от 0,75 до 1,25, следовательно, спрос и предложение имеют общие две точки, в которых пересекаются в разные моменты времени. Ценовой коридор от 0,75 и 1,25 стабилен, поэтому если установить цену равную значению из этого коридора, то излишки на рынке будут покрывать нехватки.
Задание №2.
Для заданных векторов валового выпуска и конечного потребления в начальный момент времени
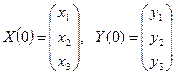
и продуктивной матрице затрат
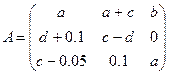 , ,
требуется:
1. рассчитать вектор валового выпуска 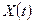 на момент времени t=2
, если все компоненты вектора конечного потребления на момент времени t=2
, если все компоненты вектора конечного потребления 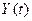 увеличиваются на увеличиваются на 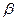 % за каждый период; % за каждый период;
2. выяснить при этом на сколько процентов необходимо увеличить компоненты вектора валового выпуска продукции 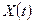 по сравнению с исходными величинами; по сравнению с исходными величинами;
3. по результатам расчета сделать выводы.
| a
|
b
|
c
|
d
|
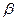
|
Y
1,
млн.ден. ед.
|
Y
2,
млн.ден. ед.
|
Y
3,
млн.ден. ед.
|
X
1
|
X
2
|
X
3
|
| 0,1
|
0,02
|
0,12
|
0,12
|
25
|
100
|
70
|
30
|
150
|
105
|
60
|
Решение.
Векторы валового выпуска и конечного потребления в начальный момент времени
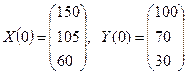
и продуктивная матрица затрат
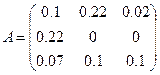
Для нахождения вектора валового выпуска воспользуемся формулой
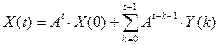 , ,
которая принимает вид 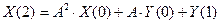 . .
Вектор конечного потребления согласно условию задачи увеличивается на 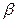 % за каждый период, т.е. имеет вид % за каждый период, т.е. имеет вид 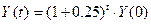 . .
Тогда  . .
Матрица А2
изменения состояния

Теперь из формулы 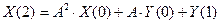 получим получим
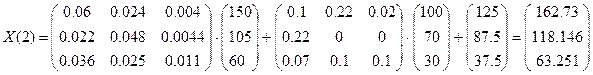
ВЫВОД
На основе линейной динамической модели Леонтьева, при заданном темпе роста продукта конечного потребления Y
(
t
)
на 25% за каждый период, через два временных цикла компоненты вектора валового выпуска X
(
t
)
необходимо увеличить соответственно на 8,49%, 12,52% и 5,42% по сравнению с исходными величинами, заданными на начальный момент времени.
ЗАКЛЮЧЕНИЕ
В контрольной работе мы исследовать динамику цены товара для пяти временных интервалов, на основании полученных данных построили диаграмму, иллюстрирующую изменение цены во времени.
По полученным результатам сделали выводы:
Равновесная цена колеблется в диапазоне от 0,75 до 1,25, следовательно, спрос и предложение имеют общие две точки, в которых пересекаются в разные моменты времени. Ценовой коридор от 0,75 и 1,25 стабилен, поэтому если установить цену равную значению из этого коридора, то излишки на рынке будут покрывать нехватки.
На основании начальных данных векторов валового выпуска и конечного потребления в начальный момент времени, а также продуктивной матрице затрат был рассчитан вектор валового выпуска на определённый момент времени, когда все компоненты вектора конечного потребления увеличиваются на 25% за каждый период.
При получении результатов расчета был сделан вывод, что при заданном темпе роста продукта конечного потребления Y
(
t
)
на 25% за каждый период, через два временных цикла компоненты вектора валового выпуска X
(
t
)
необходимо увеличить соответственно на 8,49%, 12,52% и 5,42% по сравнению с исходными величинами, заданными на начальный момент времени.
СПИСОК ЛИТЕРАТУРЫ
1. И.И. Бажин Экономическая кибернетика. Компакт-Учебник, Донецк: Консум, 2004, 292 с.
2. Крайзмер Л. П. Кибернетика. Учеб. Пособие для студ. с.-х. вузов по экон. спец. - М.: Агропромиздат,1985.
3. Монахов А.В. Математические методы анализа экономики. СПб.: Издательство «Питер», серия «Краткий курс», 2002 г.
4. Пинегина М.В. Математические методы и модели в экономике. М.: «Экзамен», 2002 г.
5. Пястолов С.М. Экономический анализ деятельности предприятий: Учебное пособие для вузов Серия: «Gaudeamus». М.: 2002 г.
6. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. М.: Издательство «Дело», серия «Наука управления», 2000 г.
|