БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра ЭТТ
РЕФЕРАТ
На тему:
«Формы представления аберраций (поперечная, продольная, волновая). Монохроматические аберрации»
МИНСК, 2008
В идеальной оптической системе все лучи, исходящие из точки A, пересекаются в сопряженной с ней точке A΄0
. После прохождения реальной оптической системы либо нарушается гомоцентричность пучка и лучи не имеют общей точки пересечения, либо гомоцентричность сохраняется, но лучи пересекаются в некоторой точке A΄, которая не совпадает с точкой идеального изображения (рисунок 1). Это является следствием аберраций. Основная задача расчета оптических систем – устранение аберраций.

Рисунок 1 – Идеальное и реальное изображения точки
Для вычисления аберраций необходимо определить точку референтного (идеального) изображения A΄0
, в которой должно находиться изображение по законам гауссовой оптики. Относительно этой точки и определяют аберрации.
Поперечные аберрации
Поперечные аберрации
 – это отклонения координат точки A΄ пересечения реального луча с плоскостью изображения от координат точки A΄0
идеального изображения в направлении, перпендикулярном оптической оси (рисунок 2): – это отклонения координат точки A΄ пересечения реального луча с плоскостью изображения от координат точки A΄0
идеального изображения в направлении, перпендикулярном оптической оси (рисунок 2):
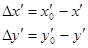 . (1) . (1)
Если точки A΄ и A΄0
совпадают, то поперечные аберрации равны нулю  . .
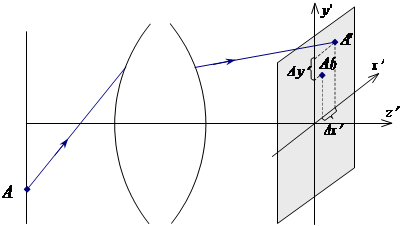
Рисунок 2 – Поперечные аберрации
Различают поперечные аберрации в сагиттальной плоскости 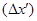 и в меридиональной плоскости и в меридиональной плоскости  . Поперечные аберрации для изображения ближнего типа выражаются в миллиметрах, для изображения дальнего типа – в угловой мере. Для изображения дальнего типа поперечная аберрация – это угловое отклонение . Поперечные аберрации для изображения ближнего типа выражаются в миллиметрах, для изображения дальнего типа – в угловой мере. Для изображения дальнего типа поперечная аберрация – это угловое отклонение  между реальным и идеальным лучом (рисунок 3). между реальным и идеальным лучом (рисунок 3).

Рисунок 3 – Поперечные аберрации для удаленного изображения
У каждого луча в пучке своя величина поперечной аберрации. Для всего пучка поперечные аберрации – это функции от зрачковых координат:
 , (2) , (2)
где 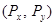 – реальные зрачковые координаты. – реальные зрачковые координаты.
Зрачковые канонические координаты.
Зрачковые координаты определяют положение луча в пучке. Канонические (относительные) зрачковые координаты определяются следующим образом:
 , (3) , (3)
где 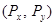 , , 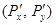 – входные и выходные реальные зрачковые координаты, – входные и выходные реальные зрачковые координаты,  , ,  – входные и выходные апертуры. Апертуры определяют максимальные значения зрачковых координат. – входные и выходные апертуры. Апертуры определяют максимальные значения зрачковых координат.
Таким образом, верхний луч пучка имеет координаты  , нижний луч пучка – , нижний луч пучка –  , главный луч пучка – , главный луч пучка –  , сагиттальный луч – , сагиттальный луч – 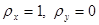 (рисунок 4). (рисунок 4).
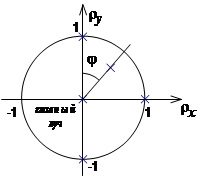
Рисунок 4 – Канонические зрачковые координаты
Канонические зрачковые координаты можно выразить через полярные координаты
ρ и φ:
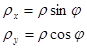 , (4) , (4)
где 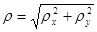 . .
Волновая аберрация
Волновая аберрация
– это отклонение реального волнового фронта от идеального (рисунок 5), измеренное вдоль луча в количестве длин волн:
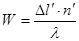 (5) (5)
Из выражения (5) следует, что волновая аберрация пропорциональна отклонениям оптических длин лучей пучка. Поэтому влияние волновой аберрации на качество изображения не зависит от типа изображения, а определяется тем, сколько длин волн она составляет.

Рисунок 5 – Волновая аберрация
Референтная сфера
– это волновой фронт идеального пучка с центром в точке идеального изображения A΄0
, проходящий через центр выходного зрачка O΄
.
При нахождении волновой аберрации с референтной сферой сравнивается ближайший к ней волновой фронт.
Для всего пучка волновая аберрация – это функция канонических зрачковых координат:
 . (6) . (6)
Поперечная и волновая аберрации – это разные формы представления одного явления, они связаны между собой соотношениями:
 . (7) . (7)
Таким образом, поперечные аберрации прямо пропорциональны первым частным производным волновой аберрации по каноническим координатам.
Продольные аберрации
Продольные аберрации
– это отклонения координаты точки  пересечения реального луча с осью от координаты точки пересечения реального луча с осью от координаты точки  идеального изображения вдоль оси (рисунок 6): идеального изображения вдоль оси (рисунок 6):
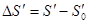 , (8) , (8)
где S΄ – положение точки пересечения луча с осью, S΄0
– положение идеальной точки пересечения.

Рисунок 6 – Продольные аберрации осевого пучка для изображения ближнего типа
Для изображения ближнего типа продольные аберрации выражаются в миллиметрах, для изображения дальнего типа (рис.8.7) продольные аберрации выражаются в обратных миллиметрах:
 . (9) . (9)

Рисунок 7 – Продольные аберрации осевого пучка для изображения дальнего типа
Продольные аберрации связаны с поперечными, и, следовательно, с волновыми тоже:
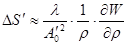 , (10) , (10)
где А΄0
– задняя апертура осевого пучка.
Выражение (10) приближенное, оно может использоваться только для случая небольших апертур.
Итак, из выражений (7) и (10) следует, что волновая, поперечная и продольная аберрация – это разные формы представления одного явления нарушения гомоцентричности пучков. При оценке качества изображения за исходную модель аберрационных свойств оптической системы берут волновую аберрацию (по величине волновой аберрации судят о качестве оптической системы). Однако, если аберрации велики, то более целесообразно использовать для оценки качества изображения поперечные аберрации.
Аберрации делятся на монохроматические
и хроматические.
Монохроматические аберрации присутствуют, даже если оптическая система работает при монохроматическом излучении.
Монохроматические аберрации делятся на несколько типов:
- сферическая,
- кома,
- астигматизм и кривизна изображения,
- дисторсия.
Обычно все последующие аберрации добавляются к уже существующим. Но мы будем рассматривать каждый тип аберрации по отдельности, как если бы только он и существовал.
Разложение волновой аберрации в ряд
Если в оптической системе присутствуют все типы аберраций, то для описания отдельных типов аберраций волновую аберрацию можно разложить в ряд по степеням относительных зрачковых координат в следующем виде:
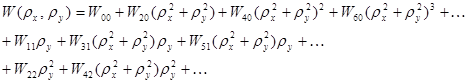 (11) (11)
или в полярных координатах:
 , (12) , (12)
где  (n – степень r, m – степень cosj) – коэффициент, значение которого определяет вклад конкретного типа (и порядка) аберрации в общую волновую аберрацию: (n – степень r, m – степень cosj) – коэффициент, значение которого определяет вклад конкретного типа (и порядка) аберрации в общую волновую аберрацию:
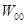 – постоянная составляющая, которая может быть сведена к нулю соответствующим выбором референтной сферы, – постоянная составляющая, которая может быть сведена к нулю соответствующим выбором референтной сферы,
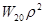 – продольная дефокусировка, – продольная дефокусировка,
 и и  – сферическая аберрация 3 и 5 порядка, – сферическая аберрация 3 и 5 порядка,
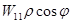 – дисторсия, – дисторсия,
 – кома 3 и 5 порядка, – кома 3 и 5 порядка,
 – астигматизм 3 и 5 порядка. – астигматизм 3 и 5 порядка.
В разложении могут участвовать и более высокие порядки, но мы их рассматривать не будем.
Порядок аберрации определяется по степени координаты ρ в разложении поперечной аберрации в ряд.
Этот ряд получаем путем дифференцирования выражения (12). Таким образом, поперечная аберрация определяется следующим образом:
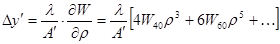 . (13) . (13)
Разложение в ряд продольной аберрации имеет вид:
 . (14) . (14)
Радиально симметричные аберрации (дефокусировка и сферическая аберрация)
Радиально симметричные аберрации (расфокусировка и сферическая аберрация) анализируются и изучаются при рассмотрении осевой точки предмета. Для описания радиально симметричных аберраций достаточно использовать одну радиальную зрачковую координату 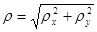 : :
 . (15) . (15)
ЛИТЕРАТУРА
1. Бегунов Б.Н., Заказнов Н.П. и др. Теория оптических систем. – М.: Машиностроение, 2004
2. Заказнов Н.П. Прикладная оптика. – М.: Машиностроение, 2000
3. Дубовик А.С. Прикладная оптика. – М.: Недра, 2002
4. Нагибина И.М. и др. Прикладная физическая оптика. Учебное пособие.- М.: Высшая школа, 2002
|