Задача 1.
По 10 сельскохозяйственным предприятием имеются данные о прибыли и производстве валовой продукции (производительности труда) на одного среднегодового работника (табл. 1).
Таблица 1 – Исходные данные.
| Прибыль на одного среднегодового работника, тыс. руб. |
23 |
19 |
13 |
25 |
27 |
19 |
10 |
14 |
22 |
24 |
| Валовая продукция (в сопоставимых ценах 1994 г.) на одного среднегодового работника, тыс. руб. |
320 |
300 |
390 |
410 |
440 |
350 |
380 |
400 |
450 |
420 |
Требуется:
1. Рассчитать параметры уравнения парной линейной регрессии зависимости прибыли от производительности труда.
2. Оценить качество уравнения с помощью средней ошибки аппроксимации.
3. Найти средний (обобщающий) коэффициент эластичности.
4. Оценить тесноту связи с помощью показателей корреляции и детерминации.
5. Оценить значимость коэффициента через t – критерий Стьюдента при a=0,05
6. Оценить статистическую надежность результатор регрессионного анализа с помощью F – критерия Фишера при a=0,05.
7. Рассчитать прогнозное значение результата, если прогнозное значения фактора увеличиться на 10% от его среднего уровня.
Решение
1. Уравнение парной линейной регрессии имеет вид:
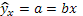 , ,
где 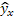 – прибыль на одного среднегодового работника, тыс. руб.; – прибыль на одного среднегодового работника, тыс. руб.;
 – производства валовой продукции на одного среднегодового работника, тыс. руб.; – производства валовой продукции на одного среднегодового работника, тыс. руб.;
a, b– параметры уравнения.
Для определения параметров уравнения a и b составим систему нормальных уравнений. Исходное уравнения последовательно умножим на коэффициенты при неизвестных a и b, и затем каждое уравнение просуммируем:

где n – число единиц совокупности.
Для расчетов построим вспомогательную таблицу (табл. 2).
Таблица 2 – Вспомогательная таблица для расчета статистических величин
| с/х предприятие |
Прибыль на 1 среднегодового работника, тыс. руб. |
Валовая продукция на одного среднегодового работника, тыс. руб. |
 |
 |
 |
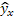 |
 |
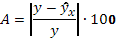 |
| у |
х |
| 1 |
23 |
320 |
529 |
102400 |
7360 |
17,7 |
5,3 |
23,04 |
| 2 |
19 |
300 |
361 |
90000 |
5700 |
17,1 |
1,9 |
9,86 |
| 3 |
13 |
390 |
169 |
152100 |
5070 |
19,7 |
-6,7 |
51,65 |
| 4 |
25 |
410 |
625 |
168100 |
10250 |
20,3 |
4,7 |
18,84 |
| 5 |
27 |
440 |
729 |
193600 |
11880 |
21,2 |
5,8 |
21,65 |
| 6 |
19 |
350 |
361 |
122500 |
6650 |
18,6 |
0,4 |
2,29 |
| 7 |
10 |
380 |
100 |
144400 |
3800 |
19,4 |
-9,4 |
94,27 |
| 8 |
14 |
400 |
196 |
160000 |
5600 |
20,0 |
-6,0 |
42,88 |
| 9 |
22 |
450 |
484 |
202500 |
9900 |
21,4 |
0,6 |
2,54 |
| 10 |
24 |
420 |
576 |
176400 |
10080 |
20,6 |
3,4 |
14,26 |
| сумма |
196 |
3860 |
4130 |
1512000 |
76290 |
- |
- |
281,28 |
Параметры уравнения регрессии можно определить и по другим формулам, которые вытекают из системы нормальных уравнений:
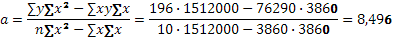

Уравнения регрессии имеет вид:
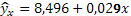
Коэффициент регрессии b=0,029показывает, что при росте производительности труда на 1 тыс. руб. прибыли на одного работника в среднем по данной совокупности хозяйств увеличивается на 0,029 тыс. руб.
2. Оценим качество уравнения с помощью средней ошибки аппроксимации по формуле:

где  - ошибка аппроксимации. - ошибка аппроксимации.
Подставляем в уравнения регрессии фактические значения х, определим теоретические (расчетные) значения 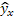 (табл. 2). Найдем величину средней ошибки аппроксимации (табл. 2). Найдем величину средней ошибки аппроксимации  . Для этого заполним две последние графы табл. 2. Отсюда: . Для этого заполним две последние графы табл. 2. Отсюда:
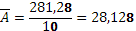
В среднем расчетные значения прибыли на одного среднегодового работника отклоняются от фактических на 28,128%. Качество уравнения регрессии можно оценить как хорошее, так как средняя ошибка аппроксимации не превышает допустимого предела ().
3. Рассчитаем средний коэффициент эластичности по формуле:
где  и и  – средние значения признаков. – средние значения признаков.
Отсюда:

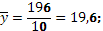

Коэффициент эластичности показывает, что в среднем при росте производительности труда на 1% прибыли на одного работника повышается на 0,571%.
4. Для определения тесноты связи между исследуемыми признаками рассчитываем корреляции. Для парной линейной зависимости формула имеет вид:

где  - средняя сумма произведения признаков; - средняя сумма произведения признаков;
 и и  – средние квадратическое отклонения по х и у. – средние квадратическое отклонения по х и у.
Данные для расчета коэффициента представлены в табл. 2 и в пункте 3 решения. Отсюда:
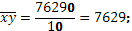

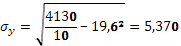

Коэффициент корреляции  =0,251 свидетельствует, что связь между признаками есть, но не очень большая. Коэффициент детерминации =0,251 свидетельствует, что связь между признаками есть, но не очень большая. Коэффициент детерминации  =0,2512
=0,063 показывает, что 6% ….. =0,2512
=0,063 показывает, что 6% …..
5. Для проверки статической зависимости (существенности) значением линейного коэффициента парной корреляции рассчитываем t– критерий Стьюдента по формуле:
Вычисленное сравним с табличным (критическим) значением  при принятом уровне значимости а=0,05 и числе степеней свободы v=n-2=10-2=8. Табличное значение по таблице распределения Стьюдента равно 2,306. при принятом уровне значимости а=0,05 и числе степеней свободы v=n-2=10-2=8. Табличное значение по таблице распределения Стьюдента равно 2,306.
Фактическое значения критерия меньше табличного, что свидетельствует о…
6. Оценим значимости уравнения регрессии и показатели тесноты связи с помощью F – критерия Фишера. Для этого сравним его фактическое значения Fфакт
с табличным (критическим) значением Fтабл.
Фактическое значение Fфакт
по формуле:
В нашем случае:
Табличное значение Fтабл.
По таблице значения F – критерия Фишера – при а=0,05, k1
=m=1и k2
=n-m-1=10-1-1=8 равно 5,32 (m – число параметров при переменной х).
Фактическое значения критерия меньше табличного, свидетельствует о …
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Рассчитаем прогнозное значения прибыли на одного работника при средним росте производительности труда на 10%.
Прогнозное значение производительности труда:

Прогнозное значение прибыли на одного работника:
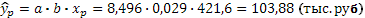
Задача 2
По 30 сельскохозяйственным предприятием имеются данные о средних значениях и вариации урожайности картофеля, количество внесенных органических удобрений и доли посадок картофеля после лучших предшественников, а так же о значениях коэффициентов парной корреляции между этими признаками (табл. 3)
Таблица 3 – Исходные данные.
| Показатель |
Признак |
Среднее значения |
Среднее квадратическое отклонения |
Линейные коэффициенты парной корреляции |
| Урожайность картофеля с 1 га, ц |
y |
120 |
24 |
- |
| Внесено органических удобрений на 1 га посадки картофеля, т |
x1
|
21 |
2 |
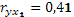 |
| Доля посадок картофеля по лучшим предшественникам, % |
x2
|
55 |
10 |


|
Требуется:
1. Построить уравнение множественной линейной регрессии зависимости урожайности картофеля от количества внесенных органических удобрений и доле посадок картофеля по лучшим предшественникам в стандартизированном масштабе и в естественной форме.
2. Определить линейный коэффициент множественной корреляции.
3. Рассчитать F – критерий Фишера при уровне значимости, а=0,05.
Решение
1. Уравнение множественной линейной регрессии имеет вид:

где  - урожайность картофеля с 1 га, ц; - урожайность картофеля с 1 га, ц;
 - внесено органический удобрений на 1 га посадки картофеля, т; - внесено органический удобрений на 1 га посадки картофеля, т;
 - доля посадки картофеля по лучшим предшественникам, %; - доля посадки картофеля по лучшим предшественникам, %;
 , ,  - параметры уравнения. - параметры уравнения.
Для расчета его параметров а,  и и  сначала построим уравнения множественной регрессии в стандартизированном масштабе: сначала построим уравнения множественной регрессии в стандартизированном масштабе:

где 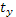 , ,  и и 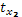 - стандартизированные переменные; - стандартизированные переменные;
 и и 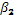 – стандартизированные коэффициенты регрессии. – стандартизированные коэффициенты регрессии.
Стандартизированные коэффициенты регрессии определим по формулам:

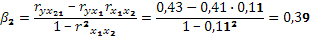
Уравнение множественной регрессии в стандартизированной форме имеет вид:
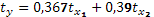
Стандартизированные коэффициенты регрессии позволяют сделать заключение о сравнительной силе влияния каждого фактора на урожайность картофеля. Наиболее значительное влияние доли посадок картофеля лучшим предшественникам. Количество внесенных органических удобрений оказывают меньшее воздействие.
Для построения уравнения в естественной форме рассчитаем  и и  , используя формулы перехода от , используя формулы перехода от 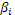 к к 
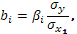
где  и и 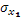 - средние квадратическое отклонения. - средние квадратическое отклонения.
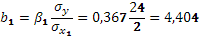
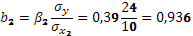
Параметры а определим из соотношения:
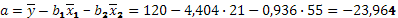
Получим уравнение:
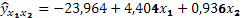
Каждый из коэффициентов уравнения регрессии определяет среднее изменение урожайности за счет изменения соответствующего фактора при фиксированном уровне другого. Так, коэффициент при х1
показывает, что увеличение (или снижение) количества внесения органических удобрений на 1 т ведет к повышению (или снижению) урожайности картофеля на 4,404 ц. Соответственно коэффициент при х2
определяет меру зависимости урожайности картофеля от доли высадки его по лучшим предшественникам.
2. Для определения линейного коэффициента множественной корреляции использует формулу:
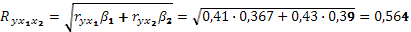
Коэффициент множественной корреляции показывает тесную зависимость между анализируемыми признаками. Коэффициент множественной детерминации 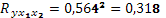 свидетельствует, что 31,8% изменения урожайности картофеля связано с анализируемыми признаками. свидетельствует, что 31,8% изменения урожайности картофеля связано с анализируемыми признаками.
3. Статистическую значимость уравнения регрессии в целом и показателя тесноты связи оценим с помощью общего F – критерий Фишера по формуле:
где  – число единиц совокупности; – число единиц совокупности;
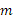 - число факторов в уравнении линейной регрессии. - число факторов в уравнении линейной регрессии.
В нашем случае:
|