Министерство
образования
Украины
Национальный
технический
университет
Украины
(Киевский
политехнический
институт)
Методические
указания
к курсовому
проектированию
по дисциплине
"Техническая
механика"
для студентов
специальностей
“Информационно-измерительная
техника"
Киев
2000 г.
Методические
указания к
курсовому
проектированию
по дисциплине
"Техническая
механика" для
студентов
специальностей
“Информационно-измерительная
техника" /Сост.
В. А. Бойко, В. C.
Детлинг.
- Киев: НТУУ КПИ.
2000.
1 ОБЩИЕ МЕТОДИЧЕСКИЕ
УКАЗАНИЯ
1.1 Цель курсового
проектирования
Курсовой проект
по курсу "Техническая
механика"
является первой
самостоятель-ной
комплексной
работой студентов
в процессе
подготовки
к инженерной
деятельности.
Цель курсового
проекта -
систематизировать
и закрепить
теоретические
знания, полу-ченные
при изучении
курсов "Инженерная
графика",
"Физика", "Химия",
"Математика",
"Техническая
механика",
приобрести
навыки проектирования
новых изделий
(в част-ности
электромеханических
устройств с
учетом современных
требований);
использова-ния
справочной
литературы,
стандартов,
единых норм
и расценок;
разработки
тексто-вой и
графической
документации;
подготовки
к выполнению
курсовых проектов
по профилирующим
предметам.
Курсовой проект
выполняется
на основании
технического
задания, выдаваемого
руководителем
проекта.
1.2. Содержание
и объем курсового
проекта
В процессе
работы над
курсовым проектом
студенты
рассчитывают
основные параметры
заданного
механизма и
разрабатывают
его конструкцию.
Конструкторская
документация
проекта состоит
из пояснительной
записки (15-20 страниц),
принципиа-льной
кинематической
схемы, сборочных
чертежей
устройства
и сборочной
единицы, рабочих
чертежей 5-8
нестандартных
деталей (вала,
зубчатого
колеса, шкалы,
пружи-ны, стакана,
стойки и т.п.).
Пояснительная
записка в общем
случае должна
содержать
следующее
разделы:
Введение.
Назначение
и область применения
проектируемого
изделия.
Техническая
характеристика
изделия.
Описание и
обоснование
выбранной
конструкции.
Расчеты, подтверждающие
работоспособность
и надежность
конструкции:
расчет мощности
и выбор электродвигателя;
расчет кинематических
параметров
(определение
общего передаточного
отношения и
передаточных
отношений
ступеней);
расчеты на
прочность;
расчеты кинематической
точности и
погрешности
мертвого хода;
выбор материалов
и покрытий;
определение
критериев
конструктивного
качества и
экономической
эффектив-ности
конструкции.
Конкретный
перечень
конструкторской
документация,
подлежащей
обязательной
разработке,
указывается
в техническом
задании на
курсовой
проект.
1.3. Оформление
документации
проекта
Вся графическая
и текстовая
документация
проекта должна
оформляться
в полном соответствии
с требованиями
Единой системы
конструкторской
документации
(ЕСКД) и СТП КПИ
2.001-83 "Курсовые
проекты. Требования
к оформлению
документации".
2.
ВЫБОР ЭЛЕКТРОДВИГАТЕЛЕЙ
ДЛЯ ПРИВОДОВ
ИСПОЛНИТЕЛЬНЫХ
МЕХАНИЗМОВ
МАЛОЙ МОЩНОСТИ
2.1
Исходные данные
1 Назначение
электропривода,
общая характеристика
режима работы
электродви-гателя,
специальные
требования.
А. Приводы
специализированных
устройств
(магнитофоны,
МТЛ устройств
ЭВМ, печатающие
машины и др.).
Режим работы
и требования
к электродвигателю
опреде-ляются
специальными
техническими
условиями.
Б. Нерегулируемые
приводы исполнительных
механизмов
управления,
операцион-ных
механизмов
и технологических
устройств,
механизмов
дистанционного
управления.
Режим работы
двигателя
длительный
или повторно-кратковременный,
нерегулируемый
по частоте
вращения,
реверсивный
или нереверсивный.
В. Нерегулируемые
приводы приборов
времени, программных
устройств,
МТЛ са-мопишущих
приборов и др.
Режим работа
двигателя
длительный
или повторно-кратко-временный
с постоянной
стабилизированной
частотой вращения,
нереверсивный.
Г. Приводы следящих
систем управления
(приводы РЛС,
графопостроителей,
ма-нипуляторов,
привод стабилизации
положения
корпусов и
др.). Режим работы
длитель-ный
или повторно-кратковременный
реверсивный,
регулируемый
по частоте
вращения.
2. Характеристика
источника
питания двигателя:
для постоянного
тока – напряже-ние
и допускаемые
токи нагрузки;
для переменного
- напряжение,
частота и вид
сети (однофазная,
трехфазная).
3. Конструктивные
требования:
способ крепления
двигателя;
количество
выходных концов
вала ротора;
наличие встроенных
элементов
(тахогенератор,
редуктор и
др.).
4. Функциональные
требования:
допускаемое
изменение
частоты вращения,
способ регулирования,
время переходного
процесса,
характеристика
режима работа
следящей системы
и входных сигналов.
5. Эксплуатационные
требования:
срок службы;
температура
внешней среды;
тре-бования
устойчивости
к линейным
ускорением,
вибрации, к
ударным перегрузкам,
к изменениям
атмосферного
давления и
влажности.
6. Характеристика
внешней нагрузки:
числовое значение
или закон изменения
ста-тического
момента нагрузки;
скорости и
ускорения вала
нагрузки.
2.2 Выбор серии
электродвигателей
По исходным
данным выбирают
серии двигателей
переменного
или постоянного
тока, соответствующих
требованиям
пп. 1 и 2 группы
привода (А, Б,
В или Г) (см. под-разд.
2.1), используя
каталоги или
ограничительные
перечни, например
таблице 2.1.
Из группы серий
и типов выбирают
двигатели,
удовлетворяющие
требованиям
пп. 1-5 исходных
данных, сравнивая
требования
с паспортными
характеристиками
конк-ретных
типов двигателей.
В первую очередь
отбирают серии,
соответствующие
напря-жению
питания, частоте
сети и требуемой
постоянной
времени (для
следящих систем),
затем, учитывая
степень обязательности,
выбирают серии
и типы, удовлетворяющие
требованиям
к конструкции,
сроку; службы
и устойчивости
к климатическим
и механи-ческим
воздействиям.
Сравнительные
характеристики
некоторых
серий двигателей
приведены
в таблицах 2.2
и 2.3. Если исходные
требования
перечнем серий
одной группы
не могут быть
удов-летворены,
используют
серии нижестоящих
групп в таблице
2.1: группу Б, например,
можно дополнить
перечнем групп
В или Г.
Таблица 2.1-Перечень
электродвигателей
предпочтительного
применения
|
Группа
|
Общая
характеристика
|
Серии
или типы
электродвигателей
|
|
переменного
тока
|
постоянного
тока
|
А
|
Специальные
|
для
аппаратуры
магнитной
записи
|
ЭДГ;
типы: АД-5; АДТ-6;
АДТ-1,6
КД-3,5
КДП-6-4;
ДК-16;
КД-б-4
|
ДКС;
ДКМ типы: Д16-06;
ВДС-02 МД-0,35-2ООО-9
|
|
интегрирующие
|
ИД-1;
ИД-2; ИД-9
|
ДИ-6-1500А |
|
для
потенциомет-рических
систем
|
РД-09 |
СЛ-267;
СЛ-367 |
|
Б
|
Нерегулируемые
|
общего
при-менения
Редук-торн.
двигатели
со встроенным
редуктором
|
УАД;
АОЛБ; АОЛ |
Дв.
авиац. Д-100; МА
Ред.:МКМ; МСВ;
МС-160; МФА; ДР-1; 5Р,
МН или ЭДН |
|
В
|
со стабилизиро-ванной
частотой вращения |
Г; ДСР;
ДСГ; ДСА; ДСМ;
ДСДР; ДСД; типы:
СД-09; ЭГ-10 |
ДПР;
ДПМ в исп. Н3;
ДРВ; ДП в исп.
Цр, |
Г
|
Управляемые
общего применения
в следящих
системах |
АДП;
ДИД; ЭМ; ДКМ; АД;
ДМ; АДИ;
ДАД;
АСМ;
с
тахоге-нераторами
АДТ; ДГ; СМА; СМБ
|
ДПМ;
ДПР; ДП, СЛ, ДП,
СД, ПЯ, |
Таблица
2.2-Электродвигатели
постоянного
тока
|
Характеристики
параметры
|
Серии
электродвигателей |
| Д |
ДРВ
|
СД
|
ДПМ |
ДПP |
МИГ |
ДА |
|
Напряжение
питания
В,
|
<
6
|
+ |
- |
- |
- |
+ |
- |
- |
| 6 |
- |
- |
- |
- |
+ |
- |
- |
| 12 |
- |
- |
- |
+ |
+ |
+ |
- |
| 27 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
| 60 |
- |
+ |
+ |
- |
- |
- |
- |
| 110 |
- |
- |
- |
- |
- |
- |
- |
|
Номиналь
ная мощно-сть,
Вт
|
от |
0,1 |
0,1 |
8,0 |
0,5 |
0,3 |
10 |
2,0 |
| до |
200 |
300 |
150 |
14 |
80 |
600 |
600 |
|
Электромехани-ческая
постоян-ная
времени, мс
|
25…
100
|
15...100 |
11...150 |
45..90 |
12..20 |
1,3…8.5 |
30….160 |
|
С регулятором
скорости
|
- |
+ |
- |
+/- |
+/- |
- |
- |
| С редуктором |
- |
- |
- |
- |
- |
- |
- |
| С
тахогенер. |
- |
- |
- |
- |
+/- |
+/- |
- |
|
С
0В "Лев" и "Пр
|
- |
- |
- |
- |
- |
- |
+ |
| С тормозной
муфтой |
- |
- |
- |
- |
- |
- |
+/- |
| Кол.
концов вала |
1/2 |
1 |
1 |
1/2 |
1/2 |
1/2 |
1 |
| С фланцевым
креплением |
+
|
+ |
+ |
- |
+ |
+ |
+ |
| С креплением
по диаметру |
+ |
- |
- |
+ |
+ |
- |
+ |
| Последовательно-го
возбуждения |
+ |
- |
- |
- |
- |
- |
+ |
| Параллельного
возбуждения |
+ |
+ |
+ |
- |
- |
- |
- |
| С постоянным
магнитом |
+ |
- |
- |
+ |
+ |
+ |
- |
| Срок
службы, тыс.
ч, макс. |
1,5 |
1,5 |
0,5 |
1,0 |
3,0 |
|
0,5 |
| Устойчивость |
к
линейн. ускор
|
35
|
15 |
15
|
50
|
100
|
|
35
|
| к вибрационным
нагрузкам |
12 |
10 |
10 |
10 |
10 |
|
15 |
| К ударным
нагрузкам |
35 |
10 |
35 |
50 |
50 |
|
35 |
| К внешн. температу-рам,
°С: |
|
85 |
85 |
60 |
60 |
60 |
|
85 |
| |
60 |
60 |
60 |
60 |
60 |
|
60 |
|
К влажности,
%
|
98 |
98 |
98 |
98 |
98 |
|
98 |
| К
внешнему
атмосферному
давлен, кПа |
2,5-150 |
2,5-150 |
2,5-200 |
50-
200
|
50-
300
|
|
2,5-
150
|
2.3. Выбор типоразмера
двигателя и
передаточного
отношения
редуктора
Энергетические,
кинематические
и динамические
показатели
привода зависят
одновременно
от характеристик
двигателя и
от параметров
редуктора.
Оптимальный
ва-риант сочетания
типоразмера
двигателя,
структуры
редуктора и
его передаточного
отно-шения
устанавливается,
на основании
энергетического,
кинематического
и динамиче-ского
расчета системы
ДВИГАТЕЛЬ-РЕДУКТОР-НАГРУЗКА.
Для приводов
группы А методика
такого расчета
разрабатывается
применительно
к конкретному
виду привода.
Таблица
2.3 Электродвигатели
переменного
тока
| Характеристи-ки,
параметры |
Серия
єлектродвигателей |
| АДП |
АДТ |
ДИД |
ДГ |
ЭМ |
ДKM |
АД |
Г |
ДСД |
ДСР |
| Видпита-ния |
1-фазн.
3-фазн.
|
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
| - |
- |
- |
- |
- |
- |
- |
+ |
- |
- |
| Частота,
Гц |
50
400
500
1000
|
+ |
- |
- |
- |
- |
- |
- |
+ |
+ |
+ |
| + |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
- |
- |
| + |
+ |
- |
- |
- |
- |
- |
- |
- |
- |
| + |
- |
+ |
+ |
- |
- |
- |
- |
- |
- |
| Напряжениепитания,
В |
36- 40
110
220
|
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
- |
- |
| + |
+ |
- |
- |
115 |
- |
- |
- |
127 |
- |
| + |
- |
- |
- |
- |
- |
- |
- |
+ |
+ |
|
Номинальная
мощность,
Вт
|
2,1 -62 |
0,3 -13 |
0,1 –10 |
0,1 –5,0 |
0,4 -50 |
0,2-60 |
0,3–3,5 |
1,0 -40 |
* |
0,2–0,3 |
| Эл.-мех.
пост. времени,
мс |
6-82 |
22-500 |
26-160 |
50-290 |
15-170 |
15-150 |
10-20 |
|
|
30-50 |
| Синхронные |
- |
- |
- |
- |
- |
- |
- |
+ |
+ |
+ |
| С редуктором |
- |
- |
- |
- |
+/- |
- |
- |
+/- |
+ |
+ |
| С тахогенерат. |
- |
+ |
- |
+ |
- |
- |
- |
- |
- |
- |
| Кол.
концов вала |
1/2 |
1 |
1 |
1 |
1/2 |
1 |
1/2 |
1 |
1 |
1 |
|
С фланцевым
креплением
|
- |
- |
+ |
+ |
+ |
+ |
- |
+ |
+ |
+ |
| С креплением
по диаметру |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
- |
+ |
|
Срок
службы,
тыс. часов
max
|
2 |
2 |
1 |
1,5 |
1 |
1 |
1 |
5 |
1 |
10 |
| Устойчивость |
К
лин. ускор. |
25 |
25 |
8 |
15 |
15 |
15 |
8 |
8 |
|
|
| К
вибрациям |
12 |
12 |
5 |
5 |
5 |
5 |
3,5 |
3,5 |
|
|
| К
ударам |
15 |
7 |
4 |
4 |
12 |
4 |
3 |
3 |
|
|
|
К внеш-ним
тем-перату-рам,С
|
|
70 |
60 |
100 |
100 |
80 |
80 |
70 |
50 |
50 |
60 |
| |
50 |
40 |
60 |
60 |
60 |
60 |
50 |
60 |
40 |
40 |
|
к
влажности
отн, %
|
98 |
98 |
98 |
98 |
98 |
98 |
98 |
98 |
98 |
98 |
| к
внешнему
атмосфер-ному
давле-нию. кПа |
2,5…
150
|
2,5…
150
|
2,5…
150
|
2,5…
150
|
2,5…
150
|
2,5…
150
|
2,5…
150
|
2,5…
150
|
2,5…
200
|
2,5…
150
|
Примечание.
Для параметров
устойчивости
указаны максимальные
значения по
сериям двигателей.
Виброуотойчивость
- для частот
200...300 Гц.
х Номинальная
мощность двигателей
ДСД около 12 мкВт.
2.3.1
Неуправляемый
привод (группы
Б и В)
Основная нагрузка
привода - постоянный
и переменный
во времени
(рисунок 1) статический
момент Тн.с(t)
на выходном
валу редуктора
в режиме нормируемого
или не-нормируемого
по времени
переходного
процесса в
периоды пуска
или изменения
нагру-зочного
момента.
 Тн
Т4
Тн
Т4
Т1
Т3
Т2
Т5
t1
t2 t3
t4
t5
t∑
Рисунок 2.1- График
изменения
статического
момента нагрузки.
Исходный
кинематический
параметр - средняя
или номинальная
угловая скорость
на выходном
валу редуктора
-н,
рад/с.
Переходный
процесс может
быть ограничен
временем tп
,с или предельным
угло-вым ускорением
вала нагрузки
н,
рад/с2, при
этом должен
быть задан
момент инерции
нагрузки Iн,
кгм2.
В качестве
рабочего режима
двигателя
принимается
номинальный,
для чего на
его обмотки
необходимо
подавать номинальное
напряжение,
а передаточное
отношение
редуктора
принимают
iр= ωдв
/ωн,
(2.1)
где
ωдв
-
номинальная
угловая скорость
двигателя,
который надлежит
выбрать в следующем
порядке.
1.Определить
эквивалентный
статический
момент сопротивления
на валу редук-тора,
H·м:
 ,
(2.2) ,
(2.2)
где Ti
среднее значение
момента в интервале
i (см. рисунок
2.1);
ti-
продолжительность
интервала, c.
При постоянном
значении момента
Tнc
принимают . Тэ
= Tнс .
2. Определить
необходимую
мощность двигателя,
Вт:
Nдв
= Тэ·
ωн·
кн
/
ηр
,
(2.3)
где кн - коэффициент
запаса: 1,05... 1,1 - если
нет ограничений
по времени
пере-ходного
процесса; 1.2...2,2
- при заданном
времени разгона;
при этом чем
больше мо-мент
инерции нагрузки,
тем больше
следует брать
запас по мощности;
ηр - ориентировочное
значение КПД
редуктора:
0,7...О,9 - для простого
цилинд-рического,
планетарного
или волнового;
0,4...О,7 - для червячного.
3. Выбрать типоразмеры
двигателей,
номинальная
мощность которых
равна Nдв
или несколько
больше. Если
время разгона
ограничено
значением
tn,
отбирают двигате-ли,
электромеханическая
постоянная
времени которых
меньше τ0=tn/6.
Для приводов
с длительном
режимом работы
предпочтение
отдают двигателям
с большим сроком
служ-бы и хорошим
КПД, для
повторно-кратковременного
режима - высокоскоростным.
4. Определить
передаточное
отношение
редуктора по
уравнению
(2.1). После раз-работки
кинематической
схемы редуктора
и геометрического
расчета его
элементов
выбранный
двигатель
необходимо
проверить:
по номинальной
мощности, используя
неравенство
Nном ≥Тэ
· ωдв / ηр
· iр,
(2.4)
где ηр - расчетное
значение КПД
редуктора;
по пусковому
моменту, чтобы
Тп ≥ Тнсп
/ (iр ηр)
+ (Ірот
+ Ір
+Ін/і2р)∙(
ωдв /tn),
(2.5)
где Тнсп -
наибольший
статический
момент нагрузки
при пуске, Н∙м;
Ірот
- момент инерции
ротора двигателя,
кг∙м2;
Ір
- момент инерции
редуктора,
приведенный
к валу двигателя,
кг∙м2;
по времени
разгона, чтобы
tр = 3∙ (Ірот
+ Ір
+Ін/і2р)
∙ ωдв/ (Тп -
Тсп) ≤ t n
, (2.6)
где Тсп -
статический
момент нагрузки
при пуске,
приведенный
к валу двигателя
Н∙м: Тсп = Тнсп/(iр
ηр).
2.3.2 Следящий
привод. Группа
Г
В следящем
приводе вал
нагрузки через
редуктор
поворачивается
по сигналам
управления,
поступающим
от усилителей
следящей системы.
Привод, т.е.
двигатель и
редутор, являясь
исполнительной
частью следящей
системы должен
обеспечивать
на нагрузочном
валу необходимые
статические
и динамические
характеристики
(переме-щения,
скорость и
ускорение) в
соответствии
с требованиями
оптимального
переход-ного
процесса либо
в точности,
повторяя закон
изменения
управляющего
сигнала. В этих
условиях выбор
передаточного
отношения
редуктора
играет решающую
роль. Оптимальное
значение
передаточного
отношения
зависит от
выбора критерия
оптими-зации
(обеспечение
максимального
ускорения
вала нагрузки,
получение
минимальной
мощности двигателя
или наименьшего
пускового
момента), а также
от соотношения
статического
и динамического
моментов.
Внешняя нагрузка
следящего
привода характеризуется
статическим
моментом Тнс,
моментом инерции
Ін,
а внутренняя
- статическим
моментом
сопротивления
в редук-торе,
учитываемым
через КПД ηр,
приведенным
моментом инерции
редуктора Ір,
момен-том инерция
ротора Ірот
электродвигателя.
Для воспроизведения
входного сигнала
двигатель
должен обеспечивать
необходи-мую
угловую скорость
ротора ω(t)
= ωн(t)∙iр
при соответствующих
значениях
вращаю-щего
момента двигателя,
равного моменту
всех сил сопротивления,
т.е. значениям
T(t) = Тнс
/(iр ηр)
+ Ін·
εн(t)/
ір + (Ірот
+ Ір)
∙ір
· εн (t)
(2.7)
и достаточную
плавность
слежения:
приведенный
к валу двигателя
момент статической
нагрузки не
должен превышать
5...1O % значения
пускового
момента электродвигателя,
а, следовательно,
передаточное
отношение
редуктора
должно удовлетворять
неравен-ству
ір
≥ γ
∙ Тнс
/Tп,
(2.8)
где γ - коэффициент
плавности
следящей системы,
а мощность
двигателя
в номи-нальном
режиме - неравенству
Nном≥
γ
·Тнс
· ωнmax
/2
(2.9)
Для систем
высокой точности
с погрешностями
установок угла
0,0002...О,001 рад принимают
γ = 10...20; при погрешностях
по углу установки
0,002...0,007 рад можно
принимать γ=
5...10.
Приведенные
методы выбора
параметров
следящего
привода не
являются общими,
а применяются
для условий,
указываемых
в наименовании
методики и во
вводной части
к ним.
А. Для режимов
с совпадающими
во времени
значениями
ωнmax
и εнmax.
Методика применима
для систем,
отрабатывающих
сигналы вида
1) θ
= ω0t;
ωнmax
=ωн
=ω0;
ε
= 0
2) θ = ω0t
+ ε0 t2
/2;ωнmax=ωн=ω0
+ ε0 tmax
; εнmax
= ε0
3) θ = θ0
(1-e-αt
); ωнmax=
ωнmax=
θ0 ·
w; |ε|нmax
= θ0 ·w2
4)
θ
= w0·t3+
w1·t2
+
w2·t;
ωнmax=;
εнmax
=
5)
θ
=2 θ0
t2
/
tn2;
ωнmax=2
θ0
/
tn;
|ε|нmax
= 2 θ0
/
tn2
используемые
в приводах
РЛС, вычислительных
механизмах,
приводах управления
и др., основной
режим работы
которых - продолжительные
или часто
повторяющиеся
пе-риоды работа
с максимальной
мощностью,
т.е. работа
двигателя в
номинальном
режиме.
Методика выбора
электродвигателя
1. Отобрать
двигатели,
быстродействие
которых, с
τ = Ірот
·
ωном
/ Тном
(2.10)
меньше требуемого
τ = ωнmax
/ εнmax
,
(2.11)
где ωном
- номинальная
угловая скорость
двигателя,
рад/c;
Tном-
номинальный
момент на валу
двигателя,
Н∙м;
ωнmax
-заданная
максимальная
угловая скорость
вала нагрузки,
рад/с;
εнmax
- заданное
максимальное
угловое ускорение
нагрузки, рад/с2.
2. Определить
полную мощность
нагрузки, Вт:
N∑ = (Tнс
/ η′р+ Iн
εнmax)
∙ωнmax
(2.12)
где Tнс
- статический
момент нагрузки,
Н∙м;
η′р - ориентировочное
значение КПД
редуктора (см.
формулу (2.3);
Iн - момент
инерции нагрузки,
кг ∙ м2.
3. Выбрать значения
коэффициента
плавности и
установить
соотношение
нагрузок:
Tнс ≥ Iн∙
εнmax
/ (0,5∙ γ-1)
(2.13)
Если Tнс
больше правой
части неравенства
(13), выбор параметров
привода выполняют
по пп.4-8, если
меньше - по пп.
9-12.
4. Определить
относительное
передаточное
отношение
αск ≥
 (2.14)
(2.14)
5. Определить
необходимую
номинальную
мощность двигателя,
Вт:
Nном
0
= (1+ α2ск)·N∑
(2.15)
и необходимый
динамический
коэффициент,
Н∙м/с2:
Кдо= (2.16)
(2.16)
6. Выбрать двигатель,
у которого
Nном ≥
Nном 0 и
Кд =
 (2.17)
(2.17)
7. Определить
оптимальное
значение
передаточного
отношения
редуктора
 (2.18)
(2.18)
8.. Если двигатель
пришлось выбрать
с большим запасом
по мощности
или Кд, проверить
возможность
применения
передаточного
отношения

при котором
обеспечивается
максимальное
быстродействие.
Его можно принять
при выполнении
условий:

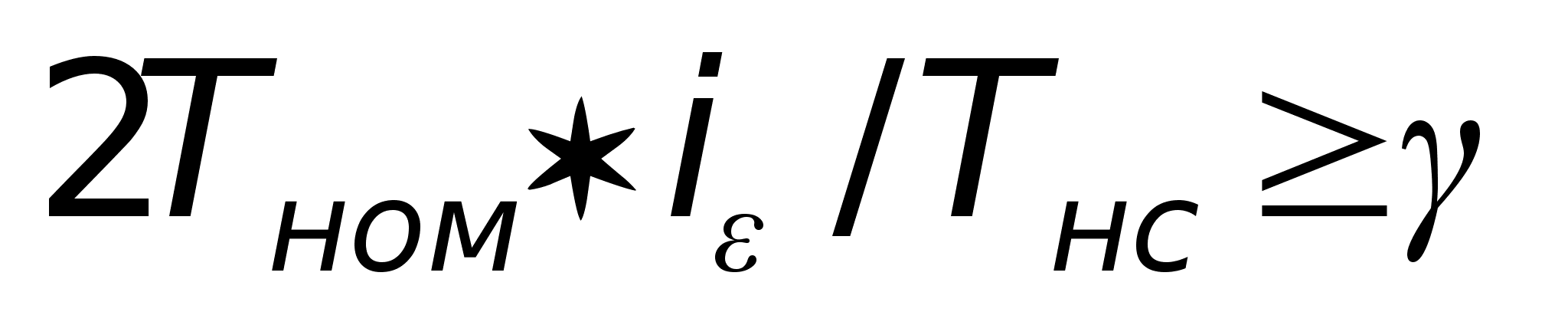 ; ;
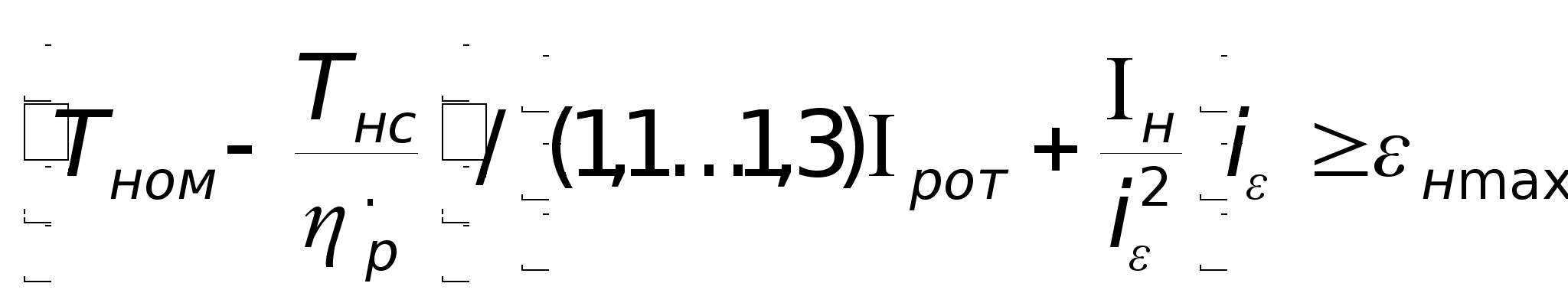 . .
9. Необходимая
мощность двигателя,
Вт:
Nном 0 =
1,5∙ N∑.
(2.20)
и необходимый
динамический
коэффициент,
Н∙м/с2,
Кдо= 4,5∙ N∑∙
εнmax
/ ωнmax.
(2.21)
10. Выбрать двигатель,
для которого
соблюдаются
условия:
 
11.
Определить
оптимальное
значение
передаточного
отношения
редуктора
из условия
 (2.22)
(2.22)
Если условие
(2.22) не соблюдается,
принять

После выполнения
геометрического
расчета редуктора
следует проверить
двига-тель по
тепловому
режиму (для
двигателей
постоянного
тока - обязательно):
Тном / Тср.кв.≥(1…1,08),
где
 (2.23)
(2.23)
Б. Для систем,
отрабатывающих
ступенчатые
входные воздействия
в опти-мальном
переходном
режиме
(εнmax
и ωнmax
совпадают во
времени)
Режим используется
в системах
дистанционного
управления,
в устройствах
ввода данных,
блоках сравнения
и согласования
и др.
Заданы: значения
входного воздействия
(угол перестановки)
Θ, рад; время
пере-ходного
процесса t,
с; момент инерции
нагрузки Iн,
кг·м2, статический
момент нагрузки
Т, Н·м; коэффициент
плавности,
принимаемый
γ = 10...20.
Методика выбора
электродвигателя,
1. Определить
параметры
оптимального
переходного
процесса:
максимальное
угловое ускорение
при пуске εнп
= 5,02∙ θн/t2п;,
расчетную
угловую скорость
ωнmax =
3,6 ∙θн/tп.
2. Определить
соотношение
нагрузок:
 .
(2.24) .
(2.24)
Если Тнс
больше правой
части неравенства
(2.24), выбор параметров
привода вы-полняют
согласно пп.3-5
(ниже), если меньше
- используют
методику А
(пп. 2; 9…11).
3. Определить
динамические
характеристики
привода:
 (2.25)
(2.25)
 (2.26)
(2.26)
4. Выбрать двигатель,
для которого
 и и

Предпочтение
следует отдавать
быстроходным
двигателям
с номинальной
часто-той вращения
ротора 6000 об/мин
и более.
5. Определить
оптимальное
передаточное
отношение
редуктора
 .
(2.27) .
(2.27)
В.- Для систем,
отрабатывающих
гармонический
сигнал вида
θ = θ0∙sinωat.
Заданы: θ0 -
амплитуда
сигнала, рад;
круговая частота,ωa=
2π/t, рад/с;
Iн, кг∙м2;
Тнс, Н∙м; γ
= 20...10, ηр.
Требование:
применять
двигатели с
линейной или
с линеаризуемой
механической
характеристикой
(см. таблица
2.1, группа Г).
Методика выбора
электродвигателя.
Определить
характеристики
управления
по выходу:
Максимальная
расчетная
угловая скорость
нагрузки:
 (2.28)
(2.28)
Нормальное
угловое ускорение
нагрузки:
 .
(2.29) .
(2.29)
Нормальная
угловая скорость
нагрузки:
 (2.30)
(2.30)
2. Определить
соотношение
нагрузок:
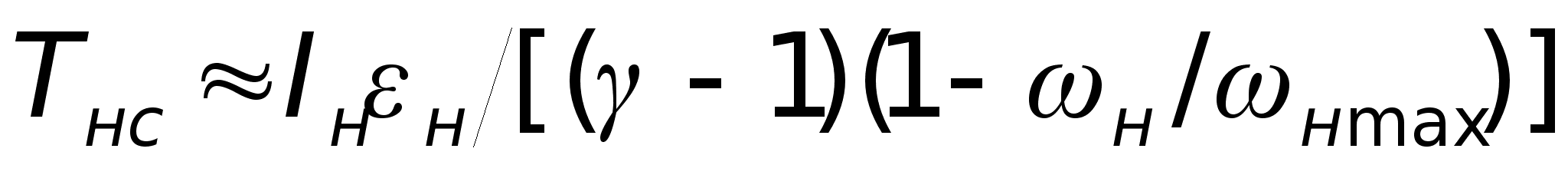 .
(2.31) .
(2.31)
Если заданный
статический
момент Тнс
больше динамического
(правая часть
не-равенства
(2.31)), выбор параметров
привода выполняют
по пп.3-5, если
меньше - по пп.6…9
3. Определить
необходимые
динамические
характеристики
двигателя
 (2.32)
(2.32)
 .
(2.33) .
(2.33)
4. Выбрать двигатель,
для которого
 ; ;
 . .
5. Определить
оптимальное
значение
передаточного
отношения
редуктора:
 . (2.34)
. (2.34)
6. Определить
необходимую
мощность двигателя,
Вт:
 .
(2.35) .
(2.35)
7.
Выбрать двигатель,
у которого
Nном≥
Nном
0.
8. Определить
оптимальное
по быстродействию
передаточное
отношение
редук-тора:
 (2.36)
(2.36)
9. Проверить
условие обеспечения
заданной
максимальной
угловой скорости:

Если условие
не выполняется,
передаточное
отношение
редуктора
 (2.37)
(2.37)
Запас по скорости
следует принимать
тем больше,
чем больше
относительное
зна-чение
статической
нагрузки.
Н  а
рисунке 2.2 изображена
нагрузочная
характеристика
привода а
рисунке 2.2 изображена
нагрузочная
характеристика
привода
 в поле механической
характеристики
двигателя
в поле механической
характеристики
двигателя
 при
гармоническом
входном сигнале.
ω при
гармоническом
входном сигнале.
ω
ір
∙ωнmax
ω A=
ір
∙ωн
A
ТТ T

 Т
Т
Рисунок 2.2
По относительному
расположению
значений
 и
и
 можно
определить
необходимое
значение
коэффициента
запаса: можно
определить
необходимое
значение
коэффициента
запаса:
 (2.38)
(2.38)
3. ОПРЕДЕЛЕНИЕ
ПЕРЕДАТОЧНЫХ
ОТНОШЕНИЙ В
ЗУБЧАТЫХ МЕХАНИЗМАХ.
С ЦИЛИНДРИЧЕСКИМИ
И КОНИЧЕСКИМИ
КОЛЕСАМИ.
3.1. Общее передаточное
отношение
механизма
определяется
по формуле:
 ,
(3.1) ,
(3.1)
где
 -
общее передаточное
отношение; -
общее передаточное
отношение;
nдв -
частота вращения
вала заданного
или выбранного
электродвигателя,
об/мин,
nвых
- частота вращение
выходного вала
механизма,
об/мин.
Значение nвых
определяется
на основании
технического
задания. При
этом возмож-ны
следующие
варианты:
1. Значение nвых
задано непосредственно
в техническом
задании.
2. Задана угловая
скорость выходного
ωвых
рад/с:
 .
(3.2) .
(3.2)
3.Задано время
движения выходного
вала tp,
с. При отом угол
поворота
выходного вала
 ,
либо задан
либо может
быть назначен
из конструктивных
соображений.
Тогда ,
либо задан
либо может
быть назначен
из конструктивных
соображений.
Тогда
  /(6
tp).
(3.3) /(6
tp).
(3.3)
4. Задан закон
движения выходного
вала
 : :
 .
(3.4) .
(3.4)
5. На выходе
механизма
осуществляется
преобразование
вращательного
движения в
поступательное
реечной парой
или парой с
гибким звеном
(лентой, тросом,
цепью):
 ,
(3.5)
,
(3.5)
где v -линейная
скорость выходного
звена, мм/с,
dk-
диаметр колеса,
преобразующего
вращательное
движение в
поступательное,
мм.
6. На выходе
механизма
осуществляется
преобразование
вращательного
движения в
поступательное
винтовой парой:
 ,
(3.6) ,
(3.6)
где
ph-
ход винтовой
линии, мм.
7.
На выходе механизма
вращательное
движение
преобразуется
в поступательное
кулачковым
механизмом:
 ,
(3.7) ,
(3.7)
где
 -
угол
поворота
кулачка (…˚),
соответствующий
времени цикла
tпост
,с
звена совершающего
возвратно-поступательное
движение. -
угол
поворота
кулачка (…˚),
соответствующий
времени цикла
tпост
,с
звена совершающего
возвратно-поступательное
движение.
8.
На выходе механизма
преобразование
вращательного
движения в
поступатель-ное
осуществляется
кривошипно-шатунным
механизмом:
 ,
(3.8) ,
(3.8)
где
 -
время цикла
звена, совершающего
возвратно-поступательное
движение. -
время цикла
звена, совершающего
возвратно-поступательное
движение.
3.2.
Выбор передаточных
отношений
ступеней в
зависимости
от функционального
назначения
механизма
заключается
в определении
рациональных
значений
состав-ляющих
уравнения:
 (3.9)
(3.9)
где
 -передаточные
отношения
первой и второй
ступеней, -передаточные
отношения
первой и второй
ступеней,
 -передаточные
отношения
предыдущей,
последующей
и последней
ступени соответственно. -передаточные
отношения
предыдущей,
последующей
и последней
ступени соответственно.
При
распределении
общего передаточного
отношения по
ступеням в
механизмах
приводов, систем
управления
и регулирования
необходимо
обеспечить:
-
минимальные
размеры и массу
механизмов,
в том случае,
если к
ним
не предъяв-ляется
требование
малоинерционности;
-
минимальный
момент инерции,
приведенный
к входному
валу механизма.
3.3
В соответствии
с функциональным
назначением
и условиями
нагружения
звеньев механизмы
при распределении
передаточных
отношений
между ступенями
делятся на 5
типов:
-
тип I: нереверсивные
силовые зубчатые
механизмы, у
которых размеры
зубчатой пары
и долговечность
определяются
контактной
прочностью
рабочих поверхностей
зубьев;
-
тип 2: реверсивные
силовые механизмы,
у которых размеры
зубчатой пары
и дол-говечность
определяются
изгибной прочностью
сердцевины
зубьев;
-
тип 3: малонагруженные
кинематические
зубчатые механизмы,
размеры звеньев
которых выбираются
из конструктивных
соображений,
а напряжения
в
материалах
нас-только
малы, что на
размеры колес
влияния практически
не оказывают;
-
тип 4: реверсивные
силовые малоинерционные
механизмы, у
которых
долговеч-ность
и размеры зубчатой
пары определяются
изгибной прочностью;
-тип
5: реверсивные
малонагруженные
кинематические
малоинерционные
зубча-тые механизмы,
у которых напряжения
малы и на размеры
колёс влияния
практически
не оказывают.
-тип
6: малонагруженнный
кинематический
механизм с
минимальной
суммарной
кинематической
погрешностью
передачи.
Формулы
для определения
составляющих
уравнения
(3.10) приведены
в таблице 3.1.
Они
получены из
условий, что
все зубчатые
колеса данного
механизма
геометри-чески
подобны, т.е.
относительная
ширина зубчатых
венцов
 одинако-ва, а
числа зубьев
всех ведущих
колес в зубчатых
парах равны.
одинако-ва, а
числа зубьев
всех ведущих
колес в зубчатых
парах равны.
3.4. Выбор и определение
чисел зубьев
зубчатых колес
в ступенях
производят
по формуле
Z2
= Z1 ik
,
(3.11)
где
Z1
и
Z2
числа зубьев
ведомого и
ведущего колес
зубчатой пары
соответственно.
Числа зубьев
ведущих колёс
выбирают одинаковыми
во всех ступенях;
по конструктив-ным
соображениям,
для силовых
механизмов
Z1=16…20,
для кинематических
Z2=
18...24.
Таблица
3.1 Распределение
суммарного
передаточного
отношения по
ступеням
Критерий
|
Вид
механизма
|
|
Силовой
|
Малонагруженный
|
|
Количество
ступеней
|
|
задано
|
не
задано
|
задано
|
не
задано
|
Минимальный
объем переда-чи
|
Не
ревер сивный
|

|
i1=i2=i3=…=
= ik=
= i = 2,89
nопт=
0,942 lni∑
|
i1
=
i2
=
i3
=…=
in=
ik
=
1,895
nопт=
1,564 lni∑
|
|
реверсивный
|

|
i1=i2=i3=…=
= ik=
= i = 2,414
nопт=
1,1346 lni∑
|
|
Минима-
льный приведен-ный
момент инерции
передачи
|
Не
ревер сивный
|
ik+1=0,854i1,2
|
i1=i2=i3=…=
= ik=
= i = 2,176
nопт=
1,286
lni∑
|

|
i1
=
i2
=
i3
=
=…= in=
ik
=
= 1,554
nопт=2,269*
*lni∑
|
|
Ревер-сивный
|

|
i1=i2=i3=…=
= ik=
= i = 1,806
nопт=
1,692 lni∑
|
|
Минимальная
сум-марная
кинемати-ческая
погрешность
|
|

ikmin=
1,202nопт=0,2*lni∑
|
3.5. Допустимые
отклонения
передаточных
отношений в
механизмах.
При реализации
разработанной
кинематической
схемы из-за
дискретности
значе-ний чисел
зубьев, которые
должны быть
целыми, чаще
всего приходится
отклоняться
от расчетных
значений
передаточных
отношений
в ступенях и
значения общего
переда-точного
отношения
механизма.
Допускаемое
отклонение
общего передаточного
отно-шения:
+2%…-5 %. В кинематических
механизмах
отсчетных
устройств
погрешность
общего передаточного
отношения
недопустима.
В силовых механизмах
типа 1 и 2 наи-более
точно должны
быть реализованы
передаточные
отношения
последних
ступеней, а в
малоинерционных
механизмах
типа 4 и 5 - первых
двух-трех ступеней.
4.
расчет геометрии
зубчатых ПЕРЕДАЧ
ЗАЦЕПЛЕНИЯ.
4.1. Эвольвентные
цилиндрические
передачи внешнего
зацепления.
Для зубчатых
цилиндрических
передач используются
термины, определения
и обозна-чения,
установленные
ГОСТ 16530-83 и ГОСТ
16531-83.
В качестве
стандартной
величины зубчатых
передач, для
обеспечения
взаимозаме-няемости
выбран модуль
зацепления
m = p/π.
Стандартный
ряд модулей
регламентиро-ван
ГОСТ 9563-60. Значения
модулей в
диапазоне от
0,1 до 5 мм, охватывающем
обла-сть механизмов
приборов, приведены
в таблице 4.1.
Таблица 4.1- Стандартные
ряды модулей
зубчатых передач,
мм
| Ряд
1 Ряд 2 |
0.1 |
0,12 |
0,15 |
0,2 |
0,25 |
0,3 |
0,4 |
0,5 |
0,6 |
| 0,11 |
0,14 |
0,18. |
0,22 |
0,28 |
0,35 |
0,45 |
0,55 |
0,7 |
| Ряд
1 Ряд 2 |
0,8 |
1,0 |
1,25 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
| 0,9 |
1,125 |
1,375 |
1,75 |
2,25 |
2,75 |
3,5 |
4,5 |
|
Исходнымым
контуром для
определения
размеров и
формы зубьев
колес эвольвент-ного
зацепления
является
теоретический
исходный контур
рейки, стандартизованный
для передач
с модулем m
≤1мм ГОСТ 9587-81, а
для m
> 1
мм
-
ГОСТ 13755-81. Стан-дартные
параметры
профилей: угол
профиля α = 20°,
коэффициент
высоты головки
зуба h*a=
1, радиального
зазора
с*
= 0,25.
4.1.2.
Смещение исходного
контура в
эвольвентных
зубчатых передачах.
Примене-ние
передач со
смещением
позволяет
существенно
повысить нагрузочную
способность
и долговечность
передачи.
Положительное
смещение исходного
контура увеличивает:
изгибную прочность,
т.к. основание
зуба становится
шире; контактную
прочность, т.
к, уменьшается
кривизна
контактирующих
профилей зубьев;
долговечность,
т.к. подбо-ром
коэффициентов
смещения можно
уменьшить
относительное
скольжение
сопрягае-мых
профилей и,
следовательно,
их износ. При
применении
оптимальных
смещений повышение
изгибной прочности
зубьев может
достигать 70
%,
контактной
30 %,
долго-вечности
по износу 50 %.
При
этом технология
и стоимость
изготовления
колес со смещением
не изменяются
по сравнению
с нулевыми
(без смещения).
Применение
смещения позволяет
также наиболее
простым способом
получить заданное
межосевое
расстояние
в передаче,
без использования
косозубых
колес, более
сложных технологи-чески
и менее точных
кинематически.
Поэтому эвольвентные
цилиндрические
передачи, у
которых качественные
показа-тели
должны быть
высокими, необходимо
проектировать
с оптимальными
коэффициен-тами
смещения.
4.2. Выбор коэффициентов
смещения исходного
контура X .
Значения
коэффициентов
смещения исходного
контура зубчатых
колес в паре
X1, и X2
должны обеспечить
изготовление
зубьев без
подрезания
и заострения,
а коэффициент
перекрытия
в передаче
должен быть
не менее 1,2; кроме
того, они определяются
назна-чением
передачи, т.е.
необходимостью
получить
максимальную
изгибную или
контакт-ную
прочность, или
максимальную
износостойкость,
а также тем,
задано межосевое
расстояние
или нет.
Значение минимально
необходимого
коэффициента
смещения Хmin,
обеспечи-вающее
отсутствие
подрезания
рабочего профиля,
может быть
рассчитано
по формуле:
Xmin=
hl*-
ha*-
0,5 ·z ·sin2
α,
(4.1)
где - hl*,
ha*коэффициенты
граничной
высоты и высоты
головки зуба,
z- число
зубьев колеса,
α - угол
профиля.
Для стандартных
исходных контуров
hl*-
ha*=
1.
В
силовых передачах
с относительно
низкой твердостью
поверхностей
зубьев НВ≤350
несущая способность
определяется
контактной
прочностью
и суммарный,
коэф-фициент
смещения
ХΣ
= X1+
Х2
должен
иметь максимально
возможное
значение. У
зубьев с высокой
твердостью
критичной
является изгибная
прочность, при
этом, для обеспечения
равной прочности
зубьев колес
пары коэффициент
смещения X1
меньшего колеса
должен быть
максимальным.
В точных силовых
и кинематических
передачах
необходимо,
чтобы износ
зубьев обоих
колес был
минимальным,
что обеспечивается
большим коэффициентом
смещения большего
колеса. Если
межосевое
расстояние
в прямозубой
передаче не
задано, коэффициенты
смещения колес
выбирают по
таблице 4.2, в
соответствии
с критерием,
который для
передачи является
определяющим:
К - условие
наибольшей
контактной
прочности, И
- условие наибольшей
изгибной проч-ности,
ИЗ - условие
наибольшей
износостойкости.
При
выборе коэффициентов
смещения по
этой таблице
обеспечиваются
относите-льная
толщина эубьев
на поверхности
вершин s*a
≥ 0,25 и коэффициент
перекрытия
εα
≥
1,2. Промежуточные
значения
коэффициентов
смещения находят
линейным
интер-полированием.
В
передачах с
заданным межосевым
расстоянием
aw
не равным
делительному
a
= 0,5 m
(z1+
z2)
рассчитывают
суммарный
коэффициент
смещения
ХΣ
(раздел 4.3), а затем
производят
его разбивку
на составляющие
X1
и Х2
в соответствии
с определяющи-ми
критериями
для передачи,
пропорционально
значениям
X1
и Х2
в
соответствующих
графах таблицы
4.2, по формулам:

 ,
(4.2) ,
(4.2)
 -
значение суммарного
коэффициента
смещения в
таблице 4.2 для
соответствующих
значений Z1
и
Z2.
-
значение суммарного
коэффициента
смещения в
таблице 4.2 для
соответствующих
значений Z1
и
Z2.
При этом должно
быть: X∑∑T
и, кроме того,
Х1 >Х1min,
X2 >X2min.
Значения минимально
необходимых
коэффициентов
смещения находят
по формуле
(4.1)
|
Таблица
4.2
|
|
Z2
|
Z1
|
|
Крите-рий
|
12
|
14
|
16
|
18
|
20
|
22
|
24
|
26
|
28
|
30
|
34
|
38
|
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
X1
|
X2
|
| 18 |
К
И ИЗ |
0,60
0,45 0,49 |
0,20
0.41 0.36 |
0,69
0,48 0,50 |
0.21
0,47 0,45 |
0,63
0,52 0,52 |
0,39
0.52 0,51 |
0,55
0,55
0,55
|
0.55
0,55
0,55
|
—
|
—
|
—
|
---
|
---
|
—
|
—
|
--- |
---
|
— |
— |
--- |
---
|
— |
— |
--- |
|
22
|
К
И ИЗ |
0,65
0,49 0,54
|
0,23
0,48 0,41
|
0,86
0,51
0,56
|
0,03
0,55 0,51
|
0,86
0,53 0.58
|
0,18
0,57
0.57
|
0,82
0,52
0,61
|
0,37
0,55 0,62
|
0,76
0,56
0,64
|
0.54
0,58
0,66
|
0,68
0,51
0,68
|
068
0,51 0,68
|
— |
— |
--- |
---
|
— |
— |
--- |
---
|
— |
— |
--- |
---
|
| 26 |
К
И ИЗ |
0,76
0.50 0,57 |
0,13
0,55 0.47 |
0,88
0.53 0,59 |
0,08
0,63 0,57 |
0,96
0,50 0,62 |
0,09
0,59
0,64
|
1,02
0,49
0,64
|
0,14
0,55
0,69
|
0,98
0,52
0,68
|
0,33
0.59
0,73
|
0,93
0.45
0.72
|
050
0.48 0,76 |
0,86
0,47 0,76 |
0,67
0,49 0,78 |
0,80
0,43 0,80 |
0,80
0,43 0,80 |
— |
— |
-- |
— |
-- |
— |
— |
— |
|
30
|
К
И ИЗ |
0,77
0,52 0,59
|
0,18
0,63 0,53
|
0,88
0.50 0,61
|
0.13
0.64 0.64
|
0,99
0,49 0,64
|
0,09
0,62
0,71
|
1,08
0,45
0.67
|
0,08
0,55
0,76
|
1,15
0,44
0,71
|
0,10
0,53
0,81
|
1,13
0.44
0,74
|
0,29
0,51 0,84
|
1,09
0,38 0,78 |
0,47
0,43 0,86 |
1,03
0,40 0,82 |
0,63
0,43 0,88 |
0,97
0,32 0,86 |
0.77
0,33
0.89
|
0,90
0,340,90
|
0,90
0,34 0,90 |
— |
— |
— |
— |
|
34
|
К
И ИЗ |
0,76
0,50 0,61
|
0,27
0,67 0,59
|
0,90
0,50 0,62
|
0.17
0,69 0,70
|
0,98
0,42 0,65
|
0,18
0,56
0,78
|
1,06
0,390,69
|
0,19
0,51
0,85
|
1,20
0,39
0,72
|
0,06
0,50
0,88
|
1,220,39
0,76 |
0,17
0,48 0,91
|
1,26
0.33 0,80 |
0,25
0,40 0,94 |
1,22
0,33 0,84 |
0,44
0,39 0,96 |
1^9
0,29 0,88 |
0,59
0,32
0,97
|
1,13
0,28
0,92
|
0,73
0,30 0,98 |
1.00
0,27
1,00
|
1,00
0,27
1.00
|
— |
--- |
|
40
|
К
И ИЗ |
0,76
0,46 0,62
|
0,37
0,65 0,68
|
0,91
0,43 0,64
|
0.24
0,63 0,81
|
1,01
0.37 0,67
|
0,19
0,51
0,89
|
1.05
0,37
0,70
|
0,31
0,54
0,95
|
1,18
0,35
0,73
|
0,17
0,50
1,00
|
1,22
0,33
0,77
|
0,27
0,47 1,03
|
1,25
0,30 0,81 |
0,35
0,41 1,05 |
1,28
0,29 0,85 |
0,43
0,37 1,07 |
1,31
0,26 0,89 |
0,49
0,33 1,09 |
1,34
0,19 0,93 |
0,54
0,23 1.10 |
1,31
0,18
1,01
|
0,76
0,20 1,12 |
1,200,19
1,09 |
1.01
0,191,13 |
| 50 |
К
И ИЗ |
0,80
0,43 0,64 |
0,40
0,70 0,83 |
0,90
0,39 0,66 |
0,31
0,64 0,97 |
1,02
0,34 0,68 |
0,29
0,56
1,07
|
1,11
0.28
0,71
|
0,26
0,44
1,13
|
1,15
0.29
0,75
|
0,38
0,49
1,18
|
1,20
0,24
0,78
|
0,43
0,38 1,22 |
1,23
0,23 0,82 |
0,52
0.37 1,24 |
1,26
0,22 0,86 |
0,60
0,34 1,26 |
1,29
0,23 0,90 |
0,67
0,30
1,28
|
1,32
0,17
0,94
|
0,72
0,26 1.30 |
1,37
0,131,01
|
0,82
0,19
1,31
|
1,42
0,091.10
|
0,90
0,13
1,32
|
|
60
|
К
И ИЗ |
0,82
0,39 0,65
|
0,49
0,66 0,97
|
0,93
0,31 0,66
|
0,43
0,50 1,12
|
1,03
0,27 0,69
|
0,37
0,44
1,22
|
1,13
0.26
0,72
|
0,32
0,46
1,30
|
1,16
0,25
0,75
|
0,34
0.48
1,35
|
1,19
0,24
0,78
|
0,53
0,48 1,39
|
1,22
0,17 0,82 |
0,66
0,31 1,42 |
1,25
0,16 0,86 |
0,76
0,30 1,45 |
1,27
0,13 0,89 |
0,84
0,241,47
|
1,30
0,12
0,93
|
0,90
0,23 1,48 |
1.35
0,091,01
|
1,00
0,171,50
|
1,40
0,06
1,09
|
1.09
0,11
1,51
|
| 80 |
К
И ИЗ |
0,83
0,30 0.65 |
0,66
0,47 1.23 |
0,93
0,26 0.69 |
0,60
0,44 1.40 |
1,04
0,21 0,69 |
0,54
0,38
1,52
|
1,12
0,21
0,72
|
0,47
0,47
1,60
|
1.12
0,19
0.75
|
0,24
0,43
1,67
|
1.13
0,17
0,78
|
0,26
0,41 1,72 |
1,20
0.10 0,81 |
0,87
0,23 1,75 |
1,20
0,11 0,84 |
0,71
0,30 1,77 |
1,22
0,12 0,88 |
0,75
0,34 1,80 |
1,25
0,08 0,92 |
0,92
0,23 1.82 |
1,32
0,10 0.99 |
1,28
0,30 1,84 |
1.37
-0,04 1.07 |
1,40
-0,01 1,85 |
| 100 |
К
И ИЗ |
0.84
0,30 0,66 |
0.82
0,62 1,46 |
0,94
0,20 0,67 |
0,74
0,28
1,66
|
1,04
0,20 0.69 |
0.67
0,45
1,79
|
1,11
0,17
0,71
|
0.58
0,40
1,88
|
1,11
0,16
0,74
|
0,31
0,44
1,96
|
1,10
0,13
0,77
|
0,12
0,41 2.00 |
1,11
0,10 0,80 |
0,16
0,33 2,05 |
1,20
0,10 0,83 |
1,10
0,37 2,08 |
1,20
0,10 0.87 |
0,93
0,39
2,10
|
1,20
0,06
0,90
|
0,78
0,29 2,12 |
1,24
0,02
0,97
|
0,95
0,1 7 2,14 |
1,30
0,04
1,04
|
1.24
0,26 2,16 |
| 120 |
К
И ИЗ |
0,84
0,30 0,66 |
0,96
0,79 1,68 |
0,94
0,20 0.67 |
0,88
0.37 1,89 |
1,04
0,20 0.69 |
0,82
0,58
2,04
|
1,50
0.10
0,70
|
0,67
0,11
2,12
|
1,10
0,11
0,73
|
0,47
0,32
2,22
|
1,10
0,10
0,76
|
0,33
0,36 2,28 |
1,10
0,10 0,79 |
0,21
0,41 2.32 |
1,20
0.00 0,82 |
1,49
0,22 2,35 |
1,20
0,09 0,85 |
1,28
0,46
2,38
|
1,20
0,00
0,88
|
1,11
0,13 2,40 |
1,20
0,00
0,92
|
0,83
0,20
2,33
|
1,30
-0,01 0,96 |
1,64
0,19
2,30
|
| 140 |
К
И ИЗ |
0,84
0,30 0,66 |
1.08
0,95 1,88 |
0,95
0.20 0,67 |
1,00
0,47 2,11 |
1,05
0.20 0,68 |
0,94
0,72
2,27
|
1,10
0,10
0,70
|
0,92
0,17
2,37
|
1,10
0,10
0,73
|
0.71
0,34
2,46
|
1,10
0,10
0,75
|
0,54
0,45 2,51 |
1,10
0,10 0,78 |
0,40
0,54 2,57 |
1,10
0,10 0.80 |
0,28
0,58 2,59 |
1,10
0,00 0,82 |
0,20
0,14
2.56
|
1,20
0,00
0,84
|
1,44
0,20 2,54 |
1,20
0,00
0:87
|
1.12
0,26
2.47
|
1,43
-0,02 0,90 |
-1,20
0,26
2,42
|
| 160 |
К
И ИЗ |
0,85
0,30 0,66 |
1,20
0,99 2,06 |
0,95
0,20 0,67 |
1,12
0,57 2,31 |
1,05
0,20 0,68 |
1,05
0,85 2,48 |
1,05
0,10 0,70 |
0,74
0,23 2,60 |
1,10
0,10 0,72 |
0,94
0,42 2,29 |
1,10
0,10 0,74 |
0,74
0,55 2,75 |
1,10
0,10
0,76
|
0,59
0,64 2,77 |
1,10
0,00 0.77 |
0,46
0,10
2,73
|
1,10
0,00 0,79 |
0,34
0,20
2,70
|
1,10
0,00
0,80
|
0,25
0,26 2,67 |
1,32
-0,03
0,83
|
-1,15
0,19
2,60
|
1,43
-0,02
0,86
|
-1,20
0,33
2,52
|
| 200 |
К
И ИЗ |
— |
— |
--- |
---
|
— |
— |
--- |
---
|
— |
— |
--- |
---
|
1,10
0,00 0.72 |
0,97
0,05 3.04 |
1,10
0,00 0.73 |
0,80
0,20 3,00 |
1,14
0,00 0.74 |
-1,07
0,31
2,94
|
1,10
0,00
0,75
|
0.54
0,39 2.91 |
1,32
0,00
0,77
|
1.16
0,49
2,82
|
1,43
- 0,10
0,79
|
-
1,21 0,02
2,75
|
| 240 |
К
И ИЗ |
— |
— |
--- |
---
|
— |
— |
--- |
---
|
— |
— |
--- |
---
|
1,10
0,00 0,69 |
1,34
0,12 3,27 |
1,10
0,00 070 |
1,14
0,29 3,21 |
1,14
0,01)
0,70
|
1,06
0.42
3.17
|
1,10
0.00
0.71
|
0,84.
0,52 3.10 |
1,32
-
0,10
0,72
|
-
1,15
-
0,07
3,02
|
1,43
-
0,10
0,74
|
-1.21
0,09
2,95
|
4.1.3. Расчет геометрических
параметров
прямозубых
цилиндрических
эвольвент-ных
передач внешнего
зацепления
производится
по формулам
таблицы 4.3
Таблица 4.3
| Наименование
параметра |
Обозначения,
расчетные
формулы, указания
|
Исходные
данные
|
| Числа
зубьев |
Шестерни
и колеса |
 ,
Z2 ,
Z2
|
| Модуль,
мм |
m- по ГОСТ
9563-60 |
| Нормальный
исходный контур |
m<1 – по
ГОСТ 9587-81
|
|
m 1
– по ГОСТ 13755-81 1
– по ГОСТ 13755-81
|
| Коэффициенты
смещения: |
Шестерни
и колеса |
 , ,
 -
в соответствии
с п.4 и таблицей
4.2 -
в соответствии
с п.4 и таблицей
4.2
|
Основные
геометрические
параметры
|
| Делительные
диаметры, мм: |
Шестерни |

|
| Колеса |

|
| Делительное
межосевое
расстояние,
мм |

|
| Коэффициент
суммы смещений |

|
| Угол
зацепления,
рад |

|
| Межосевое
расстояние,
мм |

|
| Коэффициент
воспринимаемого
смещения |

|
| Диаметры
вершин зубъев,
мм |
Шестерни |

|
| Колеса |

|
| Диаметры
впадин, мм |
Шестерни |

|
| Колеса |

|
| Высота
зубъев, мм |
Шестерни |

|
| Колеса |

|
| Передаточное
число |
u=z2/z1
|
| Начальные
диаметры, мм |
Шестерни |

|
| Колеса |
 или
или

|
Геометрические
показатели
качества
зацепления
|
| Углы
профилей на
поверхностях
вершин |
шестерни |

|
| колеса |

|
| Толщина
зубьев на
поверхностях
вершин, мм: |
шестерни |

|
| колеса |

|
|
Коэффициент
торцового
перекрытия
|
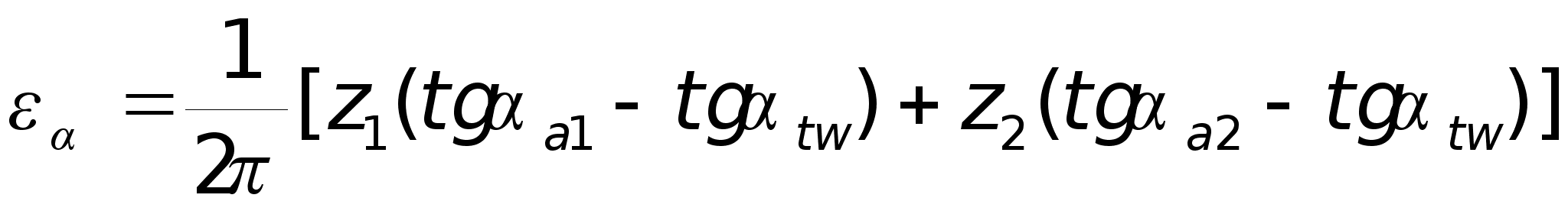
|
4.1.4 Размеры
для контроля
По размерам
для контроля
определяется
точность изготовления
зубчатого
вен-ца; эти размеры
вместе с их
предельными
отклонениями
проставляются
на рабочем
чертеже зубчатого
колеса.
1. Размер по
измерительным
роликам.
Размер по роликам
(шарикам) для
цилиндрических
прямозубых
и косозубых
ко-лес с внешними
зубьями при
их четном числе
определяеся
по формуле:
=dD
+ в .
(4.3)
То же при нечетном
числе зубьев:
M= dDcos(90/z)
+ D.
(4.4)
При этом должно
выполняться
условие: M>da.
В формулах
(4.3) и (4.4): D- диаметр
измерительного
ролика (шарика)
опреде-ляется
из условия D
1,7∙ m. При
этом стандартные
значения диаметров
роликов выбираются
из ряда: ( ГОСТ
2475-62): 0,260; 0,289; 0,346; 0,404; 0,433; 0,462; 0,577; 0,722;
0,866; 1,010; 1.023; 1,155; 1,193; 1,302; 1,432; 1,443; 1,591; 1,732;
1,790; 2.021; 2,045; 2,309; 2,387; а стандартные
значения диаметров
шариков из
ряда: (ГОСТ 3722-8I):
0,25; 0,3; 0,36; 0,4; 0,5; 0,508; 0,6; 0,635; 0,68; 0,7; 0,8; 0,85;
1,00; 1,2; 1,3; 1,5; 1,588; 1,984; 2,0; 2,381; 2,5.
dD
- диаметр окружности,
проходящей
через центр
ролика (шарика):
dD =
d cost
/cosD
; (4.5)
D - угол
профиля зуба
на окружности
диаметра dD,
который может
быть найден
из системы
уравнений
invD
= invt
+ D/(z⋅m⋅cost)
– (/2
–2⋅x ⋅tg)/z
; (4.6)
D =
1,3945(invD
+ 1,66 10-3)
0,235 –
0,183.
(4.7)
2. Расчет длины
общей нормали
Wm .
Определение
длины общей
нормали производят,
последовательно
рассчитывая:
А) угол профиля
αx в точке
на концентрической
окружности
диаметром
dx =
d +2xm:
 (4.8)
(4.8)
 
Рисунок 4.1
Б) расчетное
число зубьев
в длине общей
нормали
 . (4.9)
. (4.9)
В) действительное
число зубьев
zn,
охватываемое
при контрольном
замере, полу-чается
округлением
znr
до ближайшего
целого значения;
Г) длину общей
нормали
 (4.10)
(4.10)
Предельные
отклонения
длины общей
нормали и размера
по роликам
опреде-ляются
для мелкомодульных
передач - по
ГОСТ 9178-81, а для
передач с модулем
m ≥ 1 мм – по
ГОСТ 1643-81.
4.2 Расчет
геометрии
прямозубых
цилиндрических
эвольвент-ных
передач внутреннего
зацепления.
4.2.1. Термины,
определения
и обозначения,
модули
и параметры
исходного
кон-тура прямозубых
цилиндрических
звольвентных
передач внутреннего
зацепления
- по п 4.1.1 - 4.1.3.
4.2.2. Смещение
исходного
контура передач
внутреннего
зацепления
выбирают по
таблице 4.4.
4.2.3. Расчет геометрии
прямозубых
цилиндрических
эвольвентных
передач вну-треннего
зацепления
в соответствии
с Г'ОСТ 19274-73 приведен
в таблице 4.5,
Таблица
4.4 Коэффициенты
смещения
 для передач
внутреннего
зацепле-ния
при m=1…2
мм
для передач
внутреннего
зацепле-ния
при m=1…2
мм
|
Z2
|
Z1
|
| 16 |
20 |
25 |
32 |
40 |
50 |
63 |
80 |
100 |
| 63 |
0,5
0,6
0
|
0,5
0,6
|
0,4
0,6
|
0,4
0,6
|
0,4
0,6
|
- |
- |
- |
- |
| 80 |
0,5
1,0
|
0,5
1,0
|
0,5
1,0
|
0,5
1,0
|
0,5
1,0
|
0,5
1,0
|
- |
- |
- |
| 100 |
0,5
1,0
|
0,5
1,0
|
0,5
1,0
|
0,5
1,0
|
0,6
1,2
|
0,6
1,2
|
- |
- |
- |
| 125 |
- |
0,5
1,4
|
0,5
1,4
|
0,5
1,4
|
0,5
1,4
|
0,6
1,4
|
0,6
1,4
|
- |
- |
| 160 |
- |
- |
- |
0,5
1,0
|
0,5
1,0
|
0,6
1,0
|
0,6
1,0
|
0,6
1,0
|
0,8
1,2
|
| 200 |
- |
- |
- |
0,6
1,0
|
0,6
1,0
|
0,6
1,0
|
0,6
1,0
|
0,8
1,1
|
1,0
1,0
|
Примечание:
Обеспечиваются:
εα >1,2;
s*a
> 0,3; c*>
0,1.
Таблица 4. 5
| Наименование
параметра |
Обозначение,
расчетные
формулы, указания |
| Исходные
данные |
| Числа
зубьев |
шестерни |
Z1
|
| колеса |
Z2
|
| Модуль |
по ГОСТ
9363-60, табл.4.1 |
| Нормальный
исходный контур |
по ГОСТ
9587-81 по ГОСТ 13755-81 |
| Основные
геометрические
параметры |
| Коэффициенты
смещения |
См. таблицу
4.4 |
| Делительные
диаметры |
шестерни |

|
| колеса |

|
| Делительное
межосевое
рас-стояние |

|
| Коэффициент
разности
смеще-ний |

|
| Угол
зацепления |

|
| Межосевое
расстояние |

|
| Диаметры
вершин зубьев |
шестерни |

|
| колеса |

|
| Диаметры
впадин |
шестерни |

|
| колеса |

|
| Высота
зубьев |
шестерни |

|
| колеса |

|
| Передаточное
число |

|
| Начальные
диаметры |
шестерни |

|
| колеса |

|
| Геометрические
показатели
качества
зацепления |
| Углы
профилей на
поверностях
вершин |
шестерни |

|
| колеса |

|
|
Толщина
зубьев на
поверхностях
вершин
|
шестерни |

|
| колеса |

|
| Koэффициент
торцового
пере- тия |

|
Примечание.
Для стандартных
исходных контуров:
 ; ;

Определение
угла зацепления
 производят
так же как и
для передач
внешнего зацеп-ления
в соответствии
с формулой в
таблице 4.3, принимая
=xd/(z2
– z1). производят
так же как и
для передач
внешнего зацеп-ления
в соответствии
с формулой в
таблице 4.3, принимая
=xd/(z2
– z1).
4.3. Расчет
геометрии
реечных цилиндрических
прямозубых
передач
4.3.1. Тернины, определения
и обозначения,
модули и параметры
исходных конту-ров
реечных передач
- по пп . 4.1.1- 4.1.3.
4.3.2 Расчет геометрии
зубчатого
колеса и рейки
приведен в
таблице 4.6.
Таблица 4.6. Реечные
цилиндрические
прямозубые
передачи.
Расчет геометрических
параметров
| Наименование
параметра |
Обозначения,
расчетные
формулы, указания |
| Исходные
данные |
| Число
зубьев зубчатого
колеса |
Z1
|
| Модуль,
мм |
m-- по
ГОСТ 9563-75 |
| Нормальный
исходный контур |
m <1мм
по ГОСТ 9587-8I;m>1
по ГОСТ
13755-81
|
| Коэффициент
смещения
зубча-того
колеса |

|
| Высота
рейки, мм |
H |
|
Длина
нарезанной
части рей-ки,
мм
|
L |
|
Основные
геометрические
параметры
|
| Рейка |
| Нормальный
шаг, мм |

|
| Число
зубьев |

|
| Уточненная
длина нарезанной
части |

|
| Высота
зуба, мм |

|
| Высота
головки зуба,
мм |

|
| Толщина
зуба, мм |

|
| Расстояние
от базовой
плоско-сти
рейки до оси
колеса, мм |

|
| Диаметр
измерительного
роли-ка, мм |
 ;
принимают
по ГОСТ 2475-62 ;
принимают
по ГОСТ 2475-62
|
| Расстояние
от базовой
поверх-ности
до ролика, мм |

|
| Зубчатое
колесо |
| Делительный
диаметр, мм |

|
| Диаметр
вершин зубьев,
мм |

|
| Диаметр
впадин, мм |

|
| Геометрические
показатели
качества
задапления |
| Толщина
зубьев на
поверности
вершин, мм |

|
Коэффициент
перекрытия
|
 
|
4.4. Расчет
геометрии
конических
прямозубых
передач
4.4.1. Термины, определения
и обозначения,
относящиеся
к этим передачам,
уста-новлены
ГОСТ 16530-83 и ГОСТ
19325-73.
4.4.2. Модули конических
передач соответствуют
модулям цилиндрических
и установлены
ГОСТ 9563-75.
4.4.3. Исходный
контур конической
передачи. Аналогом
зубчатой рейки
для кони-ческой
передачи является
плоское коническое
колесо с углом
делительного
конуса
δ = 90°, профиль
зубьев которого
на внешнем
делительном
диаметре
соответствует
профилю исходного
контура. Исходные
контуры: для
m< I мм - по
ГОСТ 9587-81, для m>1мм
ГОСТ I3754-8I
(последний
практически
совпадает с
контуром
цилиндрических
передач по ГОСТ
I3755-8I) .
4.4.4. Осевая форма
зубьев. В соответствии
с ГОСТ 19325-73 различают
три фор-мы зубьев
конических
колес, определяемые
положением
вершин конусов
делительного
8 , выступов
δn и впадин
δf на оси
колеса. Наиболее
часто применяют
форму I –
пропор-ционально
понижающиеся
зубья - все вершины
конусов совпадают.
4.4.5. Выбор чисел
зубьев колес
в конических
передачах.
Понижающие
кониче-ские
передачи следует
выполнять с
передаточным
числом до 10,
повышающие
- до 3,15. Для ортогональных
конических
передач (угол
пересечения
oceй Σ
= 90°) числа зубьев
шестерни и
колеса дожны
соответствовать
друг другу:
число зубьев
шестерни
12 13 14 15 16 17
минимальное
число зубьев
колеса 30 26 20 19
18 17
4.6.6. Смещение
исходного
контура. Для
обеспечения
максимальной
износостой-кости
применяют
положительное
смещение
производящего
колеса для
шестерни и
отрицательное,
равное по модулю
предыдущему,
для колеса: x1
= -x2 (табл.
4.8).
4.4.7. Расчет геометрии
прямозубых
конических
передач с осевой
формой зубьев
I в соответствии
с ГОСТ 19624-74 приведен
в таблице 4.7.
Таблипа 4.7. Конические
прямозубые
передачи Расчет
геометрических
параметров
|
Наименование
параметра
|
Обозначение,
расчетные
формулы указания |
| Исходные
данные |
| Числа
зубьев |
шестерни |
Z1
|
| колеса |
Z2
|
| Модуль,
мм |
me-
по ГОСТ 9563-60,
|
| Нормальный
исходный контур |
me<
по ГОСТ 9587-81; me>1
по ГОСТ 13754-81
|
| Коэффициенты
смещения |
шестерни |

|
| колеса |
x2=-x1
|
| Межосевой
угол |
Σ |
| Основные
геометрические
параметры |
| Число
зубьев плоского
колеса |

|
| Внешнее
конусное
расстояние,
мм |

|
|
Ширина
зубчатого
венца, мм
|
 ; ;

|
|
Среднее
конусное
расстояние,мм
|

|
| Средний
окружной модуль,
мм |

|
|
Внешний
делитель-ный
диаметр, мм
|
шестерни |

|
| колеса |

|
| Средний
делитель-ный
диаметр, мм |
шестерни |

|
| колеса |

|
| Передаточное
число |

|
| Угол
делительного
конуса |
шестерни |

|
| колеса |

|
|
Внешняя
высота го-ловки
зуба, мм
|
шестерни |
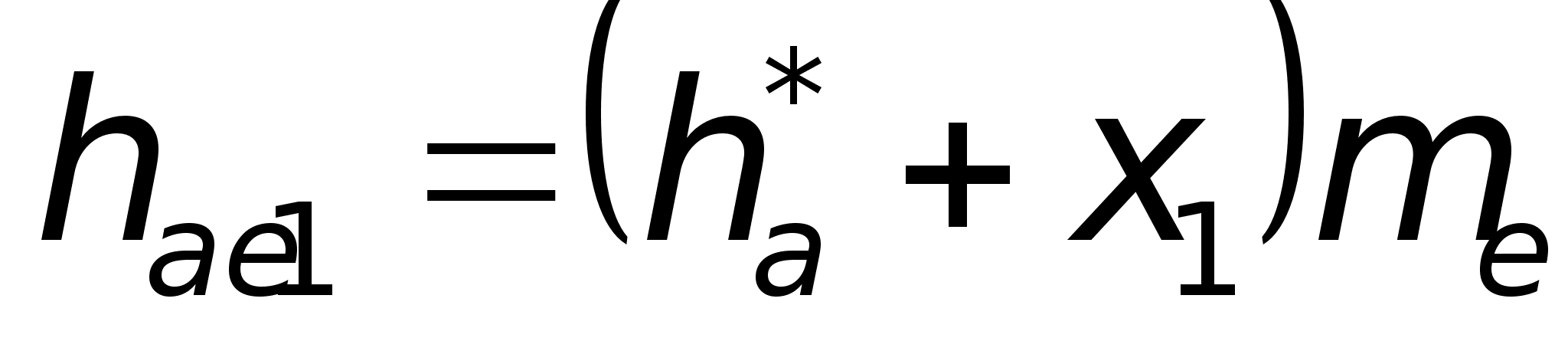
|
| колеса |

|
| Внешняя
высота но-жки
зуба, мм |
шестерни |

|
| колеса |

|
| Внешняя
высота зуба,
мм |
шестерни |

|
| колеса |

|
|
Угол
ножки зуба
|
шестерни |

|
| колеса |

|
| Угол
головки зуба |
шестерни |

|
| колеса |

|
| Угол
конуса вершин |
шестерни |

|
| колеса |

|
| Угол
конуса впадин |
шестерни |

|
| колеса |

|
| Внешний
диаметр вершин,
мм |
шестерни |

|
| Колеса |

|
| Расстояние
от вер-шины
до плоскости
внешней, окружно-сти
зубьев, мм |
шестерни |

|
| колеса |

|
Примечание.
Для стандартных
исходных контуров:
  ; ;

4.5 Расчет
геометрии
червячных
цилиндрических
передач
4.5.1 Термины, определения
и обозначения,
относящиеся
к червячным
передачам,
установлены
ГОСТ 16530-83 и ГОСТ
18498-73. В механизмах
приборов применяются,
главным образом,
ортогональные
червячные
передачи с
архимедовым
червяком (передача
ZA).
4.5.2 Модули (в осевом
сечении) и
коэффициенты
диаметра червяка,
- эти пара-метры,
определяющие
размеры червяка,
устанавливает
ГОСТ I9672-74,
значения моду-лей
в диапазоне
от 0,1…5 мм: 0.10; 0.125; 0,16; 0,20,
0,25; 0,315? 0,40; 0,50; 0,63; 0.80; 1,0;1,25; 2,0; 2,5;
3,15; 4,0; 5,0.
Коэффициенты
диаметра червяка
приведены
в таблице 4.8. Ряд
I следует пред-почитать
ряду 2.
Таблица 4.8. Коэффициенты
диаметра червяка
| Ряд I |
6,3 |
8,0 |
10,0 |
12,5 |
16,0 |
20.0 |
25,0 |
| Ряд 2 |
7,1 |
9.0 |
11,2 |
14,0 |
18,0 |
22,4 |
- |
4.5.3 Исходный
червяк. Параметры
профиля червяка,
определяющие
форму вит-ков
и зубьев червячного
колеса и образующие
профиль исходного
червяка, установ-лены
для m I мм ГОСТ
20184-81.
4.5.4. Число витков
червяка принимают
обычно z1
= 1…4; число
зубьев на колесе
z2>24.
4.5.5. Смещение в
червячной паре.
Применяется
для изменения
межосевого
рас-стояния
и определяется
коэффициентом
смещения червяка
x=(aw-a)/m
; при этом гео-метрия
червяка не
меняется; изменяются
только размеры
венца зубчатого
колеса. Пре-дельные
значения
коэффициентов
смещения, исходя
из условий
подрезания
и заострения
зубьев, рассчитывают
по формулам:
xmin=1-0,0585z2
(4.11)
xmax=0,05z2-0,12
(4.12)
4.5.6. Расчет геометрии
цилиндрических
ортогональных
передач SA,
в соответ-ствии
с ГОСТ 19650-74, приведен
в таблице 4.9.
Таблица 4. 9 Цилиндрические
ортогональные
червячные
передачи
Расчет геометрических
параметров
| Наименование
параметра |
Обозначения,
расчетные
формулы, указания |
| Исходные
данные |
| Число
витков червяка |

|
| Число
зубьев колеса |

|
| Модуль,
мм |
m- по
ГОСТ 19672-74 |
| Исходный
червяк |
m<1
по ГОСТ 20184-81 m>1по
ГОСТ 19036-81
|
| Коэффициент
диаметра червяка |
q- по
ГОСТ 19672-74 |
| Межосевое
расстояние,
мм |
aw
|
|
Основные
геометрические
параметры
червяк
|
| Делительный
угол подъема
витка |

|
|
Делительный
диаметр, мм
|

|
| Расчетный
шаг, мм |

|
| Диаметр
вершин витков,
мм |

|
|
Диаметр
впадин, мм
|

|
| Высота
витка, мм |

|
| Длина
нарезанной
части, мм |

|
| Колесо |
| Коэффициент
смещения |

|
| Делительный
диаметр, мм |

|
| Диаметр
вершин зубьев,
мм |

|
|
Диаметр
впадин, мм
|

|
| Наибольший
диаметр, мм |
 
|
|
Угол
бокового скоса
зубьев, (…˚)
|
 ;
округлить
до 5˚ ;
округлить
до 5˚
|
| Ширина
венца, мм |

|
| Передача |
|
Делительное
межосевое
рассто-яние,
мм
|

|
| Межосевое
расстояние,
мм |

|
| Передаточное
число |

|

| Начальный
диаметр, мм |
червяка |

|
| колеса |

|
| Контрольные
размеры червяка |
|
Ход витка,
мм
|

|
| Делительная
толщина по
хорде витка,
мм |

|
| Высота
до хорды витка,
мм |

|
|
Диаметр
измерительного
ролика,
мм
|
 ;
принимают по
ГОСТ 2475-62 ;
принимают по
ГОСТ 2475-62
|
| Размер
червяка по
роликам, мм |

|
Примечание.
Для стандартных
исходных червяков:
 при m<1
мм и с*=0,2
при m>1
мм.
при m<1
мм и с*=0,2
при m>1
мм.
5.
Расчет силовых
параметров
в зубчатых
передачах.
5.1.
Моменты
сил,
передаваемые
соседними
валами связаны
соотношением:
 ,
(5.1)
,
(5.1)
где
ТI
и ТII
- моменты сил
на валах I
и II соответственно,
iI-II
-
передаточное
отношение между
валом I
и II;
η1-2
-
КПД зубчатой
пары при передаче
мощности от
колеса 1 к колесу.
Аналогичное
соотношение
связывает
моменты сил
любых двух
соседних валов.
Связь между
моментами
входного вала
I
и выходного
вала IV
(рисунок.5.1)
определяется
формулой:
 ,
(5.2) ,
(5.2)
где
ТIV
- момент сил на
вале IV;
iI-II,,iII-III,iIII-IV
-
передаточные
отношения между
соседними
валами,
η1-2,
η3-4,
η5-6,
- КПД зубчатых
пар
5..2.
Формулы для
определения
усилий
в зацеп-лении
зубчатых колес
приведены в
таблице 5.1.
Рисунок
5.1
Таблица
5.1 Усилия в зацеплениях
зубчатых колес.
| Вид зубчатой
передачи |
Усилие,
Н |
| Окружное |
радиальное |
осевое |
нормальное |
| Цилиндри-ческая,
прямо-зубая |

|

|
|

|
| Коническая
прямозубая |

|
 
|
 
|

|
| червячная-цилиндри-ческая |
 
|

|

|

|
|
Примечание:
В формулах
T1 и Т2
- моменты сил
на ведущем
и ведомом колесе
соот-ветственно;
Диаметры d
W1 и dW2
в мм; в формулах
для червячннх
передач верхний
знак - при ведущем
червяке, нижний
- при ведущем
колесе, φТ
- приведенный
угол трения
профилей в
червячной
паре: φТ = arctgfпр.
|
Значения приведенного
коэффициента
трения fпp
и соответствующие
им значения
углов трения
φТ зависят
от скорости
относительного
скольжения:
 ,
(5.4) ,
(5.4)
где n1 -
частота вращения
червяка, об/мин.
Значения fпр
и φТ приведены
в таблице 5.2
Таблица 5.2
|
vs,
м/с
|
fпр
|
φТ, (…˚)
|
vs,
м/с
|
fпр
|
φТ, (…˚)
|
| 0,01 |
0,11…0.12 |
6,3…6,8 |
1,5 |
0,0400,050 |
2,3…2,9 |
| 0,1 |
0,08…0.09 |
4,5…5,2 |
2,0 |
0,035…0,045 |
2,0…2,6 |
| 0,25 |
0,063…0,075 |
3,7…4,3 |
2,5 |
0,030…0,040 |
1,7…2,3 |
| 0,5 |
0,055…0,065 |
3,2…3,7 |
3,0 |
0,028…0,035 |
1,6…2,0 |
| 1,0 |
0,045…0,055 |
2,6…3,2 |
4,0 |
0,023…0,030 |
1,3…1,7 |
5.3. Определение
КПД
Формулы для
определение
КПД приведены
в таблице 5.З
Таблица 5.З
| Вид
зубчатой передачи |
Расчетная
формула |
Коэффициент
нагрузки |
| Цилиндрическая
прямозубая |

|

|
|
Коническая
прямозубая
|

|
| Червячная
цилиндриче-ская
при веду-щем: |
Червяке |

|

|
| колесе |

|
|
Примечание:В
формулах: для
цилиндрических
и конических
зубчатых
передач:
f
- коэффициент
трения на
новерхностм
профилей зубьев.
Ориентировочные
значения f
зависят от
сочетания
материалов
колес в зубчатой
паре и приведены
ниже:
Закаленная
сталь по закаленной
стали 0,06
Сталь
по стали
0,05…0,1
Сталь
uo бронзе,
бронза по бронзе
0,07…0,1
Сталь
но текстолиту
0,12
Сталь
по полимерным
материалам
0,06…0,1
|
5.4 Реакции
в опорах
При работе
механизмов
в опорах валов
зубчатых передач
возникают
реакции, зна-
чения которых
зависят от вида
передачи, усилий
в зацеплениях
зубчатых пар
и распо ложения
зубчатых колес
относительно
опор.
1. Опоры валов
прямозубых
передач внешнего
зацепления.
Возможны три
варианта расположения
колес относительно
опор: в пролете
(рису-
нок5.2а), консольное
(рисунок 5.2б),
комбинированное
(рисунок 5.2в).

а б
в
Рисунок
5.2
Hагpyзкa
в опорах при
расположении
колес по рисунку
5.2а:
|
Номер
опоры
|
Радиальная
нагрузка, Н
|
|
I
|

|
|
II
|

|
|
III
|

|
|
IV
|

|
|
V
|

|
|
VI
|

|
Нагрузки
в опорах при
расположении
колес по рисунку
5.2б:
|
Номер
опоры
|
Радиальная
нагрузка, Н
|
|
I
|

|
|
II
|

|
|
III
|

|
|
IV
|

|
|
V
|

|
|
VI
|

|
|
Нагрузки
в опорах при
расположении
колес по рисунку
5.2в:
|
|
Номер
опоры
|
Радиальная
нагрузка, Н
|
|
I
|

|
|
II
|

|
|
III
|

|
|
IV
|

|
|
V
|

|
|
VI
|

|
|
VII
|

|
|
VIII
|

|
5.5.Конические
передачи. (рисунок
5.3)

а
б
Рисунок
5.3
Нагрузки в
опорах при
расположении
колес по рисунку
5.3а
|
Номер
опоры
|
Радиальная
нагрузка |
Осевая
нагрузка
|
| I |

|

|
| II |

|
| III |

|

|
| IV |

|
Нагрузки в
опорах при
расположении
колес по рисунку
5.3б:
|
Номер
опоры
|
Радиальная
нагрузка |
Осевая
нагрузка
|
| I |

|

|
| II |

|
| III |

|

|
| IV |

|
5.6 Червячная
передача (рисунок
5.4).

Рисунок
5.4
Составляющие
полных нагрузок:
| Номер
опоры |
Составляющие
от силы |
|

|

|

|
| I |

|

|

|
| II |

|

|
| III |

|

|

|
| IV |

|

|
Результирующие
нагрузки на
опоры:
| Номер
опо-ры |
Правое
направление
линии витка
червяка при
вращении |
| по часовой
стрелке |
против
часовой стрелки |
| Радиальная
нагрузка, Н |
Осе-вая
нагру-зка, Н |
Радиальная
нагрузка, Н |
Осе-вая
нагрузка, Н |
| I |

|
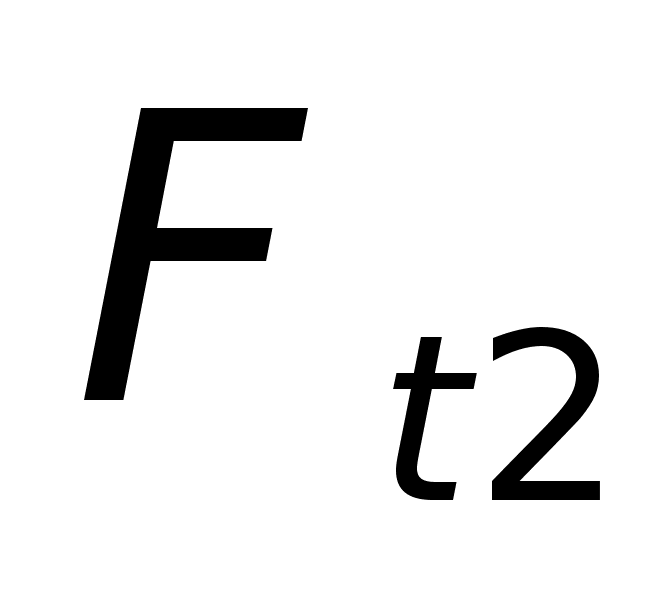
|

|

|
| II |

|

|
| III |

|

|

|

|
| IV |

|

|
| Но-мер
опо-ры |
Левое
направление
линии витка
червяка при
вращении |
| по часовой
стрелке |
против
часовой стрелки |
| Радиальная
нагрузка, Н |
Осе-вая
нагру-зка, Н |
Радиальная
нагрузка, Н |
Осе-вая
нагрузка, Н |
| I |

|

|

|

|
| II |

|

|
| III |

|

|

|

|
| IV |

|

|
Электродвигатели
Электродвигатели
- генераторы
типа ДГ
|
Технические
характеристики
|
ДГ-0,1А
|
ДГ-0.5ТА
|
ДГ-1ТА
|
ДГ-2ТА
|
ДГ-ЗТА
|
ДГ-5ТА
|
|
Напряжение
питнания,
В
|
обмоток
возбуждения
двигателя и
тахогене-ратора
|
36
|
36
|
36
|
36
|
36
|
36
|
|
управления
двигателя
|
30
|
30
|
30
|
30
|
30
|
30
|
|
Частота,
Гц
|
400
|
400
|
400
|
400
|
400
|
400
|
|
Полезная
мощность
двигателя,
Вт
|
0,07
|
0,5
|
1,0
|
2,0
|
3,0
|
5,0
|
|
Вращающий
момент • 104
, Н м
|
0,83
|
3,67
|
6,37
|
11,94
|
35,8
|
79,6
|
|
Пусковой
мо-
мент
• 104
Н·м
при температуре
|
(+20
±5)єС
|
2,548
|
9,8
|
15,68
|
33,32
|
88,2
|
215,6
|
|
(+100±5)єС
|
1,96
|
8,82
|
15,68
|
31,36
|
78,4
|
215,6
|
|
Момент
инерции вращающихся
частей •108
,кг·мІ
|
4,9
|
12,74
|
7,84
|
10,78
|
36,26
|
39,2
|
|
Электромеханическая
постоянная
времени, мс
|
120
|
100
|
68
|
68
|
36
|
30
|
|
Скорость
вращения, об/мин
|
при
нормальной
температуре
|
8000
|
13000
|
15000
|
16000
|
8000
|
6000
|
|
при
температуре
+
100 °С
|
7000
|
12000
|
14000
|
15000
|
6000
|
5000
|
|
Гарантийный
срок службы,
ч:
при
температуре
|
от
–60°С до+100єС
|
500
|
500
|
500
|
500
|
500
|
500
|
|
от
60єС до + 70єС
|
1500
|
1500
|
1500
|
1500
|
1500
|
1500
|
Электродвигатели
- генераторы
типа АДТ
Технические
характеристики
|
АДТ-1 |
АДТ-1А |
АДТ-1Б |
АДТ-С |
|
Н апряжение
питания обмоток,В апряжение
питания обмоток,В
|
тахогенератора |
110 |
5 5 |
110 |
110 |
| управления
двигателя |
110 |
110 |
110 |
110 |
| Частота,
Гц |
400 -
500 |
400 -
500 |
400 -
500 |
400 -
500 |
| Полезная
мощность
двигателя,Вт |
32 |
32 |
13 |
13 |
|
Вращающий
момент • 104,
Н м
|
78,4 |
78,4 |
194 |
194 |
|
Пусковой
момент •104
,Н∙м
|
147 |
147 |
296 |
296 |
|
Момент
инерции вращающихся
частей •108
,кг м2
|
|
|
|
|
| Скорость
вращения, об/мин |
4000 |
4000 |
4000 |
4000 |
| Гарантийный
срок службы,ч |
2000 |
2000 |
2000 |
2000 |
Электродвигатель
асинхронный
с полым ротором
управляемый
типа ДИД
|
Технические
характеристики
|
ДИД-0.
1ТА |
ДИД-0,5ТА |
ДИД-0,6ТА |
ДИД--1ТА |
ДИД-2ТА |
ДИД-ЗТА |
ДИД-5ТА |
| Напряжение
питания обмоток,
В |
возбуждения |
36 ±2,
9 |
36±2,9 |
36±2.9 |
36±2,9 |
36±2,9 |
36±2,9 |
36±2,9 |
| управления |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
| Частота,
Гц |
400 |
400±8 |
400±8 |
400±8 |
400±8 |
400±8 |
400±8 |
| Полезная
мощность
двигателя,
Вт |
0,1 |
0,5 |
0,6 |
1, 0 |
2,0 |
3,0 |
5 |
|
Вращающий
момент • 10 4,
Н ▪
м
|
1, 47 |
3,43 |
6,37 |
8,82 |
18,. 0 |
54,8 |
117,6 |
|
Пусковой
момент • 10 4,
Н ▪
м
|
2,55 |
|
9,8 |
|
34, 0 |
|
215,6 |
|
при
температуре
+20 ±5 °С
|
|
6,86 |
|
15.68 |
|
88,2 |
|
|
при
температуре
+100 5 °С
|
|
2,548 |
|
13,72 |
|
78,4 |
|
|
Момент
инерции вращающихся
частей
• 10 8 ,
кг.▪
мІ
|
2.,205 |
4,41 |
7,35 |
6,86 |
8,8 |
23,5 |
245 |
| Электромеханическая
пост. времени
, мc |
90 |
80 |
50 |
38 |
32 |
26 |
52 |
|
Скорость
вращения, об
/ мин при температуре
+20±5 °С
|
12000 |
14000 |
16000 |
18000 |
18000 |
8000 |
6000 |
|
Гарантийный
срок службы
,ч
при
температуре,
°С
|
+100 |
500 |
500 |
500 |
500 |
500 |
500 |
250 |
| от -60 до
+70 |
1500 |
1000 |
|
1500 |
1500 |
1500 |
|
Асинхронный
управляемый
электродвигатель
с полым ротором
типа АДП
Технические
характеристики
|
АДП
– 024А |
АДП
023 |
АДП
023Б |
АДП-
023А |
АДП-120 |
АДП-123 |
АДП123Б |
АДП-1 |
АДП-124А |
АДП-124Б |
АДП-
262
|
АДП-
263А
|
АДП-
362
|
АДП-
363
|
АДП
–563 |
| Напряжение
питания, В |
40 |
110 |
110 |
40 |
110 |
110 |
110 |
120 |
40 |
110 |
110 |
36 |
110 |
36 |
36 |
| Частота,
Гц |
1000 |
500 |
500 |
500 |
400 |
400 |
400 |
500 |
1000 |
1000 |
50
|
500 |
| 500 |
50 |
500 |
| Полезная
мощность
двигателя,
Вт |
4,5 |
2,1 |
4,3 |
4,3 |
2,4 |
4,1 |
8,9 |
3,7 |
5,35 |
15 |
9,5 |
27,7 |
19 |
46,4 |
62 |
|
Вращающий
момент • 104
, Н • м
|
53,9 |
44,1 |
58,9 |
58,9 |
58,8 |
98 |
142 |
39,2 |
63,76 |
122,6 |
490 |
392 |
931 |
735 |
981 |
|
Пусковой
момент • 104
, Н • м
|
|
73,5 |
73,5 |
73,5 |
|
|
167 |
53,9 |
142 |
186,4 |
833 |
588 |
1666 |
833 |
|
|
Момент
инерции вращающихся
частей
• 108 ,
кг • м 2
|
|
|
|
|
|
|
|
765 |
|
|
1660 |
1660 |
3900 |
3900 |
11800 |
| Электромеханическая
постоянная
времени, мс |
|
|
|
|
|
|
|
48 |
|
|
55 |
32 |
6 |
50 |
82 |
| Скорость
вращения, об
/ мин |
8000 |
4500 |
7000 |
7000 |
4000 |
4000 |
6000 |
9000 |
8000 |
12000 |
1850 |
6000 |
1950 |
6000 |
6000 |
| Гарантийный
срок службы,
ч |
50 |
2000 |
2000 |
2000 |
2000 |
1500 |
1500 |
200 |
50 |
50 |
2000 |
1500 |
2000 |
1500 |
|
Электродвигатель
асинхронный
с полым ротором
управляемый
типа ЭМ
Технические
характеристики
|
ЭМ-0,2
|
ЭМ-0,5
|
ЭМ-1МТ
|
ЭМ-2МТ
|
ЭМ-2М
|
эм-2-12
|
эм-4А
|
эм-4м
|
эм-8м
|
эм-8-12 |
эм-15
м |
ЭМ-15
МТ
|
ЭМ-25М |
ЭМ-50М |
| Напряжение
питания обмоток
возбуждения
, В |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
115 |
| Частота,
Гц |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
400 |
| Полезная
мощность, Вт: |
0,2 |
0,5 |
1,0 |
2,0 |
2,0 |
2,0 |
4,0 |
4,0 |
8,0 |
8,0 |
15,0 |
15,0 |
25 |
50 |
|
Вращающий
момент•10 4,
Н• м
|
9,8 |
24,5 |
44,1 |
44,1 |
47,7 |
38,2 |
137,2 |
117,6 |
196,0 |
127,4 |
362,6 |
362,6 |
568,4 |
490 |
|
Пусковой
момент•10 4,
Н• м
|
19,6 |
49,0 |
63,7 |
147 |
117,6 |
63,7 |
274,0 |
215,6 |
313,6 |
176,4 |
588 |
588 |
882 |
1176 |
|
Момент
инерции вращающихся
частей •108,
кг • м І
|
6,5 |
20,0 |
23,7 |
51,0 |
51,0 |
51,0 |
127,4 |
127,4 |
205,8 |
205,8 |
345 |
345 |
519,14 |
1421 |
| Электромеханическая
постоян-ная
времени ,с |
0,02 |
0,015 |
0,015 |
0,020 |
0,025 |
0,04 |
0,04 |
0,025 |
0,030 |
0,045 |
0,04 |
0,035 |
0,04 |
0,05 |
| Скорость
вращения, об/мин |
2500 |
2000 |
2500 |
4000 |
4000 |
5000 |
3300 |
3300 |
4000 |
6000 |
4000 |
4000 |
4200 |
5000 |
| Гарантийный
срок службы,
ч : |
|
400 |
400 |
400 |
400 |
500 |
400 |
500 |
400 |
500 |
400 |
400 |
400 |
400 |
Электродвигатель
синхронный
гистерезисный
типа Г
|
Технические
характеристики
|
Г-31
|
Г32
|
Г-33
|
Г-
201
|
Г-202
|
Г-203
|
Г-205
|
Г-210
|
ЭГ-10
|
ГСД-321-6
|
ГСД-322-6
|
МГ-30-400
|
| Напряжение
питания, В |
220 |
40(32) |
220 |
115 |
127 |
127 |
220 |
40 |
40 |
40 |
36 |
60 |
55 |
30 |
115 |
Частота,
Гц
|
50 |
500(400) |
50 |
400 |
50 |
50 |
50 |
500 |
500 |
360 |
300 |
400 |
400 |
200 |
400 |
| Полезная
мощность, Вт |
4,0 |
16(12,8) |
7,0 |
2,0 |
2 |
1,5 |
1,0 |
3,5 |
8,2 |
10 |
8 |
15 |
10 |
5 |
30 |
|
Вращающий
момент •104,
Нм
|
127,3 |
206 |
223 |
24,5 |
63,7 |
49 |
31,9 |
44,1 |
78 |
530 |
429 |
119 |
716 |
119 |
265 |
| Скорость
вращения, об/мин |
3000 |
7500
(6000)
|
3000 |
8000 |
3000 |
3000 |
3000 |
7500 |
10000 |
7200 |
6000 |
8000 |
8000 |
4000 |
11000 |
| Гарантийный
срок службы,
ч |
3000 |
1000 |
5000 |
500 |
5000 |
5000 |
5000 |
1000 |
500 |
2000 |
2000 |
2000 |
600 |
600 |
500 |
Электродвигатели
синхронные
Технические
характеристики
|
ДС
-1
|
СРД-2
|
ДСД60 |
ДСД
1/300 |
ДСД2 |
СД-09М |
Напряжение
питания, В
|
220 |
24 |
220 |
220 |
220 |
127/220 |
| Частота,
Гц |
50 |
50 |
50 |
50 |
50 |
50 |
| Полезная
мощность
двигателя,
Вт |
0,02 |
0,012 |
0,0123 |
6,85.10-5
|
0,014 |
|
| Номинальный
вращающий
момент, Н •м |
0,098 |
|
1,96.10-3
|
0,196 |
0,0687 |
0.028 |
| Максимальный
вращающий
момент,
Н•м |
|
0,0686 |
|
|
|
0.078 |
| Пусковой
момент, Н•м |
0,098 |
0,049 |
|
|
|
|
| Скорость
вращения, об
/ мин |
2,0 |
2,0 |
60 |
1/300 |
2,0 |
3000 |
| Гарантийный
срок службы,
ч: |
длит. |
1 год |
|
|
|
|
Электродвигатели
постоянного
тока типа ДПР
Тип
элект-родви-гателя
|
Ско-
рость
враще-
ния,
об/ми
|
Мо-мент
инер -
ции
рото-ра •108
кг·м2
|
Напряжение
питания, В
|
| 3,0 |
6,0 |
12,0 |
14,0 |
27,0 |
| N,Вт |
T104Н·м.
|
N,Вт |
T•104Н·м.
|
N,Вт |
T•104Н·м.
|
N,Вт |
T•104Н·м.
|
N,Вт |
T•104Н·м.
|
| ДПР-1 |
9000 |
|
0,185 |
1,962 |
0,185 |
1,962 |
|
|
|
|
|
|
| 6000 |
0,123 |
0,123 |
|
|
|
|
|
|
| 4500 |
0,092 |
— |
— |
|
|
|
|
|
|
| 2500 |
0,051 |
— |
— |
|
|
|
|
|
|
| ДПР-2 |
9000 |
7,0 |
0,74 |
7,848 |
0,924 |
9,81 |
0,924 |
9,81 |
|
|
|
|
| 6000 |
0,493 |
0,616 |
0,616 |
|
|
|
|
| 4500 |
0,37 |
0,462 |
0,462 |
|
|
|
|
| 2500 |
0,205 |
0,257 |
— |
— |
|
|
|
|
| ДПР-3 |
9000 |
20,0 |
|
|
1,387 |
14,71 |
1,85 |
19,62 |
1,85 |
19,62 |
1,85 |
19,62 |
| 6000 |
|
|
0,924 |
1,233 |
1,233 |
1,233 |
| 4500 |
|
|
0,693 |
0,924 |
0,924 |
0,924 |
| 2500 |
|
|
0,385 |
0,514 |
0,514 |
— |
— |
| ДПР-4 |
9000 |
57,0 |
|
|
3,698 |
39,24 |
4,62 |
49,05 |
4,62 |
49,05 |
4,62 |
49,05 |
| 6000 |
|
|
2,465 |
3,082 |
3,082 |
3,082 |
| 4500 |
|
|
1,85 |
2,311 |
2,311 |
2,311 |
| 2500 |
|
|
1,027 |
1,284 |
1,284 |
1,284 |
| ДПР-5 |
9000 |
170,0 |
|
|
— |
— |
9,245 |
98,10 |
9,245 |
98,1 |
9,245 |
98,1 |
| 6000 |
|
|
4,93 |
78,48 |
6,164 |
6,164 |
6,164 |
| 4500 |
|
|
3,698 |
4,623 |
4,623 |
4,623 |
| 2500 |
|
|
2,055 |
2,568 |
2,568 |
2,568 |
| ДПР-6 |
9000 |
360,0 |
|
|
— |
— |
14,79 |
157,0 |
14,79 |
157,0 |
18,49 |
196,2 |
| 6000 |
|
|
9,862 |
157,0 |
12,33 |
196,2 |
12,33 |
196,2 |
12,33 |
| 4500 |
|
|
7,396 |
9,25 |
9,25 |
9,25 |
| 2500 |
|
|
4,109 |
5,136 |
5,136 |
5,136 |
| ДПР-7 |
9000 |
780,0 |
|
|
— |
— |
27,74 |
284,3 |
27,73 |
294,3 |
36,98 |
392,4 |
| 6000 |
|
|
— |
— |
24,65 |
392,4 |
24,65 |
392,4 |
24,65 |
| 4500 |
|
|
13,87 |
294,3 |
18,49 |
18,49 |
18,49 |
| 2500 |
|
|
10,27 |
392,4 |
10,27 |
10,27 |
10,27 |
Электродвигатели
постоянного
тока типа СД,
ОД
|
Технические
характеристики
|
ОД-7
|
СД-8
|
СД-10А
|
СД-20
|
СД-10В
|
СД-10Г
|
СД-10Л
|
| Напряжение
питания, В |
27 |
27 |
27 |
27 |
27 |
27 |
27 |
| Номинальная
мощность, Вт |
7 |
8 |
20 |
20 |
20 |
20 |
20 |
|
Вращающий
момент ·104
,Н
· м
|
102 |
127 |
324 |
319 |
324 |
324 |
324 |
| Скорость
вращения, об/мин |
7000 |
5500 |
6000 |
6000 |
6000 |
6000 |
6000 |
| Режим
работы |
Длит. |
Длит. |
П/кр. |
Длит. |
П/кр. |
Длит. |
П/кр. |
| Гарантийный
срок службы,
ч |
1000 |
400 |
500 |
500 |
400 |
450 |
500 |
| Масса,
кг |
0,4 |
0,5 |
0,5 |
0,9 |
0,4 |
0,5 |
0,4 |
|
Момент
инерции вращающих-
ся частей ·10
8 , кг
· м 2
|
|
|
39 |
125 |
39 |
|
42 |
| Электромех.
постоянная,
с |
|
|
0,02 |
0,011 |
0,02 |
0,02 |
0,02 |
Электродвигатели
постоянного
тока типа
СЛ
| Технические
характеристики |
СЛ-
121
|
СЛ-161 |
СЛ-163 |
СЛ-221 |
СЛ-329 |
СЛ-261 |
СЛ-281 |
СЛ-267 |
СЛ-
367
|
| Напряжение
питания, В: |
110 |
110 |
110 |
110 |
24 |
110 |
24 |
110 |
110 |
| Полезная
мощность, Вт |
5 |
7,5 |
8,3 |
13 |
23,5 |
24 |
26 |
27 |
32 |
|
Вращающий
момент • 104
,Н • м
|
137,3 |
206 |
225,6 |
343 |
981 |
637,6 |
490,5 |
637,6 |
1226 |
| Скорость
вращения, об/мин |
3500-
5500
|
3500-
5500
|
3500-
5500
|
3600-
4200
|
2300-
2900
|
3600-
4600
|
5200-
6200
|
3800-
4400
|
2500-
3000
|
Гарантийный
срок службы,
ч
|
1500 |
1500 |
1500 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Технические
характеристики |
СЛ-
569К
|
СЛ-361 |
СЛ-369 |
СЛ-365 |
СЛ-525 |
СЛ-571К |
СЛ-563 |
СЛ-569 |
СЛ-
621
|
СЛ-
661
|
| Напряжение
питания, В: |
110 |
110 |
110 |
110 |
110 |
24 |
110 |
110 |
110 |
110 |
| Полезная
мощность, Вт |
36 |
50 |
55 |
56 |
78 |
95 |
110 |
160 |
172 |
230 |
|
Вращающий
момент • 104
,Н • м
|
4120 |
1570 |
1472 |
1668 |
1962 |
4120 |
2747 |
4660 |
6867 |
9074 |
| Скорость
вращения, об/мин |
850-
1050
|
3000
3600
|
3000-
4200
|
3240-
3960
|
3800-
4400
|
2200 |
3800-
4400
|
3300-
4000
|
2400-2700 |
2400-2750 |
| Гарантийный
срок службы,
ч |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
Электродвигатели
постоянного
тока с регулятором
скорости типа
ДРВ
| Технические
характеристики |
ДРВ-0,5 |
ДРВ-3К |
ДРВ-5
|
ДРВ-8 |
ДРВ-20 |
ДРВ-25 |
ДРВ-45 |
ДРВ-60 |
ДРВ--150
|
ДРВ-300 |
| Напряжение
питания, В |
27 |
| Полезная
мощность, Вт |
0,515 |
3,08 |
5 |
8 |
20,5 |
25 |
45 |
61,5 |
150 |
300 |
|
Вращающий
момент•104,
Н • м
|
4,9 |
29,4 |
47,6 |
76,5 |
196 |
402 |
613 |
589 |
1913 |
3826 |
| Скорость
вращения, об/мин |
10000 |
10000 |
10000 |
10000 |
10000 |
6000 |
7000 |
10000 |
7500 |
7500 |
|
Момент
инерции враща-ющихся
частей106,кгм2
|
27,47 |
2,75 |
2,2 |
2,94 |
14,7 |
24,5 |
72,6 |
72,6 |
179,5 |
571,9 |
| Электромеханическая
постоянная
времени, с |
0,3 |
0,18 |
0,2 |
0,25 |
0,48 |
0,28 |
0,45 |
0,31 |
1,43 |
1,28 |
| Гарантийный
срок службы,
ч |
200 |
75 |
200 |
100цкл |
400 |
400 |
500 |
500 |
400 |
400 |
| Масса,
кг |
0,35 |
0,22 |
0,35 |
|
0,8 |
1,5 |
|
|
3,2 |
4,7 |
|
Режим
работы
|
длит |
П-к |
длит |
Кратк. |
Длит. |
Прод. |
Длит. |
Длит. |
Прод. |
Прод. |
Электродвигатели
постоянного
тока типа Д
|
Технические
характеристики
|
Д-250-8
|
2Д-7
|
3Д-7
|
| Напряжение
питания, В |
27 |
27,5 |
27,5 |
|
Номинальный
момент •104
,Н · м
|
2943 |
102 |
102 |
| Номинальная
мощность, Вт |
250 |
7 |
7 |
| Скорость
вращения, об/мин |
8000 |
7000 |
7000 |
| Режим
работы |
Прод. |
Длит. |
П/кр. |
| Гарантийный
срок службы,
ч |
500 |
500 |
50000цикл |
| Масса,
кг |
3,6 |
|
|
Технические
характеристики
|
Д-75
|
Д-100-3
|
Д-100-8
|
Д-100-10
|
Д-120
|
Д-160
|
Д-200-8
|
| Напряжение
питания, В |
27 |
27 |
27 |
27 |
27 |
27 |
27 |
|
Номинальный
момент •10 4
,Нм
|
956 |
2649 |
1080 |
814 |
7848 |
2060 |
2354 |
| Номинальная
мощность, Вт |
75 |
100 |
90 |
80 |
120 |
160 |
200 |
| Скорость
вращения, об/мин |
7500 |
3000 |
8000 |
9500 |
1200 |
5500 |
8000 |
| Режим
работы |
П/кр. |
Прод. |
Прод. |
Прод. |
|
П/кр. |
Прод.. |
| Гарантийный
срок службы,
ч |
500 |
500 |
500 |
400 |
50 |
25цикл |
10 |
| Масса,
кг |
1,4 |
2,6 |
3,0 |
2,0 |
|
1,8 |
3,5 |
Технические
характеристики
|
Д-0,1
|
Д-0,16
А
|
Д-5
|
Д-7
|
Д-25А
|
Д-25-1С
|
Д-40
|
Д-50А
|
Д-55
|
| Напряжение
питания, В |
2,8 |
4,5 |
27 |
27,5 |
27 |
27 |
27 |
27 |
27 |
|
Номинальный
момент •10 4,Н
· м
|
4,9 |
6,37 |
41,2 |
102 |
399 |
285 |
687 |
412 |
952 |
| Номинальная
мощность, Вт |
0,092 |
0,2 |
5 |
7 |
25 |
20 |
50 |
50 |
55 |
| Скорость
вращения, об/мин |
1500 |
3000 |
12000 |
7000 |
6000 |
8400 |
7000 |
11400 |
4500 |
| Режим
работы |
Длит. |
Цикл. |
Длит. |
Длит |
Длит. |
Прод |
Прод. |
П/кр. |
Длит. |
| Гарантийный
срок службы,
ч |
200 |
|
250 |
1500 |
1000 |
1000 |
70 |
500 |
1080 |
| Масса,
кг |
0,1 |
|
|
|
0,7 |
0.9 |
0,8 |
1,3 |
1,5 |
ПРОЕКТИРОВАНИЕ
ОПОРНЫХ УЗЛОВ
ВАЛОВ И ОСЕЙ
При
проектировании
опорных узлов
последовательно
решаются такие
задачи:
1)
разработка
конструктивной
схемы расположения
опор и функциональных
элементов всего
механизма из
условий разме-щения
звеньев по
габаритам
в плоских развертках
или сечениях;
2)
разработка
конструктивной
схемы продольного
замыкания опор,
т.е. схемы ограничения
осевых смещений
валов или блоков
на осях;
3)
выбор (в особых
случаях разработка)
подшипников
качения,
4)
разработка
элементов
посадочных
мест подшипников:
определение
формы и размеров
поверхностей,
сопрягаемых
с кольцами
подшипников;
установление
допусков на
размеры, форму
и расположения
посадочных
поверхностей;
установление
требований
к твердости
и шероховатости;
5)
разработка
элементов
смазывания
и уплотнения
подшипников;
6)
пространственная
компоновка
(свертка) плоских
схем и внесение
необходимых
изменений и
уточнений в
конструкцию
опорных узлов:
отработка
формы и размеров
крышек, выбор
деталей крепления
крышек, расчет
пружин замыкания
и др.
1.1.
Разработка
конструктивной
схемы
Используя
геометрические
расчеты (зубчатых
колес, кулачковв
и др.), паспортные
и исходные
данные (для
двигателей,
потенциометров,
концов валов
и т.п.), выполнить
в масштабе 1:1
габаритные
эскизы всех
вновь разработанных,
принятых или
заданных элементов
кинематической
цепи. На основании
кинематической
схемы, пользуясь
эскизами ее
элементов и
рекомен-дациями
таблицы 1.1 составить
необходимое
количество
плоских компоновочных
схем, т.е. схем
расположения
тех элементов,
оси которых
могут быть
показаны в
одной плоскости
одной разверткой
или в одном
сечении (рисунок
1.1).

Рис.
1.1. Габаритно-конструктивная
компоновка
плоской развертки
кинемати-ческой
цепи редуктора
с параллельными
осями
Комбинируя
варианты
схем
для отдельных
осей (таблица
1.1 или [2, таблица
4.21]), следует:
а)
обеспечить
заданное
относительное
расположение
входных и выходных
звеньв
механизма
(валов, двигателей
и др.);
б)
обеспечить
расположение
подшипников
в соответствии
с возможностями
принятого типа
корпуса (для
двухплатного,
например, корпуса
подшипники
желательно
располагать
только в двух
плоскостях);
г)
исключить
накладку размеров
(например, венцов
зубчатых колес
на валики или
ступицы) и уменьшить
длину валиков,
изменяя расположение
элементов вдоль
оси вращения;
д.)
удовлетворить
требования
по сборке и
регулировке,
используя
варианты с
двухконсольным
расположением
на основе стаканов
(см. [2, рис.7.З5]), применяя
блочные конструкции
зубчатых колес
на неподвижных
осях и др.
Выбор
схемы продольного
замыкания опор
Рекомендуемые
схемы замыкания
опор приведены
в таблице 1.2.
Схема
1. Замыкание "в
распор". Внутренние
кольца подшипников
упираются в
заплечики вала,
наружные - в
торцовые поверхности
корпусных
деталей. Необходимый
осевой зазор
(натяг) в зависимости
от допуска на
его значение
(таблица 1.3)
обеспечивается:
а)
замыкающим
размером сборочной
размерной цепи
вал - корпус и
его предельными
отклонениями
методом полной
или неполной
взаимозаменяемости.
Применять для
изделий крупносерийного
и массового
производства
или при допуске
зазора более
0,1 мм;
б)
методом пригонки,
т.е. доработкой
при сборке
высоты торцового
уступа крышек
(схема I.I,
поз.2) или толщины
простановочных
колец (схема
1.2, поз.2). Применять
при допуске
осевого зазора
вала в подшипниках
10...30 мкм;
в)
методом регулировки
- набором прокладок
(колец) по толщине
(схема 1.3, поз.2).
Применять
при допуске
зазора более
30 мкм;
г)
методом регулировки
- смещением
наружных колец
подшипников
резьбовыми
пробками (схема
1.4, поз.2). Применять
при допуске
осевого зазора
(натяга) менее
15 мкм и при любом
значении допуска,
когда необходима
регулировка
положения вала
вдоль его оси
или периодическая
регулировка
зазора или
натяга
|
1.Базовые
схемы для
формирования
конструкции
опорных узлов
редукторов
и передаточных
механизмов
|
|
В
двухплатных
корпусах и
стойках
|
В
одноплатных
корпусах и
стаканах
|

о
о
о
о
|

о
о
о о
|

о
о
о о
|

о
о
о
о
|
|
2.Вспомогательные
схемы для
формирования
конструкции
опор связей,
сателлитов,
ограничителей,
отводов и т.п.
|
|

о
о
 о
о
о
о
|

о о
о о
|


О
О

О
О

|

о
о
о о
|
Таблица
1.1
Примечание:
Полная сетка
возможных
вариантов схем
опор-ных узлов
валов и осей
приведена в
[2]. Если на валу
или оси необхо-димо
установить
более двух
функ-циональных
элементов,
возможные
варианты схем
строятся на
основе приведенных
двухэлементных.1.2.
В
технических
требованиях
сборочных
чертежей в
зависимости
от принятого
метода ограничения
осевой игры
вала делается
запись по форме:
для
метода полной
взаимозаменяемости
- "Осевой зазор
в опорах валов
поз.___
(0,03...0,0б мм). Контролировать
по смеще-нию
торца вала при
осевой нагрузке
5 Н";
для
метода пригонки
- "Осевой зазор
в подшипниках
валов поз. ___
(-0,01...0,02 мм) обеспечить
доработкой
толщины простановочных
колец поз. ___.
для
методов регулировки
- "Осевой зазор
в опорах вала
поз.__
(0,02...0,06 мм)
обеспечить
подбором толщины
колец поз,__"
или "Осевой
натяг в подшипниках
валов поз.____(0,005..
.0,01 мм) обеспечить
перемещением
резьбовых
пробок поз.__.
Контрольное
смещение вала
при осевой
нагрузке 10 Н в
пределах 0,002..
.0,004 мм". •
Схема
2. Замыкание
обеспечивается
внутренними
уступами расточек
в корпусе (схема
2.1) или распорным
кольцом (схема
2.2, поз.1) и торцами
двух наружных
элементов,
закрепляемых
на валу. Необходимый
осевой зазор
или натяг достигается
сме-щением
внутренних
колец подшипника
гайками (схема
2.1, поз.2), упорными
кольцами (схема
2.3, поз.2) или ступицами
зубчатых колес,
муфт и др. (схема
2.4). В технических
требованиях
записывают:
"Осевой зазор
в опорах валов
поз.__ (0,02...0,04
мм)
обеспечить
перемещением
упорных колец
поз._. Кольца
заштифтовать
после контрольной
проверки редуктора
по моменту
трения".
Схема
3. Замыкание на
одной опоре.
Опору с двумя
подшипниками
нужно замыкать
по схеме 1 или
2. Толщина колец
между подшипниками
0,5...1,5 мм. Подшипник
плавающей опоры
фиксировать
закреплением
только внутреннего
кольца; если
используется
подшипник с
цилиндрической
дорожкой качения
(серия 640000), закрепляют
оба кольца
подшипника
(схема 3.2).
Схема
4. Замыкание
каждой опоры
осуществляют
только по схеме
1. Стакан плавающей
опоры устанавливать
в корпусном
отверстии с
натягом 0,002...0,006 мм
индивидуальной
подгонкой или
используя метод
групповой
взаимозаменяемости.
В техни-ческих
требованиях
дополнительно
к записи, соответствующей
схеме 1, указывают:
"Стакан поз.___
в отверстие
корпуса установить
с натягом
(0,003...0,006
мм). Допускается
доработка
поверхности
стакана (Ra
0,32)".
Схема
5. Осевой зазор
устраняется
перемещением
шариковой пяты
при контролируемом
усилии замыкания.
Пример записи
в технических
требованиях:
"Осевой зазор
в опорах вала
поз.__ не допускается.
Устранить
перемещением
упора регули-ровочным
винтом поз.__
".
Таблица
1.2
|
Схема
1
|
Схема
2
|
|

|
1.1.
Для двухплатных,
литых закры-тых
и открытых
корпусов, для
сбо-рок
в двухопорных
стойках на
пли-те.
Для всех типов
подшипников.
Регулирование
осевого зазора
дости-гается
подрезкой
торцов
выступов
крышек поз.
2.
|
Для
одноплатных
корпусов
и во
всех случаях,
когда опоры
монтируются
в коротких
стаканах. Для
всех основных
типов подшипников.
Осевой зазор
уста-навливается
смещением
внутренних
колец подшипников
любым способом.
|

|
|

|
1.2.
То же, по условиям
применения.
Необходимый
зазор устанавливается
доработкой
толщины колец
поз. 2 или подбором
их толщины.
Крыш-ки
могут быть
утопленными,
иметь отверстия
для выхода
вала, уплотни-тели,
смазочные
полости.
|
2.2.
То же, по применению,
но ограни-чение
смещения колец
в стакане или
в отверстии
корпуса осуществляется
рас-порными
кольцами поз.1,
которые фик-сируются
в отверстии
штифтами,
сто-порными
винтами и др.
|

|
|

|
1.3.
То же, по применению,
но кон-струкция
основана на
применении
подшипников
типа 840ооо, 860ооо
или 880ооо по
ГОСТ 10058-75 с упорным
бортом.
Зазор
регулируют
либо прокладками
поз.2, смещением
стоек на плите,
либо ступицы
на
внутреннее
кольцо
|
2.3.
Для формирования
двухопорного
узла на неподвижной
оси, для установ-ки
сателлитов
планетарных
механиз-мов
и др. Зазор или
натяг в подшипни-ках
устанавливается
смещением
коль-ца поз.
2. либо всей оси
на корпусную
деталь.
|

|
|

|
1.4.
То же, по условиям
применения
(см. схему 1.1.).
Необходимый
осе-вой
зазор или натяг
может быть
ус-тановлен
с большой
точностью
резь-бовыми
пробками поз.2.
Схема поз-воляет
регулировать
продольное
по-ложение
функциональных
элементов.
|
2.4.
По применению
и регулированию
осевого зазора
схема аналогична
схеме 2.2, но
конструктивно
основана на
при-менении
подшипников
с упорным бор-том
по ГОСТ 10058-75.
Конструктивно
и технологически
- очень
простая схема
|

|
|
Схема
3
|
|

|
3.1.
Для валов, винтов
и др. большой
длины при
значительных
перепадах
температуры
эксплуатации.
Подшипники
поз. 4 узла замыкания
- типа о84оо, о660ооо,
о88ооо с упорным
бортом, плавающей
опоры – типа
0ооо или 06оооо,
000ооо по ГОСТ
7242-70 с уменьшенными
радиальными
зазорами. Зазор
устанавливается
подбором или
доработкой
толщины колец
поз.2
|
|

|
3.2.
Применение
то же. В замыкающей
опоре используются
подшипники
типа Оооо ГОСТ
8338-75 или 6ооо ГОСТ
831-75; для плавающей
-
подшипник
с цилиндриче-ской
дорожкой качения
внутреннего
кольца типа
64ооо ГОСТ 10058-75. Для
креп-ления
этот подшипник
имеет фланец
с отверстиями.
Опора
замыкания
собрана в стакане,
зазор регулируется
резьбовым
кольцом поз.2
|
|

|
Схема
4. В условиях
применения
схемы замыкания
3, когда не допускается
радиаль-ный
зазор в плавающей
опоре, одиночный
подшипник
заменяется
плавающим
стаканом с
двумя подшипниками,
замкнутыми
внутри стакана
по схеме 1. Подшип-ники
типа 0ооо или
6ооо.
Внутренние
кольца по оси
стягивают до
отказа. Осевой
зазор в каждой
паре обеспечивается
смещением
наружных колец
подшипников
любым методом.
|
|

|
Схема
5. Для валов
счетно-решающих
механизмов
и в других
случаях, когда
необходимо
полностью
устранять
осевой зазор,
сохраняя
минимальные
потери на трение.
В опорах используются
радиальные
подшипники
типа Оооо 5-го
или 4-го класса
точности с
уменьшенными
радиальными
зазорами. Опоры
формируют в
стаканах. Осевой
зазор устраняется
специальным
винтом-упором
поз. 2;
|
|

|
Схема
6. Когда необходимо
обеспечить
постоянное
значение осевого
натяга во всем
температурном
диапазоне
эксплуатации,
в схемах замыкания
1 или 5 кинематическое
замыкание
заменяют силовым:
кольцо менее
нагруженного
подшипника
замыкается
на вал (для схемы
2) или на корпус
(для схемы 1)
через упругую
связь - пружину,
упругую
крышку
и др.
|
Схема
6. Необходимое
усилие замыкания
обеспечивается
пружиной. Схема
является вариантом
любой из пяти
ранее рассмотренных
схем, при котором
кинематическое
замыкание
заменяется
силовым. В
технических
требованиях
записывают:
"Усилие замыкания
подшипников
вала поз.___ (40,5
Н) установить
смещением
резьбовой
пробки поз.__.
Контролировать
по началу смещения
торца вала".
Конструктивные
схемы узлов
с поперечной
и комбинированной
базами можно
выбирать
по [2, рис.4.21 и 4.23].
1.3.
Выбор подшипников
качения.
Подшипники
качения выбирают
с учетом всех
требований,
предъявленных
к подшипниковым
узлам проектируемого
изделия [2].
Исходный
критерий –
относительная
частота вращения
подвижного
кольца подшипника:
если она меньше
1 об/мин, под-шипники
выбирают по
статической
грузоподъемности
(ГОСТ 18854-82), если
равна 1 об/мин
или больше - по
динамической
грузоподъемности
(ГОСТ 18855-82).
Приступая
к выбору подшипников,
следует детально
изучить стандарты
с общим наименованием
"Подшипники
качения", в
частности:
|
ГОСТ
24955-81. Термины и
определения.
|
ГОСТ
3325-85. Поля допусков
посадочных
мест валов и
отверстий.
Посадки.
|
|
ГОСТ
3395-75. Типы и конструктивные
разновидности
|
ГОСТ
20226-82 Заплечики
для установки
подшипников
качения.
|
|
ГОСТ
520-89. Технические
требования
|
ГОСТ
25256-82 Допуски.
Термины и
определения.
|
|
ГОСТ
3189-75. Система
условных
обозначений.
|
ГОСТ
18854-82 Методы расчета
статической
грузоподъемности.
|
|
ГОСТ
3478-79. Основные
размеры.
|
ГОСТ
18855-82 Методы расчета
динамической
грузоподъемности.
|
|
ГОСТ
24810-8I.
Зазоры. Размеры
|
ГОСТ
20918-75 Методы расчета
предельной
частоты вращения.
|
Выбор
подшипников
по статической
грузоподъемности
по ГОСТ
18854-82 затруднений
не вызывает.
Приведенная
далее последовательность
выбора подшипников
по динамической
грузоподъемности
применима для
всех
типов
радиальных
и радиально-упорных
шари-коподшипников.
В более общих
случаях руководствоваться
[1,
2].
Исходные
данные для
выбора типоразмеров
подшипников:
а)
принятая конструкция
узла (см.
таблица
1.2);
б)
значения и
направления
внешних нагрузок
на опоры и вал;
r)
монтажные и
эксплуатационные
требования
(осевой зазор
вала, температура,
ударно-вибрационные
параметры и
др.);
д)
диаметры вала
в зоне установки
подшипников;
и)
материалы вала
и корпуса.
Последовательность
выбора подшипников.
Выбрать
основной тип
подшипника
по таблице 1.4.
В исходной
схеме обозначения
подшипника
по ГОСТ 3189-75.
XX
- ХХХХХХХ.
XX …
записать
обозначение
принятого типа
(0; 1 или 6).
Пример
1; Двухопорный
гладкий вал
(dв
= 6
мм), конструктивная
схема 1.3; ради-альная
нагрузка правой
опоры Q2
= 35 Н, левой
– Q1=40
H;
осевая
A=
13 Н направлена
на опору 2, осевой
люфт(30...60
мкм) и другие
данные (см. далее).
По
таблице 1.4 приняты
радиальные
однорядные
шариковые
подшипники
(тип 0). Обозначение
принимает вид
XXX
– ХXХ0ХХХ.
XX ...
2.
Выбрать конструктивную
разновидность
основного типа
подшипника;
в
обозначении
подшипника
записать знаки
разновидности:
XXX
- XXXXXXX.
XX ...
Использование
разновидностей
основного типа
по ГОСТ 3395-79 (с
уплотне-ниями,
с упорным бортом
и др.) упрощает
конструкцию
узла, повышает
его надеж-ность
и точность (см.
табл.1,2 и 1.4).
Конструктивные
разновидности
00, 03, 04, 07 радиально-упорных
подшипников
отличаются
номинальным
углом контакта
и конструкцией
колец.
К примеру
1. Принятая ранее
схема замыкания
(схема 1.3) конструктивно
фор-мируется
с использованием
радиальных
подшипников
с упорным бортом
и двумя за-щитными
шайбами по ГОСТ
10058-75 (разновидность
88оооо). Обозначение
подшипника
принимает вид
ХХ - X880ХXX.
ХХ…
Таблица
1.3-Ориентировочные
данные
для
назначения
сборочного
осевого смещения
вала в
подшипниках.
Зазоры
и допуски в
мкм.
|
Элемент
узла, определяющий
уровень требований
к осевому
смещению вала
в подшипниках
|
Группа
механизма
по требованиям
к зазору
|
|
А
|
Б
|
В
|
|
Gao
|
TG
|
Ga
|
Gao
|
TG
|
Ga
|
Gao
|
TG
|
Ga
|
|
min
|
max
|
min
|
max
|
min
|
max
|
|
Цилиндрические
прямозубые
колёса
|
40-60
|
30
|
0
|
100
|
4
|
10
|
-
4
|
10
|
6
|
2
|
10
|
|
Цилиндрические
косозубые и
винто-вые колёса
|
Нереверсивные
|
40-60
|
0
|
0
|
80
|
4
|
10
|
-4
|
10
|
2
|
10
|
|
Реверсивные.
|
20-40
|
20
|
0
|
60
|
4
|
8
|
.-4
|

|
2
|

|
|
Конические
прямозубые
колёса
|

|
0
|
fАМ
|

|
-4
|

|

|
2
|

|
|
Червячные
колёса
|

|
0
|
fxr
|

|
-4
|

|

|
2
|

|
|
Червяки
|
Нереверсивные
|
20-40
|
20
|
0
|
60
|
6
|
2
|
-2
|
10
|
6
|
6
|
2
|
10
|
|
Реверсивные.
|
10-30
|
10
|
0
|
40
|
22
|
4
|
4
|
2
|
6
|
|
Винты
ходовые
|
10-30
|
10
|
0
|
0
|
|
Осевые
кулачки с
замыканием
|
Силовым
|
10-30
|
20
|
0
|
40
|
4
|
10
|
0
|
10
|
6
|
6
|
2
|
10
|
|
Кинематическим
|
6-12
|
10
|
-4
|
16
|
2
|
6
|
-2
|
8
|
4
|
4
|
2
|
8
|
|
Радиальные
кулачки с
замыканием
|
Силовым
|
20-40
|
20
|
0
|
60
|
4
|
10
|
0
|
10
|
6
|
6
|
2
|
10
|
|
Кинематическим
|
4-8
|
10
|
-4
|
16
|
0
|
4
|
-4
|
4
|
4
|
4
|
2
|
6
|
|
Маховики
стабилизаторы
скорости
|
-
|
-
|
-
|
-
|
2
|
4
|
0
|
4
|
2
|
4
|
2
|
6
|
|
Обозначения:
А - механизмы,
к которым не
предъявляются
специальные
требования
(к кинематической
точности и
моменту трения
в опорах)
Б
- механизмы,
к которым
предъявлены
требования
(прежде всего,
к кинематической
точности);
высоко-скоростные
валы (n10
об/мин) всех
групп механизмов;
В
- механизмы,
которые одновременно
должны иметь
и достаточно
высокую
кинематическую
точность, и
малые потери
на трение в
опорах;
Gao-
оптимальный
зазор или натяг
(знак "-");
fАМ
- предельное
осевое смещение
зубчатого
венца конического
колеса по ГОСT
9368-81(модуль
меньше 1 мм) или
ГОСТ
1758-81
(модуль равен
или больше
1
мм);
fxr-
смещение средней
плоскости
червячного
колеса,
допускаемое
по ГОСТ
3675-81 или
ГОСТ
9774-81;
TG
допуск сборочного
зазора;
Gamin,
Gamax-
предельные
значения
эксплуатационного
зазора
(натяга);
F‘I
-допуск
на кинематическую
погрешность
зубчатого
колеса, определяемый
по ГОСТ 9178-81 или
ГОСТ
1643-81
-
угол
наклона зубьев
косозубых
колес;
|
3.
Выбрать размер
внутреннего
диаметра подшипника
d
из размерного
ряда по ГОСТ
3478-79 или таблице
1.5, принимая его
равным диаметру
вала dв
или меньше на
1…3 мм в зависимости
от принятой
схемы замыкания
и конструкции
узла; в схеме
обозначения
заполнить знаки
внутреннего
диаметра (табл.
1.5):
XXX
– ХХХХХХХ.
ХХ ... при d<10
ми,
XXX
- ХХХХХХХ.
ХХ ... при d
10
мм.
Если
диаметр вала
не рассчитывался,
а ступицы зубчатых
колес на валу
закрепляются
штифтами, d
и dв
можно выбирать
по таблице 1.6.
Выбирая
d,
следует
учитывать
ограниченность
номенклатуры
подшипников
массового
изготовления
для принятого
типа.
Обозначение
подшипников
принимает вид
ХХ
– Х8800X4.
XX ...
Таблица
1.4 - Выбор
основного типа
подшипников
для опор малогабаритных
механизмов
приборов
|
Характеристика
нагружения
вала
|
Частота
вращения103,
об/мин
|
Подшипник
|
Примеры
элементов,
нагружающих
вал
|
|
Тип
|
Класс
точно-сти,
не ниже
|
|
Вал
нагружен только
радиальными
внешними силами
Qr
|
<10
|
0ooо
|
Р0
|
Цилиндрические
прямозубые
колёса, радиальные
кулачки, поводковые
муфты, шкалы,
рычаги и т.п.
|
|
10
|
Р6
|
|
Вал
нагружен
ради-альными
и осевой силами
при:
A
≤ 0,35Qr
|
<10
|
0ooo
|
P0
|
Конические,
косозубые
цилиндрические
и однозаходные
червячные
колёса, контактные
торцевые кольца
|
|
10
|
0ooo
(6ооо)
|
P6
|
|
Вал
нагружен
ради-альными
Qr
и осевой силами
при:
0,35Qr
r
|
<10
|
o6000
|
PO
|
То
же и винты
ходовые, червяки
и червячные
колёса
|
|
10
|
36ooo
(6000)
|
P6
|
|
То
же, при
Qr
r
|
<10
|
36000
(6000)
|
PO
|
Конические
зубчатые колёса,
червяки, винты
ходовые, осевые
кулачки, кулачковые
муфты
|
|
10
|
46000
|
P6
|
|
Вертикальные
валы
|
с
чисто осевой
односторонней
нагрузкой
|
<10
|
0oоo+
+6oоo
|
P6
|
Маховики,
опорные диски
регистраторов,
лимбы,
кодовые
диски на вертикальных
валах и т.п.
|
|
10
|
P5
|
|
С
осевым и радиальным
нагружением
|
<5
|
6000+
+6ooo
|
P6
|
То
же, но установленные
на одном валу
с зубчатыми
или фрикционными
колёсами.
|
|
5
|
Р5
|
При
длине опорной
базы валика
l
> 12dв
и относительно
боль-ших радиальных
наг-рузках, а
также
во всех
случаях, когда
трудно обеспечить
соосность
посадоч-ных
отверстий
кор-пуса для
установки
подшипников,
сле-дует применять
ша-рикоподшипники
типа 1ooo
(радиаль-ные
сферические
двухрядные).
Примечание.
При больших
осевых нагрузках
валов силовых
механизмов
взамен радиально-упорных
подшипников
(тип 6ооо) для
диаметров
больше 9 мм можно
применять
упорные (тип
8ооо) совместно
с 0ооо.
4.
Определить
расчетную
долговечность
подшипников,
млн.об.:
Lna=
Lh•n•60/106,
(1.1)
где
Lh-заданная
продолжительность
работы
подшипника
в
течение срока
службы изделия,
часов;
n-частота
относительного
вращения колец
подшипника,
об/мин; при n=
1...10 об/мин принимать
n
= 10 об/мин.
К
примеру 1. Задано
Lh=20000
ч;
n=850
об/мин. По (1.1)
Lna=2000085060/106=1020
млн. об.
5.
Определить
базовую долговечность
подшипников
 (1.2)
(1.2)
где
a1-
коэффициент
коррекции по
надежности
(таблица 1.7);
a2
– коэффициент,
учитывающий
изменение
характеристик
материала; для
стандартных
подшипников
a2=1;
a3-
коэффициент,
учитывающий
условия условия
эксплуатации
(таблица1.8):
а3=1/(КБКТ)3
(1.3)
Таблица
1.5 - Технические
характеристики
шарикоподшипников
|
Серия
по Dxd
|
Серия
по ширине для
типа
|
Размеры,
мм
|
Грузопо-дъёмность,
Н
|
[n]*103,об/мин
|
|
Х000ооо
|
Х840ооо
|
Х860ооо
|
Х880ооо
|
Х060ооо
|
Х080ооо
|
Х006ооо
|
d
|
D
|
B
|
r
|
DF
|
BF
|
Cr
*
|
C0r*
|
|
Защитные
шайбы
|
Защитные
шайбы
|
|
нет
|
есть
|
нет
|
есть
|
|
82
|
-
|
1
|
3
|
3
|
-
|
-
|
-
|
2
|
5
|
1,5
|
2,3
|
0,2
|
6,1
|
0,5
|
0,61
|
100
|
61
|
31
|
|
8/2,5
|
-
|
1
|
3
|
3
|
-
|
-
|
-
|
2,5
|
6
|
1,8
|
2,6
|
0,3
|
7,1
|
0,5
|
|
200
|
120
|
|
83
|
2
|
1
|
3
|
3
|
-
|
-
|
2
|
3
|
7
|
2,5
|
3
|
0,3
|
8,1
|
0,5
|
|
340
|
130
|
|
84
|
1
|
1
|
3
|
3
|
-
|
-
|
2
|
4
|
9
|
2,5
|
4
|
0,3
|
10,3
|
0,6
|
1,0
|
415
|
186
|
25
|
|
85
|
1
|
1
|
3
|
3
|
-
|
-
|
-
|
5
|
11
|
3
|
5
|
0,3
|
12,5
|
0,8
|
1,0
|
480
|
200
|
|
86
|
1
|
1
|
3
|
2
|
-
|
-
|
6
|
6
|
13
|
3,5
|
5
|
0,3
|
15,0
|
1,0
|
1,1
|
600
|
250
|
|
87
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
7
|
14
|
3,5
|
-
|
0,3
|
-
|
-
|
-
|
800
|
300
|
|
88
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
8
|
16
|
4
|
-
|
0,4
|
-
|
-
|
-
|
963
|
490
|
|
89
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
9
|
17
|
4
|
-
|
0,4
|
-
|
-
|
-
|
980
|
500
|
|
800
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
10
|
19
|
5
|
-
|
0,5
|
-
|
-
|
-
|
1000
|
510
|
|
801
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
12
|
21
|
5
|
-
|
0,5
|
-
|
-
|
-
|
1050
|
580
|
|
802
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
15
|
24
|
5
|
-
|
0,5
|
-
|
-
|
-
|
1435
|
830
|
20
|
|
803
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
17
|
26
|
5
|
-
|
0,5
|
-
|
-
|
-
|
1800
|
900
|
|
804
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
20
|
32
|
7
|
-
|
0,5
|
-
|
-
|
-
|
2300
|
1000
|
16
|
|
805
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
25
|
37
|
7
|
-
|
0,5
|
-
|
-
|
-
|
2830
|
1980
|
12
|
|
806
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
30
|
42
|
7
|
-
|
0,5
|
-
|
-
|
-
|
3400
|
2500
|
|
91
|
1
|
1
|
3
|
3
|
-
|
-
|
1
|
1
|
4
|
1,6
|
2,3
|
0,2
|
5,0
|
0,5
|
0,6
|
195
|
29
|
31
|
|
9/1,5
|
1
|
1
|
3
|
3
|
-
|
-
|
-
|
1,5
|
5
|
2,0
|
2,6
|
0,3
|
6,5
|
0,6
|
0,8
|
200
|
30
|
|
92
|
1
|
1
|
3
|
3
|
-
|
-
|
1
|
2
|
6
|
2,3
|
3,0
|
0,3
|
7,5
|
0,6
|
0,8
|
210
|
88
|
|
9/2,5
|
1
|
1
|
3
|
3
|
-
|
-
|
-
|
2,5
|
7
|
2,5
|
3,5
|
0,3
|
8,5
|
0,7
|
0,9
|
300
|
120
|
|
93
|
1
|
1
|
3
|
3
|
3
|
3
|
1
|
3
|
8
|
3
|
4
|
0,3
|
9,5
|
0,7
|
0,9
|
430
|
196
|
|
94
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
4
|
11
|
4
|
4
|
0,3
|
12,5
|
1
|
1
|
730
|
340
|
|
95
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
5
|
13
|
4
|
4
|
0,4
|
15
|
1
|
1
|
830
|
390
|
|
96
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
6
|
15
|
5
|
5
|
0,4
|
17
|
1,2
|
1,2
|
1130
|
558
|
|
97
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
7
|
17
|
5
|
5
|
0,5
|
19
|
1,2
|
1,2
|
1540
|
774
|
25
|
|
98
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
8
|
19
|
6
|
6
|
0,5
|
22
|
1,5
|
1,5
|
1710
|
880
|
|
99
|
1
|
-
|
-
|
-
|
1
|
1
|
1
|
9
|
20
|
6
|
6
|
0,5
|
-
|
-
|
-
|
2050
|
1040
|
|
900
|
1
|
-
|
-
|
-
|
-
|
-
|
1
|
10
|
22
|
6
|
-
|
0,5
|
-
|
-
|
-
|
2570
|
1290
|
|
901
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
12
|
24
|
6
|
-
|
0,5
|
-
|
-
|
-
|
2570
|
1290
|
|
902
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
15
|
28
|
7
|
-
|
0,5
|
-
|
-
|
-
|
2680
|
1480
|
20
|
|
903
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
17
|
30
|
7
|
-
|
0,5
|
-
|
-
|
-
|
2790
|
1640
|
|
904
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
20
|
37
|
9
|
-
|
0,5
|
-
|
-
|
-
|
5030
|
3050
|
16
|
|
16
|
0
|
-
|
-
|
-
|
-
|
-
|
0
|
6
|
17
|
6
|
-
|
0,5
|
-
|
-
|
-
|
1900
|
800
|
25
|
|
17
|
0
|
-
|
-
|
-
|
0
|
0
|
0
|
7
|
19
|
6
|
6
|
0,5
|
-
|
-
|
-
|
2190
|
1150
|
|
18
|
0
|
-
|
-
|
-
|
0
|
0
|
0
|
8
|
22
|
7
|
7
|
0,5
|
-
|
-
|
-
|
2540
|
1350
|
|
19
|
0
|
-
|
-
|
-
|
0
|
0
|
0
|
9
|
24
|
7
|
7
|
0,5
|
-
|
-
|
-
|
3000
|
1500
|
|
100
|
0
|
-
|
-
|
-
|
-
|
-
|
0
|
10
|
26
|
8
|
-
|
0,5
|
-
|
-
|
-
|
3530
|
1960
|
|
23
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
3
|
10
|
4
|
4
|
0,3
|
11,5
|
1,0
|
1,0
|
490
|
215
|
31
|
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
4
|
13
|
5
|
5
|
0,4
|
15,0
|
1,0
|
1,0
|
902
|
420
|
|
25
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
5
|
16
|
5
|
5
|
0,5
|
18
|
1,0
|
1,0
|
1470
|
740
|
|
26
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
6
|
19
|
6
|
6
|
0,5
|
22
|
1,5
|
1,5
|
2160
|
1150
|
25
|
|
27
|
0
|
-
|
-
|
-
|
0
|
0
|
0
|
7
|
22
|
7
|
7
|
0,5
|
-
|
-
|
-
|
2500
|
1350
|
|
28
|
0
|
-
|
-
|
-
|
0
|
0
|
0
|
8
|
24
|
8
|
8
|
0,5
|
-
|
-
|
-
|
2500
|
1350
|
|
34
|
0
|
-
|
-
|
-
|
0
|
0
|
-
|
4
|
14
|
5
|
5
|
0,5
|
-
|
-
|
-
|
1450
|
740
|
31
|
|
35
|
0
|
-
|
-
|
-
|
0
|
0
|
-
|
5
|
19
|
6
|
6
|
0,5
|
-
|
-
|
-
|
2120
|
1150
|
25
|
Значения Сr
и С0r
- ориентировочные.
Примечания:1.
Для подшипников
типов 840ооо, 860ooo
и 880ооо серий
95…98 r=0,3
мм
2.
Подшипники,
отмеченные
знаком “+”,
изготавливаются
класса точности
Р6, а выделенные
знаком « - « в
графе серий
по ширине - по
специальным
заказам.
Обозначения
размеров, размерных
серий и знаков
условного
обозначения
подшипников
соответствуют
приведенной
схеме:

Таблица
1.6
|
Диаметр,
мм
|
Крутящий
момент, Нм
не более
|
|
0,1
|
0,2
|
0,36
|
0,77
|
1,4
|
1,6
|
2,8
|
3,1
|
5,4
|
|
Вала
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
12
|
|
штифта
|
0,8
|
1
|
1,2
|
1,6
|
2
|
2
|
2,5
|
2,5
|
3
|
|
подшип-ника
для схемы:
|
1
|
2
|
3
|
3
|
4
|
5
|
6
|
7
|
8
|
9(10)
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
12
|
Примечания:
1. Материал валика
- сталь качественная,
HRC>32.
Штифты
по ГОСТ
3128-70.
2.Допускается
увеличение
диаметра штифта
до d/З;
при этом предельный
крутящий момент
Т= 0,05dвdш,
Нм.
К
примеру 1. При
Т=0,5 Нм:
dв
=6 мм,
dш
=1,6 мм;
для схемы1
d
=
4 мм.
Tаблица
1.7- Значения
коэффициента
а1
(ГОСТ
18855-82)
Таблица
1.8 Значения
коэффициентов
КБ
и КТ
|
Условия
нагружения
|
Значение
КБ
|
|
Спокойная
нагрузка без
толчков и ударов
|
1,0
|
|
Легкие
толчки, кратковременные
перегрузки
до 128 %
|
1,0…1,2
|
|
Умеренные
толчки, вибрация,
кратковременные
перегрузки
до 150 %
|
1,3…1,5
|
|
То
же, в условиях
повышенной
надежности
|
1,5…1,8
|
|
Значительные
толчки и вибрация,
перегрузки
до 200 %
|
1,8…2,5
|
|
Очень
сильные удары,
кратковременные
перегрузки
до 300 %
|
2,5…3,0
|
|
Коэффициент
К т
|
|
Рабочая
температура
подшип-ника,
С
|
100
|
125
|
150
|
175
|
200
|
225
|
250
|
|
Значение
коэффициента
КТ
|
1,0
|
1,05
|
1,10
|
1,15
|
1,25
|
1,35
|
1,40
|
|
Надежность,
%
|
Значение
а1
|
|
90
|
1,00
|
|
95
|
0,62
|
|
96
|
0,53
|
|
97
|
0,44
|
|
98
|
0,33
|
|
99
|
0,21
|
К примеру
1. Заданы: необходимая
надежность
98 %, температура
узла 95 С,
не более; возможны
перегрузки
до 120 %.
Из
таблиц: a1=
0,33; КБ
=
1,2; КТ
= 1.
По
(1.3):а3=1/(1,2·1)3=
=
0,578;
по
(1.2):
L10=1020/(0,33x
1x0,578)=
5347 млн.
об.
6. Определить
эквивалентную
динамическую
нагрузку.
 ,
(1.4) ,
(1.4)
где
X
и Y - коэффициенты
по таблице 1.9,
зависящие от
значения
 (или е);
(или е);
Fr
и
Fa
- радиальная
и осевая нагрузки
на один подшипник,
Н;
V=1,
если вращается
внутреннее
кольцо подшипника,
V=
1,2 - наружное.
Значение
коэффициента
е
для подшипников
0ооо, 06ооо, 36ооо
эависит от
относительной
нагрузки .
Следовательно,
точное значение
е
можно установить,
только зная
типоразмер
подшипника. .
Следовательно,
точное значение
е
можно установить,
только зная
типоразмер
подшипника.
На
конструктивной
схеме вала
каждой паре
подшипников
присвоить
индексы 1 и 2.
Радиальную
нагрузку на
каждый из в
подшипников
принять равной
заданному
значению внешней
радиальной
нагрузки
Qi:
Fr1=Qr1;
F r2=Qr2
(1.5)
Последующие
вычисления
выполнить по
одному из приведенных
вариантов.
Вариант
1. Приняты радиальные
шариковые
подшипники
типа 0ооо.
а)
Внешняя осевая
нагрузка на
подшипник Аi
=0 или Аi
0,19Qri.
Окончательное
значение
Pri=VFri.
(1.6)
б)
Внешняя осевая
нагрузка Аi>
0,19Qri.Ориентировочно
приняв e=0,21
Pri=0,56VFri+2Ai
(1.7)
Вариант
2.Приняты радиально-упорные
подшипники
типа о06ооо или
o36ooo.
Принять
e1=e2=0,3.
Вычислить
ориентировочно
Pr1
и Pr2
согласно таблице
1. l0.
Вариант
3.Приняты
подшипники
типов looo,
о46ооо, оббооо,
бооо - магнетные.
Из
таблицы
1.9 выписать значения
е, Х, и Y,соответствующие
типу подшипника,
и выполнить
вычисления
по таблице
1.10. Здесь Рri-
окончательные
значения.
Таблица
1.9 Коэффициенты
Х и У
|
Тип,
угол контакта
|

|
e
|
Fa/(FrV)>e**
|
Тип,
угол контакта
|

|
e
|
Fa/(FrV)>e**
|
|
X
|
Y
|
X
|
Y
|
|
0ooo
=0
|
0,014
|
0,19
|
0,56
|
2,30
|
36ооо
=12
|
0,014
|
0,30
|
0,45
|
1,81
|
|
0,028
|
0,22
|
1,99
|
0,029
|
0,34
|
1,62
|
|
0,056
|
0,26
|
1,71
|
0,057
|
0,37
|
1,46
|
|
0,084
|
0,28
|
1,55
|
0,086
|
0,41
|
1,34
|
|
0,110
|
0,30
|
1,45
|
0,110
|
0,45
|
1,22
|
|
0,17
|
0,34
|
1,31
|
0,17
|
0,48
|
1,13
|
|
0,28
|
0,48
|
1,15
|
0,29
|
0,52
|
1,04
|
|
0,42
|
0,42
|
1,04
|
0,43
|
0,54
|
1,01
|
|
0,56
|
0,44
|
1,00
|
0,57
|
0,54
|
|
1,00
|
|
1ооо
|
=12
|
-
|
0,32
|
0,65
|
3,06
|
46ooo
=26
|
-
|
0,68
|
0,41
|
0,87
|
|
=13
|
-
|
0,35
|
2,81
|
66ooo
=36
|
-
|
0,95
|
0,37
|
0,66
|
|
6ооо*
|
-
|
0,20
|
0,50
|
2,50
|
*Магнетные.
**Если
Fa/(V
Fr)е,
для
однорядных
подшипников
принимать Х=
1,
Y=
0. Для подшипников
типа 1ооо -
X=
1, Y=
0,45ctg.
Вариант
4. Подвижное
звено установлено
на одном радиальном
подшипнике
(А = 0) или выбирается
подшипник
плавающей опоры
(схемы 3, таблица
1.2). Окончательное
значение
Pr3=Qr3V.
(1.8)
К
примеру 1. При
замыкании по
схеме 1 А2=
13 Н. Подшипники
типа 0ооо.
По
(1.5) Fr1=
40 Н; Fr2=
35 Н; по (1.6) P1
=40 Н;
по
(1.7) P2=
0.56135
+ 213
= 45,6 Н.
7. Определить
расчетную
динамическую
грузоподъемность
для каждого
шарикоподшипника,
Н:
 ,
(1.9) ,
(1.9)
где
Pri
и L10-
ранее вычисленные
значения.
К
примеру 1.
 . .
8.
Выбрать серию
подшипника
по наружному
диаметру D
и серии по ширине
колец B;
заполнить знаки
в обозначении
подшипника:
XXX
– ХХХХ0ХХ. XX ... –
при
d<10
мм,
XXX
- ХШХХХ. XX ... - при
d
мм.
По
каталогу, зная
внутренний
диаметр подшипника
d
и тип, выбирают
наиболее легкую
серию диаметров,
при которой
еще удовлетворяются
условия:
Ср.
Cr;
(1.10)
nmax
[n] ,
(1.11)
где
Cr
и [n]-
предельные
грузоподъемность
и частота вращения
по
каталогу
(при
этом, в первую
очередь, следует
ориентироваться
на
подшипники
нормальной
ширины - серии
по ширине 1
или 0).
Характеристики
некоторых
типоразмеров
подшипников
приведены в
таблице 1.5.
Таблица
1.10 – Вычисление
эквивалентных
нагрузок.
|
Вычислить
|
Установить
соотношения
|
Вычислить
|
Установить
соотношения
|
Вычислить
|
|
S1
|
S2
|
S1S2
|
A2S2-S1
|
Fa1
|
Fa2
|

|

|
Pr1
|
Pr2
|
|
Fr1e1
|
Fr2e2
|
|
-
|
S1
|
S1+A2
|
-
|
|
Fr1V
|
Fr2
|
| |
|
-
|
>
|
X2Fr2V+Y2Fa2
|
| |
S2-A2
|
S2
|
|
-
|
Fr1V
|
Fr2V
|
|
>
|
-
|
X1Fr1V+Y1Fa1
|
|
Примечание.
Индексация
в таблице
соответствует
варианту, когда
осевая сила
А воспринимается
подшип-ником
2. При нагружении
осевой силой
подшипника
1 все индексы
"1" заменить
на "2", "2"
– на
"1". Для
узлов с осевым
сборочным
натягом при
вычислении
Fa1
и Fa2
следует добавлять
усилие натяга
Qн.
|
В
реверсируемых
механизмах
могут изменяться
значения и
направления
нагрузок (червяки,
винты). В этом
случае необходимо
просчитывать
оба режима.
К
примеру 1. По
таблице 1.5 подшипники
типа 880ооо при
d=4
мм
имеют грузоподъемность,
Н:
серия
диаметров 8,
ширины 1 - Cr=
415 < Cp1=
699;
серия
диаметров 9,
ширины 1 - Cr=
730 > Cp1=
699, но меньше Cp2;
Серия
диаметров 1
ГОСТ 10056-75 не предусмотрена;
серия
диаметров 2,
ширины 0 - Cr1=
902 > Cp2=
797 > Cp1=699.
Для
всех серий [n]
> n
= 850 об/мин.
Следовательно,
для левой опоры
можно принять
подшипник
типоразмера
1880094,
D
= 11 мм; для правой
- 0880024, D
= 13 мм.
Подшипники
одного вала
малогабаритных
редукторов
и большинства
механизмов
технологически
выгодно выбирать
либо одинаковыми,
либо одного
размера по
наружному
диаметру (таблица
1.11)
Таблица
1.11-Наружные
диаметры радиальных
и радиально-упорных
подшипников
в
зависимости
от размерной
серии по диаметру
D
(ГОСТ 3478~79), мм
|
Серия
по
D
|
Внутренний
диаметр подшипника,
мм
|
|
0,6
|
1,0
|
1,5
|
2,0
|
2,5
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
12
|
15
|
|
0
|
2
|
2,5
|
3
|
4
|
5
|
6
|
7
|
8
|
10
|
11
|
12
|
14
|
15
|
-
|
-
|
|
8
|
2,5
|
3
|
4
|
5
|
6
|
7
|
9
|
11
|
13
|
14
|
16
|
17
|
19
|
21
|
14
|
|
9
|
-
|
4
|
5
|
6
|
7
|
8
|
11
|
13
|
15
|
17
|
19
|
20
|
22
|
24
|
28
|
|
1
|
-
|
-
|
6
|
7
|
8
|
9
|
12
|
14
|
17
|
19
|
22
|
24
|
26
|
28
|
32
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
2
|
2
|
-
|
-
|
-
|
10
|
13
|
16
|
19
|
22
|
24
|
26
|
30
|
32
|
35
|
|
3
|
-
|
-
|
-
|
-
|
-
|
13
|
16
|
19
|
22
|
26
|
28
|
30
|
35
|
37
|
42
|
К
примеру 1
Можно принять
оба подшипника
типоразмера
0880024 с наружным
диаметром 13
мм, либо
для левой опоры
использовать
подшипник с
внутренним
диаметром не
4 мм, а 5 мм, т.е.
типоразмер
1880095 (D=13
мм, Cr=
830 Н). Ориентировочно
примем оба
подшипника
серии 2 по D,0
- по ширине:
dxDxB=
4х13х5 мм; Сr=
902 Н, Сor
=420 Н.
Обозначение:
XXX - 880024.
XX
*
свободные
нули слева в
основном обозначении
не записывают.
Если
значения P
определялись
как ориентировочные,
необходимо
выполнить
поверочный
расчёт. Для
этого выписывают
из каталога
или таблицы
1.5 значения
статической
грузоподъемности
Cor
принятых
подшипников,
определяют
относительную
осевую нагрузку
 ,
соответствующие
ей значения
e,
X,
и Y
в таблице 1.7 и
повторяют
вычисления
по (1.6) (для радиально-упорных
подшипников
по таблице
1.10) и (1.8) при действительных
значениях e. ,
соответствующие
ей значения
e,
X,
и Y
в таблице 1.7 и
повторяют
вычисления
по (1.6) (для радиально-упорных
подшипников
по таблице
1.10) и (1.8) при действительных
значениях e.
Сравнивая
новые значения
Сp
с допускаемыми
для ориентировочно
принятых подшипников
(см. п.8), их принимают
либо окончательно,
либо переходят
к другим сериям
по диаметру.
Если
действительное
значение eq
получится
меньше ориентировочного
ea
и после
определения
нового значения
расчётной
грузоподъёмности
будет соблюдено
условие
(1.10), можно
считать, что
подшипники
по
грузоподъёмности
выбраны правильно.
При
eq
>
ea
следует
проверить
возможность
перехода к
более лёгким
сериям.
К
примеру 1. Для
принятыx
подшипников
Со1
= Со2=
420 Н.
Fa/Cor
= 13:420 = 0,031;
eq
= 0,224, X=0,56,
Y=1,96
(промежуточные
значения e
и Y
определяют
линейной
интерполяцией).
Из уравнения
(1.6) Pr2=
45,1 Н; из
(1.9) Cp2=
789 Н < Сr2=902
Н, но больше Сr
=
730 Н
для серии 9.
Поскольку
eq>ea=0,22
и грузоподъемность
подшипников
серии
2 явно
не
используется,
следует проверить
возможность
применения
серии 9,
для
которой
Cor=340
Н
Fa/Cor
=
13:340
= 0,038;
eq
= 0,234,
X=0,56, Y=1,161.
Pr2=
0,56135
+1,6113
= 40,53 Н;
Cp2=
708
Н < Сr2=730
Н.
Следовательно,
переход
на
серию
9 возможен.
Окончательно
принимаются
подшипники
по
ГОСТ 10058-75
сверхлёгкой
серии
4х11х4.
Обозначение:
ХХХХ
– 1880094.ХХ...
9.
Выбрать класс
точности подшипника;
в обозначении
записать класс
точности (0;6;5;4
или 2) ГОСТ 520-89:
ХХХ
- XXXXXXX.
ХХ…
В
первую очередь
ориентироваться
на применение
подшипников
класса 0 (Р0) или
наиболее грубого
класса, по которому
выпускается
принятый типоразмер
(см. таблицу
1.5). Необходимость
в применения
более высоких
классов точности
уста-
Таблица
1.12 - Предельные
отклонения
размеров и
радиальные
биения дорожек
качения
радиальных
и радиалыю-упорных
шарикоподшипников.
Ограничение
ГОСТ 520–89
|
Класс
точности
|
dm
|
Отклонения,
мкм
|
D
|
Отклонения,
мкм
|
|
Св.
|
До
|
dm
|
Ri
|
B
|
Св.
|
До
|
Dm
|
Ra
|
|
EI
|
ES
|
max
|
ei
|
es
|
ei
|
es
|
max
|
|
P0
(0)
|
0,6
|
2,5
|
-8
|
0
|
10
|
-40
|
0
|
2,5
|
6
|
-8
|
0
|
15
|
|
2,5
|
10
|
-120
|
6
|
18
|
|
10
|
18
|
18
|
30
|
-9
|
|
18
|
30
|
-13
|
13
|
30
|
50
|
-11
|
20
|
|
P6
(6)
|
0,6
|
2,5
|
-7
|
0
|
5
|
-40
|
0
|
2,5
|
6
|
-7
|
0
|
8
|
|
2,5
|
10
|
6
|
-120
|
6
|
18
|
|
10
|
18
|
7
|
18
|
30
|
-8
|
9
|
|
18
|
30
|
-8
|
8
|
30
|
50
|
-9
|
10
|
|
P5
(5)
|
0,6
|
10
|
-5
|
0
|
3,5
|
-40
|
0
|
2,5
|
18
|
-5
|
0
|
5
|
|
10
|
18
|
-80
|
18
|
30
|
-6
|
6
|
|
18
|
30
|
-6
|
4
|
-120
|
30
|
50
|
-7
|
7
|
|
P4
(4)
|
0,6
|
10
|
-4
|
0
|
2,5
|
-40
|
0
|
2,5
|
18
|
-4
|
0
|
3
|
|
10
|
18
|
-80
|
18
|
30
|
-5
|
4
|
|
18
|
30
|
-5
|
3
|
-120
|
30
|
50
|
-6
|
5
|
|
P2
(2)
|
0,6
|
10
|
-2,5
|
0
|
1,5
|
-40
|
0
|
2,5
|
18
|
-2,5
|
0
|
1,5
|
|
10
|
18
|
-80
|
18
|
30
|
-4
|
2,5
|
|
18
|
30
|
2,5
|
-120
|
30
|
50
|
навливается:а)
сопоставлением
заданных требований
к отклонениям
средних значений
диаметра отверстия
dm,
наружного
диаметра Dm
и ширины колец
с соответствующими
предельными
отклонениями
по классам
точности для
принятых типоразмеров
подшипни-ков;
б)
сравнением
заданных допускаемых
значений радиального
биения
качения
внутреннего
Ri
и (или) наружного
Ra
колец c
соответствующими
предельными
биениями принятых
типоразмеров
в *Включительно
этот размер.
зависимости
от класса точности
(таблица
1.12 или ГОСТ 520-89).
dm,
Dm
-
нормируемое
среднее значение
диаметра отверстия
и наружного
диаметра подшипника,
соответственно.
EI,
ei-
нижние предельные
отклонения;
ES,
es
- верхние.
К
примеру 1.- Задано
предельное
смещение вала
в плоскости
опор
за счет радиального
биения дорожек
качения 5 мкм.
Поскольку
вращается
только вал, а
наружное кольцо
в условиях
жестких ограничений
радиального
смещения будет
устанав-ливаться
неподвижно,
класс точности
подшипника
выбирается
по биению Ri
внутреннего
кольца:
Rmax=
5 мкм
Rimax
(1.12)
Для
принятых подшипников
(d
= 4 мм) условие
(1.12) удовлетворяется
в классе точности
Р5
(Rimax
=3,5 мкм).
Обозначение
подшипника
принимает вид
ХХ5 -
1880094. XX ...
10.
Выбрать группу
подшипника
по радиальному
зазору; указать
обозначение
группы по ГОСТ
24810-60 в схеме
вба
XXX - ХХХХХХХ.
XX ...
Группу
по радиальному
задору выбирают
только для
радиальных
подшипников.
Группа, предпочтительная
для приме-нения
в общих случаях,
именуется
"основная":
в обозначении
подшипника
либо проставляется
буква М, либо
ее опускают,
если позиция
"в" схемы окажется
не заполненной.
Значения
радиальных
зазоров приведены
в таблице 1.13. Кроме
основной группы
можно использовать
и другие: группу
6 - для подшипника
плавающей опоры
в схеме
Таблица
1.13 Радиальные
зазоры шариковых
радиальных
замыкания
3; группы 7,8,9 с
увеличенным
однорядных
подшипников
Gr
мкм. Ограничение
ГОСТ 24810-80
|
d,
мм
|
Группа
зазора в подшипнике
|
|
6
|
основная
|
7
|
8
|
9
|
|
Св.
|
До
|
min
|
max
|
min
|
max
|
min
|
max
|
min
|
max
|
min
|
max
|
|
2,5
|
10
|
0
|
7
|
2
|
13
|
8
|
32
|
14
|
29
|
20
|
37
|
|
10
|
18
|
0
|
9
|
3
|
18
|
II
|
25
|
18
|
33
|
25
|
45
|
|
18
|
24
|
0
|
10
|
5
|
20
|
13
|
28
|
20
|
36
|
28
|
48
|
|
24
|
30
|
1
|
II
|
5
|
20
|
13
|
28
|
23
|
41
|
30
|
53
|
зазором
- для подшипников
вертикальных
валиков или
вали-ков
с большой осевой
нагрузкой на
радиальные
подшипники,
используемые
взамен радиально-упорных.
11.
Выбрать группу
(ряд) по
моменту трения;
заполнить
позицию "в"
схемы обозначения:
вба
ХХХ
- ХХХХХХХ. ХХ...
Группы
по моменту
трения, их
обозначения
и числовые
характеристики
уста-новлены
специальными
техническими
условиями на
подшипники
качения. В общих
условиях используется
основная группа,
обозначение
которой на
схеме не указывается.
К
примеру 1. Для
выбранного
типоразмера
приняты основные
группы по зазору
и моменту трения.
Обозначение
принимает вид:
5
- 1880094. XX…
12.
Составить
перечень специальных
требований
для оформления
заказа на подшипники
и согласования
с подшип-никовой
промышленностью.
В схеме обозначения
подшипника
г
XXX - ХХХХХХХ. XX К…
У… Т… С… Ш…
заполнить
те дополнительные
знаки справа
от основных,
которые
однозначно
установлены
в каталоге.
Позиция
"г" - знаки,
указывающие
на материал
деталей подшипника:
например, Е -
сепаратор из
текстолита.
Последующие
позиции отражают
конструктивные
изменения,
связанные с
удовлетворением
требований
быстроходности
(К…), к покрытиям
и шероховатости
поверхностей
(У…), к уровню
шумов и вибрации
(Ш…).
Позиция
Т… - температура
отпуска колец:
Т соответствует
температуре
отпуска 200 С;
Т2 - 250; ТЗ - 300; Т4 - 350, Т5 - 400
С.
Подшипники
общего применения
могут работать
при температурах
до 100 С
без снижения
их номинальной
долго-вечности.
Позиции Т…
таких подшипников
опускаются.
Позиция
С - марка смазочного
материала,
которым заполняется
закрытый подшипник
(типы 88ооо, 98оооо,
98оооо и др.) на
заводе-изготовителе
подшипника.
Можно указать,
например, знаки:
С1-подшипники
скоростных
узлов и узлов
с большим сроком
службы или
предэксплуатационного
хранения (заполняется
ОКБ 122-7);
С2-подшипники,
работающие
в агрессивных
средах (ЦИАТИМ-221);
5
- для работы
при температурах
до 200 С
(заполнен ВНИИ
НП 207).
К
примеру 1. Поскольку
температура
эксплуатации
указана меньше
100 С,
знак Т опускается.
Подшипник
принят закрытого
типа, имеет
большой срок
службы. Других
особых требования
нет. Обозначение
подшипника
следует дополнить
только знаком
CI
и указать стандарт
на типоразмер
подшипника:
5-1880094.С1
ГОСТ 10058-75.
1.4.
Посадочные
места подшипников
Номинальной
формой посадочных
мест для установки
шарикоподшипников
служат цилиндрические
поверхности
и опорные кольцевые
плоскости. Если
посадочный
цилиндр и опорная
плоскость
(заплечики)
образуются
на одной детали,
в зоне их пересечения
формируется
переходной
участок в виде
галтели (криволинейное
сопряжение)
или проточки
(См рис.1.2). Валы
и отверстия
со стороны
монтажа подшипников
должна иметь
фаски.
Номинальные
размеры.
Диаметр посадочного
цилиндра вала
принимается
равным номинальному
диаметру отверстия
подшипника
d,
а диаметр отверстия
в корпусе - наружному
диаметру подшипника
D.
Высота (длина)
посадочных
цилиндров
L
В-r,
(1.13)
где
В
- ширина
кольца подшипника,
мм;
r-
координата
фасок подшипника
(см. таблицу
1.5).
Внешний
диаметр упорных
торцовых поверхностей
вала (заплечиков,
колец, ступиц
и др.) принимается
обязательно
больше диаметра
кромки фасок:
d1>d+4r.
(1.14)
Внутренний
диаметр торцовых
поверхностей
отверстия в
корпусе или
в корпусных
деталях (крышек,
резьбовых
пробок, колец)
должен быть
меньше диаметра
кромки фаски
на наружном
кольце подшипника:
d2
<
D-5r
(1.15)
Наибольший
радиус галтели
(r1,
r2),мм:
|
r
|
0,1
|
0,15
|
0,2
|
0,3
|
0,4
|
0,5
|
1,0
|
|
r1,
r2
|
0,05
|
0,1
|
0,1
|
0,2
|
0,2
|
0,3
|
0,6
|
Ширина
проточек (рисунок
1.2): S
= 0,8 мм, глубина
h
= 0,3 мм.
Размер
фаски:
cx45
при
c
=
r.
(1.17)
Допуски
размеров.
Предельные
отклонения
размеров принятых
подшипников
определяют
по таблицам
ГОСТ 520-89. Необходимый
характер сопряжения
колец подшипников
и посадочных
цилиндров
достигается
выбором полей
допусков вала
и отверстия
в корпусе из
числа рекомендованных
ГОСТ 3325-77.
Сочетания полей
допусков отверстия
(KB)
и наружного
диаметра (h8)
подшипника
c
полями допусков
посадочных
цилиндров вала
и отверстия
в корпусе образуют
посадки с натягом,
с зазором или
переходные.
Методика выбора
посадок регламентирована
ГОСТ 3325-77. Применительно
к шарикоподшипникам
опор механизмов
приборов для
выбора полей
допусков
и посадок можно
воспользоваться
таблицей 1.15
настоящих
указаний.
При
ударных и
вибрационных
нагрузках поля
выбираются
по нормам тяжёлого
режима работы
независимо
от расчётной
долговечности.
Подшипники
точных механизмов
(счетно-решающих,
функциональных
преобразователей
и др.) устанавливаются
с жестко ограниченными
значениями
посадочных
зазоров и натягов,
определяемых
расчетом или
экспериментально.
Если предельные
значения зазоров
и (или) натягов
выходят за
границы допускаемых,
в технических
требованиях
сборочных
чертежей опытного
производства
записывают:
"Подшипники
поз.__ осей I и III
установить
на вал с натягом
0,004…0,008 мм подбором
подшипников
по разности
средних диаметров
цапфы вала и
отверстия
подшипника
в пределах
0,005…0,007 мм. Доработка
цапф
вала не допускается.
Наружные кольца
подшипников
в отверстия
стаканов поз.
___ установить
с номинально
нулевым зазором
при отклонениях
0,002
мм доработкой
посадочной
поверхности
стаканов
(Ra
0,32)".
На
длину L
посадочной
поверхности
в общих случаях
устанавливают
допуски 12…14
квалитетов.
Предельные
отклонения
радиусов галтелей
и фасок назначаются
в соответствии
ГОСТ
25670-83.
Таблица
1.15 – Выбор посадок.
|
Характер
радиальной
нагрузки
|
Вращающее-ся
кольцо
|
Вид
нагружения
колец
|
Пример
узла
|
|
внутреннего
|
наружного
|
|
Постоянная
по направлению
Fr.
|
Внутреннее
|
Циркуляционное
|
Местное
|
Уравновешенные
узлы зубчатых,
фрикционных
и кулачковых
механизмов
|
|
Наружное
|
Местное
|
Циркуляционное
|
|
Постоянная
по направлению
Fr
и вращающаяся
Ри
< Fr
|
Внутреннее
|
Циркуляционное
|
Колебательное
|
То
же, но не уравновешенные,
низкие скорости
вращения
|
|
Наружное
|
Колебательное
|
Циркуляционное
|
|
То
же, но Ри
> Fr
|
Внутреннее
|
Местное
|
Циркуляционное
|
То
же, но
при
вы-соких скоростях
вращения
|
|
Наружное
|
Циркуляционное
|
Местное
|
2.Выбор
полей допусков
вала и отверстия
в корпусе
А.
Поля допусков
стальных валов
|
Вид
нагружения
|
Режимработы
|
Примеры
узлов
|
Подшипник
|
|
Тип
и размер
|
Класс
точности
|
|
|
|
|
0;6
|
5;4
|
2
|
|
Циркуляцион-ное
или колеба-тельное
нагру-жение
внутрен-него
кольца подшипника
|
Лёгкий
или нор-мальныйP<0,15C
|
Редукторы
самописцев,
реле времени,
электроприводы
и другие при
Lh5000
ч
|
Радиальный
d18
mm
|
h6
|
h5
|
h4
|
|
Радиальный
и радиаль-но–упорный
d<100
мм
|
js6
|
js5
|
js4
|
|
Нормальный
или тяжёлый
при:0,07 C
|
Приводы
РЛС, электроприводы
исполнительные
и др. при: Lh<5000
ч
|
Радиальный
d18
mm
|
k6
|
js5
|
js4
|
|
Радиальный
и радиаль-но–упорный
d<100
мм
|
k6
|
k6
|
k4
|
|
Местное
нагру-жение
внутрен-него
кольца; вращается
нару-жное
кольцо
подшипника
|
Лёгкий
или нормальный
P<0,07Сr
|
Блоки
колес,6apaбаны
двухопорные,
сателлиты,
внутреннее
кольцо
подвижное
|
Все
размеры радиаль-ных
и радиально
– упор-ных
подшипников
|
g6
|
h5
|
h4
|
|
Нормальный
или тяжёлый
P>0,07Cr
|
То
же,
но
когда
внутреннее
кольцо
не
должно
вращаться
|
h6
|
h5
|
h4
|
|
Чисто
осевые
нагрузки при
всех режимах
работы
|
Вертикальне
валы
лимбов,
осевых кулачков,
маховиков
и др.
|
js6
|
js5
|
js4
|
|
Б.
Поля допусков
отверстий
корпусных
элементов
из стали, чугуна,
титановых
или медных
сплавов*
|
|
Вид
нагружения
|
Режим
работы
|
Примеры
узлов
|
Схема
замыкания
|
Класс
точности
подшипника
|
|
0;6
|
5;4
|
2
|
|
Местное
или колебательное
нагружение
на-ружного
кольца
|
Лёгкий
или
нормальный
P<0,15Сr
|
Редукторы
самописцев,
реле времени,
электроприводы
и другие при
Lh5000
ч
|
Сх.1
|
Н7
|
Н6
|
Н5
|
|
Сх.2
|
Js7
|
Js6
|
Js5
|
|
Нормальный
или тяжёлый
0,07C
|
Приводы
РЛС, электроприводы
исполни-тельные
и др. при: Lh<5000
ч
|
Сх.1
|
Js7
|
Js6
|
Js5
|
|
Сх.2
|
К6
|
К5
|
К4
|
|
Циркуляционное
или колебатель-ное
нагружение
внутреннего
коль-ца подшипника;
вращается
наруж-ное
кольцо или
оба
|
Лёгкий
или
нормальный
P
<
0,15
Сr
|
Блоки
колес,
6apaбаны
двухопорные,
сателлиты,
маховики
Lh5000
ч
|
Сх.1
|
|
|
|
|
Сх.2
|
|
|
|
|
Нормальный
или тяжёлый
0,07 C
|
То
же при Lh<5000
ч
|
|
|
|
|
Допуски
формы, допуски
расположения
и шероховатость
посадочных
поверхностей
должны соответствовать
значениям,
приведенным:
в таблице
1.16
Примеры
нанесения
допусков, объязателыю
указываемых
на чертежах
или оговариваемых
общем записью
в технических
требованиях,
показаны на
рис.1.2.
 
Рисунок
1. 2
Таблица
1.16 - Допуски формы,
допуски расположения
поверхностей
и посадочных
поверхностей
для установки
шарико-подшипников
|
Параметры
|
Обозначение
на чертежах
|
Допуски
и отклонения,
мкм, не
более,
для
класса
точности
подшипника
мкм,
|
|
Р0
|
Р6
|
Р5
|
Р4
|
Р2
|
|
Допуск
цилиндричности
вала или отверстия
корпуса
|

|
IT/4
|
IT/8
|
|
Допуск
круглости
вала или отверстия
корпуса
|

|
|
Допуск
соосности
отверстия
корпуса относительно
общей
оси
|

|
1,5В*
|
0,5В*
|
|
Допуск
полного торцового
бие-ния заплечиков
вала d50
мм
|
 
|
10
|
7
|
4
|
1.6
|
1.2
|
|
Допуск
полного торцового
бие-ния заплечиков
отверстия
(D80
мм)
|
|
25
|
16
|
10
|
4
|
2.5
|
|
Шероховатость
поверхности
валов, Ra
не
более
|

|
1,25
|
0,63
|
0,32
|
0,16
|
|
Шероховатость
поверхности
отверстий
корпуса, Rа
не более
|

|
1,25
|
0.63
|
0,32
|
|
Шероховатость
поверхности
заплечиков
вала и отверстия,
не более
|

|
2,5
|
1,25
|
0,63
|
*
Допуск отнесен
к размеру В/2.
Примечание.
После вычислений
допуски округлить
до меньших
ближайших
значений по
ГОСТ 24643-81.
Обозначения:
IТ-
допуск на диаметр
отверстия или
вала по ГОСТ
25347-82, мкм; В-
ширина колец
подшипника,
мм (см.
таблицу
1.5);
d,
D
-
диаметр цапфы
(шипа) вала и
отверстия в
корпусной
детали, соответст-венно.
Твердость
посадочных
поверхностей.
Стальные валы
и оси механизмов
приборов подвергаются
термохимической
обработке,
обеспечивающей,
прежде всего,
необходимые
физико-механические
характеристики
вала как несущего
элемента конструкции.
Посадочные
поверхности
валов дополнительной
обработке и
покрытиям
подвергаются
только в особых
случаях. Как
правило, принятые
для валов требования
к твердости
поверхности
удовлетворяют
и требованиям
к твердости
поверхностей
для установки
подшипников
качения:
сталь
45 - улучшение:
НRС
26...32; закалка:HRC
36...42;
сталь
20Х - закалка,
цементация:
HRC
52...56;
сталь
40Х - закалка, отпуск
до HRC
40...46;
сталь
I2XH3A
- закалка, отпуск
до 36...40 единиц
сталь
38ХМЮА
- нормализация:
HRC
32...36; или закалка,
азитирова-
ние:
HRC
56...62;
сталь
25XI3H2
- закалка,
отпуск
до HRC
38...42.
1.5
Осевое смещение
валов.
Функциональная
работоспособность
узла
“вал-опоры”
во многом зависит
от
степени ограничения
осевых
смещений
вала в
подшипниках.
Ориентировочный
осевой
зазор Gao
выбирают в
рекомендуемых
для заданных
условий пределах
(см. таблицу
1.8), учитывая
особенности
нагрузочного
и кинематического
режима: чем
больше частота
вращения и
осевые нагрузки,
чем выше требования
к кинематической
точности, тем
меньше должен
быть осевой
зазор и больше
натяг.
В
технических
требованиях
сборочных
чертежей осевые
смещения вала
оговаривают
предельными
значениями
сборочного
зазора (натяга),
мм:
Gao
min…
Gaomax,
с
указанием
способа его
обеспечения
и контроля
(примеры записей
см. разд. 1.2). При
этом
Gaomin=
Gao-
kiTG,
(1.27)
Gaomax=
Gao-
ksTG,
(1.28)
где
Gao
– по таблице
1.3; TG
– допуск сборочного
зазора, мм по
таблице 1.3;
ki
TG;
ksTG
– нижнее и верхнее
предельные
отклонения
осевого зазора
от номинального
Gao,
мм, nри
условии, что
ki+ks=1.
Если
коэффициенты
теплового
расширении
(КТР) материалов
вала и корпуса
одинаковы или
близки по значениям,
а разность
температур
вала и корпуса
не превышает
20 С,
принимают
ki=ks=0,5.
В общем случае
их выбирают
так, чтобы
выполнялись
условия:
 , ,
 (1.29)
(1.29)
 ,
(1.30) ,
(1.30)
где
Gamin,
Gamax
- наименьший
и наибольший
действительные
осевые зазоры
в подшипниках,
мм,
Gamin,
Gamax
-
наименьший
и наибольший
допускаемые
осевые зазоры,
мм (см.
таблицу
1.З)
 , ,
 - абсолютные
значения наибольших
изменений
осевого зазора
за счет
тепловых вариаций
размеров
вала и
корпуса, уменьшающих
|←|
и увеличивающих
|→|
исходный осевой
зазор, вычисляемые
для двух наиболее
неблагоприятных
режимов по
уравнению:
- абсолютные
значения наибольших
изменений
осевого зазора
за счет
тепловых вариаций
размеров
вала и
корпуса, уменьшающих
|←|
и увеличивающих
|→|
исходный осевой
зазор, вычисляемые
для двух наиболее
неблагоприятных
режимов по
уравнению:

где
d1,
d2,
D1,
D2
- внутренние
и наружные
посадочные
диаметры подшипников
1 и 2, мм;
α1,
α2 -
углы контакта
в подшипниках
(см. таблицу
1.5); для подшипников
типа 0ооо принять
α
= 8°;
α
tk,
αtв
– КТР материалов
корпуса и вала,
°С-1;
tk,
tв
– заданные
предельные
значения температуры
корпуса и вала,
°С,
при наиболее
неблагоприятных
режимах работы;
l0
– расстояние
между плоскостями
качения замыкающих
вал подшипников,
мм; верхние
знаки использовать
при замыкании
вала по схеме
1, нижние – по
схеме 2 (см. таблицу
1.2).
Если
точных данных
о тепловых
режимах узла
нет, уменьшающее
 вычисляют
для режима
пуска
при
tk=tв=
tmin
-
для схемы замыкания
1, или полагая
tk=tв=tmax
при замыкании
по схеме 2. Увеличивающее
вычисляют
для режима
пуска
при
tk=tв=
tmin
-
для схемы замыкания
1, или полагая
tk=tв=tmax
при замыкании
по схеме 2. Увеличивающее
 - вычислять
для режима
пуска при tk=tв=tmin
- для
замыкания по
схеме 2, или, приняв
tk=tв=
tmax-
при замыкании
по схеме 1.
- вычислять
для режима
пуска при tk=tв=tmin
- для
замыкания по
схеме 2, или, приняв
tk=tв=
tmax-
при замыкании
по схеме 1.
(tmin,
tmax
– заданные
предельные
значения температуры
эксплуатации).
РАСЧЕТ ТОЧНОСТИ
ЗУБЧАТЫХ ПЕРЕДАЧ
1 Общие
положения.
Наличие
первичных
погрешностей
при изготовлении
и монтаже зубчатых
передач приводит
к погрешностям
в их работе,
проявляющихся
в кинематической
погрешности
передачи,
представляющей
собой разность
между действительным
и номи-нальным
(расчетным)
углами поворота
ведомого зубчатого
колеса передачи,
а также мертвом
ходе, возникающем
при ревер-сировании
передачи. Значения
первичных
погрешностей
различных
типов зубчатых
передач ограничены
стандартами,
перечень которых
приведен в
таблице 1.1.
Стандарты
устанавливают
12 степеней точности
и 8 видов сопряжении
зубчатых колес.
В точных механизмах
применяются
зубчатые колеса
5...8 степеней
точности. При
этом для высокоточных
отсчетных и
кинематических
цепей механизмов
приборов
используются
передачи 5-й
степени точности.
Таблица
1.1
| Вид
передачи |
Модуль,
мм |
Стандарт |
Степень
точности |
Вид
сопряжения |
| Цилиндрические,
внешнего и
внутреннего
зацепления
с прямозубыми
и косозубыми
зубчатыми
колесами |
от
1 до 55 |
ГОСТ
1643-81 |
3...12 |
А,
В, С, D,
Е, Н
|
| 0.1...1.0
(исключительно) |
ГОСТ
9178-81 |
3...12 |
D,
Е, F,G, Н |
| реечные
прямозубые
и косозубые |
I...40 |
ГОСТ
I0242-8I
|
3...I2
|
А,
В, С, D, Е, Н |
|
0,1...1,0
(исключительно)
|
ГОСТ
13506-81 |
3...12 |
D,
Е, F, G, Н, |
| конические
и гипоидные
внешнего
зацепления
с прямыми,
тангенциальными
и криволинейными
зубьями |
1...56 |
ГОСТ
1768-81 |
4...12 |
А,
В, С, D. Е, Н |
| конические
мелкомодульные
внешнего
зацепления
с прямыми зубьями |
0,1...1,0
(исключительно) |
ГОСТ
9368-81 |
4...12 |
D,
Е, F, G, Н |
|
червячные
цилиндрические
с червяками
типа ZA,
Z1,
ZN.ZK
|
1...25 |
ГОСТ
3675-81 |
1...12 |
А,
В, С, D, Е, Н |
| 0,1...1,0
(исключительно) |
ГОСТ
9774-81 |
3...12 |
D,
Е, F, G, Н |
Необходимая
степень точно-сти
устанавливается
в зависимо-сти
от заданной
кинематической
погрешности
зубчатой передачи.
Вид сопряжения
зависит от
усло-вий
эксплуатации
зубчатой пере-дачи,
главным из
которых являет-ся
температурной
режим.
2 Расчет
кинематической
погрешности
Для определения
кинематической
погрешности
механизма,
составленного
из зубчатых
передач, сначала
необходимо
определить
минимальные
и максимальные
значения
кинематической
погрешности
каждой пары,
а затем произвести
суммирование
этих погрешностей
относительно
заданного вала
методом максимума-минимума
или вероятностным.
2.1 Минимальное
значение
кинематической
погрешности,
мкм
Передачи
зубчатые
цилиндрические:
 ,
(2.1) ,
(2.1)
где
 -
допуск на
кинематическую
погрешность
соответственно
ведущего и
ведомого колеса
зубчатой пары;
выби-рается
из ГОСТ 1643-81 или
ГОСТ 9178-81 в зависимости
от степени
точности колеса. -
допуск на
кинематическую
погрешность
соответственно
ведущего и
ведомого колеса
зубчатой пары;
выби-рается
из ГОСТ 1643-81 или
ГОСТ 9178-81 в зависимости
от степени
точности колеса.
Передачи
зубчатые конические:
 ,
(2.2) ,
(2.2)
где ¤
- допуск на
кинематическую
погрешность
ведущего и
ведомого колес
соответственно,
выбирается
из ГОСТ1756-81
и ГОСТ
9368-81 в зависимости
от степени
точности.
Передачи
червячные
цилиндрические:
 ,
(2.3) ,
(2.3)
где
 - допуск на
погрешность
винтовой линии
на длине нарезанной
части червяка;
- допуск на
погрешность
винтовой линии
на длине нарезанной
части червяка;
 - допуск
на погрешность
профиля витка
червяка;
- допуск
на погрешность
профиля витка
червяка;
 - допуск
на кинематическую
погрешность
червячного
колеса.
- допуск
на кинематическую
погрешность
червячного
колеса.
Значения
величин
 , ,
 , ,
 выбираются
из ГОСТ 3675-81 и ГОСТ
9774-81 в зависимости
от принятой
степени точности.
выбираются
из ГОСТ 3675-81 и ГОСТ
9774-81 в зависимости
от принятой
степени точности.
Передачи
зубчатые реечные:
 ,
(2.4) ,
(2.4)
где
  - коэффициент
фазовой компенсации,
значение которого
выбирается
из таблицы 2.2.
- коэффициент
фазовой компенсации,
значение которого
выбирается
из таблицы 2.2.
Примечание
1.1
В формулах
2.1…2.3 ks
- коэффициент
фазовой компенсации,
выбираемый
в зависимости
от передаточного
числа зубчатой
пары u=z2/z1
по таблице 2.1;
В формулах
2.1… 2.4 k1
-коэффициент,
зависящий от
степени точности;
|
Коэффициент
k1
|
| Тип
передачи |
Степень
точности |
| 5;6 |
7;8 |
| Цилиндрическая;
реечная |
0,62 |
0,71 |
| коническая |
0,67 |
0,72 |
 -
коэффициент,
учитывающий
угол поворота
ведомого зубчатого
колеса, вычисляется
по формуле: -
коэффициент,
учитывающий
угол поворота
ведомого зубчатого
колеса, вычисляется
по формуле: , ,
где
(…) - угол
поворота ведомого
колеса зубчатой
пары;
 -допуск
на кинематическую
погрешность
зубчатого
колеса:
-допуск
на кинематическую
погрешность
зубчатого
колеса:
 ,
где Fp и ff
параметры,
определяемые
по таблицам
стандартов
(см. таблицу
1.1) в зависимости
от степени
точности. Для
цилиндрических
зубчатых колёс
эти параметры
можно определить
по таблицам
Приложения
1. ,
где Fp и ff
параметры,
определяемые
по таблицам
стандартов
(см. таблицу
1.1) в зависимости
от степени
точности. Для
цилиндрических
зубчатых колёс
эти параметры
можно определить
по таблицам
Приложения
1.
| Таблица
2.1 |
| u |
ks
|
k
|
u |
ks
|
k
|
| от
1,0 до 1,5 |
0,3 |
0,98 |
св.4,0
до
4,5
|
0,90 |
0,96 |
| св.
1,5 до 2 ,0 |
0,76 |
0,85 |
св.4,5
до 5,0 |
0,87 |
0,96 |
| св.
2,0 до 2,5 |
0,75 |
0,83 |
св.
5,0 до 5,5 |
0,85 |
0,98 |
| св.2,5
до 3,0 |
0,74
|
0,93 |
св.5,5
до
6,0
|
0,88 |
0,96 |
| св.3,0
до 3,5 |
0,75 |
0,97 |
св.6,0
до 6,5 |
0,94 |
0,97 |
| св.3,5
до 4,0 |
0,80 |
0,96 |
св.
6,5 |
0,99 |
0,98 |
|
Если
передаточное
число не выражается
конеч-
ным
, числом,
а
угол
поворота ведомого
колеса
 то
принять ks=
0,98
то
принять ks=
0,98
|
| Таблица
2.2 |
| Unp |
ks
|
k |
Unp |
ks
|
k |
| от
0,25 до 0,5 |
0,07 |
0,90 |
св.
2,00 до 2.25 |
0.68 |
0,87 |
| св.
0,5 до 0,75 |
0,17 |
0,95 |
св.2,25
до 2,50 |
0.78 |
0,94 |
| св.
0.75 до 1,00 |
0,4 |
0,80 |
св.
2,50 до 2,75 |
0,72 |
0,98 |
| св.
1,00до 1,25 |
0,65 |
0,80 |
св.
2,75 до 3,00 |
0,68 |
0,92 |
| св.
1,25 до 1,50 |
0,65 |
0,95 |
св.
3,00 до 3.25 |
0,73 |
0,90 |
| св.
1,50 до 1,75 |
0,60 |
0,95 |
св.
3,25 до 3,5 |
0,83 |
0,95 |
| св.
1,75 до 2,00 |
0,59 |
0,88 |
св.
3,5 |
0,98 |
0,98 |
|
Uпр=zрейки/zколеса
|
2.2 Максимальное
значение
кинематической
погрешности
передач, мкм.
Передачи
зубчатые
цилиндрические
и конические
 ,
(2.5) ,
(2.5)
где k
- коэффициент
фазовой компенсации,
значение которого
выбирается
из таблицы 2.1
в зависимости
от передаточного
числа в зубчатой
паре и.
 -
суммарная
приведенная
погрешность
монтажа, мкм. -
суммарная
приведенная
погрешность
монтажа, мкм.
Передачи
червячные
цилиндрические:
 ,
(2.6) ,
(2.6)
Передачи
зубчатые реечные:
 ,
(2.7) ,
(2.7)
где k -
коэффициент
фазовой компенсации,
значение которого
выбирается
из таблицы 2.2
в зависимости
от приведенного
передаточного
числа
2.3 Суммарная
приведенная
погрешность
монтажа
 Рисунок
2.1а Рисунок
2.1а

Рисунок
2.1б
Нормируемый
стандартами
допуск кинематической
точности зубчатой
передачи
 обеспечивается
технологическим
процессом
изготовления
и контроля
зубчатых колес,
валов (осей),
опорных поверхностей
корпусных
элементов и
процессом
сборки с использованием
выбранных по
классу точности
подшипников
качения. Однако
уже на стадии
проектирования
зубчатой передачи
необходимо
соблюдать
рациональное
соотношение
между принятой
степенью точности
зубчатых колес
и допусками
на размеры
формы и расположения
поверхностей,
которые прямо
или косвенно
определяют
положение
рабочей поверхности
зубьев. В таблице
2.3 приведены
рекомендуемые
значения допусков
на элементы
зубчатых колес
и валов, оказывающих
влияние на
степень точности
зубчатой передачи.
На рисунке
2.1 и рисунке 2.2
показаны обозначения
допусков формы
и расположения
поверхностей
отдельных
зубчатых колес
(рисунок 2.1) и
собранных в
узел (рисунок
2.2).
обеспечивается
технологическим
процессом
изготовления
и контроля
зубчатых колес,
валов (осей),
опорных поверхностей
корпусных
элементов и
процессом
сборки с использованием
выбранных по
классу точности
подшипников
качения. Однако
уже на стадии
проектирования
зубчатой передачи
необходимо
соблюдать
рациональное
соотношение
между принятой
степенью точности
зубчатых колес
и допусками
на размеры
формы и расположения
поверхностей,
которые прямо
или косвенно
определяют
положение
рабочей поверхности
зубьев. В таблице
2.3 приведены
рекомендуемые
значения допусков
на элементы
зубчатых колес
и валов, оказывающих
влияние на
степень точности
зубчатой передачи.
На рисунке
2.1 и рисунке 2.2
показаны обозначения
допусков формы
и расположения
поверхностей
отдельных
зубчатых колес
(рисунок 2.1) и
собранных в
узел (рисунок
2.2).

Рисунок
2.2
Для реечных,
конических,
червячных и
винто-вых
передач соотношение
уровней точности
при выборе
классов точности
подшипников,
посадок колёс
на вал, допусков
на диаметр
поверхности
вершин и шероховатостей
поверхностей
также можно
использовать
рекомендации
таблицы 2.3.
При назначении
на элементы
зубчатых колес
и валов допусков
в соответствии
с рекомендациями
таблицы 2.3 суммарная
приведенная
погрешность
монтажа отсутствует
 ,
В случае назначения
(с целью удешевления
деталей) более
грубых значений
допусков, необходимо
вычислить
значение возможной
суммарной
погрешности
монтажа. ,
В случае назначения
(с целью удешевления
деталей) более
грубых значений
допусков, необходимо
вычислить
значение возможной
суммарной
погрешности
монтажа.
|
Таблица
2.3 - К выбору допусков
на элементы
монтажа цилиндрических
эвольвентных
зубчатых колес
на валах по
рисунке
2.1 и рис.2.2
|
| Рекомендуемые
параметры и
характеристики |
Степень
точности передачи
по
ГОСТ 1643-81 или ГОСТ
9178-81
|
Обозначения:
IT-
допуск на диаметр
d2 (по
ГОСТ 25346-89);
Fr-
допуск радиального
биения зубча-того
венца, в мкм
(по ГОСТ 1643-81, - для
m > 1 мм или
по ГОСТ9178-81, - для
m <1 мм );
d
- делительный
диаметр, мм;
b-
ширина венца
зубчатого
колеса, мм;
F
- допуск на
направление
зуба, мкм (по
ГОСТ 9178-81, таблице
7 - для
m
<1 мм или ГОСТ
1643-81, табли- це 11
для т
1 мм).
|
| 5- |
6 |
7 |
8 |
| Класс
точности
подшипников
качения |
Р4
|
P5 |
P6 |
P6
|
|
Посадка
ступицы колеса,
на вал d2;
(НQ/ТQ)
|
H5/k5* |
H6/k6 |
Н7/js6
|
|
Радиальное
биение посадочной
поверхности
вала FR1
мкм
|
IT5/4 |
IT6/4 |
IT6/2 |
|
Радиальное
биение поверхности
вершин зубьев
FR2,
мкм
|
FR2=0,6Fr
|
|
Предельное
отклонение
диаметра
окружности
вершин hQ
|
h7
|
h8
|
|
Биение
базового торца
шестерни или
колеса Fa1
мкм; d,
мм
|

|
|
Биение
базового торца
колеса после
сборки Fa2
мкм
|
Fa2=1,2Fa1
|
|
Радиальное
биение зубчатого
венца FR3
,мкм
|
FR3=0,75Fr,
|
| Шероховатость
поверхности |
рабочих
профилей зубьев
- а
|
0,63 |
1,25 |
|
посадочной
поверхности
вала -б
|
0,32 |
0,63 |
1,25 |
|
посадочной
поверхности
ступицы колеса
-в
|
0,63 |
1,25 |
|
поверхности
цапф вала -г
|
0,32 |
0,63 |
1,25 |
Для зубчатых
цилиндрических,
конических
и червячных
колес:
 ,
(2.8) ,
(2.8)
где
er
- монтажное
радиальное
биение зубчатого
колеса;
ea
- монтажное
осевое биение
зубчатою колеса.
- угол
профиля исходного
контура зубчатого
колеса; (=20);
- угол
наклона линии
зуба зубчатого
колеса;
Монтажное
радиальное
биение может
быть определено
по формуле:
 ,
(2.9) ,
(2.9)
где
 -
избыточное
радиальное
биение посадочной
поверхности
вала, мкм. -
избыточное
радиальное
биение посадочной
поверхности
вала, мкм.
 ,
(2.10) ,
(2.10)
где
 принятое
значение радиального
биения посадочной
поверхности
вала, отличное
от табличного
значения принятое
значение радиального
биения посадочной
поверхности
вала, отличное
от табличного
значения
 . .
 -
избыточное
радиальное
биение зубчатого
венца, мкм: -
избыточное
радиальное
биение зубчатого
венца, мкм:
 ,
(2.11) ,
(2.11)
 принятое
значение радиального
биения зубчатого
венца отличное
от табличного принятое
значение радиального
биения зубчатого
венца отличное
от табличного
 ; ;
 избыточное
радиальное
биение дорожек
качения внутреннего
кольца шарикоподшипников,
на которых
установлен
вал данного
колеса: избыточное
радиальное
биение дорожек
качения внутреннего
кольца шарикоподшипников,
на которых
установлен
вал данного
колеса:
 ,
(2.12) ,
(2.12)
где
 принятое радиальное
биение дорожек
качения внутреннего
кольца в случае
применения
шарикоподшипников
более грубого
класса точности,
чем рекомендуется
по таблице
2.3. Значения
радиального
биения дорожек
подшипников
выбираются
по ГОСТ 520-89
принятое радиальное
биение дорожек
качения внутреннего
кольца в случае
применения
шарикоподшипников
более грубого
класса точности,
чем рекомендуется
по таблице
2.3. Значения
радиального
биения дорожек
подшипников
выбираются
по ГОСТ 520-89
Осевое
биение зубчатого
колеса определяется
по формуле:
 ,
(2.13) ,
(2.13)
где
 избыточное
торцевое
биение базового
торца шестерни
или колеса,
мкм;
избыточное
торцевое
биение базового
торца шестерни
или колеса,
мкм;
 '
(2.I4) '
(2.I4)
где
 -
принятое торцовое
биение базового
торца шестерни
или колеса
значения -
принятое торцовое
биение базового
торца шестерни
или колеса
значения
 ,
отличное от
рекомендуемого
по таблице 2.3. ,
отличное от
рекомендуемого
по таблице 2.3.
 избыточное
торцовое биение
базового торца
колеса после
сборки, мкм избыточное
торцовое биение
базового торца
колеса после
сборки, мкм
 ,
(2.15) ,
(2.15)
где
 -принятое
торцовое биение
базового торца
колеса после
сборки отличное
от значения -принятое
торцовое биение
базового торца
колеса после
сборки отличное
от значения
 рекомендуемое
по таблице 2.3;
рекомендуемое
по таблице 2.3;
 - избыточное
торцовое биение
дорожек шарикоподшипников:
- избыточное
торцовое биение
дорожек шарикоподшипников:
 ,
(2.16) ,
(2.16)
где
 -
торцовое биение
дорожек шарикоподшипников
более грубых
классов точности, -
торцовое биение
дорожек шарикоподшипников
более грубых
классов точности,
чем
рекомендуется
по таблице 2.3.
Значения торцового
биения дорожек
выбираются
по ГОСТ 520-89.
Суммарная
приведенная
погрешность
монтажа цилиндрических
червяков может
быть определена
по формуле:
 .
(2.17) .
(2.17)
Значения
ea
и er
могут быть
вычислены по
формулам (2.9) и
(2.13).
2.4 Значение
кинематической
погрешности
зубчатой передачи
в угловых единицах.
При расчете
погрешностей
механизма в
угловых единицах,
вычисленные
по формулам
(2.1)...(2.7) значения
минимальной
и максимальной
кинематической
погрешностей
из линейных
единиц (мкм)
переводятся
в угловые (...'):
 ,
(2.18) ,
(2.18)
где
 -
минимальное
или максимальное
значение
кинематической
погрешности,
(...'); -
минимальное
или максимальное
значение
кинематической
погрешности,
(...');
 -
минимальное
или максимальное
значение
кинематической
погрешности,
мкм; -
минимальное
или максимальное
значение
кинематической
погрешности,
мкм;
d
- делительный
диаметр ведомого
колеса зубчатой
пары, мм.
2.5
Суммарная
кинематическая
погрешность
зубчатого
механизма
2.5.1
При расчете
по методу
максимума-минимума
 ,
(2.19) ,
(2.19)
где
 -
максимальное
значение
кинематической
погрешности
зубчатой пары,
вычисленное
в зависимости
от вида передачи; -
максимальное
значение
кинематической
погрешности
зубчатой пары,
вычисленное
в зависимости
от вида передачи;
 -
передаточное
отношение от
вала, на котором
находится
ведомое колесо
данной
зубчатой пары,
до вала, к которому
приводится
погрешность. -
передаточное
отношение от
вала, на котором
находится
ведомое колесо
данной
зубчатой пары,
до вала, к которому
приводится
погрешность.
Полученное
по формуле (2.
19) значение
кинематической
погрешности
должно быть
меньше или
равно допустимому
значению погрешности,
заданному для
данной кинематической
цепи механизма.
2.5.2 При
расчете по
вероятностному
методу
Координата
середины поля
рассеяния
кинематической
погрешности
зубчатой пары:
 ,
(2.20) ,
(2.20)
где i
- номер зубчатой
пары.
Поле
рассеяния
кинематической
погрешности
зубчатой пары:
  .
(2.21) .
(2.21)
Координата
середины поля
рассеяния
кинематической
погрешности
рассматриваемой
цепи механизма:
    .
(2.22) .
(2.22)
Суммарное
вероятностное
значение
кинематической
погрешности
рассматриваемой
цепи механизма:
 ,
(2.23) ,
(2.23)
| Процент
риска р,% |
10 |
4.5 |
1,0 |
0,27 |
|
Коэффициент
t1
|
0,26 |
0,35 |
0,46 |
0,57 |
где t1
- коэффициент,
зависящий от
процента риска,
значение его
выбирается
из следующей
таблицы
Вероятностное
значение
кинематической
погрешности
цепи, состоящей
из одной зубчатой
пары, определяется
по формуле:
 ,
(2.24) ,
(2.24)
где Kp-
вероятностный
коэффициент,
значение которого
выбирается
из таблиц
(2.4)...(2.6), в зависимости
от вида передачи,
|
Таблица
2.4-Значение
коэффициента
Кp для
цилиндрических
и конических
зубчатых
передач
|
|
Процент
риска
|
Передаточное
число |
| от
1,0 |
св.
1,5 |
св.2,0 |
св.2,0 |
св.3,0 |
св.3,5 |
св.4,0 |
св.4,5 |
св.5,0 |
св.5,5 |
св.6,0 |
св |
| до
1,5 |
до
2,0 |
ДО
2,5 |
ДОЗ |
до
3.5 |
до
4,0 |
до
4,5 |
до
5,0 |
до
5,5 |
до
6,0 |
до.6,5 |
6,5 |
| 32 |
0,58 |
0,68 |
0,60 |
0,74 |
0,71 |
0,71 |
0,68 |
0,71 |
0,78 |
0,70 |
0,78 |
0,80. |
| 10 |
0,92 |
0,78 |
0,73 |
0,88 |
0,82 |
0,32 |
0,80 |
0,82 |
0,90 |
0,88 |
0,91 |
0,94 |
| 4,5 |
0,95 |
0,83 |
0,81 |
0,91 |
0,91 |
0,91 |
0.88 |
0,92 |
0,94 |
0,94 |
0,94 |
0,96 |
| 1,0 |
0,96 |
0,84 |
0,82 |
0,92 |
0,95 |
0,95 |
0,94 |
0,95 |
0,97 |
0,95 |
0,96 |
0,96 |
|
Таблица
2.6--Значение
коэффициента
Кp
для
червячной
передачи
|
| Процент
риска р,% |
Коэффициент
Кр |
|
32
|
0,79
|
|
10
|
0,87
|
|
4,5
|
0,89
|
|
1,0
|
0,92
|
|
0,25
|
0,93
|
процента
риска и передаточного
числа.
|
Таблица
2.5 - Значение
коэффициента
К для зубчатой
реечной передачи
|
| Процент
риска |
Приведенное
передаточное
число |
| От
0,25 до0,50 |
св.
0,5 до0,75 |
св.0,75
до 1,00 |
св.1,00
до 1,25 |
св.1,25
до1,50 |
св.1,50
ДО 1,75 |
св.1,75
до2,00 |
св.2,00до2,25 |
св.2,25
до2,50 |
св.2,50
до 2,75 |
св.2,75
до 3,00 |
|
32
10
4,5
1,0
|
0,54
0,81 0,85 0,88 |
0,62
0,83 0,87 0,89 |
0,42
0,75 0,77 0,78 |
0,54
0,70 0,76 0,78
|
0,70
0,86 0,88 0,89 |
0,70
0,86 0,86 0,89 |
0,76
0,86 0,84 0,86 |
0,73
0,81 0,84 0,86 |
0,76
0,84 0,90 0,93 |
0,76
0,91 0,93 0,95 |
0,73
0,82 0,86 0,88 |
2 .6
Кинематическая
погрешность
планетарных
механизмов .6
Кинематическая
погрешность
планетарных
механизмов
При
проектировании
механизмов
часто возникает
требование
компоновки,
при которой
входной и выходной
валы были бы
соосны. Такая
задача лучше
других способов
решается
планетарными
зубчатыми
механизмами.
Одной из наиболее
распротра-ненных
является
кинематическая
схема механизма,
представленная
на рисунке 2.3.
При этом вопрос
о том, какое из
центральных
колее должно
быть неподвижным
(а или с), решается
в зависимости
от требуемой
ориентации
входного и
выходного вала
Рисунок
2.3
Передаточное
отношение
механизма по
схеме 2.3а при
ведущем водиле
h определяется
по формуле:
 ,
(2.25) ,
(2.25)
а для
механизма по
схеме рис. 2.3:б
 .
(2.26) .
(2.26)
Суммарная
кинематическая
погрешность
планетарного
механизма
рассчитывается
в соответствии
с вышеприведенной
методикой, но
при этом водило
условно считается
неподвижным,
а кинематическая
погрешность
суммируется
от вала неподвиж-ного
центрального
колеса до вала
подвижного
центрального
колеса.
2.7. Методы
достижения
заданной
кинематической
погрешности
В случае
если расчетное
значение суммарной
кинематической
погрешности
превышает
заданное, его
можно уменьшить
за счет следующих
мероприятий:
1. Применением
зубчатых колее
более высоких
степеней точности,
начиная с последних
(выходных) ступеней.
2. Уменьшением
приведенной
погрешности
монтажа за счет
выбора подшипников
более высокого
класса точности
и уменьшением
допусков на
погрешность
формы и размеров
посадочных
мест зубчатых
колес.
3. Перераспределением
передаточных
отношений между
ступенями
механизма с
целью увеличения
передаточных
отношений
последних
ступеней при
соответствующем
уменьшении
передаточных
отношений
первых ступеней.
4. Увеличение
процента риска
и соответствующим
уменьшением
значения
коэффициента
t1
в формуле
2.23.
2.8. Рекомендации
по расчету
кинематической
погрешности
| Номер
колеса |
d |
u |
Fr
|
Fp
|
ff
|

|
fhk
|
k1
|
ks
|
k |
k
|
|
ii
|
t1
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет
кинематической
погрешности
зубчатого
механизма
производится
после определения
геометрических
размеров зубчатых
колес, составляющих
механизм. Далее
в зависимости
от типов зубчатых
передач (цилиндрические,
конические,
червячные,
реечные) и степени
точности по
соответствующим
стандартам
(см. таблицу
1.1) составить
таблицу первичных
погрешностей,
а также параметров
и коэффициентов,
учитываемых
при расчете
кинематической
погрешности
После
этого произвести
расчет кинематической
погрешности
заданной
кинематической
цепи.
3. Расчет
погрешности
мертвого хода
Мертвый
ход возникает
в механизмах,
работающих
в реверсивных
режимах. Составляющими
погрешности
мертвого хода
зубчатых механизмов
являются зазоры
между рабочими
поверхностями
зубьев, зазоры
в опорах валов
и упругие деформации:
скручивание
и изгиб валов.
3.1 Определение
вида сопряжения.
В зависимости
от вида сопряжения
в зацеплении
устанавливается
значение
гарантированного
бокового зазора
Jnmin,,
кoтоpoе
в свою очередь
определяется
в зависимости
от условий
эксплуатации
с учетом температурного
режима, способа
смазывания
и окружной
скорости работы
зубчатых колес.
В мелкомодульных
зубчатых колесах
основным критерием
для выбора вида
сопряжения
является
температурная
деформация.
Минимальный
боковой зазор
из условий
предотвращения
заклинивания
зубьев при
температурных
деформациях
пр
определяется
в зависимости
от типа передач
по следующим
формулам:
3.1.1 Передачи
цилиндрические
зубчатые и
червячные:
 ,
(3.1) ,
(3.1)
где пр
- допустимый
зазор, мкм;
d1
,d2
-диаметры делительной
окружности
шестерни и
колеса соответственно,
мм;
1,
2,
k,-
температурный
коэффициент
теплового
расширения
материала
шестерни, колеса
и корпуса
соответственно,
"С;
t0-
нормальная
температура,
°С (t0= 20°C);
t -
рабочая температура,
°С;
tw-
угол зацепления
шестерни и
колеса;
т - модуль
зацепления,
мм.
Для
цилиндрических
зубчатых и
червячных
передач, у которых
имеются колеса
из искусственных
смол или других
пласт-масс,
необходимо
учитывать
набухания венца
во влажной
атмосфере. В
этом случае
минимальный
допустимый
зазор равен:
 ,
(3.2) ,
(3.2)
где d-
ширина части
колеса, изготовленной
из пластмассы,
мм;
- коэффициент
набухания
пластмассы
(для полиамидных
смол
= 0,05 %).
3.1.2. Передачи
зубчатые конические
 (3.3)
(3.3)
где е1,
е2 - угол
делительного
конуса шестерни
и колеса соответственно;
dei,de2-
внешний делительный
диаметр шестерни
и колеса соответственно.
Значения
температурных
коэффициентов
линейного
расширения
различных
материалов,
приведены в
таблице 3.1
Таблица
3.1
| Материал |
Марка |
105С-1
|
Материал |
Марка |
105С-1
|
| Чугун |
белый |
0,8 |
Алюми-
ниевый
сплав
|
АМг |
2,36 |
| серый |
1,05
|
Д16-Т |
2,27 |
| ковкий |
1,1 |
В95 |
2,31 |
| Сталь |
10…20 |
1,16
|
АЛ2 |
2,11 |
| 30,45,А12 |
1,06 |
АЛ3 |
2/2 |
| 40Х |
1,34 |
АЛ9 |
2,3 |
| 40Х13 |
1,1 |
Бронза |
БрОФ6,5-1,5 |
1,72 |
| Х18Н9Т |
1,6 |
БрОЦ4-3 |
1,8 |
| ШХ15 |
1,4 |
БрАЖ9-4 |
1,62 |
| 30ХГСА |
1,1 |
БрБ2 |
1,66 |
| 12ХН3А |
1,2 |
Латунь |
Л62 |
2,06 |
| 25Х13Н2А |
1,2 |
ЛС59-1 |
2,06 |
Минимальное
значение бокового
зазора, определяющее
вид сопряжения,
назначается
из условия:
Jnmin
Jпр
и выбирается
по таблицам
соответствующих
стандартов
(см. таблицу
1.1)
3.2 Минимальное
значение мертвого
хода передачи
Для всех
видов передач
минимальное
значение мертвого
хода, приведенное
к дуге делительной
окружности,
определяется
по формуле:
 (3.4)
(3.4)
где
Jt
min
-
гарантированный
боковой зазор,
мкм
аt,-
торцовый угол
профиля;
- делительный
угол подъема
винтовой линии
червяка. Для
косозубых колес
=
для прямозубых
=0.
3.3 Максимальное
значение мертвого
хода передач
3.3.1 Передачи
зубчатые
цилиндрические:
 ,
(3.5) ,
(3.5)
где EHS1,
EHS1
-наименьшее
дополнительное
смещение исходного
контура шестерни
и колеса соответственно,
мкм;
TH1,
TH2
-смещение исходного
контура шестерни
и колеса соответственно,
мкм;
fа
- предельное
отклонение
межосевого
расстояния,
мкм;
Gr1
и Gr2
- радиальный
зазор в опорах
шестерни и
колеса соответственно,
мкм.
3.3.2 Передачи
зубчатые конические:

 ,
(3.6) ,
(3.6)
где
 - наименьшее
отклонение
средней делительной
толщины зуба
по хорде шестерни
и колеса соответственно,
мкм;
- наименьшее
отклонение
средней делительной
толщины зуба
по хорде шестерни
и колеса соответственно,
мкм;
fAM1,
fAM2
-- предельное
осевое смещение
зубчатого венца
шестерни и
колеса соответственно,
мкм;
E
- предельное
отклонение
межосевого
угла передачи;
 -
допуск на среднюю
делительную
толщину зуба
по хорде в шестерне
и колесе соответственно,
мкм; -
допуск на среднюю
делительную
толщину зуба
по хорде в шестерне
и колесе соответственно,
мкм;
Ga1,
Ga2-
осевой зазор
в опорах шестерни
и колеса, мкм;
1, 2-
угол делительного
конуса шестерни
и колеса соответственно.
3.3.3 Передачи
червячные
цилиндрические:
 ,
(3.7) ,
(3.7)
где
 - наименьшее
отклонение
толщины витка
по хорде, мкм;
- наименьшее
отклонение
толщины витка
по хорде, мкм;
 -
допуск на толщину
витка, мкм;
-
допуск на толщину
витка, мкм;
fa
- предельное
отклонение
межосевого
расстояния
червячной
передачи, мкм;
fac
- предельное
отклонение
межосевого
расстояния
в обработке
fac
= 0,75 fa.
3.3.4 Передачи
зубчатые реечные:
 .
(3.8) .
(3.8)
Все значения
величин, входящих
в формулы
(3,5)...(3,8), выбираются
по таблицам
стандартов,
указанных в
таблице 1.1 в
зависимости
от типа передач,
степени точности
и вида сопряжения.
Значения радиальных
Gr,. и
осевых Ga
зазоров назначаются
в зависимости
от типа опор.
3.4 Погрешность
мертвого хода
в угловых единицах
(...')
При
необходимости
получения
погрешности
мертвого хода
в угловых единицах,
вычисленные
по формулам
(3.5) ... (3.8) значения
минимальной
и максимальной
погрешностей,
из линейных
единиц (мкм)
переводятся
в угловые (...'):

 (3.9) (3.9)
где J
- минимальное
или максимальное
значение погрешности
мертвого хода
в угловых единицах
(...');
Jt-
минимальное
или максимальное
значение погрешности
мертвого хода
в мкм,
d - делительный
диаметр ведомого
колеса зубчатой
пары, мм.
3.5 Суммирование
погрешностей
мертвого хода,
вызванных
боковым зазором
в передаче.
3.5.1 При
расчете по
методу максимума-минимума:
 ,
(3.10) ,
(3.10)
где J
max i
- максимальное
значение мертвого
хода i-ой ступени,
рассматриваемой
кинематической
цепи;
ii
передаточное
отношение между
валом ведомого
колеса зубчатой
пары и валом,
к которому
приводится
погрешность
3.5.2 При
расчёте по
вероятностному
методу:
1. Определить
координату
середины поля
рассеяния
погрешности
мертвого хода
каждой ступени:
 .
(3.11) .
(3.11)
2. Определить
поле рассеяния
погрешности
мертвого хода
каждой ступени:
 .
(3.12) .
(3.12)
3. Определить
суммарную
координату
середины поля
рассеяния,
рассматриваемой
кинематической
цепи
 ,
(3.13) ,
(3.13)
где EVj
- координата
середины поля
рассеяния i-ой
ступени.
4. Суммарное
вероятностное
значение погрешности
мертвого хода,
рассматриваемой
кинематической
цепи:
 ,
(3.14) ,
(3.14)
|
Процент
риска р,%
|
10 |
4,5 |
1,0 |
0,27 |
|
Коэффициент
t2
|
0,21 |
0,28 |
0,39 |
0,46 |
где Vji
- поле рассеяния
i-ой ступени,
t2-
коэффициент,
учитывающий
процент риска.
Его значение
вбирается по
таблице:
3.6 Погрешность
упругого мертвого
хода
3.6.1. Погрешность
упругого мертвого
хода от скручивания
валов
Эта погрешность
определяется
как двойной
угол скручивания
вала при нагружении
его крутящим
моментом:
 (3.15)
(3.15)
где
 -
двойной угол
скручивания
вала, рад; -
двойной угол
скручивания
вала, рад;
Т-
крутящий момент
на валу, Н-мм;
l
- расстояние
между средними
плоскостями
зубчатых колес,
установленных
на валу, или
расстояние
между средними
плоскостями
колеса и места
съема движения
с вала, мм;
Jp-
полярный момент
инерции поперечного
сечения вала,
мм4. Для вала
круглого сечения
Jp =л•d4/32•,
G -
модуль упругости
материала вала
при кручении,
МПа. Для стали
G = 8104
МПа.
Значение
погрешности
упругого мертвого
хода от скручивания
для стального
вала круглого
сечения в угловых
минутах (...') определяется
по формуле:
 ,
(3.16) ,
(3.16)
где
dв-
диаметр вала,
мм.
Суммарная
погрешность
мертвого хода
от скручивания
валов кинематической
цепи определяется
по формуле:
 (3.17)
(3.17)
где
 -
погрешность
упругого мертвого
хода от скручивания
отдельных
валов, -
погрешность
упругого мертвого
хода от скручивания
отдельных
валов,
 -
передаточное
отношение между
i-тым
валом и выходным
валом, рассматриваемой
кинематической
цепи. -
передаточное
отношение между
i-тым
валом и выходным
валом, рассматриваемой
кинематической
цепи.
3.6.2 Погрешность
упругого мертвого
хода от изгиба
валов, приведенная
к оси ведомого
колеса зубчатой
пары в угловых
минутах (...') для
стальных валов
круглого сечения
определяется
по формуле:

а
б
Рисунок
3.1
 ,
(3.18) ,
(3.18)
где Т2
- крутящий
момент на валу
ведомого колеса
зубчатой пары,
Н-мм;
dw2
- диаметр начальной
окружности
ведомого колеса,
мм;
 , , - диметры валов,
на которых
установлены
ведущее и ведомое
колеса данной
зубчатой пары,
мм;
- диметры валов,
на которых
установлены
ведущее и ведомое
колеса данной
зубчатой пары,
мм;
k1,
k2
- коэффициенты,
учитывающие
расположение
зубчатых колес
относительно
опор вала, мм.
Для схемы на
рисунке. 3.1а
 ,
для схемы на
рисунке. 3.16 ,
для схемы на
рисунке. 3.16
 . .
Если
 ,
то погрешность
упругого мертвого
хода от изгиба
валов не учитывается. ,
то погрешность
упругого мертвого
хода от изгиба
валов не учитывается.
Суммарная
погрешность
упругого мертвого
хода от изгиба
валов может
быть определена
по формуле:
 (3.19)
(3.19)
 - погрешность
упругого мертвого
хода от изгиба
валов i-ой
зубчатой пары;
- погрешность
упругого мертвого
хода от изгиба
валов i-ой
зубчатой пары;
 - передаточное
отношение между
валом ведомого
колеса данной
пары и валом,
к которому
приводится
погрешность.
- передаточное
отношение между
валом ведомого
колеса данной
пары и валом,
к которому
приводится
погрешность.
3.7 Полная
погрешность
мертвого хода
Полная
погрешность
мертвого хода
представляет
собою сумму
погрешностей
мертвого хода
от зазоров
между зубьями,
определяемую
по формулам
(3.10) или (3.14), и погрешностей
упругого мертвого
хода, определяемой
по формулам
(3.17) и (3,19),
Таким
образом
 (3.20)
(3.20)
или
 ,
(3.21) ,
(3.21)
где
 - допустимое
значение погрешности
мертвого хода
кинематической
цепи.
- допустимое
значение погрешности
мертвого хода
кинематической
цепи.
3.8 Погрешность
мертвого хода
в планетарных
механизмах
Погрешность
мертвого хода,
вызванная
боковым зазором
между зубьями
в отдельно
взятых зубчатых
парах, составляющих
планетарный
механизм,
определяется
по формулам
(3.1)...(3.8). Суммарная
погрешность
(максимальная)
мертвого хода
в (...') между водилом
и подвижным
центральным
колесом для
схемы на рисунке
2.За может быть
определена
по формуле:
 (3.22)
(3.22)
а для
схемы на рисунке
2.3б по формуле
 (3.23)
(3.23)
где
da,
dc-
диаметры делительных
окружностей
центральных
колес, мм;
 , , -
максимальная
погрешность
мертвого хода
в зубчатых
парах,
мкм; -
максимальная
погрешность
мертвого хода
в зубчатых
парах,
мкм;
 , , - передаточные
отношения
планетарного
механизма,
вычисляемые
по формулам
(2.25) или (2.26).
- передаточные
отношения
планетарного
механизма,
вычисляемые
по формулам
(2.25) или (2.26).
При
суммировании
вероятностным
методом:
для схемы
на рисунке
2.3а:
 ;
(3-24) ;
(3-24)
-для схемы
на рисунке
2.3.6:,
 ,
(3.25) ,
(3.25)
где
 - координата
середины поля
рассеяния
погрешности
мертвого хода
для планетарного
механизма на
рисунке 2.3,а:
- координата
середины поля
рассеяния
погрешности
мертвого хода
для планетарного
механизма на
рисунке 2.3,а:
 ,
(3.26)
,
(3.26)
где - координата
середины поля
рассеяния
погрешности
мертвого хода
для планетарного
механизма на
рисунке. 2.36:
- координата
середины поля
рассеяния
погрешности
мертвого хода
для планетарного
механизма на
рисунке. 2.36:
Eva-g
и Evf-c
- координаты
середины поля
рассеяния
погрешности
мертвого хода
зубчатых пар
a-g и f-c,
вычисляемые
по фор-
муле
(3.11);
Va.g,
Vf-c
- поле рассеяния
погрешности
мертвого хода
зубчатых пар
a-g и f-c, вычисляемых
по формуле
(3.12);
t2-
коэффициент,
учитывающий
процент риска.
Его значения
выбираются
по таблице
3.2.
3.9 Способы
уменьшения
погрешности
мертвого хода.
В случае
превышения
расчетной
суммарной
погрешности
над допустимой
необходимо
принять меры
по уменьшению
погрешности
мертвого хода.
Основные из
них следующие:
1. Уменьшение
зазора в опорах
валов.
2. Применение
специальных
конструкций
зубчатых колес,
уменьшающих
или устраняющих
боковой зазор
между зубьями.
Наиболее эффективными
являются безлюфтовые
зубчатые колеса,
состоящие из
2-х колес: основного
и поджимного
и устанавливаемых
между ними
пружинами
(винтовыми или
плоскими).
Рабочее
усилие пружины
(в Н) определяется
из условия:
 ,
(3.28) ,
(3.28)
где Ткр
- момент, передаваемый
валом, на котором
устанавливается
бсзлюфтовое
зубчатое колесо,
Н мм;
l2-
расстояние
между осями
пружины и зубчатого
колеса, мм;
n
- количество
пружин.
Расчет
усилия пружины
по формуле
(3.28) производится
в случае применения
пружин сжатия
или растяжения.
В случае использования
конструкций
безлюфтовых
колес с пружинами,
создающими
вращающий
момент, пружина
выбирается
по условию:
 .
(3.29)
.
(3.29)
Конструкции
и размеры элементов
безлюфтовых
колес в зависимости
от потребного
усилия пружины
приведены в
Приложении
2.
3.10 Рекомендации
по расчету
погрешности
мертвого хода
Номер
колеса
|
d |
aW
|
Jnmin
|
fa
|
EH
|
TH
|

|
faM
|
E
|
TŜ
|
fac
|
Gr
|
Ga
|
t2
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет
погрешности
мёртвого хода
производится
после определения
геометрических
размеров зубчатых
колес и выполнения
компоновки
механизма с
целью определения
положения
зубчатых колес
на валах и значений
пролетов валов.
Далее необходимо
определить
минимальный
боковой зазор
из условий
предотвращения
заклинивания
зубьев при
температурных
деформациях
по формулам
(3.1)...(3.3), выбрать вид
сопряжения,
значения
величин, входящих
в формулы
(3.4)...(3.8), в зависимости
от видов передач
по стандартам
(таблица 1.1). Значения
этих величин
свести в таблицу,
куда также
занести значения
других параметров,
входящих в
формулы (3.4)...(3.8):
После
составления
таблицы исходных
данных произвести
суммирование
погрешностей
в заданной
кинематической
цепи
| Таблица
1-Нормы кинематической
точности |
| Степень
точности |
Обозначение |
Модуль
т,
мм
|
Делительный
диаметр d,
мм
|
| До
12 |
Св.
12 до 20 |
Св.
20 до32 |
Св.
32 до 50 |
Св.
50 до 80 |
Св.
80 до 125 |
Св.
125 до 200 |
Св.
200 до 315 |
Св.
315 до 400 |
| мкм |
| 5 |
Fr |
От
0,1 до 0,5 |
7 |
8 |
9 |
10 |
12 |
14 |
16 |
— |
— |
| Св..
0,5 до 1,0 |
9 |
10 |
11 |
12 |
14 |
16 |
19 |
22 |
22 |
| Fp |
От
0,1до<1,0
|
10 |
11 |
12 |
14 |
16 |
19 |
22 |
25 |
30 |
| 6 |
Fr |
От
0,1 до 0,5 |
11 |
12 |
14 |
16 |
19 |
22 |
26 |
— |
— |
|
Св.0,5до<1,0
|
15 |
16 |
18 |
20 |
22 |
25 |
30 |
35 |
36 |
| Fp |
От0,1до<1,0
|
16 |
17 |
19 |
22 |
25 |
30 |
36 |
40 |
45 |
| 7 |
Fr |
От
0,1 до 0,5 |
16 |
18 |
20 |
22 |
26 |
30 |
36 |
— |
— |
|
Св.
0,5 до < 1,0
|
21 |
22 |
24 |
26 |
30 |
36 |
42 |
48 |
50 |
| Fp |
От0,1до<1,0
|
22 |
24 |
26 |
30 |
35 |
42 |
50 |
56 |
63 |
| 8 |
Fr |
От
0,1 до 0,5 |
19 |
21 |
25 |
28 |
32 |
38 |
45 |
— |
— |
|
Св,0,5до<1,0
|
26 |
28 |
30 |
34 |
38 |
45 |
50 |
55 |
63 |
| Fp |
От0,1до<1,0
|
32 |
34 |
38 |
42 |
50 |
60 |
70 |
80 |
90 |
|
*-
для этих диапазонов
диаметров
числовые значения
допусков
относятся к
зубчатым
колесам с
модулями свыше
0,5 мм
Fr
-допуск на
радиальное
биение зубчатого
колеса;
Fp
-допуск на
накопленную
погрешность
шага зубчатого
колеса
|
|
Таблиц
2-Нормы плавности
работы
(показатель
ff-допуск
на погрешность
профиля
зуба)
|
|
Обозна-
чения
|
Модуль
т.
мм
|
Степень
точности
|
| 5 |
6 |
7 |
8 |
| мкм |
|
ff
|
От
0,1 до 0,5 |
5 |
7 |
9 |
11 |
|
Св.
0,5 < 1
|
3 |
4 |
10 |
13 |
Приложение
1
|
Таблица
3-Нормы контакта
зубьев (показатель
f)
|
| Обоз
наче ния |
Ширина
зубчатого
венца bw,
мм
|
Степень
точности |
| 5 |
6 |
7 |
8 |
| мкм |
|
f
|
До
10 |
6 |
7 |
9 |
13 |
| Св.
10 до 20 |
7 |
9 |
11 |
15 |
| Св.
20 до 40 |
7 |
9 |
11 |
17 |
|
Таблица
5 - Нормы
бокового зазора
(показатели
–EWms
или +EWmi
cлагаемое
I и –EWs
или EWi)
|
| Вид
сопряжения |
Степень
точности
по
нормам плавности
|
Делительный
диаметр d,
мм |
| До 12 |
Св. 12 до
20 |
Св. 20 до32 |
Св. 32 до
50 |
Св. 50 до
80 |
Св. 80 до
125 |
Св. 125 до
180 |
Св. 180 до
250 |
Св. 250 до
315 |
Св. 315 до
400 |
| мкм |
| H |
3-7 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
9 |
10 |
10 |
| G |
3-6 |
8 |
9 |
11 |
13 |
15 |
17 |
19 |
25 |
28 |
30 |
| 7 |
11 |
12 |
13 |
15 |
17 |
19 |
21 |
26 |
28 |
32 |
| 8 |
15 |
16 |
17 |
18 |
20 |
22 |
24 |
30 |
32 |
35 |
| F |
3-6 |
12 |
15 |
18 |
21 |
24 |
26 |
30 |
36 |
40 |
45 |
| 7 |
15 |
16 |
19 |
22 |
25 |
28 |
32 |
36 |
40 |
45 |
| 8 |
18 |
20 |
22 |
25 |
28 |
32 |
36 |
40 |
42 |
45 |
| E |
3-7 |
19 |
22 |
26 |
30 |
36 |
42 |
48 |
55 |
63 |
70 |
| 8 |
24 |
26 |
30 |
35 |
40 |
45 |
50 |
60 |
63 |
70 |
| 9 |
28 |
32 |
36 |
40 |
45 |
50 |
55 |
60 |
63 |
70 |
| D |
3-7 |
28 |
34 |
40 |
48 |
55 |
63 |
75 |
85 |
95 |
105 |
| 8 |
34 |
38 |
42 |
48 |
55 |
63 |
80 |
85 |
95 |
105 |
| 9 |
38 |
42 |
48 |
55 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Таблица
4 -Нормы бокового
зазора (показатели
Jnmin,fa)
|
| Вид
сопряжения |
Класс
отклонений
межосевого
расстояния* |
Обозначения |
Межосевое
расстояние
aw,
мм
|
| До
12 |
Св.
12 до 20 |
Св.
20 до32 |
Св.
32 до 50 |
Св.
50 до 80 |
Св.
80 до 125 |
Св.
125 до 180 |
Св.
180 до250 |
Св.
250 до 315 |
Св.
315
до 400
|
| мкм |
| H |
II |
Jnmin
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| G |
III |
6 |
8 |
9 |
11 |
13 |
15 |
18 |
20 |
23 |
25 |
| F |
IV |
9 |
11 |
13 |
16 |
19 |
22 |
25 |
29 |
32 |
36 |
| E |
V |
15 |
18 |
21 |
25 |
30 |
35 |
40 |
46 |
52 |
57 |
| D |
VI |
22 |
27 |
33 |
39 |
46 |
54 |
63 |
72 |
81 |
89 |
| H |
II |
fa
|
±8 |
±9 |
±11 |
±14 |
±16 |
±18 |
±20 |
±22 |
±25 |
±28 |
| G |
III |
±11 |
±14 |
±16 |
±20 |
±22 |
±28 |
±30 |
±35 |
±40 |
±45 |
| F |
IV |
±18 |
±22 |
±25 |
±32 |
±35 |
±45 |
±50 |
±55 |
±60 |
±70 |
| E |
V |
±30 |
±36 |
±40 |
±50 |
±60 |
±70 |
±80 |
±90 |
±100 |
±110 |
| D |
VI |
±45 |
±55 |
±63 |
±80 |
±90 |
±110 |
±120 |
±140 |
±160 |
±180 |
| *
Класс отклонений
межосевого
расстояния
используется
при измерении
соответствия
между видом
сопряжения
и классом
отклонения
межосевого
расстояния |
|
Таблица
6- Нормы
бокового зазора
(показатели
EHS-
lдля зубчатых
колёс
с внешними
зубьями; EHI-
для зубчатых
колёс с внутрен-
ними
зубьями
|
| Вид
сопряжения |
Степень
точности
по
нормам плавности
|
Делительный
диаметр d,
мм |
| До 12 |
Св. 12 до
20 |
Св. 20 до32 |
Св. 32 до
50 |
Св. 50 до
80 |
Св. 80 до
125 |
Св. 125 до
180 |
Св. 180 до
250 |
Св. 250 до
315 |
Св. 315 до
400 |
| мкм |
| H |
3-7 |
5 |
6 |
7 |
6 |
9 |
11 |
13 |
14 |
16 |
18 |
| G |
3-6 |
12 |
14 |
16 |
18 |
22 |
25 |
28 |
38 |
40 |
45 |
| 7 |
16 |
18 |
20 |
22 |
26 |
28 |
30 |
40 |
40 |
45 |
| 8 |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
45 |
50 |
50 |
| F |
3-6 |
18 |
22 |
26 |
30 |
35 |
40 |
45 |
55 |
60 |
63 |
| 7 |
22 |
24 |
28 |
32 |
36 |
42 |
48 |
55 |
60 |
63 |
| 8 |
26 |
30 |
34 |
38 |
42 |
45 |
53 |
60 |
63 |
70 |
| E |
3-7 |
28 |
32 |
38 |
45 |
53 |
60 |
70 |
80 |
90 |
100 |
| 8 |
35 |
40 |
45 |
50 |
55 |
63 |
75 |
85 |
95 |
105 |
| 9 |
42 |
48 |
55 |
60 |
63 |
70 |
80 |
90 |
100 |
110 |
| D |
3-7 |
40 |
55 |
60 |
70 |
80 |
90 |
110 |
130 |
140 |
150 |
| 8 |
50 |
55 |
60 |
70 |
80 |
95 |
118 |
130 |
150 |
160 |
| 9 |
55 |
60 |
70 |
80 |
90 |
100 |
120 |
130 |
150 |
160 |
|
Таблица7-Нормы
бокового зазора
(Twm - допуск
на среднюю
длину
общей
нормали)
|
| Вид
сопряжения |
Допуск
на радиальное
биение зубчатого
венца Fr |
| Вид допуска
бокового зазора |
До 6 |
Св. 6 до
8 |
Св. 8 до
10 |
Св. 10 до
12 |
Св. 12 до
16 |
Св. 16 до
20 |
Св. 20 до
25 |
Св. 25 до
32 |
Св. 32 до
40 |
Св. 40 до
50 |
Св. 50 до
60 |
Св. 60 до
80 |
Св. 80 до
100 |
Св. 100 до
125 |
Св. 125 до
160 |
Св. 160 |
| мкм |
| Н |
h |
6 |
7 |
7 |
8 |
9 |
10 |
11 |
12 |
14 |
16 |
18 |
21 |
25 |
28 |
35 |
38 |
| G |
g |
8 |
8 |
9 |
9 |
11 |
12 |
14 |
15 |
16 |
20 |
21 |
28 |
32 |
40 |
48 |
50 |
| F |
f |
9 |
10 |
10 |
11 |
12 |
14 |
16 |
19 |
21 |
22 |
28 |
35 |
38 |
45 |
56 |
63 |
| E.D |
e |
11 |
11 |
12 |
14 |
15 |
17 |
21 |
22 |
26 |
30 |
38 |
45 |
53 |
67 |
80 |
85 |
| Таблица
8-Нормы бокового
зазора (Tw
- допуск на длину
общей нормали) |
| Вид
сопряжения |
Вид
допуска бокового
зазора
|
Допуск
на радиальное
биение зубчатого
венца Fr |
| До 6 |
Св. 6 до
8 |
Св. 8 до
10 |
Св. 10 до
12 |
Св. 12 до
16 |
Св. 16 до
20 |
Св. 20 до
25 |
Св. 25 до
32 |
Св. 32 до
40 |
Св. 40 до
50 |
Св. 50 до
60 |
Св. 60 до
80 |
Св. 80 до
100 |
Св. 100 до
125 |
Св. 125 до
160 |
Св. 160 |
| мкм |
| Н |
h |
10 |
11 |
12 |
14 |
17 |
20 |
22 |
26 |
34 |
40 |
48 |
60 |
75 |
95 |
112 |
130 |
| G |
g |
11 |
12 |
14 |
15 |
19 |
22 |
26 |
30 |
36 |
45 |
50 |
67 |
80 |
100 |
130 |
140 |
| F |
f |
12 |
14 |
15 |
17 |
20 |
24 |
28 |
34 |
40 |
48 |
56 |
75 |
90 |
110 |
140 |
160 |
| E,D |
e |
14 |
15 |
17 |
20 |
22 |
28 |
32 |
38 |
48 |
53 |
67 |
85 |
100 |
130 |
160 |
180 |
|
Таблица
9-Нормы бокового
зазора
(ТН-
допуск на
смещение
исходного
контура)
|
| Вид
сопряжения |
Вид допуска
бокового зазора |
Допуск
на радиальное
биение зубчатого
венца Fr
|
| До 6 |
Св. 6 до
8 |
Св. 8 до
10 |
Св. 10 до
12 |
Св. 12 до
16 |
Св. 16 до
20 |
Св. 20 до
25 |
Св. 25 до
32 |
Св. 32 до
40 |
Св. 40 до
50 |
Св. 50 до
60 |
Св. 60 до
80 |
Св. 80 до
100 |
Св. 100 до
125 |
Св. 125 до
160 |
Св. 160 |
| мкм |
|
Н
|
h
|
14
|
16
|
18
|
20
|
25
|
30
|
34
|
40
|
50
|
60
|
70
|
90
|
110
|
140
|
170
|
190
|
|
G
|
g
|
16
|
18
|
20
|
22
|
28
|
32
|
38
|
45
|
53
|
67
|
75
|
100
|
120
|
150
|
190
|
210
|
|
F
|
f
|
18
|
20
|
22
|
25
|
30
|
36
|
42
|
50
|
60
|
70
|
85
|
110
|
130
|
160
|
200
|
230
|
|
E,D
|
e
|
20
|
22
|
25
|
30
|
34
|
40
|
48
|
56
|
70
|
80
|
100
|
125
|
150
|
190
|
240
|
260
|
|
Таблица
9-Нормы бокового
зазора
(ТН-
допуск на
смещение
исходного
контура)
|
| Вид
сопряжения |
Вид допуска
бокового зазора |
Допуск
на радиальное
биение зубчатого
венца Fr
|
| До 6 |
Св. 6 до
8 |
Св. 8 до
10 |
Св. 10 до
12 |
Св. 12 до
16 |
Св. 16 до
20 |
Св. 20 до
25 |
Св. 25 до
32 |
Св. 32 до
40 |
Св. 40 до
50 |
Св. 50 до
60 |
Св. 60 до
80 |
Св. 80 до
100 |
Св. 100 до
125 |
Св. 125 до
160 |
Св. 160 |
| мкм |
|
Н
|
h
|
14
|
16
|
18
|
20
|
25
|
30
|
34
|
40
|
50
|
60
|
70
|
90
|
110
|
140
|
170
|
190
|
|
G
|
g
|
16
|
18
|
20
|
22
|
28
|
32
|
38
|
45
|
53
|
67
|
75
|
100
|
120
|
150
|
190
|
210
|
|
F
|
f
|
18
|
20
|
22
|
25
|
30
|
36
|
42
|
50
|
60
|
70
|
85
|
110
|
130
|
160
|
200
|
230
|
|
E,D
|
e
|
20
|
22
|
25
|
30
|
34
|
40
|
48
|
56
|
70
|
80
|
100
|
125
|
150
|
190
|
240
|
260
|
ПРИЛОЖЕНИЕ
2.
Параметры
и конструктивные
элементы безлюфтовых
зубчатых колес.
В зависимости
от конструктивных
особенностей
механизма и
допустимых
его габаритов
люфтовыбиращее
устройство
может устанавливаться
либо на ведущем
колесе зубчатой
пары, либо на
ведомом. Тип
безлюфтового
зубчатого
колеса и размеры
его элементов
зависят от
значения момента,
передаваемого
валом, на котором
установлено
данное зубчатое
колесо. На рисунке
1 даны размеры
винтовых пружин
растяжения
в зависимости
от рабочей
нагрузки,
определяемой
по формуле
(3.28), а на рисунке
2 даны размеры
мест установки
этих пружин
на зубчатых
колесах. На
рисунке 3 даны
размеры пружины
кручения в
зависимости
от потребного
значения крутящего
момента пружины,
определяемого
по формуле
(3.29), а на рисунке
4 показана
конструкция
безлюфтового
колеса с пружиной
кручения и даны
размеры элементов
для ее установки.
Рисунок 1
|

|
|
b
|
R
|
l
|
l1
|
l2
|
l3
|
d
|
k
|
s
|
| 4 |
2,0 |
9 |
1,0 |
13,9 |
2,0 |
0,8 |
2,5 |
0,6 |
| 5 |
2,5 |
11 |
1,5 |
14 |
4,4 |
0,9 |
3,0 |
0,7 |
| 6 |
3,0 |
12 |
12,7 |
2,5 |
1,0 |
| 7 |
3,5 |
18 |
2,5 |
14,6 |
6,9 |
1,2 |
5,0 |
0,9 |
| 7 |
14,5 |
15,2 |
5,5 |
1,0 |
4,0 |
1,0 |
| 9 |
4,5 |
21 |
13,5 |
8,7 |
1,2 |
4,5 |
| 11 |
5,5 |
23,5 |
16 |
9,5 |
1,3 |
|
Рисунок 2

|
Р исунок
3 исунок
3
|
мм |
| D |
D1
|
b |
d |
| 17 |
14 |
1,2 |
1,3 |
| 22 |
19 |
| 27 |
24 |
1,8 |
1,7 |
| 32 |
29 |
1,5 |
1,5 |
| 37 |
34 |
| 42 |
39 |
| 45 |
43,5 |
2,3 |
2,0 |
| 50 |
48,5 |
|

|
Размеры,
мм |
|
Угол
заrру-чивания
()
|
Крутя-
щий
момент, Нмм
|
| D |
d |
h |
h1
|
R |
| 15 |
0,8 |
2,5 |
4,0 |
0,8 |
27 |
23 |
48 |
| 20 |
38 |
32 |
49 |
| 25 |
1,2 |
47 |
39 |
163 |
| 30 |
1,0 |
59 |
49 |
96 |
| 35 |
3,0 |
5,0 |
1,0 |
69 |
57 |
| 40 |
78 |
65 |
| 45 |
1,6 |
5,0 |
10 |
1,5 |
84 |
50 |
291 |
| 50 |
97 |
55 |
270 |
| Рисунок
4 |
Литература
Детали
и механизмы
приборов: Справочник
/Б.М. Уваров,
В.А. Бойко,
В.Б. Подаревский,
Л.И. Власенко./-
К.:
Техн1ка,
1987.
*2.
Куцоконь
В.А. Точность
кинематических
цепей приборов.-Л.:
Машиностроение,
1980 г.
3. ГОСТ
21098-82. Цепи кинематические.
Методы расчет
точності.
|