Федеральное агентство по образованию российской федерации
Новгородский государственный университет имени Ярослава Мудрого
Институт экономики и управления
Кафедра СЭММ
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №4
ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ
Вариант №16
Выполнил:
Студент группы 8431
Яросвет И.В.
Проверил:
Орлов А.С.
ВЕЛИКИЙ НОВГОРОД 2010
Задание 4
:
1. Проанализировать автокорреляцию уровней временного ряда, выявить и охарактеризовать его структуру.
2. Построить аддитивную и мультипликативную модель временного ряда, характеризующую зависимость уровней ряда от времени.
3. На основе лучшей модели сделать прогноз на следующие два квартала с учетом выявленной сезонности.
Таблица 1
Данные о предприятии
| № наблюдения |
год |
квартал |
Стоимость ОПФ на конец квартала, млн.руб. |
| 6 |
2001 |
2 |
898 |
| 7 |
2001 |
3 |
794 |
| 8 |
2001 |
4 |
1441 |
| 9 |
2002 |
1 |
1600 |
| 10 |
2002 |
2 |
967 |
| 11 |
2002 |
3 |
1246 |
| 12 |
2002 |
4 |
1458 |
| 13 |
2003 |
1 |
1412 |
| 14 |
2003 |
2 |
891 |
| 15 |
2003 |
3 |
1061 |
| 16 |
2003 |
4 |
1287 |
| 17 |
2004 |
1 |
1635 |
Таблица 2
Вспомогательные расчеты по определению коэффициента автокорреляции первого порядка

Таким образом,
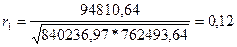 , ,
Таблица 3
Вспомогательные расчеты по определению коэффициента автокорреляции второго порядка

Таким образом,
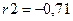 , ,
Таблица 4
Вспомогательные расчеты по определению коэффициента автокорреляции третьего порядка
| t |
Yt |
Yt-3 |
Yt-Ytср |
Yt-3-Yt-3ср |
(Yt-Ytср) 2 |
(Yt-3-Yt-3ср) 2 |
(Yt-Ytср)*(Yt-3-Yt-3ср) |
| 1 |
898 |
- |
- |
- |
- |
- |
- |
| 2 |
794 |
- |
- |
- |
- |
- |
- |
| 3 |
1441 |
- |
- |
- |
- |
- |
- |
| 4 |
1600 |
898 |
375,83 |
-291,67 |
141250,69 |
85069,44 |
-109618,0556 |
| 5 |
967 |
794 |
-257,17 |
-395,67 |
66134,69 |
156552,11 |
101752,2778 |
| 6 |
1246 |
1441 |
21,83 |
251,33 |
476,69 |
63168,44 |
5487,444444 |
| 7 |
1458 |
1600 |
233,83 |
410,33 |
54678,03 |
168373,44 |
95949,61111 |
| 8 |
1412 |
967 |
187,83 |
-222,67 |
35281,36 |
49580,44 |
-41824,22222 |
| 9 |
891 |
1246 |
-333,17 |
56,33 |
111000,03 |
3173,44 |
-18768,38889 |
| 10 |
1061 |
1458 |
-163,17 |
268,33 |
26623,36 |
72002,78 |
-43783,05556 |
| 11 |
1287 |
1412 |
62,83 |
222,33 |
3948,03 |
49432,11 |
13969,94444 |
| 12 |
1635 |
891 |
410,83 |
-298,67 |
168784,03 |
89201,78 |
-122702,2222 |
| сумма |
14690 |
10707 |
x |
x |
608176,92 |
736554,00 |
-119536,67 |
| среднее знач. |
1224,17 |
1189,67 |
- |
- |
- |
- |
- |
Таким образом, r3=-0.18,
Таблица 5
Вспомогательные расчеты по определению коэффициента автокорреляции четвертого порядка
| t |
Yt |
Yt-4 |
Yt-Ytср |
Yt-4-Yt-4ср |
(Yt-Ytср)^2 |
(Yt-4-Yt-4ср)^2 |
(Yt-Ytср)*(Yt-4-Yt-4ср) |
| 1 |
898 |
- |
- |
- |
- |
- |
- |
| 2 |
794 |
- |
- |
- |
- |
- |
- |
| 3 |
1441 |
- |
- |
- |
- |
- |
- |
| 4 |
1600 |
- |
- |
- |
- |
- |
- |
| 5 |
967 |
898 |
-257,17 |
-329,00 |
66134,69 |
108241,00 |
84607,83333 |
| 6 |
1246 |
794 |
21,83 |
-433,00 |
476,69 |
187489,00 |
-9453,833333 |
| 7 |
1458 |
1441 |
233,83 |
214,00 |
54678,03 |
45796,00 |
50040,33333 |
| 8 |
1412 |
1600 |
187,83 |
373,00 |
35281,36 |
139129,00 |
70061,83333 |
| 9 |
891 |
967 |
-333,17 |
-260,00 |
111000,03 |
67600,00 |
86623,33333 |
| 10 |
1061 |
1246 |
-163,17 |
19,00 |
26623,36 |
361,00 |
-3100,166667 |
| 11 |
1287 |
1458 |
62,83 |
231,00 |
3948,03 |
53361,00 |
14514,5 |
| 12 |
1635 |
1412 |
410,83 |
185,00 |
168784,03 |
34225,00 |
76004,16667 |
| сумма |
14690 |
9816 |
x |
x |
466926,22 |
636202,00 |
369298,00 |
| среднее знач. |
1224,17 |
1227,00 |
- |
- |
- |
- |
- |
Таким образом, r4=0,68,
Таблица 6
Автокорреляционная функция и коррелограмма временного ряда объема выпуска товара фирмой
| лаг |
коэфавтокорреляции |
коррелограмма |
| 1 |
0,12 |
* |
| 2 |
-0,71 |
******* |
| 3 |
-0,18 |
** |
| 4 |
0,68 |
******* |
Построение аддитивной модели временного ряда с сезонными колебаниями
.
Таблица 7
Расчет оценок сезонной компоненты в аддитивной модели
| t |
Yt |
итого за 4 квартала |
скольз.сред. |
центрсколсред |
оценка сезонной компоненты |
| 1 |
898 |
- |
- |
- |
- |
| 2 |
794 |
4733 |
1183,25 |
- |
- |
| 3 |
1441 |
4802 |
1200,5 |
1191,875 |
249,125 |
| 4 |
1600 |
5254 |
1313,5 |
1257 |
343 |
| 5 |
967 |
5271 |
1317,75 |
1315,625 |
-348,625 |
| 6 |
1246 |
5083 |
1270,75 |
1294,25 |
-48,25 |
| 7 |
1458 |
5007 |
1251,75 |
1261,25 |
196,75 |
| 8 |
1412 |
4822 |
1205,5 |
1228,625 |
183,375 |
| 9 |
891 |
4651 |
1162,75 |
1184,125 |
-293,125 |
| 10 |
1061 |
4874 |
1218,5 |
1190,625 |
-129,625 |
| 11 |
1287 |
- |
- |
- |
- |
| 12 |
1635 |
- |
- |
- |
- |
Таблица 8
Расчет значений сезонной компоненты в аддитивной модели
| показатели |
год |
1 кв |
2 кв |
3 кв |
4 кв |
| 1 |
- |
- |
249,125 |
343 |
| 2 |
-348,625 |
-48,25 |
196,75 |
183,375 |
| 3 |
-293,125 |
-129,625 |
- |
- |
| итого за i кв |
-641,75 |
-177,875 |
445,875 |
526,375 |
| средняя оценка сезонной компоненты для i квартала, Sср |
-320,875 |
-88,9375 |
222,9375 |
263,1875 |
| скорректированная сезонная компонента, Si |
-397,19 |
-88,94 |
222,94 |
263,19 |
Для данной модели имеем:
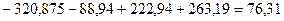
Определим корректирующий коэффициент:
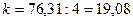
Проверим условие равенства нулю суммы значений сезонной компоненты:
-397,19-88,94+222,94+263,19=0
Таблица 9
Расчет выровненных значений T и ошибок E в аддитивной модели

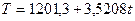 , ,
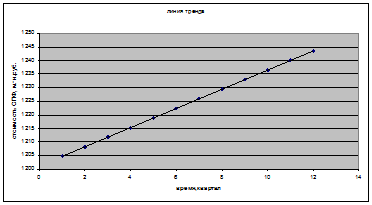
Рисунок 1 – стоимость ОПФ, млн. руб. (фактические, выровненные и полученные по аддитивной модели значения уровней ряда)
Для оценки качества построенной модели или для выбора наилучшей модели используется ошибка е.
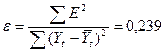
Следовательно, можно сказать, что аддитивная модель объясняет 76,1% общей вариации временного ряда.
Построение мультипликативной модели временного ряда
Таблица 10
Расчет оценок сезонной компоненты в мультипликативной модели
| t |
Yt |
итого за 4 квартала |
скольз. сред. |
Центр скол. сред |
оценка сезонной компоненты |
| 1 |
898 |
- |
- |
- |
- |
| 2 |
794 |
4733 |
1183,25 |
- |
- |
| 3 |
1441 |
4802 |
1200,5 |
1191,875 |
1,21 |
| 4 |
1600 |
5254 |
1313,5 |
1257 |
1,27 |
| 5 |
967 |
5271 |
1317,75 |
1315,625 |
0,74 |
| 6 |
1246 |
5083 |
1270,75 |
1294,25 |
0,96 |
| 7 |
1458 |
5007 |
1251,75 |
1261,25 |
1,16 |
| 8 |
1412 |
4822 |
1205,5 |
1228,625 |
1,15 |
| 9 |
891 |
4651 |
1162,75 |
1184,125 |
0,75 |
| 10 |
1061 |
4874 |
1218,5 |
1190,625 |
0,89 |
| 11 |
1287 |
- |
- |
- |
- |
| 12 |
1635 |
- |
- |
- |
- |
Таблица 11
Расчет сезонной компоненты в мультипликативной модели
| показатели |
год |
1 кв |
2 кв |
3 кв |
4 кв |
| 1 |
- |
- |
1,21 |
1,27 |
| 2 |
0,74 |
0,96 |
1,16 |
1,15 |
| 3 |
0,75 |
0,89 |
- |
- |
| итого за i кв |
1,49 |
1,85 |
2,37 |
2,42 |
| средняя оценка сезонной компоненты для i квартала, Sср |
0,745 |
0,925 |
1,185 |
1,21 |
| скорректированная сезонная компанента, Si |
0,73 |
0,91 |
1,17 |
1,19 |
Имеем:
0,745+0,925+1,185+1,21=4,07
Определим корректирующий коэффициент: 
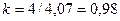 . .
Проверим условие равенства 4 суммы значений сезонной компоненты:
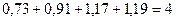
Таблица 12
Расчет выровненных значений Ф и ошибок Е в мультипликативной модели
| t |
Yt |
Si |
T*E=Y/S |
T |
T*S |
E=Yt/(T*S) |
E^2 |
(Yt-T*S)^2 |
| 1 |
898 |
0,73 |
1230,137 |
1183,465 |
863,9295 |
1,039437 |
1,0804287 |
1160,802377 |
| 2 |
794 |
0,91 |
872,5275 |
1190,5 |
1083,355 |
0,732908 |
0,5371548 |
83726,31603 |
| 3 |
1441 |
1,17 |
1231,624 |
1197,535 |
1401,116 |
1,028466 |
1,0577421 |
1590,737444 |
| 4 |
1600 |
1,19 |
1344,538 |
1204,57 |
1433,438 |
1,116197 |
1,2458965 |
27742,79991 |
| 5 |
967 |
0,73 |
1324,658 |
1211,605 |
884,4717 |
1,093308 |
1,1953226 |
6810,928554 |
| 6 |
1246 |
0,91 |
1369,231 |
1218,64 |
1108,962 |
1,123573 |
1,2624159 |
18779,30381 |
| 7 |
1458 |
1,17 |
1246,154 |
1225,675 |
1434,04 |
1,016708 |
1,0336956 |
574,0935801 |
| 8 |
1412 |
1,19 |
1186,555 |
1232,71 |
1466,925 |
0,962558 |
0,9265175 |
3016,74464 |
| 9 |
891 |
0,73 |
1220,548 |
1239,745 |
905,0139 |
0,984515 |
0,9692704 |
196,3879918 |
| 10 |
1061 |
0,91 |
1165,934 |
1246,78 |
1134,57 |
0,935156 |
0,8745171 |
5412,515472 |
| 11 |
1287 |
1,17 |
1100 |
1253,815 |
1466,964 |
0,877322 |
0,7696946 |
32386,87933 |
| 12 |
1635 |
1,19 |
1373,95 |
1260,85 |
1500,412 |
1,089701 |
1,1874484 |
18114,06433 |
| итого |
14690 |
12 |
14665,85 |
14665,89 |
14683,2 |
11,99985 |
12,140104 |
199511,5735 |
| Ср знач |
1224,17 |
Т=7,035t+1176,43
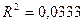
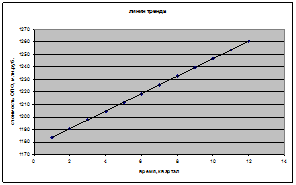
Рисунок 2 – стоимость ОПФ, млн. руб. (фактические, выровненные и полученные по мультипликативной модели значения уровней ряда)
Следовательно, ошибка е мультипликативной модели составит:
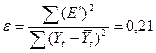
Таким образом, доля объясненной дисперсии уровней ряда в мультипликативной модели составит 79%
Прогнозирование
Для прогнозирования из двух рассмотренных моделей необходимо выбрать ту, у которой ошибка е наименьшая. Следовательно, при прогнозировании будет использоваться мультипликативная модель, так как 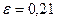
Таким образом, прогнозное значение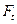 уровня временного ряда в мультипликативной модели есть сумма трендовой и сезонной компонент.
уровня временного ряда в мультипликативной модели есть сумма трендовой и сезонной компонент.
Объем товаров, выпущенного фирмой в течение первого полугодия ближайшего следующего, т. е. четвертого года, рассчитывается как сумма объемов выпущенных товаров в I и во II кварталах четвертого года, соответственно 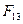 и и 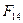 . Для определения трендовой компоненты воспользуемся уравнением тренда: . Для определения трендовой компоненты воспользуемся уравнением тренда:
Т=7,035t+1176,43
Получим:
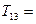 7.035*13+1176.43=1267.885 7.035*13+1176.43=1267.885
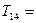 7.035*14+1176.43=1274.92 7.035*14+1176.43=1274.92
Значения сезонной компоненты равны:
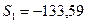 (I квартал); (I квартал);
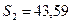 (II квартал) (II квартал)
Таким образом,
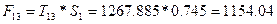 ; ;
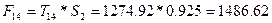 . .
|