Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего
профессионального образования
«Санкт-Петербургский государственный
политехнический университет»
Факультет экономики и менеджмента
Кафедра «Предпринимательство и коммерция»
КУРСОВОЙ ПРОЕКТ
по дисциплине «Статистика»
на тему «Статистический анализ рядов распределения. Проверка гипотезы о законе распределения»
Выполнил____________
(подпись)
Принял:Магистр коммерции
____________
(подпись)
«__» _________ 2010 г.
Санкт-Петербург
2010 
ДАННЫЕ, ВАРИАЦИОННЫЙ РЯД, РАНЖИРОВАНИЕ, ВЫБРОСЫ, ГИСТОГРАММА, ПОЛИГОН, КУМУЛЯТА, ИНТЕРВАЛЬНЫЕ РЯДЫ , СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ, СГЛАЖИВАНИЕ ИМПЕРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ, ГИПОТЕЗА
В курсовом проекте рассмотрена реализация анализа распределений с использованием программы STATISTICA, а также произведены расчеты основных статистических показателей.
СОДЕРЖАНИЕ
Введение…………………………………………………………………стр.4
1. Табличное и графическое представление вариационного ряда распределения………………………………………………………стр.5
2. Расчет основных характеристик вариационного ряда………...стр.17
3. Сглаживание эмпирического распределения, проверка гипотезы о законе распределения……………………………………………...стр.21
Заключение………………………………………………...……………стр.25
Список использованных источников…………………………………..стр.26
Введение
Ряд распределения – это распределение единиц совокупности по значению того или иного признака в конкретных условиях места и времени.
Ряды распределения могут быть вариационным, если они строятся на основе количественного признака, или атрибутивным, если они строятся на основе атрибутивного признака.
Изучение вариационных рядов распределения позволяет: определить типический уровень признака в изучаемой совокупности; определить наличие выбросов и решить вопрос о необходимости их самостоятельного изучения; оценить степень разброса значений признака вокруг типического уровня; изучить структуру совокупности; охарактеризовать форму распределения, а также подобрать теоретическое распределение, на основе которого можно моделировать поведение распределения изучаемой совокупности.
На основе статистических рядов распределения вычисляются основные величины статистических исследований: индексы, коэффициенты; абсолютные, относительные, средние величины и т.д., с помощью которых можно проводить прогнозирование, как конечный итог статистических исследований. Таким образом статистические ряды распределения являются базисным методом для любого статистического анализа. Понимание данного метода и навыки его использования необходимы для проведения статистических исследований.
Ряды распределения могут быть представлены в табличной форме и графически.
Целью проекта является освоение методики и приобретение практических навыков анализа распределений, включающего расчет основных статистических характеристик, графическое и табличное представление рядов распределения.
В курсовом проекте рассматривается реализация анализа распределений с использованием программы STATISTICA.
STATISTICA – это универсальная интегрированная система, предназначенная для статистического анализа и визуализации данных, управления базами данных и разработки пользовательских приложений, содержащая широкий набор процедур анализа для применения в научных исследованиях, технике, бизнесе, а также специальные методы добычи данных.
1. Табличное и графическое представление
вариационного ряда
Проект выполнен на основе исследования данных о числе собственных легковых автомобилей на 1000 человек по различным округам, республикам, краям в 2001 году.
Исходные данные приведены в Табл. 1.1
.
Табл.1.1
Число собственных легковых автомобилей
на 1000 человек в 2001г.
| Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
| 1 |
147 |
16 |
122,2 |
31 |
46,6 |
46 |
110,1 |
61 |
158,6 |
76 |
115,4 |
| 2 |
62,1 |
17 |
100,3 |
32 |
56,4 |
47 |
118,5 |
62 |
132,3 |
77 |
114,1 |
| 3 |
112,8 |
18 |
197 |
33 |
96,6 |
48 |
68,3 |
63 |
112,5 |
78 |
120,2 |
| 4 |
172,9 |
19 |
166 |
34 |
118,3 |
49 |
107 |
64 |
81,7 |
79 |
115,1 |
| 5 |
93,8 |
20 |
115,7 |
35 |
104,9 |
50 |
97,9 |
65 |
94,1 |
80 |
187,7 |
| 6 |
121 |
21 |
92,7 |
36 |
115,6 |
51 |
112,8 |
66 |
166 |
81 |
134,6 |
| 7 |
105 |
22 |
69,7 |
37 |
34,4 |
52 |
150,8 |
67 |
126,1 |
82 |
150,7 |
| 8 |
114,7 |
23 |
121 |
38 |
172 |
53 |
107,5 |
68 |
120,5 |
83 |
197,7 |
| 9 |
132,7 |
24 |
216,9 |
39 |
136,8 |
54 |
165,4 |
69 |
50,4 |
84 |
19,6 |
| 10 |
183,4 |
25 |
141,4 |
40 |
119,3 |
55 |
129,5 |
70 |
10,8 |
85 |
173,1 |
| 11 |
119,8 |
26 |
149,7 |
41 |
131,2 |
56 |
122,8 |
71 |
140 |
86 |
196 |
| 12 |
119 |
27 |
106,2 |
42 |
142,8 |
57 |
122 |
72 |
34 |
87 |
124,9 |
| 13 |
107,4 |
28 |
127,7 |
43 |
134 |
58 |
104,3 |
73 |
117,4 |
88 |
20,8 |
| 14 |
135,4 |
29 |
168,1 |
44 |
86,7 |
59 |
180,4 |
74 |
94,8 |
| 15 |
133,8 |
30 |
147,6 |
45 |
85,7 |
60 |
113,2 |
75 |
130,7 |
Построение ряда распределения начинается с ранжирования ряда распределения по величине соответствующего признака. Ранжирование – это расположение единиц совокупности в порядке возрастания или убывания значений признака. Для этого выбираем в меню Data опцию Sort. Далее в поле Direction выбираем тип сортировки – по возрастанию значений признака (Ascending). Получим значения признака, упорядоченные по возрастанию (см. Табл.1.2
). Построение ранжированного ряда позволяет увидеть наличие в совокупности выбросов. Выбросы - значения признака, резко отличающиеся в меньшую или большую сторону от основной массы значений признака.
Табл. 1.2
Исходные данные, ранжированные по возрастанию значений признака
| Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
| 1 |
10,8 |
16 |
93,8 |
31 |
112,8 |
46 |
120,2 |
61 |
133,8 |
76 |
166 |
| 2 |
19,6 |
17 |
94,1 |
32 |
112,8 |
47 |
120,5 |
62 |
134 |
77 |
166 |
| 3 |
20,8 |
18 |
94,8 |
33 |
113,2 |
48 |
121 |
63 |
134,6 |
78 |
168,1 |
| 4 |
34 |
19 |
96,6 |
34 |
114,1 |
49 |
121 |
64 |
135,4 |
79 |
172 |
| 5 |
34,4 |
20 |
97,9 |
35 |
114,7 |
50 |
122 |
65 |
136,8 |
80 |
172,9 |
| 6 |
46,6 |
21 |
100,3 |
36 |
115,1 |
51 |
122,2 |
66 |
140 |
81 |
173,1 |
| 7 |
50,4 |
22 |
104,3 |
37 |
115,4 |
52 |
122,8 |
67 |
141,4 |
82 |
180,4 |
| 8 |
56,4 |
23 |
104,9 |
38 |
115,6 |
53 |
124,9 |
68 |
142,8 |
83 |
183,4 |
| 9 |
62,1 |
24 |
105 |
39 |
115,7 |
54 |
126,1 |
69 |
147 |
84 |
187,7 |
| 10 |
68,3 |
25 |
106,2 |
40 |
117,4 |
55 |
127,7 |
70 |
147,6 |
85 |
196 |
| 11 |
69,7 |
26 |
107 |
41 |
118,3 |
56 |
129,5 |
71 |
149,7 |
86 |
197 |
| 12 |
81,7 |
27 |
107,4 |
42 |
118,5 |
57 |
130,7 |
72 |
150,7 |
87 |
197,7 |
| 13 |
85,7 |
28 |
107,5 |
43 |
119 |
58 |
131,2 |
73 |
150,8 |
88 |
216,9 |
| 14 |
86,7 |
29 |
110,1 |
44 |
119,3 |
59 |
132,3 |
74 |
158,6 |
| 15 |
92,7 |
30 |
112,5 |
45 |
119,8 |
60 |
132,7 |
75 |
165,4 |
В данной совокупности выбросами являются значения регионов под номерами 1, 2, 3, 88, т.е. данные 10,8; 19,6; 20,8 и 216,9 резко отличаются от основной части значений признака. Поэтому при анализе совокупности в дальнейшем исключим эти значения признака. Каждое из них выделяется и стирается простым нажатием кнопки Delete на клавиатуре. Также удаление значений (выбросов) из ячеек, можно провести как удаление наблюдений, то есть строк. В итоге изучаемая совокупность будет состоять из 84 значений признака (см.Табл.1.3
).
Табл.1.3
Исходные данные за исключением выбросов,
ранжированные по возрастанию значений признака
| Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
Номер региона |
Число легковых автомобилей |
| 1 |
34 |
16 |
96,6 |
31 |
114,1 |
46 |
121 |
61 |
135,4 |
76 |
172 |
| 2 |
34,4 |
17 |
97,9 |
32 |
114,7 |
47 |
122 |
62 |
136,8 |
77 |
172,9 |
| 3 |
46,6 |
18 |
100,3 |
33 |
115,1 |
48 |
122,2 |
63 |
140 |
78 |
173,1 |
| 4 |
50,4 |
19 |
104,3 |
34 |
115,4 |
49 |
122,8 |
64 |
141,4 |
79 |
180,4 |
| 5 |
56,4 |
20 |
104,9 |
35 |
115,6 |
50 |
124,9 |
65 |
142,8 |
80 |
183,4 |
| 6 |
62,1 |
21 |
105 |
36 |
115,7 |
51 |
126,1 |
66 |
147 |
81 |
187,7 |
| 7 |
68,3 |
22 |
106,2 |
37 |
117,4 |
52 |
127,7 |
67 |
147,6 |
82 |
196 |
| 8 |
69,7 |
23 |
107 |
38 |
118,3 |
53 |
129,5 |
68 |
149,7 |
83 |
197 |
| 9 |
81,7 |
24 |
107,4 |
39 |
118,5 |
54 |
130,7 |
69 |
150,7 |
84 |
197,7 |
| 10 |
85,7 |
25 |
107,5 |
40 |
119 |
55 |
131,2 |
70 |
150,8 |
| 11 |
86,7 |
26 |
110,1 |
41 |
119,3 |
56 |
132,3 |
71 |
158,6 |
| 12 |
92,7 |
27 |
112,5 |
42 |
119,8 |
57 |
132,7 |
72 |
165,4 |
| 13 |
93,8 |
28 |
112,8 |
43 |
120,2 |
58 |
133,8 |
73 |
166 |
| 14 |
94,1 |
29 |
112,8 |
44 |
120,5 |
59 |
134 |
74 |
166 |
| 15 |
94,8 |
30 |
113,2 |
45 |
121 |
60 |
134,6 |
75 |
168,1 |
Вариационным называется ряд распределения, построенный по количественному признаку. Он может быть представлен в виде таблицы и графически. Табличное представление позволяет не только выявить ту или иную закономерность распределения, но и подробно охарактеризовать структуру изучаемой совокупности.
Для построения таблицы вариационного ряда выбираем следующий путь: меню Statistics/Basic Statistic Tables. Впоявившемсядиалоговомокневыбираемпункт Frequency tables. Выбрав переменную, содержащую ранжированный ряд с учетом выбросов, переходим на закладку Advanced. Задаем параметры построения таблицы. Нажимаем кнопку Summary, и появляется расчетная таблица частот (см.Табл.1.4
).
Табл.1.4
Рассчитанная таблица частот с интервалом 10 (k = 10)

Далее представлены таблицы вариационного ряда, построенные с использованием разного числа интервалов (k = 15, k = 5 и k = 8).
Табл.1.5
Рассчитанная таблица частот с интервалом 15 (k = 15)

Табл.1.6
Рассчитанная таблица частот с интервалом 5 (k = 5)

Табл.1.7
Рассчитанная таблица частот с интервалом 8 (k = 8)

Для графического представления рядов распределения используются, в основном, три вида графиков:
1. Полигон распределения.
2. Гистограмма распределения.
3. Кумулята распределения.
Наряду с этим, STATISTICA дает возможность получать графические представления эмпирического распределения, широко используемые в зарубежной статистической литературе, как учебной, так и профессиональной. Речьидетографиках Box-and- Whisker Plot, Hanging Bars.
Гистограмма (или столбиковая диаграмма) строится только для интервальных вариационных рядов. Основаниями столбиков гистограммы, являются интервалы значений варьирующего признака, а высота столбиков соответствует частоте каждого интервала.
Для построения гистограммы удобно воспользоваться кнопкой Histograms на закладке Advanced меню Frequency Tables, которым мы пользовались для построения таблиц. При этом условия построения гистограмм должны полностью соответствовать условиям построения таблиц.
На построенных графиках (рис. 1.1, 1.2, 1.3, 1.4) помимо гистограммы нанесена кривая нормального распределения (обозначена красным цветом).

Гистограмма регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2005 г. с наложенными на них кривыми нормального распределения: с числом интервалов k = 10
Рис. 1.1

Гистограмма регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2005 г. с наложенными на них кривыми нормального распределения: с числом интервалов k = 15
Рис. 1.2

Гистограмма регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2005 г. с наложенными на них кривыми нормального распределения: с числом интервалов k = 5
Рис. 1.3

Гистограмма регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2005 г. с наложенными на них кривыми нормального распределения: с числом интервалов k = 8
Рис. 1.4
При k = 10 получено много малонаполненных групп, наблюдаются две вершины и получается плосковершинное распределение (равные частоты в двух группах). Такой интервал нам не подходит.
При k = 15 получено еще больше малонаполненных групп, чем при k = 10, а также у 2, 3 и 5 групп соответственно равные частоты, что приводит в плосковершинному распределению. Интервал, равный 15, тоже не подходит.
При k = 8 наблюдаются две вершины, в двух группах равные частоты. И вообще распределение не является нормальным, т.к. частота в третьей группе ниже, чем во второй. Этот интервал также не подходит нам.
Выбирая окончательный вариант табличного представления вариационного ряда в нашем примере, следует остановиться на группировке с использованием 5 групп. Все группы вполне наполнены, наблюдается одна вершина, нет плосковершинного распределения.
Ниже представлены полигон и кумулята для вариационного ряда с использованием 5 групп.
Полигон распределения целесообразнее использовать для рядов, построенных по дискретному признаку. Если полигон строится по интервальному вариационному ряду, то в качестве значения признака берется середина интервала. По оси Х откладываются значения признака, по оси Y – частоты (частости).
Для построения полигона на основе абсолютных частот необходимо выделить столбец Count в таблице частот и щелкнуть на нем правой кнопкой мыши.

Полигон регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2001г. при k=5
Рис. 1.5
Для построения полигона по относительным частотам, кумуляты по абсолютным и относительным частотам выбираются соответственно столбцы Percent, Cumulative count , Cumulative percent в таблице частот.

Кумулята регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2001г. при k=5
Рис. 1.6

Полигон регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2001г. при k=5
Рис. 1.7

Кумулята регионов России по значению показателя «Число собственных легковых автомобилей на 1000 человек» в 2001г. при k=5
Рис. 1.8
Одним из приемов компактного изображения статистической совокупности, находящимся вне отечественной традиции, является "Box-and-Whisker Plot" — "ящик с усами". Рассматриваемая процедура обеспечивает как диагностическую, так и описательную информацию об исследуемой совокупности.
Для ее реализации запускаем процедуру Graphs/2D Graphs/Box Plots. В появившемся окне удобно сразу же выбрать интересующий нас тип графика (в поле Graph Type выбираем Box-Whiskers). Остальные свойства графика удобнее всего настроить, перейдя на закладку Advanced.
График появляется в вертикальном виде, однако, на практике принято рассматривать его горизонтально. Для того чтобы повернуть график на 90 градусов, нужно щелкнуть в поле графика правой кнопкой мыши и выбрать меню Graph Properties (All options). Далеепереходимкзакладке Graph layout: вполе Axis position вместофункции Standard выбираем Reserved, тоестьобратноеположениеосиабсцисс. НажимаемОК.

Диаграмма "Box-and-Whisker Plot" — "ящик с усами"
Рис.1.9
Метод "Box-and-Whisker Plot" также дает полезную информацию о концентрации, дисперсии и асимметрии распределения, но наряду с этим исследователь получает наглядное представление о том, что происходит на концах распределения.
В качестве дополнения отметим, что система дает также возможность получить нетрадиционное графическое представление о том, как соотносятся между собой эмпирическое распределение и его нормальная аппроксимация. Речь идет о графике "Hanging Histobars" или “Hanging Bars” (в весьма вольном переводе – «висячие полоски»). Канонизированного термина на русском языке нет, потому будем обозначать рассматриваемую процедуру как "HH-график".
Для его представления необходимо запустить процедуру Graphs/2D Graphs/Histograms и далее перейти к закладке Advanced.

Диаграмма “Hanging Bars”
Рис.1.10
HH-процедура выводит на экран изображение близкое к гистограмме, с тем только различием, что столбцы гистограммы не опираются на горизонтальную ось, а "подвешены" (Hanging) к кривой нормального распределения в точках, соответствующих серединам интервалов группировки.
2. Расчет основных характеристик вариационного ряда
Статистический анализ вариационных рядов распределения предполагает расчет характеристик центра распределения, его структуры, оценку степени вариации и дифференциации изучаемого признака, изучение формы распределения.
В качестве показателей центральной тенденции распределения используются: среднее арифметическое значение, мода и медиана. Основными показателями вариации являются: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Для характеристики структуры распределения используются следующие показатели: медиана, квартили, децили и прочие перцентили. Изучение формы распределения предполагает оценку асимметрии и эксцесса (куртозиса). Перечисленные показатели имеют самостоятельное аналитическое значение, поскольку отражают разные свойства изучаемой совокупности, а все вместе они позволяют получить комплексную характеристику эмпирического распределения.
В программе STATISTICA, как и в других статистических ППП, есть возможность получить все перечисленные показатели, пользуясь одной процедурой. В главном меню раздел Statistics, активизируем опцию Basic Statistics/Tables. Затем, в появившемся контекстном окне, выбирается процедура Descriptive statistics – описательные статистики. Закладка Advanced предлагает пользователю сформировать набор вычисляемых статистик, отвечающих целям анализа.
Ниже приведены результаты расчета основных статистических характеристик.
Табл.2.1
Основные характеристики распределения регионов России по значению
показателя «Число собственных легковых автомобилей на 1000 человек» в 2001 г.

Valid N
– объем выборки (число единиц в совокупности). У нас 84 региона.
Mean
– средняя арифметическая. 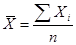 , ,
где n – объем совокупности (число единиц);
Хi – значение признака у I-ой единицы совокупности.
Средняя арифметическая величина – отношение объема признака к объему совокупности. Данная средняя используется для расчета средних значений абсолютных показателей по не сгруппированным данным.
Median
– медиана. Это значение признака у единицы, делящий ранжированный ряд пополам.


Mode
– мода определяется непосредственно по исходным данным (запись в строке Multiple означает, что распределение имеет не одну моду). Это наиболее часто встречающееся значение признаков совокупности.
Frequency
– частота модального значения.
Sum
– сумма значений признака в совокупности.
Variance
– дисперсиия.

Показатель дисперсии в экономических исследованиях содержательно не интерпретируется, но благодаря своим свойствам широко используется для расчета многих статистических характеристик.
Standard deviation
– среднее квадратическое (стандартное) отклонение.

Minimum
– минимальное значение признака в совокупности: x min .
Maximum
– максимальное значение признака в совокупности: x max.
Range
– размах вариации.

Lower (Lower quartile)
–
нижний (первый) квартиль.

Upper (Upper quartile)
–верхний (третий) квартиль.

Quartile (Interquartile range)
– межквартильныйразмах: Q3 – Q1.
Skewness
–асимметрия.
Табл.2.2
Сравнение статистических показателей, рассчитанных
различными способами
| № п/п |
Показатель |
Значение в ППП
STATISTICA
|
Значение после ручного расчета |
| 1 |
Средняя арифметическая |
122,2202 |
122,2202 |
| 2 |
Мода |
Multiple |
Multiple |
| 3 |
Медиана |
120,0000 |
120,0000 |
| 4 |
Дисперсия |
1239,130 |
1239,130 |
| 5 |
Среднее квадратическое отклонение |
35,20128 |
35,20128 |
| 6 |
Частота модального значения |
2 |
2 |
| 7 |
Сумма значений признака |
10266,50 |
10266,50 |
| 8 |
Верхний квартиль |
140,7000 |
140,7000 |
| 9 |
Нижний квартиль |
105,6000 |
105,0000 |
Среди рассчитанных характеристик нет такого важного показателя вариации, как коэффициент вариации
(принято рассчитывать в процентах):

В нашем случае коэффициент вариации равен:
V = (35,20128/122,2202)*100 = 28,8 %.
Заключение
В данном курсовом проекте была рассмотрена реализация анализа распределений с использованием программы STATISTICA, а также произведены расчеты основных статистических показателей.
Таким образом, по итогам курсового проекта я освоила методику и приобрела практические навыки анализа распределений, включающего расчет основных статистических характеристик, графическое и табличное представление рядов распределения.
|