БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра информатики
РЕФЕРАТ
На тему:
«Переключательные функции одного и двух аргументов
»
МИНСК, 2008
1.Переключательные функции одного аргумента.
Существует четыре переключательные функции одного аргумента, которые приведены в табл. 1.
Таблица 1
Переключательные функции одного аргумента
 x x
f(x)
|
0 |
1 |
Условное обозначение |
Название функции |
| f0
(
x)
|
0 |
0 |
0 |
Константа нуль |
| f1
(x)
|
0 |
1 |
x
|
Переменная x
|
| f2
(
x)
|
1 |
0 |
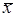 |
Инверсия x
|
| f3
(
x)
|
1 |
1 |
1 |
Константа единица |
Функция f0
(x)
тождественно равна нулю. Она называется константой нуль
и обозначается f0
(x)=
0.
Функция f1
(x)
повторяет значения аргумента и поэтому тождественно равна переменной x
.
Функция f2
(x)
принимает значения, противоположные значениям аргумента: если x
=0, то f2
(x)
=1; если x
=1, то f2
(x)
=0. Эту функцию называют инверсией x
или отрицанием x
и вводят для нее специальное обозначение f2
(x)
= 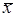 . .
Функция f3
(x)
тождественно равна единице. Она называется константой единица
и обозначается f3
(x)=
1.
2. Переключательные функции двух аргументов.
Существует шестнадцать различных переключательных функций двух аргументов, каждая из которых определена на четырех наборах. Эти функции представлены в табл. 2.
В число шестнадцати переключательных функций входят функции, рассмотренные в п.1:
f0
(x,y) =
0 — константа нуль;
f15
(x,y) =
1 —
константа единица;
f3
(x,y) = x —
переменная x
;
f5
(x,y) = y —
переменная y
;
f12
(x,y) = 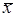 —
инверсия x; —
инверсия x;
f10
(x,y) = 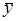 —
инверсия y
; —
инверсия y
;
Таблица 2
Переключательные функции двух аргументов
| x
|
0 |
0 |
1 |
1 |
Название функции |
Обозначение |
| y
|
0 |
1 |
0 |
1 |
| f0
(x,y)
|
0 |
0 |
0 |
0 |
Константа нуль |
0 |
| f1
(x,y)
|
0 |
0 |
0 |
1 |
Произведение (конъюнкция) |
x∙y; x
Ùy;
x&
y
|
| f2
(x,y)
|
0 |
0 |
1 |
0 |
Функция запрета по y
|
x
D
y
|
| f3
(x,y)
|
0 |
0 |
1 |
1 |
Переменная x
|
x
|
| f4
(x,y)
|
0 |
1 |
0 |
0 |
Функция запрета по x
|
y
D
x
|
| f5
(x,y)
|
0 |
1 |
0 |
1 |
Переменная y
|
y
|
| f6
(x,y)
|
0 |
1 |
1 |
0 |
Сумма по модулю 2 (логическая неравнозначность) |
x
Å
y
|
| f7
(x,y)
|
0 |
1 |
1 |
1 |
Логическое сложение (дизъюнкция) |
x+y; x
Ú
y
|
| f8
(x,y)
|
1 |
0 |
0 |
0 |
Операция Пирса (стрелка Пирса) |
x
¯
y
|
| f9
(x,y)
|
1 |
0 |
0 |
1 |
Эквивалентность (логическая равнозначность) |
x
~
y
|
| f10
(x,y)
|
1 |
0 |
1 |
0 |
Инверсия y
|
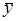 |
| f11
(x,y)
|
1 |
0 |
1 |
1 |
Импликация от y
к x
|
y
®
x
|
| f12
(x,y)
|
1 |
1 |
0 |
0 |
Инверсия x
|
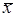 |
| f13
(x,y)
|
1 |
1 |
0 |
1 |
Импликация от x
к y
|
x
®
y
|
| f14
(x,y)
|
1 |
1 |
1 |
0 |
Операция Шеффера (штрих Шеффера) |
x
½
y
|
| f15
(x,y)
|
1 |
1 |
1 |
1 |
Константа единица |
1 |
Рассмотрим некоторые переключательные функции двух аргументов.
Функция f1
(x,y)
называется конъюнкцией, или логическим умножением. Таблица истинности этой функции совпадает с таблицей умножения двух одноразрядных двоичных чисел. Можно ввести функцию n аргументов, соответствующую произведению n одноразрядных двоичных чисел. Такая переключательная функция равна единице тогда и только тогда, когда все ее аргументы равны единице. Для конъюнкции справедливы следующие соотношения:
x
× 0 = 0;
x
× 1 = x
;
x
×
x
= x
;
x
×
y
=y
×
x
;
x
×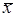 = 0. = 0.
Функция f7
(x,y)
называется дизъюнкцией или логическим сложением. Эта функция равна нулю только в том случае, когда все ее аргументы равны нулю. Можно ввести функцию n аргументов, соответствующую логическому сложению n одноразрядных двоичных чисел. Такая переключательная функция равна нулю тогда и только тогда, когда все ее аргументы равны нулю. Для конъюнкции справедливы следующие соотношения:
x
Ú 0 = x
;
x
Ú 1 = 1;
x
Ú
x
= x
;
x
Ú
y
=y
Ú
x
;
x
Ú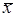 = 1. = 1.
Таблица истинности функции f6
(x,y)
совпадает с таблицей сложения двух одноразрядных двоичных чисел по модулю два. Можно ввести функцию n аргументов, соответствующую сумме по модулю два n одноразрядных двоичных чисел. Такая переключательная функция определяется следующим условием: она равна единице, если число аргументов, равных единице, нечетно, и равна нулю, если число таких аргументов четно. Приведем некоторые соотношения для суммы по модулю два:
x
Å 0 = x
;
x
Å 1 = 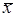 ; ;
x
Å x
= 0;
x
Å x
Å x
= x
;
x
Å y
= y
Å x
.
Рассмотренные шестнадцать функций двух аргументов (будем называть их элементарными) позволяют строить новые переключательные функции следующим образом:
· путем перенумерации аргументов;
· путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f
1
,
f
2
, …,
fk
путем применения (возможно многократного) этих двух правил, будем называть суперпозицией
функций f
1
,
f
2
, …,
fk
. Например, имея элементарные функции инверсии, конъюнкции, дизъюнкции, импликации, запрета, сложения по модулю два, можно составить новую переключательную функцию:
f
(
x
,
y
,
z
) = ((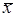 Ú
y
)
D
z
)
Å
((
y
®
z
)
×
x
).
Ú
y
)
D
z
)
Å
((
y
®
z
)
×
x
).
Используя таблицы, определяющие элементарные функции, можно задавать в виде таблицы любую переключательную функцию, являющуюся суперпозицией этих функций.
Пример 1. Представить в виде таблицы функцию
f
(
x
,
y
,
z
) = ((
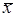 Ú
y
)
D
z
)
Å
((
y
®
z
)
×
x
).
Ú
y
)
D
z
)
Å
((
y
®
z
)
×
x
).
Решение. Функцию f (x,y,z)
будем представлять последовательно, записывая в столбцы табл. 1.5 промежуточные результаты, получаемые после выполнения каждой операции:
Таблица 3
Таблица истинности функции f
(
x
,
y
,
z
) = ((
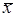 Ú
y
)
D
z
)
Å
((
y
®
z
)
×
x
).
Ú
y
)
D
z
)
Å
((
y
®
z
)
×
x
).
| x
|
y
|
z
|
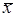
|
(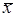 Ú
y)
Ú
y)
|
(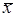 Ú
y)
D
z)
Ú
y)
D
z)
|
(y
®
z)
|
(y
®
z)
×
x
|
((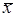 Ú
y)
D
z)
Å
((y
®
z)
×
x)
Ú
y)
D
z)
Å
((y
®
z)
×
x)
|
| 0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
| 0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
| 1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
| 1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1. Конституенты.
В п. 2 был рассмотрен один из возможных способов представления переключательной функции – задание ее в виде таблицы истинности. В этом разделе будем решать обратную задачу, а именно представление переключательной функции, заданной таблицей истинности, через элементарные функции, образующие базис.
Рассмотрим переключательные функции, называемые конституентами.
Определение 1.
Конституентой единицы называют переключательную функцию
n
аргументов, которая принимает значение, равное единице на одном единственном наборе аргументов.
Из определения следует, что число различных конституент единицы среди функций n аргументов равно 2n
. Конституенты единицы обозначаются так: Ki
(x1
, …, xn
)
, где i
– номер набора, на котором конституента равна единице. Например, запись K7
(x1
, x2
, x3
, x4
)
означает функцию четырех аргументов, равную единице на наборе (0111).
Конституента единицы может быть выражена через конъюнкцию всех аргументов, каждый из которых входит в произведение со знаком отрицания или без него. Приведенную выше конституенту единицы можно представить через конъюнкцию аргументов следующим образом:
K
7
(
x
1
,
x
2
,
x
3
,
x
4
) =
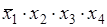 .
.
Чтобы записать в виде произведения конституенту Ki
(
x
1
, …,
xn
),
можно воспользоваться следующим правилом: записать n
-разрядное двоичное число (n
– число аргументов), равное i
, и конъюнкцию n
переменных; над переменными, места которых совпадают с позициями нулей в двоичном числе i
, поставить знак отрицания.
Пример 2. Записать конституенту, равную единице на двенадцатом наборе для функции пяти переменных.
Решение. Пятиразрядное двоичное число, равное двенадцати, записывается в виде: 01100. Запишем произведение пяти аргументов, располагая их в порядке возрастания индексов: x
1
×
x
2
×
x
3
×
x
4
×
x
5
. Сопоставляя это произведение с двоичным числом 01100, определяем, что знаки отрицания необходимо поставить над первым, четвертым и пятым аргументами:
K
12
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
) =
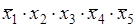 .
.
Определение 3.
Конституентой нуля называют переключательную функцию
n
аргументов, которая принимает значение, равное нулю, на одном единственном наборе аргументов.
Из определения следует, что число различных конституент нуля среди функций n аргументов равно 2n
. Конституенты нуля обозначаются так: Mi
(
x
1
, …,
xn
)
, где i
– номер набора, на котором конституента равна нулю. Конституента нуля может быть выражена через дизъюнкцию всех аргументов, каждый из которых входит в произведение со знаком отрицания или без него.
Чтобы записать в виде произведения конституенту Mi
(
x
1
, …,
xn
),
можно воспользоваться следующим правилом: записать n
-разрядное двоичное число (n
– число аргументов), равное i
, и дизъюнкцию n
переменных; над переменными, места которых совпадают с позициями единиц в двоичном числе i
, поставить знак отрицания.
Пример 3. Записать конституенту нуля, равную нулю на двадцать пятом наборе для функции пяти переменных.
Решение. Пятиразрядное двоичное число, равное двадцати пяти, записывается в виде: 11001. Запишем дизъюнкцию пяти аргументов, располагая их в порядке возрастания индексов: x
1
Ú
x
2
Ú
x
3
Ú
x
4
Ú
x
5
. Сопоставляя это произведение с двоичным числом 11001, определяем, что знаки отрицания необходимо поставить над первым, вторым и пятым аргументами:
M
25
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
) =
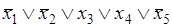 .
.
2. Представление переключательной функции в виде полинома Жегалкина.
Теорема Жегалкина
.
Любая переключательная функция может быть представлена в виде полинома (многочлена), т. е. записана в форме
f(x1
, . . . , xn
) =
ао
Å
a1
x1
Å
a2
x2
Å
…
Å
an
xn
Å
an+1
x1
x2
Å
…
Å
aN
x1…
xn
,
(1)
где a0
, a1
x1
, … a
N
—
константы, равные нулю или единице;
Å
—
операция сложения по модулю два.
При записи конкретной переключательной функции в виде многочлена коэффициенты a0
, a1
x1
, … a
N
выпадают, так как члены, при которых коэффициенты равны нулю, можно опустить, а коэффициенты, равные единице, не писать.
Для доказательства теоремы Жегалкина предположим, что задана произвольная переключательная функция п
аргументов f
(
x
1
, . . . ,
xn
),
равная единице на некотором числе наборов с номерами m
1
, …
mp
.
Покажем, что переключательная функция f
(
x
1
, . . . ,
xn
)
равна сумме конституент единицы, которые равны единице на тех же наборах, что и данная функция:
f(x1
, . . . , xn
) = Km1
Å
Km2
Å
. . .
Å
Kmp
.
(2)
Действительно, на каждом из наборов с номерами m
1
, …
mp
равна единице только одна конституента, стоящая в правой части выражения (2), а остальные равны нулю. Следовательно, на этих наборах и только на них правая часть выражения (2) принимает значение, равное единице.
Для того чтобы перейти от выражения (2) к виду (1), достаточно представить конституенты единицы в виде произведений и, используя соотношение 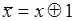 ,
заменить все переменные с отрицаниями (так как отрицания в выражение (3.1) не входят). Пусть например, конституента единицы записана в виде ,
заменить все переменные с отрицаниями (так как отрицания в выражение (3.1) не входят). Пусть например, конституента единицы записана в виде
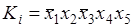 . .
Тогда получим
Ki
= (1
Å
x
1
)
x
2
(1
Å
x
3
)
x
4
x
5
.
Раскрывая скобки и приводя подобные члены в соответствии со свойствами операции сложения по модулю два, получаем запись заданной функции в форме (1), что и доказывает теорему.
Приведенное доказательство теоремы позволяет сформулировать правило представления любой переключательной функции в виде многочлена.
Чтобы переключательную функцию, заданную таблицей истинности, представить в виде полинома Жегалкина, достаточно записать функцию в виде суммы конституент единицы, равных единице на тех же наборах, на которых равна единице заданная функция. Затем все аргументы, входящие в полученное выражение с отрицанием, заменить с помощью соотношения 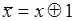 , раскрыть скобки и привести подобные члены с учетом тождества; , раскрыть скобки и привести подобные члены с учетом тождества;
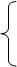 x
,
если п
нечетно, x
,
если п
нечетно,
x
Å
x
Å
. . .
Å
x =
0, если п
четно.
Пример 3. Представить в виде полинома Жегалкина функцию f
58
(
x
1
,
x
2
,
x
3
)
.
Функция f
58
(
x
1
,
x
2
,
x
3
)
равна единице на втором, третьем, четвертом и шестом наборах, и может быть записана в виде суммы соответствующих конституент единицы:
f
58
(
x
1
,
x
2
,
x
3
) =
K
2
Å
K
3
Å
K
4
Å
K
6
=
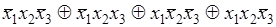 . .
Используя соотношение 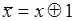 , получаем , получаем
f58
(x1
,x2
,x3
)=(1
Å
x1
)x2
(1
Å
x3
)
Å
(1
Å
x1
)x2
x3
Å
x1
(1
Å
x2
)(1
Å
x3
)
Å
x1
x2
(1
Å
x3
).
Приводя подобные члены, окончательно находим
f
58
(
x
1
,
x
2
,
x
3
)=
x
1
Å
x
2
Å
x
1
x
2
Å
x
1
x
3
.
3. Совершенная дизъюнктивная нормальная форма переключательной функции.
В общем виде переключательная функция п
аргументов может быть задана таблицей истинности. Обозначим через f(
i
)
(i=0, … ,2n
-1) значение функции на i-м наборе аргументов. Напомним, что каждая из величин f(
i
)
принимает значение нуль или единица. В соответствие i-му набору аргументов можно поставить конституенту единицы Ki
,
которая принимает значение, равное единице только на данном f
(
i
)
наборе. Умножим каждую конституенту единицы Ki
на
значение функции f(
i
)
и рассмотрим дизъюнкцию произведений fi
Ki
:
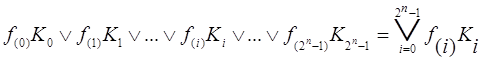 . (3) . (3)
Если подставить в выражение (3) значения f(i)
,
то получим дизъюнкцию конституент, которые равны единице на тех же наборах, что и заданная функция. Действительно, ввиду того, что 0×x
=0 и 0Úх=х,
члены выражения (2), в которых коэффициенты f
(
i
)
=0, можно опустить, а так как x
×
1 =
x
, то коэффициенты f
(
i
)
=
1можно не писать. Тогда
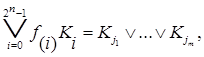
где j1
, …,jm
– номера наборов, на которых функция равна единице;
m
– число таких наборов.
Определение 3. Дизъюнкция конституент единицы, равных единице на тех же наборах, что и заданная функция, называется совершенной дизъюнктивной нормальной формой переключательной функции.
Любую переключательную функцию f
(
x
1
, . . . ,
xn
)
(кроме константы ноль) можно представить в совершенной дизъюнктивной нормальной форме. Заметим, что любая переключательная функция имеет единственную совершенную дизъюнктивную нормальную форм у: это непосредственно следует из выражения (3).
Совершенную дизъюнктивную нормальную форму переключательной функции удобно находить в такой последовательности:
· выписать ряд произведений всех аргументов и соединить их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в единицу;
· записать под каждым произведением набор аргументов, на котором функция равна единице, и над аргументами, равными нулю, поставить знаки отрицания.
Это правило называют иногда правилом записи переключательной функции по единицам.
Пример 4. Представить в совершенной дизъюнктивной нормальной форме переключательную функцию четырех аргументов f
23805
(
x
1
,
x
2
,
x
3
,
x
4
)
(см. табл. 2).
Решение. Из табл. 2 видно, что переключательная функция принимает значения, равные единице, на следующих наборах аргументов:
0001, 0011, 0100, 0101, 1000, 1001, 1010, 1011, 1100, 1101, 1111.
Таким образом, совершенная дизъюнктивная нормальная форма функции f
23805
(
x
1
,
x
2
,
x
3
,
x
4
)
будет состоять из одиннадцати дизъюнкций, каждая из которых представляет собой конъюнкцию четырех элементов:
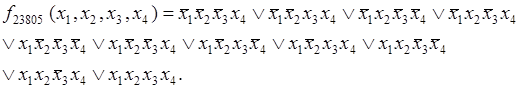
4. Совершенная конъюнктивная нормальная форма переключательной функции.
Если заданная переключательная функция равна единице на большинстве наборов аргументов, то представление функции в совершенной дизъюнктивной нормальной форме может оказаться достаточно громоздким. В этих случаях удобнее использовать другую форму представления функции – совершенную конъюнктивную нормальную форму. Для представления функций в этой форме используется функция конституенты нуля.
Рассмотрим выражение
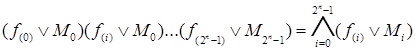 , (4) , (4)
где f
(
i
)
– значение переключательной функции на i
-м наборе.
Ввиду справедливости соотношений 1Úx
= 1 и 0
Ú
х= х,
при подстановке в выражение (4) значений функции f(i)
, сомножители, у которых f(i)
, == 1, можно опустить, а значения функции f(i)
=0 не писать. Тогда
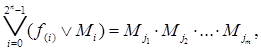 (5) (5)
где j1
, j2
, …,jm
–номера наборов, на которых функция равна нулю;
т -
число таких наборов.
Определение 4.
Произведение конституент нуля, которые равны нулю на тех же наборах, что и заданная функция, называется совершенной конъюнктивной нормальной формой.
Любая переключательная функция f
(
x
1
, . . . ,
xn
)
(кроме константы единицы) может быть представлена в совершенной конъюнктивной нормальной форме. Любая переключательная функция имеет единственную совершенную конъюнктивную нормальную форму.
Сформулируем правило представления переключательной функции в совершенной конъюнктивной нормальной форме. Чтобы представить переключательную функцию п
аргументов в совершенной конъюнктивной нормальной форме, достаточно:
· выписать произведение дизъюнкций всех аргументов с количеством сомножителей, равным числу наборов, на которых заданная функция обращается в нуль;
· выписать под каждым сомножителем набор аргументов, на котором функция равна нулю, и над аргументами, равными единице, поставить знаки отрицания;
Это правило иногда называют правилом записи переключательной функции по нулям.
Пример 5. Представить в совершенной конъюнктивной нормальной форме функцию f
23805
(
x
1
,
x
2
,
x
3
,
x
4
)
(см. табл. 2).
Решение. Из табл. 2 видно, что переключательная функция принимает значения, равные нулю, на следующих наборах аргументов:
0000, 0010, 0110, 0111, 1110.
Таким образом, совершенная конъюнктивная нормальная форма функции f
23805
(
x
1
,
x
2
,
x
3
,
x
4
)
будет состоять из пяти конъюнкций, каждая из которых представляет собой дизъюнкцию четырех элементов:
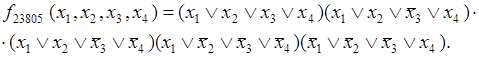
ЛИТЕРАТУРА
1. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).
2. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика.– М.: Наука, Физматлит, 2000.– 544 с.– ISBN 5-02-015238-2.
3. Зарубин В.С. Математическое моделирование в технике: Учеб. для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.– 496 с. (Сер. Математика в техническом университете; вып. XXI, заключительный).
|