Задача №1.
Двумерная случайная величина (X,Y) имеет равномерное распределение вероятностей в треугольной области ABC:

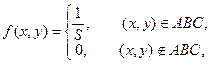
где S – площадь треугольника ABC.
Определить плотности случайных величин X и Y, математические ожидания M(X) и M(Y), дисперсии D(X) и D(Y), а также коэффициент корреляции 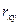 . Являются ли случайные величины X и Y независимыми? . Являются ли случайные величины X и Y независимыми?
Решение.
Разделим область ABC на две равные части вдоль оси OX, тогда из условия
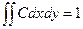 или или 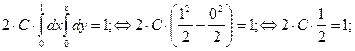
следует, что 
Тогда плотность двумерной случайной величины (X,Y):
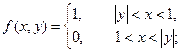
Вычислим плотность составляющей X:
при 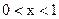 , , 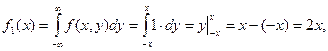
откуда плотность составляющей X–
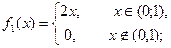
Вычислим плотность составляющей Y:
при 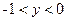 , , 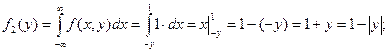
при 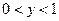 , , 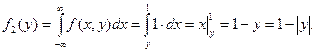
Поэтому плотность составляющей Y –
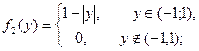
Найдем условную плотность составляющей X:
при 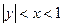 , , 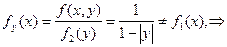 случайные величины X и Y зависимы. случайные величины X и Y зависимы.
Найдем математическое ожидание случайной величины X:
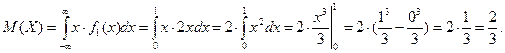
Найдем дисперсию случайной величины X:
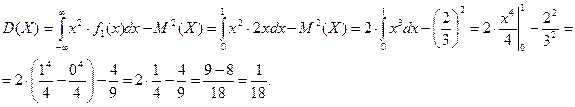
Найдем среднеквадратическое отклонение случайной величины X:
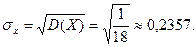
Найдем математическое ожидание случайной величины Y:
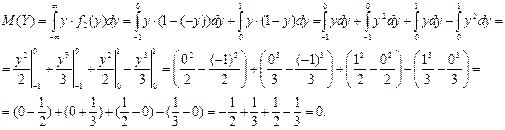
Найдем дисперсию случайной величины Y:
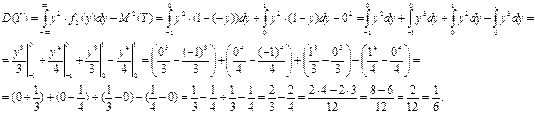
Найдем среднеквадратическое отклонение случайной величины Y:
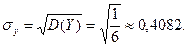
Найдем математическое ожидание двумерной случайной величины (X,Y):
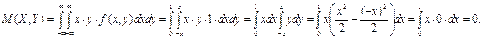
Тогда ковариация: 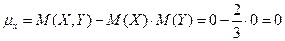 , ,
а значит и коэффициент корреляции 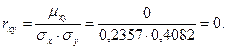
Следовательно, случайные величины X и Y - зависимые, но некоррелированные.
Задача №2
Двумерная случайная величина (X,Y) имеет следующее распределение вероятностей:
| Y |
X |
| 3 |
6 |
8 |
9 |
| -0,2 |
0,035 |
0,029 |
0,048 |
0,049 |
| 0,1 |
0,083 |
0,107 |
0,093 |
0,106 |
| 0,3 |
0,095 |
0,118 |
0,129 |
0,108 |
Найти коэффициент корреляции между составляющими X и Y.
Решение.
Таблица распределения вероятностей одномерной случайной величины X:
| X |
3 |
6 |
8 |
9 |
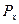 |
0,213 |
0,254 |
0,270 |
0,263 |
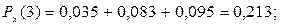
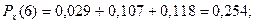
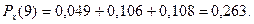 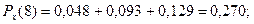
Проверка: 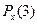 + + 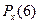 + + 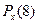 + + 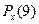 = 0,213 + 0,254 + 0,270 + 0,263 = 1. = 0,213 + 0,254 + 0,270 + 0,263 = 1.
Таблица распределения вероятностей одномерной случайной величины Y:
| Y |
-0,2 |
0,1 |
0,3 |
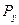 |
0,161 |
0,389 |
0,450 |
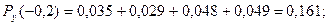
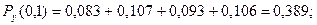
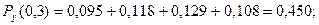
Проверка: 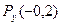 + + 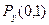 + + 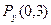 = 0,161 + 0,389 + 0,450 = 1. = 0,161 + 0,389 + 0,450 = 1.
Вычислим числовые характеристики случайных величин X и Y.
1. Математическое ожидание случайной величины X:
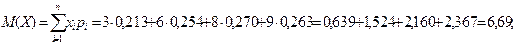 2. 2.
Математическое ожидание случайной величины Y:
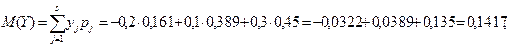
3. Дисперсия случайной величины X:
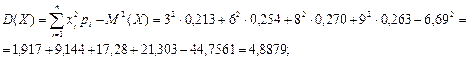
4. Дисперсия случайной величины Y:
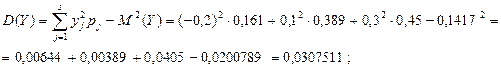
5. Среднеквадратическое отклонение случайной величины X:
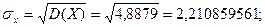
6. Среднеквадратическое отклонение случайной величины Y:
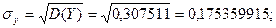
Таблица распределения вероятностей случайной величины X-M(X):
| X-M(X) |
3-M(X) |
6-M(X) |
8-M(X) |
9-M(X) |
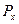 |
0,213 |
0,254 |
0,270 |
0,263 |
Таблица распределения вероятностей случайной величины Y-M(Y):
| Y-M(Y) |
-0,2-M(Y) |
0,1-M(Y) |
0,3-M(Y) |
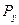 |
0,161 |
0,389 |
0,450 |
Таблица распределения вероятностей случайной величины [X-M(X)][Y-M(Y)]:
| [X-M(X)][Y-M(Y)] |
1,260873 |
0,153873 |
| P |
0,035 |
0,083 |
| -0,584127 |
0,235773 |
0,028773 |
-0,109227 |
-0,447627 |
| 0,095 |
0,029 |
0,107 |
0,118 |
0,048 |
| -0,054627 |
0,207373 |
-0,789327 |
-0,096327 |
0,365673 |
| 0,093 |
0,129 |
0,049 |
0,106 |
0,108 |
1. 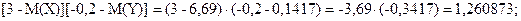
2. 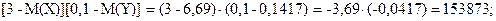
3. 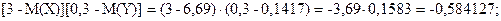
4. 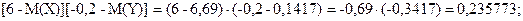
5. 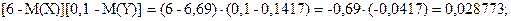
6. 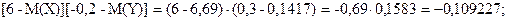
7. 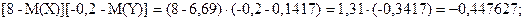
8. 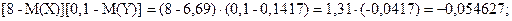
9. 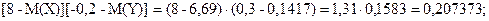
10. 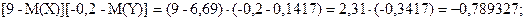
11. 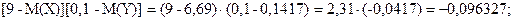
12. 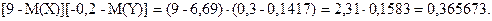
Найдем ковариацию:
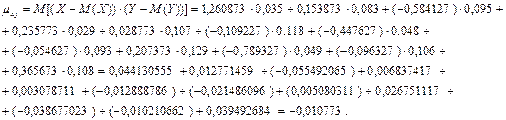
Найдем коэффициент корреляции:
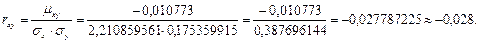
Ответ: -0,028.
Задача №3
Рост, см
(X)
|
Вес, кг (Y) |
| 22,5-25,5 |
25,5-28,5 |
28,5-31,5 |
31,5-34,5 |
34,5-37,5 |
| 117,5-122,5 |
1 |
3 |
- |
- |
- |
| 122,5-127,5 |
- |
2 |
6 |
1 |
- |
| 127,5-132,5 |
- |
1 |
5 |
5 |
- |
| 132,5-137,5 |
- |
1 |
6 |
7 |
2 |
| 137,5-142,5 |
- |
- |
1 |
4 |
2 |
| 142,5-147,5 |
- |
- |
- |
1 |
1 |
| 147,5-152,5 |
- |
- |
- |
- |
1 |
Результаты обследования 50 учеников:
По данным таблицы требуется:
- написать выборочные уравнения прямых регрессии Y на X и X на Y;
- вычертить их графики и определить угол между ними;
- по величине угла между прямыми регрессии сделать заключение о величине связи между X и Y.
Решение.
Принимая рост всех учеников, попавших в данный интервал, равным середине этого интервала, а вес – равным середине соответствующего интервала, получим так называемую корреляционную таблицу:
Для роста
X
получим:
1. Выборочная средняя
–
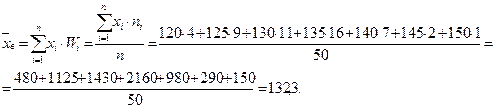
2. Дисперсия выборочная исправленная –
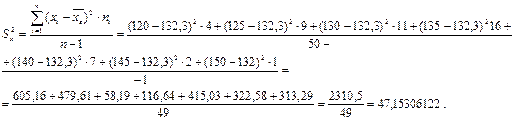
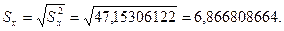
Для веса
Y
получим:
1. Выборочная средняя -
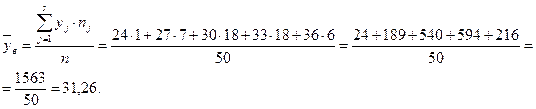
2. Дисперсия выборочная исправленная –
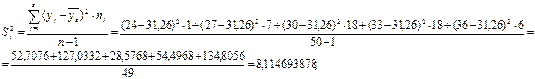
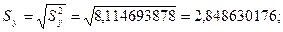
Найдем выборочный коэффициент корреляции:
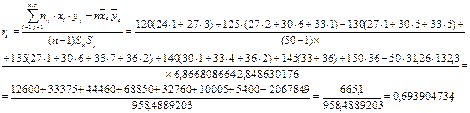
Найдем значения коэффициентов регрессии:
 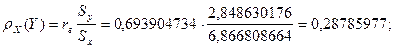
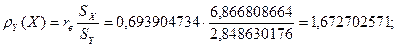
Уравнение прямой регрессии Y на X имеет вид:
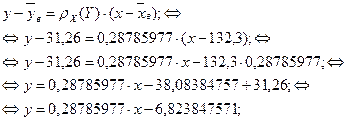
Уравнение прямой регрессии X на Y имеет вид:
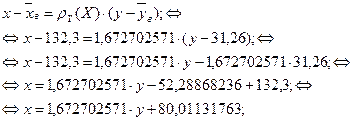
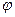 - угол между прямыми регрессии. - угол между прямыми регрессии.
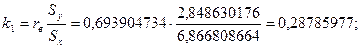
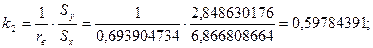
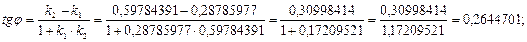
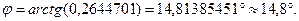
Следовательно, связь между X и Y не тесная.

|