| Тольяттинский государственный университет
Кафедра "Промышленная электроника"
РАСЧЁТ ЭЛЕКТРОМАГНИТНОГО ДЕМПФЕРА.
Пояснительная записка к курсовой работе по курсу "Методы математического анализа и расчёта электронных схем"
Вариант № 15
Студент: Моторин С.К.
Группа: Э-306
Преподаватель: Кудинов А.К.
Тольятти 2003
Содержание
ВВЕДЕНИЕ
1. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
3. Коррекция точек стыковки
4. Реализация численных вычислений И ПОЛУЧЕНИЕ РЕЗУЛЬТАТОВ
Заключение
Список используемой Литературы
ВВедение
Математическое моделирование устройств промышленной электроники проводится как альтернатива физическому моделированию с целью уменьшения производственных затрат, либо с целью оптимизации параметров разработанных схем. Задача оптимизации параметров, как правило, отличается большой сложностью и требует для своего решения значительных затрат машинного времени. Поэтому эффективность разрабатываемых программ имеет существенное значение и определяется выбором математической модели устройства, а также методов её анализа и оптимизации. Данная работа ориентирована на математическое моделирование вентильных устройств (ВУ) промышленной электроники, как наиболее сложных механических систем с переменными во времени параметрами и структурой. Целью данной работы является составление математической модели электромагнитного демпфера, проверка удовлетворительной работы демпфера при заданных начальных условиях и значениях параметров, а также определение границ допустимых значений, тех или иных параметров системы, при которых работа демпфера удовлетворительна. Работа демпфера считается удовлетворительной, если выполняются условия:
а) масса достигает опоры и остаётся лежать на ней без повторных отскоков;
б) скорость в момент удара £ 0,25 скорости, с которой бы произошло соударение при отсутствии демпфера.
1. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
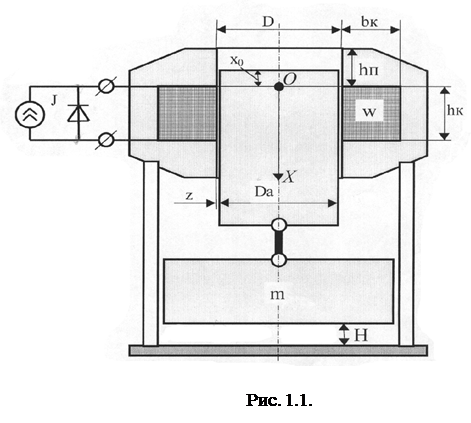
Промоделировать процессы в электромеханической системе, изображенной на рис.1.1., и построить графики зависимости во времени высоты и скорости груза, тока катушки, магнитной индукции в сердечнике при заданных значениях параметров:
Диаметр расточки: в = 0,06 м;
Зазор на сторону: z = 1мм;
Размеры катушки: hk
= 3 см;
bk
= 3см;
Диаметр провода: dпр
= 1,2 мм;
Число витков: w = 397;
Удельное сопротивление провода: r = 1,78×10-8
Ом×м;
Масса груза: m = 30 кг;
Высота груза над опорой: H = 20 мм;
Начальная скорость груза: Vo
= 0 м/с;
Начальное положение сердечника относительно катушки: хо
= -15 мм;
Ток источника: J = 3,4 А.
Построить график зависимости посадочной скорости груза (в момент удара об опору) от высоты груза Н и положения хо
. По построенным зависимостям определить диапазон допустимых значений Н и положения хо
, при которых достигается удовлетворительное демпфирование.
Исследуемая электромеханическая система.
2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
Электромеханическая система на рис. 1.1. представляет собой электромагнитный демпфер, который нужен для снижения скорости движущейся массы перед ударом. В исходном состоянии масса m поднята над опорой на высоту H. Предоставленная самой себе масса начинает двигаться в поле силы тяжести и падает на опору. Удар считается абсолютно неупругим (вся кинетическая энергия теряется). Для снижения энергии удара с массой m жёстко связан якорь электромагнитного демпфера. Индуктор с катушкой закреплёны неподвижно относительно опоры. Катушка подключена к схеме питания. Положение индуктора подобрано таким образом, что при подлёте массы к опоре электромагнитная сила, развиваемая демпфером, резко возрастает, в результате чего скорость падения массы и энергия удара снижается.
Для упрощения математической модели приняли следующие допущения:
Магнитная проницаемость стали равна бесконечности: mст
= ¥;
Электропроводность равна нулю: rст
= 0.
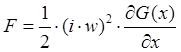
i - ток в катушке;
w - число витков в катушке;
G(x) - зависимость проводимости магнитной цепи от положения сердечника.
При таких допущениях магнитную цепь считаем линейной и электромагнитную силу направленную по оси ОХ на рис.1.1. определили по формуле:
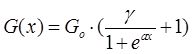 Для построения графика функции G(x) приняли, что сердечник имеет координату x=0 тогда, когда его верхний торец расположен на уровне верхнего края катушки. Поскольку аналитическое определение зависимости G(x) представляет собой сложную задачу, а погрешность расчёта магнитных цепей велика, то зависимость G(x) аппроксимировали аналитической функцией вида: Для построения графика функции G(x) приняли, что сердечник имеет координату x=0 тогда, когда его верхний торец расположен на уровне верхнего края катушки. Поскольку аналитическое определение зависимости G(x) представляет собой сложную задачу, а погрешность расчёта магнитных цепей велика, то зависимость G(x) аппроксимировали аналитической функцией вида:
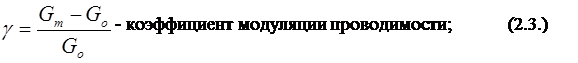 где где
 |
| - магнитная проводимость полная при
введенном якоре;
|
|
|
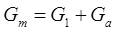 |
 |
|
|
График G(x) приведен на рис. 2.1.
Также нашли аналитические выражения для Ba - средняя индукция якоря, формула (2.9.) и Y - потокосцепление, формула (2.10.):
Соотношения 2.2. – 2.10. использовали далее при математическом моделировании электромагнитного демпфера.
На рис.2.2 приведена электрическая схема питания обмотки демпфера. В начальный момент времени диод VD закрыт и ток источника тока J бежит по обмотке демпфера. В некоторый момент времени, когда напряжение на диоде достигнет порогового, диод откроется. Энергия запасенная в обмотке демпфера будет уменьшаться, так как образуется короткозамкнутый контур. Ток через диод будет также уменьшаться, а так как сила пропорциональна току, то будет
График функции G(x).
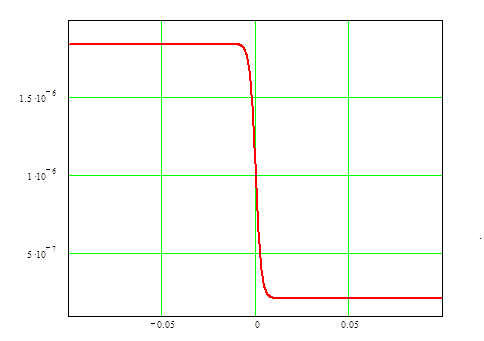 Схема питания обмотки демпфера. Схема питания обмотки демпфера.
уменьшаться и сила, то есть и скорость груза. Анализировали переходные процессы методом припасовывания. Согласно данному методу весь период работы схемы разбивается на отдельные "интервалы линейности", каждый из которых описывается линейной системой дифференциальных уравнений (ДУ). Припасовывание заключается в стыковке полученных численных решений, причём значения переменных состояния, полученные в конце n - го интервала, используются как начальные значения этих же переменных состояния для (n+1) - го интервала. Зная, что количество ключевых элементов в схеме определяет количество интервалов линейности, а для исследуемой схемы этих элементов 2, диод и контакт между грузом и опорой, определили количество интервалов линейности. Получили четыре возможных интервала линейности. Для упорядочения состояний ввели логические переменные:
«0» - если диод закрыт;
«1» - если диод открыт;
«0» - если контакта нет;
«1» - если контакт есть.
Определили номер состояния по формуле:
n = VD + 2Cont. (2.11.)
Для каждого из состояний получили математическую модель в виде системы дифференциальных уравнений и системы условий, определяющих нахождение системы в этом состоянии. Переменными состояния являются потокосцепление, скорость движения груза относительно опоры и координата сердечника. Перед началом численного интегрирования им присваивали начальные значения, взятые из предыдущего состояния. Также составили условия перехода от одного состояния к другому.
Составили математические модели для состояний исследуемой системы:
Состояние n = 0 (диод закрыт, контакта между грузом и опорой нет). Данное состояние описывается системой дифференциальных уравнений 2.12. Условиями перехода от этого состояния к другим являются неравенства 2.13 – 2.14. Схема замещения для этого состояния показана на рис. 2.3.
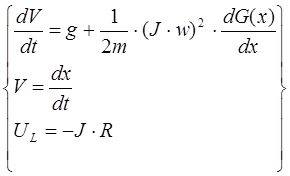 Условие открытия диода:
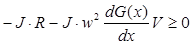 Условие летящего груза:
Если выполняются условия 2.13 - 2.14, то схема переходит к состоянию n=1 (открылся диод, контакта нет).
Состояние n=1 (диод открыт, контакта нет). Данное состояние описывается системой дифференциальных уравнений 2.15. Условиями перехода от этого состояния к другим являются неравенства 2.16 и 2.17. Схема замещения для этого состояния показана на рис.2.4.
Условие закрытия диода:
Схема замещения для состояния n=0.
Схема замещения для состояния n=1.
Условие груза лежащего на опоре:
Если выполняются условия 2.16 и 2.17, тогда схема переходит к состоянию n=2.
Состояние n=2 (диод заперт, контакт есть). Данное состояние описывается уравнением 2.18. Схема замещения для данного состояния показана на рис. 2.3.
IL
= J (2.18.)
Если система пришла в данное состояние, то ни в какое другое состояние она уже перейти не может, то есть переход системы в данное состояние означает завершение её работы.
Состояние n=3 (диод открыт, контакт есть). Данное состояние описывается уравнением 2.19. Условиями перехода от этого состояния к другим будут неравенства 2.14 и 2.16. Схема замещения для данного состояния показана на рис.2.4.
Получены системы дифференциальных уравнений (СДУ) для всех состояний исследуемой системы. Перед началом численного интегрирования переменным состояния, входящим в эти СДУ, присваивали начальные значения переменных состояния из предыдущего состояния.
3. КОРРЕКЦИЯ ТОЧЕК СТЫКОВКИ
Точный момент переключения из одного состояния в другое можно определить достижением точного равенства в условиях переключения. Однако при численном интегрировании условия переключения проверяются не в каждый момент времени, а дискретно, то есть с каким - то шагом интегрирования. Поэтому добиться точного равенства в условиях переключения практически невозможно. Для уменьшения ошибки определения момента переключения и, соответственно, ошибки определения начальных условий для следующего состояния можно уменьшить шаг интегрирования. Однако, это приводит к возрастанию времени расчёта и возрастанию погрешности округления.
В данной работе использован следующий подход. Пусть условие переключения выглядит следующим образом:
Р £ 0,
где Р - это критерий переключения;
Пусть на к - ом шаге интегрирования Рк
> 0, а на к +1 - ом шаге Рк
< 0. В этом случае очевидно, что точный момент переключения находится между рассматриваемыми моментами времени tк
и tк+1
:
tк
= k × h (3.1.)
tк+1
= (k + 1) × h (3.2.)
где h - это шаг интегрирования.
Предположим, что параметр Р изменяется линейно (рис.3.1), из подобия треугольников находим:
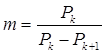 t* = tк
+ mh (3.3.) t* = tк
+ mh (3.3.)
где (3.4.)
m - коэффициент деления шага интегрирования.
Аналогично должны быть уменьшены приращения, полученные всеми переменными состояния на к+1 - ом шаге интегрирования:
График определения момента переключения.
(3.5.)
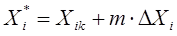
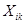 - значение i - ой переменной состояния в момент времени tк
; - значение i - ой переменной состояния в момент времени tк
;
DXi
- приращение i - ой переменной состояния на k+1 - ом шаге интегрирования;
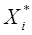 - точное значение i - ой переменной состояния в момент переключения. - точное значение i - ой переменной состояния в момент переключения.
Используя данный подход, удалось существенно снизить погрешность определения начальных условий, причём время расчёта практически не увеличилось.
4. РЕАЛИЗАЦИЯ ЧИСЛЕННЫХ ВЫЧИСЛЕНИЙ И ПОЛУЧЕНИЕ РЕЗУЛЬТАТОВ
Для численного интегрирования систем дифференциальных уравнений полученных в пункте 2 данной работы использовали метод Кутта-Мерсона. Данный метод применяется при анализе цепей с вентильными элементами, когда вентильные элементы рассматриваются как идеальные, а исследуемая электромеханическая система содержит такие элементы.
Нижеприведенная программа рассчитывает ток, магнитную индукцию, высоту груза над опорой и скорости ее перемещения. Также данная программа строит графики зависимостей этих величин от времени. При запуске программы ЭВМ предлагает пользователю выбрать рассчитываемую величину и указать диапазон значений в пределах которых будет изменяться выбранная величина. По окончанию работы программа выводит график зависимости выбранной величины от времени. Программу следует запускать столько раз, сколько зависимостей требуется получить.
Графики тока, индукции, скорости и высоты в зависимости от времени приведены на рис. 4.1.- 4.4. Также с помощью данной программы построили графики зависимости скорости в момент удара об опору от Н и Хо
рис.4.5. и 4.6. и определили допустимых значений Н и Хо на уровне 1/4V. Получили диапазоны: по Н – от 18,2 до 22,4 мм; по Хо – от 13,2 до 17,7 мм.
Текст программы представлен ниже. Блок схема изображена на рис.4.7. Основные переменные программы и их назначение приведены в таблице 4.1.
Таблица 4.1.
Таблица идентификаторов.
| Имя переменной
|
Назначение переменной в программе
|
| Cont, VD
|
Логические переменные.
|
| P, i, j, egavga, mode
|
Вспомогательные целочисленные переменные.
|
| dpr, z, rr, w,hp, hk, bk, d, m, R
|
Исходные параметры демпфера заданные в техническом задании.
|
| k1,k2,k3,k4,k5,k11,k22,k33,k44,k55,kk1,kk2,kk3,kk4,kk5,kv,kv2,kv3,kv4,kv5
|
Переменные коэффициенты численного интегрирования.
|
| Ymax, Ymin, Vmax, Vmin, Xmin, Xmax, Fmin, Fmax, bmax, bmin, hmax, hmin
|
Переменные обозначающие диапазон изменения соответствующей величины.
|
| h
|
Шаг интегрирования.
|
| IL, Y, V,X
|
Динамические переменные состояния ЭМД.
|
| Step
|
Момент интегрирования.
|
| Go, gm, g1
|
Магнитные проводимости.
|
Блок-схема программы.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе был исследован электромагнитный демпфера. Были получены зависимости от времени высоты и скорости груза, тока в обмотке и магнитной индукции в сердечнике. При заданных параметрах электромеханической системы достигается удовлетворительное демпфирование, то есть скорость в момент удара массы об опору не превышает ¼ от посадочной скорости массы без демпфера. Удовлетворительное демпфирование достигается лишь в небольшом диапазоне значений Н и Хо, близких к заданным.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Методические указания к выполнению курсовой работы по курсу "Математическое моделирование устройств промышленной электроники на ЭВМ".-ТПИ,1995;
2. Конспект лекций по "Методам математического анализа и расчёта электронных схем".
|