|
Теоретические методы познания в обучении физике
ПОЗНАНИЕ
, воспроизведение в сознании (индивидуальном и коллективном) характеристик объективной реальности. Познание носит социально и культурно опосредованный исторический характер и в большинстве случаев предполагает более или менее ярко выраженное осознание используемых средств и способов познавательной деятельности.
Цикл научного познания
:
наблюдение и анализ фактов " формулировка проблемы " выдвижение гипотезы " теоретический вывод следствий " экспериментальная проверка следствий " установление эмпирических законов " применение теории на практике.
Практика преподавания физики в средней школе показывает, что изучаемый материал лучше усваивается и
учащиеся приобретают необходимые навыки в самостоятельном пополнении знаний, если они глубоко разбираются в сути методов, с помощью которых добываются те
или иные физические знания. Методы познания, используемые и физике, нашли отражение в учебниках по физике и в соответствующих методических руководствах.
МЕТОД
– способ достижения цели, определённым образом, упорядоченная деятельность, средство познания.
Для выбора метода необходимо знать обо всех методах (их возможностях).
Теоретические методы познания в физике
1.
Абстрагирование
2.
Идеализация
3.
Аналогия
4.
Моделирование
5.
Мысленный эксперимент
6.
Гипотеза
1.
Абстрагирование
Абстрагирование
– мысленное отвлечение от ряда свойств предметов (явлений) и отношений между ними, либо выделение существенных свойств и отношений.
Под абстрагированием понимается отвлечение от несущественных в данном исследовании свойств исследуемого объекта или же выделение у объекта свойства или совокупности свойств, которые должны стать предметом самостоятельного исследования. Например, изучая законы взаимодействия электрически заряженных частиц, можно абстрагироваться от гравитационного их взаимодействия, ибо оно во много раз слабее электромагнитного.
Абстрагирование обладает объективной основой. Действительно, явление никогда не вступает одновременно во все возможные для него отношения. Поэтому оно не проявляет одновременно все свои свойства. Тем самым явления как бы абстрагируют сами себя.
Изучать абстрактный объект — это значит изучать модель, в которой интересующие нас свойства реального объекта не затемнены второстепенными свойствами и явлениями.
Всякое научное понятие есть абстракция. Оно всегда абстрагирует какую-либо сторону действительности, которая и фиксируется в понятии. Без абстрагирования теоретическое мышление невозможно. Абстрагирование — это движение мысли в глубь предмета, выделение его существенных моментов.
Вопрос о том, что в объективной действительности выделяется абстрагирующей работой мышления и от чего мышление отвлекается, в каждом конкретном случае решается в прямой зависимости, прежде всего от природы изучаемого объекта и тех задач, которые ставятся практикой, перед исследователем. Так, в механике выделяют массу тел и количественное выражение действующих сил, отвлекаясь от других физических свойств тел.
 Но абстрагирование имеет спой предел, определяемый природой самих вещей, их свойств и отношений. Переход за этот предел ведет к бесплодным идеалистическим спекуляциям. Но абстрагирование имеет спой предел, определяемый природой самих вещей, их свойств и отношений. Переход за этот предел ведет к бесплодным идеалистическим спекуляциям.
Например, если нам надо рассчитать объём воздушного шарика, то нам абсолютно не важно какого он цвета, где его надували, и каким газом он заполнен.
 При определении химических элементов иногда используют фенолфталеин. В данном случае нам важен цвет в который окраситься вещество. Нас не будет интересовать какой объём мы взяли. При определении химических элементов иногда используют фенолфталеин. В данном случае нам важен цвет в который окраситься вещество. Нас не будет интересовать какой объём мы взяли.
2.
Идеализация
Идеализация
, т.е. мысленное конструирование понятий об объектах, не существующих в действительности, но для которых имеются прообразы в реальном мире.
Идеализации широко используются при исследовании законов природы. Дело в том, что во многих случаях для изучения физического закона необходимо исключить из рассмотрения ряд таких свойств и отношений изучаемых физических объектов, без которых эти объекты реально могут существовать, но учет которых заслонил бы существо изучаемого физического процесса. Так, в механике и электродинамике во многих случаях целесообразно отвлечься от размеров объектов и рассматривать соответствующие законы для «материальных точек» и «точечных зарядов», причем в одних случаях «точками» оказываются атомы, а в других планеты солнечной системы.
Формирование у школьников теоретического метода идеализации представляет собой длительный и сложный процесс.
Идеализации в основном предстают перед учащимися в готовом виде без показа в школьном курсе их происхождения. Идеализация предполагает умение не только абстрагировать, но отделять в каждом данном явлении существенное от второстепенного.
Овладение учащимися методом идеализации предполагает определенный мыслительный процесс, который включает целый ряд этапов:
1) выделение среди множества объектов или явлений предмета идеализации;
2) отделение в выделенном объекте или явлении существенных аспектов (свойств) от второстепенных, с учетом того, что идеализация должна служить хорошим приближением реального процесса;
3) доведение выделенного свойства (аспекта) до предельного значения;
4) формулировка этого идеализированного объекта или явления;
5) включение идеализированного объекта в физический закон, теорию и т. д.;
6) использование полученной идеализации
На протяжении курса физики учащиеся неоднократно знакомятся с данным методом теоретического исследования, а это позволяет им усвоить мысль, что умение правильно идеализировать изучаемые процессы и объекты является важным методологическим условием, обеспечивающим успех в их учебной работе.
 Одним из примеров идеализации является понятие материальной точки. На примере учат школьника абстрагироваться от реальных свойств, затемняющих те существенные стороны вещей и явлений, которые изучаются. Если не акцентировать внимание учащихся на том факте, что материальная точка есть идеализация реальных тел, связанная с пренебрежением размерами тела, но обладающая массой и другими характеристиками движения, то может возникнуть опасность, что школьники будут представлять материальную точку только в геометрическом смысле (они и говорят часто: «материальная точка — это точка...»). Одним из примеров идеализации является понятие материальной точки. На примере учат школьника абстрагироваться от реальных свойств, затемняющих те существенные стороны вещей и явлений, которые изучаются. Если не акцентировать внимание учащихся на том факте, что материальная точка есть идеализация реальных тел, связанная с пренебрежением размерами тела, но обладающая массой и другими характеристиками движения, то может возникнуть опасность, что школьники будут представлять материальную точку только в геометрическом смысле (они и говорят часто: «материальная точка — это точка...»).
  Например: рассматривая движение планет Солнечной системы вокруг Солнца их можно считать мат. точками, т.к. их размеры планет малы по сравнению с радиусами их орбит. Но когда предметом рассмотрения является движение автомобиля по поверхности Земли, наши планеты уже нельзя считать мат. точками, сам автомобиль при этом рассматривается, как точка, потому что пройденный им путь много больше его собственных размеров. Когда автомобиль занимает место на автостоянке, его нельзя считать мат. точкой, иначе на любой автостоянке можно было бы уместить бесконечное количество автомобилей. Например: рассматривая движение планет Солнечной системы вокруг Солнца их можно считать мат. точками, т.к. их размеры планет малы по сравнению с радиусами их орбит. Но когда предметом рассмотрения является движение автомобиля по поверхности Земли, наши планеты уже нельзя считать мат. точками, сам автомобиль при этом рассматривается, как точка, потому что пройденный им путь много больше его собственных размеров. Когда автомобиль занимает место на автостоянке, его нельзя считать мат. точкой, иначе на любой автостоянке можно было бы уместить бесконечное количество автомобилей.
3.
Аналогия
Аналогия
– вид умозаключения; выявление свойств одного предмета на основании сходства с другим.
Сравнение (установление сходства и различия между объектами) лежит в основе аналогии. Если обнаруживается, что один из сравниваемых объектов имеет свойства a,
b,
c, а
, а другой a,
b,
c,
d
, то мы можем предположить, что свойство d
присуще и первому объекту, ибо оно не могло появиться вне связи со свойствами a,
b,
c.
Теснейшая связь и взаимозависимость свойств материальных систем являются объективным основание для применения метода аналогии. Аналогичными могут быть, как отдельные свойства, отношения, условия существовании и т. д. Аналогии бывают качественные и количественные. Необходимо учитывать, что общие признаки могут быть абсолютно тождественными и просто сходными. Последнее встречается в большинстве случаев.
Тот факт, что звук и свет сопровождаются одними и теми же явлениями – отражение, преломление, дисперсия, интерференция и др., привёл Гюйгенса к мысли о волновой природе света.
В арсенале дидактических средств у учителя имеются такие аналогии, как рой комаров или дрейф льдин в реке при объяснении движения «электронного газа» в металлах; процесс испарения жидкости при объяснении термоэлектронной эмиссии и др. Знакомя учащихся с этими аналогиями, следует подчеркивать, что речь идет не о процессах единой природы, а о внешнем сходстве или единстве математического аппарата разных по существу явлений.
В зависимости от природа сравниваемых предметов и характера общих признаков умозаключение по аналогии может привести как к истинному, так и к ложному выводу.
Условия успешности применения аналогии являются:
а) сходные признаки объектов должны быть существенными, и их число должно быть максимальным;
б) разные признаки у объектов должны быть несущественными, и их число должно быть минимальным.
 Правильность аналогии всегда проверяется, в конечном счете, практикой (прямо или опосредованно). Ценность аналогии заключается в том, что она ведет к выдвижению гипотез. Правильность аналогии всегда проверяется, в конечном счете, практикой (прямо или опосредованно). Ценность аналогии заключается в том, что она ведет к выдвижению гипотез.
В настоящее время в методике преподавания физики не реализована еще одна аналогия, использование которой позволило бы осуществить единый, обобщенный подход к формированию у школьников понятия о поле. Изучение гравитационного поля (на примере гравитационного поля Земли) позволило бы построить изучение электростатического поля по аналогии с гравитационным (с обращением внимания на принципиальное отличие этих типов взаимодействия: гравитационные силы всегда силы притяжения, электрические же — силы притяжения и отталкивания). Использование этой аналогии облегчит усвоение школьниками таких сложных понятий, как напряженность, потенциал, работа и энергия электрического поля и т. д. Конечно, закон всемирного тяготения (равно как и закон Кулона) опирается на идею дальнодействия — основную идею механической картины мира, однако было бы полезным показать ограниченность этой идеи уже при изучении классической механики, введя здесь предварительные представления о близкодействии (поле). Так можно провести аналогию, что у электромагнитной волны и света скорость распространения является схожей, и свету присуще некоторые корпускулярно-волновые свойства, из чего следует, что свет является электромагнитной волной.
4. Моделирование
Моделирование
– замена исследуемого объекта другим, специально для этого созданного, но сохраняющим характеристики реального объекта, необходимого для изучения. Объекты, которыми заменяется реальный объект, называются моделями
.
Различают идеальные и материальные модели.
Материальная модель может создаваться или из элементов той же физической природы, что и объект (модель самолета), или из элементов другой физической природы (модель сердца — искусственное сердце). Материальная модель объективна как по форме, так и по содержанию.
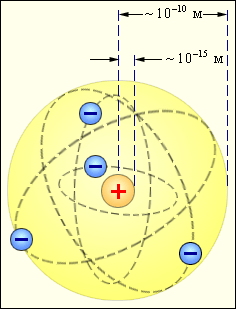
Идеальное моделирование широко распространено в теоретических науках. В физике идеальные модели часто являются наглядно-образными (например, модель атома, предложенная Резерфордом и Бором).
Моделирование обладает принципиальной ограниченностью. Так как модель воспроизводит не все, а лишь некоторые свойства оригинала, то не всякий вопрос может быть выяснен с помощью модели. Так, модель атома Резерфорда в принципе не могла ответить на вопрос, почему атом устойчив. Из таких ситуаций есть только один выход — переход к новым моделям изучаемого объекта. Например, чтобы обосновать устойчивость атома, надо было перейти к модели атома Бора. Это обстоятельство требует одновременно с вводом модели установить и точные границы ее применимости.
Никакое явление не может быть полностью объяснено какой-нибудь одной моделью.
Удачно построенная модель упрощает выводы из известных фактов и позволяет ставить новые опыты, ведущие науку вперед. Однако физическая модель — вовсе но точный образ явления, а упрощенная схематическая картина, основанная на аналогии.
На теоретическом уровне физические объекты исследования — это внутренние определяющие связи в физических явлениях, т. е. основные законы. Единственным способом выражения таких физических объектов служат математические уравнения. Поэтому во всех случаях такие уравнения могут рассматриваться как заменители объекта исследования, т. е, как его идеальные модели.
 Например: модели оптических приборов: Например: модели оптических приборов:
а) Модель глаза.
Выпускаемая промышленностью для кабинетов
анатомии модель глаза может быть использована при изучении оптики в X классе. Сначала демонстрируют модель в собранном виде
(рис. 1), а затем при рассмотрении строения глаза показывают основные оптические его элементы — роговицу, хрусталик, зрачок, стекловидное тело и др.
б) Модель перископа.
Принцип действия зеркального перископа
может быть продемонстрирован на простой модели, собранной из
имеющегося в школьном кабинете оборудования. Для этого берут два
плоских зеркала, закрепляют их в лапки штатива под углом 45°.
Зеркальные поверхности должны быть обращены навстречу друг другу. С помощью полученной модели можно рассматривать различные
предметы.
 в) Модель микроскопа.
Простейшая модель микроскопа (рис. 2) в) Модель микроскопа.
Простейшая модель микроскопа (рис. 2)
может быть продемонстрирована на приборе по геометрической оптике. Для этого на прямоугольном экране сначала устанавливают
малую собирающую линзу с фокусным расстоянием 70 мм, служащую объективом микроскопа. На нее с помощью поворотных зеркал направляют две пары узких пучков света, каждый из которых выходит из одной точки (точки пересечения перед линзой). Наблюдают пересечение этих лучей после прохождения линзы. Затем устанавливают вторую линзу с фокусным расстоянием 140 мм, которая выполняет роль окуляра микроскопа. После прохождения окуляра лучи расходятся, их продолжения дают мнимые изображения первоначальных точек. Обращают внимание учащихся на то, что окуляр действует так же, как и обычная лупа.
г) Модель телескопа.
Модель телескопа собирают аналогично модели микроскопа. Сначала устанавливают длиннофокусную линзу (
F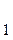 — 140 мм) - объектив, а затем короткофокусную линзу - окуляр (F
2
= 70 мм). Направляют пучки света на объектив и демонстрируют увеличение угла зрения при прохождении света через линзу телескопа.
— 140 мм) - объектив, а затем короткофокусную линзу - окуляр (F
2
= 70 мм). Направляют пучки света на объектив и демонстрируют увеличение угла зрения при прохождении света через линзу телескопа.
- Мысленный эксперимент
Мысленный эксперимент –
анализ ситуации, которую невозможно осуществить реально.
Под мысленным экспериментом понимают специфический вид умственной деятельности, при которой человек в целях познания оперирует модельными представлениями. При этом тот или иной объект ставится мысленно в различные положения, и подбираются такие «экспериментальные» ситуации, в которых, как и в обычном опыте, должны проявиться наиболее важные или почему-либо интересные особенности данного явления.
Мысленный эксперимент строится по типу реального и имеет аналогичную с ним структуру: осознание проблемы исследования, постановка познавательной задачи и разработка ее программы, осуществление эксперимента, проверка результатов.
Можно выделить два основных типа мысленного эксперимента: во-первых, мысленный эксперимент, тесно связанный с реальным, и предшествующий ему; во-вторых, мысленный эксперимент, неосуществимый принципиально на практике (в виде реального эксперимента) в силу оперирования идеализированными объектами.
 Он ведет к глубокому пониманию действительных экспериментов, к установлению новых законов природы и более глубокому проникновению в сущность физических теорий. Он ведет к глубокому пониманию действительных экспериментов, к установлению новых законов природы и более глубокому проникновению в сущность физических теорий.
Мысленные эксперименты условно могут быть разделены на исторические и эксперименты чисто учебного характера, которые предлагают учитель или учащиеся в процессе объяснения какого-либо явления.
Мысленные эксперименты учебного характера применяются, например, при выводе формулы архимедовой силы, действующей на тело кубической формы, полностью погруженное в жидкость (рис. 1); при выводе основного уравнения кинетической теории идеального газа (рис. 2) и т. д.
  Исторические мысленные эксперименты следует излагать, используя хрестоматийный материал: отрывки из сочинений ученых, исторические рисунки и др. Исторические мысленные эксперименты следует излагать, используя хрестоматийный материал: отрывки из сочинений ученых, исторические рисунки и др.
Пример мысленного эксперимента Симона Стевина. Стевин придерживался убеждения о невозможности создания вечного двигателя, т. е. такого механизма, который мог бы давать выигрыш в работе. И закон наклонной плоскости ученый получает, исходя из «золотого правила» механики, являющегося одним из проявлений закона сохранения энергии. Приводим рассуждения Стевина, используя рисунки 3, а, б, несколько видоизмененные по сравнению с историческим.
Если бы сила, действующая на шары, расположенные на плоскости АВ, равнялась их общей силе тяжести, то, так как число шаров на плоскости АВ больше, чем на плоскости ВС, то под действием силы, равной разности сил тяжести, действующих слева и справа, они скатывались бы вниз, заставляя ожерелье непрерывно вращаться против часовой стрелки. Таким образом, можно было бы запустить вечный двигатель, работающий без поступления энергии бесконечно долго. Но ввиду того что вечный двигатель невозможен, сила, действующая на шары, лежащие на плоскости АВ, должна быть меньше их общей силы тяжести. В случае равновесия шаров на наклонной плоскости эта сила должна равняться силе тяжести, действующей на шары, касающиеся плоскости ВС. Та часть 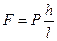 ожерелья, которая свисает ниже основания АС, симметрична относительно АВ и ВС, и ею можно пренебречь (просто отрезать). Можно легко получить соотношение ожерелья, которая свисает ниже основания АС, симметрична относительно АВ и ВС, и ею можно пренебречь (просто отрезать). Можно легко получить соотношение
Так же примером может служить мысленный опыт Галилея при изучении закона инерции.
В качестве примера рассмотрим методику изложения закона инерции, состоящую из двух взаимосвязанных этапов, включающих мысленный эксперимент.
а) Подготовительный этап, связанный с реальным экспериментом. Учащиеся проводят усложненную лабораторную работу по изучению равнопеременного движения.
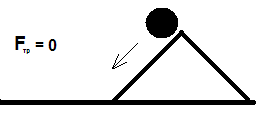 Необходимое оборудование: наклонный желоб, линейка, секундомер, транспортир. Сначала изучают движение шарика по желобу вниз и вверх, выясняют зависимость полученного ускорения от угла наклона желоба. Затем исследуют движение шарика под действием первоначального толчка по желобу, расположенному горизонтально. Делают вывод о причинах ускорения в рассмотренных случаях. Необходимое оборудование: наклонный желоб, линейка, секундомер, транспортир. Сначала изучают движение шарика по желобу вниз и вверх, выясняют зависимость полученного ускорения от угла наклона желоба. Затем исследуют движение шарика под действием первоначального толчка по желобу, расположенному горизонтально. Делают вывод о причинах ускорения в рассмотренных случаях.
б) Этап мысленного экспериментирования. В качестве постановки
проблемы приводят утверждение Аристотеля: для поддержания механического движения обязательно действие силы, причем под действием постоянной силы тело движется с постоянной скоростью, т. е.
равномерно. Прав ли Аристотель? Далее вспоминают описанную выше
лабораторную работу и ее результат: неравномерное движение шарика
обусловлено наклоном желоба и наличием трения между желобом и
шариком. После этого проводят мысленный опыт Галилея.
Представим себе идеально гладкий желоб и такой же идеально гладкий шарик, скатывающийся без трения. Расположим желоб под некоторым углом к горизонту и поместим на него шарик. Спрашивают, в каком состоянии будет находиться шарик, предоставленный самому себе. Обобщая результаты лабораторной работы, учащиеся приходят к выводу, что шарик будет двигаться вниз с постоянным положительным ускорением, скорость его равномерно возрастает. При уменьшении угла наклона желоба ускорение шарика уменьшается, а скорость возрастает медленнее.
^Затем разбирают движение шарика по тому же желобу вверх под действием толчка. Учащиеся сразу заявляют, что в этом случае шарик будет двигаться равнозамедленпо (с отрицательным ускорением), скорость его непрерывно уменьшается. Чем меньше угол наклона желоба, тем медленнее убывает скорость.'
И наконец, рассматривается случай движения шарика по идеально горизонтальному желобу. В этом случае под действием толчка шарик получает некоторую скорость, которая дальше изменяться не будет ни по модулю, ни по направлению (нет причин ни для увеличения, ни для уменьшения скорости). По традиционной методике формулируют закон инерции, приводят примеры его проявления.
- Гипотеза
Гипотеза
– выдвигаемое на основе известных фактов предположение о непосредственно ненаблюдаемых формах связи явлений или внутренних механизмах, обусловливающих эти явления и присущие им формы связи. Гипотеза не просто регистрирует и суммирует известные старые и новые факты, а пытается дать им объяснение, в силу чего ее содержание значительно богаче тех данных, на которые она опирается.
Гипотезы, принципиально не проверяемые, не имеют права на существование в науке (например, гипотеза теплорода, магнитной жидкости), однако они часто стимулируют поиск ученых, наталкивая их на новые эксперименты и, подобно строительным лесам, помогают строить здание физической науки. Учащихся следует познакомить еще с одним свойством научной гипотезы — ее плодотворностью.
Выдвинутая вначале для объяснения одного-единственного явления, гипотеза надежно служит в дальнейшем при исследовании целого ряда процессов. Таковы фундаментальные гипотезы об атомах, о квантах.
Так же примерами могут являться гипотеза Коперника о движении Земли вокруг Солнца, составившая основу гелиоцентрической системы; гипотеза Галилея об одинаковости падения тел в безвоздушном пространстве, получившая простую интерпретацию в механике Ньютона; гипотезы Бора о характере поведения электронов в атоме, включенные в виде постулатов в атомную теорию, и т. д.
 Научная гипотеза как предположительное знание требует своего экспериментального подтверждения, а поэтому должна быть принципиально проверяема. Пусть гипотеза не проверена сегодня (она, например, неактуальна для данного состояния науки, или технический уровень не позволяет это сделать), тогда она будет проверена в будущем, но до этого времени ученые относятся к ней с недоверием и не делают, как правило, эту гипотезу предметом исследования. В истории физики бывали случаи, когда гипотеза ждала своего подтверждения целые столетия (например, гипотеза Гюйгенса о волновых свойствах света, выдвинутая в XVII в., получила экспериментальное подтверждение в XIX в. и т. д.). Гипотеза, не подтвержденная экспериментально, не включается в научное знание. Так, гипотеза Ампера, согласно которой «атомы обтекаются токами», позволила объяснить постоянный магнетизм, но она оставалась гипотезой еще почти 100 лет, пока эксперименты Резерфорда не подтвердили наличие электронной оболочки атома. Научная гипотеза как предположительное знание требует своего экспериментального подтверждения, а поэтому должна быть принципиально проверяема. Пусть гипотеза не проверена сегодня (она, например, неактуальна для данного состояния науки, или технический уровень не позволяет это сделать), тогда она будет проверена в будущем, но до этого времени ученые относятся к ней с недоверием и не делают, как правило, эту гипотезу предметом исследования. В истории физики бывали случаи, когда гипотеза ждала своего подтверждения целые столетия (например, гипотеза Гюйгенса о волновых свойствах света, выдвинутая в XVII в., получила экспериментальное подтверждение в XIX в. и т. д.). Гипотеза, не подтвержденная экспериментально, не включается в научное знание. Так, гипотеза Ампера, согласно которой «атомы обтекаются токами», позволила объяснить постоянный магнетизм, но она оставалась гипотезой еще почти 100 лет, пока эксперименты Резерфорда не подтвердили наличие электронной оболочки атома.
Между теорией и гипотезой, положенной в основу данной теории, нет качественного различия. Гипотеза служит отправной точкой, первой ступенью в построении физической теории. Экспериментальное подтверждение следствий теории является одновременно подтверждением тех основных посылок теории, которые были выдвинуты вначале как гипотезы. Это можно проиллюстрировать при изучении теории всемирного тяготения, теории электромагнитного поля, элементов теории относительности.
В учебном процессе логический процесс формирования гипотезы состоит в ее выводе из ранее изученных законов, теорий, идей. При этом происходит дедуктивная экстраполяция этих знаний на объяснение новых фактов и результатов экспериментальной деятельности учащихся.
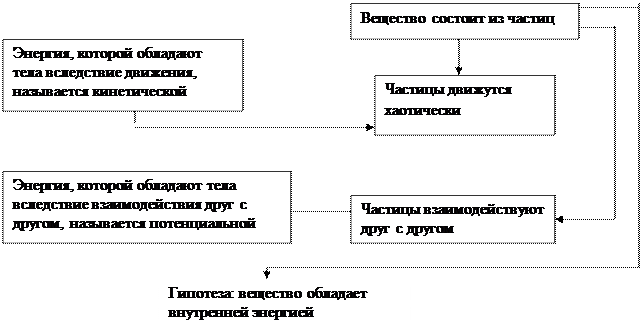 Приведем несколько обобщенных схем, отражающих логику включения гипотезы в процесс объяснения нового материала. Приведем несколько обобщенных схем, отражающих логику включения гипотезы в процесс объяснения нового материала.
|