ВВЕДЕНИЕ
В качестве проводников электрического тока могут быть использованы как твердые тела, так и жидкости, а при соответствующих условиях и газы. Важнейшими практически применяемыми в электротехнике твердыми проводниковыми материалами являются металлы и их сплавы.
Из металлических проводниковых материалов могут быть выделены металлы высокой проводимости, имеющие удельное сопротивление r при нормальной температуре не более 0,05 мкОм×м, и сплавы высокого сопротивления, имеющие r при нормальной температуре не менее 0,3 мкОм×м. Металлы высокой проводимости используются для проводов, токопроводящих жил кабелей, обмоток электрических машин и трансформаторов и т. п. Металлы и сплавы высокого сопротивления применяются для изготовления резисторов, электронагревательных приборов, нитей ламп накаливания и т. п.
К жидким проводникам относятся расплавленные металлы и различные электролиты. Для большинства металлов температура плавления высока; только ртуть, имеющая температуру плавления около минус 39°С, может быть использована в качестве жидкого металлического проводника при нормальной температуре. Другие металлы являются жидкими проводниками при повышенных температурах.
Механизм прохождения тока в металлах — как в твердом, так и в жидком состоянии — обусловлен движением (дрейфом) свободных электронов под воздействием электрического поля; поэтому металлы называют проводниками с электронной электропроводностью или проводниками первого рода. Проводниками второго рода, или электролитами, являются растворы (в частности, водные) кислот, щелочей и солей. Прохождение тока через эти вещества связано с переносом вместе с электрическими зарядами ионов в соответствии с законами Фарадея, вследствие чего состав электролита постепенно изменяется, а на электродах выделяются продукты электролиза. Ионные кристаллы в расплавленном состоянии также являются проводниками второго рода.
Все газы и пары, в том числе и пары металлов, при низких напряженностях электрического поля не являются проводниками. Однако, если напряженность поля превзойдет некоторое критическое значение, обеспечивающее начало ударной и фотоионизации, то газ может стать проводником с электронной и ионной электропроводностью. Сильно ионизированный газ при равенстве числа электронов числу положительных ионов в единице объема представляет собой особую проводящую среду, носящую название плазмы.
1. Электропроводность металлов.
Классическая электронная теория металлов представляет твердый проводник в виде системы, состоящей из узлов кристаллической ионной решетки, внутри которой находится электронный газ из коллективизированных (свободных) электронов. В свободное состояние от каждого атома металла переходит от одного до двух электронов. К электронному газу применялись представления и законы статистики обычных газов. При изучении хаотического (теплового) и направленного под действием силы электрического поля движения электронов был выведен закон Ома. При столкновениях электронов с узлами кристаллической решетки энергия, накопленная при ускорении электронов в электрическом поле, передается металлической основе проводчика, вследствие чего он нагревается. Рассмотрение этого вопроса привело к выводу закона Джоуля—Ленца. Таким образом, электронная теория металлов дала возможность аналитически описать и объяснить найденные ранее экспериментальным путем основные законы электропроводности и потерь электрической энергии в металлах. Оказалось возможным также объяснить и связь между электропроводностью и теплопроводностью металлов. Кроме того, некоторые опыты подтвердили гипотезу об электронном газе в металлах, а именно:
1. При длительном пропускании электрического тока через цепь, состоящую из одних металлических проводников, не наблюдается проникновения атомов одного металла в другой.
2. При нагреве металлов до высоких температур скорость теплового движения свободных электронов увеличивается, и наиболее быстрые из них могут вылетать из металла, преодолевая силы поверхностного потенциального барьера.
3. В момент неожиданной остановки быстро двигавшегося проводника происходит смещение электронного газа по закону инерции в направлении движения. Смещение электронов приводит к появлению разности потенциалов на концах заторможенного проводника, и стрелка подключаемого к ним измерительного прибора отклоняется по шкале.
4. Исследуя поведение металлических проводников в магнитном поле, установили, что вследствие искривления траектории электронов в металлической пластинке, помещенной в поперечное магнитное поле, появляется поперечная ЭДС и изменяется электрическое сопротивление проводника.
Однако выявились и противоречия некоторых выводов теории с опытными данными. Они состояли в расхождении температурной зависимости удельного сопротивления, наблюдаемой на опыте и вытекающей из положений теории; в несоответствии теоретически полученных значений теплоемкости металлов опытным данным. Наблюдаемая теплоемкость металлов меньше теоретической и такова, как будто электронный газ не поглощает теплоту при нагреве металлического проводника. Эти противоречия удалось преодолеть, рассматривая некоторые положения с позиций квантовой механики. В отличие от классической электронной теории в квантовой механике принимается, что электронный газ в металлах при обычных температурах находится в состоянии вырождения. В этом состоянии энергия электронного газа почти не зависит от температуры, т. е. тепловое движение почти не изменяет энергию электронов. Поэтому на нагрев электронного газа теплота не затрачивается, что и обнаруживается при измерении теплоемкости металлов. В состояние, аналогичное обычным газам, электронный газ приходит при температуре порядка тысяч Кельвинов. Представляя металл как систему, в которой положительные ионы скрепляются посредством свободно движущихся электронов, легко понять природу всех основных свойств металлов: пластичности, ковкости, хорошей теплопроводности и высокой электропроводности.
2. Свойства проводников.
К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся:
1) удельная проводимость g или обратная ей величина — удельное сопротивление r,
2) температурный коэффициент удельного сопротивления ТКr
или ar
,
3) коэффициент теплопроводности gт
,
4) контактная разность потенциалов и термоэлектродвижущая сила (термо-ЭДС),
5) работа выхода электронов из металла,
6) предел прочности при растяжении sр
и относительное удлинение перед разрывом Dl/l
.
Удельная проводимость и удельное сопротивление проводников. Связь плотности тока J
(в амперах на квадратный метр) и напряженности электрического поля (в вольтах на метр) в проводнике дается известной формулой:
(дифференциальная форма закона Ома); здесь g (в сименсах на метр) параметр проводникового материала, называемый его удельной проводимостью: в соответствии с законом Ома у металлических проводников не зависит от напряженности электрического поля Е при изменении последней в весьма широких пределах. Величина r = 1/g, обратная удельной проводимости и называемая удельным сопротивлением, для имеющего сопротивление R
проводника длиной l
с постоянным поперечным сечением S
вычисляется по формуле
Удельное сопротивление измеряется в ом-метрах. Для измерения r проводниковых материалов разрешается пользоваться внесистемной единицей Ом×мм2
/м; очевидно, что проволока из материала длиной 1 м с поперечным сечением 1 мм2
имеет сопротивление в омах, численно равно r материала в Ом×мм2
/м.
Диапазон значений удельного сопротивления r металлических проводников (при нормальной температуре) довольно узок: от 0,016 для серебра и до примерно 10 мкОм×м для железохромоалюминиевых сплавов, т.е. он занимает всего три порядка. Удельная проводимость металлических проводников согласно классической теории металлов может быть выражена следующим образом:
| g = (e2
n0
l)/(2mvT
)
|
(2-3)
|
где е —
заряд электрона; n0
— число свободных электронов в единице объема металла; l —
средняя длина свободного пробега электрона между двумя соударениями с узлами решетки; т —
масса электрона; vT
—
средняя скорость теплового движения свободного электрона в металле.
Преобразование выражения (2-3) на основе положений квантовой механики приводит к формуле
где K
— численный коэффициент; остальные обозначения — прежние.
Для различных металлов скорости хаотического теплового движения электронов v
T
(при определенной температуре) примерно одинаковы. Незначительно различаются также и концентрации свободных электронов п0
(например, для меди и никеля это различие меньше 10 %). Поэтому значение удельной проводимости у (или удельного сопротивления r) в основном зависит от средней длины свободного пробега электронов в 
Рис. 2-1. Зависимость удельного сопротивления r меди от температуры
данном проводнике l,
которая, в свою очередь, определяется структурой проводникового материала. Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси, искажая решетку, приводят к увеличению r. К такому же выводу можно прийти, исходя из волновой природы электронов. Рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием около четверти длины электронной волны. Нарушения меньших размеров не вызывают заметного рассеяния волн. В металлическом проводнике, где длина волны электрона около 0,5 нм, микродефекты создают значительное рассеяние, уменьшающее подвижность электронов, и, следовательно, приводит к росту r материала.
Температурный коэффициент удельного сопротивления металлов. Число носителей заряда (концентрация свободных электронов) в металлическом проводнике при повышении температуры практически остается неизменным. Однако вследствие усиления колебаний узлов кристаллической решетки с ростом температуры появляется все больше и больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т. е. уменьшается средняя длина свободного пробега электрона l.
уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов и возрастает удельное сопротивление (рис. 2-1). Иными словами, температурный коэффициент удельного сопротивления металлов, (кельвин в минус первой степени)
| TKr =ar
= (1/r) (d
r/dT
)
|
(2-5)
|
положителен. Согласно выводам электронной теории металлов значения ar
., чистых металлов в твердом состоянии должны быть близки к температурному коэффициенту расширения идеальных газов, т.е. 1/273»0,0037 К-1
. При изменении температуры в узких диапазонах на практике допустима кусочно-линейная аппроксимация зависимости r (Т); в этом случае принимают, что
| r2
= r1
[1+ar
(T2
–T1
)]
|
(2-6)
|
где r1
, и r2
— удельные сопротивления проводникового материала при температурах Т1
, и T2
, соответственно (при этом T2
> Т1
);
ar
— так называемый средний температурный коэффициент удельного сопротивления данного материала в диапазоне температур от Т1
, до Т2
.
Изменение удельного сопротивления металлов при плавлении. При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления r, как это видно, например для меди, из рис. 2-1; однако у некоторых металлов r при плавлении уменьшается. Удельное сопротивление увеличивается при плавлении у тех металлов, у которых при плавлении увеличивается объем, т. е. уменьшается плотность; и, наоборот, у металлов, уменьшающих свой объем при плавлении, — галлия, висмута, сурьмы r уменьшается.
Удельное сопротивление сплавов.
Как уже указывалось, примеси и нарушения правильной структуры металлов увеличивают их удельное сопротивление. Значительное возрастание r наблюдается при сплавлении двух металлов в том случае, если они образуют друг с другом твердый раствор, т. е. при (утверждении совместно кристаллизуются, и атомы одного металла входят в кристаллическую решетку другого.
Теплопроводность металлов.
За передачу теплоты через металл в основном ответственны те же свободные электроны, которые определяют и электропроводность металлов и число которых в единице объема металла весьма велико. Поэтому, как правило, коэффициент теплопроводности gT
металлов намного больше, чем коэффициент теплопроводности диэлектриков. Очевидно, что при прочих равных условиях, чем больше удельная электрическая проводимость у металла, тем больше должен быть и его коэффициент теплопроводности. Легко также видеть, что при повышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость g уменьшаются, отношение коэффициента теплопроводности металла к его удельной проводимости gT
/g должно возрастать. Математически это выражается законом Вчдемана—Франца—Лоренца:
где Т
—термодинамическая температура, К; Lo —число Лоренца, равное
| Lo=(p2
k
2
)/(3e
2
)
|
(2-8)
|
Подставляя в формулу (2-8) значения постоянной Больцмана k
= 1.38 ×10-23
Дж/К и заряда электрона е
= 1,6×10-19
Кл, получаем Lo = 2,45×10-8
B2
K2
.
Термоэлектродвижущая сила.
При соприкосновении двух различных металлических проводников между ними возникает контактная разность потенциалов. Причина появления этой разности потенциалов заключается в различии значений работы выхода электронов из различных металлов, а также в том, что концентрация электронов, а следовательно, и давление электронного газа у разных металлов и сплавов могут быть неодинаковыми. Из электронной теории металлов следует, что контактная разность потенциалов между металлами А
и В
равна
| UAB
=UB
- UA
+ (kT/e) ln (n0A
/n0B
)
|
(2-9)
|
где UA
и UB
—
потенциалы соприкасающихся металлов; n0A
и n0B
— концентрации электронов в металлах А
и В; k —
постоянная Больцмана; e —абсолютная величина заряда электрона.
Если температуры «спаев» одинаковы, то сумма разности потенциалов в замкнутой цепи равна нулю. Иначе обстоит дело, когда один из спаев имеет температуру T1
, а другой —температуру Т2
(
рис. 2-2).

Рис. 2-2. Схема термопары
В этом случае между спаями возникает термо-ЭДС, равная
| U = (k/e) (T1
- T2
) ln (n0A
/n0B
)
|
(2-10)
|
Что можно записать в виде
где y — постоянный для данной пары проводников коэффициент термоЭДС, т. е. термо-ЭДС должна быть пропорциональна разности температур спаев.
Температурный коэффициент линейного расширения проводников.
Этот коэффициент, интересен не только при рассмотрении работы различных сопряженных материалов в той или иной конструкции (возможность растрескивания или нарушения вакуум-плотного соединения со стеклами, керамикой при изменении температуры и т. п.). Он необходим также и для расчета температурного коэффициента электрического сопротивления провода
| TKR
= aR
= ar
- al
|
(2-12)
|
3. Материалы высокой проводимости.
Медь.
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
1) малое удельное сопротивление (из всех материалов только серебро имеет несколько меньшее удельное сопротивление, чем медь);
2) достаточно высокая механическая прочность;
3) удовлетворительная в большинстве случаев стойкость по отношению к коррозии (медь окисляется на воздухе даже в условиях высокой влажности значительно медленнее, чем, например, железо; интенсивное окисление меди происходит только при повышенных температурах);
4) хорошая обрабатываемость (медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра);
5) относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После нескольких плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехники, обязательно проходит процесс электролитической очистки. Полученные после электролиза катодные пластины меди переплавляют в болванки массой 80—90 кг, которые прокатывают и протягивают в изделия требующегося поперечного сечения. При изготовлении проволоки болванки сперва подвергают горячей прокатке в так называемую катанку диаметром 6,5—7,2 мм; затем катанку протравливают в слабом растворе серной кислоты, чтобы удалить с ее поверхности оксид меди СuО, образующийся при нагреве, а затем уже протягивают без подогрева в проволоку нужных диаметров — до 0,03—0,02 мм.
Стандартная медь, в процентах по отношению к удельной проводимости которой иногда выражают удельные проводимости металлов и сплавов, в отожженном состоянии при 20 °С имеет удельную проводимость 58 МСм/м, т. е. r = 0,017241 мкОм×м. Твердую медь употребляют там, где надо обеспечить особо высокую механическую прочность, твердость и сопротивляемость истиранию (для контактных проводов, для шин распределительных устройств, для коллекторных пластин электрических машин и пр.). Мягкую медь в виде проволок круглого и прямоугольного сечения применяют главным образом в качестве токопроводящих жил кабелей и обмоточных проводов, где важна гибкость и пластичность (не должна пружинить при изгибе), а не прочность. Медь является сравнительно дорогим и дефицитным материалом. Поэтому она должна расходоваться весьма экономно. Отходы меди на электротехнических предприятиях необходимо тщательно собирать; важно не смешивать их с другими металлами, а также с менее чистой (не электротехнической) медью, чтобы можно было эти отходы переплавить и вновь использовать в качестве электротехнической меди. Медь как проводниковый материал все шире заменяется другими металлами, в особенности алюминием.
Сплавы меди
. В отдельных случаях помимо чистой меди в качестве проводникового материала применяются ее сплавы с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз,
при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь: sр
бронз может быть 800—1200 МПа и более. Бронзы широко применяют для изготовления токопроводящих пружин и т. п. Введение в медь кадмия при сравнительно малом снижении удельной проводимости значительно повышает механическую прочность и твердость. Кадмиевую бронзу
применяют для контактных проводов и коллекторных пластин особо ответственного назначения. Еще большей механической прочностью обладает бериллиевая бронза
(sр
—до 1350 МПа). Сплав меди с цинком — латунь —
обладает достаточно высоким относительным удлинением перед разрывом при повышенном по сравнению с чистой медью пределе прочности при растяжении. Это дает латуни технологические преимущества перед медью при обработке штамповкой, глубокой вытяжкой и т. п. В соответствии с этим латунь применяют в электротехнике для изготовления всевозможных токопроводящих деталей.
Алюминий
является вторым по значению (после меди) проводниковым материалом. Это важнейший представитель так называемых легких металлов (т. е. металлов с плотностью менее 5 Мг/м3
); плотность литого алюминия около 2,6, а прокатанного —2,7 Мг/м3
. Таким образом, алюминий приблизительно в 3,5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата теплоты, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами — как механическими, так и электрическими. При одинаковых сечении и длине электрическое сопротивление алюминиевого провода больше, чем медного, в 0,028 : 0,0172 = 1,63 раза. Следовательно, чтобы получить алюминиевый провод такого же электрического сопротивления, как и медный, нужно взять его сечение в 1,63 раза большим, т. е. диаметр должен быть в » 1,3 раза больше диаметра медного провода. Отсюда понятно, что если ограничены габариты, то замена меди алюминием затруднена. Если же сравнить по массе два отрезка алюминиевого и медного проводов одной длины и одного и того же сопротивления, то окажется, что алюминиевый провод хотя и толще медного, но легче его приблизительно в два раза:
8,9/(2,7×1,63) »2.
Поэтому для изготовления проводов одной и той же проводимости при данной длине алюминий выгоднее меди в том случае, если тонна алюминия дороже тонны меди не более чем в два раза. Весьма важно, что алюминий менее дефицитен, чем медь.
Для электротехнических целей используют алюминий, содержащий не более 0,5 % примесей, марки А1. Еще более чистый алюминий марки АВОО (не более 0,03 % примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов оксидных конденсаторов.
Алюминий наивысшей чистоты АВОООО имеет содержание примесей, не превышающее 0,004 %. Разные примеси в различной степени снижают удельную проводимость g алюминия. Добавки Ni, Si, Zn или Fe при содержании их 0,5 % снижают y отожженного алюминия не более чем на 2—3 %. Более заметное действие оказывают примеси Сu, Ag и Mg, при том же массовом содержании снижающие v алюминия на 5—10 %. Очень сильно снижают g алюминия добавки Ti и Мп.
Прокатка, протяжка и отжиг алюминия аналогичны соответствующим операциям над медью. Из алюминия может прокатываться тонкая (до 6—7 мкм) фольга, применяемая в качестве электродов бумажных и пленочных конденсаторов.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет алюминий от дальнейшей коррозии, но создает большое переходное сопротивление в местах контакта алюминиевых проводов и делает невозможной пайку алюминия обычными методами. Для пайки алюминия применяются специальные пасты-припои или используются ультразвуковые паяльники. В местах контакта алюминия и меди возможна гальваническая коррозия. Если область контакта подвергается действию влаги, то возникает местная гальваническая пара с довольно высоким значением ЭДС, причем полярность этой пары такова, что на внешней поверхности контакта ток идет от алюминия к меди и алюминиевый проводник может быть сильно разрушен коррозией. Поэтому места соединения медных проводников с алюминиевыми должны тщательно защищаться от увлажнения (покрытием лаками и тому подобными способами).
Иногда, например для замены свинца в защитных кабельных обо
лочках, используется алюминий с содержанием примесей не более
0,01 % (вместо 0,5 % для обычного проводникового алюминия).
Такой особо чистый алюминий сравнительно с обычным более мягок
и пластичен и притом обладает повышенной стойкостью по отношению к коррозии.
Алюминиевые сплавы
обладают повышенной механической прочностью. Примером такого сплава является альдрей
содержащий 0,3-0,5 % Mg, 0,4-0,7 % Si и 0,2-0,3 % Fe (остальное Аl). Высокие механические свойства альдрей приобретает после особой обработки (закалки катанки—охлаждение в воде при температуре 510—550°С волочение и последующая выдержка при температуре около 150 °С). В альдрее образуется соединение Mg2
Si, которое сообщает высокие механические свойства сплаву; при указанной выше тепловой обработке достигается выделение MgoSi из твердого раствора и перевод его в тонкодисперсное состояние.
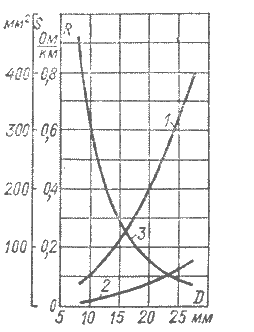
Рис. 3-1. Зависимость полного сечения сталеалюминиевого провода марки АС (кривая 1), сечения стального сердечника (кривая 2) и активного электрического сопротивления (при частоте 50 Гц) единицы длины провода (кривая 3) от внешнего диаметра провода D
Сталеалюминиевый провод, широко применяемый в линиях электропередачи, представляют собой сердечник, свитый и из стальных жил и обвитый снаружи алюминиевой проволокой. В проводах такого типа механическая прочность определяется главным образом стальным сердечником, а электрическая проводимость — алюминием. Увеличенный наружный диаметр сталеалюминиевого провода по сравнению с медным на линиях передачи высокого напряжения является преимуществом, так как уменьшается опасность возникновения короны вследствие снижения напряженности электрического поля на поверхности провода. На рис. 3-1 приведены некоторые характеристики сталеалюминиевого провода марки АС.
Железо (сталь) как
наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление r (около 0,1 мкОм-м); значение r стали, т. е. железа с примесью углерода и других элементов, еще выше.
При пер еменном токе в стали как в ферромагнитном материале заметно сказывается поверхностный эффект,
поэтому в соответствии с известными законами электротехники активное сопротивление стальных проводников переменному току выше, чем постоянному току. Кроме того, при переменном токе в стальных проводниках появляются потери мощности на гистерезис. В качестве проводникового материала обычно применяется мягкая сталь с содержанием углерода 0,10—0,15 %, имеющая предел прочности при растяжении sр
=700—750 МПа, относительное удлинение перед разрывом Dl
/l
= 5 —8 % и удельную проводимость g ,
в б—7 раз меньшую по сравнению с медью. Такую сталь используют в качестве материала для проводов воздушных линий при передаче небольших мощностей. В подобных случаях применение стали может оказаться достаточновыгодным, так как при малой силе тока сечение провода определяется не электрическим сопротивлением, а его механической прочностью.
Сталь как проводниковый материал используется также в
виде шин, рельсов трамваев, электрических железных дорог (включая «третий рельс» метро) и пр. Для сердечников сталеалюминиевых проводов воздушных линий электропередачи (см. выше) применяется особо прочная стальняя проволока, имеющая ар
=1200—1500 МПа и Dl
/l
= 4—5 %. Обычная сталь обладает малой стойкостью к коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком. Непрерывность слоя цинка проверяется опусканием образца провода в 20 %-ный раствор медного купороса; при этом на обнаженной стали в местах дефектов оцинковки откладывается медь в виде красных пятен, заметных на общем сероватом фоне оцинкованной поверхности провода. Железо имеет высокий температурный коэффициент удельного сопротивления. Поэтому тонкую железную проволоку, помещенную для защиты от окисления в баллон, заполненный водородом или иным химическим неактивным газом, можно применять в бареттерах,
т. е. в приборах, использующих зависимость сопротивления от силы тока, нагревающего помещенную в них проволочку, для поддержания постоянства силы тока при колебаниях напряжения.
Биметалл. В некоторых случаях для уменьшения расходов цветных металлов в проводниковых конструкциях выгодно применять так называемый проводниковый биметалл.
Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно по всей поверхности их соприкосновения. Для изготовления биметалла применяют два способа: горячий
(стальную болванку ставят в форму, а промежуток между болванкой и стенками формы заливают расплавленной медью; полученную после охлаждения биметаллическую болванку подвергают прокатке и протяжке) и холодный,
или электролитический
. Холодный способ обеспечивает равномерность толщины медного покрытия, но требует значительного расхода электроэнергии; кроме того, при холодном способе не обеспечивается столь прочное сцепление слоя меди со сталью, как при горячем способе.
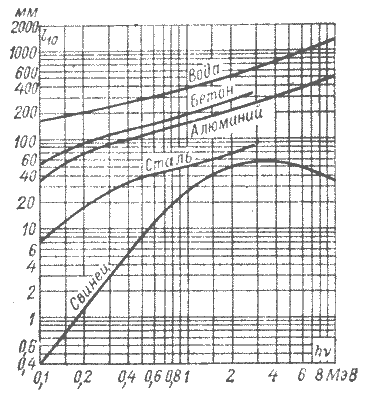
Рис. 3-2. Слои десятикратного ослабления для различных материалов в зависимости от энергии квантов излучения
Биметалл имеет механические и электрические свойства, промежуточные между свойствами сплошного медного и сплошного стального проводника того же сечения; прочность биметалла больше, чем меди, но электрическая проводимость меньше. Расположение меди в наружном слое, а стали внутри конструкции, а не наоборот, весьма важно: с одной стороны, при переменном токе достигается более высокая проводимость всего провода, в целом, с другой — медь защищает расположенную под ней сталь от коррозии. Биметаллическая проволока выпускается наружным диаметром от 1 до 4 мм содержанием меди не менее 50 % полной массы проволоки. Значение Стр (из расчета на полное сечение проволоки) должно быть не менее 550—700 МПа, а Dl
/l
не более 2 %. Сопротивление 1 км биметаллической проволоки постоянному току (при 20 °С) в зависимости от диаметра от 60 (при 1 мм) до 4 Ом/км (при 4 мм).
Такую проволоку применяют для линий связи, линий электропередачи и т. п. Из проводникового биметалла изготовляются шины для распределительных устройств, полосы для рубильников и различные токопроводящие части электрических аппаратов.
Защитные свойства стали от излучений высокой энергии приведены на рис. 3-2.
4. Сверхпроводники и криопроводники
В 1911 г. нидерландский физик X. Камерлинг-Оннес, незадолго перед тем (в 1908 г.) впервые получивший жидкий гелий (гелий был последним газом, который до того еще не удавалось перевести в жидкое состояние), исследовал электропроводность металлов при «гелиевых» температурах (температура сжижения гелия при нормальном давлении около 4,2 К; еще более низкие температуры могут быть получены при испарении жидкого гелия). При этом Камерлинг-Оннес сделал поразительное открытие: он обнаружил, что при охлаждении до температуры, примерно равной температуре сжижения гелия, сопротивление кольца из замороженной ртути внезапно, резким скачком падает до чрезвычайно малого, не поддающегося измерению, значения.
Такое явление, т. е. наличие у вещества практически бесконечной удельной проводимости, было названо сверхпроводимостью, температура Тс
, при охлаждении до которой вещество переходит в сверхнроводящее состояние, — температурой сверхпроводящего перехода, а вещества, переходящие в сверхпроводящие состояние, — сверхпроводниками.
Переход в сверхпроводящее состояние является обратимым; при повышении температуры до значения Тс
сверхпроводимость нарушается и вещество переходит в нормальное состояние с конечным значением удельной проводимости g .
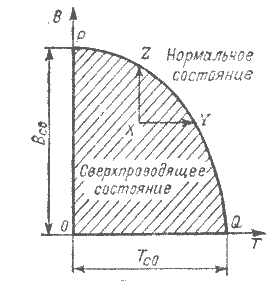
Рис. 4-1. Общий вид диаграммы состояния сверхпроводника первого рода
В настоящее время известно уже 35 сверхпроводниковых металлов и более тысячи сверхпроводниковых сплавов и химических соединений различных элементов. В то же время многие вещества, в том числе и такие, обладающие весьма малыми значениями r при нормальной температуре металлы, как серебро, медь, золото, платина и другие, при наиболее низких достигнутых в настоящее время температурах (около милликельвина) перевести в сверхпроводящее состояние не удалось.
Явление сверхпроводимости связано с тем, что электрический ток, однажды наведенный в сверх проводящем контуре, будет длительно (годами) циркулировать по этому контуру без заметного уменьшения своей силы, и притом без всякого подвода энергии извне (конечно, если не учитывать неизбежного расхода энергии на работу охлаждающего устройства, которое должно поддерживать температуру сверхпроводящего контура ниже значения Тс
, характерного для данного сверхпроводникового материала); такой сверхпроводящий контур создает в окружающем пространстве магнитное поле, подобно постоянному магниту. Поэтому обтекаемый электрическим током сверх проводящий соленоид должен представлять собой сверхпроводниковый электромагнит, не требующий питания от источника тока. Однако первоначальные попытки изготовить практически пригодный сверхпроводниковый электромагнит, создающий в окружающем пространстве магнитное поле с достаточно высокими напряженностью Н и магнитной индукцией В, закончились неудачей. Оказалось, что сверхпроводимость нарушается не только при повышении температуры до значений, превышающих Тс
, но и при возникновении на поверхности сверхпроводника магнитного поля с магнитной индукцией, превышающей индукцию перехода В0
(в первом приближении, по крайней мере для чистых сверхпроводниковых металлов, безразлично, создается ли индукция Вс
током, идущим по самому сверхпроводнику, или же сторонним источником магнитного поля). Это поясняется диаграммой состояния сверхпроводника, изображенной на рис. 4-1. Каждому значению температуры Т данного материала, находящегося в сверх проводящем состоянии, соответствует свое значение индукции перехода Вс
. Наибольшая возможная температура перехода Тс
(критическая температура) данного сверхпроводникового материала достигается при ничтожно малой магнитной индукции, т. е. для сверхпроводникового электромагнита — при весьма малой силе тока, идущего через обмотку этого электромагнита. Соответственно и наибольшее возможное значение Вс0
магнитной индукции перехода (критическая магнитная индукция) соответствует температуре сверхпроводника, ничтожно отличающейся от нуля Кельвина.
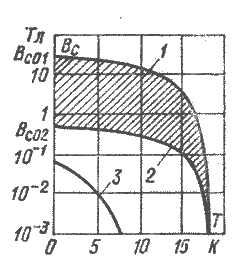
Рис. 4-2. Диаграммы состояния сверхпроводника II рода — станнида ниобия Nb3
Sn (кривые 1 и 2) и сверхпроводника I рода — свинца РЬ (кривая 3)
В 50-х годах нашего столетия были открыты новые сверхпроводники, представляющие собой уже не чистые металлы, а сплавы или химические соединения. Эти сверхпроводники в отличие от чистых сверх проводниковых металлов (сверхпроводников I рода),
названные сверхпроводниками II рода,
обладают рядом особенностей. Переход из нормального в сверх проводящее состояние при охлаждении у них происходит не скачком (как у сверхпроводников I рода), а постепенно; у них существует промежуточное состояние между нижним ВС1
и верхним BС2
значениями критической магнитной индукции перехода для значений температур Т < TС0
. В промежуточном состоянии сверхпроводимость при постоянном напряжении сохраняется, т. е. r = 0, но относительная магнитная проницаемость сверхпроводника mr
> 0; при воздействии на сверхпроводник переменного напряжения в нем наблюдаются некоторые потери энергии и т. п. Кроме того, свойства сверхпроводников II рода в большой степени зависят от технологического режима изготовления и т. п. Из чистых металлов к сверхпроводникам II рода относятся лишь ниобий Nb, ванадий V и технеций Тс.
На рис. 4-2 представлена диаграмма состояния типичного сверхпроводника II рода — интерметаллического соединения, стан-нида ниобия Nb3
Sn. Кривая 1 дает значения BС01
, кривая 2—
значения ВC02
; заштрихована область промежуточного состояния. Для сопоставления здесь же приведена диаграмма состояния для типичного сверхпроводника I рода—свинца Рb.
Криопроводники.
Помимо явления сверхпроводимости, в современной электротехнике все шире используется явление криопроводимости, т. е. достижение металлами весьма малого значения удельного сопротивления при криогенных температурах (но без перехода в сверхпроводящее состояние). Металлы, обладающие таким свойством, называются криопроводниками.
Очевидно, что физическая сущность криопроводимости не сходна с физической сущностью явления сверхпроводимости. Криопроводимость — частный случай нормальной электропроводности металлов в условиях криогенных температур.
Весьма малое, но все же конечное значение r криопроводников ограничивает допустимую плотность тока в них, хотя эта плотность может быть все же гораздо выше, чем в обычных металлических проводниках при нормальной или повышенной температуре. Криопроводники, у которых при изменении температуры в широком диапазоне р меняется плавно, без скачков, не могут использоваться в устройствах, действие которых основано на триггерном эффекте возникновения и нарушения сверхпроводимости (например, в сверхпроводниковых запоминающих устройствах).
Применение криопроводников вместо сверхпроводников в электрических машинах, аппаратах и других электротехнических устройствах может иметь свои преимущества. Использование в качестве хладагента жидкого водорода или жидкого азота (вместо жидкого гелия, который значительно дороже других хладагентов) упрощает и удешевляет выполнение тепловой изоляции устройства и уменьшает расход мощности на охлаждение. Кроме того, в сверхпроводящем контуре с большим током накапливается большое количество энергии магнитного поля, равное LI2
/2 Дж (L —
индуктивность, Гн; I —ток, А). При случайном повышении температуры или магнитной индукции свыше значений, соответствующих переходу сверхпроводника в нормальное состояние хотя бы в малой части сверхпроводящего контура, сверхпроводимость будет нарушена, что приведет к внезапному освобождению большого количества энергии. Для криопроводящей цепи такой опасности нет, так как повышение температуры может повлечь за собой лишь постепенное, плавное увеличение сопротивления. Наибольший интерес для применения в качестве криопроводникового материала представляют собой: при температуре жидкого водорода — алюминий, а при температуре жидкого азота —бериллий.
Таким образом, проблема выбора оптимального (т. е. имеющего при рабочей температуре наименьшее удельное сопротивление при наилучших других технико-экономических показателях) криопроводникового материала сводится в основном к следующему: применить легко доступный и дешевый алюминий и получить наименьшее возможное для криопроводника значение удельного сопротивления, но пойти на использование для охлаждения устройства жидкого водорода, что все же требует преодоления некоторых затруднений и, в частности, необходимости учета взрывоопасности водородо-воздушной смеси; или же применять более дорогой, дефицитный, сложный в технологическом отношении бериллий, но зато использовать в качестве хладагента более дешевый и легко доступный жидкий азот и тем самым уменьшить затраты мощности на охлаждение.
Во всех случаях для получения высококачественных криопроводннков требуются исключительно высокая чистота металла (отсутствие примесей) и отсутствие наклепа (отожженное состояние). Вредное влияние примесей и наклепа на удельное сопротивление металлов при криогенных температурах выражено значительно более сильно, чем при нормальной температуре.
ЛИТЕРАТУРА
1. Боородицкий Н. П. Электротехнические материалы.- Л.: Энергоатомиздат, 1985
2. Проводниковые материалы / Под ред. Л. Ш. Казарновского. –М.: Энергия, 1970
3. Методические разработки к курсам “Конструкционные Материалы” и “Материаловедение” / Под ред. А. А. Клыпина. –М.: Издательство МАИ, 1993
4. Учебное пособие к лабораторным работам по металловедению. /Под ред. О. Х. Фаткуллина.- М.: Издательство МАИ
|