Лабораторная работа: Изучение вращательного и поступательного движений на машине Атвуда
|
Название: Изучение вращательного и поступательного движений на машине Атвуда Раздел: Рефераты по физике Тип: лабораторная работа | |||||||||||||||||||||||||||||||||||||||||||||||||
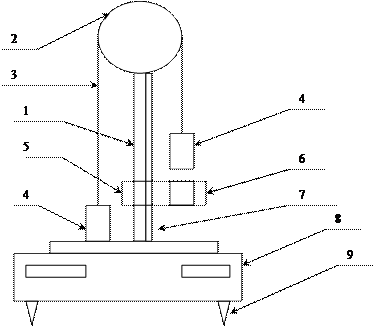
| Федеральное Агентство по образованию ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра физики ОТЧЕТ Лабораторная работа по курсу "Общая физика" ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЙ НА МАШИНЕ АТВУДА Преподаватель Студент группы Ф-1-108 ___________ /А.В. Гураков / __________ /Лузина С.И. / ___________2009 г. 31 марта 2009 г. 2009 1. ЦЕЛЬ РАБОТЫ Целью настоящей работы является изучение основных законов динамики поступательного и вращательного движений твердых тел, экспериментальное определение момента инерции блока и сравнение его с расчетным значением. 2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА Схема экспериментальной установки на основе машины Атвуда приведена на рис. 3.1. На вертикальной стойке 1 крепится массивный блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы, равной 80 г. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. Риска на корпусе среднего кронштейна совпадает с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положение грузов. За начальное, принимают положение нижнего среза груза, за конечное - риску на корпусе среднего кронштейна. Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Опоры 9 используют для регулировки положения установки на лабораторном столе. Принцип работы машины Атвуда заключается в следующем. Когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если же на один из грузов (обычно на правый) положить перегрузок, то система выйдет из равновесия, и грузы начнут двигаться с ускорением. Машина Атвуд а
1 – стойка; 2 – блок; 3 – нить; 4 – грузы; 5 – средний кронштейн; 6 – фотодатчик; 7 – линейка; 8 – миллисекундомер; 9 – регулировочная опора. Рис. 3.1 3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Случайная погрешность: Коэффициент Стьюдента: t = 2,1 (доверительная вероятность a=0,9 Среднеквадратичное отклонение: σ(t)сис – систематическая погрешность (погрешность измерительного прибора в данном случае милисекундомера). σ(t)сис = 1мс = 0,001с Общая погрешность измерений: Расчет погрешности измерений t2 : σ(t2 )=2t σ(t) (3,4) Момент инерции блока Масса блока m = Vp, где p-плотность латунного блока 8400кг/м3 (3,6)
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ. Измеренные значения и результаты их обработки приведены в таблице. Таблица Результаты измерений времени прохождения груза
1. Случайная погрешность. По формуле 3,1, где t=2,1 (доверительная вероятность a=0,9) Среднеквадратичное отклонение по формуле 3,2
σ(<t>) =
2. Абсолютная погрешность прибора равна 1 в младшем разряде прибора. Для миллисекундомера деление шкалы равно 1 мс. Поэтому: σ(t)сис = 1мс = 0,001с 3. Общая погрешность
4. Погрешность t2 σ(t2 )=2t σ(t) = 2 * 2,1 * 0,019 = 0,0798 ≈ 0,08 с2 5. Доверительный интервал 1,967 – 0,019 ≤ х ≤ 0,019 + 1,967 Для построения графика воспользуемся методом наименьших квадратов. По формулам k = nS3 -S1 S2 /D и b = S2 S4 -S1 S3 /D где S1 = Σxi = 16.489, S2 =Σyi = 88.88, S3 =Σxi yi = 325.12, S4 =Σx2 i = 57.625, D=nS4 -S1 2 = 1353.71 Отсюда k=0,12, b=-0,18 у1 (х1 ) = kх1 +b = 0,12 * 3,869 – 0,18 = 0,28 тогда х1 =3,869 и у1 (х1 ) =0,28 у5 (х5 ) = kх1 +b = 0,12 * 18,079 – 0,18 = 1,99 тогда х5 =18,079 и у5 (х5 ) =1,99 По этим координатам строим график t2 (h)
6. Масса блока По формуле 3,7 m = V * p, V = πR2 d = 3.14 * 0.005625 * 0.006 = 0.000106 м3 m= 0,000106 * 8400 = 0,8904 кг I – инерция блока I = mR2 /2 = 0.8904 * 0.005625/2 = 0.0025
5. ВЫВОДЫ С помощью машины Атвуда убедились на опыте в справедливости законов вращательного и поступательного движения тел. Проверка: t2 =kn где k=65,969 t2 1 = 65,969*0,0564≈3,720 t2 2 = 65,969*0,1294≈8,536 t2 3 = 65,969*0,1802≈11,888 t2 4 = 65,969*0,2374≈15,661 t2 5 = 65,969*0,2854≈18,827 Причины несовпадения экспериментальных результатов с расчетными связано с приборной и случайной погрешностью. 6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое момент сил и момент инерции? Моментом силы называют произведение модуля силы, вращающей тело, на ее плечо. Измеряется в 1Нм. Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающему его против часовой стрелки. I = Mn R2 n – момент инерции. Всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения, пока действия со стороны других тел не изменят этого состояния. 2. Моменты каких сил действуют на блок? Момент сил и момент инерции. 3. Как рассчитать момент инерции блока? Сформулировать теорему Штейнера. I = I +Ma2 , момент инерции твердого тела относительно произвольной оси равен сумме момента инерции тела относительно оси проходящей через центр инерции тела параллельно заданной оси и величины Ma2 , гду а – расстояние между осями. 4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными. Приборная и случайная погрешность 1. ПРИЛОЖЕНИЕ Результаты измерений Измерение №19: 17.03.2009 21:54 Начальное положение груза: 46,1 см Конечное положение груза: 40,4 см Время движения груза: 1,977 с Измерение №20: 17.03.2009 21:54 Начальное положение груза: 46,0 см Конечное положение груза: 40,4 см Время движения груза: 1,982 с Измерение №21: 17.03.2009 21:54 Начальное положение груза: 46,0 см Конечное положение груза: 40,4 см Время движения груза: 1,961 с Измерение №22: 17.03.2009 21:54 Начальное положение груза: 46,1 см Конечное положение груза: 40,4 см Время движения груза: 2,017 с Измерение №23: 17.03.2009 21:54 Начальное положение груза: 46,0 см Конечное положение груза: 40,4 см Время движения груза: 1,899 с Измерение №24: 17.03.2009 21:55 Начальное положение груза: 46,1 см Конечное положение груза: 33,1 см Время движения груза: 2,904 с Измерение №25: 17.03.2009 21:55 Начальное положение груза: 46,0 см Конечное положение груза: 33,1 см Время движения груза: 2,926 с Измерение №26: 17.03.2009 21:55 Начальное положение груза: 46,0 см Конечное положение груза: 33,1 см Время движения груза: 3,005 с Измерение №27: 17.03.2009 21:55 Начальное положение груза: 46,1 см Конечное положение груза: 33,1 см Время движения груза: 2,782 с Измерение №28: 17.03.2009 21:55 Начальное положение груза: 46,0 см Конечное положение груза: 33,1 см Время движения груза: 2,770 с Измерение №29: 17.03.2009 21:56 Начальное положение груза: 46,1 см Конечное положение груза: 28,0 см Время движения груза: 3,444 с Измерение №30: 17.03.2009 21:56 Начальное положение груза: 46,0 см Конечное положение груза: 28,0 см Время движения груза: 3,573 с Измерение №31: 17.03.2009 21:56 Начальное положение груза: 46,0 см Конечное положение груза: 28,0 см Время движения груза: 3,516 с Измерение №32: 17.03.2009 21:57 Начальное положение груза: 46,0 см Конечное положение груза: 28,0 см Время движения груза: 3,506 с Измерение №33: 17.03.2009 21:57 Начальное положение груза: 46,0 см Конечное положение груза: 28,0 см Время движения груза: 3,496 с Измерение №34: 17.03.2009 21:57 Начальное положение груза: 46,1 см Конечное положение груза: 22,3 см Время движения груза: 3,838 с Измерение №35: 17.03.2009 21:57 Начальное положение груза: 46,0 см Конечное положение груза: 22,3 см Время движения груза: 3,931 с Измерение №36: 17.03.2009 21:58 Начальное положение груза: 46,0 см Конечное положение груза: 22,3 см Время движения груза: 3,743 с Измерение №37: 17.03.2009 21:58 Начальное положение груза: 46,1 см Конечное положение груза: 22,3 см Время движения груза: 3,921 с Измерение №38: 17.03.2009 21:58 Начальное положение груза: 46,0 см Конечное положение груза: 22,3 см Время движения груза: 3,999 с Измерение №39: 17.03.2009 21:59 Начальное положение груза: 46,1 см Конечное положение груза: 17,5 см Время движения груза: 4,347 с Измерение №40: 17.03.2009 21:59 Начальное положение груза: 46,0 см Конечное положение груза: 17,5 см Время движения груза: 4,110 с Измерение №41: 17.03.2009 21:59 Начальное положение груза: 46,0 см Конечное положение груза: 17,5 см Время движения груза: 4,161 с Измерение №42: 17.03.2009 22:00 Начальное положение груза: 46,1 см Конечное положение груза: 17,5 см Время движения груза: 4,348 с Измерение №43: 17.03.2009 22:00 Начальное положение груза: 46,0 см Конечное положение груза: 17,5 см Время движения груза: 4,296 с |
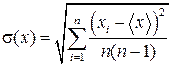 (3,2)
(3,2)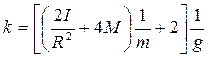 (3,7)
(3,7)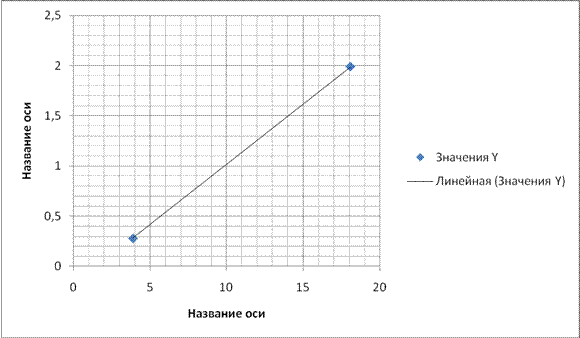
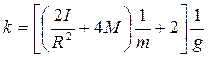 = 65,969
= 65,969