| 4.Расчетная часть
4.1. Расчет наматывателя, тормозного устройства и перематывателя
В целях сохранности фильмокопий особое внимание должно быть уделено наматывающему и тормозному устройству, обеспечивающих плотную намотку рулонов, в которых отсутствует межвитковое скольжение, а усилия на межперфорационные перемычки не должны превышать 5Н. К наматывающим устройствам предъявляются следующие требования:
1) Наматывающее устройство должно обеспечивать формирование рулона заданной емкости и плотности без затягивания витков.
2) Наматывающее устройство должно обеспечивать постоянную в пределах рулона и не превышающую допустимых значений нагрузки на межперфорационные перемычки наматываемой кинопленки.
3) Наматывание кинопленки должно производиться плавно без рывков.
Аналогичные требования предъявляются и к тормозному устройству, когда оно работает в режиме перемотки.
Исходные данные:
- формат киноленты – 35 (мм)
- емкость рулона – 1800 (м)
- скорость наматываемой киноленты – 0,456 (м/с)
- максимальное натяжение киноленты – 8 (Н)
- скорость перематываемой ленты – 6 (м/с)
- толщина киноленты – 1,6 .
10-4
(м).
4.1.1. Выбор радиуса сердечника
Выбор начального радиуса рулона имеет важное значение. Известно, что с увеличением начального радиуса R0
снижается характеристический коэффициент N для разных типов наматывателей. Увеличение R0
целесообразно и для создания условий наматывания рулона без затягивания витков. Оптимальное соотношение конечного RК
и начального R0
радиусов рулонов равно двум. Конечный радиус рулона определяем по формуле:

где S – толщина киноленты;
LK
– емкость рулона.
Если задаться соотношением ________ , то получим выражение для оптимального радиуса сердечника:
_________________________-
_________________________
В рулоне, наматываемом на сердечник такого радиуса, должно отсутствовать затягивание витков. В литературе [5] приведена таблица размеров, применяемых в соответствии с ГОСТ 11669-75 сердечников. Из нее видно, что ни один из применяемых сердечников не обеспечивает оптимальных условий наматывания киноленты.
Поэтому принимаем __________
Рассчитываем конечный радиус рулона:
___________________________
4.1.2. Выбор величины минимального натяжения ленты
В кинопроекционной аппаратуре эксплуатируется, как правило, сильнокоробленая лента, обладающая большой величиной жесткости на изгиб. Поэтому, чтобы достигнуть оптимальной плотности рулона, необходимо обеспечить большие величины натяжения киноленты. В процессе эксплуатации фильмокопии подвергаются многократному перематыванию на кинопроекторе или перематывателе. В этом случае требования к плотности рулона также высоки, что и обеспечивает высокие значения ___________
Исходя из сказанного, выбираем ___________ , обеспечивающую плотность рулона 96%.
4.1.3. Условия отсутствия затягивания витков в формируемом рулоне
Причиной возникновения затягивания витков в наматываемом рулоне, как показали многочисленные исследования, являются, в основном, такие дефекты киноленты, как сабельность и коробленность. Вследствие этих дефектов при наматывании киноленты в рулон имеет место неплотное прилегание витков друг к другу, что делает возможным их затягивание.
Подробный анализ этого процесса, выполненный А.М.Мелик-Степаняном и подтвержденный экспериментально на кафедре киновидеоаппаратуры, позволил найти условия, при которых возможно наматывание рулона без затягивания витков. Важно отметить, что при этом нет необходимости полностью устранять межвитковое пространство в формируемом рулоне – для этого требуются чрезмерно высокие значения натяжения ленты (порядка 70-80 Н). Достаточно достичь равновесия моментов, с одной стороны, развиваемого наматывателем, с другой стороны - моментов трения между витками в процессе наматывания всего рулона.
Исходя из этого, было получено выражение для граничных условий затягивания витков в наматываемом рулоне [1]:
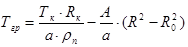 , (4.1) , (4.1)
где Тк
– конечное натяжение наматываемой ленты;
R0
, Rк
– конечный и начальный радиусы рулона;
ρn
– радиус формируемого витка.
Коэффициенты А и а характеризуют физико – механические свойства наматываемой ленты:
А=9,8ּВּγּμ,
Где В – ширина киноленты;
γ – удельная плотность ее материала;
μ – коэффициент трения между витками.
а=2ּπּμ+1.
Подставим числовые значения в выражение (4.1):

Таблица 4.1
Расчет граничной кривой наматывателя
| R,м
|
Tгр,Н
|
| 0,1
|
5,32
|
| 0,11
|
4,74
|
| 0,12
|
4,25
|
| 0,13
|
3,81
|
| 0,14
|
3,41
|
| 0,15
|
3,04
|
| 0,16
|
2,69
|
| 0,17
|
2,36
|
| 0,18
|
2,05
|
| 0,19
|
1,74
|
| 0,2
|
1,45
|
На (рис.4.1) показана кривая Тгр
, ограничивающая зону скольжения, или так называемая “граничная кривая”, которая получена из выражения (4.1). Рис.4.1.
Предварительно выбираем характеристику наматывателя в виде прямой, проходящей через точки Тнач
=8 Н и Ткон
=6 Н.
Вывод: так как характеристика наматывателя расположена выше граничной кривой, то затягивания витков не происходит.
4.2.Расчет наматывающего электродвигателя глубокого скольжения (ЭДГС)
Выражение характеристики наматывателя – ЭДГС в общем виде:
 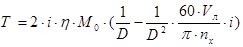 , (4.2) , (4.2)
где М0
– статический момент электродвигателя(начальный момент, когда ротор находится в покое);
nx
– число оборотов ротора электродвигателя на холостом ходу;
i – передаточное отношение редуктора;
η – КПД редуктора;
Vл
– скорость движения киноленты в установившемся режиме.
Для определения рабочего участка введем понятие "коэффициент начального скольжения а ".
  , (4.3) , (4.3)
где n0
– число оборотов вала электродвигателя в начале намотки рулона.
Тогда
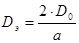 , (4.4) , (4.4)
причем
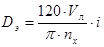 , (4.5) , (4.5)
Нетрудно видеть, что при а=2 Dэ
= D0
, т.е. начало характеристики будет совмещено с экстремальной точкой, а вид характеристики – убывающий. Анализ показывает, что с возрастанием а величина N также возрастает и, следовательно, целесообразно при выборе параметров наматывающего электродвигателя руководствоваться величиной а=2, т.е. началом рабочего участка D0
= Dэ
.
Тогда выражение для характеристики наматывателя приобретет более простой вид:
 , (4.6) , (4.6)
причем передаточное отношение редуктора можно определить из выражения
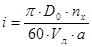 . (4.7) . (4.7)
Или, учитывая, что а=2,
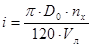 . (4.8) . (4.8)
Максимальное натяжение, развиваемое наматывающим электродвигателем, определяется из выражения
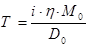 . (4.9) . (4.9)
Характеристический коэффициент наматывающего электродвигателя, работающего в таком режиме, определяется следующим образом:
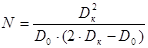 . (4.10) . (4.10)
Рассчитаем наматывающий электродвигатель.
Исходные данные
: формат киноленты 35 мм; емкость рулона Lк
=600 м; минимальное натяжение ленты Tmin
=6 Н; диаметр сердечника D0
=0,2 м; скорость движения ленты Vл
=0,456 м/с; толщина киноленты s=0,15ּ10-3
м; КПД редуктора η=0,9.
1. Определим конечный диаметр рулона Dк
:
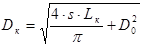 ; (4.11) ; (4.11)

Dк
=0,393 м.
2. Выберем предварительно электродвигатель глубокого скольжения, который устраивает нас числом оборотов холостого хода (nx
) и габаритами (см. табл.4.1[1]).
Пусть, достаточно приемлемым будет nx
=1400 об/мин.
Пригоден такой электродвигатель, статический момент М0
которого будет достаточным для обеспечения требуемой величины натяжения ленты.
Поэтому дальнейший ход расчета будет следующим:
3. Определим необходимое передаточное отношение редуктора, воспользовавшись выражением (4.8), подставив все необходимые данные:
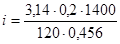
i=16,07.
Округлим i до целого числа. Возьмем i=16.
4. Исходя из того, что нам задано Тmin
, и помня, что требуется убывающая характеристика наматывателя, будем иметь в виду, что Тmin
= Тк
. Тогда, подставив в выражение (4.6) D=Dк
, найдем необходимое значение момента электродвигателя М0
:
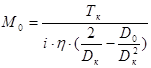 ; (4.12) ; (4.12)
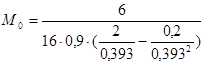
М0
=0,11 Нּм.
По имеющимся теперь М0
и nx
выберем электродвигатель. В данном случае нам подходит ЭДГС АСМ_400 (см. табл.4.1[1]). Его размеры следующие: D=60 мм, l=120 мм.
5. Найдем максимальное значение натяжения, так как Dэ
=D0
, то
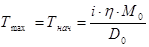 ; (4.13) ; (4.13)
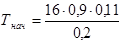
Тнач
=7,92 Н.
6. Найдем значение характеристического коэффициента N, который определим, воспользовавшись выражением (4.10):
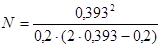
N=1,32.
7. Найдем выражение характеристики наматывателя – ЭДГС в общем виде, воспользовавшись выражением (4.2):
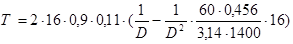
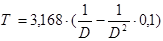
Таблица 4.2
Расчет характеристики ЭДГС наматывателя
| D,м
|
T,H
|
Tгр,Н
|
| 0,2
|
7,92
|
5,32
|
| 0,22
|
7,85
|
4,74
|
| 0,24
|
7,7
|
4,25
|
| 0,26
|
7,5
|
3,81
|
| 0,28
|
7,27
|
3,41
|
| 0,3
|
7,04
|
3,04
|
| 0,32
|
6,81
|
2,69
|
| 0,34
|
6,58
|
2,36
|
| 0,36
|
6,36
|
2,05
|
| 0,38
|
6,14
|
1,74
|
| 0,393
|
6
|
1,45
|
На (рис.4.2) показана характеристика ЭДГС наматывателя.
Рис.4.2.
4.3.Пусковой период наматывающих устройств
Расчет пускового периода наматывателя – электродвигателя глубокого
скольжения
Скорость приема ленты в течение пускового периода определяется следующим выражением:
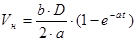 , (4.14) , (4.14)
где 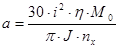 , (4.15) , (4.15)
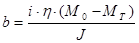 . (4.16) . (4.16)
В выражениях (4.15) и (4.16) присутствуют уже известные величины, определенные при расчете установившегося режима наматывающего электродвигателя: М0
– статический момент ЭДГС; nx
– число оборотов на холостом ходу; i – передаточное отношение редуктора; η – КПД редуктора.
Однако в эти выражения входят также и неизвестные еще величины:
J – момент инерции вращающихся частей наматывателя;
МТ
– момент трения в опорах вала наматывателя.
Момент трения в подшипниках качения достаточно мал, и, как правило, его принимают равным нулю.
Момент инерции вращающихся частей наматывателя определяется следующим образом:
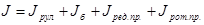 , (4.17) , (4.17)
где Jрул
– момент инерции рулона;
 , (4.18) , (4.18)
здесь q – масса одного прогонного метра киноленты;
Jред.пр.
– момент инерции редуктора, приведенный к валу наматывателя;
Jрот.пр.
– момент инерции ротора, приведенный к валу наматывателя.
Рассчитаем пусковой период ЭДГС
для двух случаев:
1) в начале намотки, когда R=R0
,
2) в случае пуска почти полного рулона, например, если имел место обрыв ленты (R=Rк
).
Исходные данные
: М0
=0,11 Нּм; nx
=1400 об/мин; i=16; η=0,9; Lк
=600 м.
1. Определим момент инерции вращающихся частей наматывателя, пользуясь выражением (4.17). В нашем случае, когда пусковой период определяется для начала намотки R=R0
и, следовательно, рулон еще не намотан, так что Jрул
=0. Тогда выражение (4.17) будет выглядеть следующим образом:
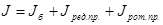 (4.19) (4.19)
Момент инерции бобины Iб
, найдем по формуле (20):
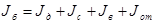 , (20) , (20)
где Jд
– момент инерции дисков бобины;
Jс
- момент инерции сердечника бобины;
Jв
- момент инерции втулки бобины;
Jот
- момент инерции отверстий дисков.
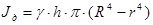 ; (4.21) ; (4.21)
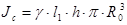 ; (4.22) ; (4.22)
 ; (4.23) ; (4.23)
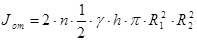 . (4.24) . (4.24)
В формулах (4.21 – 4.24):
R=0,5.
D – наружного диаметра дисков,
r=0,5.
d – внутреннего диаметра дисков, принимаем равным наружному диаметру втулки;
r1
=0,5.
d1
– внутреннего диаметра втулки;
R1
=0,5.
D1
–диаметра отверстий, сделанных в дисках бобины;
R2
=0,5.
D2
–диаметра осевой линии, проходящей через центры отверстий дисков;
γ =7,8.
103
кг.
м3
– плотность стали;
h – толщина дисков;
l – длина втулки бобины;
l1
– длина сердечника бобины;
n – количество отверстий в диске.
Подставим значения в формулы (4.21 – 4.24):
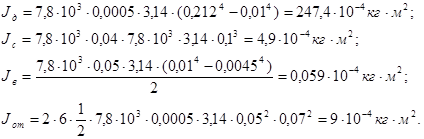
Подставим полученные значения в выражение (4.20):
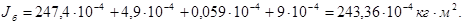
Момент инерции редуктора будет зависеть от его вида и количества ступеней. При заданном передаточном отношении i=16 воспользуемся двухступенчатой цилиндрической зубчатой передачей (рис.4.3)
Схема двухступенчатого зубчатого редуктора
Рис.4.3.
Приведем геометрический расчет редуктора, необходимый как для проектирования наматывателя, так и для расчета момента инерции вращающихся частей наматывателя.
i = iб
.
iт
.
Пусть iб
= iт
= i1/2
; iб
= iт
=4.
Выберем минимальное число зубьев шестерни, находящейся на валу ЭДГС. Возьмем Z1
=25; тогда число зубьев колеса быстроходной ступени
Z2
=i.
Z1
; Z2
=25.
4=100.
Модуль зацепления m выбираем по стандарту СЭВ [9]. Чтобы не увеличивать габариты редуктора, желательно выбирать m не очень большим, но не меньше единицы. Возьмем m=1 и определим приближенно диаметры делительных окружностей шестерни и колеса:
d1
=Z1
.
m; d1
=25.
1=25мм=0,025м;
d2
=Z2
.
m; d2
=100.
1=100мм=0,1м.
Ширину венцов шестерни и колеса определим по формуле [9]:
b=ψbd
.
d + (0,2÷0,4).
m,
где в – диаметр колеса или шестерни;
ψbd
– коэффициент колеса. ψbd
зависит от способа крепления колеса на валу, расположения опор, твердости материала шестерни [9].
Примем ψbd
=0,4, тогда
b1
=0,4.
25 + (0,2÷0,4).
1=10мм.
Теперь рассчитаем тихоходную передачу. Возьмем число зубьев шестерни Z2’
=25; тогда число зубьев колеса тихоходной ступени
Z3
=i.
Z2’
; Z3
=25.
4=100.
Возьмем m=1 и определим приближенно диаметры делительных окружностей шестерни и колеса:
d2’
=Z2’
.
m; d2’
=25.
1=25мм=0,025м;
d3
=Z3
.
m; d3
=100.
1=100мм=0,1м.
Примем ψbd
=0,4, тогда
b2’
=0,4.
25 + (0,2÷0,4).
1=10мм.
Приближенное значение момента инерции можно определить по формуле [9]:
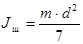 ; (4.25) ; (4.25)
где m – масса шестерни (колеса);
d – диаметр его делительной окружности.
Масса шестерни (колеса) m=V.
ρ=πּr2
ּbּρ.
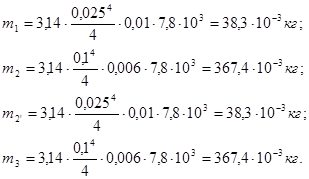
Подставим значения в формулу (4.25):
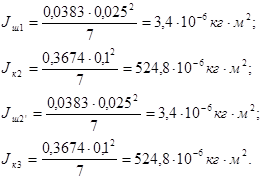
Необходимо привести моменты инерции колес к валу наматывателя:
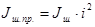 . (4.26) . (4.26)
Тогда приведенные моменты инерции будут:
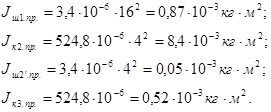
Суммарный момент инерции редуктора, приведенный к валу наматывателя, составит:
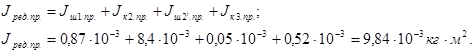
Определим момент инерции ротора Jрот
. Момент инерции ротора можно рассчитать приближенно, как момент инерции цилиндра, выполненного из алюминиевого сплава и занимающего порядка 50% объема электродвигателя. Для ЭДГС АСМ_400 длина корпуса составляет 120 мм; диаметр – 60мм. Его объем найдем таким образом:
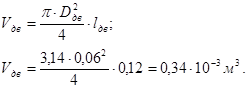
Тогда 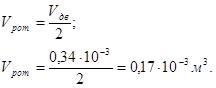
Момент инерции ротора можно найти по следующей формуле:
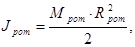 (4.27) (4.27)
где Мрот
=Vрот
.
ρрот
, где ρрот
– удельная плотность материала ротора.
Для алюминиевых сплавов ρ=2,8.
103
кг/м3
.
Подставим найденные значения в выражение (4.27):
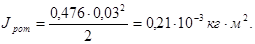
Момент инерции ротора, приведенный к валу наматывателя, определяется так же, как и приведенный момент инерции шестерни.
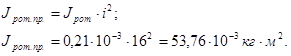
А суммарный момент инерции вращающихся частей наматывателя найдем по формуле (4.19):

Вернемся к выражениям (4.15) и (4.16), подставим в них все известные нам величины и получим значения коэффициентов a и b:
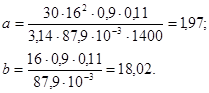
Тогда выражение (4.14) с учетом того, что R=R0
=0,1м, преобретает следующий вид:
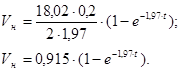
Таблица 4.3
Расчет скорости наматываемой ветви киноленты (R=R0
)
| t,c
|
a.
t
|
e(-at)
|
1-e(-at)
|
Vн,м/с
|
| 0
|
0
|
1
|
0
|
0
|
| 0,1
|
0,197
|
0,821
|
0,179
|
0,164
|
| 0,25
|
0,493
|
0,611
|
0,389
|
0,356
|
| 0,5
|
0,985
|
0,373
|
0,626
|
0,574
|
| 0,75
|
1,478
|
0,228
|
0,771
|
0,707
|
| 1
|
1,97
|
0,139
|
0,86
|
0,788
|
| 1,25
|
2,463
|
0,085
|
0,915
|
0,837
|
| 1,5
|
2,955
|
0,052
|
0,948
|
0,867
|
| 1,75
|
3,448
|
0,032
|
0,968
|
0,886
|
| 2
|
3,94
|
0,0190
|
0,981
|
0,897
|
| 3
|
5,91
|
0,003
|
0,997
|
0,913
|
| 4
|
7,88
|
0,0004
|
1
|
0,915
|
| 5
|
9,85
|
0
|
1
|
0,915
|
| 6
|
11,82
|
0
|
1
|
0,915
|
| 7
|
13,79
|
0
|
1
|
0,915
|
Построим график зависимости Vн1
(t) – скорости приема ленты наматывателем и Vл
(t) – скорости подачи ленты механизмом транспортирования.
Рис.4.4. Вывод: провисания ленты не будет, поскольку значение функции Vн1
(t) в любой момент времени превосходит значение функции Vл
(t).
Теперь проведем подробные расчеты для полного рулона, т.е. для случая, когда R=Rк
=0,201м.
Общий момент инерции вращающихся частей наматывателя определится в этом случае из выражения (4.17), т. е. В него будет входить Jрул
– момент инерции полного рулона, который найдем по формуле (4.18). В нашем случае, если учесть, что q=7.
10-3
кг/м для 35-мм киноленты,
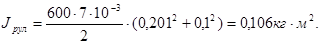
Тогда полное значение J составит:

Тогда значения коэффициентов a и b соответственно составят:
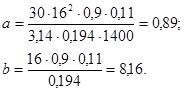
Тогда выражение (4.14) с учетом того, что R=Rк
=0,201м, преобретает следующий вид:
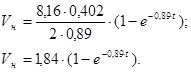
Таблица 4.4
Расчет скорости наматываемой ветви киноленты (R=Rк
)
| t,c
|
a.
t
|
e(-at)
|
1-e(-at)
|
Vн,м/с
|
| 0
|
0
|
1
|
0
|
0
|
| 0,1
|
0,089
|
0,915
|
0,085
|
0,157
|
| 0,25
|
0,223
|
0,801
|
0,199
|
0,367
|
| 0,5
|
0,445
|
0,641
|
0,359
|
0,661
|
| 0,75
|
0,668
|
0,513
|
0,487
|
0,896
|
| 1
|
0,89
|
0,411
|
0,589
|
1,084
|
| 1,25
|
1,113
|
0,329
|
0,671
|
1,235
|
| 1,5
|
1,335
|
0,263
|
0,737
|
1,356
|
| 1,75
|
1,558
|
0,211
|
0,789
|
1,452
|
| 2
|
1,78
|
0,168
|
0,831
|
1,529
|
| 3
|
2,67
|
0,069
|
0,931
|
1,713
|
| 4
|
3,56
|
0,028
|
0,972
|
1,788
|
| 5
|
4,45
|
0,012
|
0,988
|
1,819
|
| 6
|
5,34
|
0,005
|
0,995
|
1,831
|
| 7
|
6,23
|
0,002
|
0,998
|
1,836
|
Построим график зависимости Vн2
(t) – скорости приема ленты наматывателем и Vл
(t) – скорости подачи ленты механизмом транспортирования.
Рис.4.5.
Вывод: провисания ленты не будет, поскольку значение функции Vн2
(t) в любой момент времени превосходит значение функции Vл
(t).
|