МИНИСТЕРСТВО ВЫСШЕГО СРЕДНЕГО СПЕЦИАЛЬНОГО
ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТЕРЛИТАМАКСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
ИНСТИТУТ
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ТЕОРЕТИЧЕСКОЙ ФИЗИКИ
Ахтямов Рустам Расихович
РАЗРАБОТКА ТЕОРИИ
РАДИОГЕОХИМИЧЕСКОГО ЭФФЕКТА
ДИПЛОМНАЯ РАБОТА
Научный руководитель: д. т. н.,
профессор А.И. Филиппов.
Стерлитамак
Содержание
Введение. 3
Обозначения. 4
1. Результаты экспериментального исследования радиогеохимического эффекта
6
1.1. Описание и способы регистрации радиогеохимического эффекта. 6
1.2. Примеры экспериментального обнаружения радиогеохимического эффекта7
1.3. Выводы.. 11
2. Основные уравнения
. 12
2.1. Уравнение неразрывности. 12
2.2. Закон Фика. 14
2.3. Уравнение конвективной диффузии. 16
2.4. Метод характеристик. 18
2.5 Слабые растворы.. 26
2.6. Равновесие по отношению к радиактивному веществу веществу. 28
2.7. Химический потенциал. 30
3. Разработка теории радиогеохимического эффекта
. 32
3.1. Общие предположения теории. 32
3.2. Математические модели радиогеохимического эффекта. 34
3.3. Рельзультаты расчетов и их анализ. 41
3.3.1. График модели. 41
3.3.2 Условие возникновения радиогеохимического эффекта. 43
Заключение. 44
Литература. 45
В настоящее время к числу нерешенных проблем в области контроля методами промысловой геофизики за процессами обводнения следует отнести выделение коллекторов, заводняемых закачиваемой водой, по скважинам, выходящим из бурения, и по скважинам, обводнившимися в период эксплуатации закачиваемой или пластовой водой.
Перспективным направлением исследований с целью решения этих вопросов является использование эффекта увеличения естественной гамма-активности в заводняемом пласте. Эффект был экспериментально обнаружен более десяти лет назад и получил название «радиогеохимический», он заключается в многократном увеличении естественной гамма активности пород в интервале продуктивных пластов в процессе их обводнения, что проявляется в возникновении аномалий на кривых гамма-каротажа. Из-за недостаточной изученности условий отложения радиоактивных веществ эффект не находит широкого применения.
Цель данной работы заключается в разработке теории радиогеохимического эффекта.
Задачи:
– анализ экспериментальных исследований опубликованных в печати;
– вывод основных уравнений;
– формулировка задач математической физики, описывающих динамику радиоактивных примесей при вытеснении нефти водой;
– решение основных задач и проведение численных расчетов на их основе;
– определение условий возникновения радиогеохимического эффекта;
– анализ результатов расчетов, исследование зависимости величины эффекта от пористости, коэффициента равновесия растворенного вещества между жидкостью и скелетом и от плотности радиоактивных примесей в этих средах.
Практическая значимость заключается в возможности использования результатов исследования в нефтедобывающей промышленности .
Работа состоит из двух глав.
В первой главе описывается радиогеохимический эффект, рассматриваются способы регистрации и примеры результатов экспериментального обнаружения радиогеохимического эффекта.
Во второй главе вводятся основные понятия и уравнения: уравнение неразрывности, химический потенциал, закон Фика, координаты Эйлера и Лагранжа, слабые растворы и равновесия в них по отношению к растворенному веществу, уравнение конвективной диффузии, метод характеристик с рассмотрением частных случаев.
В третьей главе разрабатывается теория эффекта. Здесь строится математическая модель: постановка задач и их решение методом характеристик. Производятся расчёты и на основе их анализа строятся графики, выводится условие возникновения радиогеохимического эффекта. Глава завершается определением выражения для его величины эффекта.
Выражаю глубокую признательность за помощь в написании работы профессору А. И. Филиппову.
 – объем занимаемый порами и скелетом соответственно, м3
; – объем занимаемый порами и скелетом соответственно, м3
;
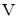 – общий объем, м3
; – общий объем, м3
;
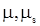 – химический потенциал растворенных радиоактивных веществ относительно жидкости и скелета, Дж/кг; – химический потенциал растворенных радиоактивных веществ относительно жидкости и скелета, Дж/кг;
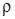 ,
,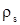 – плотность радиоактивных веществ в насыщающей жидкости и скелете, кг/ м3
; – плотность радиоактивных веществ в насыщающей жидкости и скелете, кг/ м3
;
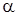 – коэффициент массообмена между скелетом и жидкостью, кг2
/(Дж м3
с); – коэффициент массообмена между скелетом и жидкостью, кг2
/(Дж м3
с);
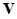 – скорость фильтрации насыщающей жидкости, м/c. – скорость фильтрации насыщающей жидкости, м/c.
1. Результаты экспериментального исследования
радиогеохимического эффекта
В этой главе приводятся результаты экспериментальных исследований полученных при замерах скважин в период и после их эксплуатации. Проводится анализ практических материалов гамма-каротажа , который показывает, что в процессе длительной закачки сточных вод в продуктивные горизонты образуются аномалии, связанные с радиогеохимическим эффектом.
В скважинах, обводняющихся вследствие заводнения пластов закачиваемой или пластовой водой, с заколонной циркуляцией и работающих практически без воды, часто наблюдается повышение радиоактивного излучения, достигая максимального значения в интервале контакта нефти с водой. Отсюда такое название - «радиогеохимический эффект».
Возникновение гамма-аномалии на границе вода-нефть связано с повышением концентрации радиоактивных веществ в пласте, источником которых является неподвижная пористая среда.
Существует несколько способов регистрации радиогеохимического эффекта. Но наиболее точным является гамма-кароттаж скважин.
Гамма-кароттаж- это метод исследования геологического разреза буровой скважины по радиоактивному гамма излучению горных пород. Он заключается в следующем. В скважину опускается снаряд (рис.1), который заключает в себе приемник гамма-излучения. В качестве приемника используют счетчик Гейгера-Мюллера, который соединяется с пультом управления и питания. Счетчик представляет собой металлическую трубку, по оси которой натянута металлическая нить. Нить и трубка соединены с полюсами источника высокого напряжения. При попадании в трубку гамма-излучения в цепи трубки возникают импульсы тока, по которым можно судить об интенсивности излучения.

Рис. 1.
Общий вид прибора для исследования радиогеохимического эффекта.
По результатам исследований строится диаграмма зависимости интенсивности излучения от глубины. Диаграмму, зарегистрированную после определенного периода эксплуатации скважины, сравнивают с замером, полученным непосредственно после выхода скважины из бурения. По сопоставлению этих двух диаграмм определяются интервалы гамма-аномалий.
По результатам производственных измерений можно говорить об изменении естественной гамма-активности по разрезу скважины в том случае,
если показания в интервале неколлекторов возросли практически до уровня глин или более, а в интервале коллекторов (глинистые разности) – превышают уровень глин не менее чем на 30-50%.
На рис.2 приведены результаты исследований по трем скважинам. В скважине 3890 в пласте песчаника 1740—1758 м водонефтяной контакт находится на глубине 1751,3м, интервал перфорации 1740-1744 мм. Пласт «а» (1723—1725 м) представлен алевролитом, вскрыт перфорацией, но в работе скважины участия он не принимает. Скважина вступила в работу с водой.

Рис. 2.
Повышение естественной гамма – активности в период эксплуатации скважины.
а – скв. 3890; б – скв.3892; в – скв. 3865.
1 – интервал повышения гамма – активности; 2 – интервал перфорации.
Обводненность продукции связана с поступлением воды из водонасыщеной части пласта «гд». В 1963 г. обводненность продукции резко возросла в результате начавшегося заводнения пласта закачиваемой водой. В пределах основной части пласта произошло резкое увеличение естественной гамма-активности; наиболее высокий уровень излучения зарегистрирован в интервале, вскрытом перфорацией (в 10 раз превышает уровень в глинах). Кроме того, увеличение гамма-активности отмечается и выше кровли этого пласта в интервале, представленном неколлектором (до глубины 1736 м). Возможно, несколько увеличилась гамма-активность и в интервале неработающего пласта «а». В скважине 3892 перфорацией вскрыт также пласт с подошвенной водой (водонефтяной контакт на глубине 1669 м). Скважина вступила в работу с водой. В 1964 г., судя по резкому увеличению обводненности продукции, началось заводнение коллектора пластовой водой. В заводняемом пласте, в основном в пределах интервала перфорации, отмечается увеличение гамма-активности до уровня глин. Кроме того, повышение гамма-активности произошло в интервале 1752—1753 м, который представлен неколлектором. В скважине 3865 работают два верхних пласта — «а» (1779—1786 м) и «б» (1789—1794 м). В 1965 г. пласт «а» начал заводняться закачиваемой водой. По замеру ГМ отложение солей радиобарита произошло в подошвенной части заводняемого пласта и в аргиллитах, залегающих над пластом «б».
При обводнении скважин закачиваемой водой гамма-аномалии в интервале заводняемого пласта, выделены по 55% скважин. В пределах коллекторов, заводняемых пластовой водой, образование гамма-аномалий отмечено по 75% скважин, т. е. в этом случае вероятность отложения солей радиобарита больше. Отсутствует какая-либо связь между вероятностью образования гамма-аномалии в заводняемом пласте и количеством отобранной воды или нефти из этого пласта. Величина аномалии также не зависит от количества отобранной воды или нефти. При заводнении нижних пластов повышение гамма - активности в интервале пласта отмечено в 70% случаев, а при заводнении верхних пластов – в 40% случаев. По нижним пластам отложение радиобарита обычно наблюдается в интервале мощностью не менее 4 – 6 м (см. рис.1, а и б).
Если заводняется верхний пласт, то повышение показаний ГМ обычно отмечается в интервале мощностью до 2 м, который бывает приурочен к подошвенной части коллектора (рис.1, в).
При сопоставлении результатов измерений естественной гамма-активности по верхним нижним пластам создается впечатление, что основным источником изотопов радия являются пласты с подошвенной водой. По-видимому, на контакте нефти с водой содержание радия в воде существенно больше, чем в пластах, значительно удаленных от водонефтяного контакта. Например, на Арланском месторождении по диаграммам ГМ, зарегистрированным после выхода скважины из бурения, граница нефть-вода в пласте выделяется характерным максимумом интенсивности естественного гамма-излучения. Возможно, на этом месторождении существовали наиболее -благоприятные условия для адсорбции радиоактивных-элементов на границе нефти с водой. Содержание изотопов радия в зоне водонефтяного контакта должно возрастать на участках интенсивного движения подошвенной воды. Например, на Павловской площади до начала разработки залежи скорость фильтрации воды по пласту была больше, чем на Абдрахмановской и Южно-Ромашкинской площадях. Этим можно объяснить, почему по скважинам Павловской площади вероятность появления гамма-аномалий при заводнении коллекторов больше и интенсивность их выше по сравнению с данными, полученными по Абдрахмановской и Южно-Ромашкинской площадям.
По скважинам, эксплуатирующим пласты с подошвенной водой и обводняющимся вследствие поступления воды по затрубному пространству или прискважинной зоне коллектора, вероятность образования гамма-аномалий составляет 50%, т. е. меньше, чем в случае заводнения коллекторов в интервале нижних пластов.
Повышение естественной гамма-активности часто наблюдается в интервалах, которые не являются источником поступления воды в скважину. Гамма-аномалии, не совпадающие по глубине с интервалом притока воды в скважину, выделены по 158 скважинам, причем 32 скважины ко времени проведения измерений работали без воды. Из числа-рассмотренных скважин в 47 гамма-аномалии приурочены к работающему пласту, из которого в скважину поступает безводная нефть. В 47 скважинах гамма-аномалии выделяются в интервале пластов, вскрытых перфорацией, но эти пласты в работе скважины не участвуют. В остальных 64 скважинах отложение радиобарита отмечается в интервале неколлекторов.Из приведенных данных следует, что в 70% случаев повышение гамма -активности отмечается в интервалах, из которых нет притока жидкости в скважину (неработающие пласты и интервалы неколлекторов). В 30% случаев из пласта поступала безводная нефть, но в пределах этого коллектора выделяется гамма-аномалия. Возможно, в подобных случаях работает не вся мощность пласта и в неработающих интервалах происходит отложение солей радиобарита.
Анализ образования гамма-аномалий после определенного периода эксплуатации скважин показывает, что отложение солей радиобарита не по всем скважинам происходит в интервале заводняемого коллектора и в 40% рассмотренных скважин заводняемые коллекторы не выделяются повышением естественной гамма-активности.
На основе всего выше сказанного можно сделать следующие выводы:
1. Радиогеохимический эффект наблюдается на границе нефть-вода в пласте. Таким образом, в нефтяном пласте содержание радиоактивных веществ повышается.
2. Вероятность появления гамма-аномалии при заводнении нижних пластов больше, чем при заводнении верхних пластов.
3. Интенсивность гамма-аномалий зависит от скорости фильтрации воды по пласту.
4. Аномальная радиоактивность часто наблюдается в пластах, которые не являются источниками поступления воды в скважину. Образование этих гамма-аномалий, по-видимому, связано с адсорбцией бария и радия из жидкости, движущейся по стволу, на участках обсадной колонны, подвергшихся коррозии, и на цементе за колонной в интервале пластов, вскрытых перфорацией.
5. Радиогеохимический эффект можно применять при исследованиях в интервале пластов, не вскрытых перфорацией.
2. Основные уравнения
Содержанием этой главы являются основные понятия и уравнения, и их решения, необходимые разработки теории на основе математической модели.
В замкнутой изолированной системе полная масса остается постоянной, т.е. она не возникает и не исчезает сама по себе.
Закон сохранения массы означает, что для любого 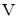 с поверхностью с поверхностью 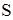 изменение массы в изменение массы в 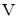 должно равняться количеству массы протекающему через должно равняться количеству массы протекающему через 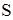 . .
Плотностью 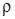 в точке в точке 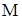 пространства называют предел отношения массы пространства называют предел отношения массы 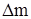 в элементарном объеме в элементарном объеме 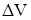 этому объему, охватывающему точку этому объему, охватывающему точку 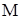 , при стягивании его в эту точку, т.е.: , при стягивании его в эту точку, т.е.:
 , , |
(2.1) |
Тогда
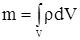 , , |
(2.2) |
где m - интегральный параметр, удовлетворяющий закону аддитивности, 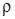 -
локальный параметр. -
локальный параметр.
Выделим в пространстве неподвижную замкнутую поверхность 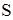 ограничивающую объем ограничивающую объем 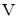 .
Каждой точке выделенного объема .
Каждой точке выделенного объема 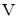 сопоставим вектор сопоставим вектор 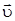 . .

Рис.3.
Выберем на поверхности 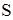 ориентированный элемент поверхности, где ориентированный элемент поверхности, где 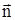 –
вектор внешней нормали, –
вектор внешней нормали, 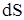 -
площадь выбранной площадки. -
площадь выбранной площадки.
Тогда через элемент площади 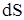 входит или выходит количество массы сплошной среды входит или выходит количество массы сплошной среды 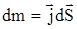 , где , где 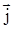 – вектор потока массы. – вектор потока массы.
Через всю поверхность войдет или выйдет количество массы
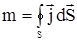 |
(2.3) |
Будем предполагать, что источники и стоки отсутствуют, тогда закон сохранения массы запишется в виде:
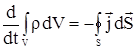 |
(2.4) |
В (2.4) знак минус в правой части объясняется тем, что если 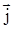 образует с образует с 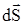 острый угол, т.е. острый угол, т.е.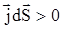 , то , то 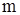 проходит через проходит через 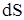 изнутри наружу, т.е. масса в изнутри наружу, т.е. масса в 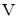 убывает. убывает.
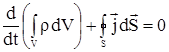 |
(2.5) |
Уравнение (2.5) – уравнение неразрывности для массы в интегральной форме.
Проведем в первом интеграле (2.5) дифференцирование по 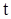 как по параметру (поскольку как по параметру (поскольку 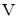 не зависит от не зависит от 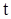 ), т.е. внесем производную под знак интеграла и заменим ее частной производную, поскольку подынтегральная функция ), т.е. внесем производную под знак интеграла и заменим ее частной производную, поскольку подынтегральная функция 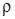 зависит от переменной интегрирования, получим: зависит от переменной интегрирования, получим:
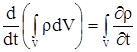 |
(2.6) |
Второй интеграл в равенстве (2.5) преобразуем в объемный, воспользовавшись теоремой Остроградского-Гаусса. Получим
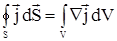 |
(2.7) |
где
Подставим (2.6), (2.7) в (2.5), и объединяя интегралы получим
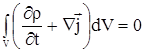 |
(2.8) |
Учитывая в (2.8) произвольность объема 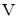 ,
получаем ,
получаем
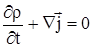 |
(2.9) |
Уравнение (2.9)– уравнение неразрывности для массы в дифференциальной форме.
2.2.
Закон Фика
Закон Фика необходим для описания диффузии растворенного(радиоактивного) вещества пропорциональной градиенту их плотности. Плотность радиоактивных примесей является функцией от химического потенциала 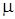
В уравнении (2.9) предыдущего параграфа вектор потока имеет вид
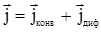 |
(*) |
где 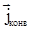 – конвекционная компонента вектора потока, связанная с потоком вещества (массы). Для случая, когда движение массы происходит только за счет конвекции, поток записывается в виде – конвекционная компонента вектора потока, связанная с потоком вещества (массы). Для случая, когда движение массы происходит только за счет конвекции, поток записывается в виде
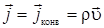 |
(2.10) |
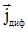 – диффузионная компонента, возникает при наличии в системе градиента концентрации. Для диффузионного компонента справедлив I Закон Фика: – диффузионная компонента, возникает при наличии в системе градиента концентрации. Для диффузионного компонента справедлив I Закон Фика:
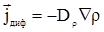 |
(2.10*) |
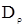 – коэффициент концентрационной диффузии, (далее – коэффициент концентрационной диффузии, (далее 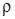 будем опускать). будем опускать).
Диффузионный поток пропорционален градиенту плотности, взятому с обратным знаком.
Подставим (2.10) и (2.10*) в (*), получим
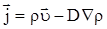 |
(2.11) |
Подставим (2.11) в (2.9), получим
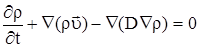 |
(2.12) |
В (2.12) каждое слагаемое записали отдельно:
Преобразуем второе слагаемое в (2.12):
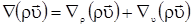 |
(2.13) |
Во втором слагаемом в (2.13) осуществим круговую перестановку (знак не меняется, т.к. скалярное произведение).
Из выражения (2.13), получим
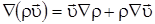 |
(2.14) |
Преобразуем второе слагаемое в (2.12):
Условие не сжимаемости жидкости:
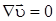 |
(2.15) |
Подставив (2.14) и (2.15) в (2.12) получим
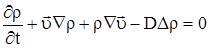 |
(2.16) |
Если в (2.16) то получим уравнение диффузии (II Закон Фика):
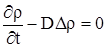 |
(2.17) |
2.3.
Уравнение конвективной диффузии
Пусть имеется раствор с плотностью растворителя 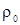 и плотностью растворенного вещества – и плотностью растворенного вещества –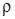 , тогда плотность раствора запишется в виде , тогда плотность раствора запишется в виде
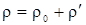 |
(2.18) |
Запишем уравнение неразрывности для растворителя:
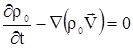 |
(2.19) |
Диффузию не учитываем, потому что в жидкостях коэффициент диффузии мал.
Будем считать, что растворитель является несжимаемым, т.е. 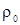 не зависит от пространственных координат и не зависит от пространственных координат и
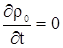 |
(2.20) |
Тогда из выражения (2.19), получим
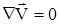 |
(2.21) |
Запишем уравнение неразрывности для раствора:
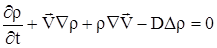 |
(2.22) |
В (2.22) подставим (2.18), получим
Учитывая (2.20), (2.21) и независимость 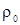 от пространственных координат, получим от пространственных координат, получим
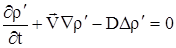 |
(2.23) |
Опустим штрих, предполагая в дальнейшем 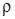 – плотность примеси. – плотность примеси.
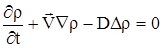 |
(2.24) |
Поясним в (2.24) значение каждого слагаемое:
Первое слагаемое 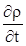 описывает изменение массового содержания в рассматриваемой точке; описывает изменение массового содержания в рассматриваемой точке;
Второе слагаемое 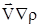 отвечает за конвекцию; отвечает за конвекцию;
Третье слагаемое 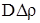 отвечает за диффузию. отвечает за диффузию.
Физический смысл уравнения (2.24) заключается в следующем: изменение концентрации, со временем, в рассматриваемой точке происходит за счет конвекции и диффузии.
На практике в (2.24) слагаемым 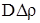 можно пренебречь, в силу его малости. можно пренебречь, в силу его малости.
Пусть движение несущей жидкости происходит вдоль оси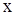 , тогда уравнение без диффузионной конвекции запишется
, тогда уравнение без диффузионной конвекции запишется
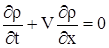 . . |
(1) |
Одномерное уравнение без диффузионной конвекции (или конвекционное уравнение).
Задача Коши для уравнения (1).
Требуется найти функцию 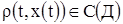 , где , где 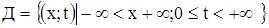 и удовлетворяющую условиям: и удовлетворяющую условиям:
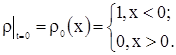 |
(2) |
Получим решение задачи методом характеристик.
Метод характеристик заключается в переходе от эйлеровых переменных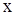 и
и 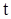 к лагранжевым.
Связь производных в эйлеровых и лагранжевых координатах записывается в виде: к лагранжевым.
Связь производных в эйлеровых и лагранжевых координатах записывается в виде:
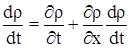 . . |
(3) |
Уравнение (1) таким образом можно записать как систему двух уравнений:
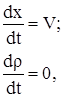 |
(4)
(5)
|
где уравнение (4) – уравнение для характеристик.
Из (5) следует, что 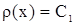 ,
где ,
где 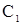 некоторая постоянная. Но т.к. некоторая постоянная. Но т.к. 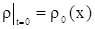 , то , то 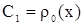 . .
Из (4) получаем
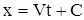 . . |
(6) |
Равенство (6) – решение уравнений характеристик.
Интегральные линии уравнения (4) на мировой плоскости 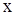 , ,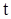 , т.е. графики движения частиц при заданной скорости , т.е. графики движения частиц при заданной скорости 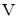 ,
называются характеристиками уравнения (1). ,
называются характеристиками уравнения (1).
Пусть при 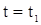 , , 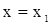 , т.е. , т.е.
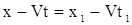 ; ; |
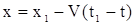 . . |
(7) |
Подставляя (7) в (2), получим
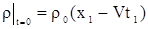 . . |
(8) |
Для того, чтобы получить решение задачи Коши нужно решить систему двух уравнений:
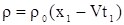 , , |
(9) |
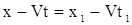 . . |
(10) |
Подставим уравнение (10) в (9), получим
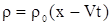 . . |
(11) |
Выражение (11) является решением задачи Коши для уравнения (1).
Решение (11) представляет собой волну бегущую вправо со скоростью 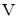 . .
Начально-краевая задача для уравнения (1) (смешанная задача)

Рис.4.
На рисунке 4 изображены характеристики уравнения (1), где при 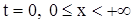 начальное условие, а при начальное условие, а при 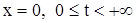 граничное условие, граничное условие, 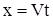 граничная характеристика. граничная характеристика.
Для задачи Коши решенной ранее,
Получим решение для граничного решения.
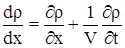 |
(5) |
Запишем уравнения (1) в виде
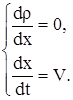 |
(6)
(7)
|
Из (6) следует, что 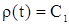 , где , где 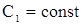 . .
Учитывая (3) получим 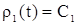 . .
Интегрируя (7) получаем
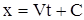 . . |
(8) |
Пусть при 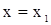 , , 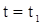 тогда тогда
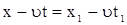 |
(9) |
Разделим обе части (9) на  получим получим
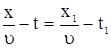 . . |
(10) |
При 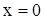 , ,
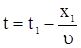 . . |
(11) |
Подставляя (11) в (3) получаем
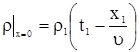 . . |
Тогда решая систему
получаем решение граничной задачи в виде
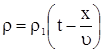 . . |
(12) |
В (12) 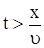 . .
Решение начально-краевой задачи будет иметь вид
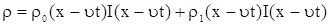 , , |
где 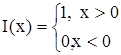 , единичная функция Хевисайда. , единичная функция Хевисайда.
Решение задачи Коши для неоднородного конвекционного уравнения
Построим формулу Даламбера для уравнения
Уравнение (1) – уравнение эволюции локального параметра.
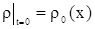 . . |
(2) |
Тогда уравнение (1) запишем в виде системы двух уравнений:
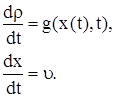 |
(3)
(4)
|
Интегрируя (4), получим
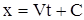 |
(5) |
Пусть при 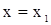 , , 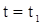 , тогда , тогда
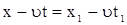 . . |
Подставим (5) в (3), получим
Исключим в (6) 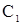 для этого учтем начальное условие (7). для этого учтем начальное условие (7).
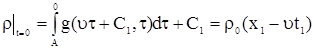 , , |
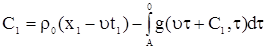 . . |
(9) |
Подставим (9) в (6), получим
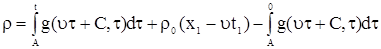 , , |
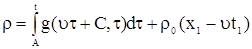 . . |
(10) |
Исключим в (10) 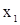 и и 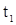 ,
потом ,
потом 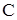 : :
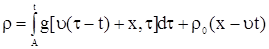 . . |
(11) |
Выражение (11) – формула Даламбера (решение задачи Коши для неоднородного конвекционного уравнения).
Покажем что (11) является решением (1).
Продифференцируем формулу (11) по 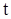 , получим , получим
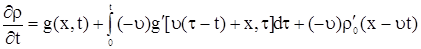 . . |
(12) |
Продифференцируем формулу (11) по 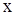 , получим , получим
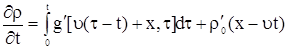 . . |
(13) |
Подставляя (13) и (12) в (1), получаем
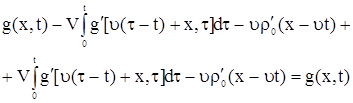 . . |
Откуда получаем тождество: 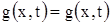 .
Следовательно, выражение (11) является решением уравнения (1). .
Следовательно, выражение (11) является решением уравнения (1).
Начально-краевая задача для неоднородного конвективного уравнения
Найдем решение граничной задачи для неоднородного конвекционного уравнения (1).
Решение будем искать в виде 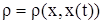 дифференцируя которое по дифференцируя которое по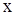 ,получим
,получим
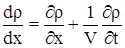 . . |
Умножая правую и левую части на 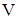 , приходим к выражению , приходим к выражению
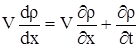 . . |
(4) |
Перепишем уравнение (1) в виде двух уравнений:
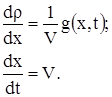 |
(5)
(6)
|
Из (6) следует, что 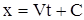 .
Пусть при .
Пусть при 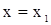 , , 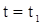 , тогда , тогда 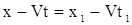 . .
Откуда получим
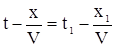 . . |
(7) |
Подставим уравнение (7) в уравнение (5), получим
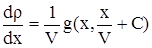 . . |
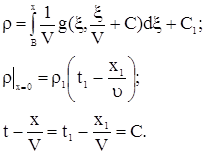 |
(8)
(9)
(10)
|
Исключим в (8) 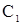 , для этого учтем граничное условие (9). , для этого учтем граничное условие (9).
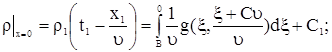 |
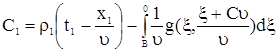 . . |
Подставим (11) в (8), получим
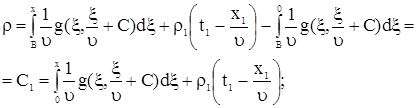 |
(12) |
Исключим в (12) 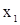 , , 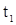 и и 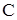 получим получим
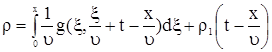 . . |
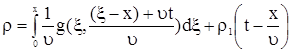 , , |
(13) |
Выражение (13) – формула Даламбера (решение граничной задачи для неоднородного конвекционного уравнения (1)).
Покажем, что (13) является решением (1). Для этого продифференцируем формулу (13) по 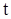 , получим , получим
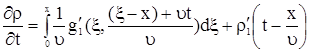 . . |
(14) |
Продифференцируем формулу (13) по 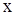 , получим , получим
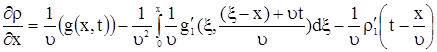 . . |
(15) |
Умножая (15) на  и складывая с (14), получим, после сокращений, что и складывая с (14), получим, после сокращений, что
то есть, (13) является решением граничной задачи для неоднородного конвекционного уравнения (1).
Решение смешанной задачи запишем, в виде
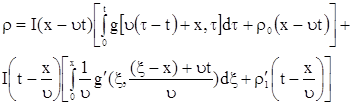 . . |
2.5
Слабые растворы
Рассмотрим термодинамические свойства слабых растворов, т. е. таких растворов, в которых число молекул растворенных веществ значительно меньше числа молекул растворителя. Рассмотрим сначала случай раствора с одним растворенным веществом; обобщение для раствора нескольких веществ можно будет произвести непосредственно [1].
Пусть 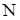 – число молекул растворителя в растворе, а – число молекул растворителя в растворе, а 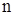 – число молекул растворяемого вещества. Концентрацией раствора назовем отношение – число молекул растворяемого вещества. Концентрацией раствора назовем отношение 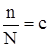 ; согласно сделанному предложению ; согласно сделанному предложению 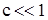 . .
Найдем выражение для термодинамического потенциала раствора. Пусть 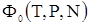 есть термодинамический потенциал чистого растворителя (в котором ничего не растворено). Согласно формуле есть термодинамический потенциал чистого растворителя (в котором ничего не растворено). Согласно формуле 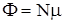 (справедливой для чистых веществ) его можно написать в виде, (справедливой для чистых веществ) его можно написать в виде,
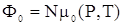 . . |
(1) |
где 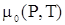 – химический потенциал чистого растворителя. Обозначим посредством – химический потенциал чистого растворителя. Обозначим посредством 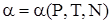 малое изменение, которое испытал бы термодинамический потенциал при введении в растворитель одной молекулы растворяемого вещества. В силу предполагаемой слабости раствора молекулы растворенного вещества в нем находятся на сравнительно больших расстояниях друг от друга, и поэтому их взаимодействие слабо. Пренебрегая этим взаимодействием, можно утверждать, что изменение термодинамического потенциала при введении в растворитель малое изменение, которое испытал бы термодинамический потенциал при введении в растворитель одной молекулы растворяемого вещества. В силу предполагаемой слабости раствора молекулы растворенного вещества в нем находятся на сравнительно больших расстояниях друг от друга, и поэтому их взаимодействие слабо. Пренебрегая этим взаимодействием, можно утверждать, что изменение термодинамического потенциала при введении в растворитель 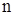 молекул растворяемого вещества равно молекул растворяемого вещества равно 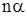 . Однако в получаемом таким путем выражении . Однако в получаемом таким путем выражении 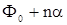 еще не учтена должным образом одинаковость всех молекул растворенного вещества. Это есть выражение, которое получилось бы по формуле (2), если бы при вычислении статического интеграла все частицы растворенного вещества считались отличными друг от друга. Вычисленный таким образом статический интеграл должен в действительности еще быть поделен на еще не учтена должным образом одинаковость всех молекул растворенного вещества. Это есть выражение, которое получилось бы по формуле (2), если бы при вычислении статического интеграла все частицы растворенного вещества считались отличными друг от друга. Вычисленный таким образом статический интеграл должен в действительности еще быть поделен на 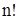 . .
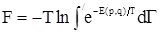 . . |
(2) |
где 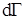 – элемент объема фазового пространства, деленный на – элемент объема фазового пространства, деленный на 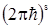 : :
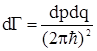 . . |
(3) |
Это приводит к появлению в свободной энергии, а потому и в потенциале 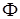 дополнительного члена дополнительного члена 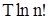 . Таким образом, . Таким образом,
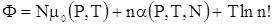 . . |
(3) |
Далее, поскольку 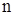 – само по себе очень большое число, хотя и малое по сравнению с – само по себе очень большое число, хотя и малое по сравнению с 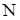 , в последнем члене можно заменить , в последнем члене можно заменить  . Тогда . Тогда
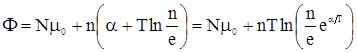 . . |
(3) |
Учтем теперь, что 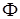 должно быть однородной функцией первого порядка по отношению к должно быть однородной функцией первого порядка по отношению к 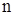 и и 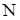 . Для этого, очевидно, стоящая под знаком логарифма функция . Для этого, очевидно, стоящая под знаком логарифма функция 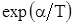 должна иметь вид должна иметь вид 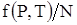 . Таким образом, . Таким образом,
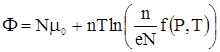 . . |
(3) |
Вводя новую функцию от 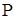 и и 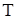 : :
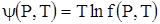 , , |
(3) |
находим окончательно для термодинамического потенциала раствора выражение
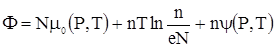 . . |
(8) |
Сделанное в начале этого параграфа предположение относительно прибавления члена вида 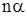 к потенциалу чистого растворителя есть в сущности не что иное, как разложение в ряд по степеням к потенциалу чистого растворителя есть в сущности не что иное, как разложение в ряд по степеням 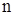 с оставлением только первых членов. Член следующего порядка по с оставлением только первых членов. Член следующего порядка по 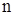 пропорционален пропорционален 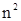 , а с учетом однородности по переменным , а с учетом однородности по переменным 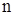 и и 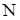 должен иметь вид должен иметь вид 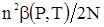 , где , где 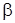 – функция только от – функция только от 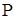 и и 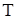 . Таким образом, с точностью до членов второго порядка термодинамический потенциал слабого раствора имеет вид . Таким образом, с точностью до членов второго порядка термодинамический потенциал слабого раствора имеет вид
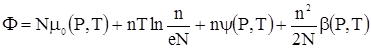 . . |
(3) |
Обобщение этого выражения на случай раствора нескольких веществ очевидно:
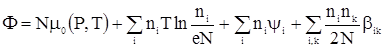 . . |
(3) |
где  – число молекул различных растворенных веществ. – число молекул различных растворенных веществ.
Из (8) легко найти химические потенциалы для растворителя (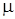 ) и растворенного вещества ( ) и растворенного вещества (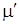 ) в растворе: ) в растворе:
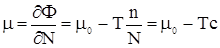 , , |
(3) |
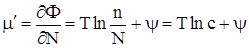 . . |
(12) |
Рассмотрим систему, состоящую из двух соприкасающихся растворов одного и того вещества в различных растворителях (например, в двух несмешивающихся жидкостях). Их концентрации обозначим буквами 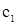 и и 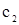 . .
Условием равновесия этой системы является равенство химических потенциалов растворенного вещества в обоих растворах. С помощью (12, см. 2.5) это условие можно написать в виде
 . . |
(1) |
Функции 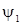 и и 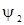 для различных растворителей, конечно, различны. Отсюда находим для различных растворителей, конечно, различны. Отсюда находим
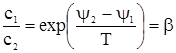 . . |
(2) |
Коэффициент равновесия растворенного вещества между растворами 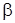 есть функция только от есть функция только от 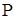 и и 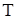 . Таким образом, растворенное вещество распределяется между двумя растворителями так, чтобы отношение концентраций было (при заданных давлении и температуре) всегда одинаково, независимо от полного количества растворенного вещества и растворителей (закон распределения). Этот же закон относится, очевидно, и к растворению одного вещества в двух соприкасающихся фазах одного и того же растворителя. . Таким образом, растворенное вещество распределяется между двумя растворителями так, чтобы отношение концентраций было (при заданных давлении и температуре) всегда одинаково, независимо от полного количества растворенного вещества и растворителей (закон распределения). Этот же закон относится, очевидно, и к растворению одного вещества в двух соприкасающихся фазах одного и того же растворителя.
Далее рассмотрим равновесие между газом (который будем считать идеальным) и его раствором в некотором конденсированном растворителе. Условие равновесия, т.е. равенство химических потенциалов газа чистого и растворенного напишется (с помощью (12) из 2.1.5) в виде
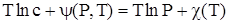 , , |
(2) |
откуда
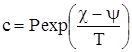 . . |
(4) |
Функция 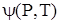 характеризует свойство жидкого (или твердого) раствора; однако при небольших давлениях свойства жидкости очень слабо зависят от давления. Поэтому и зависимость характеризует свойство жидкого (или твердого) раствора; однако при небольших давлениях свойства жидкости очень слабо зависят от давления. Поэтому и зависимость 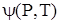 от давления не играет роли, и можно считать, что коэффициент при от давления не играет роли, и можно считать, что коэффициент при 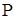 в (4) есть постоянная, не зависящая от давления: в (4) есть постоянная, не зависящая от давления:
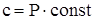 . . |
(4) |
Таким образом, при растворении газа концентрация раствора (слабого) пропорциональна давлению(подразумевается, что молекулы газа переходят в раствор в неизменном виде. Если при растворении молекулы распадаются (например, при растворении водорода Н2
в некоторых металлах), то зависимость концентрации от давления получается иной).
Для учета изменения термодинамических функций при изменении количества вещества в системе, необходимо к дифференциалу каждого термодинамического потенциала добавить член 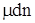 , где , где 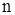 – число частиц вещества в системе, а – число частиц вещества в системе, а 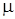 – коэффициент пропорциональности. – коэффициент пропорциональности.
В этом случае термодинамические функции будут описывать также и те системы, в которых совершаются процессы с изменением количества вещества.
Например,
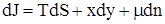 , , |
(1) |
отсюда
 . . |
(2) |
где 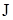 – тепловая функция, или энтальпия ( – тепловая функция, или энтальпия (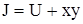 ). ).
Так все термодинамические потенциалы имеют размерность энергии, то согласно формуле (2) коэффициент пропорциональности 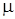 может быть определен как энергия, отнесенная к одному молю. Этот коэффициент получил название химического потенциала. может быть определен как энергия, отнесенная к одному молю. Этот коэффициент получил название химического потенциала.
Выражение (1) справедливо для системы, состоящей из однородных молекул. Если же система состоит из разнородных веществ, последний член в формуле (1) надо представить в виде суммы
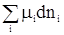 . . |
(3) |
Здесь
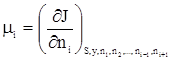 |
(4) |
характеризует изменение энергии при изменении количества данного компонента вещества в системе на один моль.
Понятно, что химический потенциал можно определить, исходя не только из выражения тепловой функции 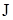 (2), но и из выражения любой другой термодинамической функции. При этом по определению (2), но и из выражения любой другой термодинамической функции. При этом по определению
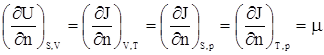 . . |
(5) |
Таким образом, химический потенциал характеризует изменение энергии при изменении количества вещества в системе на один моль.
3.
Разработка теории радиогеохимического эффекта
В данной главе сформулированы общие предположения теории радиогеохимического эффекта, приведена его математическая модель. Здесь решается задачи для нахождения результирующей плотности радиоактивных веществ в пористой среде, которые иллюстрируются на графиках. Определяются величина этого эффекта и условие его возникновения.
В данной работе предпринята попытка исследования особенностей формирования радиогеохимического эффекта на основе концепции, согласно которой диффузия радиоактивных веществ определяется химическим потенциалом и изучения новых возможностей практического использования этого эффекта.
В основу теории положено следующие общенаучные предположения:
– диффузия растворенного вещества пропорциональна градиенту химического потенциала 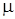
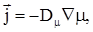 |
(3.1) |
где 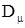 – коэффициент диффузии химического потенциала, – коэффициент диффузии химического потенциала,
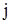 – вектор плотности потока диффундирующих радиоактивных компонентов, – вектор плотности потока диффундирующих радиоактивных компонентов,
в частности поток радиоактивных примесей между скелетом и насыщающим флюидом определяется ньютоновским законом для химического потенциала
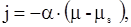 |
(3.2) |
– плотность растворенных изотопов 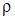 предполагается малой в сравнении с плотностью несущей фазы, которая не изменяется в процессе фильтрации. Перенос растворенных изотопов определяется скоростью фильтрации несущей фазы. Динамика растворенного вещества определяется уравнением неразрывности, следующим из закона сохранения массы предполагается малой в сравнении с плотностью несущей фазы, которая не изменяется в процессе фильтрации. Перенос растворенных изотопов определяется скоростью фильтрации несущей фазы. Динамика растворенного вещества определяется уравнением неразрывности, следующим из закона сохранения массы
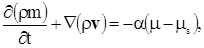 |
(3.3) |
соответственно для плотности радиоактивных веществ в скелете ρs
имеет место следующее уравнение
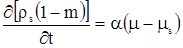 . . |
(3.4) |
Диффузией радиоактивных примесей, кроме массообмена жидкости со скелетом, в уравнениях (3) и (4) пренебрегается;
–для несущей жидкости, предполагаемой несжимаемой, соответствующее уравнение неразрывности предполагается квазистационарным
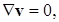 |
(3.5) |
– период полураспада предполагается настолько большим, что за все время процесса вытеснения не происходит заметного изменения плотности радиоактивных примесей за счет радиоактивного распада. Это позволяет пренебречь соответствующими источниками в уравнениях неразрывности и упростить задачу.
Для простоты также предполагается поршневой режим вытеснения водой нефти. Основные закономерности радиогеохимического эффекта без ограничения общности осуществлены на основе плоского одномерного течения, которое хорошо применимо в пластах на больших расстояниях от нагнетательной скважины, т. е. в зоне расположения добывающих скважин, где обычно указанный эффект и регистрируется. Естественным предполагается и пренебрежение диффузионным массообменом пласта с покрывающими и подстилающими породами.
Заметим, что в предполагаемом подходе к скелету отнесена реликтовая вода и другие составляющие, не подвижные в процессе вытеснения, поэтому плотность радиоактивного вещества в скелете включает и содержание радиоактивных веществ в указанных компонентах, что впрочем, улучшает условия применимости разработанной теории.
Математическая постановка задачи в указанных выше предположениях в одномерном случае включает уравнение для радиоактивных примесей в несущей жидкости
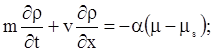 |
(3.6) |
и в скелете пористой среды
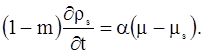 |
(3.7) |
где 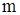 – пористость, – пористость,
 , , |
(3.8) |
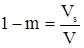 . . |
(3.9) |
Складывая (3.6) в (3.7), получим идентичные уравнения для плотности радиоактивного вещества в жидкости
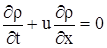 |
(3.10) |
и скелете пористой среды
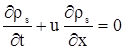 , , |
(3.11) |
где скорость конвективного переноса примесей 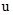 определяется выражением определяется выражением
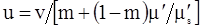 . . |
(3.12) |
Так как химический потенциал является функцией от концентрации, то разложим его в ряд Тейлора вблизи точки равновесия растворенного вещества 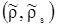
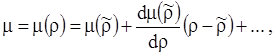
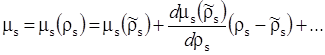 . .
|
(3.13) |
Предполагается, что в равновесии химические потенциалы радиоактивных веществ равны 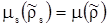 .
Пренебрегая в (3.13) слагаемыми порядка выше первого, получаем .
Пренебрегая в (3.13) слагаемыми порядка выше первого, получаем
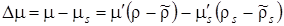 , , |
(3.14) |
где 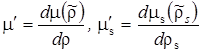 . .
Для простоты считаем, что процесс фильтрации равновесный, так что концентрации радиоактивных веществ в жидкости и скелете пористой среды определяются из условия равенства химических потенциалов
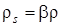 . . |
(3.15) |
Такое же условие и для нефти в скелете 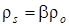 . .
3.1.1.
Постановка задачи
Исследование динамики примесей при поршневом вытеснении нефти водой из пористой среды приводит к краевым задачам математической физики. В общем случае разработка данной теории требует совместного рассмотрения уравнений (3.10) и (3.11) с краевыми условиями. Однако плотности в скелете 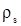 и насыщающей жидкости и насыщающей жидкости 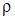 связаны равенством связаны равенством 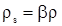 . Это соотношение позволяет отыскивать решение только одного из уравнений, поскольку второе решение находится умножением или делением на . Это соотношение позволяет отыскивать решение только одного из уравнений, поскольку второе решение находится умножением или делением на 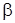 . Можно показать, что найденное таким образом второе решение будет удовлетворять соответствующему дифференциальному уравнению в частных производных. . Можно показать, что найденное таким образом второе решение будет удовлетворять соответствующему дифференциальному уравнению в частных производных.
Краевые условия задачи определяются из очевидных соображений.
Требуется найти решение уравнения для жидкости
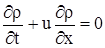 , , |
(3.16) |
в виде функции 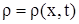 , удовлетворяющие граничным условиям, в подобласти , удовлетворяющие граничным условиям, в подобласти 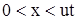 . Предполагается, что на левом конце стержня поддерживается постоянная концентрация радиоактивного вещества . Предполагается, что на левом конце стержня поддерживается постоянная концентрация радиоактивного вещества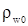 , поэтому для подобласти
, поэтому для подобласти 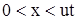 граничное условие имеет вид граничное условие имеет вид
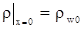 . . |
(3.18) |
Требуется найти решение уравнения для скелета
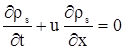 , , |
(3.17) |
в виде функции 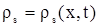 , удовлетворяющие граничным условиям, в подобласти , удовлетворяющие граничным условиям, в подобласти 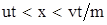 . .
В подобласти 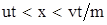 на правой подвижной границе поддерживается неизменной плотность радиоактивного вещества в скелете, поэтому граничное условие для уравнения скелета имеет вид на правой подвижной границе поддерживается неизменной плотность радиоактивного вещества в скелете, поэтому граничное условие для уравнения скелета имеет вид
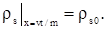 |
(3.19) |
Это условие определяет перенос радиоактивных веществ из нефтенасыщеной зоны пористой среды в водонасыщенную.
3.1.2 Решение задач
Найдем решение уравнения (3.16) в более общем виде. То есть для уравнения
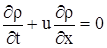 , , |
с граничным условием
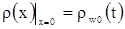 . . |
(3.20) |
для области 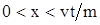
Решение уравнений (3.16) находится методом характеристик.
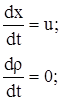 |
(3.21) |
Интегрируя первое уравнение системы (16), получаем
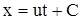 |
(3.22) |
Из второго уравнения следует, что 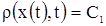 , где , где 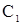 – некоторая постоянная. Но т.к. – некоторая постоянная. Но т.к.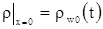 , то , то 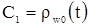 . .
Найдем границы области в котором есть решение.
Пусть при 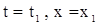 , тогда , тогда
Для начального момента, при 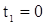 и и 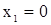
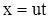 |
(3.23) |
Уравнение (3.23) представляет собой границу.
Параметризуем уравнение (3.22).
Зададим 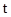 так, чтобы получить значение при так, чтобы получить значение при 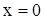 , т. е. , т. е. 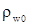 . .
При 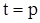 , , 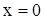
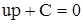 |
(3.24) |
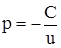 |
(3.25) |
Подставляя значение параметра в (15) получим
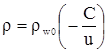 |
(3.26) |
Так как 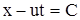 , то , то
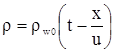 |
(3.27) |
Таким образом это выражение (3.27) есть решение уравнения (3.16) в более общем виде.
Для частного случая, т. е. 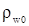 не зависит от не зависит от 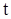 , решение , решение
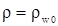 |
(3.28) |
Полученное решение (8) для плотности радиоактивного вещества в вытесняющей жидкости, удовлетворяет граничному условию для жидкости в подобласти 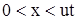 . .
Решение для плотности радиоактивного вещества в скелете в той же области получим из условия равенства химических потенциалов
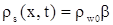 . . |
(3.29) |
Таким же образом, в более общем виде решим уравнение для скелета
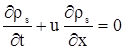 , , |
(3.30) |
с граничным условием
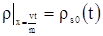 , , |
(3.31) |
для области 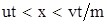 . .
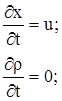 |
(3.32) |
Интегрируя первое уравнение (3.32), получаем
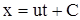 . . |
(3.33) |
Из второго уравнения следует, что 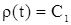 , где , где 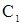 – некоторая постоянная. Но т.к. – некоторая постоянная. Но т.к.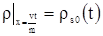 , то , то 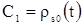 . .
Параметризуем уравнение (3.33): при 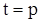 , , 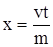 . Тогда . Тогда
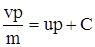 ; ; |
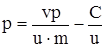 ; ; |
Так как
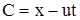 . . |
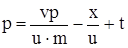 . . |
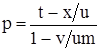 . . |
(3.34) |
Подставим значение параметра (3.34) в граничное условие для скелета пористой среды
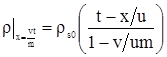 , , |
То теперь
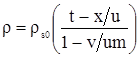 , , |
(3.35) |
Выражение (3.35) есть решение уравнения для скелета (3.30) в общем виде. Частное решение получаем из (3.35) исключая 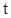 . .
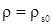 . . |
(3.36) |
Полученное решение (3.36) для плотности радиоактивного вещества в скелете, удовлетворяет граничному условию подобласти 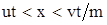 . .
Используя соотношение (3.15) находим решение для плотности радиоактивного вещества в вытесняющей жидкости подобласти 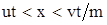 получим из условия равенства химических потенциалов получим из условия равенства химических потенциалов
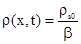 . . |
(3.37) |
Проверка значений на границах подобласти
При 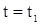 , , 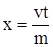 на правой границе на правой границе
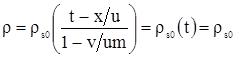 ; ; |
(3.38) |
при 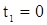 и и 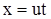 на левой границе на левой границе
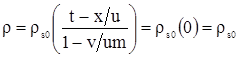 . . |
(3.39) |
Окончательное выражение для плотности радиоактивного вещества в вытесняющей жидкости имеет вид:
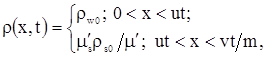 |
(3.40) |
и для плотности радиоактивного вещества в скелете в той же области получим
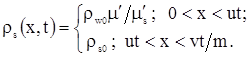 |
(3.41) |
Для области 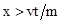 , занимаемой вытесняемой нефтью плотности радиоактивного вещества в скелете и нефти остаются неизменными:
, занимаемой вытесняемой нефтью плотности радиоактивного вещества в скелете и нефти остаются неизменными:
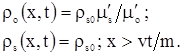 |
(3.42) |
Результирующая плотность радиоактивных веществ в пористой среде ρ+
складывается из плотности в насыщающей жидкости, скелете и нефти, поэтому окончательное выражение имеет вид
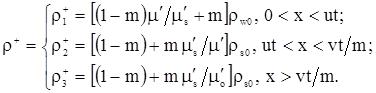 |
(3.43) |
На рисунке приведена зависимость относительной плотности радиоактивного вещества 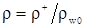 от координаты от координаты 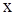 в фиксированный момент времени. В расчетах принято: в фиксированный момент времени. В расчетах принято:  =0.2, μ΄/μs
΄=0.05, μo
΄/μw
΄=10, ρs
0
/ρw0
=5. Сплошной линией изображен график зависимости относительной результирующей плотности радиоактивных веществ, а пунктирной ‑ их плотность в скелете. =0.2, μ΄/μs
΄=0.05, μo
΄/μw
΄=10, ρs
0
/ρw0
=5. Сплошной линией изображен график зависимости относительной результирующей плотности радиоактивных веществ, а пунктирной ‑ их плотность в скелете.
Из рисунка видно, что в области 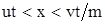 образуется зона II с повышенным содержанием радиоактивных веществ. Отметим, что на границах зон наблюдается скачкообразное изменение плотности радиоактивного вещества. В реальных условиях эти скачки нивелируются диффузией, которая в рассматриваемом случае для простоты не учитывается. образуется зона II с повышенным содержанием радиоактивных веществ. Отметим, что на границах зон наблюдается скачкообразное изменение плотности радиоактивного вещества. В реальных условиях эти скачки нивелируются диффузией, которая в рассматриваемом случае для простоты не учитывается.
 |
| Рис.5.
Зависимость относительной плотности радиоактивного вещества в пористой среде от пространственной координаты в фиксированный момент времени: I – промытая зона, II – зона радиогеохимического эффекта; III – нефтенасыщенная зона; 1 – результирующие значения плотности в пористой среде, 2 – составляющая плотности в скелете |
Из анализа кривых, приведенных на рисунке, следует, что возникновение зоны с повышенной радиоактивностью объясняется вымыванием радиоактивных веществ, первоначально сосредоточенных в скелете, водой.
Из изложенного выше следует, что область радиогеохимического эффекта представляет зону обратного массового влияния вытесняемой жидкости на вытесняющую. Это происходит за счет взаимодействия жидкостей через скелет. Дело состоит в том, что скорость движения границы вытеснения 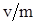 превышает скорость конвективного переноса примесей в пористой среде превышает скорость конвективного переноса примесей в пористой среде  , с которой только и возможно движение разрывов. В результате размеры области радиогеохимического эффекта увеличиваются со временем со скоростью , с которой только и возможно движение разрывов. В результате размеры области радиогеохимического эффекта увеличиваются со временем со скоростью 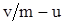 , которая, как показывают оценки, в несколько раз превышает скорость , которая, как показывают оценки, в несколько раз превышает скорость  . Процессы, аналогичные описываемым, происходят при формировании черенковского излучения. . Процессы, аналогичные описываемым, происходят при формировании черенковского излучения.
В реальных условиях возможность измерения распределения радиоактивности в пласте ограничена только определенным числом скважин, в области расположения которых происходит обводнение пласта. В этих скважинах возможно измерение зависимости радиоактивности от времени. Отметим, что наблюдаемая при этом временна̀я развертка радиоактивности соответствует пространственной, изображенной на рисунке.
Условие возникновения радиогеохимического эффекта заключается в повышении радиоактивного фона, математическим выражением которого является неравенство 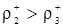 , откуда с использованием (20) получим , откуда с использованием (20) получим
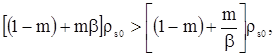 |
(3.44) |
После соответствующих преобразований получим
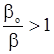 . . |
(3.45) |
Неравенство (3.45) определяет соотношение производных химического потенциала, при котором наблюдается радиогеохимический эффект. В условие (3.45) не входит пористость, это означает, что радиогеохимический эффект должен наблюдаться в пластах с любой пористостью. Отметим, однако, что величина эффекта согласно предлагаемой теории пропорциональна пористости
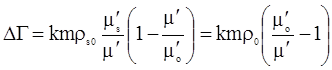 , , |
(3.46) |
где 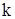 – коэффициент, зависящий от выбора единиц измерения. – коэффициент, зависящий от выбора единиц измерения.
Заключение
Таким образом, предложенная теория в достаточной мере отражает механизм перекачки радиоактивных веществ и образование зоны радиогеохимического эффекта. Полученные результаты могут быть использованы при интерпретации результатов геолого-промысловых исследований для определения принимающих и отдающих интервалов пластов. Они позволяют также более глубоко понять процессы, происходящие с растворенными веществами при движении пресных питьевых вод в подземных пластах.
Литература
1. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. – М.: Наука. – 1986. – 773 с.
2.
Орлинский Б.М. Котроль за разработкой нефтяных месторождений. – М.:Недра, 1982.
3. Хуснуллин М.Х. Геофизические методы контроля разработки нефтяных пластов. –М: Недра, 1989.
4. Валиуллин Р.А., Шарафутдинов Р.Ф., Азизов Ф.Ф., Никифоров А.А., Зелеев М.Х.
Исследование закономерностей формирования радиогеохимического эффекта в пласте//Изв. ВУЗов. Нефть и газ. №3, 2000. С 26-31.
5. Советский энциклопедический словарь. – М.: «Советская энциклопедия», 1985. Под ред. Прохорова А.М.
|