ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Амурский государственный университет»
(ГОУВПО «АмГУ»)
Кафедра энергетики
КУРСОВАЯ РАБОТА
на тему: Расчёт статической и динамической устойчивости системы
по дисциплине: Электромеханические переходные процессы
Исполнитель
студент группы 244
Р.И. Москвичева
Руководитель
Доцент, канд. техн. наук
А.Н. Козлов
Нормоконтроль:
В.А. Клемис
Благовещенск 2006

Рисунок 1 – Схема электропередачи
Таблица 1 – Характеристики элементов электропередачи
| Генератор |
| Тип |
Sн
, МВА |
Xd
|
Xq
|
X’d
|
X2
|
Tj
, c |
Td0
, c |
Te
,c |
| ТГ |
235 |
1,88 |
– |
0,27 |
0,23 |
8 |
6,38 |
0,3 |
| Трансформаторы |
| Т1 |
Т2 |
| Sн
, МВА |
Uк,
% |
Группа соед. |
Sн
, МВА |
Uк,
% |
Группа соед. |
| 250 |
11 |
 |
2´125 |
10,5 |
 |
| Нагрузка |
Линия |
| Рн
,МВт |
сosjн
|
Скольжение, S0
|
Tj
, c) |
L,км |
Uн
, кВ |
| 150 |
0,87 |
0,018 |
4 |
60 |
220 |
РЕФЕРАТ
Работа 25 страниц, 2 таблицы, 13 рисунков.
Относительные единицы, АРВ, короткое замыкание, сопротивление, нагрузка, мощность, угол, ЭДС, статическая устойчивость, динамическая устойчивость, коэффициент запаса по статической устойчивости.
Построение векторных диаграмм, угловых характеристик. Расчёт запаса статической устойчивости, динамической устойчивости, допустимого времени перерыва по условиям устойчивости.
Содержание
Введение
1. Определение параметров схемы замещения и расчёт исходного установившегося режима
1.1 Общие положения
1.2 Определение параметров элементов схемы замещения
1.3 Расчёт исходного установившегося режима
2. Расчёт статической устойчивости
3. Расчет динамической устойчивости
3.1 Общие положения
3.2 Расчёт ДУ по правилу площадей
3.3 Приближённый расчет ДУ методом последовательных интервалов
4. Расчёт устойчивости узла нагрузки
4.1 Статическая устойчивость типовой нагрузки
4.2 Динамическая устойчивость асинхронной нагрузки
Заключение
Библиографический список
Введение
В то время, как теория установившихся режимов развивалась в правильном направлении и быстро приспособилась к нуждам практики, сущность переходных процессов оставалась невыявленной. На примере развития электромашиностроения нетрудно проследить, насколько важен учёт явлений переходных процессов, в частности при коротких замыканиях.
Первоначальные конструкции электрических машин выполнялись лишь в соответствии с требованиями нормальной работы. Пока мощности машин были малы, их конструкции обладали как бы естественным запасом устойчивости против механических и тепловых действий токов короткого замыкания. Однако такое положение существовало недолго. По мере роста мощности машин и особенно после осуществления их параллельной работы, размер повреждений машин при коротких замыканиях резко возрос. Успех предлагаемых конструкций зависел от достоверности знаний самого процесса КЗ. Так постепенно создавались всё более совершенные конструкции электромашин. В современном исполнении они являются одним из надёжных элементов системы.
Более серьёзная разработка теории переходных процессов в электрических машинах начиналась с первых лет двадцатого века. Наряду с теоретическими исследованиями значимо важной являлась разработка практических методов расчёта переходных процессов.
1.
Определение параметров схемы замещения ирасчёт исходного установившегося режима
1.1 Общие положения
При выполнении расчётов устойчивости необходимо составить расчётную схему замещения электропередачи, которая составляется из схем замещения отдельных элементов. Элементы электропередачи представляются индуктивными сопротивлениями. Нагрузка представляется в комплексном виде. Элементы схемы замещения и параметры режима определяются в относительных единицах (о.е.). При этом за базисные величины берём номинальную мощность генератора и напряжение на шинах нагрузки. Ряд величин оставляем в именованных единицах: время t(с), постоянные инерции Т(с), углы d(град) и j(град). Этим определяется форма записи уравнений движения, приводимых далее. При определении параметров будем использовать приближённое приведение по средним коэффициентам трансформации.
1.2 Определение параметров элементов схемы замещения
Хл
Хт2
Хг
Хт1
                                           Eг
Хл
Хт2 Eг
Хл
Хт2
Рисунок 2 – Схема замещения
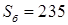 МВА; МВА;
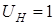 о.е. о.е.
Переводу в о.е. подлежат значения всех мощностей, напряжений и ЭДС. При этом учитываем, что к базисным условиям приводятся как полные мощности, так и их составляющие.
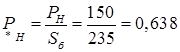 о.е.; о.е.;
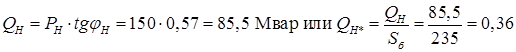 о.е.; о.е.;
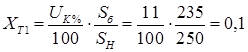 о.е. о.е.
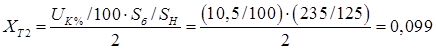 о.е.; о.е.;
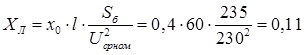 о.е. о.е.
1.3 Расчет исходного установившегося режима
Генератор при расчётах в схеме замещения представляется индуктивным сопротивлением ХГ
и приложенной за ним ЭДС ЕГ
. Величины сопротивления и ЭДС зависят от типа генератора, отсутствия или наличия АРВ и способа регулирования.
1) При отсутствии АРВ: ХГ
=Хd
=1,88 о.е.; ЕГ
=Еq
– синхронные сопротивления и ЭДС.
Расчёт величин ведётся по формуле:
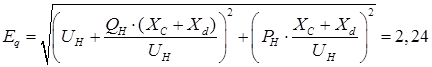 о.е, о.е,
где 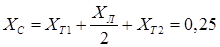 ; ;
По формуле
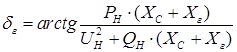 ; ;
определяются углы d0
, d’
0
, d0
U
, характеризующие сдвиг вектора соответствующей ЭДС ЕГ
относительно вектора напряжения UH
.
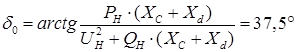 . .
2) При наличии АРВ ПД: ХГ
=Хd
'=0,27 о.е.; ЕГ
=Е' – переходные сопротивления и ЭДС.
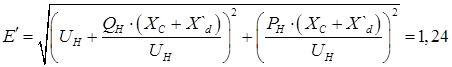 о.е.; о.е.;
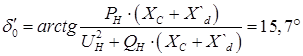
3) При наличии АРВ СД: ХГ
=0; ЕГ
=UГ
– напряжение генератора.
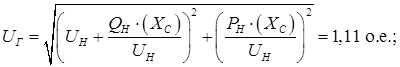
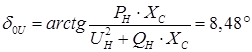 . .
Продольная составляющая переходной ЭДС:
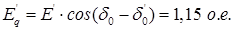
По рассчитанным значениям ЭДС и углов и заданному значению U*
н
=1 в координатной плоскости (d, q) в масштабе строим векторную диаграмму
Рисунок 3 – Векторная диаграмма неявнополюсного генератора
2. Расчет статической устойчивости
При выполнении расчётов предполагается, что устройства АРВ безинерционны и обеспечивают отсутствие самораскачивания. Предел передаваемой мощности определяется максимумом статической угловой характеристики мощности 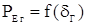 . Учёт действия устройств АРВ производится путём введения соответствующих ЭДС ЕГ
=const, приложенных за соответствующими сопротивлениями ХГ
. . Учёт действия устройств АРВ производится путём введения соответствующих ЭДС ЕГ
=const, приложенных за соответствующими сопротивлениями ХГ
.
Коэффициент запаса статической устойчивости по мощности определяется как
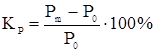
1) При расчёте запаса статической устойчивости при отсутствии АРВ турбогенератор представляется в схеме замещения синхронным индуктивным сопротивлением по продольной оси Xd
и приложенной за ним синхронной ЭДС Eq
. Угловая характеристика мощности при этом имеет вид
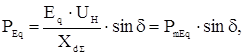
где PmEq
– идеальный предел мощности нерегулируемой передачи;
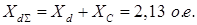 ; ;
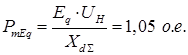 ; ;
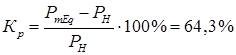 . .
2) Идеальный предел передаваемой мощности при наличии АРВ ПД определяется приближённо и без учёта явнополюсности при Е'q
=const и ХГ
=Х'd
=0,37.
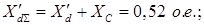
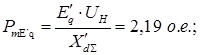
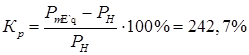 . .
3) При наличии АРВ СД (UГ
=const; ХГ
=0)
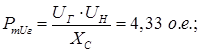
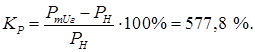
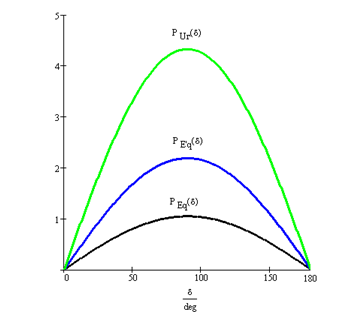
Рисунок 4 – Характеристики мощности
Вывод: наличие АРВ разных видов увеличивает запас статической устойчивости рассматриваемой электропередачи; наибольший запас статической устойчивости имеет место при наличии АРВ СД.
3.
Расчёт динамической устойчивости
3.1 Общие положения
Исследования динамической устойчивости (ДУ) основываются на методах численного решения дифференциального уравнения относительного движения ротора генератора.
При выполнении упрощённых расчётов принимаются следующие основные допущения:
- мощность турбины считается неизменной в течении всего переходного режима;
- мощность, вырабатываемая генератором, считается изменяющейся мгновенно при изменении в схеме электропередачи в следствии КЗ или коммутации;
- апериодические моменты, обусловленные потерями мощности, не учитываются.
С учётом указанных допущений, для простейшей схемы электропередачи, дифференциальное уравнение относительного движения ротора может быть записано в виде:
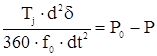 , ,
где Тj
(c) – постоянная инерции ротора генератора; t (c) – время; f0
=50 Гц;
d (эл. град); Р0
=РН
– мощность турбины.
Электрическая мощность генератора Р без учёта явнополюсности определяется по угловой характеристике мощности
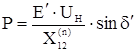
где 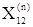 – взаимное сопротивление между точкой приложения ЭДС Е' и шинами системы UH
для состояния «n» схемы. – взаимное сопротивление между точкой приложения ЭДС Е' и шинами системы UH
для состояния «n» схемы.
Величина 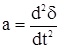 представляет собой ускорение рассматриваемого генератора. представляет собой ускорение рассматриваемого генератора.
В данной курсовой работе выполняются два расчёта динамической устойчивости электропередачи: без учёта (приближённый расчёт по правилу площадей и методом последовательных интервалов) и с учётом реакции якоря генератора и действия АРВ (уточнённый расчет методом последовательных интервалов).
3.2 Расчёт ДУ по правилу площадей
При выполнении приближённого расчёта по формуле строятся угловые характеристики мощности при Е'=const. Генератор вводится в схему замещения своим переходным сопротивлением X'd
. Взаимное сопротивление 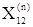 определяется с учётом сопротивления аварийного шунта DХ(
n
)
, зависящего от вида КЗ. определяется с учётом сопротивления аварийного шунта DХ(
n
)
, зависящего от вида КЗ.
Нормальный режим.
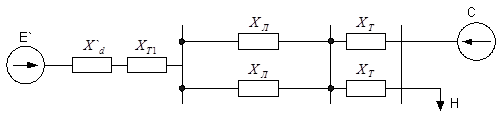
Рисунок 5 – Нормальный режим
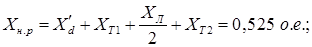
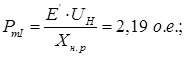
Первый аварийный режим.
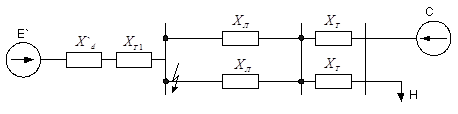
Рисунок 6 – Аварийный режим
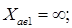
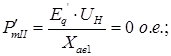
Второй аварийный режим.
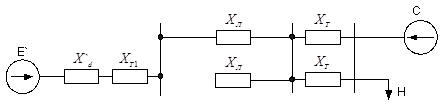
Рисунок 7 – Отключение одного выключателя
Проведя те же преобразования, что и первом аварийном режиме, получим суммарное сопротивление Хш2
.
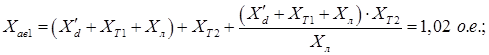
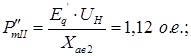
Послеаварийный режим.

Рисунок 8 – Послеаварийный режим
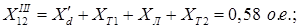
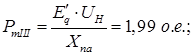
По результатам вычислений строим характеристики нормального PI
, первого P`II
и второго аварийного P``II
и послеаварийного PIII
режимов.

Рисунок *9 – Характеристики мощностей
Исходя из равенства площадок, характеризующих избыточные кинетические энергии ускорения и торможения, определим предельный угол отключения КЗ dпр.откл
:
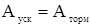 ; ;
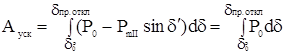 ; ;
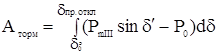 ; ;
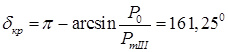 ; ;
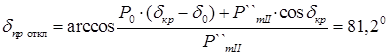 ; ;
По отношению площадки возможного торможения к площадке фактического ускорения оценивается запас динамической устойчивости:
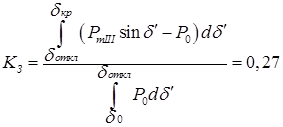 . .
3.3 Приближённый расчет ДУ методом последовательных интервалов
При приближённом расчёте метод последовательных интервалов используется для численного интегрирования дифференциального уравнения. В результате определяются зависимости d=f(t) и a=f(t). При этом переходный процесс разбивается на малые отрезки времени (Dt=0,05 c), на протяжении которых ускорение а считается неизменным.
Порядок расчёта следующий:
1. Для начала переходного процесса по разности мощностей турбины и генератора DР(0)
находится изменение угла за первый расчётный интервал
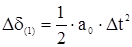 , ,
где 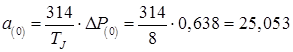 ; ;
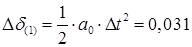 . .
Определяется значение угла в конце первого интервала:
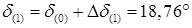 . .
2. При новом значении угла d(1)
вычисляется разность мощностей в начале второго интервала 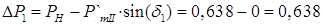 о.е. и определяется приращение угла за второй интервал времени: о.е. и определяется приращение угла за второй интервал времени:
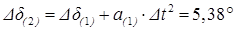 ; ;
Новое значение угла равно
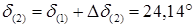 , ,
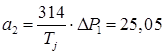
Т.к. на данном промежутке времени происходит отключение выключателя Q1, то на второй аварийной характеристике определяется приращение мощности и ускорение.
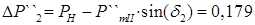 о.е.; о.е.;
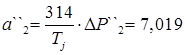 ; ;
3. Приращение угла во всех последующих интервалах определяется по формуле
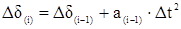 . .
При отключении КЗ, когда разность мощностей внезапно изменяется от 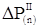 до до 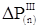 , приращение угла в n+1 интервале определяется по выражению , приращение угла в n+1 интервале определяется по выражению
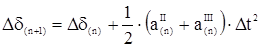 . .
По этому алгоритму расчёт продолжается либо до начала уменьшения угла d, что свидетельствует о сохранении устойчивости, либо до предельного по условиям устойчивости угла dкр
.
Результаты расчёта записываем в таблицу 1.
Таблица 2 – Расчёт динамической устойчивости
| t, c |
d, град. |
DP, о.е. |
a |
Dd, град. |
| 0 |
16,967 |
0,638 |
25,053 |
1,794 |
| 0,05 |
18,761 |
0,638 |
25,053 |
5,383 |
| 0,1 |
24,144 |
0,638 |
25,053 |
7,68 |
| 0,15 |
31,824 |
0,046 |
1,804 |
6,66 |
| 0,2 |
38,484 |
-0,597 |
-23,451 |
3,301 |
| 0,25 |
41,784 |
-0,685 |
-26,883 |
-0,55 |
| 0,3 |
41,234 |
-0,671 |
-26,323 |
-4,321 |
| 0,35 |
36,914 |
-0,554 |
-21,761 |
-7,778 |
| 0,4 |
29,136 |
-0,427 |
-16,747 |
-10,177 |
| 0,45 |
18,959 |
-0,072 |
-2,84 |
-10,583 |
| 0,5 |
8,376 |
0,32 |
12,547 |
-8,786 |
| 0,55 |
-0,41 |
0,654 |
25,668 |
-5,109 |
По результатам данного расчёта строим зависимости d=f(t) и a=f(t) с обозначением характерных углов и соответствующих значений времени.
Рисунок 10 – Зависимость угла от времени
Рисунок 11 – Зависимость ускорения от времени
3.4 Уточненный расчет динамической устойчивости
Первый интервал 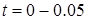 . .
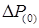 - небаланс мощности в начале первого интервала. - небаланс мощности в начале первого интервала.
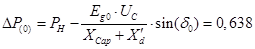 о.е о.е
Под действием 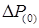 на роторе генератора возникает ускорение которое считается по формуле: на роторе генератора возникает ускорение которое считается по формуле:
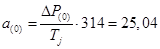 о.е. о.е.
Изменение угла 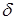 за первый интервал: за первый интервал:
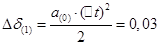 . .
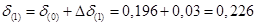 . .
Изменение вынужденной ЭДС к концу интервала, где принимаем 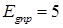 , а t берется равным правой границе соответствующего интервала: , а t берется равным правой границе соответствующего интервала:
 о.е о.е
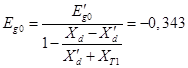 о.е о.е
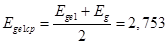 о.е о.е
Изменение переходной ЭДС за первый интервал
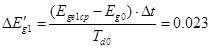 о.е о.е
Переходная ЭДС к концу первого интервала
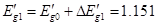
Приращение угла стало отрицательным, следовательно, угол будет уменьшаться и машина сохранит динамическую устойчивость. По результатам данного расчёта строим зависимости d=f(t) и a=f(t) с обозначением характерных углов и соответствующих значений времени. К базисным условиям приводится постоянная времени обмотки возбуждения
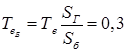
Задаемся пределами изменения ЭДС
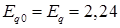
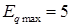 о.е.; о.е.;
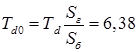
4.
Расчёт устойчивости узла нагрузки
4.1 Статическая устойчивость асинхронной нагрузки
В случае отключения выключателя В баланс мощности в оставшейся части системы сохранится. Не изменится также и напряжение на шинах нагрузки, однако теперь оно и будет зависеть от режима работы эквивалентной асинхронной нагрузки. При определении запаса устойчивости в качестве независимой переменной теперь должна рассматриваться ЭДС Ег, зависящая от вида регулирования. Генератор вводится в схему замещения соответствующим сопротивлением 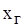 . .
Нагрузка представлена в виде комплексного сопротивления

Активное сопротивление схемы замещения 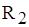 эквивалентного асинхронного двигателя определяется как эквивалентного асинхронного двигателя определяется как
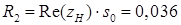
Для обеспечения устойчивости асинхронной нагрузки необходимо выполнение прямого критерия устойчивости:
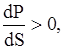
что эквивалентно условиям: 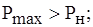 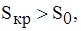
Для генератора без АРВ:
Условие устойчивости может, записано в виде 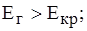 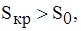
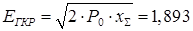
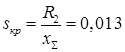
Условие не проходит, значит, нагрузка статически не устойчива.
По известному значению ЭДС 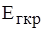 можно найти соответствующее ей критическое напряжение на шинах нагрузки и определить запас статической устойчивости нагрузки по напряжению можно найти соответствующее ей критическое напряжение на шинах нагрузки и определить запас статической устойчивости нагрузки по напряжению
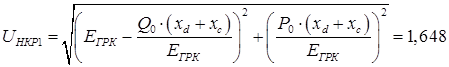
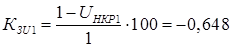
Для генератора с АРВ ПД:
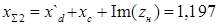
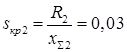
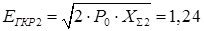
Условия не выполняются - нагрузка статически не устойчива.
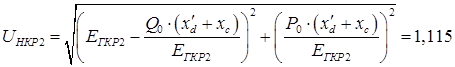
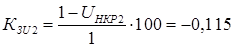
Для генератора с АРВ СД:
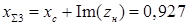
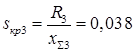
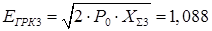
Условия выполняются - нагрузка статически не устойчива.
По известному значению ЭДС 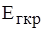 можно найти соответствующее ей критическое напряжение на шинах нагрузки и определить запас статической устойчивости нагрузки по напряжению можно найти соответствующее ей критическое напряжение на шинах нагрузки и определить запас статической устойчивости нагрузки по напряжению
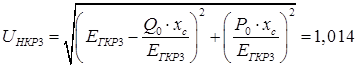
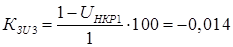
4.2
Динамическая устойчивость асинхронной нагрузки
При расчетах динамической устойчивости не учитываются электромагнитные переходные процессы в обмотках двигателей. Изменение скольжения, обусловленное изменением режима, определяется численным интегрированием уравнения движения асинхронного двигателя:
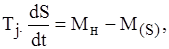
где 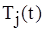 - постоянная инерции, приведенная к номинальной мощности двигателя; - постоянная инерции, приведенная к номинальной мощности двигателя;
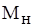 - номинальный механический момент сопротивления; - номинальный механический момент сопротивления;
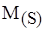 - электромагнитный момент двигателя; - электромагнитный момент двигателя;
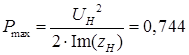
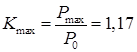

В случае к.з. на двигателе напряжение Uд
уменьшается и для его определения необходимо рассматривать схему замещения.
Напряжение Uд
на зажимах двигателя, в зависимости от скольжения определится по формуле:
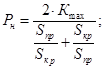
решив полученное уравнение, найдем
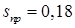

Заключение
При выполнении курсовой работы по дисциплине «Электромеханические переходные процессы в электрических сетях» были приобретены навыки практических расчётов статической и динамической устойчивости систем и узлов нагрузки.
В ходе выполнения курсовой работы были произведены следующие расчёты:
- расчёт исходного режима и построение векторной диаграммы синхронного генератора;
- определение запаса статической устойчивости по пределу передаваемой мощности при отсутствии АРВ, при наличии АРВ ПД и при наличии АРВ СД;
- расчёт динамической устойчивости по методу площадей и определение её запаса;
- расчёт динамической устойчивости методом последовательных интервалов (приближённый и уточнённый расчёт);
- расчёт допустимого времени перерыва электроснабжения по условиям устойчивости эквивалентной асинхронной нагрузки.
Библиографический список
1. Веников В.А. Переходные электромеханические процессы. Москва. Энергия, 1970.
2. Переходные процессы в системах электроснабжения. Часть II. Электромеханические переходные процессы. Шабад В.К. Москва. ВЗПИ, 1990.
3. Степанов А.С. Методические указания к курсовой работе по дисциплине «Электромеханические переходные процессы в электрических сетях». Благовещенск. 1989.
4. Ульянов С.А. Электромагнитные переходные процессы. Москва. Энергия, 1970.
|