| Министерство образования и науки Республики Казахстан Костанайский государственный университет им. А. Байтурсынова
Факультет экономический
Кафедра информационных систем
Доклад
Дисциплина: Эконометрика
На тему: Автокорреляция в остатках.
Критерий Дарбина-Уотсона
Выполнила: студентка 2 курса
050509-Финансы,08-501-45 группы
Бимурзина Бахытгуль
Проверил: Жуаспаев Т.А.
Костанай,2010 год
СОДЕРЖАНИЕ:
1.Критерий Дарбина-Уотсона.
2.Уравнение автокорреляции в остатках путем расчета критерия Дарбина-Уотсона.
1. Критерий Дарбина-Уотсона (или DW-критерий) — статистический критерий, используемый для нахождения автокорреляции остатков первого порядка регрессионной модели. Критерий назван в честь Джеймса Дарбина и Джеффри Уотсона. Критерий Дарбина-Уотсона рассчитывается по следующей формуле:
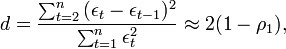
где ρ1
— коэффициент автокорреляции первого порядка.
В случае отсутствия автокорреляции ошибок d
= 2, при положительной автокорреляции в стремится к нулю, а при отрицательной стремится к 4:
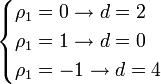
На практике применение критерия Дарбина—Уотсона основано на сравнении величины d
с теоретическими значениями dL
и dU
для заданного числа наблюдений n
, числа независимых переменных модели k
и уровня значимости α.
Если d
< dL
, то гипотеза о независимости случайных отклонений отвергается (следовательно присутствует положительная автокорреляция);
Если d
> dU
, то гипотеза не отвергается;
Если dL
< d
< dU
, то нет достаточных оснований для принятия решений.
Когда расчетное значение d
превышает 2, то с dL
и dU
сравнивается не сам коэффициент d
, а выражение (4 − d
).
Также с помощью данного критерия выявляют наличие коинтеграции между двумя временными рядами. В этом случае проверяют гипотезу о том, что фактическое значение критерия равно нулю. С помощью метода Монте-Карло были получены критические значения для заданных уровней значимости. В случае, если фактическое значение критерия Дарбина—Уотсона превышает критическое, то нулевую гипотезу об отсутствии коинтеграции отвергают.
Недостатки:
Неприменим к моделям авторегрессии
.
Не способен выявлять автокорреляцию второго и более высоких порядков.
Даёт достоверные результаты только для больших выборок]
.
Критерий h
Дарбина применяется для выявления автокорреляции остатков в модели с распределёнными лагами:
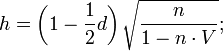
где n
— число наблюдений в модели;
V
— стандартная ошибка лаговой результативной переменной.
При увеличении объёма выборки распределение h
-статистики стремится к нормальному с нулевым математическим ожиданием и дисперсией, равной 1. Поэтому гипотеза об отсутствии автокорреляции остатков отвергается, если фактическое значение h
-статистики оказывается больше, чем критическое значение нормального распределения.
Критерий Дарбина—Уотсона для панельных данных
Для панельных данных используется немного видоизменённый критерий Дарбина—Уотсона:

В отличие от критерия Дарбина—Уотсона для временных рядов в этом случае область неопределенности является очень узкой, в особенности, для панелей с большим количеством индивидуумов.
2. Рассмотрим уравнение регрессии вида:
y t = a + ∑ b j ⋅ x jt + ε t
Для каждого момента (периода) времени t = 1,..., n значение компоненты εt
определяется из соотношения
ε t = y t − y t = y t − (a + ∑ b j ⋅ x jt ).
Рассматривая последовательность остатков как временной ряд, можно построить график их зависимости от времени. В соответствии с предпосылками
МНК остатки εt должны быть случайными. Однако при моделировании временных рядов нередко встречается ситуация, когда остатки содержат тенденцию или циклические колебания. Что свидетельствует о том, что каждое следующее значение остатков зависит от предшествующих. В этом случае говорят о наличии автокорреляции остатков.
Автокорреляция остатков может быть вызвана несколькими причинами,
имеющими различную природу:
1) наличие ошибок измерения в значениях результативного признака;
2) модель может не включать фактор, окапывающий существенное воздействие на результат, влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени t. Кроме того, в качестве таких существенных факто-
ров могут выступать лаговые значения переменных, включенных в модель;
3) модель не учитывает несколько второстепенных факторов, совместное
влияние которых на результат существенно ввиду совпадения тенденций их изменения или фаз циклических колебаний;
4) неправильная спецификация функциональной формы модели. В этом
случае следует изменить форму связи факторных и результативного признаков,
а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции остатков.
Существуют два наиболее распространенных метода определения авто-
корреляции остатков.
Первый метод — это построение графика зависимости остатков от време-
ни и визуальное определение наличия или отсутствия автокорреляции.
Второй метод – использование критерия Дарбина — Уотсона и расчет
величины
n
∑ (ε t − ε t −1 )2
в = i =2 n
Величина в есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии. Практически во всех статистических ППП значение критерия Дарбина – Уотсона указывается наряду с коэффициентом детерминации, значения-
ми t- и F-критериев.
Коэффициент автокорреляции остатков первого порядка определяется как
n
∑ (ε t − ε 1 )(ε t −1 − ε 2 )
i=2
Между критерием Дарбина–Уотсона и коэффициентом автокорреляции остатков первого порядка имеет место следующее соотношение:
в ≈ 2 ⋅ (1 − r1ε ).
Таким образом, если в остатках существует полная положительная автокорреляция и rε1 = 1, то в = 0. Если в остатках полная отрицательная автокорреляция, то rε1 = – 1 и, следовательно, в = 4. Если автокорреляция остатков отсутствует, то rε1 = 0 и в = 2. Следовательно,
0 ≤ в ≤ 4.
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина–Уотсона следующий. Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков. Альтернативные гипотезы Н1 и Н1* состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина–Уотсона dL и dU для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков.
Если фактическое значение критерия Дарбина – Уотсона попадает в зону
неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу H0.
y t = a + b ⋅ xt + ε t ;
Примем некоторые допущения относительно этого уравнения:
• пусть уt и хt не содержат тенденции, например, представляют собой отклонения выровненных по трендам значений от исходных уровней временных
рядов;
• пусть оценки а и b параметров уравнения регрессии найдены обычным
МНК;
• пусть критерий Дарбина – Уотсона показал наличие автокорреляции в
остатках первого порядка.
Основной подход к оценке параметров модели регрессии в случае, когда
имеет место автокорреляция остатков, заключается в следующем: исходная модель регрессии (6.1) с помощью замены переменных приводится к виду
y t′ = a ′ + b ⋅ x t′ + u t , где y t′ = y t − r1ε ⋅ y t −1 ; x t′ = x t − r1ε ⋅ x t −1 ;
u t = ε t − r1ε ⋅ ε t −1 ; a ′ = a (1 − r1ε ).
Здесь rε1 – коэффициент автокорреляции первого порядка.
Поскольку ut, – случайная ошибка, то для оценки параметров преобразованного уравнения можно применять обычный МНК.
Итак, если остатки по исходному уравнению регрессии содержат автокор-
реляцию, то для оценки параметров уравнения используют обобщенный МНК.
Его реализация разбивается на следующие этапы:
1. Перейти от исходных переменных уt и хt к переменным у’t и х’t по фор-
мулам.
2. Применив обычный МНК к уравнению, определить оценки пара-
метров а’ и b.
3. Рассчитать параметр а исходного уравнения из соотношения как
a = a ′ /(1 − r1ε ).
Одним из методов расчета параметров уравнения авторегрессии является
метод инструментальных переменных. Сущность этого метода состоит в том,
чтобы заменить переменную yt-1 из правой части модели, для которой нарушаются предпосылки МНК, на новую переменную ŷt-1, включение которой в модель регрессии не приводит к нарушению его предпосылок.
Искомая новая переменная, которая будет введена в модель вместо yt-1,
должна иметь два свойства.
Во-первых, она должна тесно коррелировать с yt-1, во-вторых, она не должна коррелировать с остатками ut.
Существует несколько способов получения такой инструментальной переменной.
1 способ. Поскольку в модели переменная yt зависит не только от yt-1, но и от xt, можно предположить, что имеет место зависимость yt-1 от xt-1, т. е.
y t −1 = в 0 + в 1 ⋅ x t −1 + u t .
Таким образом, переменную yt-1 можно выразить следующим образом:
y t −1 = y t −1 + u t , где
y t −1 = в 0 + в 1 ⋅ x t −1 .
Распределение этой величины приблизительно можно аппроксимировать
стандартизованным нормальным распределением. Поэтому для проверки гипотезы о наличии автокорреляции остатков можно либо сравнивать полученное фактическое значение критерия h с табличным, воспользовавшись таблицами
стандартизованного нормального распределения, либо действовать в соответствии со следующим правилом принятия решения.
1. Если h > 1,96, нуль–гипотеза об отсутствии положительной автокорреляции остатков отклоняется.
2. Если h < –1,96, нуль–гипотеза об отсутствии отрицательной автокорреляции остатков отклоняется.
3. Если –1,96 < h < 1,96, нет оснований отклонять нуль–гипотезу об отсутствии автокорреляции остатков.
Список использованной литературы:
1. Суслов В. И., Ибрагимов Н. М., Талышева Л. П., Цыплаков А.А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с.
2. Эконометрика. Учебник / Под ред. Елисеевой И.И.. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с.
3. Кремер Н.Ш., Путко Б.А. Эконометрика. — М.: Юнити-Дана, 2003-2004. — 311 с.
4. Ратникова Т.А. Введение в эконометрический анализ панельных данных (рус.) // Экономический журнал ВШЭ. — 2006. — № 3. — С. 492-519.
|