| Задание 1
Необходимо средствами MS Excel подобрать подходящий вариант аппроксимации (линейная, логарифмическая, степенная, полиномиальная, экспоненциальная функция) для заданных табличным способом данных, доказать оптимальность выбора путем сравнения коэффициентов достоверности и аппроксимации для каждого варианта.
Исходные данные
| Год
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
| Объем производства (млн.т)
|
7,07
|
5,1
|
3
|
2,1
|
2,33
|
4,13
|
7
|
Обработанные данные представлены в таблице ниже:
| №
|
Название аппроксимации
|
Уравнение
|
Величина достоверности аппроксимации R2
|
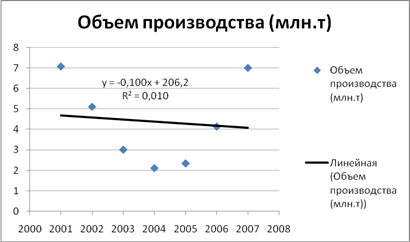
| 1
|
Линейная
|
y = -0,1007x + 206,22
|
0,0109
|
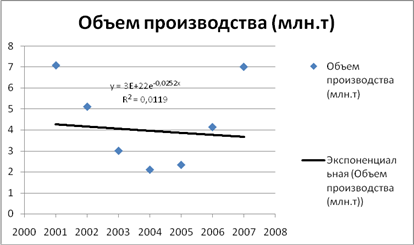
| 2
|
Экспоненциальная
|
y = (3×1022
)e-0,0252x
|
0,0119
|
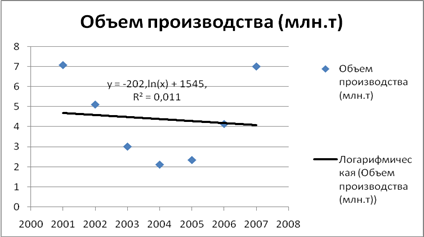
| 3
|
Логарифмическая
|
y = -202,65lnx + 1545,1
|
0,011
|
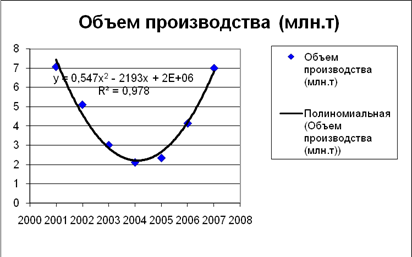
| 4
|
Полиномиальная
|
y = 0,5471x2
- 2193x + 2000000
|
0,9786
|
| 5
|
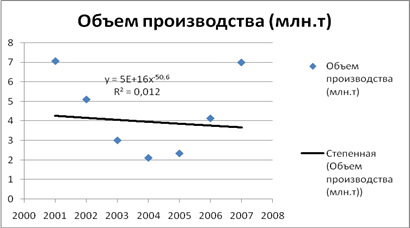
Степенная
|
y = (5×10167
)x-50,615
|
0,012
|
Наиболее оптимальная аппроксимация для исходных данных – полиномиальная кривая (квадратная парабола), так как величина достоверности наиболее близка к единице. Общий вид графика близок к фактическому расположению исходных данных в виде точек на плоскости.
Построенные графики представлены ниже.
Линейная аппроксимация
Экспоненциальная аппроксимация
Логарифмическая аппроксимация
Полиномиальная аппроксимация
Степенная аппроксимация
Задание 2
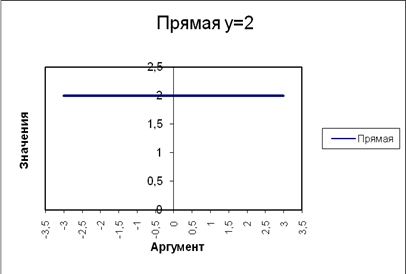
Построить прямую, параллельную оси абсцисс (Ох) и пересекающую ось ординат (Оу) в точке (0; 2) в диапазоне xÎ[-3; 3] с шагом D=0,5.
Так как абсцисса точки, через которую проходит прямая параллельная оси Ох равна 0, а ордината – 2, то уравнение прямой будет у=2.
Для построения прямой в MS Excel представим числовые данные в виде таблицы ниже, а также график функции. Шаг изменения х равен 0,5
Х
|
Y
|
| -3
|
2
|
| -2,5
|
2
|
| -2
|
2
|
| -1,5
|
2
|
| -1
|
2
|
| -0,5
|
2
|
| 0
|
2
|
| 0,5
|
2
|
| 1
|
2
|
| 1,5
|
2
|
| 2
|
2
|
| 2,5
|
2
|
| 3
|
2
|
Задание 3
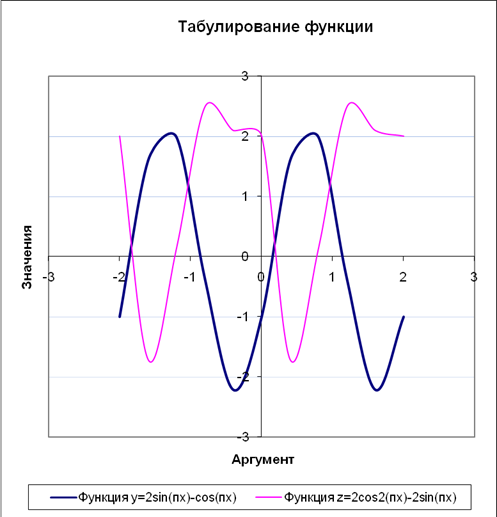
Построить в одной системе координат при xÎ[-2; 2] графики функций:
у=2sin(px)-cos(px), z=2cos2
(px)-2sin(px).
Заданные функции являются периодическими с периодом изменения, равным 2. Примерные значения нулей для каждой функции:
- функция у:
1-ый корень 0,2+2n, где nÎZ, 2-ой корень 1,2+2n, где nÎZ.
- функция z:
1-ый корень 0,3+2n, где nÎZ, 2-ой корень 0,8+2n, где nÎZ.
График и исходные данные для построения находятся ниже в таблицах и на рисунке.
| Функция у=2sin(пx)-cos(пx)
|
Х
|
Y
|
| -2
|
-1
|
| -1,6
|
1,593096038
|
| -1,2
|
1,984587499
|
| -0,8
|
-0,36655351
|
| -0,4
|
-2,21113003
|
| 0
|
-1
|
| 0,4
|
1,593096038
|
| 0,8
|
1,984587499
|
| 1,2
|
-0,36655351
|
| 1,6
|
-2,21113003
|
| 2
|
-1
|
| Функция z=2cos2(пx)-2sin(пx)
|
Х
|
Z
|
| -2
|
2
|
| -1,6
|
-1,71113003
|
| -1,2
|
0,13344649
|
| -0,8
|
2,484587499
|
| -0,4
|
2,093096038
|
| 0
|
2
|
| 0,4
|
-1,71113003
|
| 0,8
|
0,13344649
|
| 1,2
|
2,484587499
|
| 1,6
|
2,093096038
|
| 2
|
2
|
Задание 4
Создать макрос, который выполняет следующее форматирование документа MS Word:
| Ориентация страницы
|
Книжная
|
| Поля (в см)
|
Верхнее – 1
Нижнее – 1,5
Слева – 1
Справа – 1
|
| Гарнитура
|
Arial
|
| Цвет текста
|
синий
|
| размер
|
14
|
| Интервал между символами
|
-
|
| подчеркивание
|
есть
|
| выравнивание
|
По правому краю
|
| Интервал между абзацами
|
Перед 6 пт
|
| Интервал междустрочный
|
полуторный
|
| Номер страницы
|
Внизу слева
|
Запись макроса
1. Открыть новый документ MS Word.
2. В меню Сервис выделите пункт Макрос, а затем выберите команду Начать запись.
3. В поле Имя макроса введите имя нового макроса, например, «Макрос_задание_4».
4. В списке Макрос доступен для выберите Помилка! Неприпустимий об'єкт гіперпосилання.
или документ, в котором будет храниться макрос. В раскрывающемся списке Макрос доступен для
следует выбрать файл или шаблон, в который будет сохранен макрос. Если макрос предполагается использовать неоднократно в различных документах, то нужно выбрать параметр Всех документов (Normal.dot).
5. Введите описание макроса в поле Описание.
6. Если макросу не требуется назначать кнопку Помилка! Неприпустимий об'єкт гіперпосилання.
, команду Помилка! Неприпустимий об'єкт гіперпосилання.
или Помилка! Неприпустимий об'єкт гіперпосилання.
, нажмите кнопку OK, чтобы начать запись макроса.
7. С помощью мыши и клавиатуры выполните действия, указанные в таблице задания 4. При записи нового макроса допускается применение мыши только для выбора команд и параметров. Для записи таких действий, как выделение текста, необходимо использовать клавиатуру. Например, с помощью клавиши F8 можно выделить текст, а с помощью клавиши END — переместить курсор в конец строки.
8. Для завершения записи макроса нажмите кнопку Остановить запись.
9. Закрыть Новый документ (можно без сохранения).
10. Открыть какой-нибудь документ, который следует отформатировать указанным образом.
11. В меню Сервис выберите команду Макрос, а затем — команду Макросы.
12. В списке Имя выберите имя Помилка! Неприпустимий об'єкт гіперпосилання.
, который требуется выполнить.
13. Нажмите кнопку Выполнить. Форматирование документа изменится согласно параметрам, указанным в макросе.
Задание 5
Задача оптимизации (линейное программирование). Имеются корма 2 видов: сено и силос. Их можно использовать для скота в количестве не более 50 и 85 кг соответственно. Требуется составить кормовой рацион минимальной стоимости, в котором содержится не менее 30 кормовых единиц, не менее 1000 г протеина, не менее 100 г кальция, не менее 80 г фосфора. Данные о питательности кормов и их стоимости в расчете на 1 кг приведены в следующей таблице:
| Питательные вещества
|
Корма
|
Нижняя норма содержания питательных веществ
|
| Сено
|
Силос
|
| Кормовые единицы, кг
|
0,5
|
0,3
|
30
|
| Протеин, г
|
40
|
10
|
1000
|
| Кальций, г
|
1,25
|
2,5
|
100
|
| Фосфор, г
|
2
|
1
|
80
|
| Стоимость 1 кг, руб.
|
12
|
8
|
-
|
Составим математическую модель данной задачи, предварительно переведя весовые единицы измерения в килограммы:
| Корм.ед., кг
|
Протеин, кг
|
Кальций, кг
|
Фосфор, кг
|
Нижняя граница нормы, кг
|
Цена за кг, руб.
|
| Сено
|
0,5
|
0,04
|
0,00125
|
0,002
|
50
|
12
|
| Силос
|
0,3
|
0,01
|
0,0025
|
0,001
|
85
|
8
|
| Нижняя граница
|
30
|
1
|
0,1
|
0,08
|
Х1 (кг) – количество сена,
Х2 (кг) – количество силоса.
Система ограничений:
0,5Х1+0,3Х2≥30,
0,04Х1+0,01Х2≥1,
0,00125Х1+0,0025Х2≥0,1,
0,002Х1+0,001Х2≥0,08,
Х1≤50, Х2≤85.
Целевая функция: F=12Х1+8Х2®min

Ячейки G2:G3 – искомое решение задачи. Ячейки В5:Е5 – формулы ограничений:
=B2*$G$2+B3*$G$3,
=C2*$G$2+C3*$G$3,
=D2*$G$2+D3*$G$3,
=E2*$G$2+E3*$G$3.
В ячейках F2:F3 – значения, ограничивающие количество сена и силоса. В задании условий используются такие формулы:
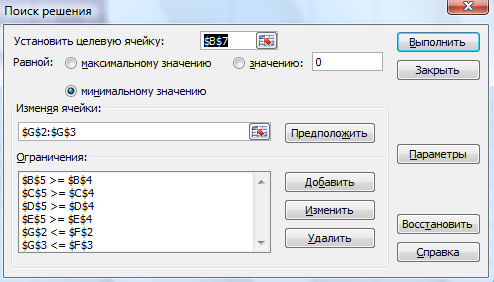
В целевой ячейке находится формула: =H2*G2+H3*G3.
Задание 6
В Сочи существует спрос на следующие товары
| Наименование товара
|
Спрос, единиц
|
| Товар 1
|
1000
|
| Товар 2
|
2500
|
| Товар 3
|
2000
|
| Товар 4
|
2500
|
Товары находятся в разных городах на складах. Запасы товара на складах (единиц) в различных городах представлены в следующей таблице:
| Наименование товара
|
Ростов
|
Москва
|
Ставрополь
|
Краснодар
|
| Товар 1
|
800
|
50
|
250
|
120
|
| Товар 2
|
120
|
100
|
500
|
1200
|
| Товар 3
|
860
|
1500
|
500
|
1300
|
| Товар 4
|
400
|
3050
|
500
|
200
|
Стоимость доставки единицы товара в г. Сочи (руб.) представлена в следующей таблице:
Наименование товара
|
Ростов
|
Москва
|
Ставрополь
|
Краснодар
|
| Товар 1
|
7
|
10
|
4
|
2
|
| Товар 2
|
10
|
40
|
32
|
20
|
| Товар 3
|
70
|
75
|
65
|
50
|
| Товар 4
|
15
|
40
|
25
|
20
|
В столбце «Итого» находятся формулы суммарного объема перевозок по каждому товару:
=СУММ(B20:E20),
=СУММ(B21:E21),
=СУММ(B22:E22),
=СУММ(B23:E23).
В столбце «Max» находятся формулы для расчета предельных объемов перевозок:
=СУММ(B4:E4),
=СУММ(B5:E5),
=СУММ(B6:E6),
=СУММ(B7:E7).
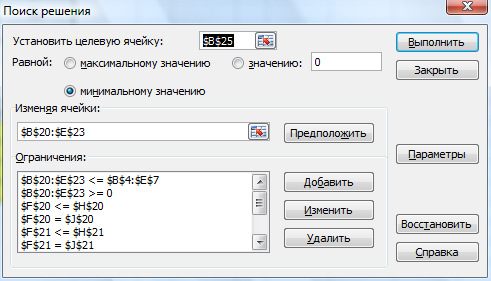
В ячейке В25 находится формула целевой функции:
=СУММПРОИЗВ(B20:E23;B12:E15)

Система ограничений для данной задачи представлена ниже на рисунке:

|