| Реферат по геометрии на тему
«Вписанные и описанные окружности в треугольниках и четырехугольниках
2009 год
Цели:
Углубить знания по теме «Вписанная и описанная окружности в треугольниках и четырехугольниках»
Задачи:
Систематизировать знания по этой теме
Подготовиться к задачам повышенной сложности в ЕГЭ
Теория
Вписанная окружность
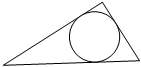 Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности. Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
Теорема: в любой треугольник можно вписать окружность, и притом только одну.
Центр окружности, вписанной в треугольник, находится на пересечении биссектрис треугольника.
Свойство: в любом описанном четырехугольнике суммы противоположных сторон равны.
Признак: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Описанная окружность
 Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
Теорема: около любого треугольника можно описать окружность, и притом только одну.
Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.
Свойство: в любом вписанном четырехугольнике сумма противоположных углов равна 180˚.
Признак: если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность.
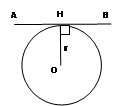 Взаимное расположение прямой и окружности: Взаимное расположение прямой и окружности:
AB – касательная, если OH = r
Свойство касательной:
AB ┴ OH (OH – радиус, проведенный в точку касания H)
 Свойство отрезков касательных, проведенных из одной точки: Свойство отрезков касательных, проведенных из одной точки:
AB = AC
ﮮ BAO = ﮮ CAO
 Теорема Пифагора: Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2 = a2 + b2
Медиана
 Медиана (от лат. mediana — средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Медиана (от лат. mediana — средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
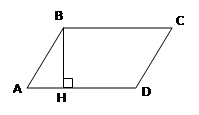 Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Площадь параллелограмма
Площадь параллелограмма равна произведению его основания на высоту:
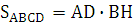
Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними:

Площадь треугольника
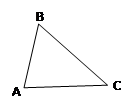 Площадь треугольника равна половине произведения двух его сторон на синус угла между ними: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:
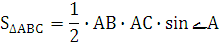
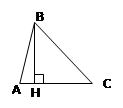 Площадь треугольника равна половине произведения его основания на высоту: Площадь треугольника равна половине произведения его основания на высоту:
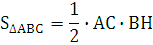
 Площадь прямоугольного треугольника равна половине произведения его катетов: Площадь прямоугольного треугольника равна половине произведения его катетов:
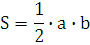
Если высоты двух треугольников равны, то их площади относятся как основания.
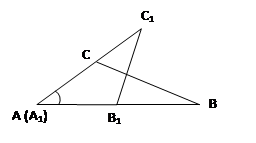 Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы:

Площадь трапеции
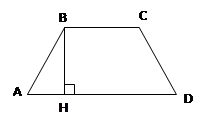 Площадь трапеции равна произведению полусуммы её оснований на высоту: Площадь трапеции равна произведению полусуммы её оснований на высоту:
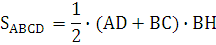
Прямоугольный треугольник
 Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой: Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой:
 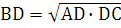
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы:
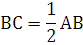
Задачи:
Задача 1: окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
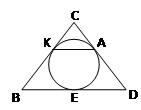
Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10
Найти: KA
Решение:
CD = CB = BK + KC, CD = CB = 15 + 10 = 25
CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD – CA, AD = 25 – 10 = 15
BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30
∆ CKA ~ ∆ CBD (ﮮC – общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12
Ответ: KA = 12
Задача 2: Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O. Найдите ее радиус, если площадь треугольника BOC равна 16.
Дано: ∆ ABC – равнобедренный, AC – основание, ﮮ ACB = 75˚,
 площадь ∆ BOC равна 16 площадь ∆ BOC равна 16
Найти: радиус описанной окружности
Решение:
Проведем медианы AF, CE, BH
∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный
ﮮ HBC = 90˚ - ﮮ ACB, ﮮ HBC = 90˚ - 75˚ = 15˚
BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚
ﮮ COB = 180˚ - (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ - (15˚ + 15˚) = 150˚
S =  ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника), SBOC = ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника), SBOC =  ∙ R ∙ R ∙ sin 150˚ = ∙ R ∙ R ∙ sin 150˚ =  ∙ R ∙ R ∙ ∙ R ∙ R ∙  = =  ∙ R2 ; ∙ R2 ;  ∙ R2 = 16; R2 = 16 : ∙ R2 = 16; R2 = 16 :  = 64; R = = 64; R = 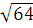 = 8 = 8
Ответ: R = 8
Задача 3: периметр прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.
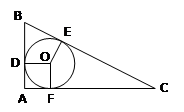 Дано: ∆ ABC – прямоугольный, P = 72 м, r = 6 м Дано: ∆ ABC – прямоугольный, P = 72 м, r = 6 м
Найти: BC
Решение:
DO = OF = OE = r = 6 м, следовательно AD = AF = 6 м
FC = EC, BD = BE (отрезки касательных, проведенные из одной точки)
Пусть BD = x, FC = y, тогда AB = x + 6, AC = y + 6, BC = x + y
По теореме Пифагора AB2 + AC2 = BC2
 P = AB + BC + AC, P = x + 6 + x + y + y + 6 = 2x + 2y + 12 P = AB + BC + AC, P = x + 6 + x + y + y + 6 = 2x + 2y + 12
2x + 2y + 12 = 72
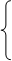 (x + 6)2 + (y + 6)2 = (x + y)2 (x + 6)2 + (y + 6)2 = (x + y)2
2x + 2y = 60 I: 2
x2 + 12x + 36 + y2 + 12y + 36 = x2 + 2xy + y2
 x + y = 30 x + y = 30
12x – 2xy + 12y + 72 = 0 I: 2
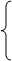 y = 30 – x y = 30 – x
6x – xy + 6y + 36 = 0
6x – x(30 – x) + 6(30 – x) + 36 = 0
6x – 30x + x2 + 180 – 6x + 36 = 0
x2 – 30x + 216 = 0
D = (-30)2 – 4 ∙ 1 ∙ 216 = 900 – 864 = 36
x1 = 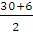 = = 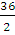 = 18, x2 = = 18, x2 = 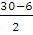 = =  = 12 = 12
  y = 30 – x y = 30 – x
x = 18
y = 12
x = 12
y = 18
BC = x + y
BC = 18 + 12 = 30 (м)
Ответ: 30 м – диаметр описанной окружности
Задача 4: вся дуга окружности радиуса R разделена на 4 большие и 4 малые части, которые чередуются одна за другой. Большая часть в два раза длиннее малой. Определить площадь восьмиугольника, вершинами которого являются точки деления дуги окружности.
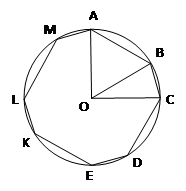 Дано: окружность, разделенная на 4 большие и 4 малые части, радиус = R, большая часть в два раза длиннее малой. Дано: окружность, разделенная на 4 большие и 4 малые части, радиус = R, большая часть в два раза длиннее малой.
Найти: 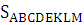
Решение:
Пусть ﮮAOB = 2x, ﮮBOC = x, тогда по условию 8x + 4x = 360°, x = 30°, 2x = 60°, ﮮAOB = 60°, ﮮBOC = 30°

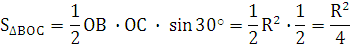
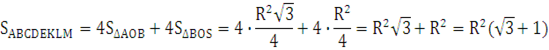
Ответ: 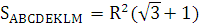

Задача 5: в ромб вписана окружность радиуса R. Найти площадь ромба, если его большая диагональ в 4 раза больше радиуса вписанной окружности.
Дано: ромб, радиус вписанной окружности – R, BD  r в 4 раза r в 4 раза
Найти: 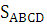
Решение:
Пусть OE = R, BD = 4OE = 4R
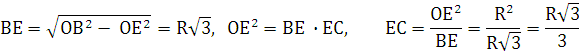

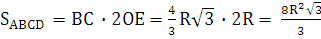
Ответ:
Задача 6: внутри правильного треугольника со стороной a расположены три равные окружности, каждая из которых касается двух сторон треугольника и двух других окружностей. Найти площадь части треугольника, расположенной вне этих окружностей.
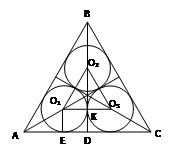
Решение:
Пусть AB = BC = AC = a.
Обозначим O1E = O1K = ED = r, тогда AD = AE + ED = AE + r =  . .
AO1 – биссектриса угла A, следовательно, ﮮ O1AE = 30˚ и в прямоугольном ∆AO1E имеем AO1 = 2O1E = 2r и AE = = = = =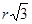 . Тогда AE + r = = . Тогда AE + r = = = =  , откуда , откуда  . .
Площадь части треугольника, расположенной вне окружностей, равна площади ∆ ABC без утроенной площади круга:

Ответ: 
Задача 7: найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.

Дано: ABCD – равнобедренная трапеция, r = 4, AB = 10
Найти: 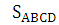
Решение:
AB = CD = 10 по условию
AB + CD = AD + BC по свойству вписанной окружности
AD + BC = 10 + 10 = 20
FE = 2r = 2 · 4 = 8

Ответ:
Литература
1. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
2. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
3. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»
|