Вариант 11.
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ ФИРМЫ, ИЗОКВАНТА И ИЗОКОСТА.
1.Производственная функция фирмы, ее построение.
2.Свойства изоквант. Субституция факторов производства.
3.Изокоста и условия равновесия фирмы.
Задача.
В паутинообразной модели функция спроса: QD
= 200 – P, а функция предложения: QS
= 0,5P – 10.
Товар продается в течении пяти дней. Определите равновесную цену товара. Найдите объемы спроса и предложения, а также цену по дням недели, если в первый день цена была равновесной, а на второй день спрос вырос на 30 ед. товара?. Запишите полученные результаты в таблицу:
| День |
Р |
D |
S |
Характер предложения |
Изменение цены |
| 1 |
140 |
60 |
60 |
| 2 |
110 |
90 |
60 |
| 3 |
120 |
80 |
60 |
| 4 |
130 |
70 |
60 |
| 5 |
140 |
60 |
60 |
Какова равновесная цена после увеличения спроса?
1.Производственная функция фирмы, ее построение.
2. Свойства изоквант. Субституция факторов производства.
Для того чтобы на предприятии организовать выпуск продукции, необходимо обеспечить взаимодействие факторов производства.
Так, факторы производства для выпуска телевизора включают: производственные помещения, станки, машины, оборудование, труд работников, участок земли, на котором построены производственные здания и сооружения и т.д.
В зависимости от скорости, с которой может изменяться количество вовлекаемых в производство ресурсов, они подразделяются на постоянные и переменные. Те из них, которые в течение определенного промежутка времени остаются неизменными, формируют постоянные факторы производства, а те, количество которых меняется — переменные факторы производства.
Все производственные ресурсы, участвующие в процессе производства, имеются в ограниченном количестве. Вследствие этого объем производства товаров и услуг ограничен количеством доступных ресурсов. Поэтому перед обществом в целом и каждым товаропроизводителем в частности всегда стоит задача их наиболее эффективною использования, Таким образом, объем произведенных товаров определяется наличием необходимых ресурсов. Причем различные варианты их использования позволяют товаропроизводителю получить большее или меньшее количество товаров или услуг. Поэтому предприятие должно быть заинтересовано, обеспечить наиболее полное использование трудовых, материальных и финансовых ресурсов и их оптимальное сочетание.
Соотношение между объемом выпуска продукции и объемом привлекаемых факторов производства отражает производственная функция.
Производственная функция указывает на возможный максимальный выпуск продукции (Q) при определенном сочетании факторов производства в рамках использования конкретного вида технологии:
Q=f(L;K),
Где Q – объем выпуска продукции, L – масса привлеченной рабочей силы (труда); К – объем используемого капитала (средств производства).
Вместе с тем в современных условиях технология рассматривается как вполне самостоятельный фактор производства. Тогда производственная функция принимает следующий вид:
Q=f(L;K;M),
Где новый символ М обозначает технологию производства.
Влияние экономического порядка. Понятно, что любое предприятие функционирует в конкретных экономических условиях, испытывает прямое воздействие со стороны национальной экономической системы. Поэтому не лишено смысла, если при анализе производственной функции экономические условие хозяйствования будут восприниматься как отдельный специфический фактор производства. Считается , что для его обозначения в формуле производственной функции используется символ f.
Производственная функция позволяет:
- определить долю участия каждого из них в создании товаров и услуг.
- меняя соотношение факторов, можно найти такое их сочетание, при котором будет, достигнут максимальный объем производства товаров и услуг.
- проследить, как изменяется выпуск продукции при увеличении или уменьшении использования тех или иных факторов производства на одну единицу, и, таким образом, выявить производственные возможности предприятия.
- определить экономическую целесообразность производства той или иной продукции.
Отметим, что производственная функция, как правило, рассчитывается для конкретной технологии.
Для различных видов производств (автомобилей, сельскохозяйственной продукции, кондитерских изделий и т.д.) производственная функция будет разной, но все они имеют следующие общие свойства:
* существует предел увеличения объема производства, которое может быть достигнуто за счет увеличения затрат одного ресурса при прочих равных условиях;
* существует определенная взаимная дополняемость ресурсов производства и их взаимозаменяемость (субституция). Взаимодополняемость ресурсов означает, что отсутствие одного или нескольких из них делает невозможным производственный процесс — производство останавливается. В то же время факторы производства в известной степени взаимозаменяемы. Нехватка одного из них может быть возмещена дополнительным количеством другого, т.е. ресурсы могут комбинироваться между собой в процессе производства в различных пропорциях;
* дифференцированная оценка влияния каждого из факторов на динамику выпуска продукции дается применительно к определенным промежуткам времени.
Производственная функция может быть выражена графически в виде изокванты — кривой, отражающей различные варианты комбинации ресурсов, которые могут быть использованы для производства данного объема продукции. Например, производство 1 т картофеля (Q) можно обеспечить за счет использования разного сочетания количества живого труда (L) и технических средств — капитала (К).
В качестве основных свойств производственной функции укажем на то, что:
1) для каждой отрасли производства складывается своя производственная функция;
2) в рамках определенной технологии могут допускаться разные варианты сочетания основных факторов производства;
3) радикальное изменение технологии неизбежно вызывает переход от одной к другой производственной функции;
4) анализ производственной функции предполагает поиск такого варианта организации производства, который обеспечивает максимальную экономическую эффективность.
Вывод: через сочетание факторов производства отражается технологический способ производства.
Производственная сетка.
Производственная функция обращает наше внимание на три важных обстоятельства:
1) чем больше объем вовлекаемых факторов производства, тем больше объем выпуска;
2) один и тот же объем выпуска можно обеспечить при разных сочетаниях факторов производства;
3) сокращая масштабы применения одного фактора, необходимо увеличить объем привлечения другого фактора производства.
Все эти положения подтверждает производственная сетка (таблица 1).
По горизонтали в таблице 1 указан объем вовлекаемой в производство рабочей силы, а по вертикали – объем капитала.
Перемещаясь по диагонали вниз и слева на право и увеличивая объем факторов производства, мы наращиваем объем выпуска продукции с 20 до 115 единиц.
Таблица 1. Изменение выпуска продукции при изменении объема вовлекаемых факторов производства (производственная сетка)
| Затраты капитала |
Затраты труда |
| 1 |
2 |
3 |
4 |
5 |
| 1 |
20 |
35 |
50 |
65 |
75 |
| 2 |
40 |
50 |
65 |
75 |
85 |
| 3 |
55 |
60 |
75 |
85 |
95 |
| 4 |
65 |
75 |
85 |
100 |
110 |
| 5 |
75 |
85 |
100 |
110 |
115 |
Перемещаясь по диагонали слева направо и вверх, объем выпуска (Q=75) остается постоянным
Изокванта. Такую зависимость между фиксированным объемом выпуска и соотношением двух факторов – труда и капитала – отразим на специальном графике. В итоге мы получаем линию, которая называется изоквантой (рис. 2)
К
|
5
|
 |
Q=75 |
4
|
3
|
2
|
1
|
| 0 |
1 |
2 |
3 |
4 |
5 |
L |
Рис. 2 Построение изокванты при объеме выпуска в 75 единиц.
На рис. изображена изокванта, соответствующая производству 1 т картофеля. Она показывает, что существует много вариантов использования ресурсов для производства данного объема картофеля. В одном случае может быть использовано больше ручного труда (L) — 70 чел-ч и лишь 2 машино-часа (К) (точка А), в другом — 40 чел-ч Lи 3 К (точка В), в третьем — 20 чел-ч L к 6 ч К (точка С) и т.д.

Для определения максимального объема производства, который может быть достигнут при каждой комбинации факторов, используется карта изоквант.
Анализ изоквант можно использовать для определения предельной нормы технологического замещения, т.е. возможности замещения одного ресурса другим в процессе их использования. Эта возможность зависит от функции производства. Существуют функции, в которых ресурсы легко заменяются, а есть и такие, где ресурсы имеют жесткие, неизменные пропорции.
Предельная норма технологической замены (MPTS) выражает количество единиц данного ресурса, которое может быть замещено единицей другого ресурса при сохранении неизменным объем производства.
Предположим, что технология производства одного автомобиля предусматривает использование 1000 ч труда и 500 ч работы станков и оборудования. Отношение труда к капиталу при этом составит 2 ч труда к 1 ч работы машин (точка А).

Чтобы механизировать и автоматизировать производство, предприятие переходит к использованию более капиталоемкого производственного процесса, т.е. на производство одного автомобиля потребуется меньше затрат живого труда и больше — овеществленного труда (машин, оборудования). В данном примере предельная норма технологического замещения труда капиталом определяется величиной капитала, которая может заменить каждую единицу труда, не вызывая увеличения или сокращения объема производства автомобилей. Предельная норма технологического замещения в любой точке изокванты равна наклону касательной в этой точке, умноженной на -1:
MPTS = - DK / DL (const Q),
где DК — сокращение или увеличение ресурса капитала;
DL — сокращение или увеличение ресурса труда;
Q — объем производства.
Кривизна изокванты помогает менеджеру точно определить, какое сокращение затрат труда потребуется при внедрении новой технологии производства. В точке В для производства автомобиля потребуется только 500 ч труда и 1000 ч работы машин. Отношение капитала к труду здесь составляет только 0,5 ч труда на каждый час работы станков и оборудования.
Изокванта – линия, отражающая варианты комбинации факторов производства, которые могут быть использованы при выпуске фиксированного объема продукции за конкретный период времени.
Изокванта является графической формой выражения двухфакторной производственной функции. Имеет объективный характер, так как отражает реальные экономические процессы.
Закон изокванты: чем в больших размерах используется один фактор производства, тем меньше применяется другой фактор.
Особые конфигурации изокванты. При определенных обстоятельствах изокванта может принять вид прямой линии. Прямолинейная изокванта предполагает, что замена одного фактора другим осуществляется в пропорции, которая неизменна на всем протяжении изокванты.
Если есто возможность организовать производство, ограничиваясь использованием только одного вида экономического ресурса (ситуация абсолютной заменяемости), то в этом случае изокванта будет касаться оси противоположного фактора производства.
Сплошной характер линии означает, что у каждого варианта всегда есть альтернативные варианты комбинирования факторов производства.
Вогнутая изокванта отражает то обстоятельство, что дело приходится иметь с гибкой производственной функцией, когда сокращение объема использования одного фактора производства компенсируется лишь при более высоких темпах прироста объема применения другого фактора (т.е. соотношение между объемом труда и капитала непрерывно изменяется).
В условиях, когда выпуск фиксированного объема продукции возможен только при единственном варианте сочетания факторов производства, приходится констатировать – имеем дело с жесткой производственной функцией. При таком сочетании обстоятельств изокванта приобретает форму прямого угла.
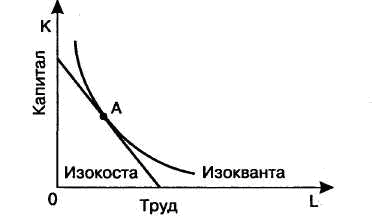
3 Изокоста и условия равновесия фирмы
Изокоста - линия, демонстрирующая комбинации факторов производства, которые можно купить за одинаковую общую сумму денег. Изокосту иначе называют линией равных издержек. Изокосты являются параллельными прямыми, поскольку допускается, что фирма может приобрести любое желаемое количество факторов производства по неизменным ценам. Наклон изокосты выражает относительные цены факторов производства. Каждая точка на линии изокосты характеризуется одними и теми же общими издержками. Эти линии прямые, поскольку факторные цены имеют отрицательный наклон и параллельны.
Совместив изокванты и изокосты, можно определить оптимальную позицию фирмы. Точка, в которой изокванта касается (но не пересекает) изокосты, означает наиболее дешевую по стоимости комбинацию факторов, необходимых для выпуска определенного объема продукта. На рисунке показан метод определения точки, в которой минимизируются издержки производства заданного объема производства продукта. Эта точка расположена на самой нижней изокосте, где изокванта соприкасается с ней.
Условия равновесия фирмы.
Следует подчеркнуть, что о разделении издержек на постоянные и переменные можно говорить только применительно к краткосрочному периоду функционирования фирмы. Другими словами, исходя из анализа видов издержек и их динамики, мы можем провести различие между краткосрочным и долгосрочным периодами функционирования фирмы. В краткосрочном периоде постоянные издержки остаются неизменными, фирма может изменять объем выпускаемой продукции только с помощью изменения величины переменных издержек. В долгосрочном периоде все издержки становятся переменными, то есть это достаточно длительный временной интервал для того, чтобы фирма могла изменить свои производственные мощности. Так при наличии безработицы и нахождении на рынке труда работников соответствующей квалификации легко увеличить объем производства за счет массы живого труда. Аналогичная ситуация может иметь место при использовании дополнительных ресурсов сырья или энергии. Естественно, что при этом приходится учитывать специфику производства. Так, прирост объема продукции можно легко получить путем привлечения дополнительных рабочих. Но совершенно иная ситуация складывается, когда необходимо расширить производственные мощности, площади производственных помещений и т.п. Здесь необходимое время измеряется месяцами, а иногда, скажем, в тяжелом машиностроении или металлургии – годами. В рамках краткосрочного периода невозможно ввести в строй новые производственные мощности, но возможно повысить степень их использования. В пределах долгосрочного периода можно расширить производственные мощности. Конечно, рамки этих периодов для различных отраслей различны. Деление на два периода имеет большое значение при определении стратегии и тактики фирмы в максимилизации прибыли.
В одной и той же отрасли действуют не одинаковые, а совершенно разные фирмы с разными масштабами, организацией и технической базой производства, а значит, и с разным уровнем издержек. Сравнение средних издержек фирмы с уровнем цены дает возможность оценить положение этой фирмы на рынке.
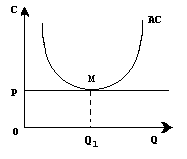
Ниже показаны три возможных варианта положения фирмы на рынке. Если линия цены Р
лишь касается кривой средних издержек АС
в минимальной точке М
, то фирма в состоянии лишь покрыть свои минимальные издержки. Точка М
в данном случае является точкой нулевой прибыли.
  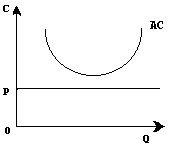
Следует особо подчеркнуть, что говоря о нулевой прибыли, мы не имеем в виду, что фирма вообще не получает никакой прибыли. Как уже было показано, в издержки производства включаются не только затраты на сырье, оборудование, рабочую силу, но и процент, который фирмы могли бы получить на свой капитал, если бы вкладывали его в другие отрасли.
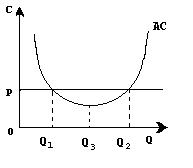
Если средние издержки ниже цены, то фирма при определенных объемах производства (от Q
1
до Q
2
) получает в среднем прибыль более высокую, чем нормальная прибыль, т.е. сверхприбыль.
Наконец, если средние издержки фирмы при любом объеме производства выше рыночной цены, то данная фирма терпит убытки и разорится, если не будет реорганизована или не уйдет с рынка.
Динамика средних издержек характеризует положение фирмы на рынке, однако сама по себе не определяет линии предложения и точки оптимального объема производства. Действительно, если средние издержки ниже цены, то на этом основании мы можем лишь утверждать, что в интервале от Q
1
до Q
2
находится зона прибыльного производства, а при объеме производства Q
3
, которому соответствуют минимальные средние издержки, фирма получает максимальную прибыль на единицу продукта. Однако означает ли это, что точка Q
3
– это точка оптимального объема производства, где фирма достигает своего равновесия. Производителя, как известно, интересует не прибыль на единицу продукции, а максимум общей массы получаемой прибыли. Линия средних издержек не показывает, где достигается этот максимум. В связи с этим необходимо рассмотреть так называемые предельные издержки, т.е. дополнительные издержки, связанные с производством дополнительной единицы продукции наиболее дешевым способом. Предельные издержки получаются как разность между издержками производства n
единиц и издержками производства n
-1
единиц:
МС=ТС
n
-ТС
n
-1
,
валовые общие издержки.  Ниже показана динамика предельных издержек. Ниже показана динамика предельных издержек.
Кривая предельных издержек не зависит от постоянных издержек, потому, что постоянные издержки существуют независимо от того, производится ли дополнительная единица продукции. Сначала предельные издержки сокращаются, оставаясь ниже средних издержек. Это объясняется тем, что если издержки на единицу продукции убывают, следовательно, каждый последующий продукт стоит меньше средних издержек предшествующих продуктов, т.е. средние издержки выше предельных. Последующий рост средних издержек означает, что предельные издержки становятся выше предшествующих средних издержек. Таким образом, линия предельных издержек пересекает линию средних издержек в ее минимальной точке М
.
Производство дополнительной единицы продукции, порождая дополнительные издержки, с другой стороны, приносит и дополнительный доход, выручку от ее продажи. Величина этого дополнительного, или предельного дохода(выручки) представляет собой разность между валовой выручкой от продажи n
и n
-1
единиц продукции:MR
=
TRn
-
TRn
-1
. В условиях свободной конкуренции, как известно, производитель не может повлиять на уровень рыночной цены, и, следовательно, продает любое количество своей продукции по одной и той же цене. Это значит, что в условиях свободной конкуренции дополнительный доход от продажи дополнительной единицы продукции будет при любом объеме одинаков, т.е. предельный доход будет равен цене: MR
=
P
.
Введя понятия предельных издержек и предельного дохода, мы можем теперь более точно определить точку равновесия фирмы, или точку, где она прекращает производство, добившись максимально возможной при данной цене массы прибыли. Очевидно, что фирма будет расширять объем производства, пока каждая дополнительно произведенная единица продукции будет приносить дополнительную прибыль. Другими словами, пока предельные издержки будут меньше, чем предельный доход, фирма может расширять производство. Если предельные издержки начнут превышать предельный доход, фирма будет нести убытки.
Ниже показано, что с увеличением производства кривая предельных издержек (МС
) идет вверх и пересекает горизонтальную линию предельного 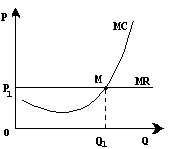 дохода, равного рыночной цене Р1
, в точке М
, соответствующей объему производстваQ
1
. Любое отклонение от этой точки приводит к потерям для фирмы либо в виде прямых убытков при большем объеме производства, либо в результате сокращения массы прибыли при уменьшении выпуска продукции. дохода, равного рыночной цене Р1
, в точке М
, соответствующей объему производстваQ
1
. Любое отклонение от этой точки приводит к потерям для фирмы либо в виде прямых убытков при большем объеме производства, либо в результате сокращения массы прибыли при уменьшении выпуска продукции.
Таким образом, условие равновесия фирмы, как в краткосрочном, так и в долгосрочном периоде можно сформулировать следующим образом: МС=
MR
. Любая фирма, добивающаяся прибыли, стремится установить такой объем производства, при котором соблюдается это условие равновесия. На рынке совершенной конкуренции предельный доход всегда равен цене, поэтому условие равновесия фирмы приобретает вид МС=Р
.
Соотношение предельных издержек и предельного дохода – это своего рода сигнальная система, которая информирует предпринимателя о том, достигнут ли оптимум производства или можно ожидать дальнейшего роста прибыли. Однако нельзя точно определить получаемую фирмой массу прибыли на основании динамики предельных издержек, поскольку, как уже отмечалось, они не учитывают постоянных издержек.
Общая прибыль, получаемая фирмой, может быть определена как разность между валовой выручкой (TR
) и валовыми издержками (ТС
). В свою очередь, валовая выручка вычисляется как произведение количества продукции на цену (TR
=
Q
*
AC
). Таким образом, лишь соединив проведенный ранее анализ предельных издержек и предельного дохода с анализом динамики средних издержек, можем точно определить объем получаемой прибыли.
Рассмотрим три возможных рыночных ситуации.
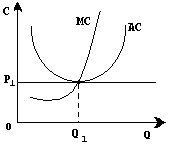  
Когда линия предельного дохода лишь касается кривой средних издержек, валовая выручка в точности равна валовым издержкам. Прибыль фирмы будет нормальной, поскольку цена ее продукции равна средним издержкам.
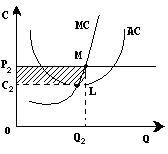
Если на каком-то интервале линия цены и предельного дохода располагается выше кривой средних издержек, то в точке равновесия М
фирма будет получать квазиренту, т.е. прибыль, превышающую нормальный уровень. При оптимальном объеме производства Q
2
средние издержки будут равны С2
, следовательно, валовые издержки составят площадь прямоугольника OC
2
LQ
2
. Валовая выручка (прямоугольник OP
2
MQ
2
) будет больше, и площадь заштрихованного прямоугольника C
2
P
2
ML
покажет нам общую массу получаемой сверхприбыли.
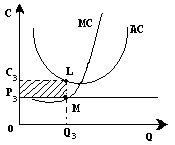
На третьем рисунке показана иная ситуация: средние издержки при любом объеме производства превышают рыночную цену. В этом случае даже при оптимальном объеме производства (МС=Р
) фирма несет убытки, хотя они и меньше, чем при других объемах производства (площадь заштрихованного прямоугольника P
3
C
3
LM
минимальна именно при объеме производства Q
3
).
Рассмотрим эту последнюю ситуацию подробнее. От убытков в рыночной экономике не застрахован никто. Поэтому, если в силу тех или иных причин (например, неблагоприятной конъюнктуры рынка). Фирма не получает прибыли, то она должна минимизировать убытки. Если рассматривать поведение фирмы в краткосрочной перспективе, когда она по-прежнему остается на данном рынке, то, что для нее предпочтительнее – продолжать работать и производить продукцию или временно остановить производство? В каком случае убытки будут меньше?
Обратим внимание, что когда фирма ничего не производит, она несет только постоянные издержки. Если же она производит продукцию, то к постоянным издержкам добавляются переменные, но при этом фирма получает и некоторый доход от продаж. Поэтому, чтобы понять, когда фирма минимизирует убытки, надо сопоставить уровень цены не только со средними издержками (AC
), но и со средними переменными издержками (AVC
). Рассмотрим ситуацию, показанную ниже:
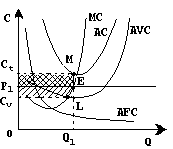 Рыночная цена Р1
ниже минимальных средних издержек, но выше минимальных средних переменных издержек. При оптимальном объеме производства Q
1
величина средних издержек производства составит отрезок Q
1
M
, величина средних переменных издержек – отрезок Q
1
L
. Следовательно, отрезок ML
– это средние постоянные издержки. Если фирма продолжает работать, то ее валовая выручка (прямоугольник OP
1
EQ
1
) будет меньше полных издержек (прямоугольник OC
т
MQ
1
), но при этом будут покрыты переменные издержки (прямоугольник OCv
LQ
1
) и часть постоянных издержек. Размер убытков будет измеряться площадью прямоугольника P
1
C
1
ME
. Если же фирма остановит производство, то убытки составят всю величину постоянных издержек (прямоугольник Cv
C
т
ML
). Таким образом, пока цена выше минимальных средних издержек, фирме в краткосрочном периоде выгоднее продолжать производить продукцию, поскольку в этом случае минимизируются убытки. Если цена равна минимальным средним переменным издержкам, то для нее безразлично, продолжать производство или останавливать его. Если же цена упадет ниже минимальных средних переменных издержек, тогда производство продукции должно быть прекращено. Рыночная цена Р1
ниже минимальных средних издержек, но выше минимальных средних переменных издержек. При оптимальном объеме производства Q
1
величина средних издержек производства составит отрезок Q
1
M
, величина средних переменных издержек – отрезок Q
1
L
. Следовательно, отрезок ML
– это средние постоянные издержки. Если фирма продолжает работать, то ее валовая выручка (прямоугольник OP
1
EQ
1
) будет меньше полных издержек (прямоугольник OC
т
MQ
1
), но при этом будут покрыты переменные издержки (прямоугольник OCv
LQ
1
) и часть постоянных издержек. Размер убытков будет измеряться площадью прямоугольника P
1
C
1
ME
. Если же фирма остановит производство, то убытки составят всю величину постоянных издержек (прямоугольник Cv
C
т
ML
). Таким образом, пока цена выше минимальных средних издержек, фирме в краткосрочном периоде выгоднее продолжать производить продукцию, поскольку в этом случае минимизируются убытки. Если цена равна минимальным средним переменным издержкам, то для нее безразлично, продолжать производство или останавливать его. Если же цена упадет ниже минимальных средних переменных издержек, тогда производство продукции должно быть прекращено.
Известно, что при изменении цены фирма будет изменять объемы производства, двигаясь вдоль кривой МС.
Суммируя индивидуальные кривые предложения всех фирм какой-то одной отрасли, получаем кривую совокупного отраслевого предложения. По мере постепенного повышения цены различные фирмы, работающие в данной отрасли, расширяют свое производство и свое предложение. Изменение рыночной цены на какой-либо товар будет происходить до тех пор, пока совокупный спрос на продукцию отрасли не сравняется с совокупным отраслевым предложением. Такое равенство достигается при определенном уровне цены, которая после этого имеет тенденцию сохранять этот уровень в течение краткосрочного периода.
Решение задачи
Определим равновесную цену товара в первый день, для этого приравняем функцию спроса к функции предложения QD
=QS
;
200-P=0.5P-10
0.5P+P=200+10
1.5P=210
P=140 - равновесная цена
Найдем объем спроса и предложения в первый день
QD
=200-P
QD
=200-140=60ед.
QS
=0.5P-10
QS
=0.5*140-10=60ед.
Находим объем спроса на второй день
QS
=60+30=90ед.
Значит равновесная цена после увеличения спроса стала
QS
=0.5P-10
P= (QS
+10)/0.5
P=(90+10)/0.5=200
|