СОДЕРЖАНИЕ
Реферат.....................................................................................................................2
Введение...................................................................................................................3
Глава 1. Обработка результатов полевых измерений..........................................4
1. Составление схемы ходов.............................................................................4
2. Вычисление горизонтальных углов и длин линий между точками хода.4
3. Вычисление горизонтального проложения линии 8-1...............................5
4. Вычисление недоступного расстояния 5-6.................................................5
5. Решение обратных геодезических задач по линии 1-2 и 4-5....................7
Глава 2. Обработка ведомости вычисления координат и составление плана теодолитной съёмки .............................................................................................10
1. Обработка ведомости вычисления координат основного хода..............10
2. Расчёт координатной сетки для построения плана..................................15
3. Нанесение точек съёмочного обоснования по координатам..................17
4. Нанесение ситуации на план......................................................................17
Глава 3. Вычисление площадей...........................................................................19
1. Вычисление площади аналитическим способом......................................19
2. Вычисление площади механическим способом.......................................20
Заключение.............................................................................................................23
Список используемой литературы.......................................................................24
РЕФЕРАТ
Данная курсовая работа является важным элементов в изучении дисциплины «Геодезия». Первокурснику данная курсовая даст знания не только об основах геодезии, но и как выполняются курсовые проекты в целом. Она должна помочь закрепить полученные знания и дать новые.
Курсовая работа состоит из 22 листов, 3 рисунков, 6 таблиц, 54 формул и 5 приложений.
Основная часть работы содержит:
1. Обработка результатов полевых измерений.
2. Обработка ведомости вычисления координат и составление плана теодолитной съёмки.
3. Вычисление площадей разными способами.
4. Учебно-исследовательская работа.
В приложении курсовой работы содержатся:
1. Журнал измерения углов способом приёмов.(Приложение А)
2. Ведомость вычисления координат.(Приложение Б)
3. Ведомость вычисления площадей.(Приложение В)
4. Схема теодолитных ходов.(Приложение Г)
5. План участка теодолитной съёмки.(Приложение Д)
Выполнение курсовой работы даёт очень много практических навыков, которые с теоретическими откладываются в памяти студена гораздо лучше чем по раздельности. После выполнения работы появляются навыки обработки полевых материалов теодолитной съёмки, построение плана теодолитной съёмки и навыки по определения площадей.
ВВЕДЕНИЕ
Геодезия- наука изучающая форму и размеры поверхности Земли или отдельных её частей, путём измерений вычислительной обработки их и создание картографического материала в виде карт, планов и профилей.
Необходимость геодезических работ у человека возникла за несколько тысячелетий до нашей эры. Её использовали в целях строительства каналов, различных сооружений и деления земельных участков, это продолжается до сих пор. Конечно, не в таком виде как это было раньше, год за годом появляется более совершенное оборудование, которое быстрее, точнее и легче помогает выполнить работу.
Существуют следующие виды топографических съёмок:
· Топографическая съемка сверхкрупных масштабов 1:50, 1:100 – геоподоснова для ландшафтного проектирования
· Топографическая съемка общего и специального назначения
· Топографическая съемка участков общего и специального назначения, а также геодезическая топографическая съемка подземных и надземных сооружений
· Топографическая съемка земельного участка масштабов 1:5 000, 1:10 000 используется для разработки генеральных плановгородов и проектов планировки сельских населенных пунктов
Теодолитная съемка, как и съемки других видов, является полевой работой, при выполнении которой сначала создается съёмочное обоснование, а затем производится съёмка ситуации. Теодолитной она называется потому, что основным прибором, с помощью которого она выполняется, является теодолит.
На данном этапе обучения, тема курсовой работы актуальна. Т.к. после выполнения работы я должен научиться измерять углы, и делать полный комплекс заданий связанных с камеральной обработкой.
ОСНОВНАЯ ЧАСТЬ
ГЛАВА1 – ОБРАБОТКА РЕЗУЛЬТАТОВ ПОЛЕВЫХ ИЗМЕРЕНИЙ
1.
Составление схемы ходов
В схему ходов заносят измеренные значения углов и длин линий, а так же условные знаки, дороги, реки и другие элементы которые должны быть размещены на карте. Особо отмечают пункты геодезической сети с известными координатами, к которым привязаны теодолитные ходы, длины линий, исходные дирекционные углы, координаты пунктов, примычные углы.(Приложение А, Приложение Г)
2.
Вычисление горизонтальных углов
Для вычисления горизонтальных углов воспользуемся углами данными нам в таблице, вычисляем углы до секунд, как показано на образце. При этом расхождение в полуприёмах не должны превышать 1’.(Приложение А)
Таблица 1 Измерение горизонтальных углов
| Станция |
Точки наблюдения |
Углы в полуприемах |
Средний угол |
| ° |
' |
° |
' |
| 2 |
1 |
225 |
47 |
225 |
47 |
| 3 |
| 1 |
225 |
47 |
| 3 |
| 3 |
2 |
101 |
17 |
101 |
17’30” |
| 4 |
| 2 |
101 |
18 |
| 4 |
Для измерения длин линий воспользуемся данными в таблице, и вычислим линию 2-3.
Измерение прямо – 806,50 м
Измерение обратно – 806,70 м
Находим среднее арифметическое : (806,50+806,70)/2=806,60 м(Dср
)
Теперь проверим допустимо ли наше значение, оно не должно превышать 1:2000 от длин линий.
∆
D=806,70-806,50=0,2 м
0,20/806,60=1/4033<1/2000
Если значения допустимы, то записываем среднее арифметические в журнал, для линии 2-3 : 806,60 м
3.
Вычисления горизонтального проложения линии 8-1
Для вычисления горизонтального проложения можно воспользоваться двумя способами:
Дано:
D
изм
= 1030, 07 м β=4
°
1) Способ: d8-1
= Dизм *
cos β= 1030,07*
0,997564=1027,5608 м (1)
2) Способ: d8-1
=Dизм
-∆D(2)
∆Dизм
=2*
Dизм*
sin2
β/2(3)
∆Dизм
=2*
1030,07*
sin2
4/2=2,51 м
d8-1
=1030,07-2,51=1027,56 м

Рисунок
1
- Определение горизонтального проложения.
4.
Вычисление недоступного расстояния 5-6
Если встречаются недоступные для измерения лентой расстояния, то их вычисляют по теореме синусов.
Недоступным расстоянием является линия 5-6. Находим ее длину по формулам:
а
= в
∙sin6/sin5 (3)
s
= в
∙sink
/sin5 (4)
s
= a
∙
sink
/sin6 (5)

Рисунок 2 -
Схема определения недоступного расстояния.
Дано: в
= 566,20 м  = 33º22'30” = 33º22'30”  = 69º18'30” = 69º18'30”  = 77º20'30”, = 77º20'30”,
Проверяем допустимы ли данные углы и увязываем их.
∑пр=180º1,5'
∑т=180º ,
так как сумма углов в треугольнике равна 180º
ƒβ =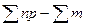 (6) (6)
где ƒβ невязка углов, то есть расхождение практики с теорией.
ƒβ =180º1,5'-180º =0º1,5'
Увязываем углы равномерно распределяя значение невязки
Увязанные углы:
5 = 33º22'
6 = 69º18'
k
= 77º20'
Таблица 2 Вычисление неприступного расстояния по теореме синусов
| Формулы |
Значения |
| а
= в
∙sin6/sin5 |
в
= 566,20 м
5 = 33º22' sin5 = 0,549995
6 = 69º18' sin6 = 0,935444
а
=
963,01 м
|
| s
= в
∙sink
/sin5 |
в
= 566,20 м
5 = 33º22' sin5 = 0,549994
k
= 77º20' sink
= 0,975662
S = 1004,41 м
|
| s
= a∙
sink
/sin6 |
а
=
963 м
6 = 69º18' sin6 = 0,935444
k
= 77º20' sink
= 0,975662
S = 1004,41 м
|
Таким образом длина линии 5-6 равна 1004,41 м.
5.
Решение обратных геодезических задач по линии 1-2 и 4-5
· 1-2
Дано: Х1
=7600,00м Х2
=7048,89м
У1
=5600,00м У2
=5274,01м
α1-2
=218°16’
Чтобы воспользоваться формулой tgr=∆Y/∆X, нужно найти ∆Y и ∆X, это делается по формулам :
Укон
-Унач
=∆У (7)
Хнач
-Хкон
=∆Х (8)
в нашем случае получтся
∆Х=5200,76-5600,00=-551,11 м
∆У=7099,39-7600,00=-325,99 м
tgr=-325,99/-551,11=0,591515305
r=30,60496434
d1
=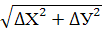 (9) (9)
d2
=∆Х/cosr (10)
d3
=∆У/sinr (11)
d1
= = =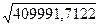 =640,31 м =640,31 м
d2
=551,11/0,860697921=640,31 м
d3
=325,99/0,509115987=640,31 м
Горизонтальное проложение линии 1-2 равно 640,31м.
С помощью рисунка схемы ходов мы получаем приблизительное изображения теодолитных ходов и всего полигона в целом, включая полностью всю ситуацию. По простейшим формулам легко рассчитываем горизонтальные углы и расстояния между точками. Существуют недоступные расстояния, которые вычисляются по теореме синусов. А также производили решение обратных геодезических задач.
ГЛАВА2- ОБРАБОТКА ВЕДОМОСТИ ВЫЧИСЛЕНИЯ КООРДИНАТ И СОСТАВЛЕНИЕ ПЛАНА ТЕОДОЛИТНОЙ СЪЁМКИ
1.
Обработка ведомости вычисления координат основного хода
Обработка начинается с контроля правильности измерения горизонтальных углов.(Приложение Б)
 = =
практическая сумма углов 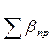 -рассчитывается путём сложения всех углов в ходе -рассчитывается путём сложения всех углов в ходе
теоретическая сумма углов для разомкнутого хода рассчитывается по формуле (12) для правых по ходу (12) для правых по ходу
где n-кол-во углов в ходе
αкон
и αнач
– конечные и начальные дирекционные углы исходных сторон.
β – горизонтальные углы.
Угловая невязка  рассчитывается по формуле рассчитывается по формуле
 (13) (13)
Рассчитаем невязку для главного хода №1
 =448°51’-448°52’=-1’ =448°51’-448°52’=-1’
Вычисленная невязка сравнивается с допустимой, допустимая невязка рассчитывается по формуле
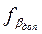 =2t* =2t*
 (14) (14)
Где t – точность прибора
В нашем случае она будет равна
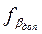 =2*
30’’* =2*
30’’*
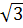 =1’*
1,7=1,7’ =1’*
1,7=1,7’
При это должно выполняться условие:
 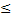 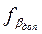
-1’ 1,7’ 1,7’
Допустимая невязка распределяется в измерённые углы поровну. Принимая что все углы измерены с одинаковой точностью. Распределяем невязку по углам с обратным знаком поровну. 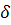 =- =- /n (однако невязка редко делится на n без остатка). Большие поправки вводятся в углы образованные короткими сторонами, поправки имеют знак противоположный невязки. Сумма поправок должна равняться невязки с обратным знаком. /n (однако невязка редко делится на n без остатка). Большие поправки вводятся в углы образованные короткими сторонами, поправки имеют знак противоположный невязки. Сумма поправок должна равняться невязки с обратным знаком.
 =- =- (15) (15)
Таблица 3 Исправление горизонтальных углов
| № угла |
Углы |
| измеренные |
исправленные |
| 3 |
101°17’30’’ +30” |
101°18’ |
| пп4 |
121°46’30’’ +30’’ |
121°47’ |
После введения поправок в измеренные углы находим их сумму
 =101°18’+121°47’+225°47’=448°52’ =101°18’+121°47’+225°47’=448°52’
Сравниваем  и и  448°52’=448°52’, они равны. 448°52’=448°52’, они равны.
Исправив углы поправками вычисляют дирекционные углы по формулам передачи дирекционного угла на линию.
αпосл
=αпред
+180°-βпр. по ходу
(16)
При этом β – исправленный
Контролем вычисления дирекционных углов является получение в конце вычислений исходного дирекционного угла. Записываем в ведомость посчитанные дирекционные углы, после чего по формулам связи переходим к румбам. По названию румба определяют знаки приращений координат.
III. четверть: r = a - 180° (19)
IV. четверть: r = 360° - a (20)
где r –румб, α – дирекционный угол
Для главного хода это будет выглядеть так:
1-2 a=210°36', тогда ЮЗ: r=30°36'
2-3 a=164°49', тогда ЮВ:r=15°11'
3-4 a=243°31', тогда ЮЗ: r=63°31'
4-5 a=301°44', тогда СЗ: r=59°44'
Переходим к приращениям координат по осям Х и У:
∆Х=d*
cosr (21)
∆Y=d*
sinr (22)
Так как координаты точек 1, 2, 4 и 5 нам даны из таблицы, их считать совсем не имеет смысла. Для нашего хода это будет выглядеть следующим образом:
Для линии 2-3: ∆Х=806,60*
0,965092721=-778,44м
∆У=806,60*
0,261908456=211,26м
Для линии 3-4: ∆Х=948,45*
0,445937468=-422,95м
∆У=948,45*
0895064117=-848,92м
Контролем правильности вычисления приращений координат служит сумма 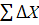 пр
= пр
=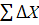 теор теор
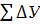 пр
= пр
=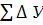 теор теор
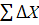 теор
=Хкон
- Хнач
(23) теор
=Хкон
- Хнач
(23) 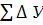 теор
=Укон
- Унач
(24) теор
=Укон
- Унач
(24)
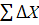 пр
=-1201,39 м пр
=-1201,39 м 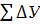 пр
=-637,66м пр
=-637,66м
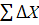 теор
=5847,56-7048,89=-1201,33м теор
=5847,56-7048,89=-1201,33м 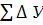 теор
=4636,18-5274,01=-637,83м теор
=4636,18-5274,01=-637,83м
 = =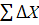 пр
- пр
-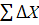 теор
(25) теор
(25)  = =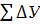 пр
- пр
-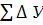 теор
(26) теор
(26)
 =-1201,39-(-1101,33)=-0,06м =-1201,39-(-1101,33)=-0,06м  =-637,66-(-637,83)=0,17м =-637,66-(-637,83)=0,17м
Прежде чем распределять невязки приращений координат нужно убедиться в их допустимости. Судя не по каждой в отдельности  и и  , а по невязки по всему периметру которая называется абсолютная невязка. , а по невязки по всему периметру которая называется абсолютная невязка.
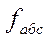 = = (27) (27)
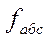 = =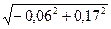 =0,18 =0,18
Затем относительную невязку
 = =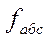 / / (28) или (28) или =1/ =1/ : :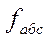 (29) (29)
Где 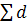 - периметр хода = 1755,05 м - периметр хода = 1755,05 м
Относительная невязка не должна превышать 1/2000 для первого разряда и 1/1500 для вторых разрядов. Рассчитаем для хода №1
 =1/1755,05:0,18=1/9750 =1/1755,05:0,18=1/9750  1/2000 1/2000
Если невязки допустимы, как в нашем случае, они распределяются по приращениям координат пропорционально длинам линий с обратным знаком.
 *
dn
(30) *
dn
(30)
 *
dn
(31) *
dn
(31)
В нашем случае приращения для Х будут равны:
δ1
=-(-0,06)*
806,60/1755,05=0,03м
δ2
=-(-0,06)*
948,45/1755,05=0,03м
Для Y:
δ1
=-0,17*
806,60/1755,05=-0,08м
δ1
=-0,17*
948,45/1755,05=-0,09м
Контролем будут являться формулы
 (32) (32)  (33) (33)
Для первого хода будет выглядеть так:
Х: 0,06=-0,06 Y: -0,17=0,17
Если условие равенства выполняется, тогда вычисляем исправленные приращения координат.
∆Хi
испр
=∆Хi
+𝛅I
(34) ∆Х1испр
=-800,21+0,03=-778,41м
∆Yi
испр
=∆Yi
+𝛅I
(35) ∆Y1испр
=101,33-0,08=211,18м
После чего проверяем
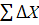 пр
= пр
=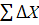 теор
(36) -1201,33=-1201,33 теор
(36) -1201,33=-1201,33
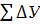 пр
= пр
=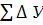 теор
(37) -637,83=-637,83 теор
(37) -637,83=-637,83
По справленным приращениям вычисляют координаты точек хода:
Хпосл
=хпред
+Dх (38)
Упосл
=упред
+Dу (39)
Где Хпосл
Упосл
координаты последующей точки, хпред
упред
соответственно предыдущей, а Dх и Dу приращения соответствующие линиям. Координаты точек 1,2,4 и 5 нам даны из методических указаний. Получим:
Х3
=4899,89-778,41=6270,48м
У3
=5274,01+211,18=5485,19м
Контроль в разомкнутом ходе: получение в конце вычислений координат конечного исходного пункта. В полигоне получение координат начального исходного пункта.
Х4
=6270,48-422,92=5847,56м
У4
=5485,19-849,01=4636,18м
2.
Расчёт координатной сетки для построения плана
Расчёт для размещения плана полигона симметрично относительно краёв листа на котором будет составлен план. Нам нужно составить план в масштабе 1:10000. (Приложение Б, Д)
Выбираем из координат основного хода максимальные и минимальные значения
Хmax
=8418,11 м Хmin
=5847,56 м
Уmax
=5600 м Уmin
=3730,76 м
m=100 (т.к. в 1 см 100 метров)
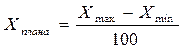 (40)Хплана
=8418,11-5847,56/100=25,70см (40)Хплана
=8418,11-5847,56/100=25,70см
 (41) Уплана
=5600-3730,76/100=18,69см (41) Уплана
=5600-3730,76/100=18,69см
Затем определяем размеры листа бумаги
Хлиста
=41,9см Улиста
=29,7см
Определяем размеры нижней, верхней и боковых полос Dхн
, Dхв
и Dу за пределами полигона при условии его симметричного расположения относительно боковых сторон рамки по формулам:
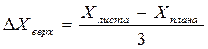 (42) ∆Хниз
=2∆Хверх
(43)
(42) ∆Хниз
=2∆Хверх
(43)
 (44) (44)
∆Xверх
=(41,9-25,70)/3=5,4 см ∆Хниз
=2*
5,4=10,8 см
∆У=(29,7-18,69)/2=5,5 см
Полученные отрезки откладываем от рамки листа и получаем прямоугольник, в котором должен разместиться полигон. От этих границ рассчитываем удаление ближних линий координатной сетки по оси абсцисс 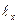 и по оси ординат и по оси ординат  под условием: координаты линий сетки – Х и У должны быть кратны заданному интервалу, в данном случае одному километру. Этот интервал получается как произведение длины стороны квадрата сетки на число метров в одном сантиметре заданного масштаба. В курсовой работе масштаб 1:10000, а 1см- 100 м, сторона квадрата 10 см, поэтому интервал между линиями координатной сетки будет 10 см-1000м, или один километр. под условием: координаты линий сетки – Х и У должны быть кратны заданному интервалу, в данном случае одному километру. Этот интервал получается как произведение длины стороны квадрата сетки на число метров в одном сантиметре заданного масштаба. В курсовой работе масштаб 1:10000, а 1см- 100 м, сторона квадрата 10 см, поэтому интервал между линиями координатной сетки будет 10 см-1000м, или один километр.
lx
=(Xсетки
-Хmin
)/m (45)
ly
=(Yсетки
-Ymin
)/m (46)
lx
=(6000-5847,56)/100=1,5244см
ly
=(4000-3730,76)/100=2,6924 см
Вычисленные отрезки откладываем в левом нижнем углу полученного прямоугольника по координатам соответственно. Затем строим сетку 10х10 см. При небольших размерах плана координатная сетка строится при помощи циркуля и масштабной линейки. Одну из осей проводят с помощью линейки, а вторую строят перпендикулярно ей при помощи засечек. Отклонение фактической длины сторон квадрата от заданной 10 см не должно превышать 0,2 мм, а диагонали от 14,14 см  0,2 мм. 0,2 мм.
3.
Нанесение точек съёмочного обоснования по координатам
Для нанесения точек съёмочного обоснования по координатам пользуются наиболее точным способом – накладка теодолитного хода по прямоугольным координатам. Для нанесения точек на план по координатам пользуются измерителем и масштабной линейкой. Тысячи выбирают по координатной сетке, сотни, десятки и единицы берут по масштабной линейке, т.к. масштаб 1:10000, то нужно воспользоваться масштабом на линейке 1:1, затем проводят координату Х, после чего на ней отмечают У, это и будет искомая точка. Контролем правильности нанесения точек на план будет расстояние между ними, которое мы рассчитывали ранее.(Приложение Б, Д)
4.
Нанесение ситуации на план
После проложения теодолитных ходов по границам землепользования снимают контуры ситуации внутри участка. Проложение точек контуров определяют с меньшей точностью, поэтому для съёмки точек контуров применяют методы обеспечивающие быстроту работы. Для этого пользуемся абрисом или полевым журналом.
· Метод прямоугольных координат:
Применяется при съёмки ручьёв, извилистых контуров или отдельных точек ситуации, расположенных вдоль или не вдалеке от линии хода. Для нанесения на план пользуемся треугольником, измерителем и масштабной линейкой. Треугольником пользуемся для построения перпендикуляров. Расстояния до оснований перпендикуляров и длины перпендикуляров определяем при помощи линейного масштаба.
· Метод полярных координат:
Состоит в том, что с точки теодолитного хода принятой за полюс, положение каждой из характерных точек контуров ситуации определяется парой полярных координат(направление на точку и расстояние до неё). Для этого нам понадобится транспортир, масштабная линейка и измеритель. Центр транспортира ставим на точку, затем нуль наводим на другую точку которая и будет полярной, затем отмечаем градусы углов, после чего проводим отрезки с помощью масштабной линейки.
· Метод засечек:
Применяется редко, чаще при съёмки отдельных объектов. Так же пользуются транспортиром и масштабной линейкой. Измеряют углы, после чего от точек до измеренных углов проводят линии, в точке пересечения линий будет находиться данный предмет.
При помощи геодезических формул, в ведомости координат рассчитываем дирекционные углы, румбы, горизонтальные проложения, приращения координат и сами координаты. которые в дальнейшем наносим на план с более высокой точностью чем на схеме ходов. При помощи различных методов так же на план наносится полностью вся ситуация.
ГЛАВА 3 - ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
1.
Вычисление площади аналитическим способом
Площади вычисляют по результатам измерений линий и углов на местности с применением формул геометрии, площади разбивают на простейшие фигуры. Если площадь небольших участков, их вычисляют по функциям – приращений координат и координатам вершин хода.
 (47) (47)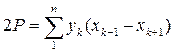 (48) (48)
Где 2P двойная площадь, 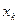 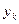 соответствующие координаты, и разности соответственно соответствующие координаты, и разности соответственно   . .
Произведение округлить до целых м2
, а окончательное значение площади – до 0,01 га. Вычисления произвести в координатной ведомости, формулы и результаты произведены в таблице
Таблица4 Определение площади полигона по координатам аналитическим способом
| № точек |
Координаты, м |
Разности |
Произведения |
| X |
Y |
 |
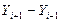 |
 |
 |
| 1 |
7600,00 |
5600 |
1369,22 |
295,72 |
7667632 |
2247472 |
| 2 |
7048,89 |
5274,01 |
1329,52 |
-114,81 |
7011901,775 |
-809283,0609 |
| 3 |
6270,48 |
5485,19 |
1201,33 |
-637,83 |
6589523,303 |
-3999500,258 |
| 4 |
5847,56 |
4636,18 |
11,37 |
-1514,53 |
52713,3666 |
-8856305,047 |
| 5 |
6259,11 |
3970,66 |
-1386,94 |
-905,42 |
-5507067,18 |
-5667123,376 |
| 6 |
7234,5 |
3730,76 |
-2005,21 |
-81,74 |
-7480957,26 |
-5911348,03 |
| 7 |
8264,32 |
3888,92 |
-1183,61 |
1247,53 |
-4602964,601 |
10309987,13 |
| 8 |
8418,11 |
4978,29 |
664,32 |
1711,08 |
3307177,613 |
14404059,66 |
| =0,0 |
=0,0 |
=7037959,017 |
=7037959,018 |
| P = 3518933,9м² = 351,897га |
При получении произведений получаем двойную площадь, соответственно сначала нужно найти среднее между произведениями, а потом площадь (49) , где Р- площадь (49) , где Р- площадь
Таким образом площадь всего полигона равно 351,897га.
2.
Вычисление площади механическим способом
Механический способ основан на использовании специального прибора- планиметра.
Планиметр- механический прибор которым можно определять площади контуров на плане или карте.
Цена деления планиметра находится по средней разности с пятью десятичными знаками по формуле:
p=P0
/U2
-U1
(50)
Где U1
- начало отсчёта, U2
-отсчёт после обвода контура. При этом раасхождение разностей отсчетов не должно быть больше пяти делений.
Если P0
выражено в гектарах, то P будет относительной ценой деления планиметра.
Дробная цена деления P1
, приводится к округлённой, удобной для пользования Р2
, для которой длина обводного рычага R2
находится из выражения:
R2
=P2*
R1
/P1
(51)
Для определения площади нужно обвести каждый контур дважды при одном положении полюса. Расхождение разностей отчётов не должно быть больше трёх делений. Если это условие выполнено, то вычисляется средняя разность, по которой определяется площадь по формуле:
P=р(U2
-U1
) (52)
Значение площади фигур округлить до сотых долей гектара.
Оценим точность определения площадей контуров планиметром и произведем увязку. Для этого находим сумму площадей контуров  , измеренных планиметром, и сравниваем ее с общей площадью участка в границах полигона, вычисленной по координатам, приняв ее за теоретическую , измеренных планиметром, и сравниваем ее с общей площадью участка в границах полигона, вычисленной по координатам, приняв ее за теоретическую 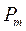 . .
 (53) (53)
есть абсолютная практическая невязка площади; она сравнивается с допустимой , которая рассчитывается по формуле: , которая рассчитывается по формуле:
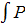 доп
=0,7*
р* доп
=0,7*
р*
 +0,05*
M* +0,05*
M*
 /10000 (54) /10000 (54)
Где p- относительная цена деления планиметра
n- число контуров, куда не входят те, площади которых определены геометрическим способом
M- знаменатель численного масштаба плана
Р- площадь участка, га
Невязка считается допустимой, если выполнено условие

Вычисленную невязку приближённо проверить по выражению:
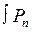  P/300 P/300
Допустимую невязку распределяют пропорционально коэффициентам поправок, выбираем для масштаба 1:10 000 со знаком, обратным знаку полученной невязки 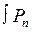 . Вычисляем увязанные площади фигур, сумма которых должна дать площадь теоретическую . Вычисляем увязанные площади фигур, сумма которых должна дать площадь теоретическую 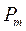 . .
На плане участка по полученным площадям угодий заполняем таблицу «Экспликация». Здесь также для контроля подсчитываем сумму этих площадей, которая тоже должна быть равна общей площади участка 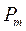 . .
Наиболее точный - аналитический способ, так как на точность определения площади при этом способе влияют только погрешности измерений на местности, в то время как при механическом способе, помимо погрешностей измерений на местности, влияют погрешности составления плана, определения площадей по плану и деформации бумаги. Однако аналитический способ требует измерения линий и углов по границам участков, значительных вычислений, зависящих от количества углов. Вместе с этим его целесообразно применять, если площадь надо получить с повышенной точностью и, не дожидаясь составления плана. Менее точен, но наиболее распространен механический способ, так как, пользуясь им, можно быстро и просто определять по плану площадь участка любой формы.
ЗАКЛЮЧЕНИЕ
При помощи журнала и полевых измерений создаётся схема теодолитных ходов, в которой нанесены точки, горизонтальные углы, длины линий и общая ситуация. После чего переходят к заполнению ведомости вычисления координат.
Когда находят координаты, на листе составляют план, на котором точно размещают точки с известными координатами. Нанесение плана координатным способ является самым удобным и простым способ решения задачи, а ещё он точнее всех других способов. Нанесение ситуации на план, разными способами, даёт возможность показать ситуацию на плане в целом.
Аналитический способ очень удобен, точен и быстр, но он в отличии от механического не позволяет измерять любые контуры, поэтому аналитическим способом можно измерить только площадь всего полигона, он удобен для применения на местности.
Качество определения геодезических данных проектного хода не даёт 100% точности и этот способ очень трудоёмкий.
После выполнения курсовой работы я приобрёл следующие знания:
Технология работ по горизонтальной съёмке и камеральной обработке съёмочных данных.
Производить увязку углов и приращений координат в теодолитных ходах, находит площади различными способами, решать обратные геодезические задачи.
27.12.2009 Жарич Е.В.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1) Маслов А.В., Гордеев А.В., Батраков Ю.Г. Геодезия. Учеб. Пособие для вузов. – М.: Недра, 1980. 616с.
2) Условные знаки для топографической карты масштаба 1:10000. – М.: Недра, 1997. – 142 с.
3) Лекции прочитанные старшим преподавателем кафедры геодезия Прониной Л.А
4) Куштин И.Ф. Геодезия / И.Ф. Куштин. – М.: Приор, 2001. – 448 с.
|