|
ВВЕДЕНИЕ
ЗАДАНИЕ
ПОДГОТОВКА ПЛАНА ПРОВЕДЕНИЯ ОДНОФАКТОРНОГО ЭКСПЕРИМЕНТА
ПЛАН ЭКСПЕРИМЕНТА И РЕЗУЛЬТАТЫ ОПЫТОВ
УРАВНЕНИЕ РЕГРЕССИИ
РЕЗУЛЬТАТЫ ОПЫТОВ В ГРАФИЧЕСКОМ ВИДЕ
ПРОВЕРКА АДЕКВАТНОСТИ И РАБОТОСПОСОБНОСТИ МОДЕЛИ
ВЫВОД
ЛИТЕРАТУРА
Современный этап научных исследований характеризуется тем, что наряду с классическим натурным экспериментом все шире применяется вычислительный эксперимент, проводимый на математической модели с помощью ЭВМ. Проведение вычислительного эксперимента значительно дешевле и мобильнее, чем проведение аналогичного натурного, и в ряде случаев вычислительный эксперимент является единственным возможным инструментом исследователя.
Математический аппарат теории планирования и обработки результатов экспериментов в полной мере может быть применен как к натурным, так и к вычислительным экспериментам. В данной контрольно-курсовой работе под проводимым экспериментом будем понимать эксперимент на математической модели, выполненный при помощи ЭВМ.
Основная задача теории планирования и обработки результатов экспериментов – это построение статистической модели изучаемого процесса в виде Y = f(X1
, X2
,…Xk
), где X – факторы, Y – функция отклика. Полученную функцию отклика можно использовать для оптимизации изучаемых процессов, то есть определять значения факторов, при которых явление или процесс будет протекать наиболее эффективно.
Объект исследования – одноцилиндровый четырехтактный дизельный двигатель ТМЗ-450Д.
Предмет исследования– процесс функционирования двигателя.
Цель исследования – анализ влияния одного из параметров двигателя на показатели его работы и получение соответствующей функциональнойзависимости
Область планирования фактора X: Xmin
= 0,012 м, Xmax
= 0,055 м.
План проведения эксперимента:
| № опыта |
xj
|
| 1 |
-1 |
| 2 |
-0,8 |
| 3 |
-0,6 |
| 4 |
-0,4 |
| 5 |
-0,2 |
| 6 |
0 |
| 7 |
0,2 |
| 8 |
0,4 |
| 9 |
0,6 |
| 10 |
0,8 |
| 11 |
1 |
Используя приведенные исходные данные и программу расчета функционирования двигателя, проанализировать влияние радиуса кривошипа (X) на величину максимальной температуры (Y) рабочего тела в цилиндре двигателя. Получить функциональные зависимости между указанными величинами.
Используя указанный в задании план проведения эксперимента в кодовом виде, а также область планирования фактора Х (Хmin
, Хmax
), подготовим план проведения данного однофакторного эксперимента.
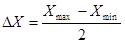 ; ; 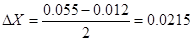 ; ;
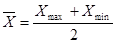 ; ; 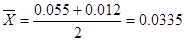 ; ;
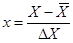 ; ; 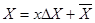 ; ;
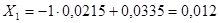 ; ; 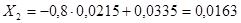 ; ;
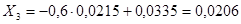 ; ; 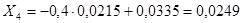 ; ;
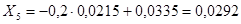 ; ; 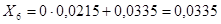 ; ;
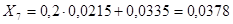 ; ; 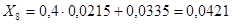 ; ;
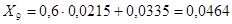 ; ; 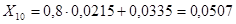 ; ;
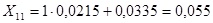 . .
где 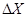 - интервал (шаг) варьирования фактора; - интервал (шаг) варьирования фактора;
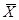 -натуральное значение основного уровня фактора;
-натуральное значение основного уровня фактора;
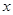 - кодированное значение фактора x; - кодированное значение фактора x;
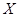 - натуральное значение фактора в j-ом опыте, где j = 1, 2,…, N; N – число опытов. - натуральное значение фактора в j-ом опыте, где j = 1, 2,…, N; N – число опытов.
В дальнейших расчетах будем использовать только натуральные значения факторов и функции отклика.
Используя выданную преподавателем программу расчета (математическую модель) проведем на ЭВМ необходимое количество опытов N. Полученные результаты представим в виде таблицы 1.
Табл. 1
| № опыта |
Xj
|
Yj
|
| 1 |
0,012 |
3601,8348 |
| 2 |
0,0163 |
2712,4310 |
| 3 |
0,0206 |
2195,4343 |
| 4 |
0,0249 |
1855,3637 |
| 5 |
0,0292 |
1626,8644 |
| 6 |
0,0335 |
1461,2450 |
| 7 |
0,0378 |
1339,577 |
| 8 |
0,0421 |
1250,5135 |
| 9 |
0,0464 |
1173,9877 |
| 10 |
0,0507 |
1126,4606 |
| 11 |
0,055 |
1092,5573 |
Получим функциональную зависимость Y = f(X) (уравнение регрессии) с помощью метода наименьших квадратов (МНК). В качестве аппроксимирующих функций использовать линейную (Y = a0
+ a1
X) и квадратичную зависимости (Y = a0
+ a1
X + a2
X2
). Посредством МНК значения a0
, a1
и a2
найдем из условия минимизации суммы квадратов отклонений измеренных значений отклика Yj
от получаемых с помощью регрессионной модели, т. е. путем минимизации суммы:
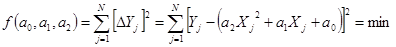 . .
Проведем минимизацию суммы квадратов с помощью дифференциального исчисления, путем приравнивания к 0 первых частных производных по a0
, a1
и a2
.
Рассмотрим реализацию метода наименьших квадратов применительно к уравнению вида Y = a0
+ a1
X. Получим:
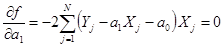 ; ;
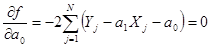 . .
Выполнив ряд преобразований, получим систему нормальных уравнений метода наименьших квадратов:
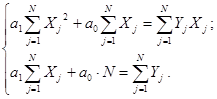
Решая эту систему, найдем коэффициенты a1
и a0
:
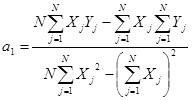 ; ; 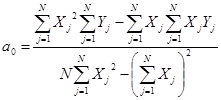 . .
Для квадратичной зависимости Y = a0
+ a1
X + a2
X2
система нормальных уравнений имеет вид:
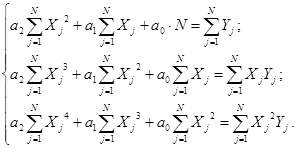
Вычислим из N опытов необходимые суммы и данные представим в виде таблицы 2.
Табл. 2
| № опыта |
Xj
|
Yj
|
Xj
2
|
Xj
Yj
|
Xj
2
Yj
|
Xj
3
|
Xj
4
|
| 1 |
0,012 |
3601,8348 |
0,000144 |
43,222017 |
0,5186642 |
0,0000017 |
0,000000020736 |
| 2 |
0,0163 |
2712,4310 |
0,0002656 |
44,212625 |
0,7204216 |
0,0000043 |
0,0000000705433 |
| 3 |
0,0206 |
2195,4343 |
0,0004243 |
45,225946 |
0,9315227 |
0,0000087 |
0,0000001800304 |
| 4 |
0,0249 |
1855,3637 |
0,00062 |
46,198556 |
1,1503254 |
0,0000154 |
0,0000003844 |
| 5 |
0,0292 |
1626,8644 |
0,0008526 |
47,50444 |
1,3870645 |
0,0000248 |
0,0000007269267 |
| 6 |
0,0335 |
1461,2450 |
0,0011222 |
48,951707 |
1,6398091 |
0,0000375 |
0,0000012593328 |
| 7 |
0,0378 |
1339,577 |
0,0014288 |
50,63601 |
1,9139876 |
0,000054 |
0,0000020414694 |
| 8 |
0,0421 |
1250,5135 |
0,0017724 |
52,646618 |
2,2164101 |
0,0000746 |
0,0000031414017 |
| 9 |
0,0464 |
1173,9877 |
0,0021529 |
54,473029 |
2,52747781 |
0,0000998 |
0,0000046349784 |
| 10 |
0,0507 |
1126,4606 |
0,0025704 |
57,111552 |
2,8954543 |
0,0001303 |
0,0000066069561 |
| 11 |
0,055 |
1092,5573 |
0,003025 |
60,090651 |
3,3049858 |
0,0001663 |
0,000009150625 |
| Σ |
0,3685 |
19436,266 |
0,0143782 |
550,27311 |
19,206122 |
0,0006174 |
0,0000282173998 |
Для уравнения регрессии вида Y = a0
+ a1
X найдем коэффициенты a1
иa0
:
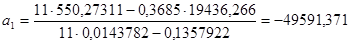 . .
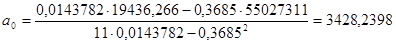 . .
Для уравнения регрессии вида
Y =
a0
+ a1
X + a2
X2
найдем коэффициенты a1
, a2
иa0
:
Решим систему нормальных уравнений способом Крамера:
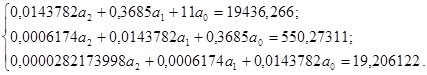
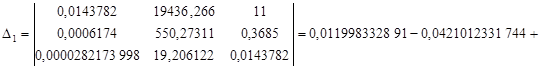
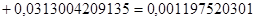 . .
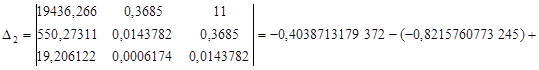
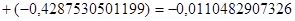 . .
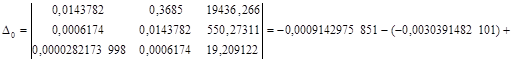
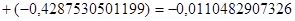 . .
Найдем определитель (
det) матрицы:
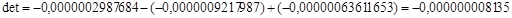 . .
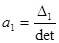 ;
; 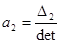 ;
; .
.
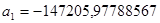 ; ; 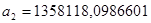 ; ; 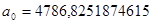 . .
Построим графики функций Y = a0
+ a1
X ; Y = a0
+ a1
X + a2
X2
:
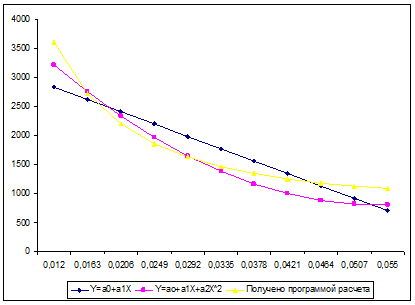
| X |
0,012 |
0,0163 |
0,0206 |
0,0249 |
0,0292 |
0,0335 |
0,0378 |
0,0421 |
0,0464 |
0,0507 |
0,055 |
| Y=ao
+a1
X |
2833,143 |
2619,9 |
2406,658 |
2193,415 |
1980,172 |
1766,929 |
1553,686 |
1340,443 |
1127,2 |
913,9573 |
700,7144 |
| Y=a0
+a1
X+a2
X2
|
3215,923 |
2748,207 |
2330,714 |
1963,444 |
1646,397 |
1379,574 |
1162,973 |
996,5962 |
880,4424 |
814,5117 |
798,8043 |
Для проверки адекватности модели определим абсолютные DYj
и относительные погрешности 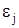 в каждом из опытов. в каждом из опытов.
DYj
= 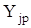 - Yj
; - Yj
; 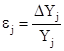 , ,
где 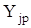 – расчетное значение функции (отклика) в j-ой точке. – расчетное значение функции (отклика) в j-ой точке.
Данные представим в виде таблицы 3.
Табл. 3
| j |
Y = a0
+ a1
X |
Y = a0
+ a1
X + a2
X2
|
| DYj
|
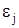 |
DYj
|
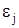 |
| 1 |
-768,6918 |
-0,21342 |
-385,9118 |
-0,10714 |
| 2 |
-92,531 |
-0,03411 |
35,776 |
0,01319 |
| 3 |
211,2237 |
0,09621 |
135,2797 |
0,06162 |
| 4 |
338,0513 |
0,1822 |
108,0803 |
0,05825 |
| 5 |
353,3076 |
0,21717 |
19,5326 |
0,012 |
| 6 |
305,684 |
0,20919 |
-81,671 |
-0,05589 |
| 7 |
214,109 |
0,15983 |
-176,604 |
-0,13183 |
| 8 |
89,9295 |
0,07191 |
-253,9173 |
-0,20305 |
| 9 |
-46,7877 |
-0,0398 |
-293,5453 |
-0,25004 |
| 10 |
-212,5033 |
-0,1886 |
-311,9489 |
-0,27693 |
| 11 |
-391,8429 |
-0,35865 |
-293,753 |
-0,26887 |
Просматривая значения этих погрешностей, исследователь может легко понять, какова погрешность предсказания в точках, где проводились опыты, устраивают его или нет подобные ошибки. Таким образом, путем сопоставления фактических значений отклика с предсказанными по уравнению регрессии можно получить достаточно надежное свидетельство о точностных характеристиках модели.
С помощью анализа работоспособности регрессионной модели выясним практическую возможность ее использования для решения какой-либо задачи. Это анализ будем проводить, вычисляя коэффициент детерминации (квадрат корреляционного отношения). Коэффициент детерминации R2
вычисляется по формуле:
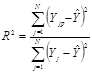
где 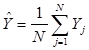 – общее среднее значение функции отклика. – общее среднее значение функции отклика.
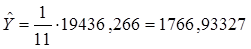 . .
Вычислим из N опытов необходимые суммы и данные представим в виде таблицы 4.
Табл. 4
| Y = a0
+ a1
X |
Y = a0
+ a1
X + a2
X2
|
| j |
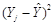 |
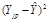 |
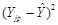 |
| 1 |
3366863,62479 |
1136803,18835 |
1952571,23764 |
| 2 |
893965,95743 |
727552,24249 |
853898,13319 |
| 3 |
183613,13271 |
409247,73017 |
312848,71152 |
| 4 |
7819,94095 |
181886,66602 |
37616,467 |
| 5 |
19619,28834 |
45470,75597 |
14328,99238 |
| 6 |
93445,31841 |
0,00002 |
147047,20405 |
| 7 |
182633,3815 |
45474,39816 |
359786,00774 |
| 8 |
266689,37885 |
181893,9504 |
589419,20142 |
| 9 |
351584,44898 |
409258,65674 |
602866,06259 |
| 10 |
410205,24101 |
727568,0054 |
801506,847 |
| 11 |
454782,94891 |
1136822,67874 |
759273,70255 |
| Σ |
6231222,66188 |
5001978,27246 |
5732724,84892 |
Для уравнения регрессии Y = a0
+ a1
X:
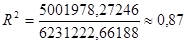
Для уравнения регрессии Y = a0
+ a1
X + a2
X2
:
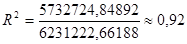
Т.к. в уравнениях регрессии 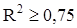 оба уравнения принято считать работоспособными. В уравнении регрессии вида Y = a0
+ a1
X + a2
X2 оба уравнения принято считать работоспособными. В уравнении регрессии вида Y = a0
+ a1
X + a2
X2
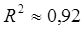 , а в уравнении регрессии вида Y = a0
+ a1
X , а в уравнении регрессии вида Y = a0
+ a1
X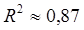 . Из этого следует, что в уравнении вида Y = a0
+ a1
X + a2
X2
найденное значение регрессии лучше объясняет вариацию в значениях Y (N >> (d+1)), чем в уравнении вида Y = a0
+ a1
X. . Из этого следует, что в уравнении вида Y = a0
+ a1
X + a2
X2
найденное значение регрессии лучше объясняет вариацию в значениях Y (N >> (d+1)), чем в уравнении вида Y = a0
+ a1
X.
ВЫВОД
В процессе выполнения контрольно-курсовой работы мы научились:
-
разрабатывать план проведения вычислительного эксперимента;
-
проводить вычислительный эксперимент на ЭВМ и накапливать статистическую информацию;
-
обрабатывать полученные статистические данные с помощью регрессионного анализа и получать формульные зависимости, связывающие значение выходной переменной (отклика) объекта с входными переменными (факторами);
-
графически представлять и анализировать полученные результаты (проверять адекватность и работоспособность регрессионной модели);
-
вычислять коэффициент детерминации (квадрат корреляционного отношения) и анализировать полученные результаты.
1. Гурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1972.
2.Красовский Г.И., Филаретов Г.Ф. Планирование эксперимента. – Минск, 1982.
3.Румшинский Л.З. Математическая обработка результатов эксперимента. Справочное руководство. – М.: Наука, 1971.
|