Контрольная работа: Основные расчеты в технической механике

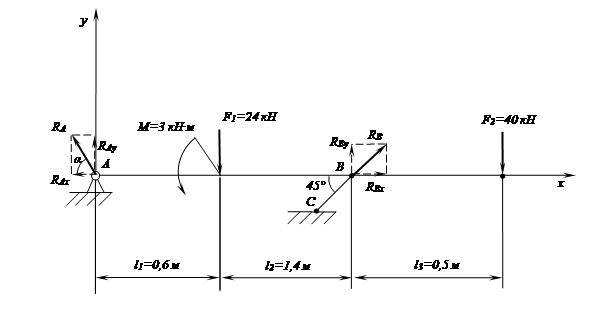
Задача №1 (рис. 2)

Балка закреплена шарнирно в точка А и удерживается в горизонтальном положении стержнем ВС, нагружена силами F_{1 ,} F₂ и парой сил с моментом М

Определить реакции шарнира А и стержня ВС

Решение:

Зададимся системой координат с центром в точке А.

Обозначим реакцию стержня ВС в точке В вектором R_B , направление же реакции шарнира А не известно.

Составим уравнение моментов в точке А:

Σ_МА = 0

Σ_МА =М_А (F₁ )+ М_А (F₂ ) - М_А (R_B )+ М_А (R_A ) + M=0

Заметим, что момент реакции шарнира в точке А будет равен нулю, так как плечо l=0

М_А (F₁ )= F₁ ∙ l₁ =24 ∙ 0,6 = 14,4 кН∙м

М_А (F₂ )= F₂ ∙ (l₁ + l₂ +l₃ )= 40 ∙ 2,5 = 100 кН∙м

М_А (R_A )= 0 кН∙м

М = - 3 кН∙м

получаем уравнение:

14,4 + 100 - 3 - М_А (R_B ) = 0

- М_А (R_B ) = - 14,4 - 100 + 3

- М_А (R_B ) = - 111,4 кН∙м

М_А (R_B ) = 111,4 кН∙м

Найдем реакцию R_B :

М_А (R_B ) = R_B ∙ cos 45º · (l₁ + l₂ )

R_B =

R_B = = 78,8 кН

Определим проекцию реакции R_A на ось x из уравнения суммы проекций:

ΣР_х = 0

ΣР_х = F_1x +R_Bx +F_2x +R_Ax =0

F_1x = F₁ ∙ cos 90° = 0

F_2x = F₂ ∙ cos 90° = 0

R_Bx = R_B ∙ cos 45°= 79,6 · 0,7 = 55,72

ΣР_х = 55,72 + R_Ax =0

R_Ax = - 55,72

Определим проекцию реакции R_A на ось yиз уравнения суммы проекций:

ΣР_y = 0

ΣР_y = F_{1 y} +R_By +F_{2 y} +R_Ay =0

F_1y = - F₁ ∙ cos 0° = - 24

R_By = R_B ∙ cos 45° = 78,8 · cos45° = 55,72

F_2y = - F₂ ∙ cos 0° = - 40 ∙ 1 = - 40

ΣР_y = -24 + 55,72 – 40 + R_Ay = 0

R_Ay = 24 - 55,72 + 40 = 8,28

Реакцию R_A найдем из прямоугольного треугольника по теореме Пифагора :

R_A = кН

Найдем угол между вектором реакции R_A и осью xпо косинусу угла α

cosα ==

α ≈ 8,5°

Для проверки определим сумму моментов сил и реакций в точке В, которая для тел находящихся в равновесии должна равняться нулю.

Σ_МВ = М_B (F₁ )+ М_В (F₂ )+M+ М_В (R_A )

М_В (F₁ ) = - F₁ ∙l₂ = - 24 ∙ 1,4 = - 33,6 кН∙м

М_В (F₂ ) = F₂ ∙ l₃ = F₂ ∙ l₃ = 40 ∙ 0,5 = 20 кН∙м

М_В (R_A ) = R_A ∙ sin 8,44º · (l₁ + l₂ ) = 56,332 · sin 8,5° · 2 = 16,65 кН∙м

M = - 3 кН∙м

Σ_МВ = - 33,6 + 20 + 16,6 - 3 ≈ 0

Задача № 2 (рис. 19)

Определить место положения центра тяжести сечения составленного из прокатных профилей

Решение:

А₁ = 34,8 см² = 3480 мм²

А₂ = 115 ∙ 10 = 1150 мм²

y₁ = 130

x₁ = 0

y₂ = 10 : 2 = 5

x₂ = 0

Так как сечение симметрично относительно оси yдостаточно определить только координату y_с

y_с = = 98,95 мм

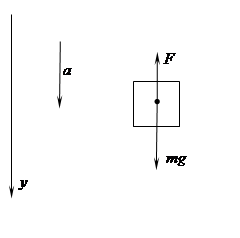
x_c = 0

Задача №3 (№23)

Груз массой 100 кг опускается равноускоренно с помощью невесомого троса, перекинутого через блок и в первые 4 секунды проходит 8 м. Определить силу натяжения троса.

Решение:

На груз действует сила натяжения троса F и сила тяжести mg , под действием которых он движется с ускорением а . Следовательно по второму закону Ньютона

mg + F = ma

Так как все силы направлены по вертикали, выберем вертикальную ось у с положительным направлением по ускорению (вниз)

Проектируем

mg + F = ma

mg – F = ma илиF = m(g – a)

Из кинематики :

h = at² /2

Следовательно :

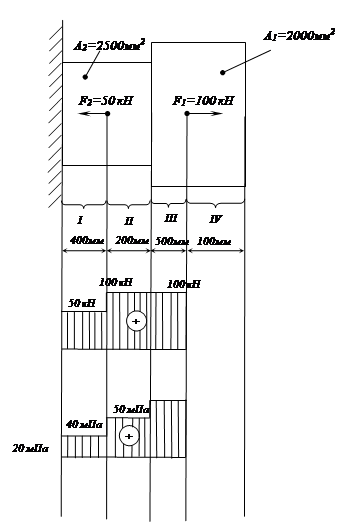
F = m(g – 2h/t² ) = 100 · (9,8 – ) = 880 H

Задача № 4 (рис. 37)

Для ступенчатого стального бруса требуется:

а) определить значение продольной силы и нормального напряжения по длине бруса.

б) построить эпюру.

в) определить удлинение (укорочение) бруса.

Модуль продольной упругости: E = 2 ∙10⁵ мПа

Решение:

Разобьем брус на участки начиная от свободного конца. Границы участков определяются точками приложения сил и местами изменения размеров поперечного сечения.

Всего будет 4-ре участка. Проведя сечение и отбрасывая левые части бруса можно определить продольные силы в его поперечных сечениях.

Участок I – не деформируется и продольные силы в нем будут равны нулю.

N₁ = 0

N₂ = N₃ = 100 кН

N₄ = F₁ – F₂ = 100 – 50 = 50 кН

т.е. на всех участках брус растянут, а продольные силы будут равны:

на участках II и III – 100 кН

на участке IV – 50 кН

Чтобы определить нормальные напряжения в поперечных сечениях бруса нужно разделить значения продольных сил на площади сечений.

для участка II : σ_II =

для участка III : σ_III =

для участка IV : σ_IV =

Определим относительное удлинение на разных участках бруса. По закону Гука, относительное удлинение:

ε_II =

ε_III =

ε_II =

Абсолютное удлинение на участках:

II = 0,00025 ∙ 500 = 0,125 мм

III = 0,0002 ∙ 200 = 0,04 мм

IV = 0,0001 ∙ 400 = 0,04 мм

Общее удлинение бруса будет равно:

0,125 + 0,04 + 0,04 = 0,205 мм

Задача №5 (рис.43)

Для заданной консольной балки построить эпюру изгибающих моментом и подобрать из условий прочности размеры поперечного сечения в двух вариантах:

- сдвоенный швеллер

- прямоугольник с отношением

Сравнить массы балок по обоим расчетным вариантам.

Материал балки – сталь Ст.3 [σ] = 160 мПа

Решение:

Разобьем балку на участки, границы которых определим точками приложения внешних сил.

На первом участке балки момент будет равен:

- в точке D

М₁ = - М = - 10 кН· м

- в точке С

М₁ = - М = - 10 кН· м

На втором участке:

- в точке С

М₂ = - М = - 10 кН· м

- в точке В

М₂ = - М – F₂ · z₂ = - 10 – 8 · 0,8 = - 16,4 кН · м

На третьем участке:

- в точке В

М₃ = - М – F₂ · z₂ = - 10 – 8 · 0,8 = - 16,4 кН · м

- в точке А

М₃ = - М – F₂ · (z₂ + z₃ ) – F₁ · z₃ = - 10 – 8 · (0,4 + 0,8) – 24 · 0,4 = - 29,2

Наибольший по величине изгибающий момент наблюдается в месте жесткой заделки балки в точке Aи равен он:

Найдем требуемый момент сопротивления

W_x ≥

Подбираем сечение балки в двух вариантах:

1. Сечение – сдвоенный швеллер

W_x ≥ 182,5 см³ см³

Подходит швеллер № W_x = см³

2. Сечение - прямоугольник с отношением сторон

для прямоугольника

W_x =;

подставив сюда и приняв W_x равным требуемому значению, получим:

W_x == = 182,5 см³

отсюда

h = 11,8 см

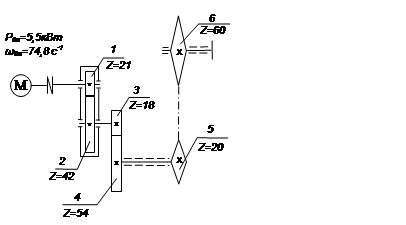
b = 11,8 : 3 = 3,9 см

Задача № 6 (рис.55)

Для заданного привода машины необходимо

а) дать характеристику привода и его отдельных передач

б)определить общие КПД и передаточные отношения.

в)определить мощность, вращающие моменты и угловые скорости для всех валов.

При расчетах принять следующие средние значения КПД (с учетом потерь на трение в опорах валов) передач:

зубчатая цилиндрическая - 0,97 (закрытая)

- 0,96 (открытая)

зубчатая коническая - 0,96 (закрытая)

- 0,95 (открытая)

червячная - 0,8 (закрытая)

цепная - 0,92 (открытая)

клиноременная - 0,95 (открытая)

Решение:

I ступень – закрытая зубчатая цилиндрическая передача с числом зубьев на ведущем колесе Z=21, на ведомом – Z = 42;

II ступень – открытая зубчатая цилиндрическая передача с числом зубьев на ведущем колесе Z=15, на ведомом – Z=54;

II ступень – цепная передача с числом зубьев на ведущем колесе Z=20, на ведомом – Z=60;

Определим передаточные отношения на отдельных передачах и на всем приводе:

i_1-6 = i_1-2 ∙ i_2-4 ∙i_5-6 = 2 ∙3 ∙3 = 18

Для определения КПД, нам требуется значение угловой скорости каждой передачи и всего привода.

ω₁ = ω_дв = 74,8 с^-1

из определения передаточного числа знаем:

i_1-2 =

отсюда:

ω₃ = ω₂ = 37,4 с^-1

ω₅ = ω₄ = 12,47 с^-1

Определим мощности для каждой передачи и всего привода:

Р₁ =Р_дв =5,5 кВт ; η_I = 0,97 (по условию)

Р₂ =η_I ∙ Р₁ = 0,97 ∙ 5,5 = 5,335 кВт

аналогично для остальных передач:

Р₃ =Р₂ = 5,335 кВт ; η_II = 0,96 (по условию)

Р₄ =η_II ∙ Р₃ = 0,96 ∙ 5,335 = 5,122 кВт

Р₅ = Р₄ = 5,122 кВт ; η_III = 0,92 (по условию)

Р₆ =η_III ∙ Р₅ = 0,92 ∙ 5,122 = 4,71 кВт

η_прив. = η_I ∙ η_II ∙ η_III = 0,97 ∙0,96 ∙0,92 = 0,857

Определим вращающие моменты для каждого вала