Курсова робота на тему: "Дослідження якостей лінійного ланцюга"
ЗМІСТ
Завдання до курсової роботи
Нормування параметрів ланцюга
1. Аналіз ланцюга в тимчасовій області методом змінних станів при постійних впливах
2. Аналіз ланцюга операторным методом при аперіодичному впливі
3. Якісний аналіз ланцюга частотним методом при аперіодичному впливі
4. Аналіз ланцюга частотним методом при періодичному впливі
Висновок
Література
ЗАВДАННЯ ДО КУРСОВОЇ РОБОТИ
1. Аналіз ланцюга в тимчасовій області методом змінних станів при постійних впливах;
2. Аналіз ланцюга операторним методом при аперіодичному впливі;
3. Якісний аналіз ланцюга частотним методом при аперіодичному впливі;
4. Аналіз ланцюга частотним методом при періодичному впливі.

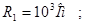 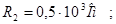 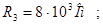 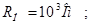
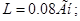 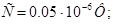 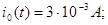 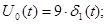
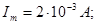 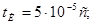 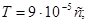
 
НОРМУВАННЯ ПАРАМЕТРІВ ЛАНЦЮГА
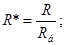 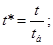
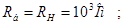 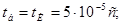 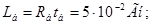 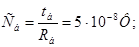
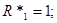 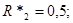 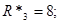 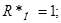
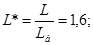 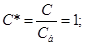
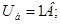 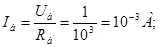
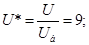 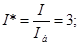
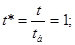 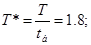 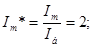
Далі індекс "*" опускається
1.
Аналіз ланцюга в тимчасовій області методом змінних станів при постійних впливах
Складання рівнянь стану ланцюга для 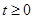
Зведемо динамічний ланцюг до резистивної (замінимо З-Елемент джерелом напруги, а L-Елемент замінимо на джерело струму):

Виразимо змінні стани (ic
і UL
), використовуючи метод вузлових напруг

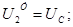
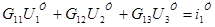
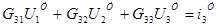
Визначаємо коефіцієнти:
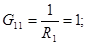 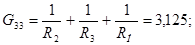 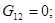 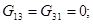 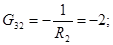
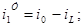 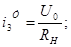
Після підстановки чисельних значень одержуємо:
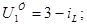
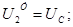
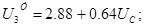
Всі змінні виражаємо через змінні стани й впливи:
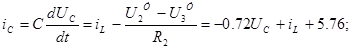
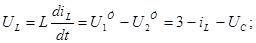
Рівняння стану ланцюга:
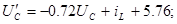
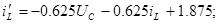
Знаходження точних рішень рівнянь стану
Загальний вид рішень рівнянь стану:
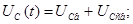
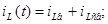
1) Незалежні початкові умови 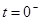

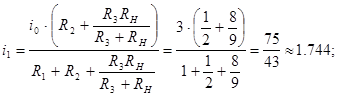
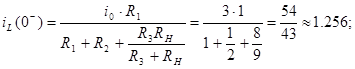
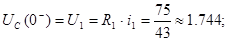
2) Визначаємо змушенні при 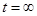
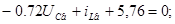
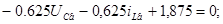
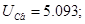
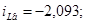
3) Визначаємо корінь характеристичного багаточлена
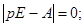
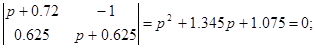
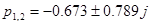
4) Визначаємо постійні інтегрування 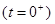
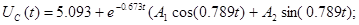
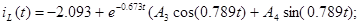
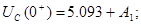
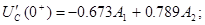
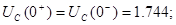
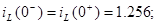
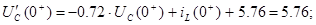
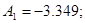
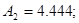
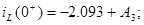
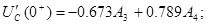
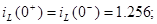
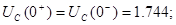
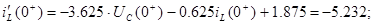
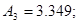
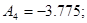
Точне рішення рівнянь стану:
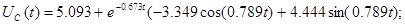
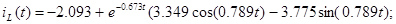
Побудова точних рішень рівнянь стану
2.
Аналіз ланцюга операторним методом при аперіодичному впливі
Операторна схема заміщення:
 
Визначення функції передачі.
Застосуємо метод пропорційних величин для знаходження функції передачі
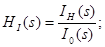
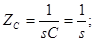 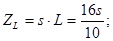
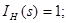 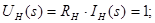
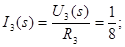 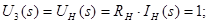
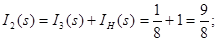
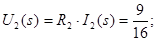
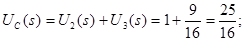
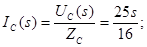
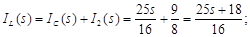
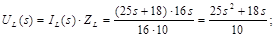
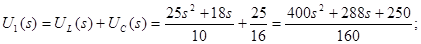
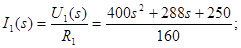
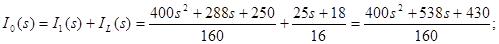
Функція передачі:
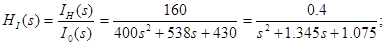
Знаходження нулів і полюсів функції передачі й нанесення їх на площину комплексної частоти
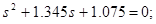
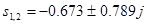
- полюси функції передачі;
Кінцевих нулів функція передачі не має;

Визначення з функції передачі перехідної 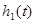 й імпульсної й імпульсної 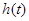 характеристики для вихідного сигналу характеристики для вихідного сигналу
1) імпульсна характеристика 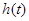 : :
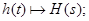
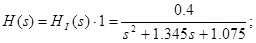
Зворотне перетворення Лапласа:
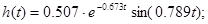
2) перехідна характеристика 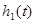 : :
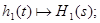
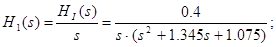
Зворотне перетворення Лапласа:
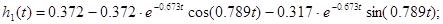
Визначення зображення по Лапласові вхідного одиночного імпульсу
Одержимо зображення сигналу шляхом диференціювання 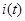
 
Для одержання самого сигналу, двічі інтегруємо 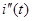 в s-області: в s-області:
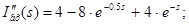
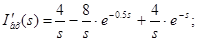
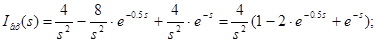
Визначення струму 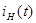 на виході ланцюга, використовуючи функцію передачі на виході ланцюга на виході ланцюга, використовуючи функцію передачі на виході ланцюга 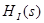
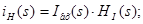
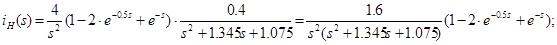
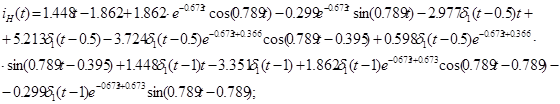
Побудова графіків перехідної й імпульсної характеристик ланцюга, а також вхідного й вихідного сигналів
3.
Якісний аналіз ланцюга частотним методом при аперіодичному впливі
Знаходження й побудова амплітудно-фазової (АФХ), амплітудно-частотної (АЧХ) і фазочастотній (ФЧХ) характеристик функції передачі ланцюга
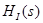
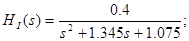
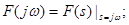
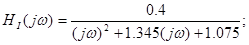
АЧХ: 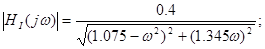
ФЧХ: 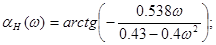
Визначення смуги пропущення ланцюга за рівнем
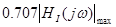
Смуга пропущення визначена за графіком 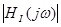

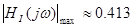
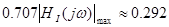
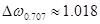 с-1 с-1
Знаходження й побудова амплітудного й фазового спектрів аперіодичного вхідного сигналу й визначення ширини спектра за рівнем
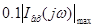

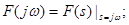

Комплексний спектр вхідного сигналу:
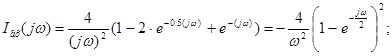
Приведемо вираження в дужках до синуса по Ейлеру (помножимо й розділимо на
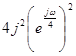 ): ):
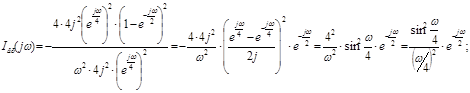
Амплітудний спектр вхідного сигналу: 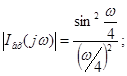
Фазовий спектр вхідного сигналу: 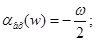
Ширина спектра визначається за графіком:
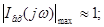
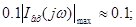
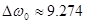 с-1
; с-1
;
Зіставляючи відповідно спектри вхідного сигналу із частотними характеристиками ланцюга, дамо висновок про очікувані перекручування сигналу на виході ланцюга.
Можна встановити, що приблизно одна десята частина амплітудного спектра вхідного сигналу укладається в смугу пропущення, а фазочастотна характеристика в цій смузі має гіперболічну залежність, на відміну від прямолінійної фазочастотної характеристики вхідного сигналу. Таким чином, при проходженні через ланцюг вхідний сигнал буде в значній мірі перекручений. На виході ланцюга можна чекати сигнал, значно більше слабкий, чим поданий на вхід, і більше виражений по своїй тривалості. Цей якісний висновок підтверджується точним розрахунком у п.2.
4.
Аналіз ланцюга частотним методом при періодичному впливі
Розкладемо в ряд Фур'є заданий вхідний періодичний сигнал. Побудуємо його амплітудний і фазовий спектри.
 
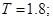 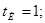
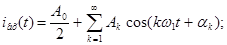
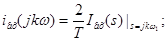 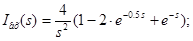
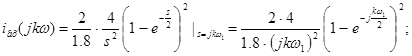
Для одержання амплітудного й фазового дискретного спектра виділимо модуль і фазу, для цього вираження зведемо до синуса по Ейлеру (помножимо й розділимо на 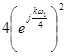 ): ):
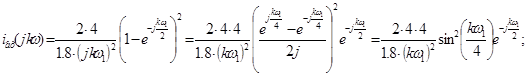
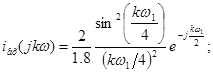
Амплітудний дискретний спектр: 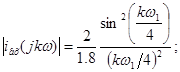
Фазовий дискретний спектр: 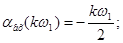
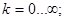 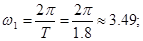
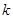 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
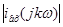 |
1.111 |
0,856 |
0,354 |
0,041 |
0,011 |
0,052 |
0,03 |
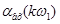 |
0 |
-1.745 |
-3.491 |
-5.236 |
-3,84 |
-8.727 |
-10.472 |
Побудова вхідного періодичного сигналу і його апроксимації відрізком ряду Фур'є
Число гармонік ряду Фур'є визначається шириною спектра за рівнем 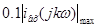 : 2 гармоніки : 2 гармоніки
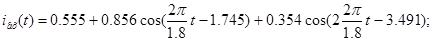
Побудова амплітудного й фазового спектрів вихідного періодичного сигналу, використовуючи розраховані в п.3.1 АЧХ і ФЧХ функції передачі ланцюга. Запис струму
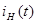 на виході ланцюга у вигляді відрізка ряду Фур'є на виході ланцюга у вигляді відрізка ряду Фур'є
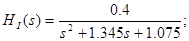
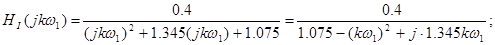
АЧХ: 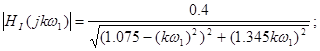
ФЧХ: 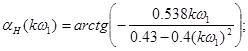
Амплітуди й початкові фази гармонік вихідної напруги:
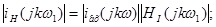
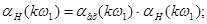
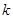 |
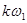 , c-1 , c-1
|
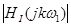 |
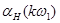 |
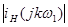 |
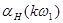 |
| 0 |
0 |
0,372 |
0 |
0.413 |
0 |
| 1 |
3,491 |
0,033 |
-2,742 |
0.028 |
-4.487 |
| 2 |
6,981 |
0,008 |
-2,947 |
0.003 |
-6.438 |
| 3 |
10,480 |
0,004 |
-3,013 |
0.0002 |
-8.249 |
Відповідно до прийнятого критерію ширини спектра:
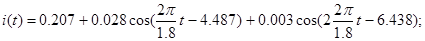
Побудова графіка струму 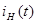 на виході ланцюга у вигляді суми гармонік знайденого відрізка ряду Фур'є на виході ланцюга у вигляді суми гармонік знайденого відрізка ряду Фур'є


ВИСНОВОК
При дослідженні лінійного ланцюга, можна зробити висновок, що при проходженні трикутного імпульсу через ланцюг він спотворюється: розтягується в часі, змінюється його амплітуда. На виході при періодичному впливі імпульсу отримані слабо виражені коливання струму.
ЛІТЕРАТУРА
1. Афанасьєв В.В. і ін. Трансформатори струму. – К., 2003
2. Методичні вказівки до курсового проекту по курсу: "Електричні системи і мережі". – Суми, 2005
3. Руководящие указания по релейной защите. Вып. 13а. Релейная защита понижающих трансформаторов и автотрансформаторов 110 – 500 кВ.
4.Макаров Е.Ф. Обслуживание и ремонт электрооборудования электростанций и сетей. - М.: Академия, 2003 г.
5.Дьяков В.И. Типовые расчеты по электрооборудованию. - М.: Высшая школа, 1980 г.
6. Димків А.М., Кибель В. М., Тишенін Ю.В. Трансформатори напруги. – К., 1997
|