| Федеральное агентство по образованию Российской Федерации
Орловский государственный технический университет
Кафедра "Электрооборудование и энергосбережение "
Пояснительная записка
к курсовой работе по дисциплине АСУТП
Работу выполнил
студент группы 41-ТК: Чернышова В.А.
Шифр 030917
Руководитель работы:
Комаристый А.С.
Курсовая работа защищена
с оценкой _____________
2007 г.
Содержание
Введение. 3
1. Схема и основные характеристики технологической установки. 5
2. Составление функциональной схемы автоматизации технологической установки. 6
3. Построение кривой разгона объекта по каналу регулирования, выбор типа регулятора. 8
4. Определение пригодности регулятора и параметров его настроек. 11
5. Анализ АСР на устойчивость по критериям устойчивости Гурвица и Михайлова. 14
5. Анализ АСР на устойчивость по критериям устойчивости Гурвица и Михайлова. 14
5.1 Определение устойчивости системы по критерию Гурвица. 15
5.2 Проверка устойчивости САУ по критерию Михайлова. 16
6. Определение запаса устойчивости АСР по фазе. 19
Заключение. 23
Литература. 25
Автоматика - отрасль науки и техники, охватывающая теорию и принципы построения средств и систем управления производственным процессом. Автоматика является основой автоматизации.
Автоматизация - этап развития машинного производства, который характеризуется освобождением человека от непосредственного выполнения функций управления производственными процессами и передачей этих функций техническим устройствам.
Управление производственным процессом - это такое воздействие на него, которое обеспечивает оптимальный или заданный режим работы. Объект управления - управляемый производственный процесс. Совокупность технических средств, используемых для управления, и производственного персонала, который принимает в нем непосредственного участие, образует совместно с объектом систему управления.
Процесс управления складывается из следующих основных функций, которые выполняются системой управления:
получение измерительной информации о состоянии производственного процесса как объекта управления;
переработка полученной информации и принятии решения о необходимом воздействии на объект для достижения целей управления;
реализация принятого решения, т.е. непосредственное воздействие на производственный процесс.
Средство измерений - это средство, предназначенное для получения информации о состоянии объекта управления.
Среди автоматических систем наиболее распространены автоматические системы регулирования (АСР). АСР предназначены для поддержания заданных значений технологических параметров, которые характеризуют состояние производственного процесса как объекта регулирования. С появлением новых технических средств, в практику автоматизации вошел новый тип систем управления - автоматизированные системы управления технологическими процессами.
Широкое внедрение автоматизации пищевых производств позволяет повысить эффективность технологических процессов и обеспечить полную сохранность натуральных свойств исходного сырья, которое поступает на переработку.
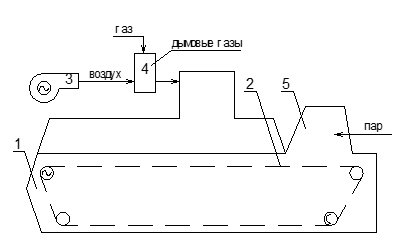
Рисунок 1.1 - Схема хлебопекарной печи
Регулируемые параметры: температура дымовых газов, подаваемых в центральную зону пекарной камеры.
Контролируемые параметры температура, давление газа.
Сушка (высушивание) материалов состоит в удалении влаги из влажных материалов путем ее диффузии из твердого материала и испарения.
Необходимость удаления влаги из материала может быть обусловлена разными причинами, например:
Влажный продукт может портиться при хранении, так как влага вредно воздействует на товарные свойства некоторых материалов: слеживание, смерзание в зимнее время, образование плесени.
Функциональная схема автоматизации (ФСА) дает представление о функционально - блочной структуре системы автоматического управления - регулирования, сигнализации, защиты технологического процесса или установки и определяет объем оснащения установки (объекта) аппаратурной автоматики. На ФСА изображены: технологическое оборудование, коммуникации, органы управления и средства автоматизации (датчики, регулирующие и контролирующие приборы, элементы управления, вычислительные устройства и пр.).
В зоне щитов и пультов условно изображают установленные средства автоматизации. От них линии связи идут к элементам схемы установки. Приборы и средства, установленные вне щитов, - местные приборы.
 
Рисунок 2 - Функциональная схема автоматизации регулирования и контроля температуры и давления газа
В соответствие с заданием для регулирования и контроля температуры и давления газа в технологической установке на выходе из топки установлен измеритель температуры (поз.4-1), имеющий сдвоенный чувствительный элемент (сдвоенная термопара), один из которых подключен ко вторичному прибору, установленному на щите (поз.4-2), осуществляющий показание и запись температуры, а другой - к электрическому регулятору (поз.4-3), имеющему датчик (поз.4-4), не встроенный в регулятор. Исполнительным механизмом (поз.4-5) можно управлять вручную с помощью кнопок управления (поз.4-5) можно управлять вручную с помощью кнопок управления (поз.3-1) через переключатель режима работы - ручное - автоматическое (поз.3-2). Исполнительный механизм изменяет подачу газа в топку. Для контроля давления на выходе в топку установлен датчик давления (поз.2-1), который подключен ко вторичному прибору на щите (поз.2-2), осуществляющему показание давление газа и имеющему задатчик (поз.2-3) и сигнализацию (поз.2-4) для обеспечения техники безопасности. Измеритель температуры подаваемого газа (поз.1-1) подключен к прибору, установленному на щите (поз.1-2), осуществляющему показания и запись температуры.
Исходные данные для построения кривой разгона объекта по каналу регулирования сведены в таблицу 1.
Таблица 1
| № п/п
|
Возмущение Y%
Р.О.
|
Относительное время кривой разгона tотн
|
Показатели качества процесса регулирования
|
| 0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1,0
|
| данные эксперимента - отклонение параметра Xэ(t)
|
X1%
|
Xост
|
Xр. отн.
|
| 1
|
10
|
0
|
0,25
|
1
|
2,3
|
3,3
|
4,1
|
4,5
|
4,8
|
5,0
|
5,1
|
5,1
|
40
|
10
|
1,5
|
Абсолютное значение времени определяется по формуле:
 , ,
где tпер. - время переходного процесса, указанное для технологической установки.

Кривую разгона объекта строим в единицах регулируемой величины по формуле:
 (t) (t) 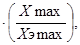 
где 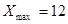 - отклонение по кривой разгона, - отклонение по кривой разгона,
 - отклонение параметра по таблице 1. - отклонение параметра по таблице 1.
Результаты пересчета t и X сводим в таблицу 2.
Таблица 2
| Параметр
|
Значение
|
| tотн
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1
|
| X э (t)
|
0
|
0,25
|
1
|
2,3
|
3,3
|
4,1
|
4,5
|
4,8
|
5,0
|
5,1
|
5,1
|
| t(М)
|
0
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
20
|
| X(t)
|
0
|
0,59
|
2,35
|
5,2
|
7,77
|
9,65
|
10,6
|
11,3
|
11,77
|
12
|
12
|
По данным таблицы строим кривую разгона объекта (рисунок 3).
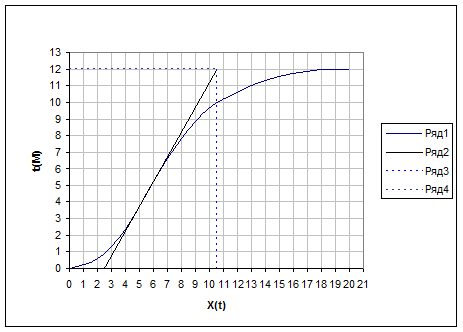
Рисунок 3 - Кривая разгона
На кривой разгона объекта проводим касательную к точке перегиба и определяем графически динамические и установившиеся параметры объекта:
t=2,5 мин,
Т=10,5 мин,
X¥ = 12.
Затем рассчитываем вспомогательные параметры:
 ; ;



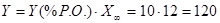
 
По номограмме  выбираем закон регулирования. выбираем закон регулирования.
 
Рисунок 4 - Номограмма 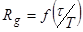
Согласно координаты точки (Rg, t/Т) и ближайшей к ней кривой - это П - регулятор.
После того, как мы выбрали закон регулирования определяем время регулирования tр и остаточное отклонение.
Время регулирования tр определяем по номограмме tр/t=f(t/Т) (рисунок 5).

Рисунок 5 - Номограмма tр/t=f(t/Т)
К оси абсцисс в точке с соответствующим значением t/Т восстанавливаем перпендикуляр до пересечения с графиком П - регулятора. По оси ординат определяем величину "С" отношения tр/t, тогда время регулирования tр определяем по формуле:
 ; ;
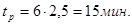
Затем проверяем неравенство:
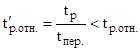 ; ;
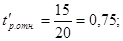

Так как.  , следовательно, регулятор выбран верно. , следовательно, регулятор выбран верно.
По графику

(рисунок 6) определяем графически остаточное отклонение.
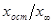 
Рисунок 6 - Номограмма

X’ост=С’X∞ C'=0,25;

X’ост< Xост 3<10;
Закон регулирования П - регулятора имеет вид:

Определяем параметры настроек регулирования по формуле:
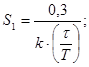

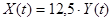 ; ;
Анализируемая АСР задана исходной структурной схемой, рисунок 7.
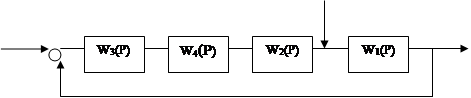 Рисунок 7 - Структурная схема
Структурную схему преобразовываем к одноконтурному виду, заменяя внутренние контуры одним звеном пользуясь правилами коммутации. Передаточные функции структурной схемы записываем в общем виде.
W(P) = W5(P) =W3(P) W4(P) W2(P) W1(P)
Заменяем параметры передаточных функций их числовыми значениями из таблицы 3.
Таблица 3
| Параметры звена
|
k1
|
T1
|
t1
|
k01
|
k2
|
T2
|
t2
|
k02
|
k3
|
t3
|
k4
|
T4
|
t4
|
| 8
|
1
|
1,2
|
0
|
0,4
|
0
|
0
|
1
|
0,9
|
0
|
0,5
|
0,7
|
0,5
|
Формулы передаточных функций имеют вид:
 
  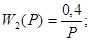
 ; ; 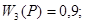
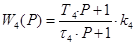 ; ; 

Записываем передаточную функцию замкнутой АСР по управлению 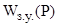 и возмущению Фf(P): и возмущению Фf(P):
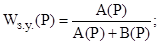



Для определения устойчивости системы по Гурвицу приравниваем к 0 знаменатель передаточной функции замкнутой по управнению системы, т.е. получаем характеристическое уравнение замкнутой по управлению системы:

В общем виде:

При положительных коэффициентах критерий Гурвица сводится к проверке неравенства:
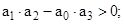

САУ по критерию Гурвица устойчива, так как определитель и диагональный минор величины положительные.
Определяем критический коэффициент усиления замкнутой по управлению системы по формуле:
 ; ;

Для проверки САУ по критерию Михайлова в характеристическом уравнении для замкнутой по управлению системы заменяем оператор дифференцирования Р на комплексную переменную jw, полученное комплексное число представляем в алгебраической форме записи:
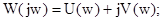
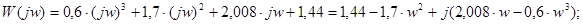 

Изменяя значение w от 0 до ¥ определяем значение функции и строим график на комплексной плоскости. На первоначальном этапе определяем точки пересечения годографа Михайлова с действительной и мнимой осями.
1)  ; ;
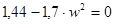 ; ;

 . .
2) 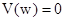 ; ;
 ; или ; или 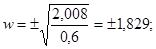
 или или 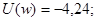
Изменяя значение w определяем U(w) и V(w), полученные данные сводим в таблицу 4.
Таблица 4.
| w
|
0,0
|
0,4
|
0,8
|
1,2
|
1,3
|
1,6
|
2,0
|
2,4
|
| U(w)
|
1,440
|
1,168
|
0,352
|
-1,008
|
-1,433
|
-2,912
|
-5,36
|
-8,352
|
| V(w)
|
0,000
|
0,765
|
1,299
|
2,410
|
1,292
|
0,755
|
-0,784
|
-3,475
|
| w
|
2,8
|
3,2
|
3,6
|
3,9
|
4,0
|
4,4
|
4,8
|
5,2
|
5,6
|
| U(w)
|
-11,888
|
-15,968
|
-20,592
|
-24,417
|
-25,76
|
-31,472
|
-37,728
|
-44,528
|
-51,872
|
| V(w)
|
-7,549
|
-13,235
|
-20,765
|
-27,76
|
-30,368
|
-42,275
|
-56,717
|
-73,923
|
-94,125
|
По данным таблицы строим годограф, рисунок 8.
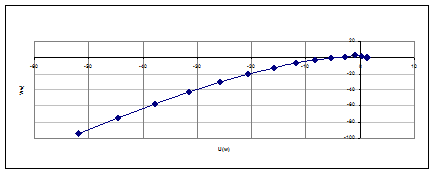
Рисунок 8 - Годограф Михайлова
Анализируя годограф Михайлова делаем следующие выводы:
САУ по критерию Михайлова устойчива, так как при показателе степени характеристического уравнения n=3, кривая (годограф), начинаясь на действительной положительной полуоси, огибает начало координат против часовой стрелки, проходя последовательно 3 квадранта.
Определенный по графику коэффициент максимального усиления kmax
 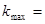 kд + kз kд + kз
kд - коэффициент усиления, = 1,44
kз - коэффициент запаса, = 4,24
Сравнения его со значением, определенным по критерию Гурвица, мы видим, что они равны:
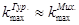
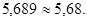
Для определения запаса устойчивости по фазе воспользуемся критерием Михайлова - Найквиста. Для этого исследуем разомкнутую по управлению систему:

Выпишем отдельно числитель и разделим его на вещественную и мнимую составляющие, заменив P на jw:




Амплитудно-частотную характеристику численно найдем по формуле:
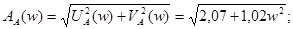
Фазово-частотную характеристику численно найдем по формуле:

Выпишем знаменатель и так же разделим его на вещественную и мнимую части:
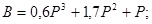


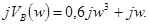
Амплитудно-частотную характеристику определим по формуле:
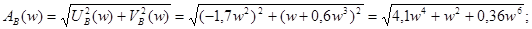
Для удобства строим АЧХ и ФЧХ в логарифмических координатах.
Чтобы система была устойчива, необходимо, чтобы логарифмические частотные характеристики разомкнутой системы удовлетворяли следующему требованию: необходимо и достаточно, чтобы при всех частотах, при которых ЛАЧХ положительна, значения фазы не превышали "-π". Иначе говоря, система устойчива, если ЛАЧХ пересечет ось lg(w) раньше, чем ЛФЧХ достигнет значения "-π".
Фазово-частотную характеристику определим по формуле:
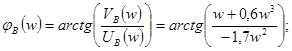
 ; ;
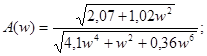

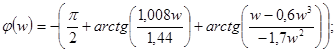
Изменяя значение w от 0 до ¥ рассчитываем значение действительной и мнимой составляющих. Затем производим операцию логарифмирования, и результаты вычислений сводим в таблицу 5.
Таблица 5
| w
|
1
|
1,25
|
1,5
|
1,75
|
2
|
2,25
|
2,5
|
| lgw
|
0
|
0,09691
|
0,176091
|
0,243038
|
0,30103
|
0,352183
|
0,39794
|
| 20lgA(w)
|
11,56588868
|
9,357563
|
7,573092
|
6,07112
|
4,770441
|
3,620912
|
2,58966
|
| φ(w)
|
0
|
-0,32548
|
-0,58501
|
-0,79662
|
-0,97266
|
-1,12171
|
-1,24986
|
По данным таблицы строим годограф, рисунок 9.

Рисунок 9 - Запас устойчивости по фазе
По графику определяем запас устойчивости по фазе
Δφ = 1,93 рад = 110,5°, следовательно, система имеет высокий запас устойчивости.
В пищевой промышленности чаще всего необходимо измерять, контролировать и регулировать следующие технологические параметры: температуру, давление (разряжение), влажность, уровни рабочих сред в аппаратах и машинах, показатели качества и состава сырья, полуфабрикатов и готового продукта.
При внедрении автоматизации технологического процесса обеспечивается рост производства, повышение качества продукции и производительности труда.
В процессе выполнения курсового проекта мы ознакомились с устройством и основными характеристиками хлебопекарной печи. Составили функциональную схему автоматизации, построили кривую разгона по каналу регулирования, выбрали тип регулятора - П - регулятор, определили пригодность регулятора и записали закон регулирования:
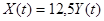 . .
Проанализировали автоматизированную систему регулирования по критериям Гурвица и Михайлова и сделали вывод:
По критерию Михайлова система устойчива, так как при показателе степени характеристического уравнения n=3, кривая, начинаясь на положительной действительной полуоси, огибает начало координат против часовой стрелки и проходит последовательно 3 квадрата;
Коэффициенты усиления k max определенный по графику и найденный по критерию Гурвица равны

При использовании критерия Михайлова - Найквиста рассчитали запас устойчивости по фазе. Δφ = 1,93 рад = 110,5°.
1. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем: Учебник для ВУЗов. М.: Машиностроение. - 1978 - 736 с.
Симонов В.П. Задания и методические указания на курсовую работу по УТС. Орел: ОрелГТУ, 1999 - 22 с.
3. Качанов А.Н. Математические основы проектирования и наладки систем автоматического управления техническими объектами и процессами. Орел: ОрелГТУ, 2001 - 143 с.
4. Автоматика и автоматизация пищевых продуктов: Учебник для ВУЗов. М.: "ВО Агропромиздат", 1991 - 239 с.
5. Малахов Н.Н. Процессы и аппараты пищевых производств. Орел: ОрелГТУ, 2001 - 686 с.
|