|  Федеральное агентство по рыболовству Федеральное агентство по рыболовству
Государственное образовательное учреждение высшего профессионального образования
“
Камчатский государственный технический университет
”
Факультет (филиал) ФИТ специальность (направление) УИ
Кафедра Систем Управления
Дисциплина: Автоматизация и проектирование средств и систем управления
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту (работе) на тему:
«Автоматизированное проектирование системы управления технологическим процессом производства цемента
»
Студент: Рунго Олег Викторович
Группа: 05-УИ
шифр_____________________________________
Обозначение курсового проекта (работы)___________________________
Проект (работа) защищен(а) на оценку_____________________________
Руководитель проекта (работы)_____________________ Пюкке Г.А.
подпись, дата инициалы и фамилия
Члены комиссии________________________________________________
подпись, дата инициалы и фамилия
_______________________________________________________________
подпись, дата инициалы и фамилия
_________________________________________________________________
подпись, дата инициалы и фамилия
ПЕТРОПАВЛОВСК-КАМЧАТСКИЙ
2009 г.
Федеральное агентство по рыболовству
Государственное образовательное учреждение высшего профессионального образования
“
Камчатский государственный технический университет
”
Факультет (филиал) ФИТ специальность (направление) УИ
Кафедра Систем Управления
Дисциплина: Автоматизация и проектирование средств и систем управления
ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ (РАБОТУ)
Студент шифр_______________группа 05-УИ
1 Тема «
Автоматизированное проектирование системы управления технологическим процессом производства цемента
»
2 Срок представления проекта (работы) к защите________________200_ г.
3 Исходные данные для разработки: Передаточная функция компоненты объекта автоматизации - 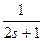 ; Передаточная функция усилительно-преобразовательного устройства - ; Передаточная функция усилительно-преобразовательного устройства - 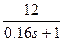 ; Передаточная функция исполнительного механизма - ; Передаточная функция исполнительного механизма - 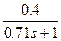 . .
4 Содержание пояснительной записки:
Титульный лист
Задание
Содержание
Введение
1 Описание технологического процесса
2 Идентификация объекта автоматизации
3 Построение системы управления технологическим процессом
4 Оптимизация параметров моделируемой системы
5 Анализ качества системы управления
Заключение
Список использованных источников
5 Перечень графического материала: Отсутствует
Руководитель проекта (работы)__________________ Пюкке Г.А.
подпись, дата инициалы и фамилия
Задание принял к исполнению___________________
подпись, дата инициалы и фамилия

Содержание
1 Описание технологического процесса
1.1 Обоснование целесообразности и необходимости автоматизации технологического процесса…………………………………………………………………………..7
1.2 Описание технологического процесса и производственного оборудования…………………………………………………………………………………………………..8
1.3 Требования к системе автоматизации технологического процесса…………………………………………………………………………………………………………..12
2 Идентификация объекта автоматизации
2.1 Особенности построения моделей технологических объектов управления……………………………………………………………………………………………………..13
2.2 Виды моделей линейных стационарных динамических объектов………………………………………………………………………………………………………..16
2.3 Виды моделей пакета System Identification Toolbox…………………………………………………………………………………………………………..20
2.4 Основные операторы и функции пакета System Identification Toolbox…………………………………………………………………………………………………………..23
2.5 Пример использования пакета System Identification Toolbox для идентификации технологических объектов управления………………………………………………………………………………………….………….25
2.6 Обработка данных при построении модели объекта управления………………………………………………………………………………………………..…….29
2.7 Оценивание статистических и частотных характеристик исходных данных……………………………………………………………………………………………………………..33
2.8 Параметрическое оценивание данных……………………………………….……38
2.9 Функции преобразование моделей……………………………………………………42
2.10 Проверка адекватности модели………………………………………….………….49
2.11 Анализ модели технического объекта управления……………….…..56
2.12 Основные результаты идентификации технического объекта идентификации……………………………………………………………………………………………..71
 3 Построение системы управления технологическим процессом 3 Построение системы управления технологическим процессом
3.1 Задание структуры системы автоматического управления, проверка системы управления на устойчивость…………………………………………………..74
3.2 Построение структуры системы автоматического регулирования установки обжига клинкера………………………………………………………………………76
4 Оптимизация параметров моделируемой системы
………………….80
5 Анализ качества системы управления
…………………………………….….85
ВВЕДЕНИЕ
Характерной особенностью современного этапа автоматизации производства состоит в том, что он опирается на революцию в вычислительной технике, на самое широкое использование микропроцессоров и контроллеров, а также на быстрое развитие робототехники, гибких производственных систем, интегрированных систем проектирования и управления, SCADA-систем разработки программного обеспечения.
Целью автоматизации является снижение объёма ручного труда, обеспечение стабильности характеристик технологического процесса, обеспечение возможности наблюдения, анализа и управления параметрами технологического процесса человеком. Результатом этого процесса является получение автоматизированной системы. Автоматизация производства позволяет повысить качество и снизить себестоимость продукции.
Автоматизированная система - это совокупность управляемого объекта и автоматизированных управляющих устройств, в которой часть функций управления выполняет человек. Автоматизированная система получает информацию от объекта управления, передаёт, преобразует и обрабатывает её, формирует управляющие команды и выполняет их на управляемом объекте. Человек определяет цели и критерии управления, корректирует их, если изменяются условия.
Применение средств и систем автоматизации позволяет решать следующие задачи:
· вести процесс с производительностью, максимально достижимой для данных производительных сил, автоматически учитывая непрерывные изменения технологических параметров, свойств исходных материалов, изменений в окружающей среде, ошибки операторов;
·  управлять процессом, постоянно учитывая динамику производственного плана для номенклатуры выпускаемой продукции путем оперативной перестройки режимов технологического оборудования, перераспределения работ на однотипном оборудовании и т. п.; управлять процессом, постоянно учитывая динамику производственного плана для номенклатуры выпускаемой продукции путем оперативной перестройки режимов технологического оборудования, перераспределения работ на однотипном оборудовании и т. п.;
· автоматически управлять процессами в условиях вредных или опасных для человека.
Решение поставленных задач предусматривает целый комплекс вопросов по проектированию и модернизации существующих и вновь разрабатываемых систем автоматизации технологических процессов и производств. Использование автоматизированной системы управления повышает надежность работы устройств и улучшает технико-экономические показатели за счет следующих усовершенствований:
· реализации системы на базе средств, отвечающих современному уровню
развития техники управления технологическими процессами;
· реализации более сложных законов автоматического регулирования, точнее и полнее учитывающих специфику протекающих технологических процессов;
· внедрения системы безопасного управления объектами повышенной опасности (розжиг, плановый и аварийный останов, опрессовка и т.д.);
· создания комфортных условий работы для оперативного персонала, снижающих нагрузку оператора, облегчающих принятие им решений по управлению. Приближения решений к оптимальным, благодаря лучшему информационному обеспечению (представление данных в требуемом объеме, в удобном для восприятия виде в реальном времени);
· повышения меры ответственности персонала за счет наличия в системе функций слежения и протоколирования действий персонала по управлению системой;
·  повышения безаварийности функционирования системы, облегчения эксплуатационного обслуживания и сокращения времени на поиск и устранение дефектов; повышения безаварийности функционирования системы, облегчения эксплуатационного обслуживания и сокращения времени на поиск и устранение дефектов;
· выдачи технико-экономических показателей и объективной информации о технологическом процессе, которая может быть использована неоперативным инженерно-техническим и административным персоналом для решения производственных и организационно-экономических задач.
В данном учебном пособии на конкретном примере одного из видов технологического процесса производства рассматривается методика анализа и синтеза системы автоматизации. Изложение материала базируется на использование возможностей современной интегрированной системы компьютерной математики MATLAB и её приложений. Рассмотренные в учебном пособии вопросы должны найти отражение в курсовом и дипломном проектировании по автоматизации технологических процессов и производств.
Целью курсового проектирования по дисциплине "Автоматизация проектирования систем и средств управления" является закрепление знаний, выработка навыков проектирования систем с использованием элементов автоматизации проектных процедур, работы с технической литературой и данными Интернета: государственными и отраслевыми стандартами, каталогами заводов-изготовителей, справочной литературой, базами данных сайтов заводов-изготовителей.
 ГЛАВА 1. ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА ГЛАВА 1. ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
1. 1. Обоснование целесообразности и необходимости автоматизации технологического процесса
В этом разделе приводится информация об области применения производимой продукции, а также информация об ее назначении (например: керамические изделия). Перечисляются этапы технологического процесса (например: производство керамических изделий состоит из нескольких этапов):
- процесс приготовления шихты;
- сушка керамического порошка;
- формовка и прессование керамических изделий;
- обжиг керамических изделий).
Описываются методы изготовления продукта и исходные материалы производства (например: пластичное формование керамических изделий, или другой метод, который применяют для формования изделий сложной формы, - метод шликерного литья).
Исходные материалы (например: глинистые и тонкомолотые материалы, каолин, глины, отощающие компоненты и плавни).
Перечисляются контролируемые параметры и допустимые пределы отклонения значений параметров (например: влажность массы для пластического формования должна быть в пределах 18-25%; влажность литейного шликера - в пределах 31-35%; отклонение влажности пластической массы от заданной средней величины не должна превышать ± 0,5%, шликера - соответственно ± 0,8%).
Делается вывод о необходимости применения автоматизированной системы контроля и управления технологическим процессом (по показателям экономичности, точности функционирования, быстродействия, инерционности, безопасности и др).
Выбирается этап технологического процесса производства, подлежащий автоматизации, обеспечивающей устойчивую работу технологического оборудования и осуществляющей управляющие воздействия для компенсации изменений в технологическом процессе (например: автоматизация процесса сушки исходного материала). Контроль влажности изделий позволяет корректировать режим сушки и поддерживать влажность керамической массы в заданных пределах).
1. 2. Описание технологического процесса и производственного оборудования
Рассматриваются различные современные устройства, используемые для реализации выбранного процесса производства. Приводится их структура и описание этапов функционирования.
Приводится мнемоническая схема автоматического регулирования процесса производства (например: для рассматриваемого примера сушки исходного материала используются распылительные сушилки). Распылительные сушилки применяют для снижения влажности массы до 7- 9% перед ее прессованием.
Математическое описание звеньев системы автоматизации следует начинать с ТОУ. В технической литературе тепловые объекты автоматизации (например, распылительная сушилка) с достаточной степенью точности описываются последовательным соединением звена чистого запаздывания и апериодического звена первого порядка. Значения постоянных времени и времени запаздывания определяются по переходным характеристикам.
Однако в ряде случаев, когда невозможно получить переходную характеристику при составлении математической модели ТОУ следует использовать статистические данные по их характеристикам, полученные экспериментально в ходе штатной работы установки методом пассивного эксперимента, когда через определенные промежутки времени фиксируются значения входной и выходной величины ТОУ. Такой путь называется идентификацией объектов автоматизации.
1. 3. Требования к системе автоматизации технологического процесса
Анализ технологического процесса позволяет построить структуру системы автоматизации и сформулировать требования, предъявляемые к системе автоматизации технологического процесса. В приведенном выше примере применение автоматического регулирования влажности шликера по температуре отходящих газов позволяет:
 - сократить расход газа; - сократить расход газа;
- уменьшить среднеквадратическое отклонение влажности шликера;
- увеличить качество керамических изделий;
- уменьшить брак при прессовании.
Для обеспечения положительного эффекта использования системы автоматизации, к ней предъявляются следующие требования:
- статическая ошибка: не более ± 5 %;
- перерегулирование: не более 10 %;
- время переходного процесса: от 0, 1 до 0, 2 с;
- запас устойчивости по амплитуде: не менее 20 дБ;
- запас устойчивости по фазе: от 20 до 80 градусов.
ГЛАВА 2. ИДЕНТИФИКАЦИЯ ОБЪЕКТА АВТОМАТИЗАЦИИ
2. 1. Особенности построения моделей технологических объектов управления
Сложность идентификации технологических процессов во многом зависит от наличия априорной информации о технологических объектах управления, их статических и динамических характеристик. Определение характеристик объекта управления выполняется различными способами, например, могут быть рассмотрены методы, связанные с проведением физичес кого эксперимента над ТОУ, в результате которого будет получен массив экспериментальных данных [ui
,
yi
], где ui
– входные переменные, yi
– выходные переменные ТОУ, i
– номер опыта. На основе массива экспериментальных данных [ui
,
yi
] в дальнейшем строится аналитическая модель посредством полиномиальной аппроксимации (например, с использованием метода наименьших квадратов или сплайнов). кого эксперимента над ТОУ, в результате которого будет получен массив экспериментальных данных [ui
,
yi
], где ui
– входные переменные, yi
– выходные переменные ТОУ, i
– номер опыта. На основе массива экспериментальных данных [ui
,
yi
] в дальнейшем строится аналитическая модель посредством полиномиальной аппроксимации (например, с использованием метода наименьших квадратов или сплайнов).
В самом общем случае, связь между входным и «теоретическим» выходным сигналами может быть задана в виде некоторого оператора Ψ. При этом наблюдаемый выходной сигнал объекта может быть описан на основе соотношения:
y
(
t
) =
Ψ[u
(
t
)
] + e
(
t
).
Принцип суперпозиции позволяет объединить все действующие помехи в одну общую e
(
t
)
и приложить ее к выходу линейной модели. При рассмотрении задач идентификации все помехи считают статически независимыми, что позволяет моделировать их в виде гауссовского процесса (шума).
Перед началом экспериментальных исследований проводят априорный анализ перечня входных переменных с целью отбора и включения в состав модели информативных параметров, т. е. оказывающих наиболее сильное воздействие на выходные переменные y
(
t
)
. В первую очередь в их состав включают управляющие входные переменные, с помощью которых осуществляется регулирующее воздействие на ТОУ.
Если в процессе идентификации структура модели не меняется, то выполняется только оценивание параметров модели (идентификация в узком смысле). Однако можно менять и структуру модели, подбирая наиболее адекватную описываемому процессу. При этом вид модели, ее структура выводится из физических представлений о сути процессов в ТОУ. Например, простейший сглаживающий фильтр (RC-цепь) описывается известными законами электротехники, для него можно записать:
u(t) = RCdy(t)/dt + y(t),
где Uin
(t) = u(t), Uout
(t) = y(t).
Если такая структура (с точностью до вектора коэффициентов β
) известна, то при известном входном сигнале u
(
t
)
описание объекта можно представить в виде:
y
(
t
) =
F
(
β
,
t
) +
e
(
t
),
где F
–
функция известного вида, зависящая от β
и времени t
.
Последнее уравнение позволяет после проведения эксперимента, заключающегося в фиксации входного и выходного сигналов на каком-то интервале времени, провести обработку экспериментальных данных и каким-либо методом (например, методом наименьших квадратов) найти оценку вектора параметров β
. Отметим, что при экспериментальном определении параметров модели необходимо обеспечить:
● подбор адекватной структуры модели;
● выбор такого входного сигнала, чтобы по результатам эксперимента можно было найти оценки всех параметров модели.
Наиболее просто задача определения параметров решается для линейных объектов, для которых выполняется принцип суперпозиции. В задачах идентификации под линейными объектами чаще понимаются объекты, линейные по входному воздействию.
Как правило, идентификация – многоэтапная процедура, состоящая из этапов:
1. Структурная идентификация, включающая определение структуры математической модели на основании теоретических соображений.
2. Параметрическая идентификация включает в себя процедуру оценивания параметров модели по экспериментальным данным.
3. Проверка адекватности – проверка качества модели в смысле выбранного критерия близости выходов модели и объекта.
Следует отметить, что в связи с многообразием объектов и различных подходов к их моделированию существует множество вариантов решения задачи идентификации.
 2. 2. Виды моделей линейных стационарных динамических объектов 2. 2. Виды моделей линейных стационарных динамических объектов
Линейные непрерывные стационарные динамические объекты могут быть представлены (без учета действия шума e
(
t
)
) в виде:
Дифференциального уравнения
. Наиболее универсальная модель, имеющая форму
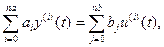
где na
– порядок модели (na
> nb
); ai
и bj
– постоянные коэффициенты (параметры модели); u
(
j
)
(
t
)
и y
(
i
)
(
t
)
– производные, соответственно, входного и выходного сигналов.
Передаточной функции.
Модель определяется как отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала
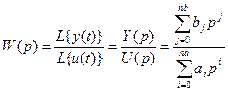 , ,
где L
{●}
– символ преобразования Лапласа, р –
переменная (оператор Лапласа).
Импульсной характеристики
w
(
t
) и
переходной функции
h
(
t
)
. Импульсная характеристика определяется как реакция объекта на входной сигнал в виде δ-функции. Переходная функция h(t) определяется как реакция объекта на входной сигнал в виде единичного скачка. Соотношения между этими характеристиками имеют следующий вид:
L
{
w
(
t
)}=
W
(
p
),
w
(
t
)=
h
’
(
t
) ,
L
{
h
(
t
)}=
W
(
p
)/
p
При нулевых начальных условиях связь между выходными и входными сигналами описывается интегралом свертки:
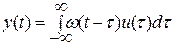 , ,
или в операторной форме:
 Y
(
p
) =
W
(
p
)*
U
(
p
)
. Y
(
p
) =
W
(
p
)*
U
(
p
)
.
Частотной характеристики.
Частотные характеристики объекта определяются его комплексным коэффициентом передачи W
(
jω
)
. Модуль комплексного коэффициента передачи │W
(
jω
)
│= A
(
ω
)
представляет собой амплитудно-частотную характеристику (АЧХ) объекта с передаточной функцией W
(
p
)
, а аргумент arg(W
(
jω
))=
φ
(
ω
)
– фазочастотную характеристику (ФЧХ). Графическое представление W
(
jω
)
, на комплексной плоскости при изменении ω
от 0 до ∞, то есть график амплитудно-фазовой характеристики (АФХ) в полярных координатах в отечественной литературе называется годографом, а в англоязычной – диаграммой Найквиста. В теории автоматического управления часто используется логарифмическая амплитудно-частотная характеристика (ЛАЧХ), равная 20 lg │W
(
jω
)
│.
В 70-е годы 20 века Розенброком был создан метод «размытых» частотных характеристик, предназначенный для автоматизированного проектирования систем с несколькими входами и выходами, ориентированный на использовании средств вычислительной техники и названный в последствие методом переменных состояния (МПС). В основе этого метода лежит представление дифференциальных уравнений в нормальной форме Коши, которое дополняется алгебраическими уравнениями, связывающими выходные переменные с переменными состояния:
x
’ =
Ax
+
Bu
y
=
Cx
, 
где u
– вектор входных воздействий; y
– вектор выходных воздействий; x
– вектор переменных состояния; A, B, C
– матрицы коэффициентов размерности n
x n
,
n
x m
,
r
x n
соответственно; n
– число переменных состояния или максимальная степень производной исходного дифференциального уравнения; m
– число входов; r
– число выходов.
 Математическим аппаратом метода переменных состояния являются матричное исчисление и вычислительные методы линейной алгебры. Метод переменных состояния содействовал значительному развитию теории управления. На языке МПС выполнена большая часть работ по оптимальному управлению, фильтрации и оцениванию. Математическим аппаратом метода переменных состояния являются матричное исчисление и вычислительные методы линейной алгебры. Метод переменных состояния содействовал значительному развитию теории управления. На языке МПС выполнена большая часть работ по оптимальному управлению, фильтрации и оцениванию.
Для систем с одним входом и одним выходом уравнения переменных состояния можно сформулировать следующим образом. При выборе n
координат системы (объекта) в качестве переменных ее состояния (такими координатами, например, могут быть выходной сигнал y
(
t
)
и n
-1
его производных) принимаем xi
,
i
=
1,2,…, n
и данную систему можно описать следующими уравнениями для переменных состояния:
х
′
(t
) =
A
х
(
t
)
+ Bu
(
t
),
y
(
t
) =
C
х
(
t
) +
Du
(
t
),
где х
(
t
) =
[x
1
(
t
),
x
2
(
t
),…,
xn
(
t
)
]t
– вектор-столбец переменных состояния; A
,
B
,
C
,
и D
при скалярных u
(
t
)
и y
(
t
)
– соответственно матрица размера n
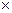 n
, векторы размера n
n
, векторы размера n
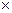 1 и 1 1 и 1 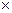 n
и скаляр (при векторных u
(
t
)
и y
(
t
)
– матрицы соответствующих размеров). n
и скаляр (при векторных u
(
t
)
и y
(
t
)
– матрицы соответствующих размеров).
Для дискретных объектов, функционирование которых представляется дискретным временем tk
=
kT
(T
– интервал дискретизации), наиболее общим видом описания является разностное уравнение (аналог дифференциального):
yk
+a1
yk-1
+ ... +ana
yk – na
= b1
uk
+ b2
uk – 1
+ b3
uk - 2
+ ... + bnb
uk – nb + 1
,
где yk – i
= y
[(k – i
)T
] , uk – j
= u
[(k – j
)T
]  . .
Связь между входом и выходом может быть отражена следующими соотношениями:
• через дискретную свертку:
  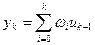 , ,
где ω –
ординаты решетчатой весовой функции объекта, или, с использованием аппарата Z
–
преобразования:
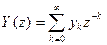 , где z
=
e
pT , где z
=
e
pT
• через дискретную передаточную функцию:
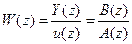 , ,
которая определяется на основании разностного уравнения после применения к обеим частям этого уравнения Z
– преобразования:
На практике в большинстве случаев измерение непрерывных сигналов производится в дискретные моменты времени, что представляет определенное удобство при последующей обработке данных на ЭВМ. Поэтому представление непрерывных объектов дискретными моделями является актуальной задачей. Хотя такое представление может быть осуществлено с некоторой степенью приближенности.
2. 3.
Виды
моделей
пакета
System Identification Toolbox
Одним из расширений MATLAB является пакет System Identification Toolbox, который содержит средства для создания математических моделей линейных динамических систем, на основе наблюдаемых входных и выходных данных. Он имеет удобный графический интерфейс, позволяющий организовывать данные и создавать модели.
Приведем несколько распространенных моделей дискретных объектов, используемых в пакете System Identification Toolbox для временной области, учитывающих действие шума наблюдения:
· Модель авторегрессии AR (AutoRegressive) – считается простым описанием:
A(z) y(t) = e(t)
, где A(z) =
1 + a
1
z
– 1
+ a
2
z
– 2
+...+ a na
z – na
.
· ARX – модель (Autoregressive with eXternal input) – более сложная модель:
A
(z
)y(t
) = B
(z
) u
(t
) + e
(t
) ,
Здесь и ниже e
(t
) – дискретный белый шум.
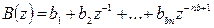 . .
· ARMAX -модель (AutoRegressive-Moving Average wiht eXternal input – модель авторегрессии скользящего среднего -модель (AutoRegressive-Moving Average wiht eXternal input – модель авторегрессии скользящего среднего
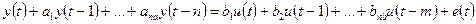 ): ):
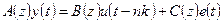 , ,
где nk
– величина задержки (запаздывания),
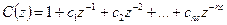 . .
· Модель «вход-выход» (в иностранной литературе такая модель называется «Output-Error», то есть «выход-ошибка», сокращенно ОЕ):
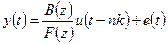 , ,
где 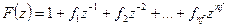 . .
· Модель Бокса-Дженкинса (BJ):
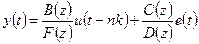 , ,
полиномы B
(z
), F
(z
), C
(z
) определены ранее, а полином D
(z
) определяется по формуле:
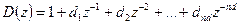 . .
Данные модели можно рассматривать, как частные случаи обобщенной параметрической линейной структуры:
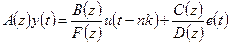 , ,
при этом все они допускают расширение для многомерных объектов (имеющих несколько входов и выходов).
· Модель для переменных состояния (State-space):
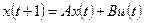 , ,
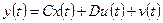 , ,
где A
,
B
,
C
,
D
– матрицы соответствующих размеров, v
(t
) – коррелированный белый шум наблюдений. Возможна и другая (так называемая о бновленная или каноническая) форма представления данной модели: бновленная или каноническая) форма представления данной модели:
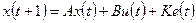 , ,
 , ,
где К – некоторая матрица (вектор столбец), е(t) – дискретный белый шум (скаляр).
В своей работе пакет System Identification Toolbox использует три внутренних вида матричного представления моделей, которые с помощью операторов и функций пакета преобразуются во все выше перечисленные виды моделей объектов:
● так называемый тета-формат (для временных моделей);
● частотный формат (для частотных моделей);
● формат нулей и полюсов.
2. 4. Основные операторы и функции пакета
System
Identification
Toolbox
Приведем основные операторы и функции пакета System Identification Toolbox, которые набираются в командной строке MATLAB или могут быть использованы при написании программ для m-файлов. Наиболее полную информацию о содержании, написании и использовании этих функций можно получить в литературе [2] и справочной части help MATLAB.
idhelp
– используется для вызова подсказаки о возможностях пакета.
iddemo
– используется для вызова демонстрационных примеров.
ident
– команда вызова графического интерфейса пользователя.
m
idprefs
– команда задает (изменяет) директорию для файла midprefs.mat,хранящего информацию о начальных параметрах графического интерфейса мользователя при его открытии.
predict
– команда осуществляет прогноз выхода объекта по его ттета-модели и сучетом информации о его предыдущих фактических значениях выхода ( рекомендуется для расчета прогноза значений временной последовательности).
 pe – вычисляет ошибку модели при заданном входе и известном выходе объекта. pe – вычисляет ошибку модели при заданном входе и известном выходе объекта.
id
sim
– возвращает выход модели тета-формата.
iddata
– создает файл объекта данных.
detrend –
удаляет тренд из набора данных.
idfilt
– команда фильтрует данные с помощью фильтра Баттерворта.
idinput
- команда генерирует входные сигналы для идентификации.
merge
– объединяет несколько экспериментов.
misdata
– оценивает и заменяет потерю входных и выходных данных в файле созданном с помощью команды iddata
.
esample
– восстанавливает форму квантованного сигнала данных прореживанием и интерполяцией и изменяет частоту дискретизации.
Функции непараметрического оценивания
:
covf
– выполняет расчет авто - и взаимных корреляционных функций совокупности экспериментальных данных.
cra –
определяет оценку импульсной характеристики методом коррелированного анализа для одномерного (один вход – один выход) объекта.
etfe
– возвращает оценку дискретной передаточной функции для обобщенной линейной модели одномерного объекта в частотной форме.
impulse
– выводит на дисплей импульсную характеристику модели.
spa
– возвращает частотные характеристики объекта и оценки спектральных плотностей его сигналов для обобщенной линейной модели объекта (возвращает модель объекта в частотном формате).
step
– выводит на дисплей переходную (временную) характеристику модели объекта (реакция на единичное ступенчатое воздействие).
Функции параметрического оценивания
:
ar
– оценивает параметры модели авторегрессии (AR), то есть коэффициенты полинома A
(z),
при моделировании скалярных временных последовательностей.
 armax
– оценивает параметры модели ARMAX. armax
– оценивает параметры модели ARMAX.
arx
– оценивает параметры моделей ARX и AR.
bj
– оценивает параметры модели Бокса-Дженкинса.
Ivar
– оценивает параметры скалярной AR-модели.
iv4
– оценивает параметры для моделей ARX с использованием четырехступенчатого метода инструментальной переменной.
n4sid
– используется для оценивания параметров моделей для переменных состояния в канонической форме при произвольном числе входов и выходов.
ivx
– оценивает параметры ARX-моделей методом инструментальной переменной.
oe
– оценивает параметры ОЕ-модели.
pem
– оценивает параметры обобщенной многомерной линейной модели.
Функции задания структуры модели
:
idpoly
– создавать модель объекта в виде полинома.
idss
– создает модель объекта в виде переменных состояния.
i
darx
– создает многопараметрическую ARX-модель объекта.
idgrey
– создает модель объекта, созданную пользователем.
arx
2
th
– создает матрицу модели тета-формата по полиномам ARX-модели многомерного объекта.
canform
– создает каноническую форму модели для переменных состояния многомерного объекта.
mf
2
th
– преобразует структуру модели для пременных состояния в тета-формат.
poly
2
th
– создает модель тета-формата из исходной модели «вход-выход».
Функции извлечения данных о моделях
:
arxdata
– возвращает матрицы коэффициентов полиномов ARX-моделей, а также их среднеквадратические отклонения.
polydata
– возвращает матрица коэффициентов полиномов.
ssdata
– функция возвращает матрицы(и величину интервала дискретизации в дискретном случае) ss-моделей (моделей переменных состояния).
tfdata
– данная функция возвращает числитель и знаменатель передаточной функции.
zpkdata
– функция возвращает нули, полюсы и обобщенные коэффициенты передачи для каждого канала модели тета-формата или LTI-модели (если используется пакет Control System Toolbox c именем sys).
idfrd
– данная функция создает частотную модель объекта в frd-формате.
idmodred
– функция уменьшает порядок модели объекта.
c2d, d2c
– первая функция преобразует непрерывную модель в дискретную. Вторая – наоборот.
ss, tf, zpk, frd
– функции создания моделей стационарных систем в виде модели переменных состояния (ss), передаточной функции по ее заданным нулям и полюсам (zpk), передаточной функции, записанной в операторном виде (tf) и в частотном виде (frd).
Функции отображения модели
:
bode
,
bodeplot
,
ffplot
– функции отображения логарифмических частотных характеристик.
plot
– отображение входных - выходных данных для данных объекта.
present
– функция отображения вида модели тета-формата с оценкой среднеквадратического отклонения, функции потерь и оценки точности модели..
pzmap
– отображает нули и полюсы модели (с областями неопределенности).
nyquist
– отображает диаграмму Найквиста (гадограф АФХ) передаточной функции.
view
– отбражение LTI-модели (при использовании пакета Control System Toolbox).
 Функции проверки адекватности модели
: Функции проверки адекватности модели
:
compare
– функция позволяет сравнить выходы модели и объекта с выводом на дисплей сравнительных графиков и указанием оценки адекватности модели.
resid
– функция вычисляет остаточную ошибку для заданной модели и соответствующие корреляционные функции.
Функции выбора структуры модели
:
aic, fpe
– функции вычисляют информационный критерий AIC и конечную ошибку модели.
arxstruc
– функция вычисляет функции потерь для ряда различных конкурирующих ARX-моделей с одним выходом.
selstruc
– функция осуществляет выбор наилучшей структуры модели
В состав библиотеки System ID Blocks блоков Simulink входят блоки, позволяющие производить оценивание ряда типовых моделей:
● модели авторегрессии AR (AutoRegressive model estimator);
● ARX-модели (AutoRegressive Moving Average with eXternal input model estimator);
● ARX-модели (AutoRegressive Moving Average with eXternal input model estimator);
● модели Бокса-Дженкинса BJ (Box-Jenkins model estimatjr);
● обобщенной линейной модели (General model estimator using Predictive Error Method);
● модели «вход-выход» OE (Output-error model estimator).
Правила работы с данными блоками аналогичны правилам для других блоков Simulink. Полученная модель отображается в основном окне MATLAB.
2. 5. Пример использования пакета
System
Identification
Toolbox
для идентификации технологических объектов управления
 В качестве примера использования пакета System Identification Toolbox для идентификации технологических объектов управления возьмем распылительную сушилку, которая рассматривается нами как технологический объект управления (ТОУ). В распылительной сушилке реализуется некоторый теплой технологический процесс, в котором входным воздействием на ТОУ является расход газа, выраженный в м3
/час, а выходным регулируемым параметром – температура в градусах Цельсия. Процесс идентификации ТОУ включает следующие этапы: В качестве примера использования пакета System Identification Toolbox для идентификации технологических объектов управления возьмем распылительную сушилку, которая рассматривается нами как технологический объект управления (ТОУ). В распылительной сушилке реализуется некоторый теплой технологический процесс, в котором входным воздействием на ТОУ является расход газа, выраженный в м3
/час, а выходным регулируемым параметром – температура в градусах Цельсия. Процесс идентификации ТОУ включает следующие этапы:
· априорный анализ ТОУ с целью выбора структуры модели;
· проведение предварительного (небольшого по объему) исследования объекта с целью уточнения оценки структуры модели (этот этап желателен, особенно при отсутствии априорной информации о ТОУ);
· разработка методики основного экспериментального исследования ТОУ, составление плана эксперимента;
· проведение основного экспериментального исследования для получения массива данных (ui
, yi
);
· математическая обработка массива данных (с использованием пакета System Identification Toolbox) с целью определения параметров модели и ее адекватности, доверительных границ параметров и выходной координаты модели.
При этом в процессе исследования ТОУ необходимо принять некоторые допущения, позволяющие применить хорошо отработанный аппарат анализа стационарных, линейных объектов:
· технологический объект управления является системой с сосредоточенными параметрами;
· технологический объект управления стационарен, т. е. статические и динамические свойства ТОУ неизменны во времени;
· уравнения моделей ТОУ линеаризуются в малом, т.е. при небольших отклонениях ± ∆
yi
от выбранной "рабочей" точки (рабочего режима) ТОУ.
Массив данных [u
i
, y
i
] образуется в результате трудоемкой операции расшифровки регистрограмм по приборам измерительной системы. Однако широкое развитие микропроцессорной и вычислительной техники и внедрение ее в производственные технологические процессы позволили существенно усовершенствовать техническое обеспечение идентификации ТОУ. Обработка массива данных с помощью пакета System Identification Toolbox предполагает следующие этапы:
· обработка и преобразование данных с целью создания файла данных;
· анализ экспериментальных данных с целью предварительного определения основных характеристик ТОУ;
· параметрическое оценивание данных с целью создания различных видов моделей (описанных во втором разделе) в тета-формате;
· задание структуры модели;
· изменение и уточнение структуры модели (если это необходимо);
· проверка адекватности и сравнение различных моделей с целью выбора наилучшей;
· преобразование модели из тета-формата в вид удобный для дальнейшего использования при анализе и синтезе системы управления.
На каждом этапе идентификации имеется возможность графического отображения результатов моделирования и извлечения необходимой информации об объекте.
2. 6. Обработка данных при построении модели объекта управления
Начнем процедуру построения аналитической модели технического объекта управления (ТОУ) – сушилки. В сушилку подводится шликер, где он распыляется. Инжекционные горелки создают высокую температуру в зоне распыления материала. Распыленные частицы, теряя влагу, уже в виде порошка собираются в днище сушилки, откуда поступают непосредственно с бункера над прессами.
Основная задача системы регулирования состоит в поддержании характеристик продукта (влажность шликера) в заданных пределах. При этом, необходимость организации процесса автоматического регулирования обусловлена и наличием также случайных возмущений (т. е. неотвратимых в реальной обстановке факторов), воздействие которых может привести к нарушению технологического процесса и отклонению характеристик продукта от заданных значений. В частности, к таким возмущениям могут относиться случайные изменения интенсивности  подачи шликера в сушилку, или случайные изменения качества топлива в горелках и т. д. Эти изменения необходимо учесть при построении модели ТОУ (сушилки). Теоретически задача будет сводиться к изучению поведение ТОУ с учетем воздействии на него и этих случайных факторов. подачи шликера в сушилку, или случайные изменения качества топлива в горелках и т. д. Эти изменения необходимо учесть при построении модели ТОУ (сушилки). Теоретически задача будет сводиться к изучению поведение ТОУ с учетем воздействии на него и этих случайных факторов.
Как было отмечено выше, аналитическая модель сложных ТОУ может быть построена на основе массива входных и выходных данных, полученных в результате физического эксперимента, проведенного над ТОУ. При этом необходимо учитывать и воздействие случайных факторов, поэтому при проведении физического эксперимента случайное воздействие должно быть смоделировано.
Для дальнейших вычислений будем использовать статистические данные, полученные при изучении теплового объекта, и содержащиеся в файле project
4,
который включает массив данных, состоящий из 159 значений входного параметра – расход газа, выраженный в м3
/час и 159 значений выходного параметра – температуры в объекте в градусах Цельсия.
Для проведения модельного эксперимента и формирования массива входных и выходных данных об объекте автоматизации следует в Simulink построить S-модель установки для снятия массивов входных и выходных данных, изображенную на рис. 2. 0.

Рис.
2.0. S-модель объекта автоматизации
Набрать в блоке Transfer Fcn передаточную функцию составляющей компоненты объекта автоматизации своего варианта и запустить моделирование. Перед запуском моделирования в раскрывающемся меню Simulation следует открыть окно Configuration Parameters и установить Stop time равным 999 (или набрать 999 непосредственно в окне модели).
Для загрузки файла в рабочую среду Workspace системы MATLAB необходимо в режиме командной строки выполнить следующую команду:
 >> load project4 >> load project4
В результате выполнения команды в рабочей области Workspace появится массив входных переменных u2 и массив выходных переменных y2. Интервал дискретизации (промежутки времени, через которые производились измерения входных и выходных величин) в ходе эксперимента был принят равным 0. 08 с, который необходимо указать дополнительно в командной строке:
>> ts=0.08
Этот массив данных при использовании в дальнейшем в пакете System
Identification
Toolbox
необходимо объединить в единый файл, содержащий необходимую информацию о входных и выходных параметрах объекта, их значениях и единицах измерения.
 Для объединения исходных данных в единый файл dan. m пользуются командой: Для объединения исходных данных в единый файл dan. m пользуются командой:
>> dan=iddata(y2,u2,ts).
Результат выполнения команды комментируется следующей фразой MATLAB:
Time domain data set with 1097 samples.
Sampling interval: 0.08
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
Сформированный файл dan. m указывает, что он содержит результаты 1097 измерений с интервалом дискретизации 0. 08 с. Входными переменными является массив u
1, а выходным параметром – y
1.
Для наглядности сформированного файла необходимо в его структуру ввести обозначения входных и выходных данных c указанием размерностей параметров:
>> dan.outputn='температура';
>> dan.inputn='расход газа';
>> dan.inputUnit='м3/ч';
>> dan.outputUnit='гр.С 100'
В конечном итоге сформированный файл данных dan.m имеет следующий вид:
Time domain data set with 1097 samples.
Sampling interval: 0.08
Outputs Unit (if specified)
температура гр.С 100
Inputs Unit (if specified)
расход газа м3/ч
Полную информацию о файле dan.m можно получить воспользовавшись командой:
>> get(dan)
Результат выполнения команды комментируется следующей фразой MATLAB:
ans =
Domain: 'Time'
Name: []
OutputData: [1097x1 double]
y: 'Same as OutputData'
OutputName: {'температура'}
OutputUnit: {'гр.С 100'}
InputData: [1097x1 double]
u: 'Same as InputData'
InputName: {'расход газа'}
InputUnit: {'м3/ч'}
Period: Inf
InterSample: 'zoh'
Ts: 0.0800
Tstart: []
SamplingInstants: [1097x0 double]
TimeUnit: ''
ExperimentName: 'Exp1'
Notes: []
UserData: [] ExperimentName: 'Exp1'
Notes: []
UserData: []
Для графического представления данных используется команда plot (dan), либо команда idplot (datta), однако в последнем случае графики не будут содержать информации о названии переменных и их размерностях. Исходные данные с использованием команды plot (dan) приведены на рис. 2. 1.
>> plot(dan)
Для дальнейшего использования полученных исходных данных необходимо провести предварительную обработку этих данных с цель удаления тренда (постоянной соста вляющей) из набора данных и если необходимо отфильтровать данные с помощью имеющихся средств в пакете System Identification Toolbox. вляющей) из набора данных и если необходимо отфильтровать данные с помощью имеющихся средств в пакете System Identification Toolbox.
Для удаления тренда пользуются функцией dtrend
:
>> zdan=dtrend(dan)
Исполнение функции приведет к появлению в командной строке записи:
Time domain data set with 1097 samples.
Sampling interval: 0.08
Outputs Unit (if specified)
температура гр.С 100
Inputs Unit (if specified)
расход газа м3/ч
а в рабочей области Workspace системы MATLAB файла zdan.
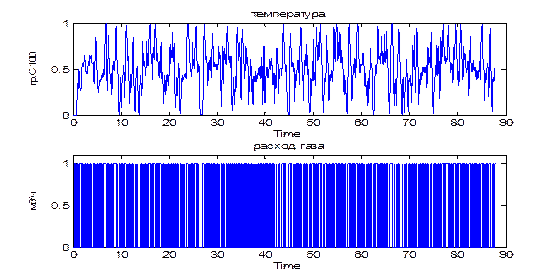
| Рис. 2. 1. Исходные данные для идентификации технического объекта управления.
|
|
 Получен новый файл zdan.m, в котором отсутствует постоянная составляющая сигналов (рис. 2. 2 получен после выполнения команды: Получен новый файл zdan.m, в котором отсутствует постоянная составляющая сигналов (рис. 2. 2 получен после выполнения команды:
>> plot(zdan)).
Файл в дальнейшем будет использован для построения моделей ТОУ. 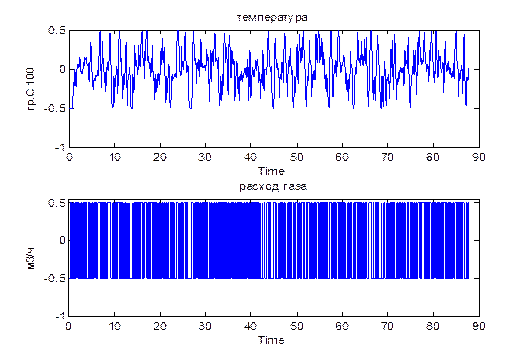

| Рис.2. 2. Исходные данные для идентификации технического объекта управления при отсутствии тренда
|
|
Кроме указанной команды удаления тренда в пакете System Identification Toolbox имеются другие функции обработки данных эксперимента, которые приведены в описании пакета System Identification Toolbox. Применение этих функций производится в тех случаях, когда проведен предварительный анализ ТОУ и определены возможные помехи либо некоторые другие динамические характеристики, либо появляется необходимость изменить интервал дискретизации в случае повышенной погрешности представления модели ТОУ в ходе параметрического оценивания ТОУ.
Следующим этапом идентификации является определение статистических и частотных характеристик массивов исходных данных.
2
. 7. Оценивание статистических и частотных характеристик исходных данных
Как уже отмечалось выше, при формировании массива исходных данных с использованием физического эксперимента над техническим объектом управления, воздействующий на объект входной сигнал был представлен случайным процессом с нулевым математическим ожиданием (т. е. центрированный после исключения тренда). Процесс будем считать эргодическим, что необходимо для практических приложений теории случайных процессов т. к. дает возможность по одной достаточно продолжительной реализации случайного процесса судить о его статистических характеристиках. В соответствие с свойствами стационарного эргодического процесса любая статистическая характеристика, полученная усреднением по ансамблю возможных реализаций, с вероятностью сколь угодно близкой к единице, может быть получена усреднением за достаточно большой промежуток времени из одной единственной реализации случайного процесса. Поэтому любая реализация исходных данных может быть использована нами для получения статистических характеристик массивов исходных данных т. к. в ходе планирования и проведения эксперимента сказать заранее, по какой реализации пойдет процесс, невозможно. Для характеристики связи между значениями случайного процесса в различные моменты времени, вводятся понятия корреляционной (автокорреляционной)
функции и спектральной плотности случайного процесса. Корреляционной функцией случайного процесса X
(t
) называют неслучайную функцию двух аргументов R
(t
1
; t
2
), которая для каждой пары произвольно выбранных значений моментов времени t
1
и t
2
равна математическому ожиданию произведения двух случайных величин случайного процесса, соответствующих этим моментам времени.
Между дисперсией случайного процесса и корреляционной функцией существует прямая связь – дисперсия случайного стационарного процесса равна значению корреляционной функции. Статистические свойства связи двух случайных процессов X
(t
) и G
(t
) можно охарактеризовать взаимной корреляционной функцией R
xg
(t
1
, t
2
). Взаимная корреляционная функция Rxg
(τ
) характеризует взаимную статистическую связь двух случайных процессов X
(t
) и G
(t
) в разные моменты времени, отстоящие друг от друга на промежуток времени τ
.
Если случайные процессы X
(t
) и G
(t
) статистически не связаны друг с другом и имеют равные нулю средние значения, то их взаимная  том, что если взаимная корреляционная функция равна нулю, то процессы невзаимосвязаны, можно сделать вывод лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения), общей же силы обратный закон не имеет. том, что если взаимная корреляционная функция равна нулю, то процессы невзаимосвязаны, можно сделать вывод лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения), общей же силы обратный закон не имеет.
Анализируя свойства корреляционной функции можно сделать вывод: чем слабее взаимосвязь между предыдущим X
(t
) и последующим X
(t
+
τ
) значениями случайного процесса, тем быстрее убывает корреляционная функция Rx
(τ
). Случайный процесс, в котором отсутствует связь между предыдущими и последующими значениями, называют чистым случайным процессом или белым шумом. В случае белого шума время корреляции τ
R
= 0 и корреляционная функция представляет собой δ-функцию.
При исследовании автоматических систем управления удобно пользоваться еще одной характеристикой случайного процесса, называемой спектральной плотностью. Спектральная плотность S
x
(ω) случайного процесса X
(t
) определяется как преобразование Фурье корреляционной функции Rx
(τ
). Физический смысл спектральной плотности состоит в том, что она характеризует распределения мощности сигнала по частотному спектру.
В пакете System Identification Toolbox имеется четыре функции cra
,
etfe
,
covf
,
и spa
непараметрического оценивания совокупности экспериментальных данных. Функция cra
выполняет расчет авто- и взаимных корреляционных функций, оценку импульсной характеристики методом корреляционного анализа для одномерного объекта массива экспериментальных данных. Написание этой функции следующее:
cra(z);
[ir,R,cl] = cra(z, M, na, plot);
cra(R)
Аргументы:
· z – матрица экспериментальных данных вида z = [y2 u2], где y2 - вектор – столбец, соответствующий выходным данным;
· u2 - вектор – столбец, соответствующий входным данным;
· М – максимальное значение дискретного аргумента для которого производится расчет оценки импульсной характеристики (по умолчанию М = 20);
· na – порядок модели авторегрессии (порядок многочлена), которая используется для расчета параметров отбеливающего фильтра (по умолчанию na = 10). При na = 0 в качестве идентифицирующего используется не преобразованный входной сигнал;
· Если plot = 0, то график отсутствует, если plot = 1, то график полученной оценки импульсной характеристики вместе с 99% - м доверительным коридором, если plot = 2, то выводятся графики всех корреляционных функций.
Возвращаемые величины:
ir – оценка (вектор значений) импульсной характеристики; R – матрица, элементы первого столбца которой – значения дискретного аргумента, элементы второго столбца – значения оценки автокорреляционной функции выходного сигнала, элементы третьего столбца – значения оценки автокорреляционной функции входного сигнала, элементы четвертого столбца – значения оценки взаимной корреляционной функции.
Для примера сушилки шликера эти величины имеют следующие значения:
М и na приняты по умолчанию [], [].
>> [ir,R,cl]=cra(zdan,[],[],2)
 ir = ir =
0.0134
0.1469
0.2256
0.1864
0.0956
0.0634
0.0457
0.0168
0.0066
0.0053
0.0046
0.0029
0.0068
-0.0068
-0.0099
-0.0099
-0.0017
0.0058
0.0150
0.0053
0.0081
R =
-20.0000 0.0011 0.0015 -0.0123
-19.0000 0.0015 -0.0021 -0.0221
-18.0000 0.0017 0.0007 -0.0370
-17.0000 0.0017 0.0069 -0.0287
-16.0000 0.0013 0.0123 0.0080
-15.0000 0.0005 0.0074 0.0289
-14.0000 -0.0003 0.0051 0.0470
-13.0000 -0.0010 0.0092 0.0236
-12.0000 -0.0018 -0.0070 0.0419
-11.0000 -0.0019 0.0064 0.0221
-10.0000 -0.0010 -0.0008 0.0000
 -9.0000 -0.0005 0.0004 -0.0054 -9.0000 -0.0005 0.0004 -0.0054
-8.0000 0.0001 0.0005 0.0018
-7.0000 0.0011 -0.0003 -0.0124
-6.0000 0.0031 0.0001 -0.0299
-5.0000 0.0065 0.0005 -0.0161
-4.0000 0.0110 0.0001 -0.0167
-3.0000 0.0163 -0.0001 0.0021
-2.0000 0.0261 -0.0007 0.0152
-1.0000 0.0393 0.0001 0.0259
0 0.0479 0.2477 0.0304
1.0000 0.0393 0.0001 0.3341
 2.0000 0.0261 -0.0007 0.5129 2.0000 0.0261 -0.0007 0.5129
3.0000 0.0163 -0.0001 0.4239
4.0000 0.0110 0.0001 0.2174
5.0000 0.0065 0.0005 0.1442
6.0000 0.0031 0.0001 0.1040
7.0000 0.0011 -0.0003 0.0382
8.0000 0.0001 0.0005 0.0150
9.0000 -0.0005 0.0004 0.0121
10.0000 -0.0010 -0.0008 0.0105
11.0000 -0.0019 0.0064 0.0066
12.0000 -0.0018 -0.0070 0.0154
13.0000 -0.0010 0.0092 -0.0155
14.0000 -0.0003 0.0051 -0.0225
15.0000 0.0005 0.0074 -0.0224
16.0000 0.0013 0.0123 -0.0038
17.0000 0.0017 0.0069 0.0131
18.0000 0.0017 0.0007 0.0341
19.0000 0.0015 -0.0021 0.0119
20.0000 0.0011 0.0015 0.0185
cl =
0.0343
 На рис. 2. 3 приведены результаты расчета автокорреляционной функции выходного сигнала (Covf for filtered y); автокорреляционной функции входного сигнала (Covf for prewhitened u); взаимная корреляционная функция (Correlation from u to y); импульсная характеристика (Impulse response estimate). На рис. 2. 3 приведены результаты расчета автокорреляционной функции выходного сигнала (Covf for filtered y); автокорреляционной функции входного сигнала (Covf for prewhitened u); взаимная корреляционная функция (Correlation from u to y); импульсная характеристика (Impulse response estimate).
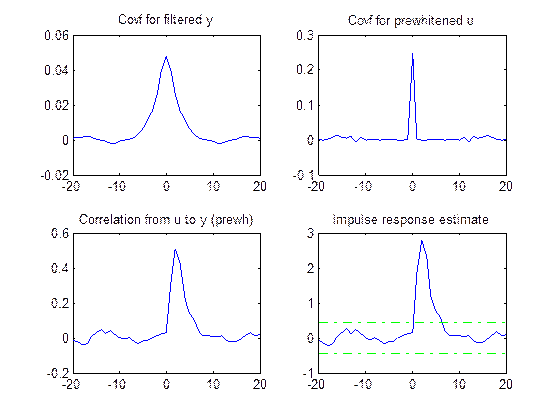 | Рис. 2. 3. Графики функций: а) автокорреляционная функция выходного сигнала; б) автокорреляционная функция входного сигнала; в) взаимная корреляционная функция; г) импульсная характеристика.
|
|
Можно получить более подробный график импульсной характеристики, если выполнить функцию cra
с одним аргументом zdan (Рис. 2. 4):
>> cra(zdan)
ans =
0.0134
0.1469
0.2256
0.1864
0.0956
0.0634
0.0457
0.0168
0.0066
0.0053
0.0046
0.0029
0.0068
-0.0068
-0.0099
-0.0099
-0.0017
0.0058
0.0150
0.0053
0.0081  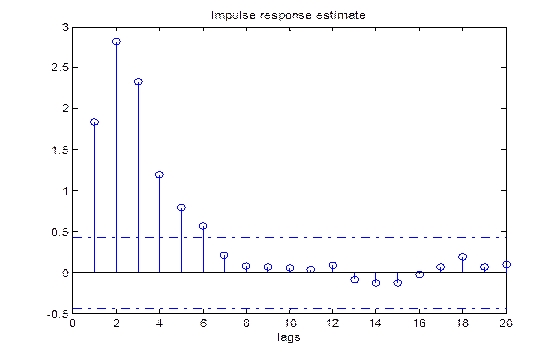
| Рис. 2. 4. Импульсная характеристика
|
|
Необходимо отметить, что на графиках по оси абсцисс откладываются промежутки времени τ
= t
i
– t
i
-1
, а по оси ординат значения корреляционных функций для входного u
2
и выходного у2
сигналов; значения взаимокорреляционой функции и импульсной характеристики. Из полученных характеристик следует, что с увеличением τ
наблюдается резкий спад корреляционной зависимости входного сигнала, что свидетельствует о слабой взаимосвязи между сечениями процесса, соответствующими произвольным моментам времени (процесс более близок к белому шуму, а автокорреляционная функция к дельта-функции). Выходная величина наоборот более плавно изменяет свои состояния от одного момента времени к другому и, следовательно, взаимосвязь между предыдущим и последующим значениями выходного сигнала более тесная, чем у входного.
Для получения частотных характеристик экспериментальных данных воспользуемся функциями оценивания частотных характеристик. Функция spa
возвращает частотные характеристики одномерного объекта  и оценки спектральной плотности его сигналов для обобщенной линейной модели объекта: и оценки спектральной плотности его сигналов для обобщенной линейной модели объекта:
[g, phiv] = spa(z)
[g, phiv, z_spe] = spa(z,M,w,maxsize,T)
Аргументы:
· z – матрица исходных данных;
· М – ширина временного окна (по умолчанию М = min(30, length(z) /10), где length(z) – число строк матрицы z);
· w – вектор частот для расчета частотных характеристик (по умолчанию [1: 128]/128*pi/T);
· Т – интервал дискретизации;
· maxsize – параметр, определяющий максимальный размер матриц, создаваемых в процессе вычислений.
Возвращаемые величины:
· g – оценка W(e jωT
) в частотном формате;
· phiv – оценка спектральной плотности шума v(t);
· z_spe – матрица спектральных плотностей входного и выходного сигналов.
Построим диаграмму Боде (АЧХ, ФЧХ), используя функции spa и bodeplot и данные, полученные при изучении теплового объекта, и содержащиеся в файле dryer2
>> load project24;
>> z=[y2 u2];
>> g=spa(z);
>> bodeplot(g)
Результаты моделирования (АЧХ построена в логарифмическом масштабе) без доверительного коридора представлены на рис. 2. 5.
 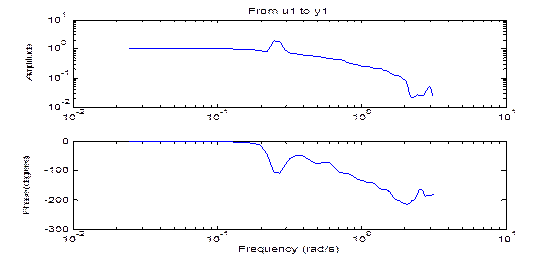
| Рис. 2. 5. Частотные характеристики технического объекта управления
|
|
Полученные зависимости подтверждают высокочастотную составляющую значений входного и выходного сигналов. Границы изменения частот на графиках установлены по умолчанию.
Для получения частотных характеристик вместе с доверительным коридором шириной в три среднеквадратических отклонения в пакете System Identification Toolbox MATLAB имеется следующие возможности:
· установка границ изменения частот с помощью команды
>> w=logspace(w1
,w2
,N),
где w1
– нижняя граница диапазона частот (10w
1
), w2
– верхняя граница диапазона частот (10w
2
) и N – количество точек графика.
· построение АФХ, ФЧХ и S
(ω
) – функции спектральной плотности шума e(
t
)
· вычисление g – оценки АФХ и ФЧХ в частотном формате и phiv – оценки спектральной плотности шума с помощью команды
>> [g,phiv]=spa(z,[],w);
Графики АФХ, ФЧХ и S
(ω
) строятся с доверительным коридором в три среднеквадратических отклонения с помощью команды
>> bodeplot([g p],'sd',3,'fill'),
где 'sd' – указывает на сплошную линию доверительного коридора (по умолчанию эта линия штриховая); 3 – величина доверительного коридора в три среднеквадратических отклонения; 'fill' – способ заливки доверительного коридора (желтым цветом).
Построим АЧХ, ФЧХ, используя функции spa, bodeplot, logspace и данные, полученные в файле Project24 с соответствующим доверительным коридором:
>> w = logspace(-2,pi,128);
>> [g,phiv]=spa(z,[],w);
>> bodeplot([g,phiv],3,'fill')
Результаты моделирования представлены на рис. 2. 6.
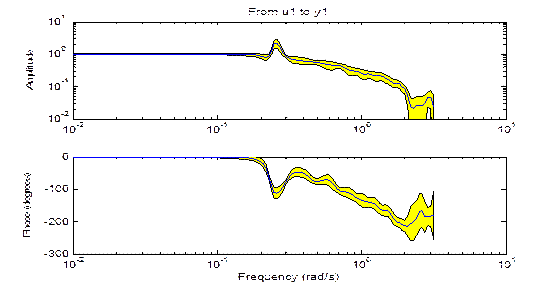
| Рис. 2.6. Оценки АЧХ и ФЧХ вместе с доверительным коридором.
|
|
 Для построения графика оценки спектральной плотности шума с доверительным коридором выполним следующую команду: Для построения графика оценки спектральной плотности шума с доверительным коридором выполним следующую команду:
>> bodeplot([phiv],'sd',3,'fill')
Результаты моделирования представлены на рис. 2. 7.
| Рис.2. 7. График оценки
S(
ω) вместе с доверительным коридором
|
|
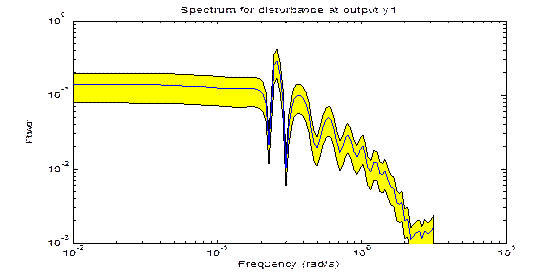 Полученный график оценки спектральной плотности шума с доверительным коридором показывает наличие равномерного распределения мощности сигнала по частотному спектру с последующим спадом мощности на частоте выше 1, 1 рад/с.
Далее необходимо выполнить параметрическое оценивание ТОУ.
2
. 8. Параметрическое оценивание данных
Параметрическое оценивание экспериментальных данных проводится с целью определения параметров модели заданной структуры путем минимизации выбранного критерия качества модели (чаще всего – среднего квадрата рассогласования выходов объекта и его постулируемой модели).
Для проведения параметрического оценивания  массив экспериментальных данных необходимо разделить условно на две части (не обязательно равные) массив экспериментальных данных необходимо разделить условно на две части (не обязательно равные)
>> zdanv=zdan(1:500);
>> zdane=zdan(501:1000).
Первая часть массива данных будет использоваться для параметрического оценивания и построения модели ТОУ. Вторая часть необходима будет для верификации (проверки качества) модели, определения адекватности полученной модели и определения погрешностей идентификации. Необходимо отметить, что параметрическая идентификация в пакете S
ystem Identification Toolbox MATLAB
выполняется в дискретном виде и полученные модели, являются дискретными.
В пакете System Identification Toolbox рассмотрены различные виды моделей ТОУ, которые с различной степенью достоверности описывают объект автоматизации. Для выбора наиболее приемлемой структуры и вида моделей при параметрическом оценивании экспериментальных данных в пакете System Identification Toolbox MATLAB имеются специальные функции
· параметрического оценивания,
· задания структуры модели,
· изменения и уточнения структуры модели и выбора структуры модели.
Функция оценивания ar
оценивает параметры модели авторегресии:
A
(
z
)
y
(
t
) =
e
(
t
)
,
где: A
(
z
) =
1 + a
1
z
– 1
+ a
2
z
– 2
+...+ a
na
z
–
na
, т.е. коэффициенты полинома A
(
z
)
, при моделировании скалярных временных последовательностей. Функция имеет синтаксис:
th = ar(y,n)
Или другое написание, позволяющее изменять параметры моделирования:
[th,refl]=ar(y,n,approach,win,maxsize,T)
где аргументы:
y – вектор-столбец данных, содержащий N элементов;
n – порядок модели (число оцениваемых коэффициентов);
approach – аргумент (строковая переменная) определяет метод оценивания:
• 'ls' – метод наименьших квадратов;
• 'yw' – метод Юла-Уокера;
• 'burg' – метод Бэрга (комбинация метода наименьших квадратов с минимизацией гармонического среднего);
• 'gl' – метод с использованием гармонического среднего;
Если любое из данных значений заканчивается нулем (например, burg0), то вычисление сопровождается оцениванием корреляционных функций.
Аргумент win (строковая переменная) используется в случае отсутствия части данных:
• win =‘now’ – используются только имеющиеся данные (используется по умолчанию, за исключением случая approach = ‘yw’);
• window = 'prw’ – отсутствующие начальные данные заменяются нулями, так что суммирование начинается с нулевого момента времени;
• window = 'pow’ – последующие отсутствующие данные заменяются нулями, так что суммирование расширяется до момента времени N + n;
• window = ‘ppw’ – и начальные, и последующие отсутствующие данные заменяются нулями (используется в алгоритме Юла-Уокера);
Арумент maxsize определяет максимальную размерность задачи; Т – интервал дискретизации.
Возвращаемые величины:
• th – полученная модель авторегрессии в тета-формате (внутреннем матричном формате представления параметрических моделей пакета System Identification);
 • relf – информация о коэффициентах и функции потерь; • relf – информация о коэффициентах и функции потерь;
 Для использования функция параметрического оценивания ar
необходимо из массива экспериментальных данных, записанных в файле dan
выделить выходную переменную у
с помощью команды Для использования функция параметрического оценивания ar
необходимо из массива экспериментальных данных, записанных в файле dan
выделить выходную переменную у
с помощью команды
>> y=dan.y,
что равносильно команде
>> y=get(dan,'y')
>> th =ar(y,4)
Discrete-time IDPOLY model: A(q)y(t) = e(t)
A(q) = 1 - 1.348 q^-1 + 0.6695 q^-2 - 0.2531 q^-3 - 0.04431 q^-4
Estimated using AR ('fb'/'now') from data set y
Loss function 0.0140559 and FPE 0.0141588
Sampling interval: 1
Полная информация о модели авторегрессии th может быть получена с помощью команды:
>> present(th)
Discrete-time IDPOLY model: A(q)y(t) = e(t)
A(q) = 1 - 1.348 (+-0.03022) q^-1 + 0.6695 (+-0.05018) q^-2
- 0.2531 (+-0.05018) q^-3 - 0.04431 (+-0.03023) q^-4
Estimated using AR ('fb'/'now') from data set y
Loss function 0.0140559 and FPE 0.0141588
Sampling interval: 1
Created: 17-Dec-2009 10:51:00
Last modified: 17-Dec-2009 10:51:00
В информации приведены сведения о том, что модель является дискретной и для оценивания ее параметров используется прямой-обратный метод (разновидность метода наименьших квадратов), на что указывает строковая переменная 'fb' (используется по умолчанию); для построения модели используются только имеющиеся данные у
, на что указывает строковая переменная 'now' (используется по умолчанию); определены: функция потерь Loss function, как остаточная сумма квадратов ошибки и так называемый теоретический информационный критерий Акейке (Akaike's Information Theoretic Criterion – AIC) FPE; интервал дискретизации Sampling interval.
Следующая функция arx
оценивает параметры модели AR и ARX: параметры модели ARX, представленной зависимостью:
A
(z
)y(t
) = B
(z
) u
(t
) + e
(t
) ,
или в развернутом виде:
y(t
) + а1
y(t-1
) + …+ аna
y(t-n
) = b1
u(t) + b2
u(t - 1) + …+ bnb
u(t - m) + e(t).
Здесь и ниже e
(t
) – дискретный белый шум.
B(z) = b1
+ b2
z-1
+ …+ bbn
z-nb + 1
Функция имеет следующий синтаксис:
dar = arx(z,nn).
Или другое написание, позволяющее изменять параметры моделирования:
dar = arx(z,nn,maxsize,T),
где z – экспериментальные данные;
nn – задаваемые параметры модели (аргумент nn содержит три параметра: na – порядок ( число коэффициентов) полинома A
(
z
)
; nb – порядок полинома B
(
z
)
; nk – величина задержки;
maxsize - максимальная размерность задачи;
Т – интервал дискретизации.
Естественно задаться вопросом: Какую степень полинома выбрать? Известно, что с увеличением порядка полиномов улучшается степень адекватности модели реальному объекту. Однако при этом получаются громоздкие выражения, и увеличивается время моделирования. Поэтому для нахождения оптимального порядка полиномов можно воспользоваться функциями выбора структуры модели:
Функция arxstruc
вычисляет функции потерь для ряда различных конкурирующих ARX моделей с одним выходом:
v = arxstruc(ze,zv,NN),
или v = arxstruc(ze,zv,NN, maxsize);
 где: ze,zv – соответственно, матрицы экспериментальных данных для оценивания и верификации моделей; где: ze,zv – соответственно, матрицы экспериментальных данных для оценивания и верификации моделей;
NN – матрица задания конкурирующих структур со строками вида nn = [na nb nk];
maxsize - максимальная размерность задачи.
Возвращаемая величина v – матрица, верхние элементы каждого столбца которой (кроме последнего) являются значениями функции потерь для ARX моделей, структура которых отображается последующими элементами столбцов (т. е. каждый столбец соответствует одной модели). Первый элемент последнего столбца – это число значений экспериментальных данных для верификации моделей.
Функция selstruc
осуществляет выбор наилучшей структуры модели из ряда возможных вариантов
[nn,vmod]=selstruc(v)
[nn,vmod]=selstruc(v,с),
где: v – матрица, возвращаемая функцией arxstruc;
с – строковая переменная, определяющая вывод графика или критерий отбора наилучшей структуры:
при с = ‘plot’ выводится график зависимости функции потерь от числа оцениваемых коэффициентов модели
при с = ‘log’ выводится график логарифма функции потерь;
при с = ‘aic’ график не выводится, но возвращается структура, минимизирующая теоретический информационный критерий Акейке (AIC).
при с = ‘mdl’ возвращается структура, обеспечивающая минимум критерия Риссанена минимальной длины описания;
при с
равном некоторому численному значению а,
выбирается структура, которая минимизирует значение функции потерь vmod
= v(1 + a(d/N)), где N – объем выборки экспериментальных данных, используемых для оценивания; в – число оцениваемых коэффициентов модели; v – значение функции потерь.
Возвращаемые величины: nn – выбранная структура; vmod – значение соответствующего критерия.
Например, для данных dryer2 можно задать пределы изменения порядка модели:
>> NN=struc(1:10,1:10,1);
Вычислить функции потерь:
>> v=arxstruc(zdane,zdanv,NN);
И выбрать наилучшую структуру порядков полиномов:
>> [nn,vmod]=selstruc(v,'plot'),
где 'plot' – строковая переменная, определяющая вывод графика зависимости функции потерь от числа оцениваемых коэффициентов модели (рис. 2. 8).

Рис. 2. 8. Окно выбора структуры модели
 В появившемся окне столбики указывают на величину функции потерь. При подведении курсора к соответствующему столбику, в правом поле окна отразятся значения порядков полиномов na, nb, nk. В поле графика появятся рекомендации по выбору цвета столбика. Воспользуемся рекомендацией, указанной в поле графика и выберем столбик, окрашенный В появившемся окне столбики указывают на величину функции потерь. При подведении курсора к соответствующему столбику, в правом поле окна отразятся значения порядков полиномов na, nb, nk. В поле графика появятся рекомендации по выбору цвета столбика. Воспользуемся рекомендацией, указанной в поле графика и выберем столбик, окрашенный  красным цветом для оптимального значения порядков полиномов и нажмем кнопку Select. красным цветом для оптимального значения порядков полиномов и нажмем кнопку Select.
Взамен строковой переменной 'plot' возможны варианты:
• 'log' – выводится график логарифма функции потерь;
• 'aic' – график не выводится, но возвращается структура, минимизирующая так называемый теоретический информационный критерий Акейке (Akaike's Information Theoretic Criterion – AIC) FPE:
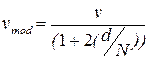 , ,
где v
– значение функции потерь, d
– число оцениваемых коэффициентов модели, N
– объем экспериментальных данных, используемых для оценивания;
• ‘mdl’ – возвращается структура, обеспечивающая минимум так называемого критерия Риссанена минимальной длины описания (Rissanen’s Minimum Description Lngth – MDL):
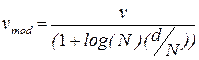 ; ;
• при строковой переменной, равной некоторому численному значению a
, выбирается структура, которая минимизирует:
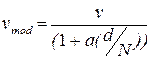 ; ;
• vmod – значение соответствующего критерия.
Выбор наилучшей структуры порядков полиномов можно осуществить и с помощью более простой команды:
>> nn=selstruc(v,0)
MATLAB возвращает:
nn =
8 2 1
С учетом выбранной структуры модели определим вид модели ARX, выполнив функцию arx
:
>> darx=arx(zdanv,nn)
Возвращается матрица из 100 столбцов и 4 строк с значениями различных критериев: vmod =
vmod =
Columns 1 through 8
0.0107 0.0078 0.0080 0.0078 0.0079 0.0079 0.0079 0.0079
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 9 through 16
0.0079 0.0079 0.0084 0.0072 0.0073 0.0073 0.0072 0.0072
1.0000 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
9.0000 10.0000 1.0000 2.0000 3.0000 4.0000 5.0000 6.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 17 through 24
0.0073 0.0073 0.0073 0.0073 0.0079 0.0070 0.0072 0.0072
2.0000 2.0000 2.0000 2.0000 3.0000 3.0000 3.0000 3.0000
7.0000 8.0000 9.0000 10.0000 1.0000 2.0000 3.0000 4.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 25 through 32
0.0072 0.0072 0.0072 0.0072 0.0073 0.0073 0.0079 0.0071
3.0000 3.0000 3.0000 3.0000 3.0000 3.0000 4.0000 4.0000
5.0000 6.0000 7.0000 8.0000 9.0000 10.0000 1.0000 2.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 33 through 40

0.0072 0.0072 0.0072 0.0072 0.0073 0.0073 0.0073 0.0073
4.0000 4.0000 4.0000 4.0000 4.0000 4.0000 4.0000 4.0000
3.0000 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 10.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 41 through 48
0.0080 0.0071 0.0071 0.0072 0.0071 0.0072 0.0073 0.0074
5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000
1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 49 through 56
0.0074 0.0074 0.0080 0.0070 0.0071 0.0071 0.0071 0.0071
5.0000 5.0000 6.0000 6.0000 6.0000 6.0000 6.0000 6.0000
9.0000 10.0000 1.0000 2.0000 3.0000 4.0000 5.0000 6.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 57 through 64
0.0073 0.0073 0.0073 0.0074 0.0080 0.0070 0.0071 0.0071
6.0000 6.0000 6.0000 6.0000 7.0000 7.0000 7.0000 7.0000
7.0000 8.0000 9.0000 10.0000 1.0000 2.0000 3.0000 4.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 65 through 72
0.0071 0.0071 0.0073 0.0074 0.0074 0.0074 0.0080 0.0070
7.0000 7.0000 7.0000 7.0000 7.0000 7.0000 8.0000 8.0000
5.0000 6.0000 7.0000 8.0000 9.0000 10.0000 1.0000 2.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 73 through 80
0.0071 0.0071 0.0071 0.0071 0.0073 0.0074 0.0074 0.0074
8.0000 8.0000 8.0000 8.0000 8.0000 8.0000 8.0000 8.0000
3.0000 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 10.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 81 through 88
0.0080 0.0070 0.0071 0.0071 0.0071 0.0071 0.0073 0.0074
9.0000 9.0000 9.0000 9.0000 9.0000 9.0000 9.0000 9.0000
1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 89 through 96
0.0074 0.0074 0.0080 0.0070 0.0071 0.0071 0.0071 0.0072
9.0000 9.0000 10.0000 10.0000 10.0000 10.0000 10.0000 10.0000
9.0000 10.0000 1.0000 2.0000 3.0000 4.0000 5.0000 6.0000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
Columns 97 through 100
 0.0073 0.0074 0.0074 0.0074 0.0073 0.0074 0.0074 0.0074
10.0000 10.0000 10.0000 10.0000
7.0000 8.0000 9.0000 10.0000
1.0000 1.0000 1.0000 1.0000
Возвращается дискретная модель, представленная в тета - формате (внутренним видом матричных моделей).
Discrete-time IDPOLY model: A(q)y(t) = B(q)u(t) + e(t)
A(q) = 1 - 1.01 q^-1 + 0.3552 q^-2 - 0.03471 q^-3 - 0.1432 q^-4
+ 0.1302 q^-5 - 0.0128 q^-6 - 0.08582 q^-7 + 0.06296 q^-8
B(q) = 0.1367 q^-1 + 0.07335 q^-2
Estimated using ARX from data set zdanv
Loss function 0.00666153 and FPE 0.00693343
Sampling interval: 0.08 
Функция armax
оценивает параметры ARMAX модели:
>> darmax = armax(zdanv,[2 2 2 1])
Аргументы функции:
zdanv – вектор экспериментальных данных; [na nb nc nk] – степени полиномов и величина задержки.
Возвращается дискретная модель, представленная в тета – формате:
Discrete-time IDPOLY model: A(q)y(t) = B(q)u(t) + C(q)e(t)
A(q) = 1 - 0.8733 q^-1 + 0.1567 q^-2
B(q) = 0.1331 q^-1 + 0.1028 q^-2
C(q) = 1 + 0.1854 q^-1 - 0.01339 q^-2
Estimated using ARMAX from data set zdanv
Loss function 0.00787129 and FPE 0.00806524
Sampling interval: 0.08
Функция oe
оценивает параметры ОЕ модели:
>> zoe=oe(zdanv,[2 2 1])
Возвращается дискретная модель, представленная в тета – формате:
Discrete-time IDPOLY model: y(t) = [B(q)/F(q)]u(t) + e(t)
B(q) = 0.1478 q^-1 + 0.1052 q^-2
F(q) = 1 - 0.8219 q^-1 + 0.1102 q^-2
Estimated using OE from data set zdanv
Loss function 0.020577 and FPE 0.0209102
Sampling interval: 0.08
Функция bj
оценивает параметры модели Бокса-Дженкинса:
>> zbj=bj(zdanv,[2 2 2 2 1])
Возвращается дискретная модель, представленная в тета – формате:
Discrete-time IDPOLY model: y(t) = [B(q)/F(q)]u(t) + [C(q)/D(q)]e(t)
B(q) = 0.1334 q^-1 + 0.101 q^-2
C(q) = 1 - 0.1222 q^-1 - 0.1405 q^-2
D(q) = 1 - 1.148 q^-1 + 0.3494 q^-2
F(q) = 1 - 0.8958 q^-1 + 0.1813 q^-2
Estimated using BJ from data set zdanv
Loss function 0.00699912 and FPE 0.0072286
Sampling interval: 0.08
Функция n
4
sid
используется для оценивания параметров моделей переменных состояния в канонической форме при произвольном числе входов и выходов:
[zn4s,AO] = n4sid(z,order,ny,auxord),
где: z – матрица экспериментальных данных
order – задает порядок модели. Если данный аргумент вводится как вектор – строка, то предварительные расчеты выполняются по моделям всех заданных порядков (по умолчанию от первого по десятый), с выводом графика, позволяющего выбрать оптимальный порядок. Если order = ‘best’(по умолчанию), то выбирается модель наилучшего порядка;
ny – количество выходов (по умолчанию ny = 1);
auxord – дополнительный порядок, используемый алгоритмом оценивания. Данный порядок должен быть больше, чем порядок, задаваемый параметром order (по умолчанию дополнительный порядок равен (1.2*order+3)). Если данный аргумент вводится как вектор – строка, то выбирается модель наилучшего порядка.
Для рассматриваемого примера project24 имеем:
>>zn4s=n4sid(zdanv,[1:10],[1:10]),
где в первых квадратных скобках задается интервал порядков модели order, и предварительные расчеты выполняются по моделям для всех заданных порядков от 1 до 10 с выводом графика, позволяющего выбрать оптимальный порядок. После этого необходимо в командной строке MATLAB набрать этот порядок и продолжить вычисление коэффициентов модели, нажав клавишу enter (рис. 2. 9). Во вторых квадратных скобках задается так называемый дополнительный порядок, используемый алгоритмом оценивания (по умолчанию дополнительный порядок равен (1.2*order+3)). При этом выбирается оптимальный порядок без вывода соответствующего графика.
 Результатом выполнения команды является вывод результатов оценивания: Результатом выполнения команды является вывод результатов оценивания:
Warning: Input arguments must be scalar.
> In n4sid>transf at 1044
In n4sid at 134
Select model order:('Return' gives default)
При нажатии In n4sid>transf at 1027, In n4sid at 134 (синий цвет: имя модели, построенной в тета - формате) появится окно редактора М-файла программы.
При нажатии Enter появится Order chosen to 3 (Закажите выбранный 3)
State-space model: x(t + Ts) = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + в u(t) + e(t)
 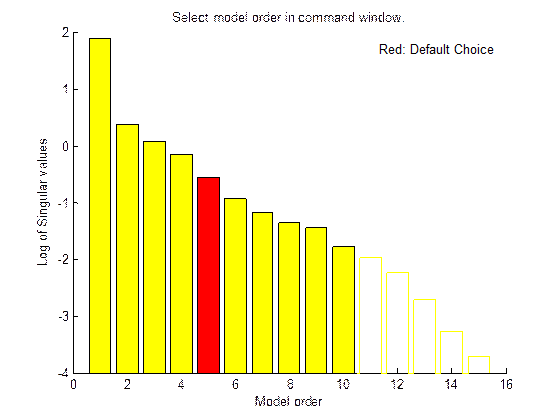
Рис.
2. 9. График для выбора оптимального порядка модели
A =
x1 x2 x3
x1 0.77993 0.54376 -0.013931
x2 -0.12996 0.073872 0.19929
x3 -0.1067 0.016064 -0.47392
B =
расход газа
x1 -0.022796
x2 -0.048006
x3 -0.034112
C =
x1 x2 x3
температура -4.6742 -0.54702 0.0027609
D =
расход газа
температура 0
K =
температура
x1 -0.20139
x2 0.075372
x3 0.02383
x(0) =
x1 0.10598
x2 0.033411
x3 -0.0020287
Estimated using N4SID from data set zdanv
Loss function 0.00753932 and FPE 0.00791011
Sampling interval: 0.08
 Функция pem
оценивает параметры обобщенной многомерной линейной модели: Функция pem
оценивает параметры обобщенной многомерной линейной модели:
>> zpem=pem(zdanv)
State-space model: x(t+Ts) = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + в u(t) + e(t)
A =
x1 x2 x3 x4 x5
x1 0.79771 0.52932 0.017441 -0.043818 -0.055481
x2 -0.089871 -0.056516 0.34751 0.4433 -0.14175
x3 0.12179 -0.31736 -0.29564 -0.43427 0.29463
x4 0.096387 -0.0086843 -0.063652 0.64711 -0.21098
x5 -0.012304 0.025405 -0.18701 0.69982 1.0514
B =
расход газа
x1 -0.021221
x2 -0.053799
x3 -0.040284
x4 -0.00059208
x5 -0.032983
C =
x1 x2 x3 x4 x5
температура -4.675 -0.54794 0.010925 0.068154 -0.1202
D =
расход газа
температура 0
K =
температура
x1 -0.22248
x2 0.037523
x3 0.024536
x4 0.11512
x5 -0.068061
x(0) =
x1 0.10985
x2 0.0039575
x3 0.071289
x4 -0.15615
x5 -0.15783
Estimated using PEM from data set zdanv
Loss function 0.00664935 and FPE 0.00720346
Sampling interval: 0.08
2
. 9. Функции преобразования моделей
Для дальнейшего использования, полученных моделей при анализе и синтезе систем автоматизации технологических процессов в пакете System Identification Toolbox MATLAB имеются специальные функции, позволяющие выполнить преобразование этих моделей из тета-формата (внутреннего вида матричных моделей, являющегося дискретным) в другие виды и в частности из дискретной в непрерывную модель в виде передаточной функции.
Функция th2a
rx
преобразует модель тета-формата в ARX модель:
Функция имеет синтаксис:
>> [A,B]=th2arx(darx)
где darx - модель тета-формата

A =
Columns 1 through 8
1.0000 -1.0105 0.3552 -0.0347 -0.1432 0.1302 -0.0128 -0.0858
Column 9
0.0630
B =
0 0.1367 0.0733
 Функция th2ff
вычисляет частотные характеристики и соответствующие стандартные отклонения по модели в тета-формате. Функция th2ff
вычисляет частотные характеристики и соответствующие стандартные отклонения по модели в тета-формате.
В качестве аргумента функции может выступать любая из рассмотренных ранее моделей, например darx:
>> [g,phiv]=th2ff(darx)
IDFRD model g.
Contains Frequency Response Data for 1 output and 1 input
and SpectrumData for disturbances at 1 output
at 129 frequency points, ranging from 0.1 rad/s to 39.27 rad/s.
Output Channels: температура
Input Channels: расход газа
Sampling time: 0.08
Estimated from data set zdanv using ARX.
IDFRD model phiv.
Contains SpectrumData for 1 signal
at 126 frequency points, ranging from 0.1 rad/s to 39.27 rad/s.
Output Channels: температура
Sampling time: 0.08
Estimated from data set zdanv using ARX.
Функция th
2
poly
преобразует матрицу модели тета-формата в матрицы обобщенной (многомерной) линейной модели:
>> [A,B,C,D,K,lan,T]=th2poly(zpem)
A = 1.0000 -2.1441 1.5148 -0.3280 0.1302 -0.1081
B = 0 0.1322 -0.0698 -0.0946 0.0197 0.0668
C = 1.0000 -1.1083 -0.0108 0.1446 0.3438 -0.0371
D =1
K = 1
lan = 0.0069
T = 0.0800
Здесь параметр lan определяет интенсивность шума наблюдений.
Функция th2ss
преобразует тета-модель в модель для переменных состояния. В качестве аргумента функции может выступать любая из рассмотренных ранее моделей, например darmax:
>> [A,B,C,D,K,x0]=th2ss(darmax)
A =
0.8733 1.0000
-0.1567 0
B =
0.1331
0.1028
C =
1 0
D =
0
 K = K =
1.0587
-0.1701
x0 =
0
0
Функция th2tf
преобразует модель тета-формата многомерного объекта в вектор передаточных функций, связанных с выбранным входом:
>> [num,den]=th2tf(zn4s)
num = 0 0.1327 0.1566 0.0575
den = 1.0000 -0.3799 -0.2810 0.0749
Команда tf
служит для представления передаточной функции в виде отношения:
>> zzn4s=tf(num,den,0.08)
Возвращает:
Transfer function:
0.1327 z^2 + 0.1566 z + 0.0575
------------------------------------
z^3 - 0.3799 z^2 - 0.281 z + 0.07493
Sampling time: 0.08
Функция thd
2
thc
преобразует дискретную модель в непрерывную
Например: преобразуем дискретную модель тета-формата zn4s (модель переменных состояния в канонической форме при произвольном числе входов и выходов) в непрерывную модель и представим ее в виде передаточной функции. Для этого необходимо сначала выполнить функцию thd
2
thc
преобразующую дискретную модель в непрерывную, затем выполнить функцию th2tf
преобразующую модель тета-формата многомерного объекта в вектор передаточных функций, связанных с выбранным входом, а затем команду tf
для представления передаточной функции в виде отношения:
>> sn4s=thd2thc(zn4s);
>> [num,den]=th2tf(sn4s);
>> sysn4s=tf(num,den)
Transfer function:
Transfer function:
-0.891 s^2 + 77.33 s + 746.9
---------------------------------
s^3 + 32.39 s^2 + 308.9 s + 891.7
 Для обратного преобразования непрерывной модели в дискретную модель существует функция thc2thd. Для обратного преобразования непрерывной модели в дискретную модель существует функция thc2thd.
Функция th2zp
рассчитывает нули, полюса и статические коэффициенты передачи (коэффициенты усиления) модели тета - формата zn4s многомерного объекта:
>> [zepo,k]=th2zp(zn4s)
 zepo = zepo =
1.0000 61.0000 21.0000 81.0000
-0.5898 + 0.2921i 0.2754 + 0.1282i -0.4946 0.6660
-0.5898 - 0.2921i 0.3531 0.6365 0.0651
Inf Inf 0.2380 0.2121
k =
1.0000
0.8376
0.0648
Информацию о нулях и полюсах модели zn4s
можно получить с помощью команды
>> [zero,polus]=getzp(zepo)
zero =
-0.5898 + 0.2921i
-0.5898 - 0.2921i
polus =
-0.4946
0.6365
0.2380
С помощью команды zpplot
можно построить график нулей и полюсов модели zn4s
>>zpplot(zpform(zepo))
На рис. 2. 10. представлен график нулей (обозначены кружком) и полюсов (обозначены крестиком) модели zn4s, который получен с помощью команды zpplot.
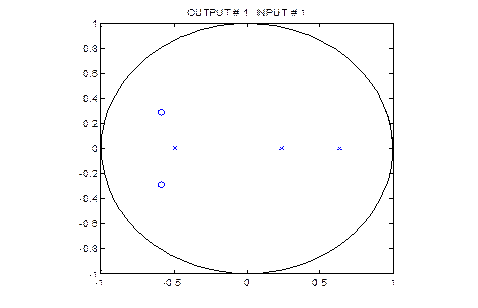
Рис.
2
.10. Графики нулей и полюсов модели zn4s
Данные графика показывают, что модель является устойчивой: полюса модели находятся внутри окружности с радиусом, равным 1 и проходящей через точку с координатами (–1; j0).
2. 10
. Проверка адекватности модели
Одним из важных этапов идентификации объектов автоматизации является проверка качества модели по выбранному критерию близости выхода модели и объекта, т.е проверка ее адекватности. В пакете System Identification Toolbox MATLAB в качестве такого критерия принята оценка адекватности модели fit, которая рассчитывается по формуле: fit = norm (yh – y)/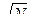 , где norm – норма вектора; yh и y – выходы модели и объекта соответственно; N – количество элементов массива данных. , где norm – норма вектора; yh и y – выходы модели и объекта соответственно; N – количество элементов массива данных.
Для проверки адекватности полученных ранее моделей воспользуемся функцией:
>> compare(zdane,zn4s,zpem,zoe,zbj,darx,darmax).
где: zdane – выход объекта;
 zn4s,zpem,zoe,zbj,darx,darmax – выходы моделей zn4s,zpem,zoe,zbj,darx,darmax zn4s,zpem,zoe,zbj,darx,darmax – выходы моделей zn4s,zpem,zoe,zbj,darx,darmax
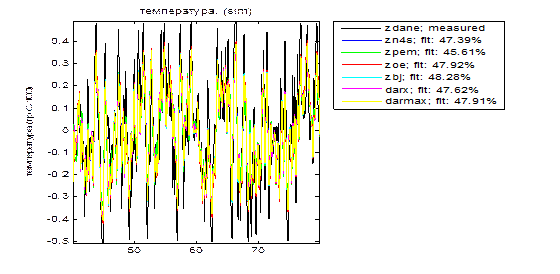
Рис.
2
. 11. Графики выходов объекта и моделей.
Результатом выполнения команды является вывод графика выходов объекта и построенных моделей (Рис. 2. 11). На графике цветными линиями представлены выходы полученных моделей и значения критерия адекватности, выраженного в процентах. Наилучшие показатели имеют модели darx, zn4s и zpem.
Для проверки адекватности модели zn4s воспользуемся функцией:
>>compare(zdane,zn4s)
Результат выполнения команды является вывод графика объекта на рис. 2. 12.
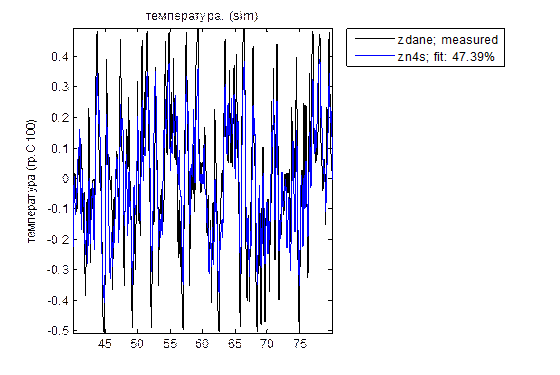
 Рис.
2
. 12. Графики выходов объекта и модели
zn4s. Рис.
2
. 12. Графики выходов объекта и модели
zn4s.
В пакете System Identification Toolbox MATLAB имеется возможность прогнозировать ошибку моделирования при заданном входном воздействии u
(
t
)
и известной выходной координате объекта y
(
t
)
. Оценивание производится методом прогноза ошибки Preictive Error Method, сокращенно PEM, который заключается в следующем. Пусть модель исследуемого объекта имеет вид так называемой обобщенной линейной модели
y
(t
) = W
(z
) u
(t
) + v
(t
),
где W
(z
) – дискретная передаточная функция любой из ранее рассмотренных моделей. При этом шум v
(t
) может быть представлен как
v
(t
) = H
(z
) e
(t
),
где e
(z
) – дискретный белый шум, который собственно и характеризует ошибку модели; H
(z
) – некоторый полином от z
, приводящий дискретный белый шум к реальным помехам при измерении выходных параметров объекта.
Из данных выражений следует, что
e
(t
) = H
-1
(z
) [y
(t
) – W
(z
) u
(t
)].
Функция resid вычисляет остаточную ошибку e для заданной модели, а также r – матрицу значений автокорреляционной функции процесса e
(t
) и значения взаимокорреляционой функции между остаточными ошибками e
(t
) и выходами объекта автоматизации y
(t
) вместе с соответствующими 99 %-ми доверительными коридорами. Кроме указанных значений выводятся графики данных функций. В качестве примера сравним остаточные ошибки и соответствующие корреляционные функции для полученных моделей darx и zbj, имеющих максимальную и минимальную оценки адекватности с помощью команд:
>> [e,r]=resid(zdan,darx)
>> [e1,r1]=resid(zdan,zbj)
Приведенные графики (рис. 2. 13 и 2 14) характеризуют равномерное распределение остаточных ошибок во всем диапазоне изменения интервалов времени τ
. Причем значения остаточных ошибок  для модели darx практически в два раза больше, чем для модели zbj. Для вывода графиков необходимо выполнить команду resid(r). для модели darx практически в два раза больше, чем для модели zbj. Для вывода графиков необходимо выполнить команду resid(r).
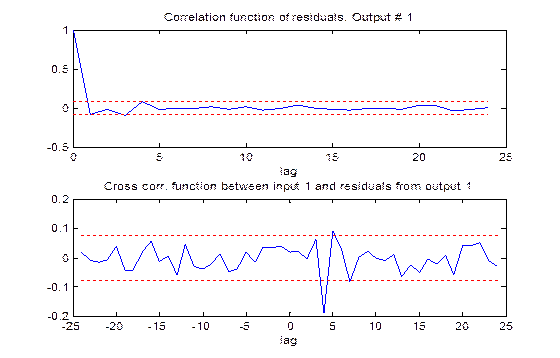
Рис. 2. 13. График автокорреляционной и взаимокорреляционной функций для модели
zbj
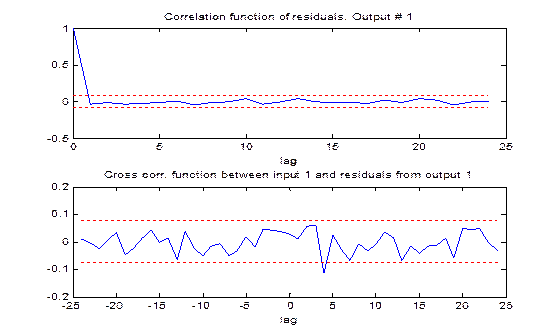
Рис.
2
. 14. График автокорреляционной и взаимокорреляционной функций для модели
darx
 После выполнения функции: После выполнения функции:
[e,r]=resid(zdan,darx)
MATLAB возвращает:
Time domain data set with 1097 samples.
Sampling interval: 0.08
Outputs Unit (if specified)
e@температура гр.С 100
Inputs Unit (if specified)
u1
r =
1.0e+003 *
Columns 1 through 8
0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000
0.0002 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000
Columns 9 through 16
-0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000
-0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000
-0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000
 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000
Columns 17 through 24
-0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000
-0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000
0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000
Columns 25 through 27
0.0000 1.0970 0.0010
-0.0000 0 0
0.0000 0 0
-0.0000 0 0
После выполнения команды >> resid(r) выводится график автокорреляционной и взаимокорреляционной функций для модели.
Таким образом, в ходе оценки адекватности различных моделей объекта автоматизации технологического процесса тепловой обработки материалов определены модели darx, zn4s и zpem, значения критерия адекватности которых максимальны и, следовательно, могут быть использованы в дальнейшем при анализе и синтезе систем автоматизации.
2. 11
. Анализ модели технического объекта управления
Для анализа модели ТОУ возьмем модель zn4s, имеющую один из наилучших показателей адекватности.
• zzn4s – дискретная модель в виде передаточной функции
0.1327 z^2 + 0.1566 z + 0.0575
------------------------------------
z^3 - 0.3799 z^2 - 0.281 z + 0.07493
• sysn4s – непрерывная модель в виде передаточной функции
-0.891 s^2 + 77.33 s + 746.9
---------------------------------
s^3 + 32.39 s^2 + 308.9 s + 891.7
Приведенные виды являются одной и той же моделью, записанной в разных формах и форматах. Проанализируем динамические характеристики модели. Построим переходную характеристику ТОУ для дискретной и непрерывной моделей и определим основные показатели переходного процесса. Для этого можно воспользоваться функцией step
. Функция step рассчитывает и строит реакцию модели на единичную ступенчатую функцию, т. е. возвращает переходную функцию системы:
step(sys)
step(sys, t)
step(sys1,sys2,….,sysN, t)
step(sys1,’PlotStyle1’,….,sysN, ’PlotStyleN’)
[y,t,x] = step(sys)
Д ля моделей, заданных в пространстве состояний, начальные условия принимаются нулевыми. Аргументы функции следующие: ля моделей, заданных в пространстве состояний, начальные условия принимаются нулевыми. Аргументы функции следующие:
- sys,sys1,sys2,….,sysN – имена моделей для которых строятся переходные функции;
- t – аргумент, задающий момент окончания моделирования – либо в форме t = Tfinal (в секундах), либо в форме t = 0:dt:Tfinal.
Для дискретных моделей значение dt должно равняться интервалу дискретизации, для непрерывных моделей – быть достаточно малым, чтобы учесть наиболее быстрые изменения переходного процесса;
- ’PlotStyle1’,….,’PlotStyleN’ – строковые переменные, задающие стили (типы линий) при выводе нескольких графиков одновременно.
Возвращаемые величины:
- графики переходных процессов;
- y, x, t – соответственно, векторы, содержащие значения переходного процесса, переменных состояния и моментов времени (при возвращении данных величин график переходного процесса не отображается).
Выполним построение переходной характеристики ТОУ, представленной дискретной zzn4s инепрерывной sysn4s моделями и определим основные показатели переходного процесса, используя функцию step:
>>step(zzn4s,sysn4s)
После выполнения команды step MATLAB возвращает графики переходного процесса (Рис. 2. 15). Нажатие левой клавиши мыши в любом месте на графике переходного процесса приводит к появлению всплывающей информационной подсказки о величине текущего численного значения переходного процесса и моменте времени.
 Нажатие правой клавиши в любом месте на графике переходного процесса приводит к появлению всплывающего меню редакции окна всплывающей информационной подсказки. Нажатие правой клавиши в любом месте на графике переходного процесса приводит к появлению всплывающего меню редакции окна всплывающей информационной подсказки.
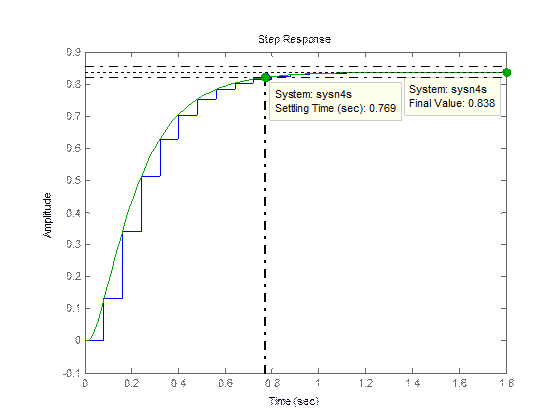
 Рис.
2
. 15. Графики переходных процессов модели
z
zn4s и
sy
sn4s Рис.
2
. 15. Графики переходных процессов модели
z
zn4s и
sy
sn4s
На графиках переходных процессов ступенчатой линией представлен переходной процесс дискретной модели, а сплошной линией – непрерывной модели. Кроме того, в поле графика указаны основные характеристики переходного процесса:
• время регулирования (Setting time) – 0,769 с для обоих моделей;
• установившееся значение выходной координаты – 0,838 для обеих моделей.
Для построения импульсной характеристики моделей необходимо воспользоваться командой:
>>impulse(zzn4s,sysn4s).
После выполнения команды impulse MATLAB возвращает графики (Рис. 2. 16).
Основными характеристиками модели ТОУ при подаче на вход единичного импульсного воздействия являются:
• пиковая амплитуда (Peak amplitude) составляет для дискретной модели 0,207 а для непрерывной – 2,79.
• время регулирования составляет для дискретной модели 0,922 и для непрерывной модели – 0,863 с.
Для определения статического коэффициента усиления модели ТОУ можно использовать команду dcgain
:
>> k=dcgain(sysn4s)
После выполнения команды получим: k = 0.8376. 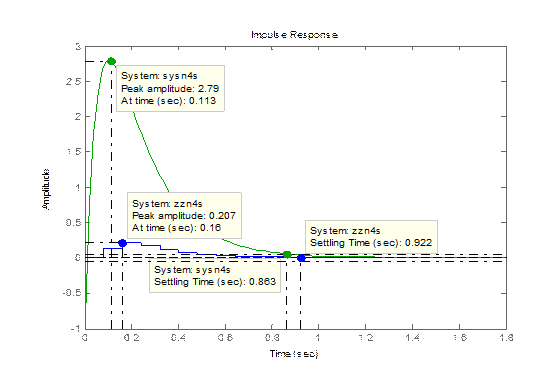
Рис.
2
. 16. Графики импульсной характеристики
Для определения частотной характеристики моделей используем команду bode:

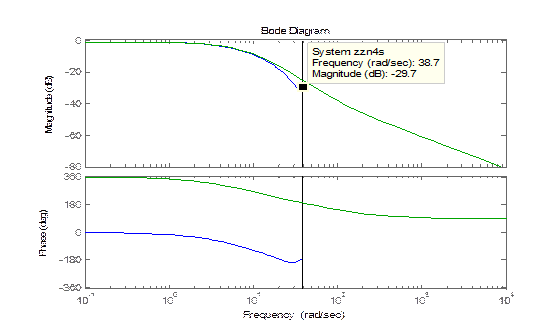
Рис.2. 17. Частотные характеристики моделей
Выполним построение частотной характеристики ТОУ, представленной дискретной zzn4s и непрерывной sysn4s моделями (Рис. 2. 17).
Н а графиках частотных характеристик указаны значения запасов устойчивости по амплитуде (Gain Margin), которые для дискретной модели составляет 29,7 dB, а для непрерывной модели – бесконечность. а графиках частотных характеристик указаны значения запасов устойчивости по амплитуде (Gain Margin), которые для дискретной модели составляет 29,7 dB, а для непрерывной модели – бесконечность.
Значения запасов устойчивости можно определить также и в режиме командной строки MATLAB с помощью команд:
>> [Gm,Pm,Wcg,Wcp]=margin(sysn4s) – для непрерывной модели:
MATLAB возвращает:
Gm =
26.5077
Pm =
Inf
Wcg =
48.5667
Wcp =
NaN
>> [Gm1,Pm1,Wcg1,Wcp1]=margin(zzn4s) – для дискретной модели:
MATLAB возвращает:
Gm1 =
9.0385
Pm1 =
Inf
Wcg1 =
21.0461
Wcp1 =
NaN
где Gm – запас устойчивости по амплитуде в натуральных величинах на частоте Wcg, Pm – запас устойчивости по фазе на частоте Wcp.
Для определения запасов устойчивости в логарифмическом масштабе необходимо выполнить следующие операции:
>> Gmlog=20*log10(Gm1) – для дискретной модели:
Gmlog =
19.1219
>> Gmlog=20*log10(Gm) – для непрерывной модели:
Gmlog =
28.4675
Как видно, определение запасов устойчивости последним способом позволяет значительно точнее вычислять эти значения, чем на графиках частотных характеристик. Анализ частотных характеристик показывает, что модели zzn4s и sysn4s являются устойчивыми с соответствующими запасами устойчивости по амплитуде. Запас устойчивости по фазе равен бесконечности.
Этот вывод подтверждается так же комплексной амплитудно-фазовой характеристикой АФХ (называется диаграммой Найквиста, Рис. 2. 18), так как годограф АФХ не пресек ает точку комплексной плоскости с координатами –1, j0. ает точку комплексной плоскости с координатами –1, j0.
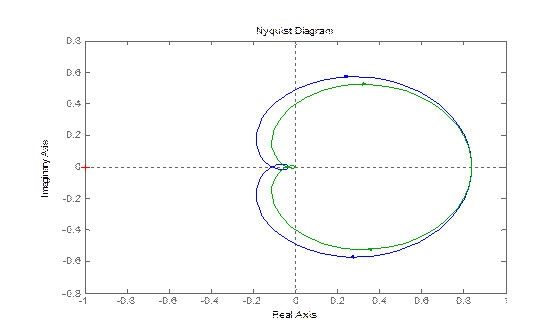 Рис.
2
. 18. Годограф АФХ для непрерывной и дискретной моделей Рис.
2
. 18. Годограф АФХ для непрерывной и дискретной моделей
Для построения АФХ необходимо воспользоваться командой:
>>nyquist(zzn4s,sysn4s),
Определить устойчивость моделей можно с помощью карты нулей и полюсов по расположению нулей моделей относительно окружности с единичным радиусом на комплексной плоскости, как это было показано на рис. 2. 10. Построить карту нулей и полюсов моделей можно так же с помощью команды pzmap(zzn4s,sysn4s), либо – pzmap(zn4s,sn4s).
Построим график изменения e
(t
) и определим основные статистические характеристики помехи с помощь команды plot (e) (Рис. 2. 19).
Для получения статистических характеристик необходимо в строке меню графика в позиции Tools
выбрать опцию Data
statistics
. Результатом выполнения команды явится окно, в котором будут указаны основные статистические характеристики случайного процесса изменения во времени e
(t
),(Рис. 2. 20), к которым относятся:
• min и max – минимальное и максимальное значения помехи.
Для нашего случая – -0,2373 и 0,2086 соответственно;
• mean – арифметическое среднее значение (0,001403);
• median – медиана процесса (0,003994);
• std – среднеквадратическое отклонение (0,0805);
• range – диапазон изменения помехи от минимального до максимального значения (1.12).Во всех случаях размерность аддитивной помехи такая же, как и выходная величина объекта автоматизации – о
С.
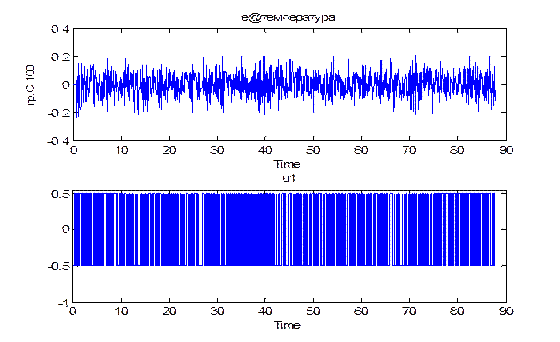
Рис. 5. 19. График аддитивной помехи
e
(
t
)

Рис. 5. 20. Статистические характеристики
e
(
t
)
Полученные статистические характеристики помехи могут быть полезны в дальнейшем при синтезе системы автоматического регулирования температуры теплового объекта автоматизации.
 Для решения задач анализа и синтеза систем управления важно знать ответ на другой не менее важный вопрос, чем полученные временные, частотные и статистические характеристики: обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область). Решение проблемы управляемости основано на анализе уравнений переменных состояния вида: Для решения задач анализа и синтеза систем управления важно знать ответ на другой не менее важный вопрос, чем полученные временные, частотные и статистические характеристики: обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область). Решение проблемы управляемости основано на анализе уравнений переменных состояния вида:
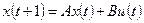 , ,
 , ,
где A
,
B
,
C
,
D
– матрицы соответствующих размеров, v
(t
) – коррелированный белый шум наблюдений. Возможна и другая (так называемая обновленная или каноническая) форма представления данной модели:
 , ,
 , ,
 где К – некоторая матрица (вектор столбец), е(t) – дискретный белый шум (скаляр), где К – некоторая матрица (вектор столбец), е(t) – дискретный белый шум (скаляр),
и формулируется следующим образом: объект называется вполне управляемым, если выбором управляющего воздействия u(t) на интервале времени [t
0
,
tk
] можно перевести его из любого начального состояния
y
(
t
0
) в произвольное заранее заданное конечное состояние
y
(
tk
).
Критерием управляемости линейных стационарных объектов является условие: для того чтобы объект был вполне управляем, необходимо и достаточно, чтобы ранг матрицы управляемости
MU
= (B AB A2
B
… An-1
B)
равнялся размерности вектора состояний n
rang MU
=
n
.
В пакете Control System Toolbox имеется функция ctrb
, формирующая матрицу управляемости в пространстве состояний. Для того, чтобы воспользоваться этой функцией необходимо вычислить матрицы A
, B
, C
, D
с помощью команды:
>>[A,B,C,D]=ssdata(sn4s)
A =
-0.8930 16.3384 4.0253
-4.7215 -22.0535 -3.5128
-1.0484 -2.5116 -9.4429
B =
0.3680
-1.5178
-0.3597
C =
-4.6742 -0.5470 0.0028
D =
0
Следует обратить внимание, что для расчета матриц используется непрерывная модель, так как дискретная модель имеет другие значения, а в критерии управляемости используются матрицы линейных непрерывных стационарных объектов.
Вычислим матрицу управляемости:
>> Mu=ctrb(A,B)
Mu =
0.3680 -26.5754 590.3514
-1.5178 32.9991 -626.2378
-0.3597 6.8234 -119.4511
Определим ранг матрицы управляемости:
>> n=rank(Mu)
 n = n =
3.
Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A
и B
равна трем и ранг матрицы управляемости MU
также равен трем, что позволяет сделать вывод о том, что объект автоматизации является вполне управляемым, т.е. для него имеется такое управляющее воздействие u(t)
, которое способно перевести на интервале времени [t0
,
tk
] объект из любого начального состояния y
(
t
0
)
в произвольное заранее заданное конечное состояние y
(
tk
)
.
При синтезе оптимальных систем с обратной связью сами управления получаются как функции от фазовых координат. В общем случае фазовые координаты являются абстрактными величинами и не могут быть исследованы. Поддается измерению (наблюдению) вектор y
=
(y
1
, …, yk
)T
, который обычно называют выходным вектором или выходной переменной, а его координаты – выходными величинами. Выходная переменная функционально связана с фазовыми координатами, и для реализации управления с обратной связью необходимо определить фазовые координаты по измеренным значениям выходной переменной. В связи с этим возникает проблема наблюдаемости, заключающаяся в установлении возможности состояния определения состояния объекта (фазового вектора) по измеренным значениям выходной переменной на некотором интервале.
Решение проблемы наблюдаемости основано на анализе уравнений переменных состояния вида 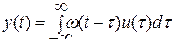 или Y
(
p
) =
W
(
p
)*
U
(
p
)
и формулируется следующим образом: объект называется вполне наблюдаемым, если по реакции y(t
1
) на выходе объекта
, на интервале
времени
[t
0
, t
1
] при заданном управляющем воздействии u(t) можно определить начальное состояние вектора переменных состояния x(t), являющихся фазовыми координатами объекта. или Y
(
p
) =
W
(
p
)*
U
(
p
)
и формулируется следующим образом: объект называется вполне наблюдаемым, если по реакции y(t
1
) на выходе объекта
, на интервале
времени
[t
0
, t
1
] при заданном управляющем воздействии u(t) можно определить начальное состояние вектора переменных состояния x(t), являющихся фазовыми координатами объекта.
Критерием наблюдаемости линейных стационарных объектов является
условие: для того, чтобы объект был вполне наблюдаемым, необходимо и достаточно, чтобы ранг матрицы наблюдаемости
 М
Y
= (CT
AT
CT
(AT
)2
CT
… (
AT
)
n
-1C
) М
Y
= (CT
AT
CT
(AT
)2
CT
… (
AT
)
n
-1C
)
равнялся размерности вектора состояния
n =
rang M
Y
.
Определим матрицу наблюдаемости и ее ранг с помощью функций пакета Control System Toolbox:
>> My=obsv(A,C)
My =
1.0e+003 *
-0.0047 -0.0005 0.0000
0.0068 -0.0643 -0.0169
0.3154 1.5712 0.4129
>> n=rank(My)
n =3
Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A
и С
равна трем и ранг матрицы наблюдаемости M
Y
также равен трем, что позволяет сделать вывод о том, что объект автоматизации является вполне наблюдаемым, т.е. для него всегда можно определить по значениям выходной величины y
(
t
)
вектор переменных состояния, необходимый для синтеза системы управления.
2. 12
. Основные результаты идентификации технического объекта автоматизации
Идентификация распылительной сушилки проводилась с целью получения модели объекта, необходимой для синтеза системы автоматизации и получения основных характеристик объекта автоматизации.
В результате проведенного эксперимента был получен массив данных, состоящий из 1097 значений входного параметра распылительной сушилки – расхода газа в м3
/час и 1097 значений выходного параметра – температуры отходящих газов в градусах Цельсия, измеренных через временные промежутки 0, 08 с.
В ходе идентификации были получены следующие результаты:
1. Обработаны и преобразованы данные в единый файл, содержащий необходимую информацию о входных и выходных параметрах объекта, их значениях и размерностях измерения. Получены графические зависимости изменения температуры отходящих газов от расхода горючего газа на входе распылительной сушилки.
2. Проведено непараметрическое оценивание исходных данных для определения статистических характеристик массивов исходных данных.
3. В результате параметри ческого оценивания экспериментальных данных, проведенного с целью определения параметров модели заданной структуры путем минимизации выбранного критерия качества модели, были получены различные структуры и виды моделей распылительной сушилки: ческого оценивания экспериментальных данных, проведенного с целью определения параметров модели заданной структуры путем минимизации выбранного критерия качества модели, были получены различные структуры и виды моделей распылительной сушилки:
– модель авторегрессии;
– модель авторегрессии с дополнительным входом;
– модель авторегрессии скользящего среднего;
– модель «вход-выход»;
– модель Бокса-Дженкинса;
– модель для переменных состояния.
4. Проверка адекватности моделей показала, что наилучшей степенью адекватности (55.28%) обладает модель для BJ. Получены значения автокорреляционной функции ошибок процесса и значения взаимокорреляционой функции между остаточными ошибками и выходами объекта автоматизации вместе с соответствующими 99 %-ми доверительными коридорами.
5. Проведенное преобразование моделей позволило получить вид передаточных функций распылительной сушилки в дискретном и непрерывном видах, необходимых для дальнейшего анализа и синтеза системы автоматизации:
0.1327 z^2 + 0.1566 z + 0.0575
W(z) = ----------------------------------------------
z^3 - 0.3799 z^2 - 0.281 z + 0.07493
-0.891 s^2 + 77.33 s + 746.9
W(s) = ----------------------------------------
s^3 + 32.39 s^2 + 308.9 s + 891.7
Проведенный анализ модели распылительной сушилки позволил определить основные статические и динамические характеристики объекта автоматизации:
– время регулирования – 0,863 с;
– запас устойчивости по амплитуде – 29,7 дБ;
– запас устойчивости по фазе
– бесконечность.
7. Анализ управляемости и наблюдаемости объекта автоматизации показал, что распылительная сушилка является вполне управляемой и наблюдаемой. На неё можно подавать управляющие воздействия для перевода её из одного начального состояния в произвольное заранее заданное конечное состояние и для этого заранее заданного управляющего воздействия можно определить (измерить) начальное состояние вектора переменных состояния.
ГЛАВА 3. ПОСТРОЕНИЕ СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМ
ПРОЦЕССОМ
3.1.
Задание структуры системы автоматического управления, проверка системы управления на устойчивость
Функция rltool
открывает графический интерфейс, позволяющий проектировать корректирующее звено в замкнутой одномерной системе управления методом корневого годографа. Функция имеет следующий синтаксис:
rltool(sys,comp,LocationFlag,FeedbackSign)
где: sys – имя модели одномерного объекта;
comp – имя корректирующего звена (компенсатора);
LocationFlag – переменная, задающая позицию компенсатора в системе: 1 – в прямом тракте системы, 2 – в цепи обратной связи;
FeedbackSign – тип обратной связи: -1 – отрицательная обратная связь, 1 - положительная обратная связь.
Но удобнее работать с окном интерфейса SISO Design for System FeedbackConfig.
Выполнение функции rltool
без аргументов приводит к появлению  основного окна интерфейса SISO Design for System FeedbackConfig, реализующего метод корневого годографа (Рис. 3. 13). Кнопка +/- позволяет установить отрицательную (-) обратную связь. Кнопка FS позволяет выбрать структуру системы и позицию компенсатора в системе. основного окна интерфейса SISO Design for System FeedbackConfig, реализующего метод корневого годографа (Рис. 3. 13). Кнопка +/- позволяет установить отрицательную (-) обратную связь. Кнопка FS позволяет выбрать структуру системы и позицию компенсатора в системе.
Выберем структуру с расположением компенсатора «С» в прямом тракте системы (Рис. 3. 13) и отрицательную обратную связь. Далее необходимо задать модели звеньев структурной схемы: «F», «C», «G», «H». Для этого следует сделать следующее:
В меню окна интерфейса SISO Design for System FeedbackConfig необходимо выполнить команды: File
Import
.
В открывшемся окне (Рис. 3. 14) загрузки модели Import
System
Data
выберем модель sysn4s. Переключатель Import from указывает, из какой области загружается модель. Модель sysn4s находится в рабочей области MATLAB, т. е. в Workspace. В поле System Data окна Import System Data (Рис. 3. 14) обозначена структурная схема замкнутой системы. В ней «F», «G», «H» звенья модели которые можно загружать. Звено, обозначенное буквой «С», это то компенсирующее динамическое звено структуру и параметры которого нужно определить.

Рис
. 3. 13.
Окна
интерфейса
SISO Design for System FeedbackConfig
.  
Рис.
3
. 14. Окно загрузки модели
Import
System
Data
Далее необходимо выполнить загрузку модели технического объекта управления sysn4s в звено «G» нажатием кнопки со стрелкой, указывающей на звено «G». Модели звеньев «F» и «H» выберем по умолчанию (это пропорциональные звенья с единичным коэффициентом передачи). Сохраним, полученную модель под именем mysys1. Подтвердим сохранение нажатием кнопки ОК. Окно загрузки при этом закроется, а основное окно интерфейса приобретет вид, показанный на рис. 3. 15.

Рис
. 6. 15.
Основное
окно
интерфейса
SISO Design for System mysys1
В графической части окна на комплексной плоскости нулей и полюсов отображены полюсы и нули замкнутой системы, а также линии их перемещения при изменении коэффициента передачи компенсатора от заданного значения до бесконечности. Система имеет три полюса и два нуля (это подтверждается видом аналитического выражения передаточной функции ТОУ, которую можно просмотреть, если щелкнуть ЛК на блоке «G» структурной схемы замкнутой системы и в открывшемся окне System
Data
в поле Plant
Model
:
sy
sn4s
нажать кнопку Show Transfer Function). Передаточная функция имеет в числителе полином второй степени, а в знаменателе полином третьей степени.
Из расположения полюсов (крестики) на комплексной плоскости следует, что замкнутая система достаточно устойчива, так как все три полюса находятся в левой полуплоскости и достаточно далеко от границы  устойчивости. В этом еще можно убедиться, просмотрев график переходного процесса замкнутой системы, если в меню Analysis
выполнить команду Response to Step Command. Данный выбор приведет к открытию окна интерактивного обозревателя LTI
-
Viewer
for
SISO
Design
Tool
(Рис. 3. 16). Как видно из графика сходящегося переходного процесса (кривая r to y) время переходного процесса достаточно мало (с данным корректирующим звеном пропорционального типа с коэффициентом пропорциональности равным единице). Система устойчива. устойчивости. В этом еще можно убедиться, просмотрев график переходного процесса замкнутой системы, если в меню Analysis
выполнить команду Response to Step Command. Данный выбор приведет к открытию окна интерактивного обозревателя LTI
-
Viewer
for
SISO
Design
Tool
(Рис. 3. 16). Как видно из графика сходящегося переходного процесса (кривая r to y) время переходного процесса достаточно мало (с данным корректирующим звеном пропорционального типа с коэффициентом пропорциональности равным единице). Система устойчива.
Однако следует отметить, что при явной устойчивости системы наблюдается некоторое перерегулирование переходного процесса. Следовательно, можно попытаться скорректировать переходный процесс, сделав его апериодическим, т. е улучшить динамические свойства системы. Сделать это можно путем подбора передаточной функции компенсирующего звена «С».
 
Рис. 3. 16. Графики переходных процессов в системе
расположенных над графическим окном.
В поле Current Compensator окна SISO Design for System mysys4 отразится текущая передаточная функция компенсатора. Необходимо также помнить, что после выполнения меню Analysis в произведенной сессии дальнейшие изменения в структуре системы не будут отражены в результатах повторного выполнения меню Analysis. Поэтому для дальнейшего анализы при коррекции системы необходимо загружать новое окно интерфейса, выполнив повторно в режиме командной строки функцию rltool
.
Далее необходимо выполнить анализ построенной замкнутой системы управления с целью определения ее параметров и, сравнив их с заданными в техническом задании параметрами, сделать вывод о необходимости корректировки системы или убедиться в отсутствии такой необходимости. Просмотреть все характеристики можно выполнив в меню Analysis окна SISO Design for System mysys4 команды: Response to Step Command; Rejection of Step Disturbance; Closed-Loop Bode; Compensator Bode; Open-Loop Nyquist. После выполнения команд появится окно обозревателя LTIViewer (Рис. 3. 17)

Рис. 3
. 17
. О
кно обозревателя
LTIViewer
При выполнении в меню Tools команды Draw Simulink Diagram (изобразить диаграмму Simulink) можно перейти к моделированию функциональной схемы в среде Simulink (Рис. 3. 18).

Рис. 3. 21. Переход в среду
Simulink
Таким образом, в пункте 3. 1. 3 мы освоили алгоритм построения структурной схемы замкнутой системы управления. Оценили устойчивость системы. Полученные навыки используем для формирования и оптимизации системы управления ТОУ (выбранного варианта объекта управления). Рассмотрим процесс построения и оптимизации системы управления сушилки клинкера (модель сушилки уже получена – это модель sysn4s).
3. 2. Построение структуры системы автоматического регулирования
установки обжига клинкера

Необходимым условием надежной устойчивой работы автоматизированной системы регулирования является правильный выбор типа регулятора и его настроек, гарантирующий требуемое качество регулирования. В зависимости от свойств объектов управления, определяемых его передаточной функцией и параметрами, и предполагаемого вида переходного процесса
выбирается тип и настройка линейных регуляторов.
Согласно исходных данных переходный процесс должен быть апериодическим с малым временем регулирования и малым перерегулированием.
На основании заданных значений передаточных функций датчика, усилительно-преобразовательного устройства, исполнительного механизма (справочные данные) и построенной модели объекта регулирования sysn4s выполним в SIMULINK построение замкнутой системы автоматического регулирования обжига клинкера.
Предварительный вариант системы автоматического регулирования уже получен. Система оптимизирована по характеру переходного процесса и представлена в среде Simulink (Рис. 6. 22). Необходимо скорректировать полученную Simulink-модель системы, включив в нее недостающие элементы: модель датчика, модель усилительно-преобразовательного устройства и модель исполнительного механизма.
Структурно - функциональная блок-схема системы автоматического регулирования представлена на рис. 3. 22.
        р р

3 22.
Структурно - функциональная блок-схема системы автоматического регулирования
ЗС
– задающий сигнал; Р
– регулятор; УПУ
– усилительно - преобразовательное устройство; ИМ
– исполнительный механизм; ОУ
– объект управления; ДОС
– датчик обратной связи.
В соответствии со структурно-функциональной блок-схемой (Рис. 3. 20) системы автоматического регулирования выполним коррекцию топологии Simulink-модели системы (Рис. 3 21, дополнив ее блоками, имеющими передаточные функции в соответствие со справочными данными: Wдос
= 0.4, Wупу
=15(0.22 + 1); Wим
= 0.19(0.37 + 1) и включим в качестве задающего сигнала единичный скачек (блок Step, Рис. 3 23.)
Выполним команду Start
simulation
в окне модели asd
99*.
В окне Output
осциллографа будем наблюдать переходный процесс (Рис. 3. 25). Регистрация параметров переходной характеристики показывает, что имеющиеся показатели качества не удовлетворяют заданным: Большое время переходного процесса, появилось перерегулирование
Заданные показатели качества и запасы устойчивости:
Время регулирования ≤0.2 с
Статическая ошибка ≤0,05
Перерегулирование ≤1 %
Время нарастания ≤0.1 с
Устойчивость по амплитуде ≥10 дБ
Устойчивость по фазе от 30 до 80 градусов.
 
3. 23.
Simulink
-
модель системы

Рис.
3. 24
. График переходного процесса
Исходя из выше изложенных рекомендаций и учитывая, что вид переходной характеристики должен соответствовать апериодическому процессу, выполним процедуру оптимизации построенной системы управления. Для оптимизации параметров регулятора воспользуемся пакетом прикладных программ для построения систем управления Nonlinear Control Design (NCD) Blockset, реализующий метод динамической оптимизации.
ГЛАВА 4 ОПТИМИЗАЦИЯ ПАРАМЕТРОВ МОДЕЛИРУЕМОЙ СИСТЕМЫ
Для оптимизации параметров регулятора воспользуемся пакетом прикладных программ для построения систем управления Nonlinear Control Design (NCD) Blockset, который реализует метод динамической оптимизации. Этот инструмент, строго говоря, представляющий собой набор блоков, разработанных для использования с Simulink, автоматически настраивает параметры моделируемых систем, основываясь на определённых пользователем ограничениях на их временные характеристики. Сеанс в среде Simulink с использованием возможностей и блоков NCD Blockset состоит из ряда стадий:
· Создание модели системы из стандартных блоков в среде Simulink.
· Соединение входа блока NCD Outport с теми точками системы, на сигналы которых накладываются ограничения. Этими сигналами могут быть, например выходы системы, их среднеквадратические отклонения и т.д.
· Задание в режиме командной строки MATLAB начальных значений параметров, подлежащих оптимизации.
· Раскрытие блоков двойным щелчком мыши на пиктограмме NCD Outport 
· Изменение конфигураций и размеров областей ограничений для сигналов с помощью мыши.
· Задание интервалов дискретизации в меню блока NCD Outport (один или два процента от длительности процесса моделирования) и указание идентификаторов параметров системы, подлежащих оптимизации.
· Задание параметров системы и указание их номинальных значений.
· Сохранение сформированных ограничений в виде файла с помощью команды Save (позднее они могут быть загружены с помощью команды load).
· Процесс оптимизации системы инициализируется нажатием кнопки Start.
 Преобразуем Simulink-модель системы, включив в нее дополнительно пропорциональное звено (П-регулятор) с коэффициентом пропорциональности kp
(Рис. 4.1, Gain1). Для этого в окне Function
Parameters
редактора компоненты Gain1 выставим kp
.
(Рис. 4. 2). Подключим к выходу системы блок Signal Constraint из библиотеки Simulink, Преобразуем Simulink-модель системы, включив в нее дополнительно пропорциональное звено (П-регулятор) с коэффициентом пропорциональности kp
(Рис. 4.1, Gain1). Для этого в окне Function
Parameters
редактора компоненты Gain1 выставим kp
.
(Рис. 4. 2). Подключим к выходу системы блок Signal Constraint из библиотеки Simulink,
 Рис.
4
. 1. Преобразованная
Simulink-модель системы управления Рис.
4
. 1. Преобразованная
Simulink-модель системы управления
 Рис. 4. 2. Окно редактора пропорционального звена Рис. 4. 2. Окно редактора пропорционального звена
содержащийся в разделе Simulink Response Optimization
. В данной операции контролируемым сигналом является реакция системы на единичный скачек, т. е. ее переходная функция. Оптимизируемым параметром является коэффициент kp
.
На переходную функцию накладываются ограничения: максимальное перерегулирование – не более 5%; время нарастания – не более 3 с; длительность переходного процесса - не более 6 с.

Для выполнения процедуры оптимизации наберем в командной строке MATLAB начальное значение настраиваемого параметра kp = 2 и введем его. Далее двойным щелчком мыши откроем рабочее окно блока Signal Constraint (Рис. 4. 3).
Рис.
4 3.
Рабочее окно блока
Signal
Constraint
.

В графической части окна показаны границы контролируемого сигнала, установленные по умолчанию. Для изменения границ в соответствии с заданными значениями используется указатель мыши, позволяющий перемещать линии в вертикальном и горизонтальном направлении. Точную установку линий ограничения можно выполнить, выделяя требуемую линию двойным щелчком левой клавиши мыши. При этом откроется окно редактора Edit
Constraint
(Рис. 4. 4), где можно установить диапазон длины и уровня выделенной линии.

Рис
. 4.4.
Окно
редактора
Edit Constraint.
Следующий этап состоит в объявлении переменных, подлежащих оптимизации. Выбор команды меню Optimization ››Tuned Parameters приведет к открытию диалогового окна задания настраиваемых параметров Tuned Parameters (Рис. 4. 5). В котором, после нажатия кнопки Add
,
появится диалоговое окно Add
Parameters
,
в нижнем поле
 
Рис.
4
. 5. Окна задания настраиваемых параметров
Tuned
Parameters
которого необходимо набрать имя коэффициента пропорциональности kp
,
подтвердив операцию нажатием кнопки ОК (Рис. 4. 6).

Рис.
4
. 6. Диалоговое окно
Add
Parameters
Появится график переходного процесса, подлежащего корректировке. Теперь необходимо запустить процесс оптимизации, нажав кнопку Start optimization. По окончании процесса оптимизации появится семейство графиков переходного процесса (Рис. 4. 7), в которых отражена динамика оптимизации при различных значениях коэффициента пропорциональности П – регулятора. Совокупность графиков содержит финальный график оптимального переходного процесса. График вписывается в установленные уровни.
Появится также окно выходной информации MATLAB (Рис. 4. 8), где содержится информация о процессе оптимизации и значение kp, соответствующее найденной оптимальной величине параметра П – регулятора. Характер оптимизированного переходного процесса можно также просмотреть на экране осциллографа (Рис. 4. 9).

Рис
. 4. 7.
Диалоговое
окно
Signal Constraint
max Directional First-order
Iter S-count f(x) constraint Step-size derivative optimality Procedure
0 1 0 2538
1 6 0 312.9 2.15 0 1 infeasible
2 9 0 1079 1.02 0 1 infeasible
3 12 0 202.2 0.831 0 1 infeasible
4 15 0 160.7 0.198 0 1 infeasible
5 18 0 203.8 0.199 0 1 Hessian modified; infeasible
6 21 0 168.6 0.203 0 1 Hessian modified twice; infeasible
7 24 0 202.8 0.202 0 1 Hessian modified; infeasible
8 27 0 163.5 0.2 0 1 Hessian modified twice; infeasible
9 30 0 203.5 0.2 0 1 Hessian modified; infeasible
10 33 0 166.7 0.202 0 1 Hessian modified twice; infeasible
11 36 0 203 0.201 0 1 Hessian modified; infeasible
12 39 0 164.6 0.2 0 1 Hessian modified twice; infeasible
13 42 0 203.3 0.201 0 1 Hessian modified; infeasible
14 45 0 166 0.201 0 1 Hessian modified twice; infeasible
15 48 0 203.1 0.201 0 1 Hessian modified; infeasible
16 51 0 165.1 0.201 0 1 Hessian modified twice; infeasible
17 54 0 203.2 0.201 0 1 Hessian modified; infeasible
 18 57 0 165.7 0.201 0 1 Hessian modified twice; infeasible 18 57 0 165.7 0.201 0 1 Hessian modified twice; infeasible
19 60 0 203.2 0.201 0 1 Hessian modified; infeasible
20 63 0 165.3 0.201 0 1 Hessian modified twice; infeasible
21 66 0 203.2 0.201 0 1 Hessian modified; infeasible
22 69 0 165.5 0.201 0 1 Hessian modified twice; infeasible
23 72 0 203.2 0.201 0 1 Hessian modified; infeasible
24 75 0 165.4 0.201 0 1 Hessian modified twice; infeasible
25 78 0 203.2 0.201 0 1 Hessian modified; infeasible
26 81 0 165.5 0.201 0 1 Hessian modified twice; infeasible
27 84 0 203.2 0.201 0 1 Hessian modified; infeasible
28 87 0 165.4 0.201 0 1 Hessian modified twice; infeasible
 29 90 0 203.2 0.201 0 1 Hessian modified; infeasible 29 90 0 203.2 0.201 0 1 Hessian modified; infeasible
30 93 0 165.5 0.201 0 1 Hessian modified twice; infeasible
31 96 0 203.2 0.201 0 1 Hessian modified; infeasible
32 99 0 165.4 0.201 0 1 Hessian modified twice; infeasible
33 102 0 203.2 0.201 0 1 Hessian modified; infeasible
34 105 0 165.5 0.201 0 1 Hessian modified twice; infeasible
35 108 0 203.2 0.201 0 1 Hessian modified; infeasible
36 111 0 165.5 0.201 0 1 Hessian modified twice; infeasible
37 114 0 203.2 0.201 0 1 Hessian modified; infeasible
38 117 0 165.5 0.201 0 1 Hessian modified twice; infeasible
39 120 0 203.2 0.201 0 1 Hessian modified; infeasible
40 123 0 165.5 0.201 0 1 Hessian modified twice; infeasible
41 126 0 203.2 0.201 0 1 Hessian modified; infeasible
42 129 0 165.5 0.201 0 1 Hessian modified twice; infeasible
43 132 0 203.2 0.201 0 1 Hessian modified; infeasible
44 135 0 165.5 0.201 0 1 Hessian modified twice; infeasible
45 138 0 203.2 0.201 0 1 Hessian modified; infeasible
46 141 0 165.5 0.201 0 1 Hessian modified twice; infeasible
47 144 0 203.2 0.201 0 1 Hessian modified; infeasible
48 147 0 165.5 0.201 0 1 Hessian modified twice; infeasible
49 150 0 203.2 0.201 0 1 Hessian modified; infeasible
50 153 0 165.5 0.201 0 1 Hessian modified twice; infeasible
51 156 0 203.2 0.201 0 1 Hessian modified; infeasible
52 159 0 165.5 0.201 0 1 Hessian modified twice; infeasible
53 162 0 203.2 0.201 0 1 Hessian modified; infeasible
54 165 0 165.5 0.201 0 1 Hessian modified twice; infeasible
55 168 0 203.2 0.201 0 1 Hessian modified; infeasible
56 171 0 165.5 0.201 0 1 Hessian modified twice; infeasible
57 174 0 203.2 0.201 0 1 Hessian modified; infeasible
58 177 0 165.5 0.201 0 1 Hessian modified twice; infeasible
59 180 0 203.2 0.201 0 1 Hessian modified; infeasible
60 183 0 165.5 0.201 0 1 Hessian modified twice; infeasible
61 186 0 203.2 0.201 0 1 Hessian modified; infeasible
 62 189 0 165.5 0.201 0 1 Hessian modified twice; infeasible 62 189 0 165.5 0.201 0 1 Hessian modified twice; infeasible
63 192 0 203.2 0.201 0 1 Hessian modified; infeasible
64 195 0 165.5 0.201 0 1 Hessian modified twice; infeasible
65 198 0 203.2 0.201 0 1 Hessian modified; infeasible
66 201 0 165.5 0.201 0 1 Hessian modified twice; infeasible
67 204 0 203.2 0.201 0 1 Hessian modified; infeasible
68 207 0 165.5 0.201 0 1 Hessian modified twice; infeasible
69 210 0 203.2 0.201 0 1 Hessian modified; infeasible
70 213 0 165.5 0.201 0 1 Hessian modified twice; infeasible
71 216 0 203.2 0.201 0 1 Hessian modified; infeasible
72 219 0 165.5 0.201 0 1 Hessian modified twice; infeasible
 73 222 0 203.2 0.201 0 1 Hessian modified; infeasible 73 222 0 203.2 0.201 0 1 Hessian modified; infeasible
74 225 0 165.5 0.201 0 1 Hessian modified twice; infeasible
75 228 0 203.2 0.201 0 1 Hessian modified; infeasible
76 231 0 165.5 0.201 0 1 Hessian modified twice; infeasible
77 234 0 203.2 0.201 0 1 Hessian modified; infeasible
78 237 0 165.5 0.201 0 1 Hessian modified twice; infeasible
79 240 0 203.2 0.201 0 1 Hessian modified; infeasible
80 243 0 165.5 0.201 0 1 Hessian modified twice; infeasible
81 246 0 203.2 0.201 0 1 Hessian modified; infeasible
82 249 0 165.5 0.201 0 1 Hessian modified twice; infeasible
83 252 0 203.2 0.201 0 1 Hessian modified; infeasible
 84 255 0 165.5 0.201 0 1 Hessian modified twice; infeasible 84 255 0 165.5 0.201 0 1 Hessian modified twice; infeasible
85 258 0 203.2 0.201 0 1 Hessian modified; infeasible
86 261 0 165.5 0.201 0 1 Hessian modified twice; infeasible
87 264 0 203.2 0.201 0 1 Hessian modified; infeasible
88 267 0 165.5 0.201 0 1 Hessian modified twice; infeasible
89 270 0 203.2 0.201 0 1 Hessian modified; infeasible
90 273 0 165.5 0.201 0 1 Hessian modified twice; infeasible
91 276 0 203.2 0.201 0 1 Hessian modified; infeasible
92 279 0 165.5 0.201 0 1 Hessian modified twice; infeasible
93 282 0 203.2 0.201 0 1 Hessian modified; infeasible
94 285 0 165.5 0.201 0 1 Hessian modified twice; infeasible
95 288 0 203.2 0.201 0 1 Hessian modified; infeasible
96 291 0 165.5 0.201 0 1 Hessian modified twice; infeasible
97 294 0 203.2 0.201 0 1 Hessian modified; infeasible
98 297 0 165.5 0.201 0 1 Hessian modified twice; infeasible
99 300 0 203.2 0.201 0 1 Hessian modified; infeasible
100 303 0 165.5 0.201 0 1 Hessian modified twice; infeasible
Maximum number of iterations exceeded.
Restart or go to Optimization Options to increase the maximum of iterations.
kp =
0.0437
Рис.
4. 8.
окно выходной информации


Рис.
4. 9
. Характер оптимизированного переходного процесса
Исходя из приоритета характеристик переходного процесса в нашем случае наилучший будет: kp = 0,0437.
ГЛАВА 5. АНАЛИЗ КАЧЕСТВА СИСТЕМЫ УПРАВЛЕНИЯ
Необходимо выполнить анализ построенной системы управления и дать оценку ее качества по основным показателям. Анализ снятой переходной характеристики системы после выполнения оптимизации показывает, что новые показатели качества переходного процесса:
Время регулирования составляет 6 с.
Установившееся значение – 0,18
Время нарастания – 3
Статическая ошибка – 0
Перерегулирование - 0 %
удовлетворяют заданным показателям.
Заключение
В данном курсовом проекте проведена идентификация объекта автоматического регулирования.
Проведена проверка на наблюдаемость и управляемость объекта управления.
На основе анализа переходных характеристик объекта управления был выбран наиболее подходящий для данного переходного процесса П – регулятор.
Проведена оптимизация настроечных параметров этого регулятора.
В результате введения в систему П - регулятора были получены следующие параметры системы:
- Время переходного процесса 11 с.;
- Время нарастания – 10 с.
- Перерегулирование – 0%;
- Статическая ошибка – нет;
- Запас по фазе – 70 градусов;
Учитывая полученные значения и принятые допущения параметров системы можно утверждать, что выполнены все поставленные в задании на курсовую работу требовани . .
|