| Знакочередующиеся и знакопеременные ряды
Содержание
1. Признак Даламбера
2. Признак Коши
3. Интегральный признак сходимости ряда
4. Знакочередующиеся ряды. Признак Лейбница
5. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды
Список использованных источников
1. Признак Даламбера
Теорема 1 (признак Даламбера). Пусть дан ряд  , где все , где все 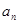 > 0. > 0. Если существует предел Если существует предел
 , ,
то при 0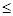  <1 ряд сходится, а при <1 ряд сходится, а при  > 1 ряд сходится. > 1 ряд сходится.
◄Пусть существует предел
 , ,
где 0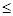  <1. Возьмем q такое, что <1. Возьмем q такое, что  < q <1. Тогда для любого числа ε > 0, например, для < q <1. Тогда для любого числа ε > 0, например, для
 ,найдется номер N такой, что для всех n ≥ N будет выполняться неравенство ,найдется номер N такой, что для всех n ≥ N будет выполняться неравенство
 < q - < q -  , ,
В частности, будем иметь
 < q - < q -  , ,
или
 < q, < q,
Откуда  < < 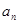 q для всех n ≥ N. Из этого неравенства, придавая n последовательно значения N, N+1,N+2, получим q для всех n ≥ N. Из этого неравенства, придавая n последовательно значения N, N+1,N+2, получим
 < <  q, q,
 < <  q < q <  q q , ,
 < <  q < q <  q q , ,
………………………….
Члены ряда
 + + + + +… +…
Не превосходят соответствующих членов ряда
 q + q + q + q + q q +… , +… ,
который сходятся как ряд, составленный из членов геометрической прогрессии со знаменателем q ,0 < q < 1. По признаку сравнения ряд
 + + + + +… +…
сходится, а значит, сходится и исходный ряд  . .
В случае  > 1, начиная с некоторого номера N, будет выполняться неравенство > 1, начиная с некоторого номера N, будет выполняться неравенство
 > 1, или > 1, или  > >  > 0. > 0.
Следовательно, 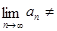 0, и ряд 0, и ряд  расходится, так как не выполнен необходимый признак сходимости. ► расходится, так как не выполнен необходимый признак сходимости. ►
Замечание. Если
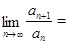 1, 1,
Или не существует, то признак Даламбера ответа о сходимости или расходимости ряда не дает.
Примеры. Исследовать на сходимость следующие ряды:
1. 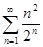 . .
◄ Для данного ряда имеем
 , ,  . .
Тогда
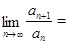   . .
По признаку Даламбера ряд сходится. ►
2.  . .
◄ Имеем
 , , 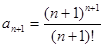 = =  ; ;
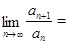 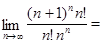 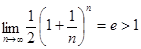 . .
Данный ряд расходится. ►
2. Признак Коши
Теорема 2 (признак Коши). Пусть дан ряд
 , , 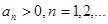 . (1) . (1)
Если существует конечный предел
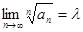 , ,
то 1) при 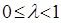 ряд сходится;2) при ряд сходится;2) при 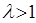 ряд расходится. ряд расходится.
◄ 1) Пусть 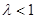 . Возьмем число q такое, что . Возьмем число q такое, что  . Так как существует предел . Так как существует предел
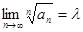 , ,
где  , то, начиная с некоторого номера N , будет выполняться неравенство , то, начиная с некоторого номера N , будет выполняться неравенство 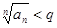 . .
В самом деле, из определенного равенства вытекает, что для любого ε ,в том числе и для
ε =  , найдется такой номер N , начиная с которого будет выполняться неравенство , найдется такой номер N , начиная с которого будет выполняться неравенство
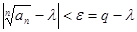 , ,
откуда    или что тоже, или что тоже,
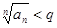 . .
Отсюда получаем
 для для  . .
Таким образом, все члены ряда, начиная с  , меньше соответствующих членов сходящегося ряда , меньше соответствующих членов сходящегося ряда 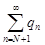 . По признаку сравнения ряд . По признаку сравнения ряд
 
сходится, а значит сходится и ряд(1).
2)Пусть 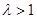 . Тогда, начиная с некоторого номера N для всех n > N , будет выполняться неравенство . Тогда, начиная с некоторого номера N для всех n > N , будет выполняться неравенство 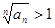 , или , или
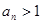 . .
Следовательно,

И ряд (1) расходится. ►
Замечание. Если 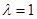 , то ряд (1) может как сходиться, так и расходиться. , то ряд (1) может как сходиться, так и расходиться.
Примеры. Исследовать на сходимость следующие ряды:
1.  . .
◄ Имеем
 , ,  ; ;
 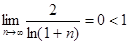 . .
Ряд сходится. ►
2. 
◄ Здесь
 , ,  ; ;
 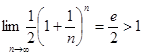
Ряд сходится. ►
3. Интегральный признак сходимости ряда
Теорема 3 (интегральный признак сходимости). Пусть функция f(x) определена, непрерывна, положительна и не возрастает на луче  . Тогда: . Тогда:
1) числовой ряд 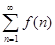 сходится, если сходится несобственный интеграл сходится, если сходится несобственный интеграл
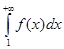 ; (1) ; (1)
2) ряд 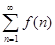 расходится, если расходится несобственный интеграл (1) расходится, если расходится несобственный интеграл (1)

◄ Возьмем на графике функции f(x) точки с абсциссами
x1=1, x2=2, x3=3, … , xn = n
и построим две ступенчатые фигуры, состоящие из выступающих и входящих прямоугольников так, как показано рис. 1. Площадь Q криволинейной трапеции, ограниченной прямыми x = 1, x = n, y=0 и кривой y = f(x) равна
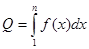 . .
Возьмем n-ю частичную сумму ряда  : :
S n = f(1) + f(2) + f(3) + … + f(n) ,
Тогда площадь Q+ выступающей фигуры будет равна
Q+= f(1) + f(2) + f(3) + … + f(n-1) = S n-1
А площадь Q- входящей фигуры равна
Q- = + f(2) + f(3) + … + f(n) = S n - f(1).
Из построения и свойств функции f(x) следует, что
Q- < Q < Q+ , т.е.
S n - f(1) <  < S n-1. < S n-1.
Так как S n-1 < S n (в силу условия 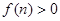 ), то ), то
S n - f(1) <  < S n, n =1,2, … . (2) < S n, n =1,2, … . (2)
1) Пусть интеграл (1) сходится. Тогда существует предел
 , ,
так как
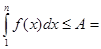 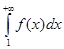
(в силу условия f(x) > 0 для  , то из неравенства (2) следует, что , то из неравенства (2) следует, что
S n < f(1) +  ≤ f(1) + A = M = const, ≤ f(1) + A = M = const,
т.е. 0 < S n < M для n = 1, 2, … .Тем самым, последовательность {S n} ограничена, и при возрастании n сумма S n возрастает, так как f(n ) > 0 для n = 1, 2, … . Поэтому она имеет предел
 , ,
Что означает сходимость ряда  . .
2) Пусть интеграл (1) расходится. Так как по условию
f(x) > 0 для  , то , то
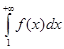 = = 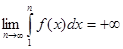 . .
Из неравенства
S n ≥  , n = 1, 2, … , , n = 1, 2, … ,
Следует, что
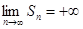 , ,
т.е. ряд 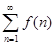 расходится. ► расходится. ►
Пример 1. Исследовать на сходимость ряд
 . .
◄ Здесь  . Известно, что несобственный интеграл . Известно, что несобственный интеграл

сходится при p > 1 и расходится при p ≤ 1. Следовательно, данный ряд сходится при p > 1 и расходится
при p ≤ 1. В частности, при p = 1 получим гармонический ряд
 ► ►
Пример 2. Исследовать на сходимость ряд
 . .
◄ В данном случае функция 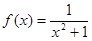 и и
 = = = = 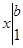 = =
= (arctg b-arctg 1)= (arctg b-arctg 1)=  , ,
т.е. интеграл

сходится, а значит, сходится и ряд. ►
Пример 3. Исследовать на сходимость ряд

◄ Так как общий член данного ряда имеет вид  , то выбираем функцию , то выбираем функцию 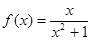 . .
Несобственный интеграл
 = = = = = =
=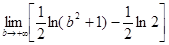 = + = +
расходится, следовательно, ряд тоже расходится. ►
Замечание. Нижний предел интегрирования в несобственном интеграле

можно взять произвольным, например, равным а, где а ≥ 1 – любое число.
Пример 4. Исследовать сходимость ряда
 , ,
◄ Так как общий член ряда

то в качестве функции 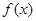 возьмем возьмем
 , где x ≥ 4. , где x ≥ 4.
Тогда
 = = = =
=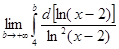 = =
=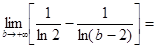  . .
Так как несобственный интеграл

сходится, то сходится и исходный ряд. ►
В случае сходимости ряда 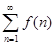 метод, примененный при доказательстве интегрального признака сходимости, позволяет получить оценку погрешности, возникающей при замене суммы ряда частичной суммой. метод, примененный при доказательстве интегрального признака сходимости, позволяет получить оценку погрешности, возникающей при замене суммы ряда частичной суммой.
Пусть функция f(x) удовлетворяет условиям теоремы 9, ряд
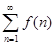
сходится и его сумма равна S. Можно показать, что в этом случае будет сходиться и несобственный интеграл
 . .
Пользуясь неравенством
 , ,
оценим остаток Rn заданного ряда, Имеем
 . .
Итак,
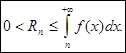
Таким образом, погрешность, получаемая при замене суммы S сходящегося ряда 
его n-й частичной суммой Sn , не превосходит интеграла  . .
Пример 5. Установить сходимость ряда
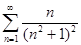
и оценить погрешность при замене его суммы S5.
◄ Здесь
 = =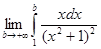 = = = = = =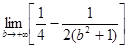 = =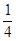
В силу интегрального признака ряд сходится. Обозначим сумму этого ряда через S и будем считать, что
S ≈ S5. Тогда
S ≈ S5 ==

Оценим погрешность R5. Имеем
  ► ►
Замечание. Обозначение

понимается так
 = =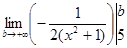 = =  = =
= . .
Пример 6. Оценить n-й остаток сходящегося ряда

где p>1.
◄ Имеем
 = = 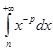 = =  = =  . ► . ►
4 Знакочередующиеся ряды. Признак Лейбница
Определение. Числовой ряд
a1 – a2 + a3 – … + (– 1) n - 1an + … ,
где все числа an положительны, называется знакочередующимся.
Пример. Ряд
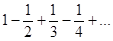
является знакочередующимся, а ряд

знакочередующимся не является.
Для знакочередующихся рядов имеет место следующий признак сходимости, который носит название признака Лейбница.
Теорема 4 (признак Лейбница). Пусть в знакочередующемся ряде
a1 – a2 + a3 – …
числовая последовательность { an } убывает,
a1 > a2> a3> …  Тогда этот ряд сходится, причем его сумма S положительна и не превосходит первого члена: Тогда этот ряд сходится, причем его сумма S положительна и не превосходит первого члена:

◄ Возьмем четную частичную сумму S2n этого ряда и запишем ее в виде
S2n = (a1 – a2) + (a3 – a4) + … + (a2n-1 – a2n).
Из условия теоремы следует, что разности в скобках положительны и, значит, S2n > 0,
причем с возрастанием n частичная сумма S2n возрастает. Эту сумму можно записать
и так:
S2n = a1 – (a2 – a3) – (a4 – a5) – … – (a2n-2 – a2n-1) – a2n.
Здесь каждая скобка положительна, откуда следует, что
S2n < a1 (n = 1, 2, … ).
Итак, последовательность { S2n } монотонно возрастает и ограничена. Следовательно,
она имеет предел
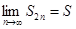 , ,
причем 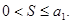
Для нечетной частичной суммы S2n+1 будем иметь
S2n+1 = S2n + a2n+1 (n = 1, 2, … ).
По доказанному
 , ,
А по условию теоремы

Поэтому существует предел
   . .
Таким образом, доказано, что
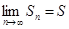 , ,
т.е. данный ряд сходится. Из неравенства 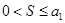 следует, в частности, положительность суммы ряда. ► следует, в частности, положительность суммы ряда. ►
Замечание. Теорема остается справедливой в части сходимости, если условие монотонности последовательности { an } будет выполняться для всех номеров n, начиная с некоторого номера N.
Пример. Знакочередующийся ряд
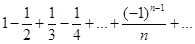
сходится, так как
 и и 
Теорема 4 позволяет оценить n-й остаток
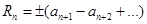
Рассматриваемого ряда, который также является знакочередующимся рядом. По абсолютной величине остаток будет не больше абсолютной величины первого своего члена,  . Так как . Так как 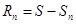 , то , то

т.е абсолютная погрешность, получающаяся при замене суммы знакочередующегося ряда его n-й частичной суммой, не превосходит абсолютной величины первого из отброшенных членов ряда 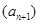 . .
Пример. Вычислить приближенно сумму ряда
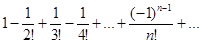 , ,
Ограничившись четырьмя членами, и оценить погрешность.
◄ Сходимость ряда очевидна. Положим приближенно

Тогда
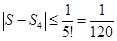 . .
Абсолютная погрешность не превосходит  .► .►
5. Знакопеременные ряды
Абсолютно и условно сходящиеся ряды
Числовой ряд
 , ,
членами которого являются действительные числа любого знака, называется знакопеременным. Знакопеременными будут, например, ряды
 , ,
(плюс, два минуса, плюс, два минуса и т.д.).
Наряду со знакопеременным рядом

рассмотрим ряд, составленный из абсолютных величин его членов, т.е.
 , ,
и докажем следующую теорему.
Теорема 5. Если сходится ряд
 , ,
то сходится и ряд

◄ Из двойного неравенства  получаем получаем
 для n = 1, 2, … . для n = 1, 2, … .
Пусть ряд

сходится. Тогда ряд

также будет сходиться, а по признаку сравнения будет сходящимся и ряд
 . .
Но ряд  есть разность двух сходящихся рядов есть разность двух сходящихся рядов
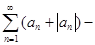 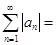  , ,
поэтому он также будет сходящимся. ►
Следствие. Если ряд

сходится, то справедливо неравенство
  . .
◄ Для любого натурального числа k имеет место неравенство
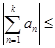  , ,
т.е.
 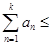 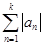 , ,
Переходя к пределу при  , получим , получим
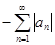 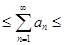  , ,
Или
  . ► . ►
При исследовании ряда

на сходимость можно применять все достаточные признаки сходимости, установленные для знакоположительных рядов.
Замечание. Из сходимости ряда

сходимости ряда

вообще говоря, не следует, т.е. доказанная теорема дает лишь достаточное условие сходимости знакопеременного ряда.
Пример 1. Ряд

сходится по признаку Лейбница, но ряд, составленный из абсолютных величин его членов,

– это гармонический ряд, который расходится.
Определение. Знакопеременный числовой ряд

называется абсолютно сходящимся, если сходится ряд
 . .
Ряд

называется условно сходящимся, если он сходится, а ряд

расходится.
Пример 2. Числовой ряд
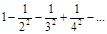
(плюс, два минуса, плюс, два минуса и т.д.) является абсолютно сходящимся, так как ряд, составленный из абсолютных величин его членов,
 , ,
сходится. Ряд из примера 1 является условно сходящимся.
Отметим следующие свойства абсолютно сходящихся и условно сходящихся рядов.
Теорема 6. Абсолютно сходящийся ряд при любой перестановке его членов остается абсолютно сходящимся, и его сумма не изменяется.
Замечание. Утверждение теоремы справедливо для любого сходящегося знакопостоянного ряда.
Условно сходящиеся ряды этим свойством не обладают.
Теорема 7. Если ряд сходится условно, то, каково бы ни было наперед взятое число A,
можно так переставить члены этого ряда, что преобразованный ряд будет иметь своей суммой число A.
Более того, члены условно сходящегося ряда можно представить так, что полученный после переустановки ряда будет расходящимся.
Пример. Рассмотрим условно сходящийся ряд
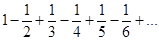 , ,
сумму которого обозначим через S. Переставим члены ряда так, чтобы за каждым положительным членом следовали два очередных отрицательных. Тогда получим ряд

Покажем, что он сходится и его сумма равна  . Рассмотрим подпоследовательность его частичных . Рассмотрим подпоследовательность его частичных
сумм 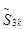 : :
 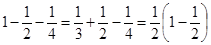 , ,
   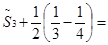
= , ,
  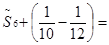 
=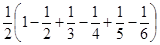 , … . , … .
Нетрудно убедится в том, что она сходится к  . А из того, что . А из того, что
 
 
получаем, что 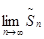 существует и он равен существует и он равен 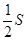 . .
Таким образом, при указанной перестановке членов ряда, мы получим сходящийся ряд, сумма которого в два раза меньше суммы исходного ряда
Список использованных источников
1. «Курс математического анализа», автор – Никольский С.М., г. Москва, изд. «Наука», 1990г.
2. «Высшая математика», автор – Щипачев А.В., г. Москва, изд. «Высшая школа», 1996г.
|