|
Низамутдинова Л. Вариант 15
ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ ПО СТАТИСТИКЕ
Ниже даны данные представленные двумя взаимосвязанными массивами информации. Требуется:
1) провести аналитическое упорядочивание исходной информации (определить Х и У, проранжировать по Х исходные данные от mim к max). Расчеты оформить в таблице. Сделайте выводы;
2) найти параметры линейного уравнения регрессии;
3) определить статистическую значимость исходной информации и полученного уравнения (Критерий Фишера, коэффициент детерминации, среднюю ошибку аппроксимации, средний коэффициент эластичности). Выводы;
4) рассчитать прогнозное значение признака-результата Ур;
5) рассчитать среднюю стандартную ошибку прогноза my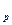 и доверительный интервал прогноза.
и доверительный интервал прогноза.
6) сделать выводы по всем рассчитанным показателям.
Примечание: 1) табличное значение критерия Фишера=4,35;
2) табличное значение критерия Стьюдента=2,08
ЗАДАЧА №16
Вариант а)
| Объем продукции, млн. руб.
|
Основные фонды, млн. руб.
|
| а
|
| 1
|
3,5
|
4,7
|
| 2
|
2,3
|
2,7
|
| 3
|
3,2
|
3,0
|
| 4
|
9,6
|
6,1
|
| 5
|
4,4
|
3,0
|
| 6
|
3,0
|
2,5
|
| 7
|
5,5
|
3,1
|
| 8
|
7,9
|
4,5
|
| 9
|
3,6
|
3,2
|
| 10
|
8,9
|
5,0
|
| 11
|
6,5
|
3,5
|
| 12
|
4,8
|
4,0
|
| 13
|
1,6
|
1,2
|
| 14
|
12,0
|
7,0
|
| 15
|
9,0
|
4,5
|
| 16
|
4,4
|
4,9
|
| 17
|
2,8
|
2,8
|
| 18
|
9,4
|
5,5
|
| 19
|
14,0
|
6,6
|
| 20
|
2,5
|
2,0
|
1) Проводим аналитическое упорядочивание исходной информации (определим Х и У, проранжируем по Х исходные данные от min к max).
X- Основные фонды
Y- Объем продукции
Чтобы проранжировать в программе MS Excel,выделяем столбик X затем выбираем “Сортировка от минимального к максимальному”,получаем:
| Объем продукции, млн. руб.
|
Основные фонды, млн. руб.
|
| Y
|
X
|
| 13
|
1,6
|
1,2
|
| 20
|
2,5
|
2
|
| 6
|
3
|
2,5
|
| 2
|
2,3
|
2,7
|
| 17
|
2,8
|
2,8
|
| 3
|
3,2
|
3
|
| 5
|
4,4
|
3
|
| 7
|
5,5
|
3,1
|
| 9
|
3,6
|
3,2
|
| 11
|
6,5
|
3,5
|
| 12
|
4,8
|
4
|
| 8
|
7,9
|
4,5
|
| 15
|
9
|
4,5
|
| 1
|
3,5
|
4,7
|
| 16
|
4,4
|
4,9
|
| 10
|
8,9
|
5
|
| 18
|
9,4
|
5,5
|
| 4
|
9,6
|
6,1
|
| 19
|
14
|
6,6
|
| 14
|
12
|
7
|
| сред
|
5,945
|
3,99
|
2)y=a+b*x;

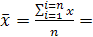
3,9900
 5,9450 5,9450
 =28,3505 =28,3505
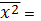 18,2270 18,2270
 15,9201 15,9201
B= (28,3505-3,9900*5,9450)/(18,2270-15,9201)=2,0070
A=5,9450-2,0070*3,9900= -2,0629
Подставляем полученные значения в уравнение парной линейной корреляционной связи и получаем значение у (расчетного):
ŷ =-2,0629+2,0070*x
3)
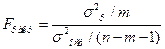
| расч(у)
|
(расч(y)-ср(y))^2
|
(Yi-расч(y))^2
|
(Yi-расч(y))/Yi
|
(Xi-ср(x))^2
|
| 0,3455
|
31,3544
|
1,5738
|
0,7841
|
7,7841
|
| 1,9511
|
15,9512
|
0,3013
|
0,2196
|
3,9601
|
| 2,9546
|
8,9425
|
0,0021
|
0,0151
|
2,2201
|
| 3,3560
|
6,7029
|
1,1151
|
-0,4591
|
1,6641
|
| 3,5567
|
5,7040
|
0,5726
|
-0,2703
|
1,4161
|
| 3,9581
|
3,9478
|
0,5747
|
-0,2369
|
0,9801
|
| 3,9581
|
3,9478
|
0,1953
|
0,1004
|
0,9801
|
| 4,1588
|
3,1905
|
1,7988
|
0,2439
|
0,7921
|
| 4,3595
|
2,5138
|
0,5768
|
-0,2110
|
0,6241
|
| 4,9616
|
0,9671
|
2,3667
|
0,2367
|
0,2401
|
| 5,9651
|
0,0004
|
1,3575
|
-0,2427
|
0,0001
|
| 6,9686
|
1,0478
|
0,8675
|
0,1179
|
0,2601
|
| 6,9686
|
1,0478
|
4,1266
|
0,2257
|
0,2601
|
| 7,3700
|
2,0306
|
14,9769
|
-1,1057
|
0,5041
|
| 7,7714
|
3,3357
|
11,3663
|
-0,7662
|
0,8281
|
| 7,9721
|
4,1091
|
0,8610
|
0,1043
|
1,0201
|
| 8,9756
|
9,1845
|
0,1801
|
0,0451
|
2,2801
|
| 10,1798
|
17,9335
|
0,3362
|
-0,0604
|
4,4521
|
| 11,1833
|
27,4398
|
7,9338
|
0,2012
|
6,8121
|
| 11,9861
|
36,4949
|
0,0002
|
0,0012
|
9,0601
|
| сумма
|
185,8461
|
51,0832
|
-1,0572
|
46,1380
|
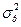 =185,8461 =185,8461
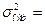 51,0832 51,0832
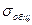 =51,0832+185,8461=236,9293 =51,0832+185,8461=236,9293
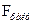 =65,4872 =65,4872
Критерий Фишера позволяет оценить значимость линейных регрессионных моделей, в нашем случае он составляет 65,4872 (табличное значение 4,35), следовательно имеется закономерность.
Коэффициент детерминации рассчитывается по формуле:
 185,8461/236,9293=0,7843 185,8461/236,9293=0,7843
Коэффициент детерминации показывает, на сколько сильно влияет наш фактор на изучаемый процесс, и он составил 78%.
Средний коэффициент эластичности:
Э=b* ; ;
Э=2,0070*(3,9900/5,9450)=0,6711
Коэффициент эластичности показывает, на сколько процентов в среднем по изучаемой совокупности изменения признак-результат (у) от своей средней величины при изменении признака фактора (х) на 1% от своего среднего значения.
Средняя ошибка аппроксимации:

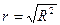 =8,0924 =8,0924
Случайные ошибки параметров:
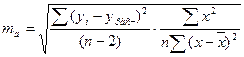 ; ;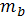 = = ; ;
Ma=1,1004
Mb=0,2480
Mr=0,0119
Доверительные интервалы показателей:
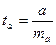 ; ;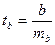 ; ;
 -2,0629/1,1004=-1,8747 -2,0629/1,1004=-1,8747
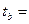 2,0070/0,2480=8,0927 2,0070/0,2480=8,0927
 0,8856/0,0119=74,4207 0,8856/0,0119=74,4207
Предельные ошибки параметров:
 ; ; ; ;
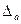 =2,2888 =2,2888
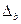 =0,5158 =0,5158
Доверительные интервалы:
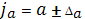 -4,3517≤ -4,3517≤ 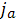 ≤ 0,2259 ≤ 0,2259
 1,4912≤ 1,4912≤  ≤ 2,5228 ≤ 2,5228
4)
прогнозные
| x
|
y
|
| 7,05
|
12,09
|
| 8,00
|
13,99
|
| 8,05
|
14,09
|
5)Xp=7,05
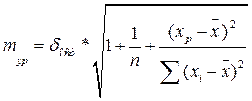
 = 8,00 = 8,00
 =16,64 =16,64
-4,55 28,73 28,73
ЗАДАЧА №48
Имеются данные о распределении населения области А и РБ по уровню располагаемых ресурсов (в среднем в месяц в 2009 г.):
| Располагаемый доход на семью,
тыс. руб. в месяц
|
Удельный вес, %
|
| Область А
|
РБ
|
| 0-9,0
|
1,1
|
1,8
|
| 9,1-13,0
|
5,4
|
7,0
|
| 13,1-17,0
|
13,1
|
10,9
|
| 17,1-21,0
|
15,5
|
14,6
|
| 21,1-25,0
|
18,1
|
16,8
|
| 25,1-29,0
|
14,7
|
13,3
|
| 29,1-33,0
|
9,6
|
10,3
|
| 33,1-37,0
|
8,3
|
7,4
|
| 37,1-41,0
|
4,6
|
5,6
|
| 41,1-45,0
|
2,7
|
3,7
|
| 45,1-50,0
|
2,5
|
2,6
|
| 50,1-60,0
|
2,7
|
3,1
|
| 60,1-70,0
|
0,5
|
1,3
|
| 70,1-90,0
|
0,6
|
1,1
|
| более 90,0
|
0,6
|
0,5
|
| Всего
|
100,0
|
100,0
|
Рассчитайте средний размер дохода семьи в месяц в области и республике, сравните полученные результаты.
Решение:
| Располагаемый доход на семью, тыс. руб. в месяц X
|
Удельный вес, %
|
| Область А F
|
РБ F
|
| 0-9,0
|
1,1
|
1,8
|
| 9,1-13,0
|
5,4
|
7
|
| 13,1-17,0
|
13,1
|
10,9
|
| 17,1-21,0
|
15,5
|
14,6
|
| 21,1-25,0
|
18,1
|
16,8
|
| 25,1-29,0
|
14,7
|
13,3
|
| 29,1-33,0
|
9,6
|
10,3
|
| 33,1-37,0
|
8,3
|
7,4
|
| 37,1-41,0
|
4,6
|
5,6
|
| 41,1-45,0
|
2,7
|
3,7
|
| 45,1-50,0
|
2,5
|
2,6
|
| 50,1-60,0
|
2,7
|
3,1
|
| 60,1-70,0
|
0,5
|
1,3
|
| 70,1-90,0
|
0,6
|
1,1
|
| более 90,0
|
0,6
|
0,5
|
| Всего
|
100,0
|
100,0
|
По формуле средней арифметической взвешенной, рассчитаем средний размер дохода семьи в месяц в области:
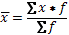 =26,2145/1=26,2145 =26,2145/1=26,2145
По формуле средней арифметической взвешенной, рассчитаем средний размер дохода семьи в месяц в республике:
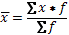 =27,4618/1=27,4618 =27,4618/1=27,4618
Вывод: средний размер дохода семьи в месяц в республике больше средней в области на 1,2473
ЗАДАЧА №59
При 5% выборочном обследовании партии поступившего товара установлено, что 320 единиц из обследованных 400 образцов, отобранных по схеме механической выборки, отнесены к стандартной продукции. Распределение образцов выборочной совокупности по весу следующее:
| Вес изделия, г.
|
Число образцов, шт.
|
| до 3 000
|
30
|
| 3 000 – 3 100
|
40
|
| 3 100 – 3 200
|
170
|
| 3 200 – 3 300
|
150
|
| 3 300 и выше
|
10
|
| И Т О Г О :
|
400
|
Определить:
1) средний вес изделия в выборке;
2) дисперсию и среднее квадратическое отклонение;
3) коэффициент вариации;
4) с вероятностью 0,997 предельную ошибку выборочной средней и границы, в которых можно ожидать средний вес изделия по всей партии товара;
5) с вероятностью 0,954 возможные пределы удельного веса стандартной продукции.
Найдем х среднее:
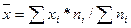 =3170г. =3170г.
Найдем дисперсию и среднеквадратичное отклонение
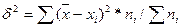 =6600 =6600
 =81,24 =81,24
Найдем предельную ошибку выборочной средней и границы, в которых можно ожидать средний вес изделия по всей партии товара:
 =0,019 =0,019
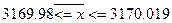
Найдем возможные пределы удельного веса стандартной продукции:
 =3,94 =3,94

ЗАДАЧА № 98
По приведенным данным рассчитать индексы добычи переменного состава, постоянного состава, структурных сдвигов.
| Шахта
|
Добыча угля, тонн на человека
|
Среднесписочная численность шахтеров, в % к итогу
|
| базисный период
X0
|
отчетный период
X1
|
базисный период
F0
|
отчетный период
F1
|
| 1
|
148
|
140
|
38,8
|
40,2
|
| 2
|
120
|
130
|
61,2
|
59,8
|
Решение:
Индекс добычи переменного состава:
I  = = = =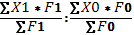 ; ;
I 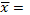 134,02/130,864=1,0241166=102,41% 134,02/130,864=1,0241166=102,41%
Следовательно, добыча в среднем увеличилась на 2,41%
Индекс добычи постоянного состава:
Ix
= = = ; ;
Ix
=134,02/131,256=1,021058=102,1058%
Следовательно, добыча в среднем увеличилась на 2,1058%
Индекс структурных сдвигов:
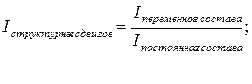 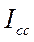 =102,41%/102,1058%=100,2979% =102,41%/102,1058%=100,2979%
Следовательно, добыча среднем увеличилась на 0,2979%
ЗАДАЧА № 123
Численность населения области А за 2000 — 2006 гг. характеризуется следующими данными (тыс. чел., на конец года):
| Годы
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
| Численность
населения
|
1173,9
|
1166,2
|
1156,4
|
1146,1
|
1135,1
|
1123,5
|
1114,1
|
По данным таблицы рассчитайте:
1) среднегодовую численность населения за 2001 — 2006 гг.;
2) аналитические показатели динамики: абсолютные приросты, темпы роста и темпы прироста (цепные и базисные), абсолютное содержание одного процента прироста (снижения). Полученные показатели представьте в виде таблицы;
3) среднегодовые показатели динамики: абсолютный прирост, темп роста и темп прироста за весь анализируемый период;
4) постройте график динамики численности населения области за 2000 — 2006 гг. и определите тип тенденции динамического ряда;
5) постройте уравнение тренда и осуществите прогноз на два года вперед.
Сформулируйте выводы.
1)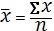 = 6841,4000/6=1140,2333 = 6841,4000/6=1140,2333
2)
| Годы
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
| Численность
|
1173,9
|
1166,2
|
1156,4
|
1146,1
|
1135,1
|
1123,5
|
| населения
|
| абс прир ц
|
-7,7
|
-9,8
|
-10,3
|
-11,0
|
-11,6
|
| абс прир б
|
-7,7
|
-17,5
|
-27,8
|
-38,8
|
-50,4
|
| темп роста ц
|
99,34%
|
99,16%
|
99,11%
|
99,04%
|
98,98%
|
| темп роста б
|
99,34%
|
98,51%
|
97,63%
|
96,69%
|
95,71%
|
| темп прироста ц
|
-0,66%
|
-0,84%
|
-0,89%
|
-0,96%
|
-1,02%
|
| темп прироста б
|
-0,66%
|
-1,49%
|
-2,37%
|
-3,31%
|
-4,29%
|
| абс знач 1%
|
11,6
|
11,6
|
11,57
|
11,458
|
11,37
|
3)
Абс прирост:
 = =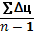 = -50,4/6= -8,4 = -50,4/6= -8,4
Абс прирост баз= = -142,2000/6=-23,7 = -142,2000/6=-23,7
Темп роста:
TРц
= 82,605%
TРб
= 81,313%
Темп прироста:
Tпрц
= -0,72%
Tпрб
= -2,02%
4)

`5)
Для построения уравнения тренда,представим таблицу в виде:
| Годы
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
| t
|
-5
|
-3
|
-1
|
1
|
3
|
5
|
| Численность населения
|
1173,9
|
1166,2
|
1156,4
|
1146,1
|
1135,1
|
1123,5
|
Уравнение имеет вид:
Y=a0+a1*t;
A0= ;a1= ;a1= ; ;
A0= 1150,2
A1= -5,08
Y=1150,2-5,08*t;
2006
- 1150,2-5,08*7=1114,64
2007
- 1150,2-5,08*9=1104,48

|