| Многие крупные проекты, такие как строительство дома, изготовление станка, разработка автоматизированной системы бухгалтерского учета и т.д., можно разбить на большое количество различных операций (работ). Некоторые из этих операций могут выполняться одновременно, другие — только последовательно: одна операция после окончания другой. Например, при строительстве дома можно совместить во времени внутренние отделочные работы и работы по благоустройству территории, однако возводить стены можно только после того, как будет готов фундамент.
Задачи планирования работ по осуществлению некоторого проекта состоят в определении времени возможного окончания как всего проекта в целом, так и отдельных работ, образующих проект; в определении резервов времени для выполнения отдельных работ; в определении критических работ, то есть таких работ, задержка в выполнении которых ведет к задержке выполнения всего проекта в целом; в управлении ресурсами, если таковые имеются и т.п.
Пусть некоторый проект W состоит из работ V1
,...,Vn
; для каждой работы Vk
, известно, или может быть достаточно точно оценено время ее выполнения t(Vk
). Кроме того, для каждой работы Vk
известен, возможно пустой, список ПРЕДШ(Vk
) работ, непосредственно предшествующих выполнению работы Vk
. Иначе говоря, работа Vk
может начать выполняться только после завершения всех работ, входящих в список ПРЕДШ(Vk
).
Для удобства, в список работ проекта W добавим две фиктивные работы s и p, где работа s обозначает начало всего проекта W. а работа p — завершение работ по проекту W. При этом будем считать, что работа s предшествует всем тем работам vÎW, для которых список ПРЕДШ(v) пуст, иначе говоря, для всех таких работ vÎW положим ПРЕДШ(v)={s}. Положим далее ПРЕДШ(s) =Æ, ПРЕДШ(p)={vÎW: v не входит ни в один список ПРЕДШ(w)}, то есть считаем, что работе p предшествуют все те работы, которые могут выполняться самыми последними. Время выполнения работ s и p естественно положить равными нулю: t(s)=t(p)=0.
Весь проект W теперь удобно представить в виде сети G=(V,E,c). Ориентированный взвешенный граф G=(V,E,c) называется сетью. Сеть может быть представлена матрицей весов дуг, массивами смежностей СЛЕД или ПРЕДШ, или списками СЛЕД[v] или ПРЕДШ[v]. При этом записи в списках смежности состоят из трех компонент: поля имени узла, поля веса соответствующей дуги и поля ссылки на следующую запись), где сеть G=(V,E,c) определим по правилам:
1. V=W, то есть множеством узлов объявим множество работ;
2. E={(v,w) : vÎПРЕДШ(w)}, то есть отношение предшествования задает дуги в сети;
3. c(v,w)=t(w).
Так построенную сеть G часто называют сетевым графиком выполнения работ по проекту W. Легко видеть, что списки смежностей этой сети ПРЕДШ[v] совпадают с заданными для проекта списками предшествующих работ ПРЕДШ(v).
Понятно, что сетевой график любого проекта не должен содержать контуров. Действительно, пусть узлы Vk
1
,Vk
2
,...,Vkr
=Vk
1
образуют контур в сети G. Это означает, что работа Vk
2
не может начаться раньше, чем будет завершена работа Vk
1
, работа Vk
3
— раньше, чем завершится работа Vk
2
, и т.д., и, наконец, Vkr
= Vk
1
— раньше, чем будет завершена работа Vkr
-1
. Но тогда никакая из работ Vk
1
,...,Vkr
никогда не сможет быть выполнена. А каждый реальный проект должен допускать возможность его завершения. Следовательно, в сетевом графике нет контуров.
Отсутствие контуров в сети G позволяет пронумеровать работы проекта W таким образом, чтобы для каждой дуги (Vi
,Vj
) сети G выполнялось условие i<j, то есть каждая дуга идёт из узла с меньшим номером в узел с большим номером. Осуществить такую нумерацию узлов сети G можно с помощью алгоритма топологической сортировки. Поэтому в дальнейшем будем считать, что узлы в сети G топологически отсортированы.
Конечной целью построения сетевой модели является получение информации о возможных сроках выполнения как отдельных работ, так и о возможном сроке выполнения всего проекта в целом. Обозначим через PBЫП(v) (соответственно PHAЧ(v)) наиболее ранний возможный срок выполнения работы v (соответственно наиболее ранний возможный срок начала работы v). Удобно считать, что PBЫП(s)=PHAЧ(s)=0. Поскольку начать выполнять работу v можно только после того, как будут выполнены все работы, предшествующие данной работе v, то получим следующие формулы для расчета значений PHAЧ(v) и PBЫП(w):
PHAЧ(v) = МАКС{PBЫП(w): wÎПРЕДШ(v)},
PBЫП(v)= PHAЧ(v) + t(v).
Значение PBЫП(p) дает наиболее ранний возможный срок завершения всего проекта в целом. Приведем запись алгоритма, непосредственно вычисляющего характеристики РНАЧ и РВЫП.
АЛГОРИТМ 1.
Данные: Сетевой график G работ V, заданный списками ПРЕДШ(v), vÎV.
Результаты: Наиболее ранние возможные сроки начала и выполнения работ РНАЧ(v), РВЫП(v), vÎV.
Шаг 1. Объявить возможные ранние сроки начала РНАЧ(v) и выполнения РВЫП(v) работ равными нулю. Текущей вершиной объявить первую вершину vk
=v1.
Шаг 2. Всем вершинам v предшествующим текущей вершине vk
,
значение РНАЧ(vk
) присвоить максимум из значений РВЫП(v) и РНАЧ(vk
). Значение РВЫП(vk
) положить равным значению РНАЧ(vk
) плюс время выполнения самой работы текущей вершины t(vk
).
Шаг 3. Если имеется следующая вершина (работа) после текущей, то объявить ее текущей вершиной vk
, иначе перейти в Шаг 5.
Шаг 4. Вернуться в Шаг 2.
Шаг 5. Выдать наиболее ранние возможные сроки начала и выполнения работ РНАЧ(v), РВЫП(v), vÎV, конец работы алгоритма.
Пусть T — плановый срок выполнения проекта W. Ясно, что Т должно удовлетворять неравенству Т >= РВЫП(Vn
+1
).
Через ПВЫП(v) (соответственно ПНАЧ(v)) обозначим наиболее поздний допустимый срок выполнения (начала) работы v, то есть такой срок, который не увеличивает срок Т реализации всего проекта.
Значения возможных и допустимых сроков выполнения работ позволяют определить резервы времени для выполнения той или иной работы. Полный резерв (иногда его называют суммарный) времени выполнения работ определяется по формуле:
PE3EPB(v)=ПHAЧ(v)-PHAЧ(v).
Значение PE3EPB(v) равно максимальной задержке в выполнении работы v, не влияющей на плановый срок Т. Понятно, что справедливо и такое равенство: РЕЗЕРВ(v)=ПВЫП(v)-РВЫП(v).
Работы, имеющие нулевой резерв времени, называются критическими. Через любую такую работу проходит некоторый максимальный s-p-путь в сети G. Критические работы характеризуются тем, что любая задержка в их выполнении автоматически ведет к увеличению времени выполнения всего проекта.
Приведем запись алгоритма, непосредственно вычисляющего характеристики ПВЫП и ПНАЧ.
АЛГОРИТМ 2.
Данные: Сетевой график G работ V, заданный списками ПРЕДШ(v), vÎV, плановый срок окончания проекта – Т.
Результаты: Наиболее поздние допустимые сроки выполнения и начала работ ПВЫП(v) и ПНАЧ(v).
Шаг 1. Объявить для всех работ vÎV значение наиболее позднего срока выполнения работ равным Т – значению планового срока окончание проекта и вершину vp
фиктивной работы p объявить текущей vk
.
Шаг 2. Присвоить значение ПНАЧ текущей работы vk
равным значению ПВЫП работы и вычесть время выполнения текущей работы.
Шаг 3. Присвоить значению ПВЫП(v) для всех работ vÎПРЕДШ(v) предшествующих текущей работе vk
минимальное значение из значений ПВЫП выполнения роботы v или ПНАЧ выполнения текущей работы vk
, если таковых нет перейти в Шаг 4.
Шаг 4. Если имеется предыдущая вершина (работа) к текущей, то объявить её текущей, иначе перейти в Шаг 6.
Шаг 5. Перейти в Шаг 2.
Шаг 6. Выдать наиболее поздние допустимые сроки выполнения и начала работ ПВЫП(v) и ПНАЧ(v), конец работы алгоритма.
Проиллюстрируем работу приведенных алгоритмов на следующих примерах:
Пример 1: Проект гаража для стоянки автопогрузчиков.
| n
|
Наименование работы
|
Предшеству-ющие работы
|
Время вы-полнения t(vk
)
|
| 1
|
Начало проекта (фиктивн. работа)
|
Нет
|
0
|
| 2
|
Срезка растительного слоя грунта
|
1
|
5
|
| 3
|
Монтаж каркаса
|
2
|
30
|
| 4
|
Обшивка стен профнастилом
|
3
|
15
|
| 5
|
Кровля из профнастила
|
3
|
12
|
| 6
|
Заполнение проема воротами
|
4
|
5
|
| 7
|
Масляная окраска ворот и профнастила
|
5,6
|
10
|
| 8
|
Щебёночное основание под полы
|
7
|
3
|
| 9
|
Асфальтовое покрытие
|
8
|
3
|
| 10
|
Уборка строительного мусора после строит.
|
7
|
3
|
| 11
|
Конец проекта (фиктивная работа)
|
9,10
|
0
|
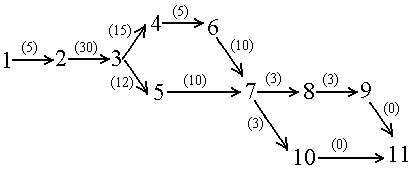
Рис 1. Проект гаража для стоянки автопогрузчиков.
Найдем значения наиболее раннего начала и выполнения работ проекта посредством алгоритма 1. Работу алгоритма изложим в виде последовательности выполняемых шагов.
| Шаг n
|
Действия выполняемые шагом
|
| 1
|
Объявление значений РНАЧ(v) и РВЫП(v), vÎV равными нулю. Текущая вершина vk
=1.
|
| 2
|
Вершин предшествующей первой нет.
РВЫП(1)=РНАЧ(1)+t(1). {РНАЧ(1) стало равным 0}
|
| 3
|
Текущая вершина vk
=2.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(2)=МАКС{РВЫП(1),РНАЧ(2)} {РНАЧ(2) стало равным 0}
РВЫП(2)=РНАЧ(2)+t(2) {РВЫП(2) стало равным 5}.
|
| 3
|
Текущая вершина vk
=3.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(3)=МАКС{РВЫП(2),РНАЧ(3)} {РНАЧ(3) стало равным 5}
РВЫП(3)=РНАЧ(3)+t(3) {РВЫП(3) стало равным 35}.
|
| 3
|
Текущая вершина vk
=4.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(4)=МАКС{РВЫП(3),РНАЧ(4)}{РНАЧ(4) стало равным 35}
РВЫП(4)=РНАЧ(4)+t(4) {РВЫП(4) стало равным 50}.
|
| 3
|
Текущая вершина vk
=5.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(5)=МАКС{РВЫП(3),РНАЧ(5)}{РНАЧ(5) стало равным 35}
РВЫП(5)=РНАЧ(5)+t(5) {РВЫП(5) стало равным 47}.
|
| 3
|
Текущая вершина vk
=6.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(6)=МАКС{РВЫП(4),РНАЧ(6)}{РНАЧ(6) стало равным 50}
РВЫП(6)=РНАЧ(6)+t(6) {РВЫП(6) стало равным 55}.
|
| 3
|
Текущая вершина vk
=7.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(7)=МАКС{РВЫП(5),РНАЧ(7)}{РНАЧ(7) стало равным 47}
РНАЧ(7)=МАКС{РВЫП(6),РНАЧ(7)}{РНАЧ(7) стало равным 55}
РВЫП(7)=РНАЧ(7)+t(7) {РВЫП(7) стало равным 65}.
|
| 3
|
Текущая вершина vk
=8.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(8)=МАКС{РВЫП(7),РНАЧ(8)} {РНАЧ(8) стало равным 65}
РВЫП(8)=РНАЧ(8)+t(8) {РВЫП(8) стало равным 68}.
|
| 3
|
Текущая вершина vk
=9.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(9)=МАКС{РВЫП(8),РНАЧ(9)}{РНАЧ(9) стало равным 68}
РВЫП(9)=РНАЧ(9)+t(9) {РВЫП(9) стало равным 71}.
|
| 3
|
Текущая вершина vk
=10.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(10)=МАКС{РВЫП(7),РНАЧ(10)}{РНАЧ(10) стало равным 65}
|
| 3
|
Текущая вершина vk
=11.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(11)=МАКС{РВЫП(9),РНАЧ(11)}{РНАЧ(11) стало равным 71}
РНАЧ(11)=МАКС{РВЫП(10),РНАЧ(11)}{РНАЧ(11) стало равным 71}
|
| 3
|
Переход в Шаг 5.
|
| 5
|
Конец работы алгоритма, выдача значений наиболее раннего начала и выполнения работ.
|
Таблица результатов работы алгоритма.
| n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
| РНАЧ(v)
|
0
|
0
|
5
|
35
|
35
|
50
|
55
|
65
|
68
|
65
|
71
|
| РВЫП(v)
|
0
|
5
|
35
|
50
|
47
|
55
|
65
|
68
|
71
|
68
|
71
|
Получили, что минимальное время, требуемое для выполнения проекта равно Т=РВЫП(11), Т=71. Теперь найдем посредством алгоритма 2 значение времени наиболее позднего начала и выполнения работ. Работу алгоритма изложим в виде последовательности выполняемых шагов.
| Шаг n
|
Действия выполняемые шагом
|
| 1
|
Объявление значений ПВЫП(v), vÎV равным Т.
Текущая вершина vk
=11.
|
| 2
|
ПНАЧ(11)=ПВЫП(11)-t(11) {ПНАЧ(11) стало равным 71}.
|
| 3
|
ПВЫП(9)=МИН{ПВЫП(9),ПНАЧ(11)}{ПВЫП(9) стало равным 71}
ПВЫП(10)=МИН{ПВЫП(10),ПНАЧ(11)}{ПВЫП(10) стало равным 71}
|
| 4
|
Текущая вершина vk
=10.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(10)=ПВЫП(10)-t(10) {ПНАЧ(10) стало равным 68}
|
| 3
|
ПВЫП(7)=МИН{ПВЫП(7),ПНАЧ(10)}{ПВЫП(7) стало равным 68}
|
| 4
|
Текущая вершина vk
=9.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(9)=ПВЫП(9)-t(9) {ПНАЧ(9) стало равным 68}
|
| 3
|
ПВЫП(8)=МИН{ПВЫП(8),ПНАЧ(9)}{ПВЫП(8) стало равным 68}
|
| 4
|
Текущая вершина vk
=8.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(8)=ПВЫП(8)-t(8) {ПНАЧ(8) стало равным 65}
|
| 3
|
ПВЫП(7)=МИН{ПВЫП(7),ПНАЧ(8)}{ПВЫП(7) стало равным 65}
|
| 4
|
Текущая вершина vk
=7.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(7)=ПВЫП(7)-t(7) {ПНАЧ(7) стало равным 55}
|
| 3
|
ПВЫП(5)=МИН{ПВЫП(5),ПНАЧ(7)}{ПВЫП(5) стало равным 55}
ПВЫП(6)=МИН{ПВЫП(6),ПНАЧ(7)}{ПВЫП(6) стало равным 55}
|
| 4
|
Текущая вершина vk
=6.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(6)=ПВЫП(6)-t(6) {ПНАЧ(6) стало равным 50}
|
| 3
|
ПВЫП(4)=МИН{ПВЫП(4),ПНАЧ(6)}{ПВЫП(5) стало равным 50}
|
| 4
|
Текущая вершина vk
=5.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(5)=ПВЫП(5)-t(5) {ПНАЧ(5) стало равным 43}
|
| 3
|
ПВЫП(3)=МИН{ПВЫП(3),ПНАЧ(5)}{ПВЫП(3) стало равным 43}
|
| 4
|
Текущая вершина vk
=4.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(4)=ПВЫП(4)-t(4) {ПНАЧ(4) стало равным 35}
|
| 3
|
ПВЫП(3)=МИН{ПВЫП(3),ПНАЧ(4)}{ПВЫП(3) стало равным 35}
|
| 4
|
Текущая вершина vk
=3.
|
| 5
|
Переход в шаг 2.
|
| 2
|
ПНАЧ(3)=ПВЫП(3)-t(3) {ПНАЧ(3) стало равным 5}
|
| 3
|
ПВЫП(2)=МИН{ПВЫП(2),ПНАЧ(3)}{ПВЫП(2) стало равным 5}
|
| 4
|
Текущая вершина vk
=2.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(2)=ПВЫП(2)-t(2) {ПНАЧ(2) стало равным 0}
|
| 3
|
ПВЫП(1)=МИН{ПВЫП(1),ПНАЧ(2)}{ПВЫП(1) стало равным 0}
|
| 4
|
Текущая вершина vk
=1.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(1)=ПВЫП(1)-t(1) {ПНАЧ(1) стало равным 0}
|
| 3
|
Переход в Шаг 4.
|
| 4
|
Переход в Шаг 6.
|
| 6
|
Конец работы алгоритма, выдача значений времени наиболее позднего начала и выполнения работ.
|
Дадим таблицу результатов работы алгоритма с результатами предыдущего алгоритма и сосчитаем резерв времени для каждой работы по формуле PE3EPB(v)=ПНАЧ(v)-PHAЧ(v) или РЕЗЕРВ(v)=ПВЫП(v)-РВЫП(v).
| Работы
|
РНАЧ
|
РВЫП
|
ПНАЧ
|
ПВЫП
|
Резерв
|
| 1
|
0
|
0
|
0
|
0
|
0
|
| 2
|
0
|
5
|
0
|
5
|
0
|
| 3
|
5
|
35
|
5
|
35
|
0
|
| 4
|
35
|
50
|
35
|
50
|
0
|
| 5
|
35
|
47
|
43
|
55
|
8
|
| 6
|
50
|
55
|
50
|
55
|
0
|
| 7
|
55
|
65
|
55
|
65
|
0
|
| 8
|
65
|
68
|
65
|
68
|
0
|
| 9
|
68
|
71
|
68
|
71
|
0
|
| 10
|
65
|
68
|
68
|
71
|
3
|
| 11
|
71
|
71
|
71
|
71
|
0
|
Из таблицы видно, что критическими работами являются 1, 2, 3, 4, 6, 7, 8, 9, 11, которые и образуют в сети G критический путь. Расчеты выполнены при Т=71.
Пример 2: Проект склада сажи и других материалов в помещение производственного цеха.
| n
|
Наименование работы
|
Предшеству-ющие работы
|
Время вы-полнения t(vk
)
|
| 1.
|
Начало проекта (фиктивн. работа)
|
Нет
|
0
|
| 2.
|
Монтаж металлоконструкций нижней обвязки каркаса
|
1
|
5
|
| 3.
|
Устройство бетона под стойки
|
2
|
3
|
| 4.
|
Монтаж стоек
|
3
|
10
|
| 5.
|
Монтаж опорных столиков
|
4
|
5
|
| 6.
|
Монтаж балок
|
2
|
7
|
| 7.
|
Монтаж металлоконструкций ворот
|
6
|
7
|
| 8.
|
Обшивка стен и кровли волнистым листом
|
6
|
12
|
| 9.
|
Монтаж козлового крана
|
7
|
5
|
| 10.
|
Устройство асфальтобетонных покрытий
|
8
|
5
|
| 11.
|
Конец проекта (фиктивн. работа)
|
5,9,10
|
0
|
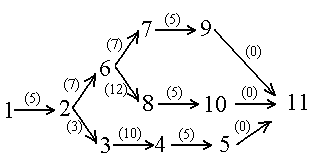
Рис 2. Проект склада сажи и других материалов в помещение производственного цеха.
Найдем значения наиболее раннего начала и выполнения работ проекта посредством алгоритма 1. Работу алгоритма изложим в виде последовательности выполняемых шагов.
| Шаг n
|
Действия выполняемые шагом
|
| 1
|
Объявление значений РНАЧ(v) и РВЫП(v), vÎV равным нулю.
Текущая вершина vk
=1.
|
| 2
|
Вершин предшествующей первой нет.
Значение РНАЧ(1)=РВЫП(1)+t(1).
|
| 3
|
Текущая вершина vk
=2.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(2)=МАКС{РВЫП(1),РНАЧ(2)} {РНАЧ(2) стало равным 0}
РВЫП(2)=РНАЧ(2)+t(2) {РВЫП(2) стало равным 5}.
|
| 3
|
Текущая вершина vk
=3.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(3)=МАКС{РВЫП(2),РНАЧ(3)} {РНАЧ(3) стало равным 5}
РВЫП(3)=РНАЧ(3)+t(3) {РВЫП(3) стало равным 8}.
|
| 3
|
Текущая вершина vk
=4.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(4)=МАКС{РВЫП(3),РНАЧ(4)} {РНАЧ(4) стало равным 8}
РВЫП(4)=РНАЧ(4)+t(4) {РВЫП(4) стало равным 18}.
|
| 3
|
Текущая вершина vk
=5.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(5)=МАКС{РВЫП(4),РНАЧ(5)} {РНАЧ(5) стало равным 18}
РВЫП(5)=РНАЧ(5)+t(5) {РВЫП(5) стало равным 23}.
|
| 3
|
Текущая вершина vk
=6.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(6)={РВЫП(2),РНАЧ(6)} {РНАЧ(6) стало равным 5}
РВЫП(6)=РНАЧ(6)+t(6) {РВЫП(6) стало равным 12}.
|
| 3
|
Текущая вершина vk
=7.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(7)=МАКС{РВЫП(6),РНАЧ(7)} {РНАЧ(7) стало равным 12}
РВЫП(7)=РНАЧ(7)+t(7) {РВЫП(7) стало равным 19}.
|
| 3
|
Текущая вершина vk
=8.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(8)=МАКС{РВЫП(6),РНАЧ(8)} {РНАЧ(8) стало равным 12}
РВЫП(8)=РНАЧ(8)+t(8) {РВЫП(8) стало равным 24}.
|
| 3
|
Текущая вершина vk
=9.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(9)=МАКС{РВЫП(7),РНАЧ(9)} {РНАЧ(9) стало равным 19}
РВЫП(9)=РНАЧ(9)+t(9) {РВЫП(9) стало равным 24}.
|
| 3
|
Текущая вершина vk
=10.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(10)=МАКС{РВЫП(8),РНАЧ(10)} {РНАЧ(10) стало равным 24}
РВЫП(10)=РНАЧ(10)+t(10) {РВЫП(10) стало равным 29}.
|
| 3
|
Текущая вершина vk
=11.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(11)=МАКС{РВЫП(9),РНАЧ(11)} {РНАЧ(11) стало равным 24}
РНАЧ(11)=МАКС{РВЫП(10),РНАЧ(10)}{РНАЧ(11) стало равным 29}
РВЫП(11)=РНАЧ(11)+t(11) {РВЫП(11) стало равным 29}.
|
| 3
|
Переход в Шаг 5.
|
| 5
|
Конец работы алгоритма, выдача значений наиболее раннего начала и выполнения работ.
|
Таблица результатов работы алгоритма.
| n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
| РНАЧ(v)
|
0
|
0
|
5
|
8
|
18
|
5
|
12
|
12
|
19
|
24
|
29
|
| РВЫП(v)
|
0
|
5
|
8
|
18
|
23
|
12
|
19
|
24
|
24
|
29
|
29
|
Получили, что минимальное время, требуемое для выполнения проекта равно Т=РВЫП(11), Т=29. Теперь найдем посредством алгоритма 2 значение времени наиболее позднего начала и выполнения работ. Работу алгоритма изложим в виде последовательности выполняемых шагов.
| Шаг n
|
Действия выполняемые шагом
|
| 1
|
Объявление значений ПВЫП(v), vÎV равным Т.
Текущая вершина vk
=11.
|
| 2
|
ПНАЧ(11)=ПВЫП(11)-t(11) {ПНАЧ(11) стало равным 29}.
|
| 3
|
ПВЫП(9)=МИН{ПВЫП(9),ПНАЧ(11)}{ПВЫП(9) стало равным 29}
ПВЫП(10)=МИН{ПВЫП(10),ПНАЧ(11)}{ПВЫП(10) стало равным 29}.
|
| 4
|
Текущая вершина vk
=10.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(10)=ПВЫП(10)-t(10) {ПНАЧ(10) стало равным 24}.
|
| 3
|
ПВЫП(8)=МИН{ПВЫП(8),ПНАЧ(10)}{ПВЫП(8) стало равным 24}
|
| 4
|
Текущая вершина vk
=9.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(9)=ПВЫП(9)-t(9) {ПНАЧ(9) стало равным 24}.
|
| 3
|
ПВЫП(7)=МИН{ПВЫП(7),ПНАЧ(9)}{ПВЫП(7) стало равным 24}.
|
| 4
|
Текущая вершина vk
=8.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(8)=ПВЫП(8)-t(8) {ПНАЧ(8) стало равным 12}.
|
| 3
|
ПВЫП(6)=МИН{ПВЫП(6),ПНАЧ(8)}{ПВЫП(6) стало равным 12}.
|
| 4
|
Текущая вершина vk
=7.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(7)=ПВЫП(7)-t(7) {ПНАЧ(7) стало равным 17}.
|
| 3
|
ПВЫП(6)=МИН{ПВЫП(6),ПНАЧ(7)}{ПВЫП(6) стало равным 12}.
|
| 4
|
Текущая вершина vk
=6.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(6)=ПВЫП(6)-t(6) {ПНАЧ(6) стало равным 5}.
|
| 3
|
ПВЫП(2)=МИН{ПВЫП(2),ПНАЧ(6)}{ПВЫП(2) стало равным 5}.
|
| 4
|
Текущая вершина vk
=5.
|
| 5
|
Переход в шаг 2.
|
| 2
|
ПНАЧ(5)=ПВЫП(5)-t(5) {ПНАЧ(5) стало равным 24}.
|
| 3
|
ПВЫП(4)=МИН{ПВЫП(4),ПНАЧ(5)}{ПВЫП(4) стало равным 24}.
|
| 4
|
Текущая вершина vk
=4.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(4)=ПВЫП(4)-t(4) {ПНАЧ(4) стало равным 14}.
|
| 3
|
ПВЫП(3)=МИН{ПВЫП(3),ПНАЧ(4)}{ПВЫП(3) стало равным 14}.
|
| 4
|
Текущая вершина vk
=3.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(3)=ПВЫП(3)-t(3) {ПНАЧ(3) стало равным 11}.
|
| 3
|
ПВЫП(2)=МИН{ПВЫП(2),ПНАЧ(3)}{ПВЫП(2) стало равным 5}.
|
| 4
|
Текущая вершина vk
=2.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(2)=ПВЫП(2)-t(2) {ПНАЧ(2) стало равным 0}.
|
| 3
|
ПВЫП(1)=МИН{ПВЫП(1),ПНАЧ(2)}{ПВЫП(1) стало равным 0}.
|
| 4
|
Текущая вершина vk
=1.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(1)=ПВЫП(1)-t(1) {ПНАЧ(1) стало равным 0}.
|
| 3
|
Переход в Шаг 4.
|
| 4
|
Переход в Шаг 6.
|
| 6
|
Конец работы алгоритма, выдача значений времени наиболее позднего начала и выполнения работ.
|
Дадим таблицу результатов работы алгоритма с результатами предыдущего алгоритма и сосчитаем резерв времени для каждой работы по формуле PE3EPB(v)=ПHAЧ(v)-PHAЧ(v) или РЕЗЕРВ(v)=ПВЫП(v)-РВЫП(v).
| Работы
|
РНАЧ
|
РВЫП
|
ПНАЧ
|
ПВЫП
|
Резерв
|
| 1
|
0
|
0
|
0
|
0
|
0
|
| 2
|
0
|
5
|
0
|
5
|
0
|
| 3
|
5
|
8
|
11
|
14
|
3
|
| 4
|
8
|
18
|
14
|
24
|
10
|
| 5
|
18
|
23
|
24
|
29
|
5
|
| 6
|
5
|
12
|
5
|
12
|
0
|
| 7
|
12
|
19
|
17
|
24
|
7
|
| 8
|
12
|
24
|
12
|
24
|
0
|
| 9
|
19
|
24
|
24
|
29
|
5
|
| 10
|
24
|
29
|
24
|
29
|
0
|
| 11
|
29
|
29
|
29
|
29
|
0
|
Из таблиы видно, что критическими работами являются 1, 2, 6, 8, 10, 11, которые и образуют в сети G критический путь. Расчеты выполнены при Т=29.
Пример 3: Проект водоснабжения и наружной канализации при застройки квартала по ул. Токарей-Синяева в г. Екатеринбурге.
| n
|
Наименование работы
|
Предшеству-ющие работы
|
Время вы-полнения t(vk
)
|
| 1.
|
Начало проекта (фиктивн. Работа)
|
Нет
|
0
|
| 2.
|
Разработка грунта экскаваторами с ковшом 0.5 м3
с погрузкой на автомобили-самосвалы.
|
1
|
16
|
| 3.
|
Зачистка дна и стенок с выкидкой грунта.
|
2
|
10
|
| 4.
|
Монтаж водопроводных колодцев
|
1
|
32
|
| 5.
|
Монтаж плит перекрытий из легкого бетона.
|
3
|
21
|
| 6.
|
Пробивка в бетонных стенах и полах отверстий.
|
5
|
5
|
| 7.
|
Оклейка плит рубероидом и гидроизолом на нефтебитуме в 1 слой.
|
4,5
|
14
|
| 8.
|
Заделка сальников при проходе труб через фундаменты или стены подвалов.
|
5
|
10
|
| 9.
|
Монтаж скоб.
|
6
|
7
|
| 10.
|
Устройство стяжек цементных.
|
9
|
5
|
| 11.
|
Конец проекта. (фиктивн. Работа)
|
7,8,10
|
0
|
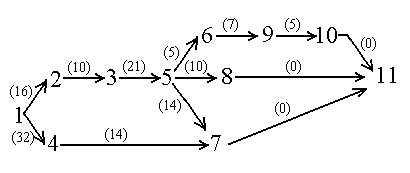
Рис 3. Проект водоснабжения и наружной канализации при застройки квартала по ул. Токарей-Синяева в г. Екатеринбурге.
Найдем значения наиболее раннего начала и выполнения работ проекта посредством алгоритма 1. Работу алгоритма изложим в виде последовательности выполняемых шагов.
| Шаг n
|
Действия выполняемые шагом
|
| 1
|
Объявление значений РНАЧ(v) и РВЫП(v), vÎV равным нулю.
Текущая вершина vk
=1.
|
| 2
|
Вершин предшествующей первой нет.
Значение РНАЧ(1)=РВЫП(1)+t(1).
|
| 3
|
Текущая вершина vk
=2.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(2)=МАКС{РВЫП(1),РНАЧ(2)}{РНАЧ(2) стало равным 0}
РВЫП(2)=РНАЧ(2)+t(2) {РВЫП(2) стало равным 16}.
|
| 3
|
Текущая вершина vk
=3.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(3)=МАКС{РВЫП(2),РНАЧ(3)}{РНАЧ(2) стало равным 16}
РВЫП(3)=РНАЧ(3)+t(3) {РВЫП(3) стало равным 26}.
|
| 3
|
Текущая вершина vk
=4.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(4)=МАКС{РВЫП(1),РНАЧ(4)}{РНАЧ(4) стало равным 0}
РВЫП(4)=РНАЧ(4)+t(4) {РВЫП(4) стало равным 32}.
|
| 3
|
Текущая вершина vk
=5.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(5)=МАКС{РВЫП(3),РНАЧ(5)}{РНАЧ(5) стало равным 26}
РВЫП(5)=РНАЧ(5)+t(5) {РВЫП(5) стало равным 47}.
|
| 3
|
Текущая вершина vk
=6.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(6)=МАКС{РВЫП(5),РНАЧ(6)}{РНАЧ(6) стало равным 47}
РВЫП(6)=РНАЧ(6)+t(6) {РВЫП(6) стало равным 52}.
|
| 3
|
Текущая вершина vk
=7.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(7)=МАКС{РВЫП(5),РНАЧ(7)}{РНАЧ(7) стало равным 47
РВЫП(7)=РНАЧ(7)+t(7) {РВЫП(7) стало равным 61}.
|
| 3
|
Текущая вершина vk
=8.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(8)=МАКС{РВЫП(5),РНАЧ(8)}{РНАЧ(8) стало равным 47}
РВЫП(8)=РНАЧ(8)+t(8) {РВЫП(8) стало равным 57}.
|
| 3
|
Текущая вершина vk
=9.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(9)=МАКС{РВЫП(6),РНАЧ(9)}{РНАЧ(9) стало равным 52}
РВЫП(9)=РНАЧ(9)+t(9) {РВЫП(9) стало равным }.
|
| 3
|
Текущая вершина vk
=10.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(10)=МАКС{РВЫП(9),РНАЧ(10)}{РНАЧ(10) стало равным 59}
РВЫП(10)=РНАЧ(10)+t(10) {РВЫП(10) стало равным 64}.
|
| 3
|
Текущая вершина vk
=11.
|
| 4
|
Переход в Шаг 2.
|
| 2
|
РНАЧ(11)=МАКС{РВЫП(7),РНАЧ(11)}{РНАЧ(11) стало равным 61}
РНАЧ(11)=МАКС{РВЫП(8),РНАЧ(11)}{РНАЧ(11) стало рвным 61}
РНАЧ(11)=МАКС{РВЫП(10),РНАЧ(11)}{РНАЧ(11) стало равным 64}
РВЫП(11)=РНАЧ(11)+t(11) {РВЫП(11) стало равным 64}.
|
| 3
|
Переход в Шаг 5.
|
| 5
|
Конец работы алгоритма, выдача значений наиболее раннего начала и выполнения работ.
|
Таблица результатов работы алгоритма.
| n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
| РНАЧ(v)
|
0
|
0
|
16
|
0
|
26
|
47
|
47
|
47
|
52
|
59
|
64
|
| РВЫП(v)
|
0
|
16
|
26
|
32
|
47
|
52
|
61
|
57
|
59
|
64
|
64
|
Получили, что минимальное время, требуемое для выполнения проекта равно Т=РВЫП(11), Т=64. Теперь найдем посредством алгоритма 2 значение времени наиболее позднего начала и выполнения работ. Работу алгоритма изложим в виде последовательности выполняемых шагов.
| Шаг n
|
Действия выполняемые шагом
|
| 1
|
Объявление значений ПВЫП(v), vÎV равным Т.
Текущая вершина vk
=11.
|
| 2
|
ПНАЧ(11)=ПВЫП(11)-t(11) {ПНАЧ(11) стало равным 64}.
|
| 3
|
ПВЫП(7)=МИН{ПВЫП(7),ПНАЧ(11)}{ПВЫП(7) стало равным 64}
ПВЫП(8)=МИН{ПВЫП(8),ПНАЧ(11)}{ПВЫП(8) стало равным 64}
ПВЫП(10)=МИН{ПВЫП(10),ПНАЧ(10)}{ПВЫП(9) стало равным 64}.
|
| 4
|
Текущая вершина vk
=10.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(10)=ПВЫП(10)-t(10) {ПНАЧ(10) стало равным 59}.
|
| 3
|
ПВЫП(9)=МИН{ПВЫП(9),ПНАЧ(10)} {ПВЫП(9) стало равным 59}.
|
| 4
|
Текущая вершина vk
=9.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(9)=ПВЫП(9)-t(9) {ПНАЧ(9) стало ранвым 52}.
|
| 3
|
ПВЫП(6)=МИН{ПВЫП(6),ПНАЧ(9)}{ПВЫП(6) стало равным 52}.
|
| 4
|
Текущая вершина vk
=8.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(8)=ПВЫП(8)-t(8) {ПНАЧ(8) стало равным 54}.
|
| 3
|
ПВЫП(5)=МИН{ПВЫП(5),ПНАЧ(8)}{ПВЫП(5) стало равным 54}.
|
| 4
|
Текущая вершина vk
=7.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(7)=ПВЫП(7)-t(7) {ПНАЧ(7) стало равным 50}.
|
| 3
|
ПВЫП(5)=МИН{ПВЫП(5),ПНАЧ(7)}{ПВЫП(5) стало равным 50}
ПВЫП(4)=МИН{ПВЫП(4),ПНАЧ(7)}{ПВЫП(4) стало равным 50}.
|
| 4
|
Текущая вершина vk
=6.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(6)=ПВЫП(6)-t(6) {ПНАЧ(6) стало равным 47}.
|
| 3
|
ПВЫП(5)=МИН{ПВЫП(5),ПНАЧ(6)}{ПВЫП(5) стало равным 47}.
|
| 4
|
Текущая вершина vk
=5.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(5)=ПВЫП(5)-t(5) {ПНАЧ(5) стало равным 26}.
|
| 3
|
ПВЫП(3)=МИН{ПВЫП(3),ПНАЧ(5)}{ПВЫП(3) стало равным 26}.
|
| 4
|
Текущая вершина vk
=4.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(4)=ПВЫП(4)-t(4) {ПНАЧ(4) стало равным 18}.
|
| 3
|
ПВЫП(1)=МИН{ПВЫП(1),ПНАЧ(4)}{ПВЫП(1) стало равным 18}.
|
| 4
|
Текущая вершина vk
=3.
|
| 5
|
Переходв Шаг 2.
|
| 2
|
ПНАЧ(3)=ПВЫП(3)-t(3) {ПНАЧ(3) стало равным 16}.
|
| 3
|
ПВЫП(2)=МИН{ПВЫП(2),ПНАЧ(3)}{ПВЫП(2) стало равным 16}.
|
| 4
|
Текущая вершина vk
=2.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(2)=ПВЫП(2)-t(2) {ПНАЧ(2) стало равным 0}.
|
| 3
|
ПВЫП(1)=МИН{ПВЫП(1),ПНАЧ(2)}{ПВЫП(1) стало равным 0}.
|
| 4
|
Текущая вершина vk
=1.
|
| 5
|
Переход в Шаг 2.
|
| 2
|
ПНАЧ(1)=ПВЫП(1)-t(1) {ПНАЧ(1) стало равным 0}.
|
| 3
|
Переход в Шаг 4.
|
| 4
|
Переход в Шаг 6.
|
| 6
|
Конец работы алгоритма, выдача значений времени наиболее позднего начала и выполнения работ.
|
Дадим таблицу результатов работы алгоритма с результатами предыдущего алгоритма и сосчитаем резерв времени для каждой работы по формуле PE3EPB(v)=ПHAЧ(v)-PHAЧ(v) или РЕЗЕРВ(v)=ПВЫП(v)-РВЫП(v).
| Работы
|
РНАЧ
|
РВЫП
|
ПНАЧ
|
ПВЫП
|
Резерв
|
| 1
|
0
|
0
|
0
|
0
|
0
|
| 2
|
0
|
16
|
0
|
16
|
0
|
| 3
|
16
|
26
|
16
|
26
|
0
|
| 4
|
0
|
32
|
18
|
50
|
32
|
| 5
|
26
|
47
|
26
|
47
|
0
|
| 6
|
47
|
52
|
47
|
52
|
0
|
| 7
|
47
|
61
|
50
|
64
|
3
|
| 8
|
47
|
57
|
54
|
64
|
10
|
| 9
|
52
|
59
|
52
|
59
|
0
|
| 10
|
59
|
64
|
59
|
64
|
0
|
| 11
|
59
|
64
|
64
|
64
|
0
|
Из таблицы видно, что критическими работами являются 1, 2, 3, 5, 6, 9, 10, 11, которые и образуют в сети G критический путь. Расчеты выполнены при Т=64.
Литература:
1. Асанов М. О. «Дискретная оптимизация», УралНАУКА, Екатеринбург 1998.
|