| ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
“СИБИРСКАЯ АКАДЕМИЯ ГОСУДАРСТВЕННОЙ СЛУЖБЫ”
ИНСТИТУТ ПЕРЕПОДГОТОВКИ СПЕЦИАЛИСТОВ
Налогооблажения и учета
(кафедра)
Статистика
(дисциплина)
Письменное контрольное задание
для студентов и слушателей дистационного обучения
Студент
Группа
Дата
Подпись
Преподаватель
Дата
Оценка
Подпись
г. Улан-Удэ 2007г.
Задание 1.
1. По данным таблицы 1 произведите группировку 30 коммерческих банков по величине прибыли, образовав 6 групп с заданными интервалами:
а) до 100, б) 100-200, в) 200-300, г) 300-500, д) 500-700, е) 700 и более.
Таблица 1.
Список крупнейших банков России по размеру капитала, млрд. руб.
| Ранг
|
Название банка
|
Город
|
Кредитные вложения
|
Объем вложений в ценные бумаги
|
Прибыль
|
| 1
|
Национальный резервный банк
|
Москва
|
2439
|
4994
|
645
|
| 2
|
ОНЭКСИМбанк
|
Москва
|
15581
|
1547
|
266
|
| 3
|
Международная финансовая компания
|
Москва
|
7612
|
510
|
512
|
| 4
|
Инкомбанк
|
Москва
|
9432
|
2975
|
744
|
| 5
|
ТОКОбанк
|
Москва
|
4318
|
852
|
282
|
| 6
|
Империал
|
Москва
|
5398
|
654
|
429
|
| 7
|
Автобанк
|
Москва
|
3900
|
1684
|
913
|
| 8
|
Международный московский банк
|
Москва
|
5077
|
1173
|
290
|
| 9
|
СБС
|
Москва
|
3256
|
4556
|
175
|
| 10
|
Международный промышленный банк
|
Москва
|
3419
|
597
|
18
|
| 11
|
Башкредитбанк
|
Уфа
|
778
|
551
|
417
|
| 12
|
Российский кредит
|
Москва
|
6019
|
1429
|
367
|
| 13
|
Мосбизнесбанк
|
Москва
|
4899
|
1837
|
481
|
| 14
|
МЕНАТЕП
|
Москва
|
9035
|
786
|
146
|
| 15
|
Московский индустриальный банк
|
Москва
|
1742
|
469
|
365
|
| 16
|
Промстройбанк России
|
Москва
|
2890
|
1115
|
239
|
| 17
|
Промышленно-строительный банк
|
Санкт-Петербург
|
1600
|
991
|
306
|
| 18
|
Уникомбанк
|
Москва
|
1605
|
439
|
57
|
| 19
|
Газпромбанк
|
Москва
|
1764
|
673
|
265
|
| 20
|
Возрождение
|
Москва
|
2236
|
532
|
158
|
| 21
|
Мост-банк
|
Москва
|
4423
|
2020
|
129
|
| 22
|
Московский деловой мир
|
Москва
|
981
|
543
|
340
|
| 23
|
Межкомбанк
|
Москва
|
2004
|
1040
|
167
|
| 24
|
Нефтехимбанк
|
Москва
|
1216
|
838
|
41
|
| 25
|
Ситибанк
|
Москва
|
1490
|
1041
|
258
|
| 26
|
Ланта-банк
|
Москва
|
545
|
44
|
35
|
| 27
|
Альба-альянс
|
Москва
|
147
|
426
|
298
|
| 28
|
ИнтерТЭКбанк
|
Москва
|
1039
|
167
|
57
|
| 29
|
Мосстройэкономбанк
|
Москва
|
1091
|
27
|
221
|
| 30
|
Росэстбанк
|
Тольятти
|
511
|
195
|
243
|
По каждой группе рассчитайте:
- средний размер прибыли;
- средний размер кредитных вложений;
- средний объем вложений в ценные бумаги.
Результаты оформите в аналитической таблице. Сделайте выводы.
2. По данным таблицы определите модальное и медианное значение прибыли.
3. По показателю размер кредитных вложений рассчитайте:
- общую дисперсию по правилу сложения дисперсий;
- эмпирическое корреляционное отношение. Сделайте выводы.
Разработаем аналитическую таблицу взаимосвязи между кредитными вложения, объемом вложений в ценные бумаги и прибылью:
Группировка банков по величине прибыли
| Группировка банков по величине прибыли
|
Число банков
|
Прибыль
|
Кредитные вложения
|
Объем вложений в ценные бумаги
|
| Всего
|
В среднем на один банк
|
Всего
|
В среднем на один банк
|
Всего
|
В среднем на один банк
|
| До 100
100-200
200-300
300-500
500-700
700 и более
|
5
5
9
7
2
2
|
208
775
2362
2705
1157
1657
|
41,6
155
262,4
386,4
578,5
828,5
|
7824
20954
32869
21417
10051
13332
|
1564,8
4190,8
3652,1
3059,6
5025,5
6666
|
2085
8934
7049
6474
5504
4659
|
417
1786,8
783,2
924,9
2752
232,5
|
| Итого
|
30
|
8864
|
295,5
|
106447
|
3548,2
|
34705
|
1156,8
|
Прибыль, кредитные вложения и объем вложений в ценные бумаги прямо зависят между собой. В увеличением прибыли возрастают кредитные вложения, но при высокой прибыли объем вложений в ценные бумаги снижается о чем подтверждают средние показатели последней группы.
2. Определим моду по формуле:
М0 = х0 +i0 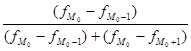 , ,
где х0 – нижняя граница модального интервала;
i0 - величина модального интервала;
fM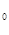 - частота модального интервала; - частота модального интервала;
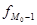 - частота интервала, предшествующего модальному; - частота интервала, предшествующего модальному;
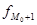 - частота интервала, следующего за модальным. - частота интервала, следующего за модальным.
Интервал с границами 200-300 в данном распределение будет модальным, так как он имеет наибольшую частоту.
М0 = 300 +200 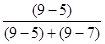 =433,33млрд. руб., =433,33млрд. руб.,
Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половины суммы накопленных частот (в нашем случае 15).
| Интервал
|
Накопленная частота
|
| До 100
100-200
200-300
300-500
500-700
700 и более
|
5
10
19
26
28
30
|
Мы определили, что медианным является интервал с границами 200-300, теперь определим медиану по формуле:
Me = x0 + i0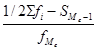
где х0 – нижняя граница медианного интервала;
i0 - величина медианного интервала;
fM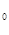 - частота медианного интервала; - частота медианного интервала;
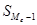 - накопленная частота интервала, предшествующего медианному. - накопленная частота интервала, предшествующего медианному.
Me =300 +200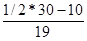 = 352,63 млрд. руб. = 352,63 млрд. руб.
На основе полученных значений структурных средних можно заключить, что больше всего банков у которых прибыль составляет 433,3 млрд. руб, а серединное значение прибыли приходится на 362,63 млрд. руб. Так как 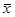 = 295,47, то М0>Ме> = 295,47, то М0>Ме>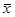 значит имеет место левосторонняя ассиметрия распределения банков по уровню прибыли. значит имеет место левосторонняя ассиметрия распределения банков по уровню прибыли.
3. Рассчитаем общую дисперсию по правилу сложения:
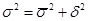 , ,
где 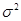 - общая дисперсия, - общая дисперсия,
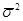 - средняя из внутригрупповых дисперсий; - средняя из внутригрупповых дисперсий;
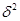 - межгрупповая дисперсия. - межгрупповая дисперсия.
Рассчитаем групповые средние: 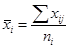
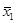 = 1564,8 = 1564,8 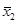 =4190,8 =4190,8
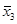 =3652,1 =3652,1  =3059,6 =3059,6
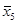 =5025,5 =5025,5 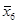 =6666 =6666
Рассчитываем общую среднюю: 
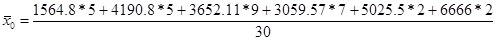 = 3548,23 = 3548,23
Рассчитываем внутригрупповые дисперсии: 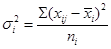
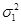 =975558,6 =975558,6 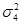 =4428905 =4428905
 = 6599476 = 6599476 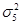 = 6689982 = 6689982
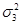 =20256031 =20256031 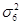 =7650756 =7650756
Вычисляем среднюю из внутригрупповых дисперсий:
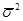 = = = 9328775,4 = 9328775,4
Определяем межгрупповую дисперсию: 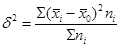
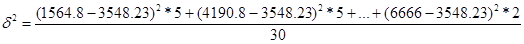 =1576950 =1576950
Находим общую дисперсию по правилу сложения
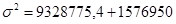 = 10905725,4 = 10905725,4
Рассчитываем эмпирическое корреляционное отношение
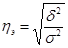 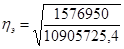 = 0,38 = 0,38
Полученная величина эмпирического корреляционного отношения свидетельствует о том, что фактор положенный в основание группировки (прибыль) средне влияет на размер кредитных вложений.
Задание 2.
Имеются следующие данные по региону за 1999 год (условные):
1. На начало года численность трудоспособного населения рабочего возраста составила 320 т. чел., работающих лиц пенсионного возраста – 15 т. чел., работающих подростков до 16 лет – 5 т. чел.
2. В течение года вступило в рабочий возраст 20 т. чел., 0,5 т. чел. из них нетрудоспособны; прибыло из других районов трудоспособных лиц 2,5 т. человек. Выбыло по естественным причинам 15 т. чел.; в другие районы – 10 т. чел. трудоспособного возраста.
Определите:
Численность трудовых ресурсов на начало и конец года.
Абсолютные и относительные показатели воспроизводства трудовых ресурсов.
Численность трудовых ресурсов на начало года.
ТРн. г. = 320 + 15 + 5 = 340 тыс. чел.
Численность трудовых ресурсов на начало конец года
ТРк. г. = 340 +20 - 0,5 +2,5 - 15 - 10 = 337 тыс. чел.
Среднегодовая численность трудовых ресурсов.
 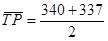 = 338,5 тыс. чел. = 338,5 тыс. чел.
2. Абсолютные показатели воспроизводства трудовых ресурсов:
а) Естественное пополнение трудовых ресурсов (Пе) складывается за счет перехода, подрастающего поколения в трудоспособный возраст.
Пе = 20 - 0,5 = 19,5 тыс. чел.
б) Естественное выбытие трудовых ресурсов (Ве) формируется из лиц вышедших за пределы трудоспособного возраста, перешедших на пенсию на льготных условиях и лиц рабочего возраста умерших в течение этого периода.
Ве = 15 тыс. чел.
в) Абсолютный естественный прирост потенциала трудовых ресурсов (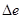 ). ).
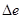 = Пе –Ве = Пе –Ве 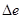 = 19,5 – 15 = 4,5тыс. чел. = 19,5 – 15 = 4,5тыс. чел.
Относительные показатели воспроизводства трудовых ресурсов:
а) Коэффициент естественного пополнения трудовых ресурсов.
КПе = 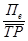 *1000. КПе = *1000. КПе = 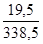 *1000 = 57,61‰ *1000 = 57,61‰
б) Коэффициент естественного выбытия трудовых ресурсов.
КВе = 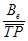 *1000. КВе = *1000. КВе = 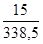 *1000 = 44,31‰ *1000 = 44,31‰
в) Коэффициент естественного прироста трудовых ресурсов
К е = е = 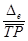 *1000. К *1000. К е = е =  *1000 = 13,29‰ *1000 = 13,29‰
Задание 3.
Имеются следующие данные по предприятию:
| Номер цеха
|
Затраты на производство продукции, тыс. р. Отчетный период
|
Изменение себестоимости единицы продукции в отчетном периоде по сравнению с базисным,%
|
| 1
2
3
4
|
1200
1800
2800
2500
|
+5,0
-3,5
-3,0
-
|
Определите в целом по предприятию:
Изменение себестоимости единицы продукции.
Изменение общих затрат на производство продукции, если физический объем производства увеличился на 8%.
Сумму экономии в связи с изменением себестоимости единицы продукции.
1. Так как нам известны данные себестоимости за отчетный период и изменение себестоимости в отчетном периоде по сравнению с базисным в%, то используем сводный индекс себестоимости в средней гармонической форме: Iz = 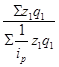
Iz = 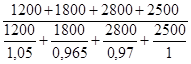 = =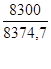 = 0,9887 = 0,9887
Cебестоимость единицы продукции по данным цехам в среднем снизилась на 1,13%.
2. Изменение общих затрат на производство продукции определим по формуле:
Izq = Iz* Iq
Izq = 0,9887 * 1,08 = 1,068
Общие затраты на производство продукции в среднем увеличились на 6,8%.
3. Е = 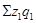 - -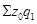 Е = 8300-8394,74 = - 94,7 тыс. руб. Е = 8300-8394,74 = - 94,7 тыс. руб.
В связи со снижением себестоимости единицы продукции по данным цехам в среднем на 1,13%, сумма экономии составила 94,7 тыс. руб.
Задание 4.
Имеются следующие данные по 3 рынкам города о продаже яблок:
| Номер рынка
|
Продано яблок, тыс. р.
|
Цена 1 кг. яблок, р.
|
| июнь
|
август
|
июнь
|
август
|
| 1
2
3
|
2500
1000
1600
|
3000
1200
2000
|
35
32
34
|
30
25
30
|
Определите изменение средней цены на яблоки по 3 рынкам города всего и в том числе за счет:
- изменения цены на каждом рынке города;
- изменения структуры продаж.
Изменение средней цены на яблоки по 3 рынкам города всего можно определить по формуле индекса переменного состава: Iп. с. = 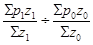
Iп. с. =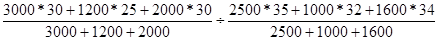 = 0,85144 = 0,85144
Средние цены на яблоки по 3 рынкам города в августе по сравнению с июнем снизились на 14,86%.
Изменения цены на каждом рынке города можно определить по формуле индекса фиксированного состава:
Iф. с. = 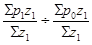
Iф. с. =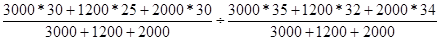 =0,85145 =0,85145
Цены на каждом рынке города в августе по сравнению с июнем снизились на 14,85%.
Изменение структуры продаж можно определить по формуле индекса структурных сдвигов: Iс. с. = 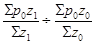
Iс. с. =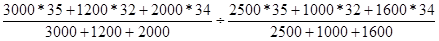 =0,99997 =0,99997
Структура продаж яблок в августе по сравнению с июнем снизилась на 0,01%.
Задание 5.
Имеются следующие данные об изменении физического объема ВВП за период с 1990 г. (1990=100%):
| Показатели
|
1991
|
1992
|
1993
|
1994
|
1995
|
| Индекс физического объема
|
95
|
81,2
|
74,2
|
64,7
|
62,2
|
Определите, как в среднем ежегодно изменяется физический объем ВВП в указанном периоде. Исчислите цепные темпы изменения ВВП (в сопоставимых ценах).
Определим средний абсолютный прирост по формуле:
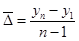 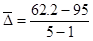 = - 8,2 = - 8,2
В среднем ежегодно индекс физического объема ВВП снижался на 8,2%.
Динамика физического объема ВВП за 1990 - 1995гг.
| Годы
|
Темпы роста(цепные),%
|
Темпы прироста (цепные),%
|
| 1991
1992
1993
1994
1995
|
-
81,2/95*100%=85,47
74,2/81,2*100%=91,38
64,7/74,2*100%=90,84
62,2/64,7*100%=96,14
|
-
85,47 - 100%= - 14,53
91,38 - 100%= - 8,62
90,84 - 100%= - 9,16
96,14 – 100% = 3,86
|
Задание 6.
Имеются следующие данные о грузообороте предприятий транспорта и перевозке грузов предприятиями транспорта за 1986-1997 гг. в одном из регионов:
| Годы
|
Грузооборот предприятий транспорта, млрд. ткм., - y
|
Перевозка грузов предприятиями транспорта, млн. т. - x
|
| 1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
|
280
304
270
305
301
307
296
299
296
269
310
286
|
285
283
321
302
316
359
334
348
333
358
305
297
|
Для изучения связи между этими рядами произведите:
· выравнивание рядов динамики по уравнению прямой;
· вычислите коэффициент корреляции;
· рассчитайте прогнозное значение грузооборота на 3 года вперед.
Произведем выравнивание рядов динамики по уравнению прямой. Для чего построим систему нормальных уравнений для нахождения параметров уравнения регрессии.
yt = a0 + a1*t xt = b0 + b1*t
na0 + a1∑t = ∑y nb0 + b1∑t = ∑x
a0∑t + a1∑t2 = ∑yt b0∑t + b1∑t2 = ∑xt
| t
|
t2
|
y
|
x
|
yt
|
xt
|
xy
|
| 1
2
3
4
5
6
7
8
9
10
11
12
|
1
4
9
16
25
36
49
64
81
100
121
144
|
280
304
270
305
301
307
296
299
296
269
310
286
|
285
283
321
302
316
359
334
348
333
358
305
297
|
280
608
810
1220
1505
1842
2072
2392
2664
2690
3410
3432
|
285
566
963
1208
1580
2154
2338
2784
2997
3580
3355
3564
|
79800
86032
86670
92110
95116
110213
98864
104052
98568
96302
94550
84942
|
| 78
|
650
|
3523
|
3841
|
22925
|
25374
|
1127219
|
12a0 + 78a1 = 3523 12b0 + 78b1 = 3841
78a0 + 650a1 = 22925 78 b0 + 650 b1 = 25374
yt = 292.42 + 0.178*t xt = 301.56 + 2.85*t
2. Определим коэффициент корреляции по формуле:
r = 
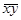 = 1127219 / 12 = 93934,92 = 1127219 / 12 = 93934,92 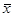 = 3841 / 12 = 320.08 = 3841 / 12 = 320.08 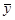 = 3523 / 12 = 293.58 = 3523 / 12 = 293.58
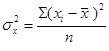 = 650.24 = 650.24  = 182.24 = 182.24
r = 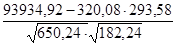 = - 0.1052 = - 0.1052
Коэффициент корреляции говорит о слабой обратной связи между рядами динамики.
3. Рассчитаем прогнозные значения грузооборота на 3 года вперед по уравнению регрессии: yt = 292.42 + 0.178*t
Прогнозное значение на 1998г. yt = 292.42 + 0.178*13 = 294,73
на 1999г. yt = 292.42 + 0.178*14 = 294,91
на 2000г. yt = 292.42 + 0.178*15 = 295,09
Задание 7.
Имеются следующие данные по группе предприятий района:
| Предприятие
|
Стоимость основных производственных фондов, млрд. руб.
|
Фондоотдача (выпуск продукции на 1 руб. основных производственных фондов), руб.
|
Производительность труда рабочих, тыс. р.
|
Фондовоо руженность труда рабочих, тыс. р.
|
| 1
2
3
|
21,0
12,5
17,4
|
1,2
1,0
0,9
|
11,0
7,1
6,8
|
9,5
7,3
8,4
|
Определите по предприятиям района среднее значение:
· стоимости основных производственных фондов на одно предприятие;
· фондоотдачи;
· производительности труда;
· фондовооруженности труда.
1. 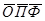 = = 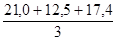 = 16,97 млн. руб. = 16,97 млн. руб.
2. 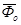 = =  = 1,03 руб. = 1,03 руб.
3. 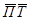 = = 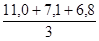 = 8,3 тыс. руб. = 8,3 тыс. руб.
4. 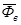 = = 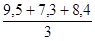 = 8,4 тыс. руб. = 8,4 тыс. руб.
По группе предприятий района среднее значение стоимости основных производственных фондов на одно предприятие составляет 16,97 млн. руб., среднее значение фондоотдачи – 1,03руб., среднее значение производительности труда рабочих – 8,3 тыс. руб., среднее значение фондовооруженности труда рабочих – 8,4 тыс. руб.
Задание 8.
С целью определения средних затрат времени при поездках на работу населением города планируется выборочное наблюдение на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 ошибка выборочной средней не превышала 1 мин. При среднем квадратическом отклонение 15 мин.
Рассчитаем необходимый объем выборки по формуле:
 => n= => n=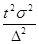 при Ф(t) = 0,954 t = 2 при Ф(t) = 0,954 t = 2
Подставим исходные данные и получим:
n=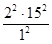 = 900. = 900.
Таким образом, численность выборки составляет 900.
Задание 9.
Имеются следующие данные о среднедушевых доходах и расходах на продукты питания по совокупности семей в базисном и отчетном периодах:
| Показатель
|
Базисный период
|
Отчетный период
|
| Среднедушевой доход за год, тыс. р. - х
Расходы на продукты питания, тыс. р. - у
|
40
28
|
45
33,5
|
Определите коэффициент эластичности расходов на питание от роста дохода.
Предположим наличие линейной зависимости между рассматриваемыми признаками.
Для расчета параметров уравнения регрессии а и b решим систему нормальных уравнений.
na + b∑x = ∑y
a∑x + b∑x2 = ∑yx
2a + b(40+45) = 28+33,5
85 a + (402 + 452) = 40*28+45*33,5 => а = - 16 b = 1,1,
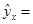 -16 + 1,1х -16 + 1,1х
Определим коэффициент эластичности по формуле:
Э = b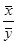 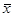 = (40+45) /2 =42,5 = (40+45) /2 =42,5 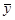 = (28+33,5) /2= 30,75 = (28+33,5) /2= 30,75
Э = 1,1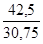 = 1,52 = 1,52
Это значит, что при увеличении среднедушевого дохода на 1% расходы на продукты питания увеличатся на 1,52%.
Задание 10.
Номинальные среднедушевые доходы населения одного из регионов составили в текущем периоде 2500 руб., за предыдущий период – 2100 руб.; доля налоговых платежей увеличилась с 20 до 22% соответственно. Цены выросли на 25%.
Как изменились реальные доходы населения.
| Показатели
|
Базисный период
|
Отчетный период
|
| Номинальные среднедушевые доходы
Доля налоговых платежей
Инфляция
Реальные доходы
|
2100
2100*20%=420
1
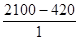 =1680 =1680
|
2500
2500*22%=550
1,25
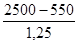 =1560 =1560
|
Реальные доходы определяются вычитанием из номинальных среднедушевых доходов суммы налоговых платежей скорректированным на индекс потребительских цен (инфляция).
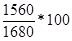 % = 92,86% % = 92,86%
Реальные доходы населения в текущем периоде по сравнению с предыдущим периодом снизились на 7,14%.
|