| Реферат
Закон Ома. История открытия. Различные виды закона Ома.
Содержание.
1. Общий вид закона Ома.
2. История открытия закона Ома, краткая биография ученого.
3. Виды законов Ома.
Закон Ома устанавливает зависимость между силой тока I
в проводнике и разностью потенциалов (напряжением) U
между двумя фиксированными точками (сечениями) этого проводника:
 (1)
 Коэффициент пропорциональности R
, зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.
Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.
Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.
В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.
В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания "Наиболее оптимальный вариант преподавания геометрии в подготовительных классах". Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием "Предварительное сообщение о законе, по которому металлы проводят контактное электричество". Статья была опубликована в 1825 году в "Журнале физики и химии", издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.
Появляется в свет его знаменитая статья "Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера", вышедшая в 1826 году в "Журнале физики и химии".
В мае 1827 года "Теоретические исследования электрических цепей" объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: "Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение".
В 1829 году появляется его статья "Экспериментальное исследование работы электромагнитного мультипликатора", в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.
В 1830 году появляется новое исследование Ома "Попытка создания приближенной теории униполярной проводимости".
Только в 1841 году работа Ома была переведена на английский язык, в 1847 году - на итальянский, в 1860 году - на французский.
16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.
Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.
В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления - 1 Ом.
В общем случае зависимость между I
и U
нелинейна, однако на практике всегда можно в определенном интервале напряжений считать её линейной и применять закон Ома; для металлов и их сплавов этот интервал практически неограничен.
Закон Ома в форме (1) справедлив для участков цепи, не содержащих источников ЭДС. При наличии таких источников (аккумуляторов, термопар, генераторов и т. д.) закон Ома имеет вид:
 (2)
где  — ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид:
 (3)
где  - полное сопротивление цепи, равное сумме внешнего сопротивления r
и внутреннего сопротивления  источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.
Закон Ома можно записать в дифференциальной форме, связывающей в каждой точке проводника плотность тока j
с полной напряжённостью электрического поля. Потенциальное. электрическое поле напряжённости Е
, создаваемое в проводниках микроскопическими зарядами (электронами, ионами) самих проводников, не может поддерживать стационарное движение свободных зарядов (ток), т. к. работа этого поля на замкнутом пути равна нулю. Ток поддерживается неэлектростатическими силами различного происхождения (индукционного, химического, теплового и т.д.), которые действуют в источниках ЭДС и которые можно представить в виде некоторого эквивалентного непотенциального поля с напряженностью E
СТ,
называемого сторонним. Полная напряженность поля, действующего внутри проводника на заряды, в общем случае равна E
+
E
СТ
.
Соответственно, дифференциальный закон Ома имеет вид:
 или  , (4)
где  - удельное сопротивление материала проводника, а  - его удельная электропроводность.
Закон Ома в комплексной форме справедлив также для синусоидальных квазистационарных токов:
 (5)
где z
-
полное комплексное сопротивление:  , r
– активное сопротивление, а x
- реактивное сопротивление цепи. При наличии индуктивности L
и емкости С
в цепи квазистационарного тока частоты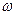 
 .
Существует несколько видов закона Ома.
Закон Ома для однородного участка цепи
(не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:
Закон Ома для замкнутой цепи:
сила тока в замкнутой цепи равна отношению ЭДС источника тока к суммарному сопротивлению всей цепи:
где R
- сопротивление внешней цепи, r
– внутреннее сопротивление источника тока.
R
- +
 
R
Закон Ома для неоднородного участка цепи
(участка цепи с источником тока):
 
R
 ; 
где  - разность потенциалов на концах участка цепи,  - ЭДС источника тока, входящего в участок.
Способность вещества проводить ток характеризуется его удельным сопротивлением  либо проводимостью  . Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
 ; 
где  — удельное сопротивление при 0°С, t
— температура по шкале Цельсия, а — коэффициент, численно равный примерно 1/273. Переходя к абсолютной температуре, получаем
При низких температурах наблюдаются отступления от этой закономерности. В большинстве случаев зависимость  от T
следует кривой 1
на рисунке.
Величина остаточного сопротивления  в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига  заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле  .
У большой группы металлов и сплавов при температуре порядка нескольких градусов Кельвина сопротивление скачком обращается в нуль (кривая 2
на рисунке). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг - Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температура Тк
,
при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поля HK
,
разрушающего сверхпроводимость, равна нулю при Т
= Тк
и растет с понижением температуры.
Полное теоретическое объяснение сверхпроводимости было дано в 1958 г. советским физиком Н. Н. Боголюбовым и его сотрудниками.
Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволоку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с точностью порядка нескольких сотых градуса как низкие, так и высокие температуры.
Список использованной литературы:
Прохоров А. М. Физический энциклопедический словарь,
М., 1983
Дорфман Я. Г. Всемирная история физики
. М., 1979
Ом Г. Определение закона, по которому металлы проводят контактное электричество
. – В кн.: Классики физической науки. М., 1989
Роджерс Э. Физика для любознательных
, т. 3. М., 1971
Орир Дж. Физика
, т. 2. М., 1981
Джанколи Д. Физика
, т. 2. М., 1989
|