| (2011 - 1 / 18)

Единый государственный экзамен по МАТЕМАТИКЕ
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2011 года по математике
подготовлен Федеральным государственным научным учреждением
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»
(2011 - 2 / 18)
Пояснения к демонстрационному варианту контрольных измерительных материалов для ЕГЭ 2011 года по МАТЕМАТИКЕ
Демонстрационный вариант ЕГЭ по математике 2011 года разработан по заданию Федеральной службы по надзору в сфере образования и науки Российской Федерации.
Демонстрационный вариант предназначен для того, чтобы дать представление о структуре будущих контрольных измерительных материалах, количестве заданий, их форме, уровне сложности. Задания Демонстрационного варианта не отражают всех вопросов содержания, которые могут быть включены в контрольно-измерительные материалы в 2011 году. Структура работы приведена в спецификации, а полный перечень вопросов – в кодификаторах требований и содержания.
Правильное решение каждого из заданий В1-В12 части 1 экзаменационной работы оценивается 1 баллом. Полное правильное решение каждого из заданий С1 и С2 оценивается 2 баллами, С3 и С4 – 3 баллами С5 и С6 – 4 баллами. Максимальный балл за выполнение всей работы – 30.
Предполагается, что верное выполнение не менее пяти заданий экзаменационной работы отвечает минимальному уровню подготовки, подтверждающему освоение выпускником основных общеобразовательных программ общего (полного) среднего образования. Конкретное значение минимального тестового балла, подтверждающего освоение выпускником основных общеобразовательных программ общего (полного) среднего образования определяется Рособрнадзором в установленном порядке.
К каждому заданию с развернутым ответом, включенному в демонстрационный вариант, дается одно-два возможных решения. Приведенные критерии оценивания позволяют составить представление о требованиях к полноте и правильности решений. Демоверсия, критерии оценивания, спецификация и кодификаторы помогут выработать стратегию подготовки к ЕГЭ по математике.
(2011 - 3 / 18)
Единый государственный экзамен по МАТЕМАТИКЕ
Демонстрационный вариант контрольных измерительных материалов
для проведения в 2011 году единого государственного экзамена по МАТЕМАТИКЕ
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 18 заданий.
Часть 1 содержит 12 заданий с кратким ответом (В1–В12) базового уровня по материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1-С6) по материалу курса математики. При их выполнении надо записать полное решение и записать ответ.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха
!
(2011 - 4 / 18)
Часть 1
Ответом к заданиям этой части (В1-В12) является целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов №1 справа от номера соответствующего задания, начиная с первой клеточки, без пробелов. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерения писать не нужно.
Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%?
На графике показано изменение температуры воздуха на протяжении трех суток. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Определите по графику наибольшую температуру воздуха 15 августа.

Найдите корень уравнения 3x
−2
= 27 .
(2011 - 5 / 18) (2011 - 6 / 18)
| Поставщик
|
Стоимость пеноблоков
(руб. за 1 м3
)
|
Стоимость доставки
(руб. за весь заказ)
|
Дополнительные условия доставки
|
| 1
|
2600
|
10000
|
| 2
|
2800
|
8000
|
При заказе товара на сумму свыше 150000 рублей доставка бесплатная.
|
| 3
|
2700
|
8000
|
При заказе товара на сумму свыше 200000 рублей доставка бесплатная.
|
  В треугольнике ABC
угол C
равен 90о
, AB
= 5, B
На рисунке изображен график функции y
= f
( )x
и касательная к этому cos A
= 0,8. Найдите BC
. графику в точке с абсциссой, равной 3. Найдите значение производной этой функции в точке x
= 3. В треугольнике ABC
угол C
равен 90о
, AB
= 5, B
На рисунке изображен график функции y
= f
( )x
и касательная к этому cos A
= 0,8. Найдите BC
. графику в точке с абсциссой, равной 3. Найдите значение производной этой функции в точке x
= 3.
Строительная фирма планирует купить 70 м3
пеноблоков у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешевую покупку с доставкой?
B9
Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания – в два раза меньше, чем у первого. Найдите
объем второго цилиндра. Ответ дайте в кубических метрах.
Найдите площадь четырехугольника, Камень брошен вертикально вверх. Пока камень не упал, высота, на которой изображенного на клетчатой бумаге с он находится, описывается формулой h t
( )=−5t
2
+18t
(h
– высота в метрах, размером клетки 1 см × 1 см (см. t
– время в секундах, прошедшее с момента броска). Найдите, сколько рисунок). Ответ дайте в квадратных секунд камень находился на высоте не менее 9 метров. сантиметрах.
Найдите наибольшее значение функции
3π ⎡ π⎤
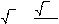 y
= 2cosx
+ 3x
− на отрезке ⎢0; y
= 2cosx
+ 3x
− на отрезке ⎢0;  2 ⎥⎦ . 2 ⎥⎦ .
3 ⎣
B12
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько
дней, работая отдельно, выполнит эту работу первый рабочий, если он за два
Найдите значение выражения log 2002
+ log2
 . дня выполняет такую же часть работы, какую второй – за три дня? . дня выполняет такую же часть работы, какую второй – за три дня?
Не забудьте перенести все ответы в бланк ответов № 1.
(2011 - 7 / 18)
Часть 2
Для записи решений и ответов на задания С1-С6 используйте бланк ответов № 2. Запишите сначала номер выполняемого задания (С1, С2 и т.д.), а затем полное обоснованное решение и ответ.
Решите уравнение
6cos2
x
−cosx
− 2 = 0.
−sin x
 Сторона основания правильной треугольной призмы ABCABC
1 1 1
равна 2, а диагональ боковой грани равна 5 . Найдите угол между плоскостью A
1
BC
и плоскостью основания призмы. Сторона основания правильной треугольной призмы ABCABC
1 1 1
равна 2, а диагональ боковой грани равна 5 . Найдите угол между плоскостью A
1
BC
и плоскостью основания призмы.
Решите неравенство  . .
На стороне BA
угла ABC
, равного 30D
, взята такая точка D
, что AD
= 2 и
BD
=1. Найдите радиус окружности, проходящей через точки A
, D
и касающейся прямой BC
.
Найдите все значения параметра a
, при каждом из которых система уравнений
 ⎧⎪a x
( 4
+ = + −1) y
2 x
, ⎧⎪a x
( 4
+ = + −1) y
2 x
,
⎨
⎪⎩
x
2
+ y
2
= 4
имеет единственное решение.
Найдите все такие пары взаимно простых натуральных чисел (то есть чисел, наибольший общий делитель которых равен 1) a
и b
, что если к десятичной записи числа a
приписать справа через запятую десятичную запись числа b
, b
то получится десятичная запись числа, равного  . .
a
(2011 - 8 / 18)
(2011 - 9 / 18)
Система оценивания экзаменационной работы по математике
Ответы к заданиям части 1
Каждое правильно выполненное задание части 1 оценивается 1 баллом. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
| № задания
|
Ответ
|
| В1
|
5
|
| В2
|
14
|
| В3
|
5
|
| В4
|
3
|
| В5
|
192000
|
| В6
|
18
|
| В7
|
3
|
| В8
|
2
|
| В9
|
9
|
| В10
|
2,4
|
| В11
|
1
|
| В12
|
20
|
Ответы к заданиям части 2
| № задания
|
Ответ
|
| С1
|
2 ,
|
 arccos 2 , . arccos 2 , .
|
| С2
|
30°
|
| С3
|
–1
|
| С4
|
1 или 7
|
| С5
|
a
= 4
|
| С6
|
a
= 2, b
= 5
|
(2011 - 10 / 18)
Решения и критерии оценивания заданий части 2
Оценки заданий части 2 зависят от полноты решения и правильности ответа.
Общие требования к выполнению заданий с развернутым ответом
: решение должно быть математически грамотным, полным, все возможные случаи должны быть рассмотрены, из него должен быть понятен ход рассуждений учащегося. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальный балл.
Эксперты проверяют математическое содержание представленного решения, а особенности записи не учитывают.
В критериях оценивания конкретных заданий содержатся общие требования к выставлению баллов. Однако они не исчерпывают всех возможных ситуаций.
Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
При выполнении задания экзаменуемый может использовать без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки Российской Федерации.
Решите уравнение
 6cos2
x
−cosx
− 2 6cos2
x
−cosx
− 2  = 0. = 0.
Решение
.
1. Уравнение равносильно системе
⎧6cos2
x
− cosx
− 2 = 0, ⎨
⎩−sin x
> 0.
Из неравенства получаем, что sin x
< 0.
В уравнении сделаем замену cosx
=t
и решим уравнение
6t
2
− −t
2 = 0. t
=−  или t
= или t
= 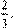
Равенствам cosx
=− и cos и cos
на тригонометрической окружности соответствуют четыре точки (см. рисунок). Две из них, находящиеся в верхней полуплоскости, не удовлетворяют условию sin x
< 0.
(2011 - 11 / 18)
Получаем решения: x
= − + 2πn
и x
= −arccos + 2πn
и x
= −arccos  + 2πn
, где n
∈Z
. + 2πn
, где n
∈Z
.
Ответ
:  2 , arccos 2 , . 2 , arccos 2 , .
| Баллы
|
Критерии оценивания выполнения задания С1
|
| 2
|
Обоснованно получен правильный ответ.
|
| 1
|
Верно найдены нули числителя, но или не произведен отбор найденных решений, или допущены ошибки в отборе.
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
 Сторона основания правильной треугольной призмы ABCABC
1 1 1
равна 2, а диагональ боковой грани равна 5 . Найдите угол между плоскостью A
1
BC
и плоскостью основания призмы. Сторона основания правильной треугольной призмы ABCABC
1 1 1
равна 2, а диагональ боковой грани равна 5 . Найдите угол между плоскостью A
1
BC
и плоскостью основания призмы.
C
1
Решение
. Обозначим H
середину ребра
ABC
равносторонний, а треугольник A
1
BC
– равнобедренный, отрезки AH
и
A
1
H
перпендикулярны BC
.
Следовательно, ∠A
1
HA
– линейный угол двугранного угла с гранями BCA
и BCA
1
.
Из треугольника A
1
AB
найдем: AA
1
=1.
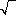  Из треугольника AHB
найдем: AH
= 3 . C
Из треугольника HAA
1
найдем: Из треугольника AHB
найдем: AH
= 3 . C
Из треугольника HAA
1
найдем:
tg .
A
Искомый угол равен 30°.
Ответ
: 30°.
Возможны другие решения.
Например, решение задачи с использованием векторов или метода координат.
| Баллы
|
Критерии оценивания выполнения задания С2
|
| 2
|
Обоснованно получен правильный ответ.
|
| 1
|
Способ нахождения искомого угла правильный, но получен неверный ответ или решение не закончено.
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
(2011 - 12 / 18)
Решите неравенство  . .
Решение.
Найдем, при каких значениях x
левая часть неравенства имеет смысл:
⎧9 − x
2
> 0, ⎧ −(3 x
)(3+ x
)> 0,
⎪ ⎪
⎪x
+ >3 0, ⎪x
>−3,
⎨ ⎨
⎪x
+ 3 ≠1, ⎪x
≠−2, ⎪⎩x
−3≠ 0; ⎪⎩
x
≠ 3.

Значит: − < <−3 x
2 или 2− < <x
3.
Поэтому
 ; ;
 . .
Сделаем замену logx
+
3
(3− x
) = y
. Получаем:
y
 y
. y
.
Таким образом, logx
+
3
(3− x
) = 2, откуда (x
+ 3)2
= 3− x
; x
2
+ 7x
+ 6 = 0.
Корни уравнения: −6 и −1. Условию − <3 x
< −2 или − <2 x
< 3 удовлетворяет только x
= −1.
Ответ
: −1.
 Решение 2.
Можно не находить область допустимых значений x
, а прийти к соотношению x
−3 = 3− x
другим способом. Тогда решение будет немного короче. Решение 2.
Можно не находить область допустимых значений x
, а прийти к соотношению x
−3 = 3− x
другим способом. Тогда решение будет немного короче.
Преобразуем неравенство:
 logx
+
3
((3− x
)(3+ x
))− 1
log2
x
+
3
x
−3 ≥ 2. logx
+
3
((3− x
)(3+ x
))− 1
log2
x
+
3
x
−3 ≥ 2.
4 Заметим, что x
+ 3> 0 и (3− x
)(3+ x
) > 0. Значит, 3− x
> 0.
 Поэтому x
−3 = 3− x
. Получаем: Поэтому x
−3 = 3− x
. Получаем:
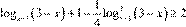 . .
(2011 - 13 / 18)
Сделаем замену logx
+
3
(3− x
) = y
. Получаем:
y
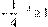 y
; y
2
− 4y
+ 4 ≤ 0; ( y
− 2)2
≤ 0; y
= 2. y
; y
2
− 4y
+ 4 ≤ 0; ( y
− 2)2
≤ 0; y
= 2.
Таким образом,
⎧⎡x
=−1,
⎧
(x
+ 3)2
= (3− x
), ⎧x
2
+ 7x
+ =6 0, ⎪
⎪
⎣
⎢
x
=−6,
⎪⎪ ⎪ ⎪
logx
+
3
(3− x
) = 2; ⎨x
+ 3 > 0, ⎨x
>−3, ⎨x
>−3, x
=−1.
⎪
⎪⎩x
+ 3 ≠1; ⎪
⎩
x
≠−2; ⎪
⎪
x
≠−2;
⎪⎩
Ответ
: −1.
| Баллы
|
Критерии оценивания выполнения задания С3
|
| 3
|
Обоснованно получен правильный ответ.
|
| 2
|
Обоснованно получен ответ, отличающийся от верного только конечным числом значений x
.
|
| 1
|
Ответ неверен, но решение содержит переход от исходного неравенства к верной системе рациональных неравенств.
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
На стороне BA
угла ABC
, равного 30D
, взята такая точка D
, что AD
= 2 и
BD
=1. Найдите радиус окружности, проходящей через точки A
, D
и касающейся прямой BC
.
Решение.
Центр O
искомой окружности принадлежит серединному перпендикуляру к отрезку AD
. Обозначим P
середину отрезка AD
, Q
– основание перпендикуляра, опущенного из точки O
на прямую BC
, E –
точку пересечения серединного перпендикуляра с прямой BC
(см. рисунок а). Из условия касания окружности и прямой BC
следует, что отрезки OA
, OD
и OQ
равны радиусу R
окружности.
Заметим, что точка O
не может лежать по ту же сторону от прямой AB
, что и точка E
, так как в этом случае расстояние от точки O
до прямой BC
меньше, чем расстояние от нее до точки A
.
Из прямоугольного треугольника BPE
с катетом BP =
2 и ∠ =B
30°
  находим, что PE =
. Так как OA = R
и AP
=1, получаем: OP
= R
2
−1 и, находим, что PE =
. Так как OA = R
и AP
=1, получаем: OP
= R
2
−1 и,
следовательно, OE
= .
Из прямоугольного треугольника OQE
, в котором ∠ =E
60°, находим:
(2011 - 14 / 18)
3 3 2
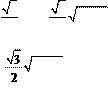 R
= OQ
= OE
= R
−1 +1. R
= OQ
= OE
= R
−1 +1.
2 2
В результате получаем уравнение для R
:
R
2
−1 = R
−1.
Возведем в квадрат обе части этого уравнения и приведем подобные члены. Получим уравнение R
2
– 8R +
7 = 0, решая которое находим два корня R
1
= 1, R
2
= 7. Если радиус равен 1, то центром окружности является точка Р
(см. рисунок б).

Ответ:
1 или 7.
Решение 2.
Пусть точка Q
касания окружности с прямой BC
лежит на луче
BC
(см. рисунок а). По теореме о касательной и секущей
 BQ
2
= BA BD
⋅ = (BD
+ DA
)⋅BD
= (1+ 2)⋅ =1 3, откуда BQ
= 3 . BQ
2
= BA BD
⋅ = (BD
+ DA
)⋅BD
= (1+ 2)⋅ =1 3, откуда BQ
= 3 .
Пусть O
– точка пересечения луча BA
и перпендикуляра к BC
, проведенного через точку Q
. Из прямоугольного треугольника BQO
находим:
BQ
1
BO
=  = 2, тогда AO
= OD
=1 и OQ
= = 2, тогда AO
= OD
=1 и OQ
=  BO
=1. cos30° 2 BO
=1. cos30° 2
Таким образом, точка O
удалена от точек A
, D
и Q
на одно и то же расстояние, равное 1. Следовательно, O
– центр искомой окружности, а ее радиус равен 1.
Пусть теперь точка Q
1
касания окружности с прямой BC
лежит на продолжении BC
за точку B
(см. рисунок б), а прямая, проходящая через
(2011 - 15 / 18)
точку Q
1
перпендикулярно BC
, пересекает прямую AB
в точке H
, а окружность вторично – в точке T
. Тогда
 BQ
1
= BA BD
⋅ = 3, ∠HBQ
1
= ∠ABC
= 30°, BQ
1
= BA BD
⋅ = 3, ∠HBQ
1
= ∠ABC
= 30°,
BQ
1
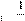 BH
= = 2, HQ
= BH
=1. BH
= = 2, HQ
= BH
=1.
cos30° 2
Если R
– радиус окружности, то Q T
1
= 2R
. По теореме о двух секущих HQ HT HA HD
1
⋅ = ⋅ , то есть 1 1⋅( + 2R
) (= 2 +3)⋅3, откуда находим, что R
= 7.

Ответ:
1 или 7.
(2011 - 16 / 18)
| Баллы
|
Критерии оценивания выполнения задания С4
|
| 3
|
Рассмотрены все возможные геометрические конфигурации и обоснованно получен правильный ответ.
|
| 2
|
Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой обоснованно получено правильное значение искомой величины.
|
| 1
|
Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неверное из-за арифметической ошибки.
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
Найдите все значения a
, при каждом из которых система
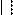 ⎧⎪a x
( 4
+1) = y
+ 2 − x
, ⎧⎪a x
( 4
+1) = y
+ 2 − x
,
⎨
⎪⎩
x
2
+ y
2
= 4
имеет единственное решение.
Решение
. Пусть система имеет решение (x
; y
). Если x
≠ 0, то система имеет второе решение (−x
; y
). Значит, решение может быть единственным, только при x
= 0.
Подставим x
= 0 в первое уравнение: y
= a
− 2. Пара (0;a
− 2) должна удовлетворять второму уравнению:
(a
− 2)2
= 4, откуда a
= 0 или a
= 4.
 Для каждого из двух найденных значений параметра проверить, действительно данная система единственное решение. Для каждого из двух найденных значений параметра проверить, действительно данная система единственное решение.
Первый случай: a
= 0. Система
принимает вид
⎧y
=| x
| 2,−
⎨ 2 2
⎩x
+ y
= 4
Графиком функции y
= x
− 2 является угол, который имеет с окружностью x
2
+ y
2
=1 три общие точки (см. рисунок). Значит, при a
= 0 система имеет три решения.
(2011 - 17 / 18)
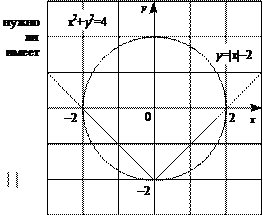
Второй случай. a
= 4. Система принимает вид
 ⎧⎪y
= 4x
4
+ +x
2, ⎧⎪y
= 4x
4
+ +x
2,
⎨ 2 2
⎪⎩x
+ =y
4.
 Из первого уравнения следует, что при x
≠ 0 y
> 2, а из второго уравнения при x
≠ 0 получаем, что y
< 2. Следовательно, при x
≠ 0 система решений не имеет. Значит, при a
= 4 есть только одно решение x
= 0, y
= 2. Из первого уравнения следует, что при x
≠ 0 y
> 2, а из второго уравнения при x
≠ 0 получаем, что y
< 2. Следовательно, при x
≠ 0 система решений не имеет. Значит, при a
= 4 есть только одно решение x
= 0, y
= 2.
Ответ
: a
= 4.
| Баллы
|
Критерии оценивания выполнения задания С5
|
| 4
|
Обоснованно получен правильный ответ.
|
| 3
|
Ответ получен, решение в целом верное, но либо недостаточно обоснованное, либо содержит вычислительные погрешности, в результате которых ответ может быть неверным.
|
| 2
|
Верно получены необходимые условия на значения a
, однако в проверке достаточных условий допущены ошибки.
|
| 1
|
Получены только необходимые условия на значения a
.
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
Найдите все такие пары взаимно простых натуральных чисел (то есть чисел, наибольший общий делитель которых равен 1) a
и b
, что если к десятичной записи числа a
приписать справа через запятую десятичную запись числа b
, b
то получится десятичная запись числа, равного .
a
Решение
. Пусть десятичная запись числа b
состоит из n
цифр. Тогда по условию задачи можно записать равенство b b
n
2
 = a
+ n
, поэтому 10 (b
−a
)= ab
. a
10 = a
+ n
, поэтому 10 (b
−a
)= ab
. a
10
Из этого уравнения следует, что b
> a
2
≥ a
. Так как числа a
и b
взаимно простые, числа b
− a
2
и ab
тоже взаимно простые. (Действительно, пусть p
– общий простой делитель этих чисел. Тогда если p
делитель a
, то p
будет делителем b
. Если же p
– делитель b
, то p
будет делителем a
2
, значит, p
– делитель a
. Противоречие.)
Поэтому b
− a
2
=1 и, следовательно, ab
=10n
. Последнее равенство при взаимно простых a
и b
возможно только в двух случаях:
1) b
=10n
, a
=1, но в этом случае не выполняется равенство b
− a
2
=1.
2) b =
5n
, a =
2n
. В этом случае равенство b – a
2
= 1 принимает вид
(2011 - 18 / 18)
n n
⎛ 5 ⎞n
⎛ 1 ⎞n
5 − 4 =1, откуда ⎜  ⎟
= +1 ⎜ ⎟
= +1 ⎜  ⎟
. ⎟
.
⎝ 4 ⎠ ⎝ 4 ⎠
n n
Функция f n
( ) = ⎛
⎜
 5
⎞
⎟
возрастает, а функция g n
( ) = +1 ⎛
⎜ 5
⎞
⎟
возрастает, а функция g n
( ) = +1 ⎛
⎜
 1
⎞
⎟
убывает. 1
⎞
⎟
убывает.
⎝ 4 ⎠ ⎝ 4 ⎠
Поэтому уравнение f
( )n
= g n
( ) имеет не более одного корня, и так как f
(1) = g
(1), единственным корнем уравнения является n
=1.
Ответ
: a
= 2, b
= 5.
Возможны другие формы записи ответа.
Например:
А) (2;5 ; )
Б)  = 2,5; = 2,5;
⎧a
= 2,
В) ⎨
⎩b
= 5.
| Баллы
|
Критерии оценивания выполнения задания С6
|
| 4
|
Обоснованно получен правильный ответ.
|
| 3
|
Получена система необходимых и достаточных условий на пару искомых чисел и найдено ее решение, но недостаточно обоснована его единственность.
|
| 2
|
Составлено верное уравнение в натуральных числах, из которого сделаны существенные выводы для нахождения искомой пары чисел, уравнение до конца не решено, но верный ответ приведен.
|
| 1
|
Составлено, но не решено верное уравнение в натуральных числах, верный ответ приведен.
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
|