A x
= b,
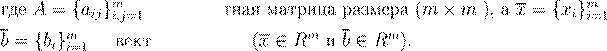
A m
{Ab
}
{Ab
} A m
{Ab
} A
m
= 2
a
11x
1 + a
12x
2 = b
1 a
21x
1 + a
22x
2 = b
2

5x
1
+ 7x
2
= 12,
7x
1
+ 10x
2
= 17,
x
1
= 1 x
2
= 1 F
t
= 2 β
= 10 t
F β F
x
1
= 2.
4 x
2
= 0 12 16.
8
0 0.
2 1.
4 −1
F x
1
= 2.
4 x
2
= 0
F

x
∈ R
m
A m
× m
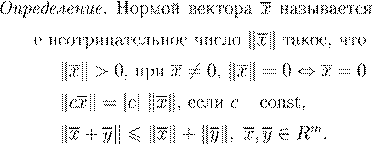

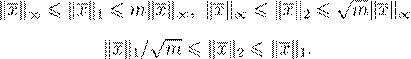 , ,
kA
k
kA
k >
0 A
6= 0 kA
k = 0 ⇔ A
= 0
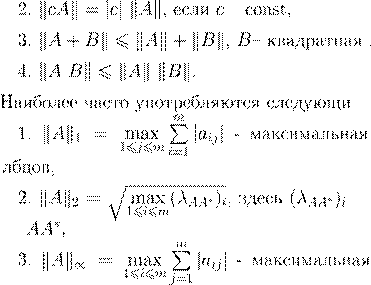 m
× m m
× m
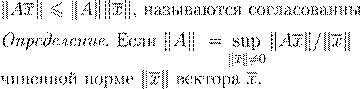 kA
k kA
k
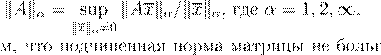
kA
kα
kx
kα
kA
kβ
kx
kα
= kx
kβ

E

E


Ax
= b
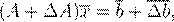
∆A
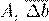

b
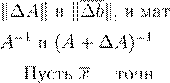 A A
+ ∆A A A
+ ∆A
x
∗
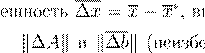
 . .
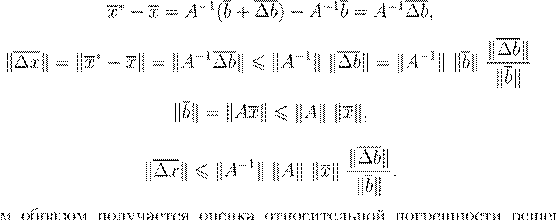 , ,
 . .
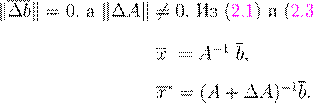
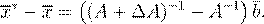
(A
+ ∆A
)−1
− A
−1
= A
−1
A
(A
+ ∆A
)−1
− A
−1
(A
+ ∆A
) (A
+ ∆A
)−1
= = A
−1
(A
− (A
+ ∆A
)) (A
+ ∆A
)−1
= −A
−1
∆A
(A
+ ∆A
)−1
.
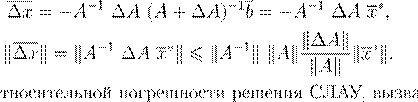

δ
(x
) 6 cond(A
)k∆A
k/
kA
k δ
(x
) 6 cond(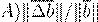 , ,
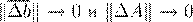 cond(A
) = kA
−1
k kA
k cond(A
) = kA
−1
k kA
k 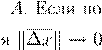
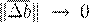
k∆A
k → 0
cond(A
) = kA
−1
k kA
k
t t
O
(2−t
)
O
(2t/
2) O
(2−t/
2)
cond(A
) = kA
−1
k kA
k
cond(A
) ≥ 1 A A
−1
= E
⇒ 1 = kE
k = kA A
−1
k > kA
k kA
−1
k = cond(A
) cond(c A
) = cond(A
) c
cond(A B
) 6 cond(A
) cond(B
) cond(A
−1
) = cond(A
)
max dii
cond(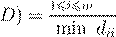 в D
= diag(dii
) в D
= diag(dii
)
16i
6m
cond(A
) = kA
k2 kA
−1
k2
cond(A
)
A
= A
∗ >
0
i
= 1,...,m
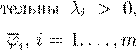
R
m
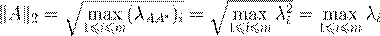 , ,
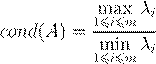 . .

b
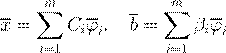 . .
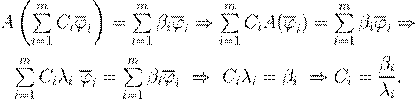
 εi εi
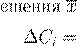
  λl λl
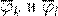

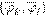
A−1
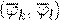
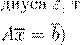 A
−1 A
−1

ε
“
δ

A x
= b,
x

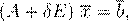

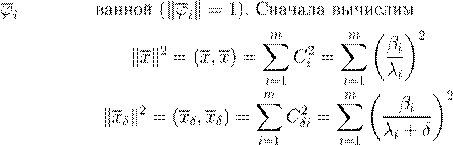

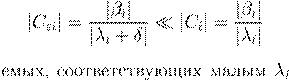
a
ij
aij
= 0 i > j
(i < j
)

U
U
T
U
−1
U
T
U
= UU
T
= E
|det(U
)| = 1 1 = det(E
) = det(UU
T
) =
det(U
) det(U
T
) = det2
(U
)
1

Pij
i j
i j P
24
5 × 5
0 0 0 1 0
| 0
A
|
0
|
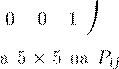
|
A
|
| i
|
j
|
A
|
  24 1 0 0 0 0 24 1 0 0 0 0
P
=0 0 1 0 0
0 1 0 0 0
Pij
Qij
(ϕ
)
i j
Q
24
(ϕ
) 5 × 5
24
1 0 0 0 0
    0 cosϕ
0 −sinϕ
0 0 cosϕ
0 −sinϕ
0
Q
(ϕ
) =0 0 1 0 0
0 sinϕ
0 cosϕ
0
0 0 0 0 1
Qij
P
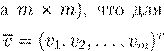 m m
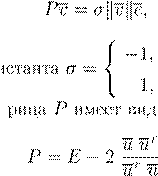 v
1
> 0, v
1
> 0,
e
= (1,
0,...,
0)T
v
1
<
0.
,
u
= v
−σ
kv
ke P
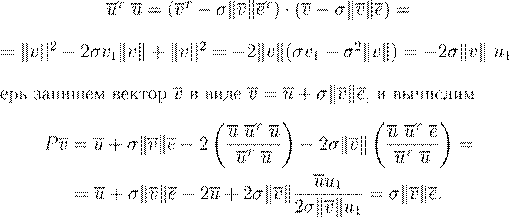 . .
 u
1
u u
1
u
P
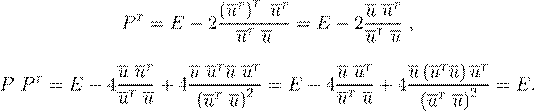
 y
= αu
+ βs y
= αu
+ βs
Aij aij
= 0 i > j
+ 1(i < j
− 1)

“
“
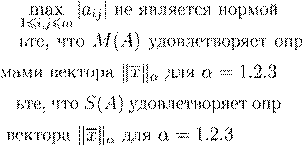
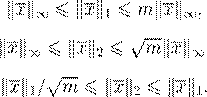 , ,
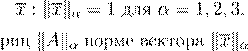
α
= 1.
2.
3
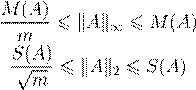
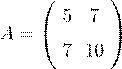
x
1
+ 0.
99 x
2
= 1.
99,
0.
99 x
1
+ 0.
98x
2
= 1.
97,
x
1
= 1 x
2
= 1
x
1
= 3 x
2
= −1.
0203

L Ux
= b.
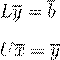 , . , .
LU

Ly
= b
l
11y
1 = b
1
,
l
21y
1+ l
22y
2 = b
2
,
... ... ... ... ... ... ...,
l
m
−1,
1y
1+ l
m
−1,
2y
2+ ...
+ ...
+ l
m
−1,m
−1y
m
−1 = b
m
−1,
l
m
1y
1+ l
m
2y
2+ ...
+ ...
+ l
m,m
−
1y
m
−
1+ l
mm
y
m
= bm
.
y
1 = b
1/l
11
yi
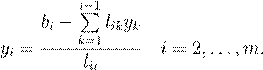
Ux
= y
u
11x
1+ u
12x
2+ u
13x
3+ ...
+ ...
+ u
1m
x
m
= y
1, u
21x
2+ u
23x
3+ ...
+ ...
+ u
2m
x
m
= y
2,
... ... ... ...,
u
m
−1,m
−1x
m
−1+ u
mm
x
m
= y
m
−1
u
mm
x
m
= y
m
.
x
m
= y
m
/u
mm
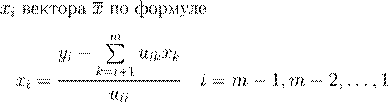 . .
Q R QR
A

QRx
= b,

Rx
= Q
T
b.
 m
× m m
× m
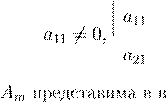 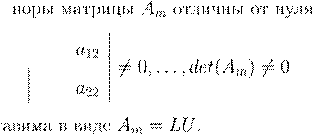 , ,
Am

 . .
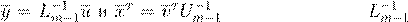
 l
mm
u
mm l
mm
u
mm
Am

LDU
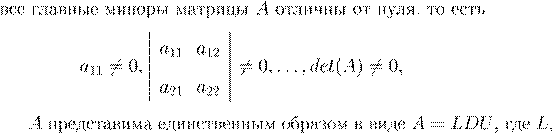
U
| l
ii
= 1 u
ii
= 1 D
|
A
= LU
|
| A
= LDU
uii
= 1
|
lii
= 1
A
= L
1D
1U
1 A
= L
2D
2U
2
|
| L
1D
1U
1 = L
2D
2U
2
|
U
1U
2−1 = D
1−1L
−1 1L
2D
2
|
| U
1U
2−1
|
D
1−1L
−1 1L
2D
2
|
U
1 U
2
U
1U
2−1 = D
= E
⇒ U
1 = U
2
D
1−1L
−1 1L
2D
2 = E L
−1 1L
2 = D
1D
2−1
L
1 L
2 L
−1 1L
2 = E
⇒ L
1 = L
2
D
1 = D
2 
 a
11 a
12 ... ... ... ... a
1m
a
11 a
12 ... ... ... ... a
1m
a
21 a
22 ... ... ... ... a
2m
A... ... ... ... ... ... ...
 ... ... ... ... ... ... ... ... ... ... ... ... ... ...
 = a
m
−1,
1 a
m
−1,
2 ... ... ... ... a
m
−1,m
= a
m
−1,
1 a
m
−1,
2 ... ... ... ... a
m
−1,m
am
1
am
2
... ... ... ... amm
 
 1 a
(1)
1222 ... ... ... ... a
1(1)
2mm
1 a
(1)
1222 ... ... ... ... a
1(1)
2mm
0 a
(1)
... ... ... ... a
(1)
A
(1) = L
1
D
1
A
=... ... ... ... ... ... ... ,
... ... ... ... ... ... ...
0 a
(1)m
−1,
2
... ... ... ... a
(1)m
−
1,m
0 a
m
(1)
2 ... ... ... ... ...a
mm
(1)
1/a
11
0 0 ...
0 1 0 0 ...
0
 D
1
= 0 1 0 ...
0 L
1
k
= 1 −a
21 1 0 A...
(k
0 . D
1
= 0 1 0 ...
0 L
1
k
= 1 −a
21 1 0 A...
(k
0 .
... ... ... ... ... ... ... ... ... ...
 0 0 0 ...
1
−am
1
0 0 ...
1 0 0 0 ...
1
−am
1
0 0 ...
1
k
− −1)
| 1
 ... ...
0
A
(k
−
1)
= L в ...L в A
= 0
|
a
(1)12
...
1
0
|
...
...
0
1
|
...
...
a
(kk
−−11),k
a
(k
−1)
|
...
...
...
...
|
...
...
...
...
|
k
a
(1)1m
1,m
...
a
(k
−
1)
−
a
(k
−
1)
|
| ...
0
|
...
0
|
...
0
|
...
a
(mk
k
−1)
|
... ...
|
... ...
... a
(mmk
−
1)
|
| A
(k
−1)
|
Dk
|
 k
−1 k
−1 1 1
k
(kkk
+11),k k
(k,mk
+11)
k
−1 k
−1 1 1
k
(kkk
+11),k k
(k,mk
+11)
0 0 0 a
−
... ... a
−
,m
Dk
= diag(1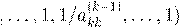 , ,
Lk
... ... ... ... ... ...
0 ...
1 0 ...
0
  k
k
 1 ... ...
k
(mk
(kk
+11)1),k
... ...
0 1 ... ...
k
(mk
(kk
+11)1),k
... ...
0
L
=.
0 ...
−a
−
1 ...
0
... ... ... ... ... ...
0 ...
−a
−
0 ...
1
A
(k
) = L
k
D
k
L
k
−1D
k
−1 ...L
1D
1A
=
− − ,m
1 ... a
11,k
1 a
11,k
... a
11,m
1 a
1
11,m
... ... ...
k
(...
k
11),k
...
k
(k
(
k,m
...k
1)1)
,m
11
(k
...
k
0 ...
1 a
−
... a
−
a
−1)
− − − −
 0 ...
0 0 m
(k
)
1,m
1
m
0 ...
0 0 m
(k
)
1,m
1
m
= 0 ...
0 1 ... a a
(k
) − k,m
... ... ... ... ... ... ...
0 ...
0 0 ... a
a
(k
)
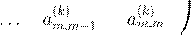 − − −1,m − − −1,m
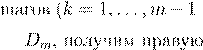 m
−1 m
−1
U
U
= Dm
Lm
−1Dm
−1 ...L
1
D
1
A
=
 − − 1,m − − 1,m
... ... ... ... ... ... ...
0 ...
1 a
−
... a
−
a
−
1)

1 ... a
11,k
1 a
(kk
11,k
11),k
... a
(kk
(k,m
11k,m
1)1),m
111 m
(a
k
(mk
111
1 ... a
11,k
1 a
(kk
11,k
11),k
... a
(kk
(k,m
11k,m
1)1),m
111 m
(a
k
(mk
111
− − − − ,m
=
0 ...
0 1 ... a a
(k
)
− k,m
... ... ... ... ... ... ...
0 ...
0 0 ...
1 a
−
1)
− ,m
 0 ...
0 0 ...
0 1 0 ...
0 0 ...
0 1
L
−1
= Dm
Lm
−1Dm
−1 ...L
1
D
1
A L
−1
A
= LU.
U
cond(U) = cond(L
−
1
A
) = cond(Dm
Lm
−1Dm
−1 ...L
1
D
1
A
) 6
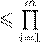 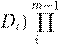 cond(cond(Li
) cond(A
) cond(cond(Li
) cond(A
)
=1
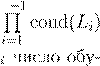 m m
cond(Li
) > 1
cond(U
) D
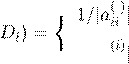 i
,
|a
(iii
)| <
1 i
,
|a
(iii
)| <
1
cond(
|aii
,
|a
(iii
)| >
1
cond(Di
) cond(U
)
cond(A
)
L
i
D
i
“
a
11x
1 + a
12x
2 + ...
+ a
1m
x
m
= b
1 a
21x
1 + a
22x
2 + ...
+ a
2m
x
m
= b
2
..............................
a
m
1x
1 + a
m
2x
2 + ...
+ a
mm
x
m
= b
m
U
xk
A
a
i,n
+1 = b
i
k
1 m
− 1
i k
+ 1 m
+ 1
r
:= a
ik
/a
kk
j
k
+ 1 m
+ 1
a
ij
:= a
ij
− r a
kj
j
i
k
x
n
:= a
n,n
+1/a
n,n
k
n
− 1 1
x
k
:= a
k,n
+1 − P a
kj
x
j
!/a
kk
n
j
=k
+1
k
Ux
= y
cond(A
)
Ux
= y U
A
k xk
|a
ln
|(k
) = 6max6 |a
ij
|(k
) k l k n
k i,j m
k n
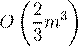
x
∗
x
(1)
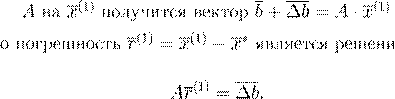
kr
(1)k 6 ε x
(1)
ε
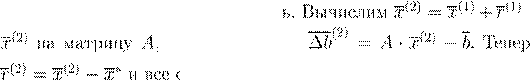
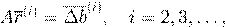
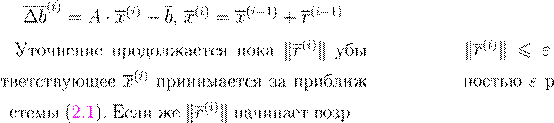
A
A
= QR,
Q R
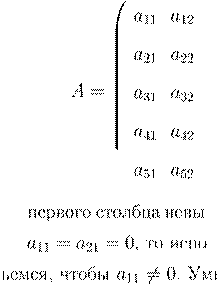 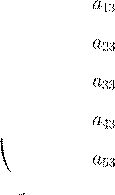 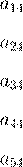 A A
a
25 a
35 a
45 a
55
a
15
 12 12 cosϕ
1212 −sinϕ
1212 0 0 0 sinϕ
cosϕ
0 0 0 12 12 cosϕ
1212 −sinϕ
1212 0 0 0 sinϕ
cosϕ
0 0 0
Q
(ϕ
) =0 0 1 0 0
 0 0 0 1 0 0 0 0 1 0
0 0 0 0 1
A
12 = Q
12A
 12
a
1111 cosϕ
1212 −514131a
2121 sinϕ
1212 ·524232 · · a
1515 cosϕ
1212 − a
2525 sinϕ
12 a
sinϕ
+ a
cosϕ
· · · a
cosϕ
+ a
sinϕ
12 12
a
1111 cosϕ
1212 −514131a
2121 sinϕ
1212 ·524232 · · a
1515 cosϕ
1212 − a
2525 sinϕ
12 a
sinϕ
+ a
cosϕ
· · · a
cosϕ
+ a
sinϕ
12
A
=a a
· · ·  a a
· · · a a
· · · a a
· · · a a
· · ·
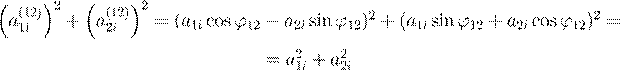
ϕ
12 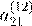 A
12 A
12
a
11 sinϕ
12 + a
21 cosϕ
12 = 0.
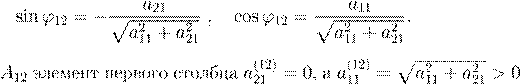

A
1

Q
3 Q
4
A
4
= Q
4
· Q
3
· Q
2
· Q
1
A
A m
× m
Am
−
1 = Qm
−
1 · ...
· Q
1
· A
= Q
e · A,
e
Q A
m
−1
A
= QR Q
= Q
e−1
R
= Am
−1
QR A
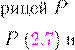
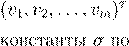 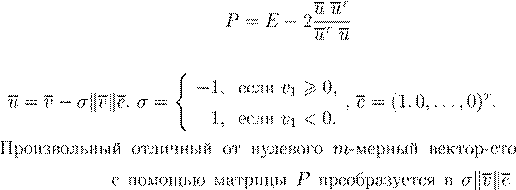 v
= v
=
m
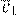 A A
v
1 = (a
11,a
21,...,a
m
1)T
P
1
m
× m
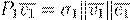
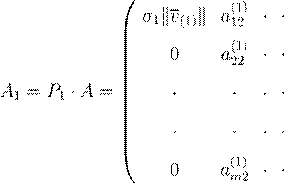 a
(1)12mm
a
(1)12mm
a
(1)
mm
·
·
a
(1)
m
− 1 v
2
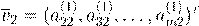
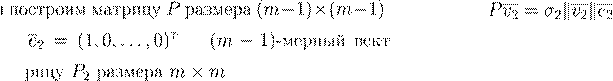
 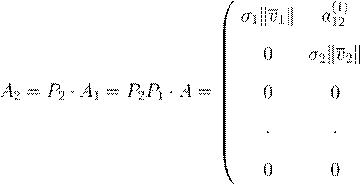 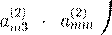 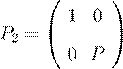 , ,
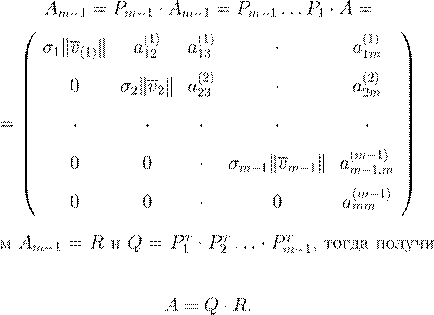
A
m
−1
Q
Pi
T
i
= 1,...,m
− 1 Q
A
= QR Q
R
Ax
= b
Rx
= Q
T
b
cond(A
) = cond(R
)
A Qij
i
j
b
(1)ik
= b
ik
cosϕ
ij
− a
jk
sinϕ
ij
k
= 1,...,m.
(1)
b
jk
= b
ik
sinϕ
ij
+ a
jk
cosϕ
ij
Q
Am
−1 = R
QR
A
QR
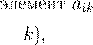 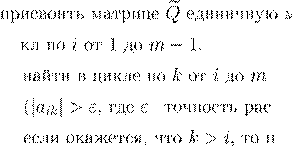 i k i k
i

i
R
= Am
−
1 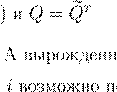 A
= Q R A
= Q R
i
A
m
−1
A
m
−1
QR
Qij
O
(2m
3
)
QR
Pi
m
× m

A
= A
∗
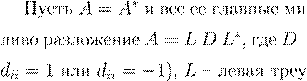
A
= L U.
A
= L U
= A
∗
= U
∗
L
∗
⇒ L U
= U
∗
L
∗
⇒ U
(L
∗
)−
1
= L
−
1
U
∗
.
U
(L
∗
)−
1
= L
−
1
U
∗
= D
⇒ U
= D L
∗
⇒ A
= L в L
∗
.
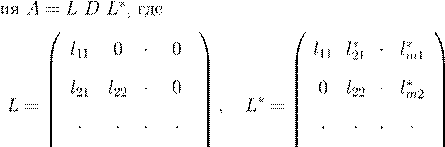 , ,
D
= diag(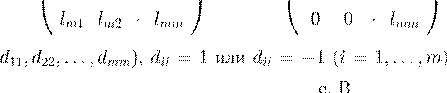
A
L
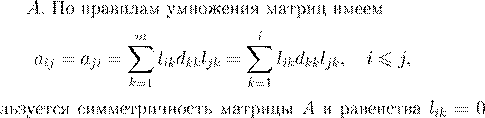
k > i
i
= 1
a
1j
= a
j
1 = l
11d
11l
j
1,

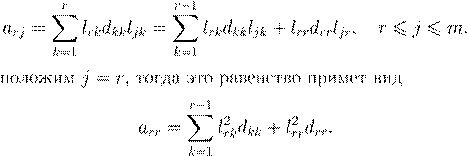
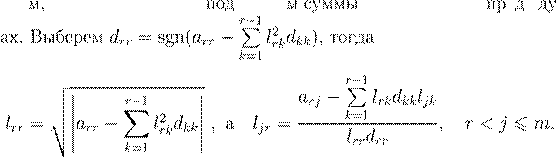
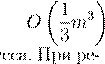
LU
LU
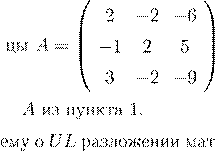

QR A
 l l
QR
x
(0) x
∗
A x
= b
“ “ x
(n
)

kx
(n
) − x
∗
k
O
(m
2
)
 B B
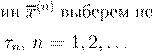
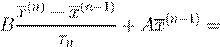 b, n
= 1,
2,... b, n
= 1,
2,...
x
(n
)
x
∗ 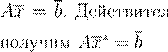 n
→ ∞ n
→ ∞
x
(n
)
τn
= τ
τn
n
= 1,
2,... B
B
−1
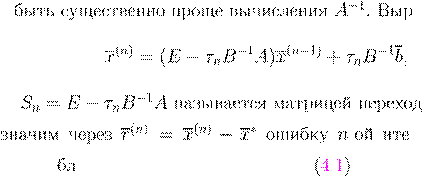 x
(n
) x
(n
)
ε
n
= n
(ε
)
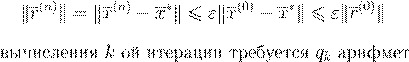 . .
ε
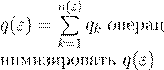 τn
n
= 1,
2,... τn
n
= 1,
2,...
r
(n
) n
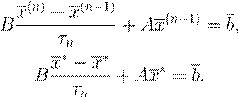
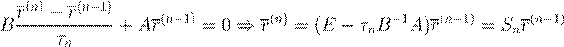
τn
= τ
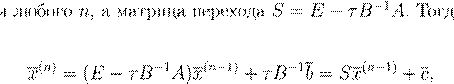
r
(n
) = Sr
(n
−1) = S Sr
(n
−2) ...
= S
n
r
(0).
S
S
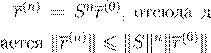 kS
k 6 1 kS
k 6 1
kr
(n
)k → 0 n
→ ∞
S S
 n
→ ∞ |µ
k
| <
1 n
→ ∞ |µ
k
| <
1  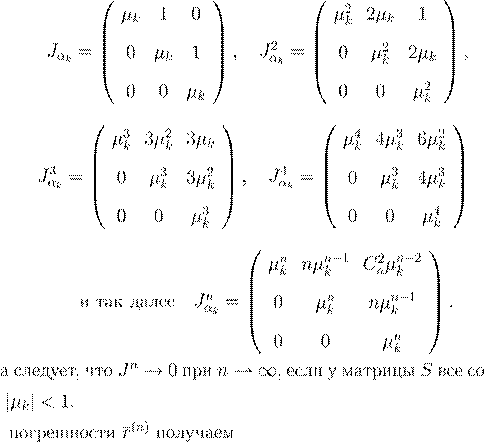 , ,
 . .
kr
(n
)k = kG
−1J
n
G r
(0)k 6 kG
−1k kJ
n
k kG
k kr
(0)k → 0 n
→ ∞.
S
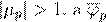
 ε ε
n
→ ∞
B
= E
S
= E
− τA
S
max|µk
| τ
max|µk
| k k
τ A
= A
∗ >
0 A
0 < γ
1
6 λk
6 γ
2
k
=
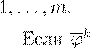 λk
S λk
S
µk
= 1 − τλk
0 < τ <
2/γ
2
|µk
| = |1−τλk
| <
1
0 < τ <
2/γ
2
τ
= τ
∗
|µ
∗| = 0<τ<
min2/γ
2 1max6k
6m
|1 − τλ
k
|

τ 
γ
1
< λ < γ
2
gλ
(τ
) = 1−τλ
τ
= τ
∗ |gλ
(τ
∗)| 6 |gλ
(τ
)| γ
1
< λ < γ
2
0 < τ <
2/γ
2
0 < τ <
1/γ
2
|gγ
2
(τ
)| 6 |gγ
1
(τ
)| τ >
1/γ
1
|gγ
1
(τ
)| 6 |gγ
2
(τ
)|
1/γ
2
6 τ
6 1/γ
1
τ
0
 |gγ
2
(τ
0
)| = |gγ
1
(τ
0
)|, τ
0 |gγ
2
(τ
0
)| = |gγ
1
(τ
0
)|, τ
0
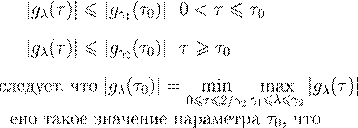
  cond(A
) cond(A
)
1
kS
k → 1 ζ
→ ∞

 aii
=6 0 i
= 1,...,m aii
=6 0 i
= 1,...,m
(n
+1)
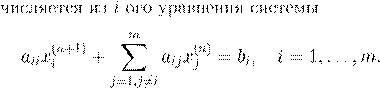
B
= diag(a
11
,...,amm
)
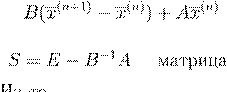 = b
⇒ x
(n
+1) = (E
− B
−1A
)x
(n
) + B
−1b, A = b
⇒ x
(n
+1) = (E
− B
−1A
)x
(n
) + B
−1b, A
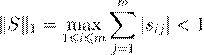 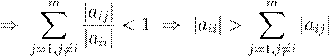 , ,
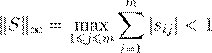 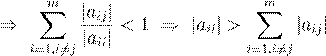 . .
x
(0)
n
:= 0
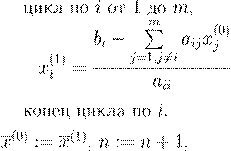
x
(1)
Ax
= b ε
n
N
n > N
A Ax
= b a
ii
=6 0
 (n
+ 1) (n
+ 1)
i
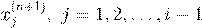
| 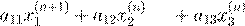
|
+ ...
|
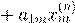
|
= b
1
|
| 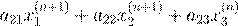
|
+ ...
|
+ a
2m
x
m
(n
)
|
= b
2
|
...................................................
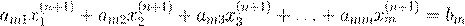
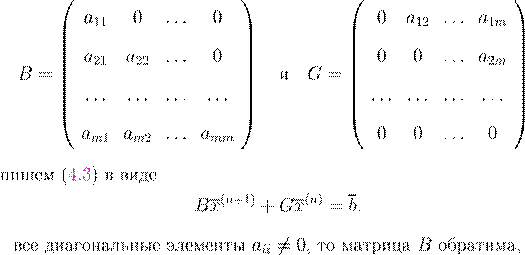 . .

m
= 2 (x
1
,x
2
)
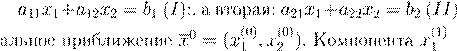
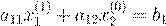 , ,
I

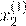
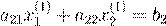 , ,
II
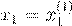

x
(0)
n
:= 0
i
1 m
 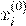
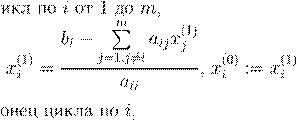
n
:= n
+ 1
 Ax
= b Ax
= b
x
∗
A
= A
∗ >
0 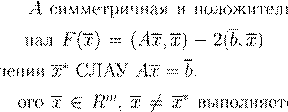
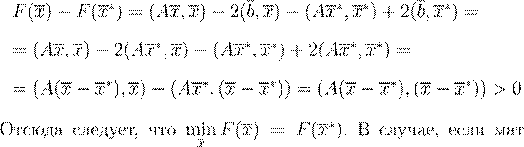 . .
Φ(x
) = (Ax
− b,Ax
− b
) x
∈ Rm
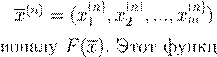 x
∗ x
∗
F
(x
) = F
(x
1
,x
2
,...,xm
).
F
(x
)
x
1
ϕ
1(x
1) = F
(x
1,x
2(n
),...,x
m
(n
)),
x
(1
n
+1)
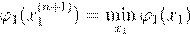 . .
x
2
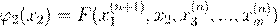
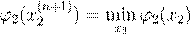 . .
(n
+ 1)
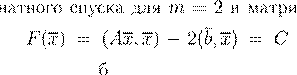 A
= A
∗ >
0 A
= A
∗ >
0
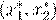
C
= 0
 a
1 a
1
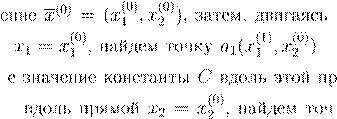
A
1
(x
(1)1
,x
(1)2
)
C
Ax
= b

Ax = b A = A∗
> 0
k
k k n
+ 1
x
(k
n
+1)
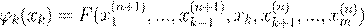 . .
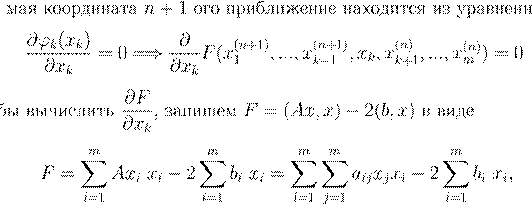 . .
 . .
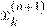
Xk
−1
a
ik
x
(in
+1) + a
kk
x
k
(n
+1) + Xm
a
ik
x
ni
= b
k
.
i
=1 i
=k
+1
A
= A
∗ >
0
F
(x
) x
grad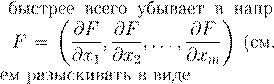 x
(n
+1) x
(n
+1)
x
(n
+1) = x
(n
) − α
n
gradF
(x
(n
)), αn
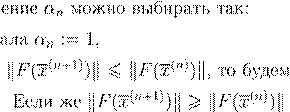 x
(n
+1) x
(n
+1)
gradF
(xn
) αn
:= αn
/
2
 x
(n
+1) x
(n
+1)
αn
αn
N
x
(n
+1)
ε ε
“
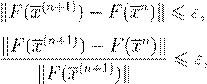 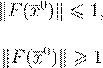 , ,
“
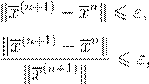 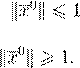 , ,
αn
|ϕ
(αn
)|
ϕ
(α
n
) = F
(x
(n
+1)) = F
(x
(n
) − α
n
gradF
(x
(n
))).
αn
A
= A
∗ >
0
grad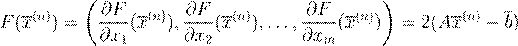
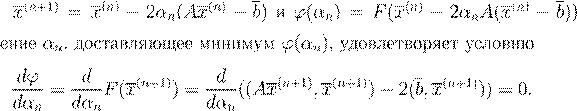
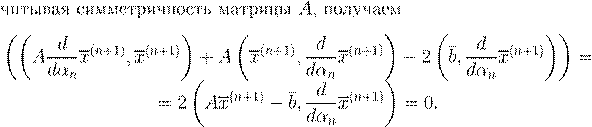
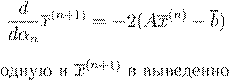 . .

αn
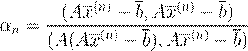

Ax = b A = A∗
> 0
A
0 = (x
01,x
02)
gradF
(x
0
) A
0A
1
A
0A
1
(x
11,x
12) A
1
A
0A
1
 A
= A
∗ >
0 A
= A
∗ >
0
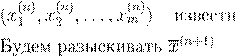 n n
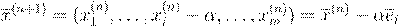 , ,

n
 , ,
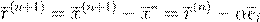 . .
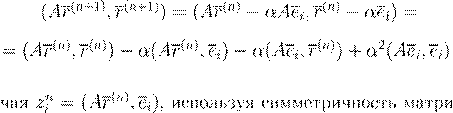 . .

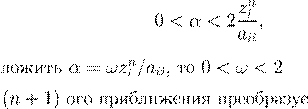
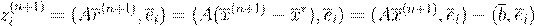 . .
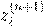
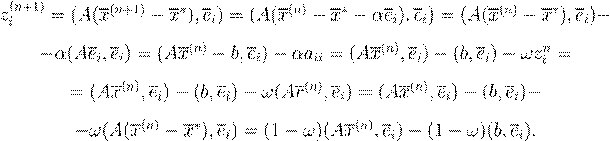
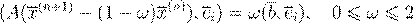 , ,
x
(n
+1)
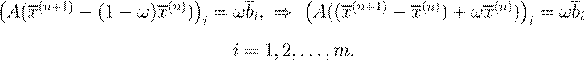 , ,
i
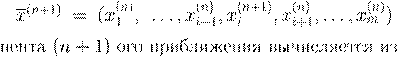
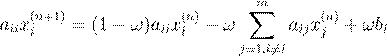
0 < ω <
1 1 < ω <
2
ω
= 1
x
(n
) = Sx
(n
−1) + c,
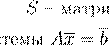 c c
| ε
|
kr
(n
)k = kx
(n
) − x
∗
k 6 ε
kr
(n
)k = kx
(n
) −x
∗
k
|
x
(n
) x
∗
|
v
(n
)
 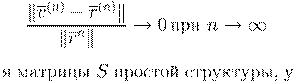 . .
R
m
µi
S
1 >
|µ
1
| >
|µ
2
| > |µ
3
| > ...
> |µm
|,
µi
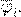
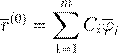 , . , .
 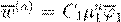 kw
(n
)k = O
(
|µ
1|n
) kw
(n
)k = O
(
|µ
1|n
)
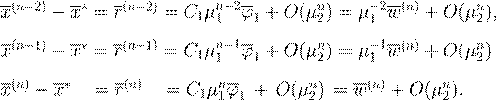 , ,
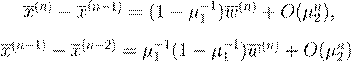 . .
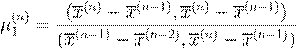 , ,
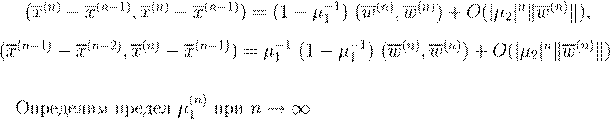 . .
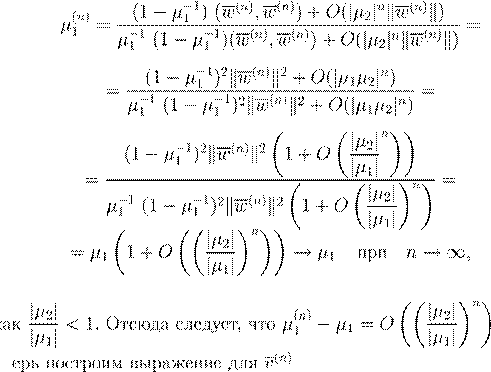
 , ,
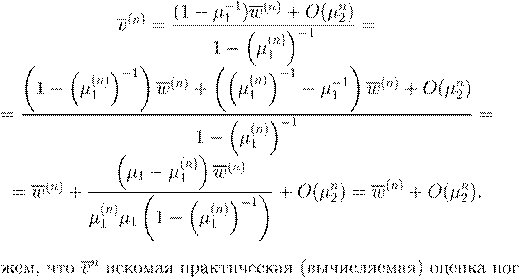
n

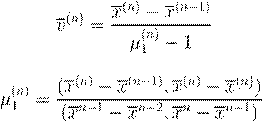 . .
kx
(n
) − x
(n
−1)k µ
1
 , ,
kv
(n
)
k 6 ε
1,
α β x
(k
+1) = S x
(k
) + c
 ? ?
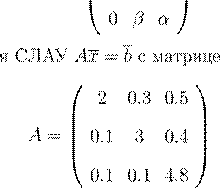 , ,
S
= E
− τA
0 < τ <
0.
4
α β
α β
α β
n
= 2
 m
× m m
× m
A
∗ A
A
 A
∗ A
∗
a
ji
AA A
−1
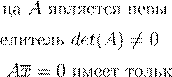
b
=6 0 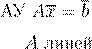
A m
λ ϕ
6= 0
A
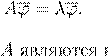
m det
(A
− λE
) = 0.
A
ρ
(A
) = max|λi
|
i
A
 trA trA
A
A
A
A
ajj
ej
= (0,...,
0,
1 ,
0,...,
0) j
|{z}
λ
k
λ
j
A λ
k
=6 λ
j
λk
ϕk
k
= 1,...,m
R
m
R
m
R
m
 A
∗ ψk
k
= 1,...,m A
∗ ψk
k
= 1,...,m
(ϕk
,ψj
) = 0, k
=6 j.
A
A B
P B
=
P
−1
AP
P B
= P
∗AP A B
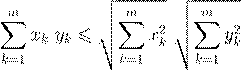 , ,
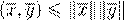 . .

grad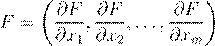
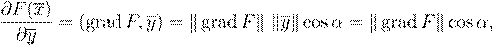
α
gradF y
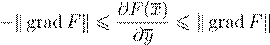 F
(x
) F
(x
)
x
F
(x
) = c
F
(x
) = c x
0
=
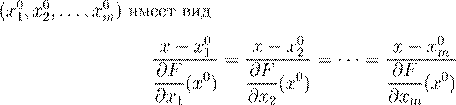 . .
max |a
ij
|
16i,j
6m
E

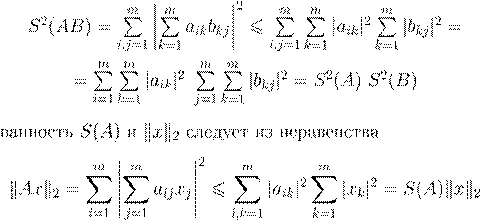


 S
(A
) = √trAA
∗ S
(A
) = √trAA
∗
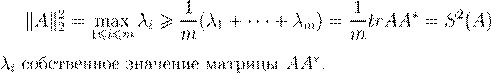
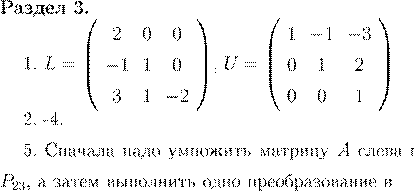
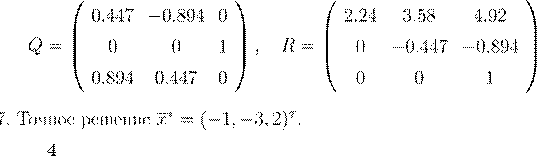
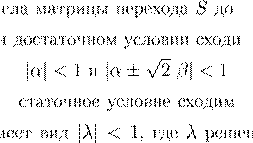
 . .
|β/α
| <
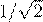
|