| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УО «БОРИСОВСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
Специальность Т 03 01 Технология, оборудование и
автоматизация машиностроения
ТЕХТРАН
— СИСТЕМА ПРОГРАММИРОВАНИЯ ОБОРУБОВАНИЯ С ЧПУ
Методические указания
предмет: «Программирование обработки на станках с ЧПУ»
Разработал: Е.К. Дыкуша
Утверждено на заседании
цикловой комиссии
Председатель цикловой комиссии В.М. Адаменко
2004
ПРЕДИСЛОВИЕ
Внедрение оборудования с числовым программным управлением (ЧПУ), средств вычислительной техники, а также создаваемых на их основе гибких производственных систем (ГПС) определяется современным развитием промышленного производства, которое характеризуют частая смена продукции, короткий жизненный цикл изделий, а также возрастающие сложность и точность обработки. В этих условиях одной из важнейших задач технологической подготовки производства является разработка управляющих программ (УП) для станков с ЧПУ.
Разработка УП − сложный и трудоемкий процесс, во многом определяющий эффективность использования оборудования с ЧПУ и качество обрабатываемых деталей, поэтому сейчас большое внимание обращается на разработку и совершенствование систем и методов автоматизированной подготовки УП. Особое внимание проблеме автоматизированной подготовки управляющих программ уделяется в составе комплексной системы САПР−АСТПП−ГПС. Управляющая программа при этом является результатом сквозного цикла обработки информации от чертежа детали до программы ее изготовления на станках с ЧПУ. Система автоматизированного программирования (САП) оборудования с ЧПУ − составная часть такой комплексной системы. Несмотря на большое число работ в области автоматизации программирования оборудования с ЧПУ в нашей стране и за рубежом, они не получили полного и систематизированного изложения в литературе. Предлагаемая книга содержит изложение основных вопросов, связанных с автоматизированной подготовкой УП для станков с ЧПУ на базе САП Техтран.
В гл. 1 дана классификация САП по различным критериям, позволяющая получить представление о направлениях развития автоматизации программирования, и приведена функциональная структура САП Техтран. Гл. 2 посвящена описанию проблемно-ориентированного языка программирования оборудования с ЧПУ Техтран. Описание приведено в полном объеме и может быть использовано на практике при разработке УП. Гл. 3 посвящена операторам постпроцессора, задающим необходимые технологические данные для выполнения УП на станке. В гл. 4 изложены особенности технологической подготовки производства в условиях использования САП, приведены примеры различных видов обработки и описание способов контроля УП.
В качестве основной задачи авторы ставили перед собой полное и систематизированное описание языка программирования оборудования с ЧПУ Техтран, изложенного в гл. 2. Гл. 1, 3, 4, включены для более глубокого восприятия основного материала.
Все замечания и пожелания авторы просят направлять по адресу: 191065, Ленин-град, ул. Дзержинского, 10, ЛО издательства «Машиностроение».
Глава 1
АВТОМАТИЗАЦИЯ ПРОГРАММИРОВАНИЯ ОБОРУДОВАНИЯ С ЧПУ
1.1 Системы автоматизации программирования
Роль систем автоматизации программирования в процессе подготовки управляющих программ для станков с ЧПУ можно сейчас сравнить с той ролью, которую сыграли компиляторы языков высокого уровня в процессе разработки программ на ЭВМ. Появление САП является логическим следствием развития вычислительной техники, программирования, станкостроения, а также обусловлено возрастающей сложностью деталей, и, следовательно, высокой трудоемкостью «ручного» программирования их обработки. За более чем двадцатилетний период, прошедший с тех пор, как начали эксплуатироваться САП, сменилось четыре поколения ЭВМ, появились микропроцессоры, разработаны и широко используются многооперационные станки типа «обрабатывающий центр» и роботы. Это естественным образом повлияло на методы подготовки управляющих программ и эволюцию развития САП.
Программирование оборудования с ЧПУ появилось совсем недавно. Результатом программирования является управляющая программа, которая представляет собой совокупность команд на языке программирования, соответствующая заданному алгоритму функционирования станка по обработке конкретной заготовки (см. ГОСТ 20523−80).
В книге будет идти речь об автоматизированном программировании, хотя последние достижения вычислительной техники и станкостроения в некоторой степени стирают грань между «ручным» и автоматизированным программированием. Рассмотрим программирование как составную часть процесса технологической подготовки производства.
«Ручное» программирование в традиционном понимании состоит в следующем. По заданному операционному технологическому процессу технолог рассчитывает траекторию движения инструмента, назначает необходимые технологические команды в соответствии с режимом обработки (например, подачу, охлаждение, смену инструмента и т. д.) и преобразует эти данные во внутреннее представление системы ЧПУ [4, 15, 17].
При автоматизированном программировании в идеальном случае все задачи ручного программирования должны решаться на ЭВМ, включая расчет режимов обработки. САП являются эффективным и надежным инструментом для их решения.
САП − это комплекс технических, программных, языковых, информационных средств, осуществляющих преобразование данных чертежа детали в коды устройства управления оборудованием с ЧПУ. Как правило, САП организованы по классической структуре: входной язык, процессор, промежуточный язык, постпроцессор. В зависимости от реализации возможны отклонения от этой структуры.
Входной язык САП − проблемно-ориентированный язык, предназначенный для описания исходных данных о детали и технологическом процессе ее обработки на оборудовании с ЧПУ.
Процессор САП − программное изделие, предназначенное для решения общих геометрических и технологических задач, а также задач управления процессом обработки данных на ЭВМ, реализация которого возможна в виде специализированного программного устройства.
Постпроцессор САП − программное изделие, предназначенное для адаптации управляющей программы к конкретному оборудованию с ЧПУ, реализация которого возможна в виде специализированного программного устройства.
Промежуточный язык процессор − постпроцессор − внутренний проблемно-ориентированный язык системы САП, служащий для представления данных, передаваемых от процессора к постпроцессору. (Все определения даны по ГОСТ 23501.603−84).
В литературе промежуточный язык процессор-постпроцессор встречается под названием CLDATA (Cutter Location Data
− данные о перемещении инструмента).
Структура САП приведена на рис. 1.1. Обычно в состав САП входит библиотека постпроцессоров, каждый из которой предназначен для определенной модели системы ЧПУ или модели станка. Разрабатываются также универсальные постпроцессоры, способные формировать УП для различных систем ЧПУ. Графические постпроцессоры предназначены для вывода траектории движения Инструмента на графические отображающие устройства.
Рассмотрим классификацию САП по различным критериям (рис. 1.2) [9]. Первый критерий классификации САП − по числу управляемых координат
− определяет
 функциональные возможности системы и класс обслуживаемого оборудования. Двух-координатные САП обеспечивают автоматизированную подготовку УП для двух-координатных станков (токарных, электроэрозионных, газорезательных и др.). Движение инструмента происходит в одной из координатных плоскостей. Движения по третьей координатной оси нет. 2,5-координатные САП обеспечивают подготовку УП для обработки произвольного плоского контура при условии, что поверхность детали является плоскостью, произвольно ориентированной в пространстве. Такие САП относятся к самому распространенному типу систем по двум причинам: во-первых, они охватывают подготовку УП для широкого класса станков (токарных, фрезерных, сверлильных и др.), во-вторых, трудоемкость разработки, сопровождения и эксплуатации такой САП не требует больших инженерных и технических ресурсов. К числу таких САП относятся ЕСПС-ТАУ, САПCM, Техтран, ADAPT (США), NELAPT (Великобритания), Autotech (ГДР), FAPT (Япония), IFAPT функциональные возможности системы и класс обслуживаемого оборудования. Двух-координатные САП обеспечивают автоматизированную подготовку УП для двух-координатных станков (токарных, электроэрозионных, газорезательных и др.). Движение инструмента происходит в одной из координатных плоскостей. Движения по третьей координатной оси нет. 2,5-координатные САП обеспечивают подготовку УП для обработки произвольного плоского контура при условии, что поверхность детали является плоскостью, произвольно ориентированной в пространстве. Такие САП относятся к самому распространенному типу систем по двум причинам: во-первых, они охватывают подготовку УП для широкого класса станков (токарных, фрезерных, сверлильных и др.), во-вторых, трудоемкость разработки, сопровождения и эксплуатации такой САП не требует больших инженерных и технических ресурсов. К числу таких САП относятся ЕСПС-ТАУ, САПCM, Техтран, ADAPT (США), NELAPT (Великобритания), Autotech (ГДР), FAPT (Япония), IFAPT
(Франция). В трех координатных САП в отличие от 2,5-координатных поверхность обрабатываемой детали может быть произвольной поверхностью второго порядка, что позволяет расширить область их применения. Типичными представителями таких САП являются MODAPT (Италия), PROMO (Франция). Многокоординатные САП в дополнение к обычным трех координатным перемещениям обеспечивают угловые перемещения вокруг одной из координатных осей. Реализация угловых перемещений производится постпроцессором и зависит от того, каким органом станка производится поворот − шпиндельной головкой или столом. Наиболее значительной из семейства многокоординатных САП является разработанная в 1961 г. в США система APT (Automatically Programmed Tools).
Следующий критерий классификации − по уровню принятия решений
− определяет уровень автоматизации решаемых в САП технологических задач. К технологическим задачам относятся реализация типовых технологических циклов точения, сверления, нарезания резьбы, фрезерования кругового и прямоугольного (внутреннего и наружного), фрезерования пазов и карманов, разбиения припуска на проходы, расчет режимов резания и др.
В настоящее время трудно назвать САП, в которой не решалась бы одна из названных задач. Поэтому основной принцип классификации по этому критерию
 состоит в том, является автоматизация технологических задач свойством, заложенным в концепцию САП при ее разработке, или такая автоматизация реализована на основе библиотеки типовых технологических процедур. В большинстве САП (например, САП-CM, APT, FAPT, IFAPT, MODAPT) автоматизация технологических задач решается при помощи технологических процедур. Среди САП со встроенной автоматизацией технологических задач можно назвать ЕСПС-ТАУ, Техтран-Т, Autotech, ЕХАРТ (ФРГ), FANUC-3T и MAZATROL (Япония). состоит в том, является автоматизация технологических задач свойством, заложенным в концепцию САП при ее разработке, или такая автоматизация реализована на основе библиотеки типовых технологических процедур. В большинстве САП (например, САП-CM, APT, FAPT, IFAPT, MODAPT) автоматизация технологических задач решается при помощи технологических процедур. Среди САП со встроенной автоматизацией технологических задач можно назвать ЕСПС-ТАУ, Техтран-Т, Autotech, ЕХАРТ (ФРГ), FANUC-3T и MAZATROL (Япония).
В зависимости от области применения
САП можно разделить на универсальные и специализированные. Универсальные САП − это системы широкого назначения, с развитым входным языком, позволяющим разрабатывать программы, имеющие сложную логическую структуру, описывать обработку произвольных контуров, производить математические вычисления, а также создавать типовые технологические процедуры для различных классов оборудования. APT является типичной САП этого класса. Она представляет собой обобщенную универсальную САП, предназначенную для программирования обработки сложных поверхностей, с управлением по трем и пяти осям [5]. APT является прототипом семейства САП, разработанных в различных странах, в том числе в СССР. В частности, за основу языка Техтран было взято подмножество языка APT. APT позволяет программировать обработку поверхностей типа конусов, цилиндров, поверхностей второго порядка (эллипсоид, эллиптический конус, гиперболический параболоид и др.), линейчатых и каркасных поверхностей, сфер. APT является многофункциональной системой, но основными областями ее эффективного применения являются авиа-, судо- и автомобилестроение, где наиболее часто встречается обработка сложных поверхностей (например, формообразующих элементов штампов, гребных винтов, элементов конструкций самолета и др.). Несмотря на высокую производительность и большие возможности, система APT не нашла широкого применения вследствие сложности в изучении и эксплуатации
[5].
Специализированные САП классифицируются по видам обработки (токарной, фрезерной, сверлильно-расточной и др.). Последние годы развитие САП идет по пути создания специализированных систем с высоким уровнем автоматизации решения технологических задач.
В ФРГ разработаны семейства САП ЕХАРТ, состоящие из технологически ориентированных подсистем, в основу которых были положены концепции APT [18].
Типичным представителем специализированных САП является ЕХАРТ (ФРГ). ЕХАРТ состоит из трех подсистем. ЕХАРТ-М01 (Basic - ЕХАРТ) - универсальная САП − ядро системы; ЕХАРТ-М02 − специализированная, технологически ориентированная САП для токарных станков, ЕХАРТ-МОЗ − для сверлильных, фрезерных и станков типа обрабатывающий центр. Программирование в ЕХАРТ-М02 состоит из следующих этапов: описания геометрии детали, описания технологических переходов, описания процесса обработки. При этом автоматизировано решение следующих задач: разбиение на проходы, расчет режимов резания, построение траектории движения инструмента при черновой и чистовой обработке, контроль на наличие столкновений.
В ЕХАРТ-МОЗ автоматизированы задачи выбора инструмента, расчета ходов инструмента при позиционной и контурной обработке, расчет режимов резания, контроль на наличие столкновений.
Система ЕХАРТ является наиболее типичным представителем семейства специализированных САП. Среди множества других САП можно назвать ориентированную на токарную обработку TAUPROG (Венгрия) и отечественные ЕСПС-ТАУ для сверлильных, токарных и фрезерных работ и Техтран-Т для токарных работ, в которых также решены перечисленные технологические задачи.
В настоящее время выпускаются системы ЧПУ типа CNC со встроенными САП − программаторы. Программаторы − это специализированные САП, предназначенные для оперативной подготовки УП непосредственно на станке. Это позволяет сократить простои станка за счет совмещения обработки детали с разработкой, отладкой и редактированием другой УП. Наибольший интерес представляют системы BOSCH-PEG (ФРГ) и FANUC-3T (Япония) − для токарных станков, FANUC 6M-MODEL Е и MAZATROL-M (Япония) − для обрабатывающих центров [14, 16].
По форме представления исходных данных
можно выделить САП со свободной структурой представления, с табличной формой и представлением в форме «меню».
Большинство известных САП имеют свободную форму представления исходных данных. Программа на языке таких САП представляет собой множество операторов, состоящих из элементов языка (служебных слов, идентификаторов, специальных символов и т. д.) и строящихся по заданному синтаксису (например, входные языки многих из названных САП соответствуют синтаксису языка APT). В дальнейшем для удобства будем отождествлять названия САП и ее входного языка.
При табличной форме представления технолог заполняет специальные бланки в форме таблиц. Каждая графа таблицы соответствует определенному виду исходных данных, например, геометрии детали, технологическим командам, управляющей информации и т. д. Имеются также САП, сочетающие обе формы представления (САДКО, АППР-АРМ).
Представления в форме «меню» − это свойство интерактивных САП. С экрана дисплея в определенном формате запрашивается требуемая информация. Технологу остается только заполнить соответствующие графы, высвечиваемые на экране дисплея, или ответить на задаваемые системой вопросы. Наиболее перспективными являются САП, сочетающие представление исходных данных со свободной структурой и в форме «меню», например, в системе ТС-АРТ [20].
Последний критерий классификации САП − по режиму работы.
В настоящее время существуют два основных режима работы САП: пакетный и интерактивный, которые находятся в прямой зависимости от типа ЭВМ и операционной системы, для которых реализована данная САП. Первые САП работали в пакетном режиме. Программа, подготовленная технологом на входном языке САП и записанная на магнитный носитель, перфоленту или перфокарты, полностью вводилась в ЭВМ и преобразовывалась в УП для станка. В случае ошибок в исходной программе эта процедура повторялась.
Разработка интерактивных САП является следствием развития вычислительной техники − появлением алфавитных и графических дисплеев, а также мини- и микро-ЭВМ. Исходные данные в интерактивных САП задаются в форме «меню» или в режиме «вопрос − ответ». Существуют интерактивные САП и со свободной формой представления (например, FAPT, где последовательно после ввода каждого оператора можно получить на экране дисплеев или печатающем устройстве результат его выполнения). Значительное преимущество таких САП перед пакетными состоит в сокращении сроков обучения технологов-программистов и технологов-операторов методам программирования за счет диалога и возможности повторения расчета УП с любой исходной позиции. Недостатком их является отсутствие универсальности в подходе к разработке УП вследствие того, что диалог ограничивает разработчика в выборе средств для решения задачи. Интерактивные САП эффективны при эксплуатации в производствах с невысокой сложностью и высоким уровнем унификации изготавливаемых деталей или их элементов.
Представленная классификация САП является попыткой систематизировать накопленный опыт и направления развития данной области инженерной деятельности за последние годы и носит условный характер. В последующие годы параллельно с развитием диалоговых, оперативных систем подготовки УП непосредственно у станка дальнейшее развитие получат системы программирования, работающие в комплексных системах автоматизированного проектирования и производства (CAD/CAM − Computer Aided. Design/Computer Aided Manufacturing).
Комплексная система состоит из ряда подсистем, с помощью которых производится формирование цифровой модели детали, вычерчивание рабочих чертежей и эскизов на графопостроителях, проектирование технологического процесса и формирование управляющей программы [19]. Объединение этих процессов в единый непрерывный процесс переработки информации и управления технологическими процессами и оборудованием дает ряд преимуществ перед описанными ранее системами и методами. Преимущества эти следующие: сокращение затрат и времени на подготовку УП; повышение качества УП; повышение эффективности использования оборудования с ЧПУ за счет быстрой загрузки программ в память системы ЧПУ и отсутствие брака в УП; высвобождение технологов-программистов, занимающихся разработкой УП; сокращение сроков подготовки производства новых изделий.
В частности, имеется опыт создания комплексной системы проектирования технологических процессов и подготовки УП для номенклатуры деталей тел вращения, функционирующей в условиях гибкой производственной системы «Группроцесс-Техтран». Подробное описание перечисленных САП приведено в работах [1, 3, 5, 7, 10, 12, 13, 14, 16, 20, 22, 23].
1.2 Структура и функциональные возможности САП Техтран
В основу организации САП Техтран был положен традиционный подход. Система состоит из входного языка, процессора, промежуточного языка и постпроцессоров. При разработке системы преследовалось несколько целей. Во-первых, САП должна быть простой в обслуживании, т. е. вмешательство оператора должно быть сведено к минимуму. Во-вторых, САП должна быть мобильной (это позволяет минимизировать затраты при адаптации САП для различных классов ЭВМ и операционных систем). В-третьих, САП должна допускать расширение выполняемых функций.
Необходимую гибкость САП Техтран приобрела благодаря модульной структуре. Для уменьшения объема оперативной памяти процессор и постпроцессор выполняют обработку данных за несколько проходов: процессор построен по трехпроходной схеме, постпроцессоры − по двухпроходной схеме. Модульная структура дает возможность вводить новые функции без существенной корректировки ранее написанных программ. Кроме того, такая структура позволяет организовать перекрытия и уменьшить тем самым объем оперативной памяти.
Требование мобильности программного обеспечения предопределило выбор языка программирования. Поскольку ко времени начала разработки (1975 г.) и вплоть
 до настоящего времени единственным языком программирования, компиляторы которого входят в состав всех операционных систем и обеспечивают необходимое качество объектного кода, был и остается Фортран, то именно ему и было отдано предпочтение. Около 95 %
программ, составляющих САП Техтран, написано на Фортране, остальные − на Ассемблере. В настоящее время синхронные версии системы эксплуатируются на ЭВМ типа ЕС с операционной системой ОС ЕС и СМ с операционной системой ОС РВ. до настоящего времени единственным языком программирования, компиляторы которого входят в состав всех операционных систем и обеспечивают необходимое качество объектного кода, был и остается Фортран, то именно ему и было отдано предпочтение. Около 95 %
программ, составляющих САП Техтран, написано на Фортране, остальные − на Ассемблере. В настоящее время синхронные версии системы эксплуатируются на ЭВМ типа ЕС с операционной системой ОС ЕС и СМ с операционной системой ОС РВ.
 Процессор
осуществляет ввод и трансляцию исходной программы на входном языке системы, выполняет заданные геометрические построения и рассчитывает траекторию движения центра инструмента. Результаты расчета выводятся в файл CLDATA. Структура процессора системы Техтран приведена на рис. 1.3. Процессор организован в виде трех последовательно выполняемых модулей: компилятора, интерпретатора и интерполятора. Каждый модуль может рассматриваться как законченная программа. Обмен данными между модулями производится только через промежуточные файлы на диске. Процессор
осуществляет ввод и трансляцию исходной программы на входном языке системы, выполняет заданные геометрические построения и рассчитывает траекторию движения центра инструмента. Результаты расчета выводятся в файл CLDATA. Структура процессора системы Техтран приведена на рис. 1.3. Процессор организован в виде трех последовательно выполняемых модулей: компилятора, интерпретатора и интерполятора. Каждый модуль может рассматриваться как законченная программа. Обмен данными между модулями производится только через промежуточные файлы на диске.
Компилятор вводит программу на Техтране, предварительно записанную на диск, и выполняет ее синтаксический контроль. На этапе компиляции проверяется, правильно ли заданы имена и служебные слова в программе, соблюдены ли требуемые форматы. Если часть текста оформлена в виде отдельного файла, то компилятор вставляет этот текст в исходную программу. Макросредства дают программисту возможность описывать типовые элементы в параметрическом виде и хранить их на магнитном диске. В процессе макрогенерации компилятор выполняет вставку тела макроса в исходную программу и заменяет формальные параметры фактическими значениями. Если обнаружена ошибка, то компилятор отмечает ее место в строке и печатает диагностическое сообщение. Затем он переходит к следующему оператору, чтобы за один прогон выявить максимальное число ошибок. Файл синтаксических
таблиц содержит описание форматов операторов Техтрана и служит для управления работой компилятора. Тексты сообщений об ошибках также хранятся на магнитном диске. Компилятор формирует на диске рабочую программу интерпретатора, в которой арифметические выражения преобразованы в польскую инверсную запись, геометрические определения преобразованы во внутренний формат и заданные в них модификаторы упорядочены. В процессе макрогенерации используется рабочий файл на диске.
Интерпретатор производит расчет канонических форм геометрических объектов. Другой функцией интерпретатора является вычисление значений арифметических и логических выражений и стандартных функций. Если в программе были использованы операторы цикла и операторы передачи управления, то интерпретатор выполняет эти операторы и тем самым приводит исходную программу к линейной. Рабочая программа интерполятора, формируемая интерпретатором, будет содержать только таблицу геометрических объектов, операторы движения и операторы постпроцессора. Интерпретатор может выполнять трассировку, т. е. распечатывать значения переменных и переходов в программе. Если в исходной программе были определены контуры, то их описания во внутреннем формате выводятся в специальный файл. При обнаружении ошибки в программе интерпретатор печатает диагностическое сообщение и продолжает обработку до заданного числа ошибок.
Интерполятор обрабатывает операторы движения и рассчитывает эквидистантную траекторию с учетом диаметра рабочего инструмента. Если интерполятор обнаруживает ошибку, то он выдает диагностическое сообщение и продолжает обработку от следующего оператора поточечного движения до заданного числа ошибок. В процессе вычислений интерполятор использует рабочую программу и файл контуров, подготовленные интерпретатором, а также файл сообщений об ошибках. Операторы постпроцессора не обрабатываются и передаются в выходной файл. Выходные данные интерполятора формируются в стандартном формате CLDATA.
Процессор рассчитан на обработку группы исходных программ за один проход. Каждый модуль процессора за один вызов обрабатывает всю группу. Программы, в которых на стадии компиляции или интерпретации обнаружены ошибки, удаляются из соответствующего выходного файла и не поступают на дальнейшую обработку. Программы с ошибками в операторах движения выводятся в файл CLDATA, но место ошибки отмечается специальной записью.
Постпроцессоры
выполняют следующие функции: чтение файла CLDATA, подготовленного процессором, и синтаксический контроль операторов постпроцессора; перевод геометрических данных в систему координат станка; проверку длины перемещений, допустимости подач и оборотов; расчет кодов подач, кодов оборотов шпинделя, коррекции; учет динамических характеристик оборудования; формирование и вывод на печать и перфоленту управляющей программы и другие функции. - САП Техтран оснащена рядом постпроцессоров, каждый из которых формирует управляющие программы для определенной системы управления. Настройка постпроцессора на конкретную модель станка производится с помощью паспорта. Структура постпроцессора приведена на рис К 4.

 Постпроцессоры построены по двухпроходной схеме. Программа первого прохода РР1
читает записи CLDATA, сглаживает траекторию, проверяет, принадлежат ли перемещения рабочей зоне станка, рассчитывает вектор коррекции и формирует в рабочем файле 1 исходные данные для второго прохода. Программа второго прохода Рсс1
выполняет синтаксический контроль операторов постпроцессора, учитывает динамические особенности оборудования, формирует на диске образ управляющей программы и другие рабочие файлы, распечатывает управляющую программу и инструкцию оператору станка. Постпроцессор формирует три рабочих файла, каждый из которых обрабатывается специальной программой: Постпроцессоры построены по двухпроходной схеме. Программа первого прохода РР1
читает записи CLDATA, сглаживает траекторию, проверяет, принадлежат ли перемещения рабочей зоне станка, рассчитывает вектор коррекции и формирует в рабочем файле 1 исходные данные для второго прохода. Программа второго прохода Рсс1
выполняет синтаксический контроль операторов постпроцессора, учитывает динамические особенности оборудования, формирует на диске образ управляющей программы и другие рабочие файлы, распечатывает управляющую программу и инструкцию оператору станка. Постпроцессор формирует три рабочих файла, каждый из которых обрабатывается специальной программой:
рабочий файл 2
содержит коды сообщений об ошибках; он обрабатывается программой РРЗ,
которая печатает таблицу сообщений об ошибках и таблицу недопустимых для данного станка операторов; рабочий файл 3
содержит таблицу инструментов; он обрабатывается программой РР5, которая печатает таблицу инструмента и таблицу времени работы каждого инструмента; рабочий файл 4
содержит управляющую программу во внутреннем формате (во внутреннем коде ЭВМ); он обрабатывается программой РР4, которая выполняет перекодировку в код системы ЧПУ и перфорирует ее.
Пользователям САП Техтран предоставлена возможность заполнять паспорта для имеющегося у них оборудования с ЧПУ при условии, что в составе библиотеки постпроцессоров имеется модуль для требуемой системы управления.
Для работы с паспортами предназначена подсистема Вопросник, состоящая из четырех программ. Структура Вопросника показана на рис. 1.5. Паспорт состоит из двух частей − характеристик оборудования и таблиц. Каждая часть паспорта обрабатывается двумя программами: одна предназначена для записи паспорта (TQ08
и TQ10),
другая − для его распечатки (TQ07
и TQ09).
Вопросник читает исходный текст паспорта и проверяет форматы и значения данных. После перекодировки паспорт в двоичном формате записывается в файл паспортов, который используется при прогоне постпроцессоров.
Графический контроль в САП Техтран решен с помощью постпроцессоров, которые либо формируют перфоленту для графопостроителей, работающих в автономном режиме, либо непосредственно выводят на экран или бумагу траекторию перемещения центра режущего инструмента.
Технологический процессор
является расширением геометрического процессора Техтран в части программирования технологических переходов, а входной язык технологического процессора − расширением базового языка, который дополняется технологическими операторами. Выделение геометрического процессора в автономный модуль позволило определить пути такого расширения системы Техтран, при котором ядро остается неизменным. Расширение функций системы осуществляется включением технологических процессоров специального назначения. Положение технологического процессора в системе Техтран показано на рис. 1.6.
Процессор формирует файл CLDATA1
, в котором содержатся геометрические и технологические данные. Технологические операторы обрабатываются процессором так же, как и операторы постпроцессора: процессор заменяет служебные слова их внутренними кодами и вычисляет арифметические выражения. Расширенный файл CLDATA1
обрабатывается технологическим процессором, на выходе которого формируется файл CLDATA2,
содержащий траекторию движения инструмента и операторы постпроцессора.
Принцип расширения функций системы Техтран реализован в системе Техтран-Т − технологическом процессоре для программирования токарных переходов.

1
Идентификация постпроцессоров осуществляется с помощью двухсимвольного кода постпроцессора ее. Например, постпроцессор для системы управления Н-33 называется Ml, а для системы Н-22− L1.
Глава 2
ВХОДНОЙ ЯЗЫК ТЕХТРАН
2.1 Основные понятия
Программа. Структура программы.
Программа на Техтране представляет собой последовательность операторов и комментариев, описывающих алгоритм обработки деталей. Программа имеет следующую структуру: ДЕТАЛЬ литерал
текст программы
КОНЕЦ
Литерал (см. п. 2.2) задает имя программы. В программу могут быть вставлены фрагменты исходного текста и тексты макросов. Программе на входном языке Техтран может соответствовать одна или несколько управляющих программ. Исходный текст программы состоит из последовательности строк. Максимальное число символов в строке равно 72. В одной строке может быть записан один или несколько операторов, между которыми должен стоять символ «точка с запятой» (;). Все символы текущего оператора должны размещаться до 72-й позиции. В противном случае часть оператора может быть перенесена на следующую строку. Для этого, после прерванной части оператора (до 72-й позиции) необходимо записать символ продолжения «процент» (%). Для совместимости с предыдущими версиями языка разрешается в качестве" символа продолжения использовать знак «коммерческое И» с пробелом (&_). Число строк продолжения не ограничивается.
Текст оператора или комментария может начинаться с любой позиции. Число пробелов между операндами не ограничено. В качестве разделителя операндов вместо запятой можно использовать пробел (_). ДЛЯ удобства чтения программ и ускорения их отладки рекомендуется располагать операторы и комментарии таким образом, чтобы текст программы являлся документом, по которому можно понять структуру и назначение программы. Желательно, чтобы имена меток и переменных, используемых в программе, отражали их назначение.
Для выделения функциональных частей программы рекомендуется использовать строки, состоящие из пробелов, знаков комментария, а также отступов.
Символические имена.
Для идентификации в программе переменных величин (геометрических, вещественных, логических, меток операторов, имен макросов) используют символические имена Символическое имя − это последовательность букв и цифр, начинающаяся с буквы. Длина его не должна превышать восьми символов. Пробелы внутри имени не разрешены. Символическое имя должно быть уникальным в программе и описывать один объект или класс объектов, например:
АБ − верно
КР15 − верно
К152АБ − верно
К 1 − неверно
К123455678910 − неверно
123К22− неверно
Операторы, метки, комментарии.
Оператор − основная функциональная единица языка. Он предназначен как для описания операций, которые предстоит выполнить, так и для установления свойств данных, идентифицируемых с помощью символических имен. Любой оператор может быть помечен меткой, для того чтобы на него можно было сослаться в других операторах данной программы.
Метка является символическим именем. Она должна предшествовать помечаемому оператору и может находиться либо в одной строке с. оператором, либо на отдельной строке. После метки всегда должен быть служебный символ «двоеточие» (:). Метка используется в операторах НАМЕТКУ.
Для пояснения действий, выполняемых в программе, используют комментарии. Комментарий не обрабатывается процессором, а только выводится на печать при распечатке исходного текста. Комментарий может находиться как в одной строке с операторами исходной программы, так и занимать целую строку. Для выделения текста комментария нужно поставить перед ним служебный символ «номер» (#).
2.2 Структура языка
Алфавит языка.
Для записи программы используют следующие символы: буквы русского алфавита А−Я; буквы латинского алфавита А−Z; цифры: 0, 1,2, 3, 4, 5, 6, 7, 8, 9; символы: «_» − пробел; «,» − запятая; «• » − точка; « = » − равно; « + » − плюс; « − » − минус; «*» − звездочка; «/» − наклонная черта; «&» − коммерческое «И»; «;» − точка с запятой; «(» − левая скобка; «)» − правая скобка; «:» − двоеточие; «'» − апостроф; «=#=» − номер; «%» − процент.
Синтаксис языка.
В связи с тем, что в описании языка не приводится формального описания синтаксиса Техтрана, этот раздел содержит основные правила и обозначения, используемые для описания форматов его операторов. Каждый оператор входного языка, формируется из операндов в соответствии с синтаксическими правилами языка. В описании языка приведена структура каждого оператора (формат).
При описании формата каждого оператора использованы следующие правила и условные обозначения:
прописные буквы используют для обозначения служебных слов;
строчные буквы используют для обозначения опорных элементов, числовых значений
параметров или арифметических выражений; необязательные служебные слова заключают в квадратные скобки [ ];
возможные варианты записи модификаторов, являющиеся альтернативными, заключают в
фигурные скобки { } и записывают в столбец или разделяют символом « | »; параметры, назначающие линейные и угловые размеры, задаются целыми и десятичными
долями миллиметров и градусов.
Элементы языка.
В языке разницы между целыми и вещественными числами не существует. Число
представляется в виде последовательности цифр, среди которых может встретиться точка или буква Е. Точка отделяет целую часть числа от дробной, а буква Е − мантиссу числа от его порядка. Перед самим числом и перед его порядком может стоять знак «минус» (.−). Пробелы и другие символы внутри числа недопустимы, например: 1.23 − верно; 2.15Е5 − верно; −ЗЕ−6 − верно; 3 Е2 − неверно; Е4 − неверно.
Служебные слова
являются зарезервированными словами и составляют словарь языка Техтран. Они используются для написания операторов программы и состоят только из букв русского алфавита. Служебные слова делятся на главные, вспомогательные и модификаторы. Главное слово определяет тип оператора. Вспомогательное слово и модификатор служат для однозначного задания оператора. Служебное слово не может использоваться в качестве имени, переменной или метки. Список служебных слов приведен в Приложениях 1−4.
Переменная
в Техтране − это символическое изображение величины, которая может принимать различные значения. Основными характеристиками переменной являются ее имя и тип.
В группу служебных символов
входят следующие символы: «_», « + », «−», «*», «/», « = », «;», «.», «,», «:», «'», «#», «&», «( )»,
«%». Употребление служебных символов в программе зависит от контекста. Описание их функций производится по мере надобности в соответствующих разделах.
Литералом
является заключенный в апострофы произвольный текст, не содержащий символа ф.
В литералах могут быть использованы любые символы (например, латинские буквы, !, > , < и т. п.). При необходимости использования апострофа его нужно записать два раза подряд, например, 'АВСДЕ" РОН' определяет литерал, состоящий из символов АВСДЕ' РОН. В основном литералы используются для задания текстовых параметров макросов, но кроме этого имеются и некоторые другие применения, например, в операторах ДЕТАЛЬ, СТАНОК и др.
2.3 Типы данных.
Возможности языка программирования в значительной степени определяются набором допустимых типов данных. Входной язык Техтран допускает применение следующих типов данных: вещественный, логический, вектор, прямая, точка, окружность, плоскость, матрица, контур. Тип каждой используемой в программе переменной фиксирован, и на протяжении всей программы каждая переменная обозначает данное только одного типа. Тип переменной описывается явно строкой вида:
тип имя
1, имя
2, имя
3, …
где тип
есть: ВЕЩ, ЛОГИЧ, ТОЧКА, ПРЯМАЯ, ВЕКТОР, ОКРУЖИ, ПЛОСК, МАТР,
КОНТУР; имя
1, имя
2, имя
3,
...− имена переменных.
Переопределение типа переменной в программе не разрешено. Если в программе встречается переменная, не описанная ранее, то имя переменной, начинающееся с символов ТЧ, считается неявно описанным, как точка; имя, начинающееся с ПР,− как прямая, с КР,− как окружность. Все остальные имена переменных определяются неявным образом, как вещественные числа.
Можно совмещать описание типа переменной и оператор присваивания, например, оператор ТОЧКА Т1 =0, 1, 2 равносилен двум операторам: ТОЧКА Tl; T1 =0, 1, 2.
2.4 Массивы
Данные одного типа могут объединяться в массивы. Массивы могут быть одномерными и двумерными. Каждый используемый в программе массив должен быть описан с указанием типа, числа индексов (размерности массива) и максимального значения каждого из индексов. Минимальным значением индекса является единица.
Оператор ВЕЩ А (16) описывает одномерный массив А, состоящий из 16 вещественных чисел. Оператор ВЕЩ В (5, 6) описывает двумерный массив, состоящий из 30 вещественных чисел. Для использования элементов массива в вычислениях следует указать имя массива, а за ним в круглых скобках − значение индексов. Индекс не может быть опущен. В частности, одно имя не представляет первый элемент массива.
В качестве индекса может использоваться любое арифметическое выражение. Число индексов и их значения должны соответствовать описанию массива. Число элементов в массиве не ограничено. Например, если значение переменной И = 2, то запись В (3, И + 3) именует элемент массива В (3,5), а запись вида В (3) также, как и запись В (1,6 + И), вызывает ошибку трансляции. В качестве элементов массива не могут использоваться объекты типов МАТР и КОНТУР.
2.5 Выражения
Арифметические выражения.
Вместо чисел в программе могут использоваться арифметические выражения. Простейшими арифметическими выражениями могут быть число; вещественная переменная; элемент вещественного массива; обращение к стандартной функции; выражение, заключенное в скобки.
Более сложные арифметические выражения могут быть образованы из простейших при помощи следующих знаков арифметических операций: « + » − сложение; « −> − вычитание; «*» − умножение; «/» − деление; «**» − возведение в степень.
Операции выполняются слева направо в соответствии с приведенными ниже приоритетами операций: вычисление функций− 1; возведение в степень − 2; умножение и деление − 3; сложение и вычитание − 4.
Приоритет используется для того, чтобы определить, какая из двух последовательных операций выполняется первой. Для изменения порядка вычислений следует применять круглые скобки.
П р и м е ч а н и е . При возведении в степень следует помнить, что отрицательное число допускается возводить только в целую степень.
 6a2 2b(c3-d3) Например, выражение записывается на входном языке Техтран так: 6a2 2b(c3-d3) Например, выражение записывается на входном языке Техтран так:
(a -\-b)sinf
(6*А**2 + 2*В* (С**3- Д**3)) / ((АА**2 + В**2) * СИН (Ф)).
Логические выражения.
Язык Техтран допускает использование логических выражений в условных операторах (ЕСЛИ), операторах цикла (ПОВТОР), операторах логического присваивания. Значением логического выражения является ЛОЖЬ или ИСТИНА.
Простейшее логическое выражение состоит из логического первичного. Логическим первичным может быть: логическая константа ЛОЖЬ и ИСТИНА; логическая переменная; элемент логического массива; оператор корректности; отношение; логическое выражение, заключенное в скобки:
Отношения образуются путем объединения двух арифметических выражений с помощью операций отношения. Шесть операций отношения изображаются следующим образом:
БЛШ или> − больше (> )
БРВ или > = − больше или равно (≥) МНШ или < − меньше (<)
МРВ или < = − меньше или равно (≤)
РВН или = − равно ( = ) НРВ или < > или < > − не равно (≠)
Например, выражение (К+1) РВН5 принимает значение ИСТИНА при К=4, в остальных случаях принимает значение ложь.
Логические выражения образуются из логических первичных путем использования логических операций. В языке Техтран существуют три логические операции: НЕ − отрицание; ЛИ − логическое умножение; ИЛИ − логическое сложение.
Вычисление логического выражения производится слева направо в соответствии с приведенными ниже приоритетами операций: вычисление функций−1; возведение в степень − 2; умножение и деление − 3; сложение и вычитание − 4; операции отношения БЛШ, БРВ, МНШ, МРВ, РВН, НРВ − 5; НЕ − 6; ЛИ − 7; ИЛИ − 8.
Для изменения порядка вычислений можно использовать круглые скобки. Логическое выражение, к которому относится операция НЕ, должно заключаться в скобки, если оно содержит не менее двух операндов.
2.6 Стандартные функции
Язык Техтран содержит ряд стандартных математических функций, часто используемых при вычислениях. Вызов математической функции производится указанием в арифметическом выражении имени функции и ее аргументов (параметров). Результат, вычисленный функцией, замещает в выражении обращение к ней. Стандартные функции в языке могут быть вещественного (табл. 2.1) и логического (табл. 2.2) типов.
Таблица 2.1
| Имя
|
Функция
|
Аргумент
|
Результат
|
| СИН
КОС
ТАН
АСИН
АКОС
АТАН
KBКОР
ЕХР ЛОГ
АБС
МОДВ
ЦЕЛ
УГОЛВ
PACT
КООРД
СКАЛПР
ДИСТ
УГОЛПР
ЛОГ10
|
Вычисление синуса
» косинуса
» тангенса
» арксинуса
» арккосинуса
» арктангенса
Извлечение квадратного корня
Вычисление экспоненты е*
Вычисление натурального логарифма
Вычисление абсолютного значения величины
Вычисление модуля век- тора
Выделение целой части переменной
Вычисление угла между двумя векторами
Вычисление расстояния между двумя точками
Извлечение составляющей канонической формы
Вычисление скалярного произведения
Вычисление расстояния от точки до прямой
Вычисление угла между прямыми
Вычисление десятичного логарифма числа
|
число
»
»
»
»
»
»
число (х)
число
»
вектор
число
или имя
вектор1
, вектор2
точка1
, точка2
число
(а), имя
вектор1
, вектор2
точка, прямая
прямая1
, прямая2
число (а)
|
Синус
Косинус
Тангенс
Арксинус
Арккосинус
Арктангенс
Квадратный корень числа
е*
Натуральный логарифм числа
Абсолютное значение ве- личины
Модуль вектора
Целая часть числа или переменной с заданным именем
Угол между двумя век- торами
Расстояние между двумя точками
Составляющая под номе- ром «а» канонической фор- мы геометрического объек- та с заданным именем
Скалярное произведение векторов
Расстояние между точкой и прямой
Угол между прямыми
lga
|
| П р и м е ч а н и я : 1. Аргументы заключаются в круглые скобки и перечисляются через запятую. 2. Вместо чисел и имен переменных в качестве аргументов могут использоваться арифметические выражения и вложенные определения. 3. Угол между векторами или прямыми отсчитывается от элемента, заданного в качестве первого аргумента. 4. Значения стандартных функций могут использоваться в качестве оператора.
|
Таблица 2.2

Пример использования логической функции КОРР: ЛОГИЧ А = КОРР ТОЧКА ТЧ1 (ПЕРЕСЕЧ, ПР1, КР1, УБ) ЕСЛИ (НЕ А) ТЧ1=ТЧ0.
Переменной ТЧ1 присваивается значение одной из точек пересечения окружности и прямой, если они пересекаются; в противном случае переменной ТЧ1 присваивается значение переменной ТЧО.
2.7 Оператор присваивания
Для присваивания значения переменным используется оператор присваивания. Он состоит из левой части, знака равенства и правой части. В результате выполнения оператора присваивания значение правой части присваивается переменной, находящейся в левой части (тип левой части должен допускать такое присваивание). Если в левой части стоит переменная вещественного (логического) типа, то и в правой части должно стоять арифметическое (логическое) выражение. Например: оператор Х = Х+1 − правильный оператор присваивания, в результате выполнения которого значение переменной X будет увеличено на 1.
2.8 Система координат
 В системе Техтран все объекты и траектория движения рассматриваются и описываются в правосторонней прямоугольной системе координат (см. рис. 2.1). На рис. 2.2, а
− в
приведены примеры отсчета координат на плоскости (рис. 2.2, а), в пространстве (рис. 2.2,6) и угловых размеров (рис. 2.2, в). Определяемые прямые и окружности всегда находятся в горизонтальной плоскости хОу,
поэтому описания геометрии и движения по контуру и поверхности детали не должны зависеть от системы координат конкретного станка. Рассчитанные процессором системы перемещения (координаты) приводятся в соответствие с фактическими направлениями и адресами координат станка при работе постпроцессора, формирующего управляющую программу. В системе Техтран все объекты и траектория движения рассматриваются и описываются в правосторонней прямоугольной системе координат (см. рис. 2.1). На рис. 2.2, а
− в
приведены примеры отсчета координат на плоскости (рис. 2.2, а), в пространстве (рис. 2.2,6) и угловых размеров (рис. 2.2, в). Определяемые прямые и окружности всегда находятся в горизонтальной плоскости хОу,
поэтому описания геометрии и движения по контуру и поверхности детали не должны зависеть от системы координат конкретного станка. Рассчитанные процессором системы перемещения (координаты) приводятся в соответствие с фактическими направлениями и адресами координат станка при работе постпроцессора, формирующего управляющую программу.
На рис. 2.3, а − г приведены примеры перехода от системы координат детали к системе координат станка для токарных
(рис. 2.3, а, б) и фрезерных (рис. 2.3, в, г)
станков.

2.9 Геометрические определения
Геометрическое определение является оператором присваивания, в левой части которого находится символическое имя определяемого геометрического объекта, а в правой − один из вариантов задания этого объекта в строгом соответствии с форматом, приведенным в данном разделе.
В общем виде геометрическое определение имеет следующий формат:
тип имя
= список параметров
где тип
− служебное слово, определяющее тип геометрического объекта; имя
−
символическое имя определяемого геометрического объекта.
Параметрами, определяющими геометрический объект, являются имена опорных элементов или вложенные геометрические определения, модификаторы, числа или заменяющие их арифметические выражения (опорным элементом называют ранее определенный геометрический объект).
Служебными словами, определяющими тип геометрического объекта, являются ТОЧКА, ПРЯМАЯ, ОКРУЖИ, ВЕКТОР, МАТР, ПЛОСК. Служебное слово, определяющее тип геометрического объекта, может отсутствовать, если тип объекта был указан ранее явно (отдельной строкой) или если используется символическое имя, определяющее тип геометрического объекта неявно.
2.9.1 Внутреннее представление геометрических объектов
Для внутреннего представления геометрических объектов в процессоре системы Техтран используются канонические формы (табл. 2.3). Таблица 2.3
Тип объекта Внутреннее представление
Точка х, у, z
− координаты точки
Прямая cos α, sin α, р
− коэффициенты нормального управления прямой (х cosα + y sinα − р = 0)
Окружность х, у, r
− координаты центра окружности и ее радиус
Вектор Δх, Δу, Δг − проекции вектора на координатные оси
Плоскость cosα, cosβ, cosγ, p
− коэффициенты нормального уравнения плоскости
(х
cos a + y
cosβ + z cosγ
− p = 0)
 Матрица a11
, a12
, ..., а34
− коэффициенты нормальных уравнений координатных плоскостей системы координат, полученной при преобразовании исходной системы координат в соответствии с заданной матрицей Матрица a11
, a12
, ..., а34
− коэффициенты нормальных уравнений координатных плоскостей системы координат, полученной при преобразовании исходной системы координат в соответствии с заданной матрицей
Внутреннее представление геометрических объектов применяют при выводе на печать результатов работы процессора в случае использования отладочных операторов СЛЕД и ПЧТ1 (см. п. 2.12.2). Для доступа к элементам канонической формы точек, прямых, окружностей и
 векторов следует использовать функцию КООРД. Например, требуется определить прямую, проходящую через центры двух окружностей, координаты которых неизвестны (рис. 2.4). Найдем эти координаты следующим образом: векторов следует использовать функцию КООРД. Например, требуется определить прямую, проходящую через центры двух окружностей, координаты которых неизвестны (рис. 2.4). Найдем эти координаты следующим образом:
X1 = КООРД (1.КР1)
У1 = КООРД (2, КР1)
Х2 = КООРД (1,КР2)
У2 = КООРД (2, КР2)
Искомая прямая имеет вид ПРА = Х1, У1, Х2, У2.
2.9.2 Определение точки
В определениях точки используют следующие группы модификаторов:
Модификаторы выбора точки из двух возможных: ХБ − выбирается точка с большей координатой х,
УБ − с большей координатой у,
ХМ − с меньшей координатой х
и УМ − с меньшей координатой у.
Модификаторы направления отсчета угла: ПОЧС − задается отсчет угла по часовой стрелке; ПРЧС − задается отсчет угла против часовой стрелки.
Модификаторы, указывающие координату точки, заданную в геометрическом определении:
ХКООРД − координата х;
УКООРД − координата у.
Точка, определенная прямоугольными координатами:
имя = координата х, координата у, координата z имя. = координата х, координата у
Например (рис. 2.5): ТЧА=-5, 15, 10.7
ТОЧКА Т3 = 24, -8,2 Точка, определенная пересечением двух прямых:
имя =
[ПЕРЕСЕЧ,] прямая1
, прямая2
Например (рис. 2.6):
ТЧ2 = ПР1, ПР2 Точка, определенная пересечением прямой и окружности:
имя =
[ПЕРЕСЕЧ,] прямая, окружность,
(ХБ|УБ|ХМ|УМ) Например (рис. 2.7):
ТОЧКА Т23= [ПЕРЕСЕЧ,] ПР7, КР2, УБ
П р и м е ч а н и е . Случай касания прямой и окружности рассматривается как пересечение этих двух объектов.

Точка, определенная пересечением двух окружностей:
имя =
[ПЕРЕСЕЧ,] окружность
1, окружность
2
{ХБ|УБ|ХМ|УМ} Например (рис. 2.8):
ТЧ4 = КР1, КР2, УМ
Точка, определенная пересечением окружности и ее радиуса, проведенного под заданным углом к оси
х:
ÏÐ×Ñ ÏÎ×Ñ
 имя
= окружность,, угол имя
= окружность,, угол
Например (рис. 2.9):
ТЧ5 = КР1, ПРЧС, 40.5
Точка, являющаяся центром ранее определенной окружности:
имя =
[ЦЕНТР], окружность
Например (рис. 2.10):
ТЧ6 = КР17
Точка, находящаяся на окружности на известном расстоянии от другой точки этой же окружности:
ÏÎ×Ñ
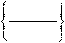 имя
= окружность, точка, расстояние
ÏÐ×Ñ имя
= окружность, точка, расстояние
ÏÐ×Ñ
Например (рис. 2.11):
ТЧ8 = КР1, ТЧА, ПОЧС, 18.6
П р и м е ч а н и е . Расстояние линейное, измеряется по дуге окружности. Точка, находящаяся на прямой и имеющая заданную координату
х
или
у:
имя = прямая,
{ХКООРД|УКООРД), число
Например (рис. 2.12):
ТЧ9 = ПР1, ХКООРД, 80
Точка, находящаяся на прямой, на определенном расстоянии от другой точки этой же прямой:
имя = прямая, точка, расстояние,
{ХБ|УБ|ХМ|УМ} Например (рис. 2.13):
ТЧ10 = ПР8, ТЧА, 23, ХМ

Точка, заданная приращениями координат известной точки:
имя = точка,
ПЕРЕНОС, приращение х, приращение у
Например (рис. 2.14):
ТЧ11=ТЧА, ПЕРЕНОС, 100, −20
Точка, находящаяся на определенном расстоянии от известной точки под углом к оси
х:
ÏÎ×Ñ
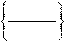 имя = точка, , угол, расстояние
ÏÐ×Ñ имя = точка, , угол, расстояние
ÏÐ×Ñ
Например (рис. 2.15):
ТЧ12 = ТЧ7, ПОЧС, 30.5, 118
Точка, координаты которой получены преобразованием координат известной точки в соответствии с указанной матрицей:
имя = точка, матрица
Например:
ТЧ16 = ТЧА, МК6
Точка, определенная ранее заданной точкой:
имя = точка
Например:
ТЧ17 = ТЧ13А
Точка, для которой ранее определенный вектор является радиус-вектором:
имя = вектор
Например (рис. 2.16):
ТЧ18 = ВЕКТ1
2.9.3 Задание координаты z в геометрических определениях точек (оператор ПЛЗ)
Оператор ПЛЗ предназначен для задания координаты z
тех точек, в геометрических определениях которых нет явно заданной третьей координаты:
Формат:
÷èñëî
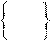 ПЗЛ_ èìÿ ПЗЛ_ èìÿ
ÎÒÌÅÍ
где имя
− имя плоскости, определенной ранее; ОТМЕН − служебное слово, обозначающее
отмену действия оператора ПЛЗ.
Действие оператора состоит в следующем. Если в операторах определения точки координата z
не задана явно, то процессор вычислит ее исходя из того условия, что определяемая точка должна лежать в плоскости, заданной оператором ПЛЗ. Если оператор ПЛЗ не был задан или был выполнен оператор ПЛЗ ОТМЕН, то все координаты z точек, не заданные явно, принимают нулевое значение. Действие оператора ПЛЗ распространяется на все точки, определенные после него, до использования другого оператора ПЛЗ или оператора ПЛЗ ОТМЕН.
 На рис. 2.17 изображены точки, определенные в приведенном ниже фрагменте программы: На рис. 2.17 изображены точки, определенные в приведенном ниже фрагменте программы:
ТЧ1=ПР5, ПР4
ПЛОСК П1, ПЛ14
ПЛ14=150
П1 = -30
ПЛЗ ПЛ14
ТЧ2 = ПР5, ПР4
ПЛЗ П1
ТЧ8 = ПР5, ПР4
ПЛЗ ОТМЕН
ТЧ100 = ПР5, ПР4
Координаты z точек ТЧ2 и ТЧ8 равны соответственно 150 и −30, так как они заданы оператором ПЛЗ с указанием плоскости, в которой лежит каждая из этих точек. Координата z
точки ТЧ1 по умолчанию равна нулю; координата точки ТЧ100 также равна нулю, так как перед ее геометрическим определением задан оператор ПЛЗ ОТМЕН, отменяющий действие последнего оператора ПЛЗ.
2.9.4 Определение прямой
В определениях прямой используют следующие группы модификаторов:
1. Модификаторы, выбирающие одну прямую из двух, касающихся окружности: ХМ − выбирается прямая, точка касания которой имеет меньшую координату по х;
ХБ− большую координату по х;
УМ − меньшую координату по у и УБ − большую координату по у.
2. Модификаторы, указывающие, с какой стороны определяемая прямая касается окружности: СПРАВА − точка касания прямой находится справа от центра окружности, если смотреть в направлении от первого геометрического объекта правой части определения ко второму; СЛЕВА − прямая касается окружности слева (при тех же условиях рассмотрения геометрических объектов).
3. Модификаторы, указывающие положение прямой относительно другой: ПАРЛЕЛ − параллельно; ПЕРП − перпендикулярно. Прямая, проходящая через две точки, заданные своими координатами:
имя
= координата
x1
, координата y1
, координата х2
, координата у2
Например (рис. 2.18):
ПР20=-15, 10, 35.6, 70 Прямая, проходящая через две точки:
имя = точка
1, точка
2.
Например (рис. 2.19):
ПР21=ТЧА, ТЧБ
Прямая, проходящая через точку и касающаяся окружности:
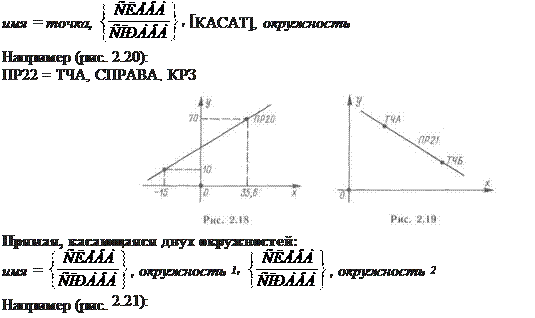
ПР23 = СЛЕВА, КР1, СПРАВА, КРЗ, Прямая, проходящая через точку под определенным углом к оси х:
имя = точка, угол
Например (рис. 2.22):
ПР23 = ТЧ5,− 15
Прямая, проходящая через точку под определенным углом к заданной прямой:
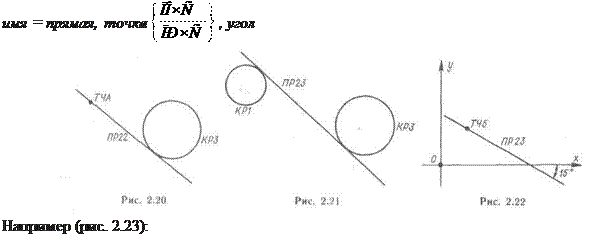
ПР25 = ПРА, ТЧВ, 44.5 Прямая, проходящая через точку и перпендикулярная к другой прямой:
имя = точка,
ПЕРП, прямая
Например (рис. 2.24):
ПР26 = ТЧ6, ПЕРП, ПР1 Прямая, проходящая через точку и параллельная другой прямой:
имя = точка,
ПАРЛЕЛ, прямая
Например (рис. 2.25):
ПР27 = ТЧ1, ПАРЛЕЛ, ПР14
Прямая, проходящая параллельно другой прямой на заданном расстоянии от нее:
имя
= прямая, расстояние,
|ХБ|УБ|ХМ|УМ) Например (рис. 2.26):
ПР28 = ПРА, 43,6, УМ Прямая, касающаяся окружности и составляющая с осью
х
заданный угол:
имя
= [КАС], окружность,
{ХБ|УБ|ХМ|УМ}, угол
Например (рис. 2.27):
ПР290 = КАС, КР1, УМ,− 15

Прямая, проходящая через точку параллельно вектору:
имя = точка, вектор
Например (рис. 2.28):
ПР310 = ТЧ1, ВЕК2

Прямая, полученная преобразованием заданной прямой в соответствии с матрицей:
имя
= прямая, матрица
 Например: Например:
ПР32 = ПР10, МАТР1
Прямая, совпадающая с прямой, определенной ранее:
имя
= прямая
Например:
ПР13 = ПР376
Прямая, параллельная одной из осей координат и находящаяся на заданном расстоянии от нее:
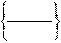 ÕÏÀÐ имя
= , расстояние
ÓÏÀÐ ÕÏÀÐ имя
= , расстояние
ÓÏÀÐ
Например (рис. 2.29):
ПР36 = УПАР, -13,6
2.9.5 Определение окружности
В определениях окружности используют следующие группы модификаторов:
1. Модификаторы БОЛШ и МЕНШ, служащие для выбора из двух окружностей одной − с большим или меньшим радиусом соответственно.
2. Модификаторы, указывающие положение определяемой окружности относительно другой, являющейся опорным элементом: ВНЕ − окружность находится вне заданной окружности; ВНУТРИ − окружность находится внутри заданной окружности.
3. Модификаторы, указывающие положение окружности относительно прямой: ХМ − центр окружности находится слева от прямой, ХБ − справа от прямой, УБ.− выше прямой и УМ − ниже прямой.
4. Те же модификаторы ХМ, ХБ, УБ, УМ, но служащие для выбора из двух окружностей одной по соответствующей координате ее центра.
Модификаторы 2 и 3-й групп относятся к следующим непосредственно за ними опорным элементам геометрического определения. Применение модификаторов ВНУТРИ и ВНЕ имеет свои особенности, отмеченные ниже.
Окружность,
совпадающая с окружностью, определенной ранее:
 имя
= окружность имя
= окружность
Например:
КР4 = КР100
Окружность, определенная координатами центра и радиусом:
имя = координата
х, координата у, радиус
Например (рис. 2.30):
КР4= − 13.6, 20, 5
Окружность, определенная радиусом и точкой, являющейся ее центром:
имя
= точка, радиус
Например (рис. 2.31):
КР4 = ТЧЗ, 15
Окружность, определенная точкой, являющейся ее центром, и касающаяся заданной прямой:
имя = точка,
[КАС], прямая
Например (рис. 2.32):
КР34 = ТЧ6, КАС, ПР8

Окружность, определенная точкой, являющейся ее центром, и проходящая через другую заданную точку:
имя
= точка1
, точка2
Например (рис. 2.33):
КР4 = ТЧА, ТЧ6 Окружность, проходящая через три точки:
имя = точка
1, точка
2, точка
3
Например (рис. 2.34):
КР55 = ТЧ1, ТЧ6, ТЧ2
Окружность, определенная точкой, являющейся ее центром, и касающаяся другой окружности:
ÌÅÍØ
 имя
= точка, ,
окружность
ÁÎËØ имя
= точка, ,
окружность
ÁÎËØ
Например (рис. 2.35):
КР6 = ТЧ1, МЕНШ, КРА1
КР6А = ТЧ1, БОЛШ, КРА1 Окружность заданного радиуса, касающаяся двух пересекающихся прямых:
ÕÁ ÕÁ
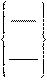 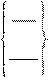 имя =
ÓÁ
, прямая1
,
ÓÁ
, прямая2
, радиус имя =
ÓÁ
, прямая1
,
ÓÁ
, прямая2
, радиус
ÕÌ ÕÌ ÓÌ ÓÌ
Например (рис. 2.36):
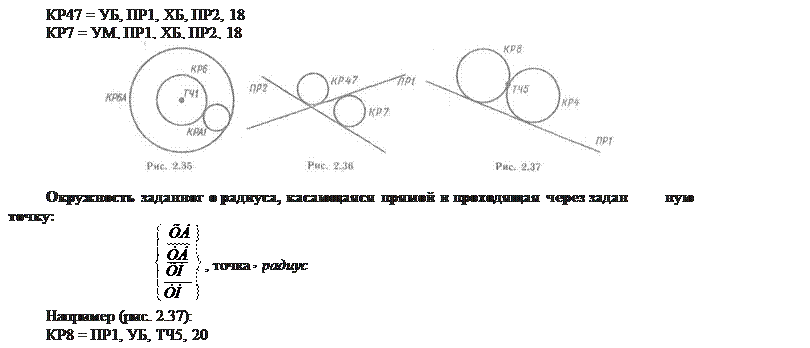 имя = прямая, имя = прямая,
КР4 = ПР1, УМ, ТЧ5, 20
Окружность заданного радиуса, касающаяся прямой
и окружности:
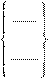 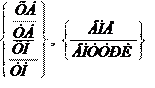 ÕÁ имя =
ÓÁ
, прямая,
, окружность, радиус ÕÁ имя =
ÓÁ
, прямая,
, окружность, радиус
ÕÌ ÓÌ
Например (рис. 2.38):
КР1=УБ, ПР1, ХМ, ВНЕ, КРО, 10
КР2 = УБ, ПР1, ХМ, ВНУТРИ, КРО, 10
КРЗ = УБ, ПР1, ХБ, ВНУТРИ, КРО, 10
КР4 = УБ, ПР1, ХБ, ВНЕ, КРО, 10 КР5 = УМ, ПР1, ХМ, ВНЕ, КРО, 10
КР6 = УМ, ПР1, ХМ, ВНУТРИ, КРО, 10
КР7 = УМ, ПР1, ХБ, ВНУТРИ, КРО, 10
КР8 = УМ, ПР1, ХБ, ВНЕ, КРО, 10
Окружность заданного радиуса, касающаяся двух других окружностей:
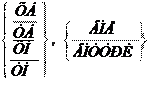 ÂÍÅ ÂÍÅ
 имя =
, окружность1
,
, окружность2
, радиус имя =
, окружность1
,
, окружность2
, радиус
ÂÍÓÒÐÈ
Например (рис. 2.39):
КР1=УБ, ВНЕ, КРА, ВНЕ, КРБ, 15
КР2 = УБ, ВНЕ, КРА, ВНУТРИ, КРБ, 15
КРЗ = УМ, ВНЕ, КРА, ВНУТРИ, КРБ, 15
КР4 = УМ, ВНЕ, КРА, ВНЕ, КРБ, 15
КР5 = УМ, ВНУТРИ, КРА, ВНЕ, КРБ, 15
КР6 = УБ, ВНУТРИ, КРА, ВНЕ, КРБ, 15
КР7 = УБ, ВНУТРИ, КРА, ВНУТРИ, КРБ, 15
КР8 = УМ, ВНУТРИ, КРА, ВНУТРИ, КРБ, 15

П р и м е ч а н и е . В тех случаях, когда определяемая окружность не может быть построена внутри опорных (слишком велик ее диаметр или опорные окружности не пересекаются), модификатор ВНУТРИ указывает положение опорных окружностей относительно определяемой окружности.
Например (рис. 2.40, а, б):
КР9 = УМ, ВНУТРИ, КР31, ВНУТРИ, КР40, 150
КР10 = УБ, ВНУТРИ, КР50, ВНЕ, КР17, 60 КР11=УМ, ВНУТРИ, КР50, ВНУТРИ, КР17, 60
Окружность, касающаяся трех прямых:
ÕÁ ÕÁ ÕÁ
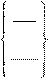  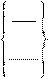 имя =
ÕÌÓÁ
, прямая
1
,
ÕÌÓÁ
, прямая
2
,
ÕÌÓÁ
, прямая
3 имя =
ÕÌÓÁ
, прямая
1
,
ÕÌÓÁ
, прямая
2
,
ÕÌÓÁ
, прямая
3
ÓÌ ÓÌ ÓÌ

Например (рис. 2.41):
КР5 = УМ, ПР1, УБ, ПР2, ХБ, ПРЗ
КР55 = УМ, ПР1, УБ, ПР2, ХМ, ПРЗ Окружность заданного радиуса, проходящая через две точки:
ÕÁ
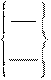 имя =
ÓÁ
, точка1
, точка2
, радиус
ÕÌ имя =
ÓÁ
, точка1
, точка2
, радиус
ÕÌ
ÓÌ
Например (рис. 2.42):
КР1=ХБ, ТЧ1, ТЧ2, 50
КР2 = ХМ, ТЧ1, ТЧ2, 30
Окружность заданного радиуса, проходящая через точку и касающаяся другой окружности:
имя = точка,
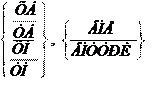 , окружность
, радиус , окружность
, радиус
Например (рис. 2.43):
КРЗ = ТЧ1, УБ, ВНУТРИ, КРА, 25
КР5 = ТЧ1, УМ, ВНУТРИ, КРА, 25
КР6 = ТЧ9, УМ, ВНУТРИ, КРБ, 14
КР9 = ТЧ9, УМ, ВНЕ, КРБ, 14
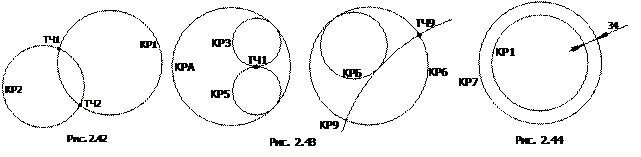
П р и м е ч ан и е . В том случае, когда точка, указанная в определении, находится внутри опорной окружности, использование модификатора ВНЕ не имеет смысла. Если опорная точка находится вне опорной окружности, возможно как внутреннее, так и внешнее касание. Модификатор ВНУТРИ в этом случае указывает положение опорной окружности относительно определяемой (окружность КР6 в приведенном примере).
Окружность, концентричная заданной окружности:
ÌÅÍØ
 имя =
ПАРЛЕЛ, , окружность, разность радиусов
ÁÎËØ имя =
ПАРЛЕЛ, , окружность, разность радиусов
ÁÎËØ
Например (рис. 2.44):
КР7 = ПАРЛЕЛ, КР1, БОЛШ, 34
Окружность, полученная преобразованием заданной окружности в соответствии с матрицей:
имя
= окружность, матрица
Например:
КР7 = КР2, МАТР6
2.9.6 Определение вектора
В определениях вектора используют модификаторы, указывающие направление вектора: ХБ
− вектор направлен в сторону возрастания координаты х;
ХМ − в сторону уменьшения координаты х;
УБ − в сторону возрастания координаты у
и УМ − вектор направлен в сторону уменьшения координаты у.
 Вектор, определенный проекциями на оси, начало которого находится в начале координат:
имя = проекция х, проекция у, [проекция z]
Например (рис. 2.45): Вектор, определенный проекциями на оси, начало которого находится в начале координат:
имя = проекция х, проекция у, [проекция z]
Например (рис. 2.45):
ВЕКТ1=50, 37, 40
ВЕКТЗ = 50, 37
Вектор, определенный своими начальной
и конечной точками:
имя = точка
1, точка
2
Например (рис. 2.46):
 ВКТР = ТЧ1, ТЧ2 Вектор, равный сумме двух других векторов:
имя = вектор
1,
ПЛЮС, вектор
2
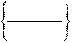
Например (рис. 2.47): ВКТР = ТЧ1, ТЧ2 Вектор, равный сумме двух других векторов:
имя = вектор
1,
ПЛЮС, вектор
2
Например (рис. 2.47):
ВЕКТ4 = ВЕКР1, ПЛЮС, ВКТ2 Вектор, равный разности двух векторов:
имя = вектор
1,
МИНУС, вектор
2
Например (рис. 2.48):
ВЕКТ5 = ВЕКР1, МИНУС, ВКТ2 Вектор, равный произведению заданного вектора и числа:
имя = число, вектор
Например (рис. 2.49):
ВЕКТ7 = 3, ВЕ2 Вектор, равный произведению двух векторов:
имя
= вектор
1
, УМНОЖ, вектор2
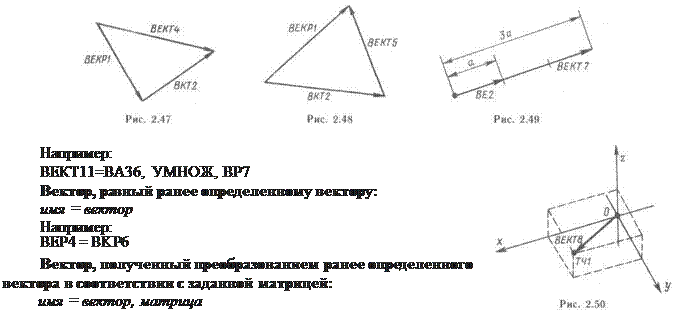
Например:
ВЕКТОР В6 = ВЕКТ, М2

Вектор, являющийся радиус-вектором заданной точки:
имя
= точка
Например (рис. 2.50):
ВЕКТ8 = ТЧ1 Вектор, заданный координатами своих начальной и конечной точек:
имя
= координата х
1, координата у
1, координата х
2, координата у
2
Например (рис. 2.51):
ВЕКТ В1 = -13, 4, 26, 28
Вектор, параллельный заданной прямой:
имя = прямая,
{ХБ|УБ|ХМ|УМ}
П р и м е ч а н и е . Длина вектора равна единице, начало его находится в начале координат, например (рис. 2.52): ВЕКТ7 = ПРА, ХМ
2.9.7 Определение матрицы
Матрица определяет способ преобразования координат. Это преобразование может быть параллельным переносом исходной системы координат, ее поворотом, симметрией или комбинацией этих преобразований. Любое преобразование координатной системы может быть описано с помощью системы трех уравнений: a
11x
1+a
12y
1+a
13z
1+a
14=x
2 a
21x
1+a
22y
1+a
23z
1+a
24=y
2 a
31x
1+a
32y
1+a
33z
1+a
34=z
2
Всегда можно определить значения таких коэффициентов a11
, a12
,
. . . , a34
, что при подстановке в систему уравнений значений координат произвольной точки x1
, y1
, z1
в локальной системе координат будут получены координаты этой точки x2
, у
2, z2
в абсолютной (исходной) системе координат.
Коэффициенты данной системы уравнений используются для представления матрицы преобразования в канонической форме и выводятся на печать в следующей последовательности:
a
11a
12a
13
a
21a
22a
23
a
31a
32a
33
a
14a
24a
34
Первые три элемента каждого столбца определяют направление осей локальной системы координат по отношению к исходной (абсолютной) системе координат: a11
, a21
, a31
− единичный вектор оси х
1; а
12, а
22, а
32
− единичный вектор оси у
1;а
13, а
23, а
33
− единичный вектор оси z1
.
Четвертая строка определяет положение начала координат локальной системы: Ом, «24, O34 − координаты х, у, z
начала локальной системы координат в исходной (абсолютной) системе.
Результатом матричного преобразования является геометрический объект, который имеет в локальной системе координат, полученной преобразованием исходной системы, параметры исходного геометрического объекта.
При использовании комбинированных матричных преобразований, задаваемых произведением матриц, следует помнить, что матричное умножение не коммутативно, т. е. конечный результат зависит от последовательности элементарных преобразований.
На рис. 2.53, а
−в
представлено последовательное преобразование исходной системы координат (о) матрицами поворота (б)
и переноса (в), а на рис. 2.53, г−е
дано преобразование системы матрицами переноса (д)
и поворота (е).
В геометрических определениях матрицы используются следующие модификаторы: ПОВХУ − определяет поворот осей х н у
вокруг оси г; ПОВУЗ − поворот осей у к г
вокруг оси * и ПОВЗХ − поворот осей z a x
вокруг оси у
(направление отсчета углов поворота − в соответствии с рисунком).
Матрица, определяющая координатную систему, полученную поворотом
на заданный угол исходной системы координат вокруг одной из ее осей:
имя
={ПОВХУ|ПОВУЗ|ПОВЗХ}, угол
Например (рис. 2.54):
МАТР МТ2 = ПОВЗХ, 30.5
Матрица, определяющая координатную систему, полученную параллельным переносом исходной системы координат:
имя =
ПЕРЕНОС, координата х, координата у,
[координата z
] Например (рис. 2.55):
МАТРЗ = ПЕРЕНОС, 10, 15, 20

Матрица, определяющая координатную систему, полученную параллельным переносом исходной системы координат и последующим поворотом на заданный угол вокруг одной из координатных осей:
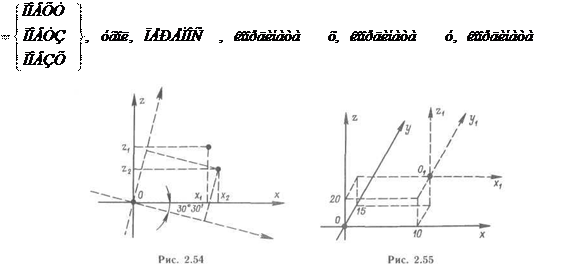 èìÿz èìÿz
Например (рис. 2.56):
МАТР = ПОВЗХ, 30.5, ПЕРЕНОС, 10, 15, 20 Матрица, являющаяся произведением двух других матриц:
имя = матрица х
1, матрица
2
Например (рис. 2.56):
МАТР=МАТР3, МТ2
П р и м е ч а н и я : 1. Произведение матриц эквивалентно применению сначала матрицы
2,
а затем преобразованию полученного результата в соответствии с матрицей
1.
2. Матрица, заданная в примере (см. рис. 2.56), является произведением матриц, определенных в первых двух примерах (см. рис. 2.54 и 2.55).

Матрица, равная ранее определенной матрице:
имя
= матрица
Например: МАТР4 = МТ6
Матрица, определяющая перенос начала координат в точку, заданную явно или вектором:
имя
= ПЕРЕНОС, {точка
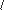 вектор}
Например (рис. 2.57): вектор}
Например (рис. 2.57):
МКТ = ПЕРЕНОС, ТЧА
МКТ = ПЕРЕНОС, ВКР4
Матрица, определяющая поворот исходной системы координат вокруг одной из осей и последующий перенос начала координат
в точку, заданную явно или вектором:
имя
= {точка
| вектор
},
{ ПОВХУ|ПОВУЗ|ПОВЗХ }, угол
Матрица, определяющая симметрию относительно заданной прямой:
имя
= прямая
Например (рис. 2.58):
МАТР8 = ПР1
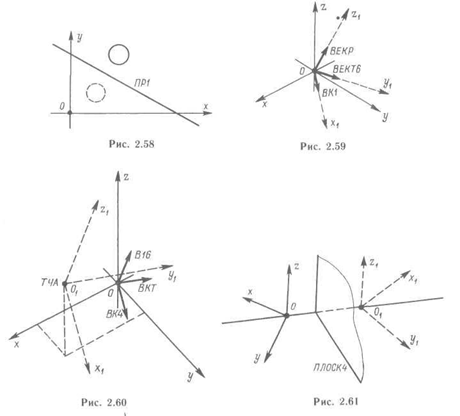
Матрица, определяющая координатную систему, начало которой совпадает с началом координат исходной системы, а направления осей заданы векторами:
имя
= вектор
1, вектор
2, вектор
3
Например (рис. 2.59):
MATP9 = BKl, BEKT6, ВЕКР
Матрица, определяющая координатную систему, начало которой находится в точке, заданной явно или вектором, а направление осей заданы соответствующими векторами:
имя = вектор1
, вектор2
, вектор3
,
ПЕРЕНОС, {точка
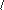 вектор4
} вектор4
}
Например (рис. 2.60):
М2 = ВК4, ВКТ, В16, ПЕРЕНОС, ТЧА
Матрица, определяющая координатную систему, являющуюся зеркальным отображением исходной относительно заданной плоскости:
имя = плоскость
Например (рис. 2.61):
МАТР2 = ПЛОСК4
Матрица, определяющая преобразование координат, обратное преобразованию, определенному заданной матрицей:
имя =
ОБРАТИ, матрица
Например; если ТЧ2 = МАТР2, ТЧ1 и М12 = ОБРАТН, МАТР2, то справедливо геометрическое определение: ТЧ1=ТЧ2, М12
2.9.8 Определение плоскости
В геометрических определениях плоскости используются следующие модификаторы: ХУПАР − определяемая плоскость параллельна плоскости ху,
УЗПАР − параллельна плоскости уz
и ЗХПАР − плоскости zх.
Отсутствие модификатора эквивалентно использованию модификатора ХУПАР.
Плоскость, параллельная одной из координатных плоскостей и проходящая через заданную точку:
имя
= {ХУПАР|УЗПАР|ЗХПАР}, точка
Например:
ПЛОСК П1=
УЗПАР, ТЧЗ
Плоскость, параллельная одной из координатных плоскостей и находящаяся на заданном расстоянии от нее:
имя
= |ХУПАР |УЗПАР |ХЗПАР}, число
Например:
ПЛОСК8 = ЗХПАР, -29.6
Плоскость, совпадающая с плоскостью, определенной ранее:
имя = плоскость
Например:
ПЛОСК ПЛТ = ПЛОСК8 Плоскость, определенная коэффициентами ее нормального уравнения:
имя = число
1, число
2, число
3, число
4
Плоскость, проходящая через три точки, не лежащие на одной прямой:
имя = точка
1, точка
2, точка
3
Например:
ПЛ54 = ТЧ1, ТЧ18, ТЧ46
Плоскость, проходящая через заданную точку перпендикулярно вектору:
имя = вектор, точка
Например (рис. 2.62):
ПЛОСК8 = ВЕКР, ТЧ2
Плоскость, параллельная двум векторам и проходящая через заданную точку:
имя
= вектор
1
, вектор2
, точка
Например (рис. 2.63):
ПЛ6 = ВЕКТ1, ВЕКИ2, ТЧ1

Плоскость, параллельная другой плоскости и проходящая через заданную точку:
имя = точка,
ПАРЛЕЛ, плоскость
Плоскость, полученная преобразованием заданной плоскости в соответствии с указанной матрицей:
имя = плоскость, матрица
2.9.9 Вложенное определение
 Вместо имени ранее определенного геометрического объекта в правой части геометрического определения или в операторе движения можно задать «вложенное определение». Оно состоит из типа определяемого объекта, необязательного имени объекта и заключенного в скобки варианта геометрического определения соответствующего типа. Вместо имени ранее определенного геометрического объекта в правой части геометрического определения или в операторе движения можно задать «вложенное определение». Оно состоит из типа определяемого объекта, необязательного имени объекта и заключенного в скобки варианта геометрического определения соответствующего типа.
Если у такого геометрического объекта отсутствует имя, то значения его геометрических параметров сохраняются временно и используются процессором только для промежуточных вычислений.
На рис. 2.64 изображена окружность К.Р2, которая описана с использованием вложенных определений:
КР2 = ТОЧКА (ПРЯМАЯ ПР2 (ТЧ1, ТЧ2), ПР1), РАДИУС, 2.5
Данное геометрическое определение равноценно трем другим определениям: ПР2 = ТЧ1, ТЧ2
ТЧА = ПР2, ПР1
КР2 = ЦЕНТР, ТЧА, РАДИУС, 2.5
Различие состоит лишь в том, что значение точки ТЧА во втором варианте записи сохранится, а при использовании вложенного определения точка пересечения прямых ПР1 и ПР2 не может быть использована в программе повторно. Глубину вложения можно увеличивать. В каждом из геометрических определений она может достигнуть двадцати.
2.10 Программирование движений инструмента
2.10.1 Общие сведения
В языке Техтран существуют два типа движения:
1) движение точка
−точка
(поточечное движение), при котором перемещение инструмента программируется прямым заданием либо целевой точки, либо величины смещения;
2) непрерывное движение, при котором перемещение программируется перечислением элементов траектории инструмента (т. е. участков прямых, окружностей, частей контуров) с указанием направления движения.
Возможность управления поверхностью детали позволяет программировать обработку контуров, имеющих наклонное «дно», благодаря чему с помощью языка Техтран возможно (с определенными ограничениями) описывать обработку деталей достаточно сложной пространственной формы. Во всех операторах движения вместо имен геометрических объектов можно использовать вложенные определения объектов тех же типов.
2.10.2 Исходное положение инструмента
Прежде чем программировать движение инструмента, необходимо задать его исходное положение. Для этого служит оператор ИЗ.
Оператор имеет следующий формат:
òî÷êà
 ÈÇ| õ, ó, z ÈÇ| õ, ó, z
где точка
− имя точки; х, у, z
− координаты точки.
В качестве координат можно использовать арифметические выражения. Если отсутствует координата z,
то она считается равной нулю. В операторе ИЗ допускается использовать вложенные определения. В одной программе может присутствовать несколько операторов ИЗ. Например, возможны следующие варианты оператора ИЗ:
ИЗ 10, 20
ИЗ А, В
ИЗ (х + у)/2, (х - у)/2
ИЗ ТЧ1
ИЗ ТОЧКА (ПР1, ПР2)
2.10.3 Движение точка
− точка
При использовании этого оператора программист явно указывает каждое перемещение инструмента либо приращениями относительно предыдущего положения, либо точкой результирующего положения центра (вершины) инструмента. Этот тип движения реализуется операторами ВТОЧКУ и ПРЙРАЩ. В дальнейшем этот тип движения в некоторых случаях будет именоваться как «поточечное движение».
 Оператор
ВТОЧКУ вызывает перемещение в заданную точку и имеет формат: òî÷êà Оператор
ВТОЧКУ вызывает перемещение в заданную точку и имеет формат: òî÷êà
ВТОЧКУ
õ, ó, z
где точка
− имя точки; х, у, z
− координаты точки.
Вместо чисел в качестве координат точки можно использовать арифметические выражения. Если в операторе указаны только две координаты, то координата z считается равной нулю. На рис. 2.65 приведен пример движения точка
− точка:
ТЧЗ = 35, 10
ИЗ 0, 0
ВТОЧКУ 0, -28
ВТОЧКУ 35, 10, 12
ВТОЧКУ ТЧЗ
  Оператором
ПРИРАЩ указывается перемещение относительно текущего положения на заданный вектор. Оператор имеет следующий формат: âåêòîð Оператором
ПРИРАЩ указывается перемещение относительно текущего положения на заданный вектор. Оператор имеет следующий формат: âåêòîð
ÏÐÈÐÀÙõ, y,[z]
z
где вектор
− имя вектора; х, у, z
− проекции вектора на координатные оси.
Вместо чисел в качестве проекций можно использовать арифметические выражения. Если в операторе ПРИРАЩ координаты х и у
или координата z
равны нулю, то перемещений по соответствующим осям не происходит. Поэтому оператор ПРИРАЩ 0, 0, А эквивалентен оператору ПРИРАЩ А.
 При многократном использовании оператора ПРИРАЩ следует соблюдать осторожность, так как ошибка в начале последовательности влияет на остальные положения инструмента. При многократном использовании оператора ПРИРАЩ следует соблюдать осторожность, так как ошибка в начале последовательности влияет на остальные положения инструмента.
Движение, изображенное на рис. 2.65, можно записать при помощи оператора ПРИРАЩ следующим образом:
ИЗ 0, 0
ПРИРАЩ 0, -28, 0
ПРИРАЩ 35, (28+10), 12
ПРИРАЩ -12
При описании движения допускается сочетание операторов ВТОЧКУ и ПРИРАЩ:
ИЗ 0, 0
ПРИРАЩ 0, -28, 0
ВТОЧКУ 35, 10, 12
ПРИРАЩ -12
Сокращенная запись операторов поточечного движения
− это замена одним оператором нескольких записанных подряд операторов поточечного движения. Операнды этих операторов разделяются в этом случае двоеточием. Можно чередовать различные формы задания точек (приращения), например:
ВТОЧКУ ТЧ1: 6.2, А + В, 0 : ТОЧКА (ПР1, ПР2) : ТЧЗ
ПРИРАЩ 5,1 : 0,3*КОС (45) : ВЕКТ1
Следует иметь в виду, что сокращенная запись этих операторов движения затрудняет понимание диагностических сообщений, имеющих ссылку на номер строки.
2.10.4 Непрерывное движение
При программировании непрерывного движения на языке Техтран описывается движение инструмента относительно трех поверхностей (рис. 2.66, а): поверхности детали (ПД);
направляющей поверхности (НП);
ограничивающей поверхности (ОП).
На рис. 2.66, б
приведено взаимное положение инструмента и поверхности. Рабочая часть инструмента при этом находится в постоянном контакте с поверхностью детали и направляющей поверхностью. Конечное положение инструмента после выполнения очередного оператора непрерывного движения определяется ограничивающей поверхностью (рис. 2.67, а). Прямые и окружности, составляющие контур детали, представляют собой проекции НП
и ОП
на горизонтальную плоскость (рис. 2.67,6).
Поверхность детали представляет собой плоскость − горизонтальную или наклонную. По умолчанию ПД
совпадает с плоскостью хОу.
В дальнейшем для простоты изложения НП
и ОП
отождествляются со своими проекциями на плоскость хОу.
Оператор
ИНСТР (описание инструмента)
предназначен для задания геометрических параметров инструмента, необходимых для расчета траектории его движения относительно контура и поверхности детали. Оператор имеет следующий формат:
  0 0
ИНСТР диаметр
ðàäèóñ
где диаметр
− диаметр инструмента; радиус
− радиус скругления режущей кромки.
Радиус скругления не может быть больше радиуса цилиндрической части фрезы. Отсутствие оператора ИНСТР эквивалентно заданию инструмента нулевого диаметра. Новый оператор ИНСТР отменяет действие предыдущего. При непрерывном движении изменение диаметра инструмента запрещено.

   На рис. 2.68 и 2.69 изображены различные резцы и фрезы и их описание на языке Техтран. На рис. 2.70, а, б
представлены схемы электроэрозионной обработки и формирования зоны резания и описания на языке Техтран (А
− ширина реза, A=d+2δ).
Точкой отмечен геометрический центр инструмента. Траекторией движения инструмента является линия, по которой перемещается в пространстве геометрический центр инструмента. На рис. 2.68 и 2.69 изображены различные резцы и фрезы и их описание на языке Техтран. На рис. 2.70, а, б
представлены схемы электроэрозионной обработки и формирования зоны резания и описания на языке Техтран (А
− ширина реза, A=d+2δ).
Точкой отмечен геометрический центр инструмента. Траекторией движения инструмента является линия, по которой перемещается в пространстве геометрический центр инструмента.
Оператор
МЕТОД используют для задания метода интерполяции и режима аппроксимации окружности отрезками прямой.
Формат оператора:
ËÈÍÅÉÍ , ÀÊÑËÈÍ ,÷èñëî1

ÌÅÒÎÄ
[ÊÂÀÄÐ
]
 ËÈÍÊÐÓÃ
,[ÌÀÊÑÐÀÄ
,÷èñëî
2
] ËÈÍÊÐÓÃ
,[ÌÀÊÑÐÀÄ
,÷èñëî
2
]
ÍÅÊÂÀÄÐ
где ЛИНЕЙН −линейная интерполяция (аппроксимация
окружностей отрезками прямых); ЛИНКРУГ − линейно-круговая интерполяция (аппроксимация кривых дугами окружностей); К.ВАДР − линейно-круговая интерполяция с делением окружностей на квадранты; НЕК.ВАДР − то же без деления на квадранты; число
1
− максимальная длина отрезков, аппроксимирующих окружность; число
2
− максимальный радиус окружности, при котором автоматически происходит переход к линейной интерполяции.
На рис. 2.71, а, б
представлены линейная (а)
и линейно-круговая (б)
интерполяции.
Параметр МАКСЛИН применяется для ограничения длины аппроксимирующих отрезков
(рис. 2.72):
МЕТОД ЛИНЕЙН, МАКСЛИН, 4, 35.

На рис. 2.73 показано применение параметра МАКСРАД в операторе МЕТОД. Точками ограничены участки траектории, заданные в управляющей программе отдельными кадрами:
МЕТОД ЛИНКРУГ, МАКСРАД, 1000.
При использовании модификатора КВАДР процессор системы разбивает дуги окружностей, составляющих траекторию, на участки, лежащие в отдельных квадрантах (рис. 2.74).
 Отсутствие в программе оператора Отсутствие в программе оператора
МЕТОД эквивалентно применению оператора МЕТОД ЛИНКРУГ, КВАДР. Круговая интерполяция разрешена только в одной из координатных плоскостей или в плоскостях, параллельных им. Круговая интерполяция с делением на квадранты возможна только в плоскостях, параллельных плоскости хОу.
Если поверхность детали не параллельна плоскости хОу,
следует задавать оператор МЕТОД, ЛИНЕЙН, даже если контур не содержит дуг окружностей.
Операторы
НАРДОП и
ВНДОП используются для задания точности линейной аппроксимации дуг окружности, которые заменяются отрезками прямых. НАРДОП число
− точность аппроксимации касательными − наружный допуск (рис. 2.75, а)
; ВНДОП число
− точность аппроксимации хордами − внутренний допуск (рис. 2.75, б).
При одновременном использовании этих операторов производится аппроксимация секущими (рис. 2.75, а). Если не заданы ни НАРДОП, ни ВНДОП, то система устанавливает следующие их значения:
НАРДОП.0, 05
ВНДОП 0
Оператор
ИДИ задает начало непрерывного движения. Оператор ИДИ выводит инструмент в рабочее положение относительно управляющих поверхностей НП, ПД
и ОП.
Положение инструмента относительно каждой из них указывается модификаторами ДО, НА, ЗА. Оператор имеет следующий формат:
ÈÄÈ 
По команде ИДИ инструмент выводится в требуемую точку по кратчайшему пути. Если НП
и ОП
имеют две точки пересечения, то выбирается ближайшая из них. На рис. 2.76 показано применение модификаторов ДО, НА, ЗА при движении с одной (а
−в) и с двумя поверхностями (г
−д)
соответственно, а иллюстрация этих примеров на языке Техтран приведена ниже:
ИЗ ТЧ1; ИДИ ДО ПР1 (а)
ИЗ ТЧ1; ИДИ НА ПР1 (б)
ИЗ ТЧ1; ИДИ ЗА ПР1 (в)
ИЗ ТЧ1; ИДИ ДО ПР1 ДО ПР2 (г)
ИЗ ТЧ1; ИДИ ДО ПР1 ЗА ПР2 (д)
При необходимости направление подхода может указываться операторами НАПРВ (в направлении вектора) или НАПРТ (в направлении точки).
На рис. 2.77, а, б
приведены соответственно иллюстрации операторов:
ИДИ НА ПРХ ДО ПЛ1 ЗА ПРЗ
ИДИ НА ПРХ НА ПЛ1 ЗА ПРЗ
Если в операторе ИДИ задана поверхность детали, то при непрерывном движении инструмент будет находиться в контакте с ней в соответствии с заданным модификатором. Команды поточечного движения (ВТОЧКУ и ПРИРАЩ), вызывающие отход от поверхности детали по координате z,
будут игнорироваться. Отвести инструмент от ПД
можно только после оператора ПОВДЕТ ОТМЕН.
Если же ПД
в операторе ИДИ опущена, то поверхностью детали становится плоскость, параллельная плоскости хОу
и отстоящая от нее на значение текущей координаты г.
При этом разрешено перемещать инструмент по вертикальной оси.

Различие в использовании оператора ИДИ с одной, двумя и тремя поверхностями иллюстрирует рис. 2.78: перемещение 0
−1:
ИЗ ТЧ1; ИДИ ДО ПР1 перемещение 0
−2:
ИЗ ТЧ1; ИДИ ДО ПР1 ДО ПР2 перемещение 0
−3:
ИЗ ТЧ1; ИДИ ДО ПР1 ДО ПЛ1 перемещение 0
−4:
ИЗ ТЧ1; ИДИ ДО ПР1 ДО ПЛ1 ДО ПР2

В операторе ИДИ с двумя или тремя поверхностями в качестве ОП
должна быть указана поверхность, которая будет направляющей в следующей команде движения.
Операторы
НАПРТ и
НАПРВ являются вспомогательными и используются совместно с оператором ИДИ в следующих случаях:
1) если при использовании оператора ИДИ с одной поверхностью (кроме поверхности детали) надо осуществить подход не к ближайшей точке поверхности;
2) если при использовании оператора ИДИ с двумя поверхностями (не считая поверхности детали) необходимо выбрать одну из двух возможных точек пересечения НП
и ОП;
3) если инструмент уже находится в требуемом положении относительно НП;
4) если в операторе ИДИ в качестве НП
указан объект типа КОНТУР.
В первом случае отсутствие оператора, задающего направление подхода, вызовет подход к ближайшей точке поверхности, а в остальных трех случаях приведет к ошибке.
Операторы НАПРТ и НАПРВ не управляют перемещением по третьей координате, т. е.
направление подхода к НП
определяется проекцией вектора подхода на горизонтальную плоскость.

 Формат оператора НАПРТ: òà÷êà Формат оператора НАПРТ: òà÷êà
НАПРТ
õ, ó
где точка
− имя точки; х, у
− переменные или арифметические выражения, значения
  которых являются соответственно координатами х
и у
точки. Формат оператора НАПРВ: âåêòîð которых являются соответственно координатами х
и у
точки. Формат оператора НАПРВ: âåêòîð
ÍÀÏÐÀÂ
õ, ó
где вектор
− имя вектора; х, у
− переменные или арифметические выражения, значения
которых являются соответственно проекциями х
и у
вектора.
На рис. 2.79, а, б
представлены методы подхода к НП в направлении точки и вектора соответственно:
(а) ИЗ ТЧО (б) ИЗ ТЧО
НАПРТ ТЧ1 НАПРВ В1
ИДИ ДО ПР1 ИДИ ДО ПР1
В случае, когда НП
и ОП
пересекаются в двух точках, целевая точка подхода выбирается с помощью операторов НАПРТ или НАПРВ. Если используется НДПРТ, то целевой выбирается точка, ближайшая к точке, заданной в этом операторе. Если используется НАПРВ, то указанный там вектор используется для выбора из двух точек так же как и модификаторы типа ХБ − УМ в геометрических определениях (рис. 2.80), например:
перемещение 0
−1 (рис. 2.80, а) −оператор ИДИ задает переход в точку ТЧ1,
так как она
ближе к ТЧЗ,
чем ТЧ2:
ИЗ ТЧО
НАПРТ ТЧЗ
ИДИ ДО ПР1 ДО КР1
перемещение 0
−2
(рис. 2.80, а) − инструмент переходит в точку ТЧ2,
так как она ближе к ТЧ4,
чем ТЧ1
ИЗ ТЧ0
НАПРТ ТЧ4
ИДИ ДО ПР1 ДО КР1

перемещение 0
−3
(рис. 2.80,6):
ИЗ ТЧ0
НАПРВ ВЕКТОР (ТЧО, ТЧ1) ИДИ ДО ПР1 ДО КР1
перемещение 0
−4
(рис. 2.80,6):
ИЗ ТЧ0
НАПРВ ВЕКТОР (1, 0, 0) ИДИ ДО ПР1 ДО КР1
Если инструмент уже подведен к НП,
то для вывода инструмента в требуемое положение относительно НП
или для задания направления, относительно которого будет выбран оператор непрерывного движения, следует указать направление подхода операторами НАПРВ или НАПРТ (рис. 2.81, а, б).
При этом запрещен вывод инструмента в направлении, встречном указанному в операторах НАПРВ или НАПРТ (рис. 2.81, в). В исходном положении инструмент может касаться НП
или его центр может находиться на НП;
вариант, показанный на рис. 2.81, г, недопустим.
Если в операторе ИДИ в качестве НП
указан объект типа КОНТУР, то следует указать направление подхода (см. п. 2.11):
ИЗ ТЧ1
НАПРВ В1
ИДИ ДО КОНТ1
Оператор
ПОВДЕТ предназначен для управления поверхностью детали при поточечном и непрерывном движении.
Оператор имеет следующий формат:
  ÷èñëî ÷èñëî
ПОВДЕТèìÿ
ÎÒÌÅÍ
число
− число или арифметическое выражение, задающее ПД
как плоскость, параллельную плоскости хОу
и отстоящую от нее на указанном расстоянии; имя
− t,
символическое имя плоскости, которая будет использоваться как ПД
в последующих; командах движения; ОТМЕН − служебное слово, вызывающее отмену ранее введенной ПД
и возврат к плоскости хОу.
При поточечном движении координата z
каждой точки будет вычисляться в соответствии с заданной ПД.
В отличие от оператора ПЛЗ, который задает координату z
при построении точек, оператор ПОВДЕТ используется с командами движения.
При непрерывном движении применение оператора ПОВДЕТ равносильно заданию в операторе ИДИ поверхности детали с модификатором НА. Вводя новые операторы ПОВДЕТ, можно переходить от одной поверхности детали к другой, не прерывая непрерывного движения. Применять одновременно операторы ПОВДЕТ и ПД
в операторе ИДИ нельзя.
Независимо от того, как в программе определена поверхность детали (в операторе ИДИ или в операторе ПОВДЕТ), инструмент будет находиться в контакте с ней до тех пор, пока ПД не будет отменена командой ПОВДЕТ ОТМЕН.

После выхода на направляющую поверхность движение по каждому из геометрических элементов контура описывается в следующем формате:
 ÂÏÅÐÅÄ ÍÀÇÀÄ ÂÏÅÐÅÄ ÍÀÇÀÄ
  ÷èñëî ÏÅÐÅÑÅ×ÎÏ ÷èñëî ÏÅÐÅÑÅ×ÎÏ
ÂËÅÂÎ ÂÏÐÀÂÎ
ВПЕРЕД, НАЗАД, ВПРАВО, ВЛЕВО − служебные слова, указывающие направление перемещения по направляющей поверхности; НП
и ОП
− направляющая и ограничивающая поверхности; число
− номер пересечения НП
с ОП,
до которого задано движение по НП;
КАС − модификатор, определяющий движение по НП
до точки касания с ОП;
ДО, НА, ЗА − модификаторы, определяющие положение инструмента относительно ОП
(аналогично модификаторам оператора ИДИ).
Направление движения выбирается относительно предыдущего перемещения в соответствии с рис. 2.82, а
−г
(секторами ограничены области действия служебных слов, указывающих направление перемещения).
 При движении по окружности направлением движения считается направление касательной к окружности в точке пересечения НП
и ОП.
Поэтому в случае касания НП
и ОП
следует применять только операторы ВПЕРЕД и При движении по окружности направлением движения считается направление касательной к окружности в точке пересечения НП
и ОП.
Поэтому в случае касания НП
и ОП
следует применять только операторы ВПЕРЕД и
НАЗАД (рис. 2.83, а, б).
Пример программирования непрерывного движения для контура, изображенного на рис.
2.84 (из положения / в положение 5):
ВПЕРЕД П1 ЗА КР1
ВЛЕВО КР1 КАС К2
ВПЕРЕД КР2 ДО ПР2
ВПРАВО ПР2 НА П1
Поверхности, указанные в операторе непрерывного движения, могут пересекаться и не один раз. Если не указывать номер пересечения, то инструмент будет выведен на (до, за) первое пересечение НП и ОП. Поэтому, когда требуется остановиться на последующих пересечениях, следует указывать номер пересечения НП с ОП.
 Номер пересечения отсчитывается для каждого оператора движения в отдельности, вне связи с предыдущими операторами непрерывного движения. Причем, если перед выполнением оператора движения инструмент уже касался НП и ОП, это пересечение считается первым. Примеры программирования непрерывного движения: Номер пересечения отсчитывается для каждого оператора движения в отдельности, вне связи с предыдущими операторами непрерывного движения. Причем, если перед выполнением оператора движения инструмент уже касался НП и ОП, это пересечение считается первым. Примеры программирования непрерывного движения:
для контура, изображенного на рис. 2.85, а,−
1−2 ВПЕРЕД ПР1 ЗА КР1 или ВПЕРЕД ПР1 ЗА 1 КР1 2−3 ВПЕРЕД ПР1 ЗА 2 КР1
для контура, изображенного на рис. 2.85, б,− 1−2 ВПЕРЕД ПР2 ДО 2 КР2
2−3 ВЛЕВО КР2 НА 2 ПР2
3−4 ВПЕРЕД КР2 НА 2 ПР2
Номер пересечения, указанный в операторе движения,
не должен превышать общего числа пересечений данных НП и ОП, в противном случае ситуация считается ошибочной (например, задание второго пересечения для двух прямых). Исключение составляет третье пересечение окружности с прямой, под которым подразумевается полный обход окружности.

Примеры программирования с «третьим» пересечением:
для контура, изображенного на рис. 2.86, а,−
ВПЕРЕД ПР1 ДО КР2
НАЗАД КР2 ДО 3 ПЕРЕСЕЧ ПР1
для контура, изображенного на рис. 2.86, б,
− ВПЕРЕД ПР2 ЗА КРЗ
ВЛЕВО КРЗ ДО 3 ПР2

Если поверхность детали является наклонной плоскостью, то команды движения следует задавать так же, как и в случае расположения обрабатываемого контура в плоскости хОу.
Истинное перемещение инструмента представляет собой результат проектирования на ПД в направлении оси z
эквидистанты к этому контуру (с учетом формы инструмента и его положения относительно ПД).
На рис. 2.87 показано программируемое и истинное перемещения инструмента при заданной поверхности детали для следующей программы:
МЕТОД ЛИНЕЙН
ИЗ ТЧ1
ИДИ ДО ПР1 ДО ПЛ1 ЗА КР1
ВЛЕВО ПР1 ДО ПР2
ВЛЕВО ПР2 ДО КР1
ВЛЕВО КР1 ДО ПР1
ПОВДЕТ ОТМЕН
ВТОЧКУ ТЧ1
Неявное определение ограничивающей поверхности
имеет место в том случае, если известно положение инструмента относительно контура обрабатываемой детали и ограничивающая поверхность и относящийся к ней модификатор в промежуточном операторе движения могут быть опущены. Они выбираются системой по направляющей поверхности следующего оператора движения. При этом необходимо задать положение инструмента относительно контура при помощи одного из операторов:
ИНСТНА − инструмент на контуре детали;
ИНСТЛВ − инструмент слева от контура (по направлению движения);

ИНСТПР − инструмент справа от контура (по направлению движения).
Несколько следующих подряд операторов движения одного типа могут заменяться одним, при этом операнды перечисляются через двоеточие. Число пересечений и ограничивающая поверхность с соответствующим модификатором задаются как обычно. При необходимости можно переходить от неявной ограничивающей поверхности к явной и наоборот.
Данный прием программирования позволяет значительно уменьшить объем исходной информации, однако при этом затрудняется понимание диагностических сообщений, связанных с номером строки.
На рис. 2.88 изображен контур, при программировании которого целесообразно использовать операторы непрерывного движения с неявной ограничивающей поверхностью:
ИЗ ТЧА
ИДИ ДО ПР1
ИНСТЛВ
ВЛЕВО ПР1
ВПЕРЕД КР1 : ПР2 ДО 2 ПЕРЕСЕЧ
ВЛЕВО КР2 : ПРЗ НА ПР7
ВЛЕВО ПР7 НА ПР2
Последний оператор движения всегда должен содержать явно заданную ограничивающую поверхность. После операторов движения, не содержащих ограничивающей поверхности, запрещено использовать операторы постпроцессора и управления интерполяцией.
Совместное применение операторов поточечного и непрерывного движений
имеет некоторые особенности. Поточечное движение прерывает непрерывное движение, поэтому после операторов ПРИРАЩ и ВТОЧКУ невозможно продолжить непрерывное движение при помощи операторов ВПРАВО, ВЛЕВО, ВПЕРЕД, НАЗАД. Для возобновления непрерывного движения следует задать оператор ИДИ.
Исключение составляет перемещение по третьей координате при незаданной поверхности детали (рис. 2.89):
ВПЕРЕД ПР1 ДО КР2
ПРИРАЩ 50
ВПРАВО КР2

Фиктивное движение,
т. е. расчет перемещений инструмента без передачи их в управляющую программу можно запрограммировать с помощью оператора НЕОБР и отменяющего его оператора ОБРАБ. Этот прием используют для того, чтобы переместить инструмент в положение, которое описать явным образом неудобно или невозможно. Например, для случая, изображенного на рис. 2.90, непосредственный переход из положения 1 в положение 3
программируется операторами:
ИЗ ТЧ1
НЕОБР
ИДИ ЗА КР2 ЗА КР1
ВЛЕВО КР1 ДО 2 КР2
ОБРАБ
ВПЕРЕД КР2 ....
При этом исключается движение по окружности КР1
из положения 2
в положение 3
2.10.5 Преобразование траектории движения инструмента
При программировании сложных деталей бывает удобно кодировать элементы контура не в базовой системе координат детали, а в некоторых местных системах координат. При этом необходимо задать положение каждой местной системы координат в базовой системе координат детали, для чего используются матричные преобразования.
Возможны два способа использования матриц: в геометрических определениях и в командах движения.
В первом случае новый геометрический объект определяется посредством матричного преобразования, производимого над ранее определенным геометрическим объектом. Во втором случае преобразованию подвергается отмеченный участок траектории, для чего используют операторы ТРАНС и ТРАНСРЕЗ.
Оператор ТРАНС предназначен для преобразования направляющих и ограничивающих поверхностей, относительно которых описывается движение. Оператор ТРАНСРЕЗ используют для преобразования точек рассчитанной траектории.
Оператор ТРАНС имеет следующий формат:
 ìàòðèöà ìàòðèöà
 ÒÐÀÍÑ ÒÐÀÍÑ
ÎÒÌÅÍ
где матрица
− символическое имя матрицы.
Матрица, заданная в этом операторе, должна быть плоской, т. е. это либо матрица поворота в плоскости хОу,
либо матрица переноса по координатам х и у ,
либо матрица симметрии относительно прямой, либо произведение матриц такого вида.
Оператор ТРАНС выполняет преобразование траектории движения инструмента в соответствии с заданной матрицей до применения нового оператора ТРАНС. Оператор ТРАНС ОТМЕН задает возврат к исходной системе координат. Если в программе последовательно применяются несколько операторов ТРАНС, то следует учесть, что каждый следующий оператор определяет преобразование исходной системы координат, а не текущей; оператор ТРАНС ОТМЕН задает возврат к исходной системе координат, а не к действовавшей ранее.
Например, необходимо обработать три одинаковых элемента (1−3),
расположенных так, как показано на рис. 2.91. Фрагмент программы на языке Техтран имеет вид:
 ... ...
команды обработки элемента 1
МАТР М1=ПОВОРОТ, 30 ТРАНС Ml
команды обработки элемента 1
МАТР М2 = ПОВОРОТ, 60
ТРАНС М2
команды обработки элемента 1
ТРАНС ОТМЕН
…
Оператор ТРАНС действует на поверхности движения (прямые, окружности и др.), а не на получаемые точки траектории. Поэтому следует иметь в виду, что неправильное употребление этого оператора в середине непрерывного движения может привести к разрыву траектории
(рис. 2.92).
Предполагается вывести инструмент последовательно из Т40 в позиции 1−4:
ИЗ Т40
ИДИ ДО КР1
ВЛЕВО КР1 ДО ПР1
 ТРАНС МАТР (ПОВОРОТ, 30) ТРАНС МАТР (ПОВОРОТ, 30)
ВПРАВО ПР1 ДО КР2
После выполнения оператора 3 инструмент оказался в позиции 2.
После выполнения оператора 4 прямая ПР1
заняла положение ПР1',
инструмент же остался в позиции 2.
В связи с этим выполнить оператор 5 невозможно.
При использовании матрицы симметрии относительно прямой операторы движения, следующие после оператора ТРАНС, должны описывать движение по исходному контуру в обратном направлении (кроме первого перемещения после оператора ТРАНС). При этом не требуется изменять положение инструмента относительно контура, если оно было задано оператором ИНСТЛВ или ИНСТПР.
Движение по контуру, изображенному на рис. 2.93 (— — → — траектория, описанная после оператора ТРАНС; → − фактическая траектория движения инструмента), программируется следующим образом (табл. 2.4).
  Оператор ТРАНСРЕЗ имеет следующий формат: èìÿ Оператор ТРАНСРЕЗ имеет следующий формат: èìÿ
ÒÐÀÍÑÐÅÇ
ÎÒÌÅÍ
где имя
− символическое имя матрицы.

отличие от оператора ТРАНС оператор ТРАНСРЕЗ осуществляет преобразование по заданной матрице рассчитанных точек траектории. Действие его распространяется до нового оператора ТРАНСРЕЗ или до оператора ТРАНСРЕЗ ОТМЕН.
Различие в результатах, полученных при использовании операторов ТРАНС и ТРАНСРЕЗ в приведенном примере, иллюстрируется на рис. 2.94 (– – – → — программируемое перемещение; → — фактическое перемещение). Например:
ТЧ0 = 0,0
ТЧ1 = −100,0
ПР1=ТЧ0, 60
МАТР М1=ПОВХУ, -90
ИЗ ТЧ1
НАПРТ ТЧ0
ИДИ НА ПР1
ТРАНС Ml
ВПРАВО ПР1 НА ОКРУЖИ (ТЧ0, 50)
Оператор ТРАНС выполняет преобразование поверхностей. Поэтому после применения оператора ТРАНС прямая ПР1
примет положение ПРГ,
а оператор ВПРАВО вызовет перемещение инструмента из ТЧ0
в точку 1 (см. рис. 2.94, а).

Если в этой же программе заменить оператор ТРАНС Ml оператором ТРАНСРЕЗ Ml, то преобразованию будет подвергнута точка траектории 2,
которая займет положение 3,
куда и переместится инструмент из ТЧ0
(см. рис. 2.94,6).
2.11 Контуры
Наряду с элементарными типами геометрических объектов в языке Техтран имеется комбинированный тип − КОНТУР. Геометрические объекты этого типа являются совокупностями отрезков прямых и дуг окружностей. Они могут использоваться в командах непрерывного движения аналогично элементарным геометрическим объектам, т. е. инструмент может быть выведен на контур оператором ИДИ, а движение по нему осуществляется с помощью операторов ВЛЕВО, ВПРАВО, ВПЕРЕД, НАЗАД.
Различают простые и составные контуры. Простой контур − комбинация элементарных геометрических объектов, а составной контур является комбинацией нескольких простых контуров.
Простой контур.
Описание простого контура состоит из последовательности операторов непрерывного движения, ограниченных заголовком контура и служебным словом КОНКОН:
[КОНТУР] имя = ИЗ точка, модификатор оператор
1 оператор
2
…
оператор
n-1 оператор
n
КОНКОН
где КОНТУР − служебное слово, задающее тип определяемого объекта (если он еще не известен); имя
− имя, присвоенное контуру; точка
− имя первой точки контура (если контур замкнутый, то любой точки контура); модификатор
− любой из модификаторов ХБ−ХМ−УБ−УМ, задающий направление, относительно которого выбирается оператор1; оператор
1, оператор2
, ..., операторп
− операторы движения.
Простой контур называется замкнутым, если начальная и конечная точки контура совпадают, и незамкнутым, если точки не совпадают. Направление движения в операторе
1
определяется относительно модификатора, указанного в заголовке контура. Проще всего в качестве оператора
1
употреблять оператор ВПЕРЕД. Направление движения в последующих операторах указывается относительно предыдущего направления движения по правилам, изложенным в п. 2.10.
Оператор,
(1 ≤ i ≤ n
) может быть оператором с двумя поверхностями
 ÂÏÅÐÅÄ ÍÀÇÀÄ ÂËÅÂÎ ÂÏÐÀÂÎ ÂÏÅÐÅÄ ÍÀÇÀÄ ÂËÅÂÎ ÂÏÐÀÂÎ
  ÏÅÐÅÑÅ×ÎÏ ÏÅÐÅÑÅ×ÎÏ
либо оператором с одной поверхностью
 ÂÏÅÐÅÄ ÍÀÇÀÄ ÂÏÅÐÅÄ ÍÀÇÀÄ
  ÷èñëî ÏÅÐÅÑÅ× ÂËÅÂÎ ÂÏÐÀÂÎ ÷èñëî ÏÅÐÅÑÅ× ÂËÅÂÎ ÂÏÐÀÂÎ
В описании замкнутого контура направляющие поверхности в первом и последнем операторах могут совпадать. В описании контуров кроме операторов движения можно использовать операторы ПОВТОР и ЕСЛИ (см. п. 2.12).
Незамкнутый контур, изображенный на рис. 2.95, описывается таким образом:
КОНТУР КОН 1= ИЗ ТЧ1, ХБ
ВПЕРЕД ПР1
ВЛЕВО КР1 2 ПЕРЕСЕЧ
ВЛЕВО ПР1 НА ПР2
КОНКОН
Применим в описании контура (рис. 2.95) условный оператор для выбора обхода верхней или нижней полуокружности в зависимости от знака переменной Р:
 КОНТУР КОН 1= ИЗ ТЧ1, ХБ КОНТУР КОН 1= ИЗ ТЧ1, ХБ
ВПЕРЕД ПР1
ЕСЛИ(Р>0)ТО
ВЛЕВО КР1 2 ПЕРЕСЕЧ
ВЛЕВО ПР1 НА ПР2
ИНАЧЕ
ВПРАВО КР1 2 ПЕРЕСЕЧ
ВПРАВО ПР1 НА ПР2
КОНЕСЛИ
КОНКОН
Замкнутый контур, изображенный на рис. 2.96, может быть задан двумя способами. Обычная форма записи следующая:
КОНТУР КОН2 = ИЗ ТЧ1, ХБ
ВПЕРЕД ПР1
ВПЕРЕД КР1
ВПЕРЕД ПР2
ВПЕРЕД КР2
ВПЕРЕД ПРЗ
ВПЕРЕД КРЗ
ВПЕРЕД ПР4
ВПЕРЕД КР4 ВПЕРЕД ПР1 КОНКОН
Сокращенная форма записи имеет вид:
КОНТУР КОШ = ИЗ ТЧ1, ХБ
ВПЕРЕД ПР1:КР1:ПР2:КР2:ПРЗ:КРЗ:ПР4:КР4:ПР1
КОНКОН
Кроме операторов движения в определении контура можно использовать и операторы постпроцессора. При этом следует соблюдать осторожность, так как если направление обхода контура не соответствует направлению, выбранному при описании, то оператор постпроцессора, записанный перед некоторым сегментом контура, будет в действительности относиться к предыдущему сегменту.
Составной контур.
Составной контур представляет собой комбинацию ранее определенных контуров. Если контур
1, контур
2, контур
3, контурп
− ранее определенные контуры, матрица
1, матрица
2, матрица
3, матрицап
− плоские матрицы, а число
1, число
2, число
3, числоп
− числа, переменные или арифметические выражения, то оператор вида
КОНТУР. имя = число1
, матрица1
, контур1
, %
, число2
, матрица2
, контур2
, %
, число3
, матрица3
, контур3
, %
……………
, числоп
, матрщап
, контурп
определяет новый контур, который строится следующим образом. Каждый i-й контур преобразуется по заданной матрице и присоединяется к предыдущему контуру начальной точкой, если число
i
положительное, или конечной точкой, если число
i
отрицательное. Если же число
i
равно нулю, то контур пропускается. По умолчанию предполагается, что числоi
= 1.
Начальной точкой результирующего контура является начальная точка контура
1,
если число
1
положительное, и конечная его точка, если число
1
отрицательное. Матрица
1
− любая плоская матрица, матрица
i
(i≥2) − матрица поворота или симметрии; сдвиг, если он есть, не учитывается. Служебное слово КОНТУР должно присутствовать в том случае, когда определение типа не было сделано ранее.
Если после знака « = » в определении составного контура нет ничего, то это означает, что контур имеет многострочный формат с ограничителем КОНКОН, где элементы составного контура отделены друг от друга концами строк или символами «;».
Например, контур К
(рис. 2.97, в), состоящий из контуров К1
и К2
(рис. 2.97, а, б), описывается следующим образом:
………..
МАТР Ml = ПОВОРОТ, 45 КОНТУР К1=ИЗ ТЧ1, ……..
……………
КОНКОН
КОНТУР К2 = ИЗ ТЧ2, ……... …………...
КОНКОН
КОНТУР К = М1, Kl, K2
Еще один пример построения составного контура приведен на рис. 2.98, б
(на рис. 2.98, а
− исходный контур):
Ml = ПОВОРОТ, −90
КОНТУР К = К1, Ml, K1, -1, К1
На рис. 2.99, б
приведен пример составного контура, который получается симметричным преобразованием исходного контура (на рис. 2.99, а − исходный контур):
КОНТУР К, К1
М1=ПРХ
М2 = ПРУ
МЗ = М1, М2
К1 =
К= + 1, К1, -1, Ml, К1, +1, МЗ, К1, -1, М2, К1
(или К = К1, -1, Ml, К1, МЗ, К1, -1, М2, К1)

В определениях составных контуров можно использовать операторы ЕСЛИ и ПОВТОР. Применим оператор цикла при построении контура К
(рис. 2.100,6), получающегося многократным повторением контура К1
(рис. 2.100, а): КОНТУР К =
ПОВТОР И = 1,5
МАТР (ПОВОРОТ, 72*(И -1)), К1
КОНЦИКЛ
КОНКОН
Частным случаем описания составного контура является оператор присваивания: А = Б или КОНТУР А = Б, где А и Б − объекты типа КОНТУР.
Определение табулированной кривой.
Табулированная кривая (СПЛАЙН, таблично заданная кривая) − это гладкая кривая, интерполирующая заданный набор точек и состоящая из отрезков прямых и дуг окружностей. Табулированная кривая имеет направление от первой заданной точки к последней (т. е. при построении кривой от точки TЧ1 к точке ТЧn и от точки ТЧn к точке ТЧ1 результаты совпадать не будут).
Табулированные кривые имеют тип КОНТУР и с ними можно осуществлять любые операции, имеющие смысл для незамкнутых контуров. Так, например, они могут быть компонентами составного контура. Их геометрическое определение в языке Техтран имеет вид: КОНТУР имя
= СПЛАЙН [, прямая1
], точка1
, точка2
,
. . . , точкап
,
[прямая2
]
где КОНТУР − служебное слово, задающее тип определяемого объекта, если он не был
объявлен ранее; СПЛАЙН − служебное слово, задающее вид определяемого контура; точка
1, точка
2, ..., точкап
− опорные точки кривой (число точек не ограничено); прямая
1, прямая
2
− имена необязательных прямых, касательных к кривой в начальной и конечной точках.
Как и в определении контура, в определении табулированной кривой можно использовать операторы ПОВТОР и ЕСЛИ. Определение с оператором цикла имеет вид:
[КОНТУР] имя =
СПЛАЙН, прямая
1 точка1
, точка2
,
..., точкак
ПОВТОР счетчик = нач, кон, шаг
массив точек (счетчик)
КОНЦИКЛ
точкак+1
, точкак+2
,
..., точкат
 пряая2
КОНКОН пряая2
КОНКОН
Например:
КОНТУР Т1=СПЛАЙН, ПР1
ПОВТОР И = 1,50
ТЧ(И)
КОНЦИКЛ
ПР2
КОНКОН
Определение табулированной кривой с условным оператором имеет вид:
[КОНТУР] имя
= СПЛАЙН [.прямая1
] точка1
, точка2
,
..., точкак
ЕСЛИ (логическое выражение)
ТО
точкак+1
, точкак+2
,
..., точка
l
ИНАЧЕ
точка
l+1, точка
l+2,
..., точкат
КОНЕСЛИ
точка
m+1, точка
m+2,
..., точка
n
КОНКОН
 Например: Например:
КОНТУР Т2 = СПЛАЙН, ПР1
ЕСЛИ (А> =В) ТО
ТЧ1, ТЧ2, ТЧ3
ИНАЧЕ
ТЧ4, ТЧ5, ТЧ6
КОНЕСЛИ
ПР2
КОНКОН
 Оператор цикла и условный оператор могут встречаться в определении табулированной кривой в различных комбинациях: Оператор цикла и условный оператор могут встречаться в определении табулированной кривой в различных комбинациях:
КОНТУР Т3 = СПЛАЙН, ПР1
ТЧ1, ТЧ2, ТЧЗ
ЕСЛИ (А> =В) ТО
ПОВТОР И=1, К
ТЧ(И)
КОНЦИКЛ
ИНАЧЕ
ПОВТОР И=1, М
ЕСЛИ (Л = 1) ТО
ТК(И)
ИНАЧЕ
ТК(М−И)
КОНЕСЛИ
КОНЦИКЛ
КОНЕСЛИ
ТЧ4, ТЧ5, ТЧ6
ПР2
КОНКОН
Подход к контуру.
Существует два способа подхода к контуру: при помощи оператора ИДИ и при помощи операторов непрерывного движения ВПЕРЕД, НАЗАД, ВЛЕВО, ВПРАВО.
При использовании оператора ИДИ следует указывать направление подхода к контуру командой НАПРВ или НАПРТ (рис. 2.101):
ИЗ ТЧ1
НАПРВ В1
ИДИ ЗА К1
При использовании операторов непрерывного движения инструмент следует вывести на контур с помощью любой команды непрерывного движения с двумя поверхностями. Число пересечений не должно превышать восьми. Если поверхность подхода совпадает с одним из сегментов контура, то инструмент выводится в первую или последнюю точку сегмента.

На рис. 2.102 приведен пример подхода к контуру по прямой, заданный следующими командами движения:
ИЗ ТЧ1
ИДИ НА ПР1
ВПРАВО ПР1 ДО КОН1

В случае многократных пересечений (рис. 2.103) вывод инструмента из позиции 1 в позицию 3
задается следующим образом:
ИЗ ТЧ1
ИДИ НА ПР1
ВПРАВО ПР1 ЗА 4 ПЕРЕСЕЧ КОН2
Перемещение инструмента из позиции 1 в позицию 4
программируется операторами: ИЗ ТЧ1
ИДИ НА ПР1
ВПРАВО ПР1 НА 7 ПЕРЕСЕЧ КОН2
Движение по контуру.
Для программирования движения инструмента по контуру можно задать любой из операторов ВПЕРЕД, НАЗАД, ВЛЕВО, ВПРАВО с двумя поверхностями, указав требуемое число пересечений. Ограничивающей поверхностью может быть только прямая или окружность (но не контур и не табулированная кривая).
Например, для контура, показанного на рис. 2.104, перемещение инструмента из позиции 1 в позиции 2
− 11
программируется следующим образом:
ИЗ ТЧ1
ИДИ ДО ПР1
ВПРАВО ПР1 ДО 2 ПЕРЕСЕЧ КОШ
ВПРАВО КОН1 НА 2 ПЕРЕСЕЧ ПР2
Аналогично можно запрограммировать и перемещение инструмента по незамкнутому контуру (рис. 2.105):
ИЗ ТЧ1
НАПРТ ТЧА
ИДИ ДО К1
ВПРАВО К1 НА ПР1

Полный обход всего контура программируется оператором непрерывного движения с одной поверхностью, которой является контур:
  ÂÏÅÐÅÄ ÍÀÇÀÄ èìÿ ÂËÅÂÎ ÂÏÐÀÂÎ ÂÏÅÐÅÄ ÍÀÇÀÄ èìÿ ÂËÅÂÎ ÂÏÐÀÂÎ
где имя
− символическое имя контура.

Совершив полный обход контура, инструмент возвращается в положение, в котором он находился перед использованием оператора этого вида.
 Например, полный обход контура представленного на рис. 2.106, задается операторами: Например, полный обход контура представленного на рис. 2.106, задается операторами:
ИЗ ТЧ1
НАПРВ В1
ИДИ ЗА КОНТ # поз 1−2
ВПРАВО КОНТ ЗА ПРА # поз. 2−3
ВПЕРЕД КОНТ #
поз. 3−2−3
Оператор обхода контура с одной поверхностью
допускается употреблять только для замкнутого контура.
Особенности движения по табулированным кривым.
Поскольку табулированная кривая является разновидностью контура, то все сказанное выше о командах движения для контуров применимо и к табулированным кривым. Необходимо помнить, что при непрерывном движении по контуру не только сами поверхности, но и их эквидистанты должны иметь требуемое число пересечений. Эквидистанта контура (и табулированной кривой) ограничена нормалями в начальной и конечной точках контура. Например, в случаях, изображенных на рис. 2.107, а, б, невозможен выход в начало табулированной кривой, так как эквидистанты к ПР1
и ТКР1
не пересекаются в начальной точке. Примеры различных способов подхода к табулированной кривой рассмотрены ниже.

Подход к табулированной кривой и отход от нее по секущей, не проходящей через граничные точки
(рис. 2.108), является наиболее простым и надежным способом движения по табулированной кривой. Он позволяет исключить начальный и конечный участки сплайна, на которых наиболее вероятно возникновение биений:
КОНТУР ТКР1 = СПЛАЙН, Т1, Т2, ТЗ, Т4, Т5, Т6, Т7, Т8
ВПЕРЕД ПР1 ДО ТКР1 ВЛЕВО ТКР1 НА ПР2 ВЛЕВО ПР2...
Подход к табулированной кривой по касательной
осуществляется с помощью прямых ПР1
и ПР2,
входящих в геометрическое определение сплайна и задающих касательные к нему в начальной и конечной точках (рис. 2.109):
КОНТУР ТКР15 = СПЛАЙН, ПР1, Т1, Т2, ТЗ, Т4, Т5, ПР2
ИДИ НА ПРЗ
ВЛЕВО ПРЗ ДО ПР1
ВЛЕВО ПР1 КАС ТКР15
ВПЕРЕД ТКР15 КАС ПР2
ВПЕРЕД ПР2 НА ПР4
Выход в начальную точку табулированной кривой по дуге окружности
(рис. 2.110) производится в следующей последовательности:
КОНТУР ТКР1=СПЛАЙН, ПР1, Т1, Т2, ТЗ, Т4, Т5, Т6, ПР2
КР1=КАС, ПР1, УБ, Т1, РАДИУС, 20 КР2 = КАС, ПР2, УБ, Т6, РАДИУС, 20
…………………………...
ВЛЕВО КР1 КАС ТКР1
ВПЕРЕД ТКР1 КАС КР2
ВПЕРЕД КР2
При построении замкнутой табулированной кривой
необходимо в качестве начальной и конечной указывать одну и ту же точку, а также общую касательную, если не допускается излома в этой точке (рис. 2.111):
КОНТУР ТК = СПЛАЙН, ПР1, Т1, Т2, ТЗ, Т4, Т5, Т6, Т7, Т8, Т1, ПР1 ИЗ ТЧ0
ИДИ НА ПР1
ВЛЕВО ПР1 КАС ТК
ВПЕРЕД ТК
При многократных пересечениях с табулированной кривой
(рис. 2.112) для выхода из позиции 1 в позицию 4
(через позиции 2
−3)
используются операторы: ИЗ ТЧО ИДИ ДО ПР1
ВЛЕВО ПР1 ДО ТКР ВЛЕВО ТКР НА 4 ПЕРЕСЕЧ ПР1

Для гладкого сопряжения двух табулированных кривых
необходимо задать вырожденное движение по их общей касательной (рис. 2.113): КОНТУР ТКР1=СПЛАЙН, Т1, Т2, ТЗ, Т4, Т5,
ПР1 КОНТУР ТКР2 = СПЛАЙН, ПР1, Т5, Т6, Т7, Т8, Т9 ВПЕРЕД ТКР1 КАС ПР1 ВПЕРЕД
ПР1 КАС ТКР2 ВПЕРЕД ТКР2
2.12 Специальные операторы
Управляющие операторы.
Эти операторы позволяют изменять порядок выполнения операторов программы, т. е. пропускать (при определенных условиях) или многократно выполнять некоторые ее участки. Такие возможности позволяют составлять на входном языке программы, имеющие сложную логическую структуру. К управляющим операторам относятся операторы НАМЕТКУ, ЕСЛИ и ПОВТОР.
Оператор
НАМЕТКУ вызывает безусловную передачу управления на помеченный оператор и имеет следующий формат:
НАМЕТКУ имя
где имя
− имя использованной в программе метки.
После этого оператора выполняется не следующий по порядку оператор, а тот, который помечен указанной меткой. Например:
ИЗ ТЧ8
НАМЕТКУ К2
ИДИ НА ПРХ
К2: В ТОЧКУ ТЧА
ПРИРАЩ 20
В приведенном фрагменте программы после оператора ИЗ будет выполнен не оператор
ИДИ, а помеченный оператор ВТОЧКУ- Оператор
ЕСЛИ имеет следующий формат:
ЕСЛИ (логическое выражение
) оператор1
[; оператор2
; …; операторn
] где оператор1
, оператор2
,
... и т. д.− операторы языка Техтран.
В том случае, если логическое выражение, заключенное в скобки, имеет значение ИСТИНА, то последовательно выполняются оператор
1, оператор
2
и т. д. Если значение логического выражения − ЛОЖЬ, то выполняется оператор2, а если он отсутствует, то выполняется оператор, находящийся в следующей строке программы. Оператор1
, оператор2
,
... и т. д. могут быть только простыми операторами входного языка. Применение составных операторов типа ПОВТОР, КОНТУР, МАКРО недопустимо. Например: ЕСЛИ (А>0.5 ИЛИ А<0) НАМЕТКУ М24
Переход на метку М24 выполняется, если значение переменной А больше 0.5 или меньше 0.
Если значения переменной К меньше 10, то будут выполнены операторы присваивания для ТЧ1 и ТЧ2:
ЕСЛИ (К МНШ 10) ТЧ1=0, 0, 5; ТЧ2 = ПРЗ, ПР4
ТЧ6 = ЦЕНТР, КР2
При других значениях переменной К логическое выражение принимает значение ЛОЖЬ, геометрическое определение точки ТЧ1 опускается и выполняются операторы ТЧ2= . . . и ТЧ6= . . .
Оператор
ЕСЛИ−ТО−ИНАЧЕ−КОНЕСЛИ имеет следующий формат:
ЕСЛИ (логическое выражение)
ТО
  [список операторов1
] ÈÍÀ×Å ñïèñîê îïåðàòîðîâ 2 [список операторов1
] ÈÍÀ×Å ñïèñîê îïåðàòîðîâ 2
КОНЕСЛИ
Если логическое выражение имеет значение ИСТИНА, то последовательно выполняются операторы списка, расположенного после слова ТО. Если же значение логического выражения − ЛОЖЬ, то выполняются операторы списка, стоящего за словом ИНАЧЕ. Любой из этих списков может быть пустым − в этом случае будет выполняться оператор, следующий за ограничителем КОНЕСЛИ. При отсутствии слова КОНЕСЛИ выдается предупреждение и ошибка корректируется. Например:
1) ЕСЛИ (А> =0) ТО
А = А
ИНАЧЕ А = - А
КОНЕСЛИ
В результате будет вычислено абсолютное значение А.
2) ЕСЛИ (Х> =0) ТО У = КВКОР (X)
ИНАЧЕ
КОНЕСЛИ
В этом примере отсутствует второй список. Оператор аналогичен оператору ЕСЛИ (X БРВ 0) У = КВКОР (X).
3) ВПЕРЕД ПРХ НА ПРУ
ПР1=ПАРЛЕЛ, ПРХ, А
ЕСЛИ (А>0) ТО
ВЛЕВО ПРУ НА ПР1
ИНАЧЕ
ВПРАВО ПРУ НА ПР1
КОНЕСЛИ
В этом примере выбирается оператор движения ВПРАВО или ВЛЕВО в зависимости от положения прямой ПР1 относительно оси х.
Оператор
ПОВТОР предназначен для многократного повторения участка программы, называемого телом цикла. Существуют две модификации оператора ПОВТОР: 1) цикл со счетчиком и 2) цикл ПОКА.
Формат 1-го варианта оператора: ПОВТОР перем = нач, кон
[, шаг
]
оператор
1
оператор
2
.
.
.
оператор
n
КОНЦИКЛ [перем
]
где перем
− идентификатор вещественной переменной, являющейся управляющей переменной цикла; нач
− число, переменная или арифметическое выражение, задающие начальное значение управляющей переменной цикла; кон
− число, переменная или арифметическое выражение, задающие конечное значение управляющей переменной цикла; шаг
− число, переменная, или арифметическое выражение, задающие приращение управляющей переменной; по умолчанию приращение равно 1; оператор1
, оператор2
,
..., операторn
− операторы входного языка, составляющие тело
цикла.
При первом исполнении цикла перем = нач,
при втором − перем = нач
+ шаг
и т. д. до тех пор, пока удовлетворяется условие: перем*шаг≤кон*шаг.
После последнего исполнения цикла управление передается оператору, следующему за оператором КОНЦИКЛ, а управляющая переменная цикла перем
принимает первое значение, не удовлетворяющее этому условию. Значение управляющей переменной цикла перем
может быть использовано при вычислениях так же, как значение любой другой вещественной переменной, например: ПОВТОР И = 1, 10
А (И)=0
КОНЦИКЛ И
В результате выполнения этого цикла первым десяти элементам массива А присваиваются нулевые значения, например:
Т = 6,5
ПОВТОР И =1,7
Т = Т-И
ЕСЛИ (Т МНШ 0) НАМЕТКУ Ml
Т = Т + 2.0
КОНЦИКЛ И
М1:Р = Т Т
В процессе выполнения цикла переменная Т
последовательно принимает следующие значения: 6,5; 5,5; 7,5; 5,5; 7,5; 4,5; 6,5; 2,5, 4,5; −0,5. Затем оператор ЕСЛИ передает управление на оператор с меткой Ml, при этом И = 5.
Если начальное значение переменной Т
принять равным 26,5, то последующие ее значения, вычисленные в цикле, будут равны: 27,5; 27,5; 26,5; 24,5; 21,5; 17,5; 12,5. Затем произойдет нормальный выход из цикла; при этом И = 8, так как это первое значение переменной И, при котором перестает выполняться условие И*1^7*1.
Формат 2-го варианта оператора:
ПОВТОР ПОКА (логическое выражение)
оператор
1
оператор
2
.
.
.
операторт
КОНЦИКЛ
Такая конструкция позволяет повторять выполнение операторов, составляющих тело цикла, до тех пор, пока логическое выражение, находящееся в заголовке цикла, сохраняет значение ИСТИНА. Для нормального завершения такого цикла необходимо, чтобы в теле цикла имелись операторы присваивания, изменяющие значения переменных, которые входят в логическое выражение. Если перед очередным повторением цикла обнаруживается, что логическое выражение имеет значение ЛОЖЬ,
то управление передается оператору, следующему за оператором КОНЦИКЛ.
Если значение выражения оказывается ложным с самого начала, то операторы, составляющие цикл, не выполняются.
 В качестве примера приведем программу вычисления значения корня кубического с использованием метода Ньютона. Полагаем хо=1 и затем вычисляем, A В качестве примера приведем программу вычисления значения корня кубического с использованием метода Ньютона. Полагаем хо=1 и затем вычисляем, A
x
1
,
3
где А
− число, из которого необходимо извлечь корень кубический.
Далее полагаем хо
= х
1
и вычисляем новое значение х2. Процесс вычислений продолжается до тех пор, пока разница между двумя последовательными значениями х
не окажется в пределах допустимой ошибки. Например, процесс вычисления корня кубического из числа 4 можно представить следующим образом: А
= 4; хо
=1; х1
= (2 + 4/1)/3 = 2; х2
=(4 + 4/4) 3=1.667; х3
= (3.333 + 4/2.778)/3= 1.591.
Если продолжить процесс вычислений, то значения х
будут приближаться к 1,5874 − корню кубическому из 4. Программа на Техтране будет иметь вид:
ХСТАР = 0
ХНОВ = 1
ПОВТОР ПОКА ( АБС ( ХНОВ-ХСТАР) БЛШ 0.0001)
ХСТАР = ХНОВ
ХНОВ = (2*ХСТАР + 4/ХСТАР**2)/3
КОНЦИКЛ
Разрешается использовать вложенные циклы. В этом случае тело внутреннего цикла полностью должно находиться в теле внешнего цикла, т. е. перекрытие циклов не допускается.
Глубина вложений должна быть не больше 10. Рассмотрим случай вложения двух циклов:
ВЕЩ А (50,6)
ПОВТОР Н=1,50
ПОВТОР И = 2,6
ХК = И
А (Н,И) = (1.0 + 0,01*ХК)**И
КОНЦИКЛ И
КОНЦИКЛ Н
Эта программа вычисляет значения А(Н,И) = (1 +И)Н
для И = 0.01; 0.02; 0.03; ... . . . ; 0,06 и И=1, 2, .... 50.
Не допускается применять операторы, лежащие вне тела цикла и передающие управление внутрь цикла. Варианты допустимых передач управления показаны на рис. 2.114.
Использование циклов должно быть согласовано с использованием макросов. Это означает, что цикл, начинающийся (кончающийся) внутри макроса, должен там же и кончаться (начинаться).
Управление печатью.
Каждая фаза процессора системы Техтран осуществляет вывод информации на печать. Для управления объемом выводимой информации в языке имеются специальные операторы: ПЕЧТЕКСТ, ПЕЧТР, СЛЕД и ПЧТ1.
   Оператор
ПЕЧТЕКСТ предназначен для управления распечаткой исходного текста программы на Техтране (результат работы первой фазы процессора). Оператор имеет следующий формат: Оператор
ПЕЧТЕКСТ предназначен для управления распечаткой исходного текста программы на Техтране (результат работы первой фазы процессора). Оператор имеет следующий формат:
ÂÊË
ПЕЧТЕКСТ ÂÑÅ
ÂÛÊË
где ВКЛ − распечатка всей вводимой информации кроме расшифровок операторов ВЫЗОВ; ВСЕ − полная распечатка, включая расшифровки операторов ВЫЗОВ; ВЫКЛ − подавление печати вводимой информации.
Отсутствие оператора ПЕЧТЕКСТ эквивалентно применению оператора ПЕЧТЕКСТ ВКЛ. Операторы ДЕТАЛЬ и КОНЕЦ, а также строки, содержащие ошибки, выводятся на печать всегда.
  Оператор
ПЕЧТР устанавливает режим распечатки траектории движения инструмента и имеет формат: ÂÊË Оператор
ПЕЧТР устанавливает режим распечатки траектории движения инструмента и имеет формат: ÂÊË
ПЕЧТР ÂÑÅ
ÂÛÊË
При отсутствии в программе оператора ПЕЧТР или при использовании оператора ПЕЧТР ВКЛ на печать выводятся следующие параметры выполняемого движения: данные об инструменте, метод интерполяции и точность линейной аппроксимации, параметры геометрических объектов, образующих контур, координаты начальной точки, координаты точек пересечения эквидистант, координаты опорных точек.
При наличии в программе таблично заданных кривых и контуров формируются сообщения «НАЧАЛО КОНТУРА», «КОНЕЦ КОНТУРА», а также параметры геометрических элементов и координаты точек пересечения этих элементов.
При использовании оператора ПЕЧТР ВСЕ дополнительно выводятся на печать следующие параметры: координаты точек разбиения окружностей на квадранты, промежуточные точки аппроксимации окружности отрезками прямых, сообщение «ДВИЖЕНИЕ ПО КОНТУРУ» и траектория движения по контуру или по таблично заданной кривой.
Использование оператора ПЕЧТР ВЫКЛ приводит к подавлению вывода информации на печать до конца программы или до следующего оператора ПЕЧТР. Исключение составляют строки, содержащие ошибки движения, которые выводятся всегда.
Данные обо всех геометрических переменных выводятся в соответствии с их внутренним представлением (см. п. 2.9).
  Оператор
СЛЕД выполняет трассировку программы, т. е. печатает результаты выполнения операторов и имеет следующий формат: ÂÊË Оператор
СЛЕД выполняет трассировку программы, т. е. печатает результаты выполнения операторов и имеет следующий формат: ÂÊË
СЛЕД ÂÑÅ
ÂÛÊË
где ВКЛ − включение распечатки результатов выполнения операторов, находящихся вне макроса; ВСЕ − включение распечатки результатов выполнения всех операторов; ВЫКЛ − выключение распечатки результатов выполнения операторов.
Таблица 2.5
| Содержание строки
|
Данные, выводимые на печать
|
|
| ЕСЛИ (логическое)
|
ЛОЖЬ или ИСТИНА
|
| НАМЕТКУ
|
ПЕРЕХОД НА МЕТКУ
|
|
| ПОВТОР
|
Минимальное и максимальное значения индекса
|
|
| КОНЦИКЛ
|
ПЕРЕХОД НА МЕТКУ
|
|
| ВЫЗОВ
|
ВХОД В МАКРО
|
|
| КОНЕЦ МАКРОСА
|
ВЫХОД ИЗ МАКРО
|
|
| Арифметическое выражение
|
Результат
|
|
| Геометрическое определение
|
Имя параметра геометрического объекта
Параметры геометрических объектов, образующих контур; координаты опорных точек табулированной кривой
|
|
| КОНТУР
|
| П р и м е ч а н и е . Перед результатом на печать выводится номер соответствующей строки.
|
| |
В режиме «1» печатаются результаты всех операторов, приведенных в табл. 2.5. В режиме «О» печатаются только результаты управляющих операторов. Вся информация выводится в процессе работы второй фазы процессора в формате, приведенном в табл. 2.5.
Оператор
ПЧТ1 используется для печати значения некоторой переменной или параметров геометрического объекта (точки, окружности, вектора или прямой) и имеет следующий формат: ПЧТ1 имя
1, имя
2, имя
3,…
где имя1
, имя2
, . . .
− имена геометрических объектов или переменных.
Аналогично оператору СЛЕД информация выводится в процессе работы второй фазы процессора в следующем формате:/
номер строки имя
1
=внутреннее представление номер строки имя2
=
внутреннее представление
Оператор
СИНОНИМ служит для замены стандартных служебных слов синонимами и имеет следующий формат:
СИНОНИМ (служебное слово1
, синоним1
),
%
[(служебное слово2
, синоним2
), %
…
(служебное словоn
, синонимn
)]
В качестве синонимов
могут употребляться только имена. Оператор должен быть задан до первого использования синонима. Например, задав оператор СИНОНИМ (ВПЕРЕД, В), (ПЕРЕСЕЧ, П), можно вместо оператора ВПЕРЕД ПР1 ДО 2 ПЕРЕСЕЧ КР1 употреблять в программе оператор В ПР1 ДО 2 П КР1.
Оператор вставки текста
«*» позволяет вставить в программу текст, хранящийся во внешней памяти, и имеет следующий формат:
* имя
* литерал
где имя
− имя модуля из библиотеки программ; литерал
− спецификация файла. Например:
*PROG1
*’SY: PROG2'
Конкретный формат оператора зависит от типа используемой ЭВМ.
2.13 Макросы
В языке Техтран можно использовать в программе отдельно подготовленные части исходного текста − макросы. В макросе разрешается применять любые операторы языка, но вместо конкретных значений переменных могут использоваться параметры.
Подключение макроса к программе осуществляется при помощи специального оператора ВЫЗОВ. При этом в тексте программы на месте оператора ВЫЗОВ появляется текст вызываемого макроса (тело), в котором формальные параметры, заданные в теле макроса, заменяются фактическими значениями, указанными в операторе ВЫЗОВ. Допускается определение макросов внутри программы. В этом случае вызов макроса должен производиться из этой же программы.
Структура макросов.
Макрос состоит из заголовка, тела и ограничителя. Заголовок макроса представляет собой специальный оператор МАКРО. Тело макроса − произвольная последовательность операторов языка Техтран (кроме операторов ДЕТАЛЬ, КОНЕЦ и ПЕЧТЕКСТ), в которых могут быть использованы параметры макроса. Тело макроса может содержать другие макросы и обращения к ним. Ограничителем макроса является служебное слово КОНМАК.
Параметры макроса.
Параметры могут быть операторными и текстовыми. Параметры записываются в произвольном порядке и отделяются друг от друга запятыми.
Операторный
параметр представляет собой оператор языка Техтран, заключенный в скобки. При вызове макроса операторные параметры выполняются непосредственно перед телом макроса. В качестве операторных параметров нельзя использовать операторы ДЕТАЛЬ, КОНЕЦ, МАКРО, КОНМАК, ВЫЗОВ, КОНТУР, КОНКОН, ПОВТОР, КОНЦИКЛ, ЕСЛИ. Операторы присваивания, не содержащие разделителей в правой части, в скобки можно не заключать.
Текстовой
параметр в отличие от операторного имеет свое имя и значение. Значением текстового параметра является произвольная последовательность символов, не содержащая символа «#». Имя текстового параметра − произвольное имя, допустимое в языке Техтран.
В теле макроса имени текстового параметра должен предшествовать символ макроподстановки «&». При вызове макроса вместо символа «&» и имени параметра в текст будет подставлено его значение. Не разрешается параметризовать часть имени, числа или литерала.
Например, вместо оператора КР& КР = 0,0,40 после текстовой подстановки значения параметра '10' получим: КР 10 = 0,0,40, что недопустимо.
Правильной является запись: &КР = 0,0,40. При значении параметра 'КРЮ' оператор будет преобразован к виду: КР10 = 0,0,40.
Значения текстовых параметров макроса задаются в операторах ВЫЗОВ или МАКРО.
Заголовок макроса.
Заголовок представляет собой специальный оператор МАКРО и имеет следующий формат:
МАКРО имя
[(список значений)
]
где имя
− имя макроса (любое имя, допущенное в языке Техтран); список значений
− список
значений текстовых параметров, установленных по умолчанию.
Если значения по умолчанию не задаются, скобки должны быть опущены. Значение по умолчанию используют в том случае, если в операторе ВЫЗОВ значение данного текстового параметра не задано. Элементы списка значений отделяются друг от друга запятыми.
Значение по умолчанию задается одним из следующих способов:
1) 'имя'
= литерал
(например, 'КР'='КР10' − параметр с именем КР принимает по умолчанию значение, равное КРЮ);
2) 'имя1
' = & имя2
(например, 'КР1' = &КР2− параметр с именем КР1 принимает то же значение, что и параметр КР2; параметр КР2 должен быть определен ранее);
3) 'имя'
= объединение литералов и текстовых параметров
(например, если значение параметра КР по умолчанию определено следующим образом: 'КР' = = 'КР'&М6&АБ'10', то при значениях параметров Мб и АБ'04' и 'В' соответственно, параметр с именем КР примет значение КР04В10).
Примеры заголовков макросов: МАКРО МТК1
Значений по умолчанию нет.
МАКРО М2 ('ПГ = '1',' П2' = 'ПР'&П1,' ПЗ' = 'КР'&П1&П1)
По умолчанию: П1 = 1; П2 = ПР1; ПЗ = КРП
МАКРО МЗ (/
ПГ = 'Г,'П2'=='ПР'&П4&П4',ПЗ' = 'КР'&П4)
По умолчанию: П1 = 1; П2 = ПР значение
П4 значение
П4; ПЗ = КР значение
П4.
Значение параметра П4 обязательно должно быть определено при вызове макроса. В противном случае возникнет ошибка. Если для параметра П4 нужно задать значение по умолчанию, то это следует сделать до присваивания значений П2 и ПЗ: МАКРО ПЗ ('ПГ = 'Г, 'П4' = '2', 'П2'='ПР'&П4&П4, % ‘ПЗ' = 'КР'&П4)
  Вызов макроса.
Для выполнения макроподстановки, т. е. вставки в текст исходной программы на Техтране тела макроса и для замены формальных "параметров фактическими предназначен оператор ВЫЗОВ. Он имеет следующий формат: èìÿ Вызов макроса.
Для выполнения макроподстановки, т. е. вставки в текст исходной программы на Техтране тела макроса и для замены формальных "параметров фактическими предназначен оператор ВЫЗОВ. Он имеет следующий формат: èìÿ
ВЫЗОВ [(список параметров)
]
ëèòåðàë
где имя
− имя макроса, использованное в операторе МАКРО; литерал
− спецификация файла, в котором находится текст макроса; список параметров
− последовательность операторных параметров и значений текстовых параметров, разделенных запятыми. Если параметры в вызове отсутствуют, скобки должны быть опущены.
Имя макроса используется в том случае, когда макрос находится в макробиблиотеке или определяется в самой программе. Если макрос содержится в отдельном файле, следует использовать литерал − спецификацию этого файла. Формат спецификации файла зависит от типа ЭВМ и операционной системы, например:
ВЫЗОВ Ml
ВЫЗОВ 'SY: MACRO 1’
С помощью оператора «:» (двоеточие) можно задавать умолчание для имени макроса. Формат оператора следующий: : литерал1
, литерал2
где литерал
1
− строка символов, присоединяемая к имени макроса слева; литерал
2
− строка
символов, присоединяемая к имени макроса справа.
Например, оператор: 'DK1: [77, 300]', '. TEH' позволяет, задавая в программе вызов в формате ВЫЗОВ МАКРО1, передать операционной системе имя файла в виде 'DK1: [77, 300] MAKRO 1. ТЕН'.
Рассмотрим следующий оператор:
ВЫЗОВ Ml (A=l, (ВЕЩ Б = 2), В = 30.5, (ТЧ1 =0,0,0))
В нем заданы четыре операторных параметра. Без скобок можно записывать только параметры, присваивающие вещественные значения.
Если в операторе ВЫЗОВ определено значение текстового параметра, которому присвоено значение по умолчанию в заголовке макроса, то значение по умолчанию игнорируется, например: ДЕТАЛЬ 'МАКРО'
МАКРО Ml ('ПГ = 'Г, 'П2' = & Ш'0')
А = &П1+& П2
ТЧ1=А, В
КР1=ТЧ1, В + & П1
ПЧТ1 А, В, ТЧ1, КР1
КОНМАК
ВЫЗОВ Ml (/
П1/
= '2/
, 'П2' = '25', В = 0)
ВЫЗОВ Ml ('П1' = '2', В = 3)
ВЫЗОВ Ml ('П2' = '35', В=2.5)
ВЫЗОВ Ml (В = 7.4)
КОНЕЦ
Таблица 2.6 Таблица 2.7
| Номер вызова макроса
|
П1
|
П2
|
В
|
А
|
|
ТЧ1
|
|
КР1
|
| 1
2
3
4
|
2
2
1
1
|
25
20
35
10
|
0
3
2,5
7,4
|
27
22
36
11
|
27
22
36
11
|
0
3
2,5
7,4
|
0
0
0
0
|
27 0 2
22 3 5
36 2,5 3,5
11 7,4 8,4
|
| Номер вызова
макроса
М2
|
П1
|
А
|
| 1
2
3
4
|
10
+
-
1+2
|
А=10-1
А=+-1
А=-1
А=1+2-1
|
| П р и м е ч а н и е . В результате 2-го вызова макроса будет выдана ошибка компиляции.
|
Значения параметров и переменных, выводимые на печать, приведены в табл. 2.6.
Вложенные вызовы.
В теле макроса может встретиться оператор ВЫЗОВ с именем другого макроса. При этом
происходит вставка тела нового макроса в тело старого. В теле внутреннего макроса нельзя использовать текстовые параметры внешнего макроса, но их можно применять в операторе ВЫЗОВ для задания значений внутренних текстовых параметров, например: МАКРО Ml ('П1' = ", П2 = ", П3 = ") ВЫЗОВ М2 ('ПГ = '&ПГ)
ВЫЗОВ М2 ('ПГ = '&П2 + &ПЗ')
КОНМАК
МАКРО М2
А = &П1 −1
КОНМАК
ВЫЗОВ Ml ('ПГ = '10')
ВЫЗОВ Ml ('П2' = 'Г, 'П3' = '2')
Значения параметра и переменной, выводимые на печать (для данного примера), приведены в табл. 2.7.
Локализация переменных в макросе.
Для обеспечения полной независимости Макросов от вызывающей программы предусмотрена возможность локализации переменных внутри макросов.
Переменная является локализованной в макросе, если ее значение доступно только внутри этого макроса. В этом случае вне макроса может существовать другая переменная с тем же именем.
Для локализации переменной внутри макроса ее необходимо там явно описать. В противном случае будет использоваться переменная, определенная вне макроса. Если переменная используется впервые, она считается локализованной на текущем уровне вложения макросов.
Приведем пример использования локальных переменных:
А=1
МАКРО М
ВЕЩ А
А = 2
КОНМАК
ВЫЗОВ М
ПЧТ1 А
Поскольку в макросе М имеется явное задание типа переменной А, то она считается локальной в макросе М. Вне макроса ее значение, равное 2, недоступно. Вне тела макроса определена другая переменная А, которой было присвоено значение, равное 1, и именно это значение будет выведено на печать:
А=1
МАКРО М
А = 2
КОНМАК
ВЫЗОВ М
ПЧТ1 А
В этом случае печатается значение А = 2, так как в теле макроса используется переменная, определенная вне его. Расположение тела макроса относительно оператора А=1 здесь не существенно:
МАКРО М
А = 2
КОНМАК
ВЫЗОВ М ПЧТ1 А
В данном примере допущена ошибка, так как значение переменной А не определено.
Операторные параметры рассматриваются как операторы, находящиеся внутри макроса.
Переменные, определяемые в операторных параметрах, должны удовлетворять тем же соглашениям, что и переменные тела макроса, например:
А=1
ВЫЗОВ М (ВЕЩ А = 2)
ПЧТ1 А
На печать будет выведено А= 1, так как в вызове определена локальная в макросе М переменная.
А=1
ВЫЗОВ М (А = 2)
ПЧТ1 А
На печать будет выведено значение А = 2.
Использование меток.
Все используемые в макросе метки локализованы внутри этого макроса. Это означает, что передачи управления в макрос и из него запрещены. Разрешены только переходы внутри тела макроса.
2.14 Примеры программ на Техтране
Примеры, приведенные ниже, иллюстрируют возможности процессора САП Техтран. Поэтому в них, как правило, отсутствуют операторы постпроцессора и некоторые вспомогательное перемещения, необходимые с точки зрения технолога.
 Пример 1.
Ниже приводится текст программы обработки простейшего контура, изображенного на рис. 2.115. ДЕТАЛЬ ‘ПРИМЕР 1’ Пример 1.
Ниже приводится текст программы обработки простейшего контура, изображенного на рис. 2.115. ДЕТАЛЬ ‘ПРИМЕР 1’
#
# ОПРЕДЕЛЕНИЕ ЭЛЕМЕНТОВ КОНТУРА
#
ТЧ0 = -30, 0
ТЧ1 = 0, 0
ПР1 = ТЧ1, 45
ПР2 = ТЧ1, -45
ТЧ2 = ПР1, ТЧ1, 50, УМ ТЧ3 = ПР2,ТЧ1, 50,УМ
ПР3 = ТЧ0, ПЕРП, ПР1
КР1 = ТЧ1, ТЧ2, ТЧЗ
КР2 = УМ, ПР1, УМ, ПР2, РАДИУС, 10
КР3 = УМ, ПР1, ХМ, ВНУТРИ, КР1, 10
КР4 = УМ, ПР2, ХБ, ВИУТРИ, КР1, 10
#
ИНСТР 6 # ДИАМЕТР ИНСТРУМЕНТА
МЕТОД ЛИНКРУГ # МЕТОД ИНТЕРПОЛЯЦИИ
ИНСТПР #
ИНСТРУМЕНТ СПРАВА
#
#
ОПИСАНИЕ ТРАЕКТОРИИ ДВИЖЕНИЯ ИНСТРУМЕНТА
#
ИЗ ТЧ0 #
НАЧАЛО ДВИЖЕНИЯ
ИДИ ДО ПР1 # ПОДХОД К КОНТУРУ
ВПРАВО ПР1 # ОБХОД КОНТУРА
ВПЕРЕД КР3 : КР1 : КР4 : ПР2 : % # СНАРУЖИ ПРОТИВ
КР2 : ПР1 НА ПРЗ # ЧАСОВОЙ СТРЕЛКИ
ВТОЧКУ ТЧ0 # ВОЗВРАТ В ИСХ. ТЧ.
KOHEЦ # КОНЕЦ ПРОГРАММЫ
|