| ЗОВНІШНЄ НЕЗАЛЕЖНЕ ОЦІНЮВАННЯ З МАТЕМАТИКИ 2009 РОКУ
(відповіді до завдань тесту)
1.
Спростіть вираз  3x
+
12
. x
2
−16 3x
+
12
. x
2
−16
3
Відповідь
:  . .
x
− 4
2.
 У трикутнику АВС
: ∠А
=65°, ВD
– бісектриса кута В
(див. рисунок). Знайдіть градусну міру кута ВCA
, якщо ∠AВD
=35°. У трикутнику АВС
: ∠А
=65°, ВD
– бісектриса кута В
(див. рисунок). Знайдіть градусну міру кута ВCA
, якщо ∠AВD
=35°.
Відповідь
: 45°.
3
128
3.
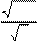 Обчисліть . Обчисліть .
3
2
Відповідь
: 4.
4.
Яка з поданих нижче послідовностей є арифметичною прогресією?
Відповідь
: 3; 7; 11; 15.
5.
У Оксани є певна кількість горіхів. Коли вона розклала їх у купки по 5 горіхів, то два горіхи залишилися, а коли розклала їх по 3, то зайвих горіхів не виявилося. Яка кількість горіхів із запропонованих варіантів МОГЛА БУТИ в Оксани?
Відповідь
: 57.
x
6.
 Розв’яжіть нерівність ⎜⎛1⎟⎞ ≤ 1
. Розв’яжіть нерівність ⎜⎛1⎟⎞ ≤ 1
.
⎝5⎠ 25
Відповідь
: [2; + ∞).
7.
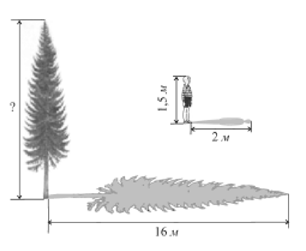
У сонячний день довжина тіні від дерева становить 16 м
. У той самий час тінь від хлопчика, який має зріст 1,5 м
, дорівнює 2 м
(див. рисунок). Визначте висоту дерева.
Відповідь
: 12 м
.
8.
За переказ грошей клієнт повинен сплатити банку винагороду в розмірі 2% від суми переказу. Скільки всього грошей (у гривнях) йому потрібно сплатити в касу банку, якщо сума переказу становить 30 000 грн
?
Відповідь
: 30 600 грн
.
9.
Якщо a
= −1  b
, то b
= c b
, то b
= c
Відповідь
: с
(1−a
).
10.
Укажіть правильну нерівність.
Відповідь
: 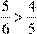 . .
11.
Укажіть рисунок, на якому зображено графік парної функції.
Відповідь
:
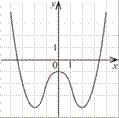
r r r r
r
12.
Знайдіть вектор c
= 2a b
− , якщо a
(3; 1;− 2), b
(−2; 2;5).
r
Відповідь
: c
(8; − −4; 1).
13.
У туриста є 10 однакових за розмірами консервних банок, серед яких 4 банки – з тушкованим м’ясом, 6 банок – з рибою. Під час зливи етикетки відклеїлися. Турист навмання взяв одну банку. Яка ймовірність того, що вона буде з рибою?
Відповідь
: 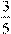 . .
14.
Знайдіть похідну функції y
= x
4
+ 3cos x
.
Відповідь
: y
′ = 4x
3
−3sin x
.
15.
Укажіть УСІ ПРАВИЛЬНІ твердження.
Через точку A
, що не належить площині α, можна провести лише одну пряму, паралельну площині α.
Через точку A
, що не належить площині α, можна провести лише одну площину, паралельну площині α.
Через точку A
, що не належить площині α, можна провести лише одну пряму, перпендикулярну до площини α.
Через точку A
, що не належить площині α, можна провести лише одну площину, перпендикулярну до площини α.
Відповідь
:
Через точку A
, що не належить площині α, можна провести лише одну площину, паралельну площині α.
Через точку A
, що не належить площині α, можна провести лише одну пряму, перпендикулярну до площини α.
16.
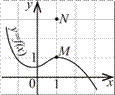 Графік функції y
= f x
( ) проходить через точку М
(1;1) (див. рисунок). При якому значенні а
графік функції y
= f x
( ) + a
проходить через точку N
(1;3)? Графік функції y
= f x
( ) проходить через точку М
(1;1) (див. рисунок). При якому значенні а
графік функції y
= f x
( ) + a
проходить через точку N
(1;3)?
Відповідь
: a
=2.
17.
Розв’яжіть рівняння 2sin x
=1.
Відповідь
: 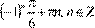 . .
18.
До складу української Прем’єр-ліги з футболу входять 16 команд. Упродовж сезону кожні дві команди грають між собою 2 матчі. Скільки всього матчів буде зіграно за сезон?
Відповідь
: 240.
19.
Гострий кут паралелограма дорівнює 60°, а його сторони – 3 см
і 4 см
. Обчисліть довжину меншої діагоналі паралелограма.
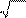 Відповідь
: 13 см
. Відповідь
: 13 см
.
20.
Свинцеву кулю радіуса 5 см
переплавили в кульки однакового розміру, радіус кожної з яких – 1 см
. Скільки таких кульок одержали? Втратами свинцю під час переплавлення знехтуйте.
Відповідь
: 125.
21.
Обчисліть 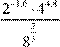 . .
Відповідь
: 64.
22.
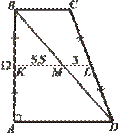 У трапеції ABCD
: ∠A
= 90o
, AB
=12 см
(див. рисунок). Діагональ У трапеції ABCD
: ∠A
= 90o
, AB
=12 см
(див. рисунок). Діагональ
BD
ділить середню лінію KL
трапеції на відрізки KM
і ML
, причому KM
= 5,5 см
і ML
= 3 см
. Обчисліть периметр трапеції ABCD
(у см
).
Відповідь
: 42.
23.
Обчисліть cosα , якщо sinα= 0,8 і 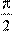 < α < π . < α < π .
Відповідь
: –0,6.
24.
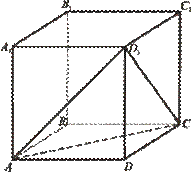 Об’єм куба ABCDA
1 1 1 1
BCD
дорівнює 216 см
3
(див. рисунок). Обчисліть об’єм піраміди D ACD
1
(у см
3
). Об’єм куба ABCDA
1 1 1 1
BCD
дорівнює 216 см
3
(див. рисунок). Обчисліть об’єм піраміди D ACD
1
(у см
3
).
Відповідь
: 36.
25.
Розв’яжіть рівняння log6
(x
− +3) log6
(x
− =8) 2.
Якщо рівняння має один корінь, то запишіть його у відповідь; якщо воно має два корені, то у відповідь запишіть їх суму.
Відповідь
: 12.
26.
У фермерському господарстві „Надія” кожен рік озимою пшеницею засівають 600 га
полів. Середня врожайність цієї культури в 2007 році становила 24 центнери з одного гектара. Завдяки сприятливим погодним умовам у 2008 році озимої пшениці було зібрано на 19 200 центнерів більше, ніж у 2007. Обчисліть середню врожайність озимої пшениці, вирощеної у господарстві „Надія” в 2008 році (у ц
/га
). (Середня врожайність сільськогосподарської культури
– це відношення маси зібраного врожаю цієї культури до загальної площі полів, на яких вона була вирощена.)
Відповідь
: 56.
27.
Знайдіть КІЛЬКІСТЬ усіх цілих розв’язків нерівності  x
2
−
x
−
12
2
≤ 0. x
2
−
x
−
12
2
≤ 0.
(x
+1)
Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100.
Відповідь
: 7.
28.
Кімната має форму прямокутного паралелепіпеда (ширина кімнати – 4 м
, довжина – 5 м
, висота – 2,5 м
). Площа стін кімнати дорівнює 0,8 площі бічної поверхні цього паралелепіпеда. Скільки фарби (у кг
) потрібно для того, щоб повністю пофарбувати СТІНИ і СТЕЛЮ цієї кімнати, якщо на 1 м
2
витрачається 0,25 кг
фарби?
Відповідь
: 14.
⎧ x
−2y
1
⎪
3 = ,
29.
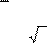 Розв’яжіть систему рівнянь⎨ 3 ⎪⎩3x
+ 32y
= 4 3. Розв’яжіть систему рівнянь⎨ 3 ⎪⎩3x
+ 32y
= 4 3.
Для одержаного розв’язку (x
0
; y
0
) системи обчисліть ДОБУТОК x
0
⋅ y
0
.
Відповідь
: 0,375.
30.
Знайдіть найбільше значення функції y
= 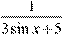 . Якщо функція не має найбільшого . Якщо функція не має найбільшого
значення, то у відповідь запишіть число 100.
Відповідь
: 0,5.
31.
Радіус основи конуса R
, твірна нахилена до площини основи під кутом α. Через вершину конуса проведено площину під кутом ϕ до його висоти. Ця площина перетинає основу конуса по хорді. Знайдіть площу утвореного перерізу.
 R
2
tgα − α ϕ1 tg2
tg2 R
2
tgα − α ϕ1 tg2
tg2
Відповідь
: .
cosϕ
32.
Задано функції f x
( ) = x
2
+1 і g x
( ) = 7 − x
.
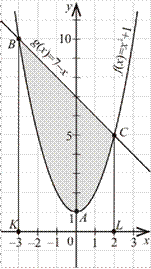
1. Знайдіть абсциси точок перетину графіків функцій f x
( ) і g x
( ) . У прямокутній системі координат зобразіть фігуру, обмежену цими графіками.
2. Обчисліть площу фігури, обмеженої графіками функцій f x
( ) і g x
( ) .
 Відповідь
: 1. –3; 2. Відповідь
: 1. –3; 2.
2. 20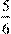 (кв
. од
.). (кв
. од
.).
33.
 Розв’яжіть нерівність 2⋅ x
2
−6x
+9 − (x
−1)2
+ 4x
≤ x
. Розв’яжіть нерівність 2⋅ x
2
−6x
+9 − (x
−1)2
+ 4x
≤ x
.
Відповідь
: [1,25; +∞).
|