ШАНОВНІ СТАРШОКЛАСНИКИ!

Ãåîìåòðіÿ – îäíà ç íàéäàâíіøèõ, íàéøëÿõåòíіøèõ, êîðèñíèõ і öіêàâèõ íàóê. Ó íіé – çãóñòîê çíà÷íîї ÷àñòèíè çàãàëüíîëþäñüêîї êóëüòóðè, íàäáàíîї ëþäñòâîì çà êіëüêà òèñÿ÷îëіòü. À ùå âîíà є íåçàìіííèì іíñòðóìåíòàðієì äëÿ íàóêîâöіâ і âèðîáíè÷íèêіâ, çàñîáîì äëÿ ðîçâèòêó ëîãі÷íîãî ìèñëåííÿ, ïðîñòîðîâîї óÿâè, ðàöіîíàëіçàòîðñüêèõ çäіáíîñòåé òà іíøèõ êîðèñíèõ ÿêîñòåé âîëі і õàðàêòåðó ìîëîäі.

Îñü ùî ïèñàâ ïðî ãåîìåòðіþ âіäîìèé àðõіòåêòîð XX ñò. Ëå Êîðáþçüє: «Òіëüêè äîòðèìóþ÷èñü çàêîíіâ ãåîìåòðії, àðõіòåêòîðè äàâíèíè ìîãëè ñòâîðèòè ñâîї øåäåâðè. Íåâèïàäêîâî êàæóòü, ùî ïіðàìіäà Õåîïñà – íіìèé òðàêòàò ç ãåîìåòðії, à ãðåöüêà àðõіòåêòóðà – çîâíіøíє âіäîáðàæåííÿ ãåîìåòðії Åâêëіäà. Ìèíóëè ñòîëіòòÿ, àëå ðîëü ãåîìåòðії íå çìіíèëàñü. ßê і ðàíіøå, âîíà çàëèøàєòüñÿ ãðàìàòèêîþ àðõіòåêòîðà». І íå òіëüêè àðõіòåêòîðà ÷è іíæåíåðà-êîíñòðóêòîðà. Öÿ íàóêà є ñâîєðіäíîþ ãðàìàòèêîþ êîæíîãî ôàõіâöÿ, ÿêèé âèêîðèñòîâóє ãåîìåòðè÷íі ôîðìè.

Ãåîìåòðіÿ ñêëàäàєòüñÿ ç äâîõ ÷àñòèí: ïëàíіìåòðії і ñòåðåîìåòðії. Ó ïîïåðåäíіõ êëàñàõ âè âèâ÷àëè â îñíîâíîìó ïëàíіìåòðіþ, òåïåð ïåðåõîäèòå äî âèâ÷åííÿ ñòåðåîìåòðії (âіä ãðåö. – ïðîñòîðîâèé), â ÿêіé ðîçãëÿäàþòüñÿ âëàñòèâîñòі ãåîìåòðè÷íèõ ôіãóð ó ïðîñòîðі.

Ñòåðåîìåòðіÿ – ãåîìåòðіÿ òðèâèìіðíîãî ïðîñòîðó. Çà çìіñòîì âîíà áàãàòøà âіä ïëàíіìåòðії і öіêàâіøà, îñêіëüêè âèâ÷àє âëàñòèâîñòі ÿê ïëîñêèõ ãåîìåòðè÷íèõ ôіãóð, òàê і íåïëîñêèõ.

Ïåðøèé ðîçäіë, çà ïðîãðàìîþ, – ìàòåðіàë äëÿ ïîâòîðåííÿ, ñèñòåìàòèçàöії òà óçàãàëüíåííÿ íàéâàæëèâіøèõ âіäîìîñòåé ç ïëàíіìåòðії.

Íîâèé íàâ÷àëüíèé ìàòåðіàë âèêëàäåíî â òðüîõ ðîçäі ëàõ і äîäàòêàõ. Êî æåí ç ðîçäіëіâ ìіñòèòü òåîðåòè÷íèé ìàòåðіàë і çàäà÷і. ×èòàþ÷è òåîðіþ, îñíîâíó óâàãó ñëіä çâåðòàòè íà ñëîâà, íàäðóêîâàíі êóðñèâîì і æèðíèì øðèôòîì. Êóðñèâîì âèäіëåíî ãåîìåòðè÷íі òåðìіíè, íàçâè ïîíÿòü. Ïîòðіáíî âìіòè ïîÿñíþâàòè їõ çìіñò, íàâîäèòè âіäïîâіäíі ïðèêëàäè. Æèðíèì øðèôòîì íà äðóêîâàíî âàæëèâі ãåîìåòðè÷íі òâåðäæåííÿ, çîêðåìà òåîðåìè.

Ó êîæíîìó ïàðàãðàôі ïіäðó÷íèêà є ðóáðèêà äîïèòëèâèõ». Âîíà ìіñòèòü äîäàòêîâі âіäîìîñòі äëÿ òèõ, õòî

õî÷å çíàòè áіëüøå. Ó ðóáðèöі «Âèêîíàєìî ðàçîì» íàâîäÿòüñÿ çàäà÷і ç ðîçâ’ÿçàííÿìè. Ðàäèìî ïåðåãëÿíóòè їõ, ïåðø íіæ âèêîíóâàòè äîìàøíє çàâäàííÿ.

Çíàòè ãåîìåòðіþ – öå íàñàìïåðåä óìіòè êîðèñòóâàòèñÿ íåþ. Â÷èòèñÿ êîðèñòóâàòèñÿ ãåîìåòðè÷íèìè çíàííÿìè íàéêðàùå ïіä ÷àñ ðîçâ’ÿçóâàííÿ ãåîìåòðè÷íèõ çàäà÷. Çàâäàííÿ, ðåêîìåíäîâàíі äëÿ äîìàøíüîї ðîáîòè, âèäіëåíî êîëüîðîì. Çàäà÷і і âïðàâè â ïіäðó÷íèêó ïîäіëåíî íà: «Âèêîíàéòå óñíî», ðіâåíü À,

ðіâåíü Á і «Âïðàâè äëÿ ïîâòîðåííÿ». Ó êîæíîìó ðîçäіëі є çàäà÷і çà ãîòîâèìè ìàëþíêàìè. Óìîâè òàêèõ çàäà÷ ïîäàíî ìàëþíêàìè і êîðîòêèìè çàïèñàìè.

Äëÿ óçàãàëüíåííÿ і ñèñòåìàòèçàöії âèâ÷åíîãî ìàòåðіàëó ïîäàíî «Ãîëîâíå â ðîçäіëі». Ïåðåâіðèòè, íàñêіëüêè âè çàñ âîїëè íîâèé ìàòåðіàë, òà ïіäãîòóâàòèñÿ äî çîâíіøíüîãî íåçàëåæíîãî îöіíþâàííÿ âè çìîæåòå, ðîçâ’ÿçóþ÷è çàäà÷і òà âèêîíóþ÷è

çàâäàííÿ ç ðóáðèê «Òåñòîâі çàâäàííÿ» і «Òèïîâі çàäà÷і äëÿ êîíòðîëüíîї ðîáîòè».

Ïðîãðàìíó òåìó «Îðòîöåíòðè÷íèé òåòðàåäð» äåùî ðîçøèðåíî і âìіùåíî â äîäàòêàõ «Åëåìåíòè ãåîìåòðії òåòðàåäðà». Òàì ìіñòèòüñÿ ùå êіëüêà òåì, â ÿêèõ ïîãëèáëåíî ðîçãëÿäàþòüñÿ äåÿêі íàéâàæëèâіøі âëàñòèâîñòі íàéïðîñòіøîãî ìíîãîãðàííèêà – òåòðàåäðà. Öі òåìè àäðåñóєìî äëÿ ñàìîñòіéíîãî îïðàöþâàííÿ òèì ó÷íÿì, ÿêі ìàþòü áàæàííÿ çàéìàòèñÿ ïîñèëüíîþ äëÿ ïî÷àòêіâöіâ íàóêîâî-äîñëіäíîþ ðîáîòîþ. À çàäà÷і, ùî є â «Äîäàòêàõ», ìîæíà ïðîïîíóâàòè âñіì ó÷íÿì.

Іíîäі ââàæàþòü, ùî íàéâàæëèâіøå â ãåîìåòðії – äîâåäåííÿ òåîðåì. Çâè÷àéíî, ó÷èòèñÿ äîâîäèòè òåîðåìè – ñïðàâà êîðèñíà. Àëå íå ìåíøó ðîëü ó öіé íàóöі âіäіãðàþòü ïîíÿòòÿ, їõ îçíà÷åííÿ і êëàñèôіêàöії; ãåîìåòðè÷íі ôіãóðè, їõ ïîáóäîâà і ïåðåòâîðåííÿ; ãåîìåòðè÷íі âåëè÷èíè, їõ âèìіðþâàííÿ òà îá÷èñëåííÿ. Îäèí ç âіäîìèõ ãåîìåòðіâ XX ñò. Ä. Ãіëüáåðò ïèñàâ: «Ó âåëè÷åçíîìó ñàäó ãåîìåòðії êîæíèé ìîæå ïіäіáðàòè ñîáі áóêåò çà ñìàêîì ».

Çàïðîøóєìî âàñ ó öåé áàãàòèé і äèâíèé ñâіò Ãåîìåòðії.

Àâòîðè

§ 1 ОПОРНІ ФАКТИ ПЛАНІМЕТРІЇ

Ïðèãàäàєìî íàéâàæëèâіøі âіäîìîñòі ç ïëàíіìåòðії, ÿêі ÷àñòî âèêîðèñòîâóþòüñÿ â ñòåðåîìåòðії.

Àêñіîìè ïëàíіìåòðії . Îñíîâíå â ãåîìåòðії – її ïîíÿòòÿ і òâåðäæåííÿ. Äëÿ áіëüøîñòі ïîíÿòü ôîðìóëþþòüñÿ îçíà÷åííÿ, àëå іñíóþòü ïîíÿòòÿ íåîçíà÷óâàíі. Öå – òî÷êà , ïðÿìà , ïëîùèíà òà äåÿêі іíøі.

Ïåðåâàæíó áіëüøіñòü ãåîìåòðè÷íèõ òâåðäæåíü äîâîäÿòü, òîáòî ïîêàçóþòü, ùî âîíè ÿê ëîãі÷íі íàñëіäêè âèïëèâàþòü ç іíøèõ іñòèííèõ òâåðäæåíü. À ÿê áóòè, êîëè íà ïî÷àòêó êóðñó ùå íåìàє «іíøèõ òâåðäæåíü»? Ó öèõ âèïàäêàõ êіëüêà òâåðäæåíü ïðèéìàþòü çà іñòèííі áåç äîâåäåíü. Їõ íàçèâàþòü àêñіîìàìè . À äîâîäæóâàíі òâåðäæåííÿ – òåîðåìàìè .

Äëÿ ïëàíіìåòðії, ÿê і äëÿ іíøèõ íàóê ÷è òåîðіé, ìîæíà îáèðàòè ðіçíі ñèñòåìè àêñіîì. Îäíà ç íèõ ìîæå áóòè òàêîþ.

1. ßêà á íå áóëà ïðÿìà, іñíóþòü òî÷êè, ùî íàëåæàòü öіé ïðÿìіé, і òî÷êè, ùî їé íå íàëåæàòü.

2. ×åðåç áóäü-ÿêі äâі ðіçíі òî÷êè ìîæíà ïðîâåñòè ïðÿìó і òіëüêè îäíó.

3. Іç òðüîõ òî÷îê ïðÿìîї îäíà і òіëüêè îäíà ëåæèòü ìіæ äâîìà іíøèìè.

4. Êîæíèé âіäðіçîê ìàє ïåâíó äîâæèíó.

5. Êîæíèé êóò ìàє ïåâíó ìіðó.

6. Ïðÿìà ðîçáèâàє ïëîùèíó íà äâі ïіâïëîùèíè.

7. Íà áóäü-ÿêіé ïðÿìіé âіä çàäàíîї òî÷êè ó çàäàíîìó íàïðÿìі ìîæíà âіäêëàñòè âіäðіçîê äàíîї äîâæèíè і òіëüêè îäèí.

8. Âіä áóäü-ÿêîãî ïðîìåíÿ ó äàíіé ïіâïëîùèíі ìîæíà âіäêëàñòè äàíèé êóò ç âåðøèíîþ ó ïî÷àòêó ïðîìåíÿ і òіëüêè îäèí.

9. ßêèé áè íå áóâ òðèêóòíèê, іñíóє ðіâíèé éîìó òðèêóòíèê ó çàäàíîìó ðîçìіùåííі âіäíîñíî çàäàíîї ïðÿìîї.

10. ×åðåç òî÷êó, ùî íå ëåæèòü íà äàíіé ïðÿìіé, ìîæíà ïðîâåñòè òіëüêè îäíó ïðÿìó, ïàðàëåëüíó äàíіé ïðÿìіé (àê ñіî ìà Åâêëіäà) .

Ðîçäіëè ïðî ãåîìåòðè÷íі âåëè÷èíè, ãåîìåòðè÷íі ïåðåòâîðåííÿ і ïîáóäîâè ïîòðåáóþòü äîäàòêîâèõ àêñіîì.

Ïàðàëåëüíі і ïåðïåíäèêóëÿðíі ïðÿìі . Äâі ïðÿìі îäíієї ïëîùèíè íàçèâàþòüñÿ ïàðàëåëüíèìè, ÿêùî âîíè íå ïåðåòèíàþòüñÿ. Äâà âіäðіçêè àáî ïðîìåíі íàçèâàþòü ïàðàëåëüíèìè, ÿêùî âîíè íàëåæàòü ïàðàëåëüíèì ïðÿìèì.

Ìàë. 3

Ãåîìåòðè÷íèì ìіñöåì òî÷îê ïëîùèíè, ðіâíîâіääàëåíèõ âіä êіíöіâ âіäðіçêà, є ñåðåäèííèé ïåðïåíäèêóëÿð äî öüîãî âіäðіçêà (ìàë. 5).

ßêùî ÀÎ  ÂÎ і ÑÎ  ÀÂ , òî ÀÑ  ÂÑ .

Ãåîìåòðè÷íå ìіñöå òî÷îê êóòà, ðіâíîâіääàëåíèõ âіä éîãî ñòîðіí, – áіñåêòðèñà öüîãî êóòà (ìàë. 6).

Òðèêóòíèêè. Òðèêóòíèê – çàìêíåíà ëàìàíà іç òðüîõ ëàíîê. ×àñòèíà ïëîùèíè, îáìåæåíà òàêîþ ëàìàíîþ, òàêîæ íàçèâàєòüñÿ òðèêóòíèêîì. Êîæíèé òðèêóòíèê ìàє òðè ñòîðîíè, òðè âåðøèíè і òðè êóòè. Ñóìó ñòîðіí òðèêóòíèêà íàçèâàþòü éîãî ïåðèìåòðîì. ßêùî ñòîðîíè òðèêóòíèêà a , b , c , à

ïðîòèëåæíі їì êóòè , , , òî:

|b – c | < a < b + c ;  +  +   180.

Îçíàêè ðіâíîñòі òðèêóòíèêіâ . Äâà òðèêóòíèêè ðіâíі, ÿêùî:

1) äâі ñòîðîíè і êóò ìіæ íèìè îäíîãî òðèêóòíèêà äîðіâíþþòü âіäïîâіäíî äâîì ñòîðîíàì і êóòó ìіæ íèìè äðóãîãî

2) ñòîðîíà і ïðèëåãëі äî íåї êóòè îäíîãî òðèêóòíèêà äîðіâíþþòü âіäïîâіäíî ñòîðîíі і ïðèëåãëèì äî íåї êóòàì äðóãîãî

3) òðè ñòîðîíè îäíîãî òðèêóòíèêà äîðіâíþþòü âіäïîâіäíî òðüîì ñòîðîíàì äðóãîãî òðèêóòíèêà.

Âіäðіçîê, ÿêèé ñïîëó÷àє ñåðåäèíè äâîõ ñòîðіí òðèêóòíèêà, – éîãî ñåðåäíÿ ëіíіÿ. Ñåðåäíÿ ëіíіÿ òðèêóòíèêà ïàðàëåëüíà éîãî òðåòіé ñòîðîíі і äîðіâíþє її ïîëîâèíі.

Òðèêóòíèêè, â ÿêèõ óñі âіäïîâіäíі êóòè ðіâíі, à âіäïîâіäíі ñòîðîíè ïðîïîðöіéíі, íàçèâàþòüñÿ ïîäіáíèìè .

Îñíîâíà òåîðåìà ïðî ïîäіáíіñòü òðèêóòíèêіâ . Ñі÷íà ïðÿìà, ïàðàëåëüíà ñòîðîíі òðèêóòíèêà, âіäòèíàє âіä íüîãî òðèêóòíèê, ïîäіáíèé äàíîìó.

Îçíàêè ïîäіáíîñòі òðèêóòíèêіâ . Äâà òðèêóòíèêè ïîäіáíі, ÿêùî:

1) äâà êóòè îäíîãî òðèêóòíèêà âіäïîâіäíî äîðіâíþþòü äâîì êóòàì äðóãîãî; àáî

2) äâі ñòîðîíè îäíîãî òðèêóòíèêà ïðîïîðöіéíі äâîì ñòîðîíàì äðóãîãî, à êóòè ìіæ íèìè ðіâíі; àáî

3) òðè ñòîðîíè îäíîãî òðèêóòíèêà ïðîïîðöіéíі òðüîì ñòî-

c ²  a ² + b ² – òåîðåìà Ïіôàãîðà ; – òåîðåìà ñèíóñіâ .

æ òіëüêè îäíå. Öåíòðîì êîëà, âïèñàíîãî â òðèêóòíèê, є òî÷êà ïåðåòèíó éîãî áіñåêòðèñ.

Êîæíèé òðèêóòíèê ÀÂÑ ìàє ìåäіàíè, áіñåêòðèñè, âèñîòè, ïіâïåðèìåòð, ðàäіóñ âïèñàíîãî і îïèñàíîãî êіë, ÿêі âіäïîâіäíî ïîçíà÷àþòü: m_a , l_a , h_a , ð , r , R . Âіäîìî, ùî:

Ïëîùà òðèêóòíèêà . Êîæíèé òðèêóòíèê (ÿê ÷àñòèíà ïëîùèíè, îáìåæåíà çàìêíåíîþ ëàìàíîþ) ìàє ïëîùó. Ôîðìóëè äëÿ âèçíà÷åííÿ ïëîùі òðèêóòíèêà:

Äëÿ ïðÿìîêóòíèõ і ðіâíîñòîðîííіõ òðèêóòíèêіâ ôîðìóëè ïðîñòіøі:

×îòèðèêóòíèêè. ×îòèðèêóòíèê – ïðîñòà çàìêíåíà ëàìàíà іç ÷îòèðüîõ ëàíîê. ×àñòèíà ïëîùèíè, îáìåæåíà òàêîþ ëàìàíîþ, òàêîæ íàçèâàєòüñÿ ÷îòèðèêóòíèêîì. Ñóìà âñіõ êóòіâ êîæíîãî ÷îòèðèêóòíèêà äîðіâíþє 360. Êîæíà ñòîðîíà ÷îòèðèêóòíèêà ìåíøà âіä ñóìè òðüîõ іíøèõ éîãî ñòîðіí.

×îòèðèêóòíèê, êîæíà ñòîðîíà ÿêîãî ïàðàëåëüíà ïðîòèëåæíіé ñòîðîíі, – ïàðàëåëîãðàì.

Îçíàêè ïàðàëåëîãðàìà. ×îòèðèêóòíèê є ïàðàëåëîãðàìîì, ÿêùî:

1) êîæíà éîãî ñòîðîíà äîðіâíþє ïðîòèëåæíіé ñòîðîíі; 2) äâі éîãî ïðîòèëåæíі ñòîðîíè ïàðàëåëüíі é ðіâíі;

3) éîãî äіàãîíàëі òî÷êîþ ïå ðåòèíó äіëÿòüñÿ íàâïіë.

Ìàë. 10

Âëàñòèâîñòі ïàðàëåëîãðàìà:

– êîæíà ñòîðîíà ïàðàëåëîãðàìà ïàðàëåëüíà ïðîòèëåæíіé

– êîæíèé êóò ïàðàëåëîãðàìà äîðіâíþє ïðîòèëåæíîìó êóòó;

– êîæíà äіàãîíàëü ïàðàëåëîãðàìà òî÷êîþ ïåðåòèíó äіëèòüñÿ

– ñóìà êâàäðàòіâ äіàãîíàëåé ïàðàëåëîãðàìà äîðіâíþє ñóìі

Îêðåìі âèäè ïàðàëåëîãðàìіâ – ïðÿìî-

– äіàãîíàëі ïðÿìîêóòíèêà (êâàäðàòà)

– äіàãîíàëі ðîìáà (êâàäðàòà) ïåðïåíäèêó-

×îòèðèêóòíèê, ó ÿêîãî òіëüêè äâі ñòî-

áі÷íі ñòîðîíè. Îêðåìі âèäè òðàïåöіé – ðіâíîáі÷íі і ïðÿìîêóòíі òðàïåöії. Âіäðіçîê, ùî ñïîëó÷àє ñåðåäèíè áі÷íèõ ñòîðіí òðàïåöії , – її ñåðåäíÿ ëіíіÿ. Ñåðåäíÿ ëіíіÿ òðàïå öії ïàðàëåëüíà її îñíîâàì і äîðіâíþє їõ ïіâñóìі.

Ñïіââіäíîøåííÿ ìіæ îêðåìèìè âèäàìè ÷îòèðèêóòíèêіâ ïîêàçàíî íà ìàëþíêó 10.

Âïèñàíі é îïèñàíі ÷îòèðèêóòíèêè (ìàë.

11 і 12)

Ïëîùі ÷îòèðèêóòíèêіâ . Ïëîùà ïðÿìîêóòíèêà äîðіâíþє äîáóòêó äâîõ éîãî ñóñіäíіõ ñòîðіí: S  ab.

S  ah_a , àáî S  ab sin ,

äå à, b – éîãî ñòîðîíè,  – êóò ìіæ íèìè, h_a – âèñîòà, îïóùåíà ßêùî äіàãîíàëі ÷îòèðèêóòíèêà äîðіâíþþòü d ₁ і d ₂ , à êóò

.

Ïëîùà òðàïåöії äîðіâíþє äîáóòêó ïіâñóìè її îñíîâ íà âè -

Êîëî. Êóòè òà âіäðіçêè, ïîâ’ÿçàíі ç êîëîì. Êîëî – ôіãóðà, ùî ñêëàäàєòüñÿ ç óñіõ òî÷îê ïëîùèíè, ðіâíîâіääàëåíèõ âіä äàíîї òî÷êè – öåíòðà êîëà . ×àñòèíà ïëîùèíè, îáìåæåíà êîëîì, – êðóã. Ðàäіóñ – âіäðіçîê, ùî ñïîëó÷àє áóäüÿêó òî÷êó êîëà ç éîãî öåíòðîì. Âіäðіçîê, ùî ñïîëó÷àє äâі äîâіëüíі òî÷êè êîëà, íàçèâàþòü õîðäîþ. Õîðäà, ùî ïðîõîäèòü ÷åðåç öåíòð êîëà, – äіàìåòð.

Ïðÿìà, ÿêà ìàє ç êîëîì òіëüêè îäíó ñïіëüíó òî÷êó і ëåæèòü ó ïëîùèíі êîëà, íàçèâàєòüñÿ äîòè÷íîþ äî êîëà.

Ìàþòü ìіñöå òàêі âëàñòèâîñòі:

• äіàìåòð êîëà, ïðîâåäåíèé ÷åðåç ñåðåäèíó õîðäè, âіäìіííîї âіä äіàìåòðà, ïåðïåíäèêóëÿðíèé äî íåї;

• äîòè÷íà äî êîëà ïåðïåíäèêóëÿðíà äî ðàäіóñà, ïðîâåäåíîãî â òî÷êó äîòèêó;

• âіäðіçêè äîòè÷íèõ, ïðîâåäåíèõ äî êîëà ç îäíієї òî÷êè, ðіâíі;

• AM  BM  CM DM (ìàë. 13);

• AK ²  AB  AC (ìàë. 14);

• âïèñàíèé êóò âèìіðþєòüñÿ ïîëîâèíîþ äóãè, íà ÿêó âіí ñïèðàєòüñÿ (ìàë. 15):

;

ëåæàòü íà îäíіé ïðÿìіé, êîëè, âðàõîâóþ÷è íàïðÿìè âіä ðіçêіâ,

Òåîðåìà ×åâè . Íåõàé A ₁ , B ₁ , C ₁ – òðè òî÷êè, ÿêі ëåæàòü âіäïîâіäíî íà ñòîðîíàõ BC , CA , AB ABC àáî íà їõ ïðîäîâæåííÿõ (ìàë. 19). Äëÿ òîãî ùîá ïðÿìі AA ₁ , BB ₁ і CC ₁ ïåðåòèíàëèñÿ â îäíіé òî÷öі àáî áóëè âñі ïàðàëåëüíі, íåîáõіäíî і äîñòàòíüî, ùîá âèêîíóâàëàñü óìîâà:

Îñòàííþ ðіâíіñòü íàçèâàþòü óìîâîþ ×åâè .

Ïðÿìà Åéëåðà . Îðòîöåíòð H òðèêóòíèêà, éîãî öåíòðîїä M і öåíòð O îïèñàíîãî êîëà ëåæàòü íà îäíіé ïðÿìіé (ìàë. 20), ïðè÷îìó OM : MH  1 : 2.

Êîëî Åéëåðà (êîëî äåâ’ÿòè òî÷îê). Îñíîâè âèñîò òðèêóòíèêà, ñåðåäèíè éîãî ñòîðіí і ñåðåäèíè âіäðіçêіâ, ÿêі ñïîëó÷àþòü îðòîöåíòð òðèêóòíèêà ç éîãî âåðøèíàìè, ëåæàòü íà

îäíîìó êîëі (ìàë. 21). Öåíòð öüîãî êîëà çáіãàєòüñÿ іç ñåðåäèíîþ âіäðіçêà, ÿêèé ñïîëó÷àє îðòîöåíòð òðèêóòíèêà і öåíòð îïèñàíîãî êîëà. Éîãî ðàäіóñ äîðіâíþє ïîëîâèíі ðàäіóñà îïèñàíîãî êîëà.

Ïðÿìà Ñіìñîíà . Îñíîâè ïåðïåíäèêóëÿðіâ, îïóùåíèõ íà ñòîðîíè òðèêóòíèêà ç òî÷êè îïèñàíîãî êîëà, ëåæàòü íà îäíіé ïðÿìіé.

Êîëî Àïîëëîíіÿ . Ãåîìåòðè÷íèì ìіñöåì òî÷îê, âіäíîøåííÿ âіäñòàíåé âіä ÿêèõ äî äâîõ äàíèõ òî÷îê ñòàëå, є êîëî.

Êîîðäèíàòè íà ïëîùèíі . Ïëîù èíó, íà ÿêіé çàäàíî ñè ñòåìó êîîðäèíàò, íàçèâàþòü êîîðäèíàòíîþ ïëîùèíîþ. Êîæíіé òî÷öі êîîðäèíàòíîї ïëîùèíè âіäïîâіäàє єäèíà ïàðà äіéñíèõ ÷èñåë (êîîðäèíàòè öієї òî÷êè), à êîæíіé ïàðі äіéñíèõ ÷èñåë – єäèíà òî÷êà êîîðäèíàòíîї ïëîùèíè.

Êîæíà êîîðäèíàòà ñåðåäèíè âіäðіçêà äîðіâíþє ïіâñóìі âіäïîâіäíèõ êîîðäèíàò éîãî êіíöіâ. Òîáòî ÿêùî êіíöі âіäðіçêà À (õ ₁ ; ó ₁ ) і  (õ ; ó ), òî ñåðåäèíîþ äàíîãî âіäðіçêà є òî÷êà ç êîîðäèíàòàìè

2

Êâàäðàò äîâæèíè âіäðіçêà äîðіâíþє ñóìі êâàäðàòіâ éîãî ïðîåêöіé íà äâі âçàєìíî ïåðïåíäèêóëÿðíі ïðÿìі.

Ðіâíÿííÿì ôіãóðè íà êîîðäèíàòíіé ïëîùèíі íàçèâàþòü ðіâíÿííÿ ç äâîìà çìіííèìè, ÿêå çàäîâîëüíÿþòü êîîðäèíàòè êîæíîї òî÷êè äàíîї ôіãóðè і òіëüêè âîíè.

Ðіâíÿííÿ êîëà ðàäіóñà r іç öåíòðîì ó òî÷öі À (à ; b ) ìàє âèãëÿä (õ – à )² + (ó – b )²  r ² .

ßêùî öåíòð êîëà ðàäіóñà r ëåæèòü ó ïî÷àòêó êîîðäèíàò, òî

éîãî ðіâíÿííÿ õ ² + ó ²  r ² .

Êîæíіé ïðÿìіé êîîðäèíàòíîї ïëîùèíè âіäïîâіäàє ëіíіéíå ðіâíÿííÿ ç äâîìà çìіííèìè ax + by + ñ  0. Òàêå ðіâíÿííÿ íàçèâàþòü çàãàëüíèì ðіâíÿííÿì ïðÿìîї.

Ðіâíіñòü y  kx + b – ðіâíÿííÿ ïðÿìîї ç êóòîâèì êîåôі öіє íòîì. Òóò k  tg, äå  – êóò, ÿêèé óòâîðþє ïðÿìà ç äîäàòíèì íàïðÿìîì îñі ÎÕ .

_– ðіâíÿííÿ ïðÿìîї, ùî ïðîõîäèòü ÷åðåç äâі

äàíі òî÷êè A (x ; y ₁ ) і  (õ ₂ ; ó ₂ ).

_– ðіâíÿííÿ ïðÿìîї ó âіäðіçêàõ íà îñÿõ (÷èñëà à і b

ïîêàçóþòü, ÿêі âіäðіçêè ïðÿìà l âіäòèíàє íà îñÿõ êîîðäèíàò). ßêùî ïðÿìі l ₁ і l ₂ çàäàíі ðіâíÿííÿìè y ₁  k ₁ x + b ₁ і y ₂  k ₂ x + b ₂ ,

òî:

1) l ₁  l ₂ òîäі і òіëüêè òîäі, êîëè k ₁  k ₂ ; 2) l ₁  l ₂ òîäі і òіëüêè òîäі, êîëè k ₁ · k ₂  –1.

Âåêòîðíі âåëè÷èíè – òі, ÿêі âèçíà÷àþòüñÿ íå òіëüêè ÷èñëîâèìè çíà÷åííÿìè, à é íàïðÿìàìè. Çíà÷åííÿ âåêòîðíèõ âåëè÷èí – âåêòîðè . Ãåîìåòðè÷íî âåêòîðè (íåíóëüîâі) çîáðàæàþòüñÿ íàïðÿìëåíèìè âіäðіçêàìè. Íàïðÿìëåíèé âіäðіçîê ìàє ïî÷àòîê і êіíåöü. Âіäñòàíü ìіæ íèìè – ìîäóëü (äîâæèíà) âåêòîðà.

Äâà âåêòîðè íàçèâàþòü êîëіíåàðíèìè, ÿêùî âіäïîâіäíі їì íàïðÿìëåíі âіäðіçêè ðîçòàøîâàíі íà îäíіé ïðÿìіé àáî íà ïàðàëåëüíèõ ïðÿìèõ. Êîëіíåàðíі âåêòîðè áóâàþòü ñïіâíàïðÿìëåíèìè àáî ïðîòèëåæíî íàïðÿìëåíèìè. Äâà âåêòîðè ðіâíі , ÿêùî âîíè ñïіâíàïðÿìëåíі і ìàþòü ðіâíі ìîäóëі. Äâà âåêòîðè íàçèâàþòü ïðîòèëåæíèìè , ÿêùî âîíè ìàþòü ðіâíі ìîäóëі і ïðîòèëåæíî íàïðÿìëåíі.

Êîîðäèíàòàìè âåêòîðà ç ïî÷àòêîì A (x ₁ ; ó ₁ ) і êіíöåì  (x ₂ ; y ₂ ) íàçèâàþòü ÷èñëà x  x ₂ – x ₁ і y  y ₂ – y ₁ .

Çàïèñóþòü òàêèé âåêòîð ó âèãëÿäі:

AB  (x ; y ), àáî a  (x ; y ), àáî AB  (x ₂ – x ₁ ; y ₂ – y ₁ ).

Ìîäóëü âåêòîðà AB  (x ; y ) ïîçíà÷àþòü ñèìâîëîì |AB |:

Ñó ìîþ âåêòîðіâ a  (x ₁ ; y ₁ ) і b  (x ₂ ; y ₂ ) íàçèâàþòü âåêòîð a + b  (x ₁ + x ₂ ; y ₁ + y ₂ ). Äëÿ äîäàâàííÿ âåêòîðіâ âèêîíóþòüñÿ ïåðåñòàâíèé і ñïîëó÷íèé çàêîíè.

Ãåîìåòðè÷íî äîäàâàòè âåêòîðè ìîæíà çà ïðàâèëîì òðèêóòíèêà àáî ïàðàëåëîãðàìà (ìàë. 22 і 23). Çàâæäè ïðàâèëüíі âåêòîðíі ðіâíîñòі:

AB + BC  AÑ , AB + BC + CD  AD .

Ðі çíèöåþ âåêòîðіâ a  (x ₁ ; y ₁ ) і b  (x ₂ ; y ₂ ) íàçèâàþòü âåêòîð a – b  (x ₁ – x ₂ ; y ₁ – y ₂ ).

Ðіçíèöÿ âåêòîðіâ AB і KP äîðіâíþє AB + PK . Ùîá âіäíÿòè âіä îäíîãî âåêòîðà äðóãèé, òðåáà äî ïåðøîãî äîäàòè âåêòîð, ïðîòèëåæíèé äðóãîìó.

ßêі íå áóëè á âåêòîðè AB і AC , çàâæäè AB – AC  CB .

Äîáóòêîì âåêòîðà a  (x ; y ) íà ÷èñëî n íàçèâàþòü âåêòîð na  (nx ; ny ). Çàâæäè ïðàâèëüíі ðіâíîñòі:

(n + m ) a  na + ma і n (a + b )  na + nb .

Ñêàëÿðíèì äîáóòêîì äâîõ íåíóëüîâèõ âåêòîðіâ íàçèâàþòü äîáóòîê ìîäóëіâ öèõ âåêòîðіâ íà êîñèíóñ êóòà ìіæ íèìè:

a b  |a | |b | cos .

ßêùî õî÷ îäèí ç âåêòîðіâ íóëüîâèé, òî їõ ñêàëÿðíèé

äîáóòîê äîðіâíþє íóëþ.

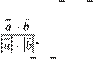Êóò  ìіæ íåíóëüîâèìè âåêòîðàìè a і b ìîæíà çíàéòè, êîðè ñòóþ÷èñü ôîðìóëîþ cos  ßêùî a  (x ₁ ; y ₁ ) і b  (x ₂ ; y ₂ ), òî a b  x ₁ x ₂ + ó ₁ ó ₂ .

a  kb àáî – óìîâà êîëіíåàðíîñòі íåíóëüîâèõ âåêòîðіâ a і b (k  0); a b  0 àáî x ₁  x ₂ + y ₁  y ₂  0 – óìîâà їõ ïåð ïåí äè êó ëÿð íîñòі.

a b

a + b b

Ìàë. 22 Ìàë. 23

ЗAПИТAННЯ І ЗAВДAННЯ ДЛЯ САМОКОНТРОЛЮ

Ùî òàêå ãåîìåòðіÿ? Ùî òàêå ïëàíіìåòðіÿ?

Íàâåäіòü ïðèêëàäè ïëîñêèõ і íåïëîñêèõ ôіãóð.

Ùî îçíà÷àþòü çàïèñè À  à ,   à ?

ßê ñëіä ðîçóìіòè âèñëіâ «òî÷êà  ëåæèòü ìіæ À і Ñ »?

Ùî òàêå ïðîìіíü? ßê ïîçíà÷àþòü ïðîìåíі?

Ùî òàêå âіäðіçîê? Ùî òàêå êіíöі âіäðіçêà?

Ùî òàêå âіäñòàíü ìіæ äâîìà òî÷êàìè?

ßêà ôіãóðà íàçèâàєòüñÿ êóòîì? ßê ïîçíà÷àþòü êóòè? ßêèé êóò íàçèâàþòü ãîñòðèì? Ïðÿìèì? Òóïèì? Ðîçãîðíóòèì?

ßêі êóòè íàçèâàþòü ñóìіæíèìè? ×îìó äîðіâíþє їõ ñóìà? ßêі êóòè íàçèâàþòü âåðòèêàëüíèìè? Ñôîðìóëþéòå òåîðåìó ïðî âåðòèêàëüíі êóòè. ßêі ïðÿìі íàçèâàþòü ïåðïåíäèêóëÿðíèìè?

Ñôîðìóëþéòå îçíà÷åííÿ ïàðàëåëüíèõ ïðÿìèõ.

Ñôîðìóëþéòå îçíàêó ïàðàëåëüíîñòі ïðÿìèõ.

Ñôîðìóëþéòå àêñіîìó Åâêëіäà ïðî ïàðàëåëüíіñòü ïðÿìèõ.

Ùî òàêå òðèêóòíèê? Íàçâіòü åëåìåíòè òðèêóòíèêà.

ßêèìè áóâàþòü òðèêóòíèêè?

Ùî òàêå áіñåêòðèñà, ìåäіàíà, âèñîòà òðèêóòíèêà?

Côîðìóëþéòå òåîðåìó ïðî ñóìó êóòіâ òðèêóòíèêà.

Ñôîðìóëþéòå îçíàêè ðіâíîñòі òðèêóò íèêіâ. ßêèé òðèêóòíèê íàçèâàþòü ðіâíîáåäðåíèì?

Ñôîðìóëþéòå êіëüêà âëàñòèâîñòåé ðіâíîáåäðåíîãî òðèêóòíèêà. ßê íàçèâàþòü ñòîðîíè ïðÿìîêóòíîãî òðèêóòíèêà?

Ñôîðìóëþéòå îçíàêè ðіâíîñòі ïðÿìîêóòíèõ òðèêóòíèêіâ.

Ùî òàêå ïåðïåíäèêóëÿð, ïîõèëà, ïðîåêöіÿ ïîõèëîї?

Ùî òàêå âіäñòàíü âіä òî÷êè äî ïðÿìîї?

Ùî òàêå êîëî? Öåíòð? Ðàäіóñ? Äіàìåòð? Õîðäà?

Ùî òàêå êðóã? ×èì âіäðіçíÿєòüñÿ êðóã âіä êîëà?

Ñôîðìóëþéòå îçíà÷åííÿ і âëàñòèâіñòü äîòè÷íîї äî êîëà.

Ùî òàêå öåíòðàëüíèé êóò? Âïèñàíèé êóò?

Ñôîðìóëþéòå òåîðåìó ïðî âïèñàíі êóòè.

ßê ïîáóäóâàòè òðèêóòíèê çà òðüîìà äàíèìè ñòîðîíàìè? ßê ïîáóäóâàòè êóò, ùî äîðіâíþє äàíîìó? ßê ïîáóäóâàòè áіñåêòðèñó äàíîãî êóòà? ßê ïîäіëèòè äàíèé âіäðіçîê íàâïіë?

ßê ÷åðåç äàíó òî÷êó ïðîâåñòè ïðÿìó, ïåðïåíäèêó ëÿð íó äî äàíîї ïðÿìîї? À ïàðàëåëüíó äàíіé ïðÿìіé?

Ùî òàêå ãåîìåòðè÷íå ìіñöå òî÷îê? Íàâåäіòü ïðèê ëàäè.

Ùî òàêå ñåðåäèííèé ïåðïåíäèêóëÿð äàíîãî âіä ðіçêà? ßê íàâêîëî äàíîãî òðèêóòíèêà îïèñàòè êîëî? ßê ó äàíèé òðèêóòíèê âïèñàòè êîëî?

Ùî òàêå ÷îòèðèêóòíèê?

Ñôîðìóëþéòå îçíà÷åííÿ ïàðàëåëîãðàìà.

ßêі âëàñòèâîñòі ìàє ïàðàëåëîãðàì? Ñôîðìóëþéòå îçíàêè ïàðàëåëîãðàìà.

Ùî òàêå ïðÿìîêóòíèê? ßêі âëàñòèâîñòі ìàє ïðÿìîêóò íèê?

Ùî òàêå ðîìá? Êâàäðàò? Íàçâіòü їõ âëàñòèâîñòі.

Ñôîðìóëþéòå òåîðåìó Ôàëåñà.

Ñôîðìóëþéòå òåîðåìó ïðî ñåðåäíþ ëіíіþ òðèêóòíèêà. Ùî òàêå òðàïåöіÿ? Ðіâíîáі÷íà òðàïåöіÿ? Ïðÿìîêóòíà òðàïåöіÿ?

Ñôîðìóëþéòå òåîðåìó ïðî ñåðåäíþ ëіíіþ òðàïåöії. ßêі òðèêóòíèêè íàçèâàþòü ïîäіáíèìè?

Ñôîðìóëþéòå îçíàêè ïîäіáíîñòі òðèêóò íèêіâ.

Ñôîðìóëþéòå òåîðåìó Ïіôàãîðà.

ßê çíàéòè êîîðäèíàòè ñåðåäèíè âіäðіçêà?

ßê çíàéòè âіäñòàíü ìіæ òî÷êàìè ç äàíèìè êîîðäèíàòàìè?

Ùî òàêå ðіâíÿííÿ ôіãóðè?

ßêå ðіâíÿííÿ ìàє êîëî? Ïðÿìà? Íàâåäіòü ïðèêëàäè âåêòîðíèõ âåëè÷èí. ßê çîáðàæàþòü âåêòîðè?

Ùî òàêå êîîðäèíàòè âåêòîðà?

Ùî òàêå äîâæèíà âåêòîðà?

ßêі âåêòîðè íàçèâàþòü ðіâíèìè? Êîëіíåàðíèìè?

Ïðîòèëåæíèìè?

Ùî òàêå ñóìà äâîõ âåêòîðіâ?

Ñôîðìóëþéòå ïðàâèëî òðèêóòíèêà äëÿ äîäàâàííÿ âåêòîðіâ.

Ñôîðìóëþéòå ïðàâèëî ïàðàëåëîãðàìà äëÿ äîäàâàí íÿ âåêòîðіâ.

Ùî òàêå ðіçíèöÿ âåêòîðіâ? ßê її çíàõîäÿòü?

Ñôîðìóëþéòå ïðàâèëî ìíîæåííÿ âåêòîðà íà ÷èñëî.

Ñôîðìóëþéòå âëàñòèâîñòі ìíîæåííÿ âåêòîðà íà ÷èñëî.

Ùî òàêå ñèíóñ, êîñèíóñ, òàíãåíñ êóòà?

Ñôîðìóëþéòå òåîðåìó êîñèíóñіâ.

Ñôîðìóëþéòå òåîðåìó ñèíóñіâ.

Ùî òàêå ìíîãîêóòíèê?

×îìó äîðіâíþє ñóìà êóòіâ îïóêëîãî n - êóòíèêà?

Ñôîðìóëþéòå îçíà÷åííÿ ïðàâèëüíîãî ìíîãîêóòíèêà.

Çà ÿêîþ ôîðìóëîþ çíàõîäÿòü äîâæèíó êîëà?

Ùî òàêå ïëîùà ìíîãîêóòíèêà?

Çà ÿêèìè ôîðìóëàìè îá÷èñëþþòü ïëîùі ïðÿìîêóòíèêà, ïàðàëåëîãðàìà, òðèêóòíèêà, òðàïåöії?

Ñôîðìóëþéòå òåîðåìó ïðî âіäíîøåííÿ ïëîù ïîäіáíèõ ìíîãîêóòíèêіâ.

Çà ÿêîþ ôîðìóëîþ çíàõîäÿòü ïëîùó êðóãà?

ПЕРЕВІРТЕ СЕБЕ

Тематичні завдання в тестовій формі

Ïðÿìі і êóòè

1. Óñòàíîâіòü, íà ñêіëüêè ÷àñòèí ìîæóòü ðîçáèòè ïëîùè íó äâі її ïðÿìі.

à) Íà 2 àáî íà 3; á) íà 2 àáî íà 4;

â) íà 3 àáî íà 4; ã) íà 3 àáî íà 5.

2. ßêùî îäèí іç ñóìіæíèõ êóòіâ íà 80 áіëüøèé âіä äðóãîãî, òî äðóãèé êóò äîðіâíþє:

à) 80; á) 140; â) 50; ã) 120.

3. Âіäîìî, ùî a  c i b  c . Óêàæіòü ïðàâèëüíå âіäíîøåííÿ.

à) a  b ; á) a  b ; â) a || b ; ã) a  b .

4. Êóò ìіæ îäíієþ ç äâîõ ïàðàëåëüíèõ ïðÿìèõ і їõ ñі÷íîþ äîðіâíþє 60. Ïіä ÿêèì êóòîì áіñåêòðèñà öüîãî êóòà ïåðåòèíàє äðóãó ïðÿìó?

à) 60; á) 40; â) 30; ã) 120.

5. Ñêіëüêè ïðÿìèõ ìîæíà ïðîâåñòè ÷åðåç äâі ðіçíі òî÷êè?

à) Îäíó; á) äâі; â) òðè; ã) æîäíîї.

6. Âïèñàíèé êóò, ùî ñïèðàєòüñÿ íà äіàìåòð, äîðіâíþє:

à) 180; á) 80; â) 45; ã) 90.

7. ßêèì çíàêîì íå ïîçíà÷àþòü âçàєìíå ðîçòàøóâàííÿ äâîõ ïðÿìèõ?

à) a  b ; á) a  b ; â) a || b ; ã) a b .

8. Ïðÿìі à і b íå ïàðàëåëüíі ïðÿìіé ñ . ×è âèïëèâàє ç öüîãî, ùî ïðÿìі à і b íå ïàðàëåëüíі?

à) Òàê; á) íі; â) òàê, ÿêùî a  ñ ; ã) íі, ÿêùî b  ñ .

9. Ñêіëüêè ïàð âåðòèêàëüíèõ êóòіâ óòâîðþþòü òðè ïðÿìі, ùî ïåðåòèíàþòüñÿ â îäíіé òî÷öі?

à) 3; á) 6; â) 9; ã) 12.

10. Íà îäíіé ñòîðîíі êóòà âіäêëàäåíî òðè âіäðіçêè À  2, ÂÑ  3 і ÑD  5. ×åðåç òî÷êè À ,  , Ñ і D ïðîâåäåíî ïàðàëåëüíі ïðÿìі ÀÀ ₁ ,  ₁ , ÑÑ ₁ і DD ₁ äî ïåðåòèíó ç іíøîþ ñòîðîíîþ êóòà. Çíàéäіòü ^ ₁ ^Ñ ₁ , ÿêùî ^À ₁ ^D ₁  20.

à) 9 ; á) 6; â) 4; ã) 10.

Òðèêóòíèêè

1. ßêùî êóòè òðèêóòíèêà ïðîïîðöіéíі ÷èñëàì 2, 3 і 4, òî éîãî íàéìåíøèé êóò äîðіâíþє:

à) 80; á) 40; â) 30; ã) 20.

2. Íàéìåíøèé çîâíіøíіé êóò ïðÿìîêóòíîãî òðèêóòíèêà äîðіâíþє:

à) 180; á) 90; â) 135; ã) 125.

3. Ïëîùà ðіâíîñòîðîííüîãî òðèêóòíèêà çі ñòîðîíîþ 2 äì äîðіâíþє:

à) 4 äì² ; á) 2 äì² ; â) äì² ; ã) 0,5 äì² .

4. Çíàéäіòü ðàäіóñ êîëà, îïèñàíîãî íàâêîëî òðèêóòíèêà ÀÂÑ , ÿêùî ÀÑ  3 ñì, B  30.

à) 3 ñì; á) 6 ñì; â) ñì; ã) 12 ñì.

5. Ìåíøà ìåäіàíà ïðÿìîêóòíîãî òðèêóòíèêà ç êàòåòàìè 5 ñì і 12 ñì äîðіâíþє:

à) 2,5 ñì; á) 6,5 ñì; â) 6 ñì; ã) 5 ñì.

6. Ó òðèêóòíèêó ïðîâåëè òðè ñåðåäíі ëіíії. Ñêіëüêè ïàð ïîäіáíèõ òðèêóòíèêіâ óòâîðèëîñÿ?

à) 4 ; á) 6; â) 10; ã) 12.

7. Çà ÿêîþ ôîðìóëîþ îá÷èñëþþòü ðàäіóñ êîëà, âïèñàíîãî â òðèêóòíèê?

à) á) â) ã)

8. 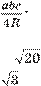Ãіïîòåíóçà ðіâíîáåäðåíîãî ïðÿìîêóòíîãî òðèêóòíèêà äîðіâíþє , à áіñåê òðè ñà, îïóùåíà íà íåї:

à) ; á) ; â) ; ã) .

9. Çíàéäіòü ïëîùó òðèêóòíèêà, äâі ñòîðîíè ÿêîãî äîðіâíþþòü 6 ñì і 14 ñì, à êóò ìіæ íèìè 30.

à) 42 ñì² ; á) 21 ñì² ; â) 21 ñì² ; ã) 21 ñì² .

10. Ïëîùі äâîõ ïîäіáíèõ òðèêóòíèêіâ âіäíîñÿòüñÿ ÿê 4 : 9. ßê âіäíîñÿòüñÿ їõíі ñòîðîíè?

à) 16 : 81; á) 2 : 4,5; â) 1 : 2,5; ã) 2 : 3.

×îòèðèêóòíèêè

1. Êіëüêіñòü îñåé ñèìåòðії êâàäðàòà äîðіâíþє:

à) 2 ; á) 3; â) 4; ã) 5.

2. Îñíîâè òðàïåöії äîðіâíþþòü 4 ñì і 10 ñì, à її ñåðåäíÿ ëіíіÿ:

à) 4 ñ;ì á) 7 ñì; â) 10 ñì; ã) 3,5 ñì.

3. Ïåðèìåòð ïàðàëåëîãðàìà äîðіâíþє 16 ñì. Îäíà éîãî ñòîðîíà – 5 ñì, à äðóãà:

à) 5 ñì; á) 6 ñì; â) 11 ñì; ã) 3 ñì.

4. Çíàéäіòü êóòè ðîìáà, ÿêùî âîíè ïðîïîðöіéíі ÷èñëàì 2 і 7.

à) 30 і 70; á) 20 і 140; â) 40 і 140; ã) 80 і 280.

5. Ìåíøà ñòîðîíà ïðÿìîêóòíèêà äîðіâíþє 5 ñì. Çíàéäіòü äîâæèíó äіàãîíàëі, ÿêùî âîíà óòâîðþє ç áіëüøîþ ñòîðîíîþ êóò 30.

à) 10 ñì; á) 5 ñì; â) 2,5 ñì; ã) 20 ñì.

6. Çíàéäіòü ïëîùó ðîìáà, ÿêùî éîãî ìåíøà äіàãîíàëü і ñòîðîíà äîðіâíþþòü 4 ì.

à) 4 ì² ; á) 6 ì² ; â) 8 ì² ; ã) 2 ì² .

7. ßêùî áіñåêòðèñà êóòà ïðÿìîêóòíèêà äіëèòü éîãî íà ÷àñòèíè, ïëîùі ÿêèõ ïðîïîðöіéíі ÷èñëàì 1 і 3, òî éîãî ñóìіæíі ñòîðîíè âіäíîñÿòüñÿ ÿê:

à) 1 : 2; á) 1 : 3; â) 1 : 4; ã) 2 : 3.

8. Ïåðèìåòð ðіâíîáі÷íîї òðàïåöії, îïèñàíîї íàâêîëî êîëà, äîðіâíþє 20 ñì. Çíàéäіòü áі÷íó ñòîðîíó òðàïåöії. à) 5 ñì; á) 6 ñì; â) 11 ñì; ã) 3 ñì.

9. Çíàéäіòü íàéáіëüøèé êóò ïðÿìîêóòíîї òðàïåöії, ÿêùî îäèí ç її êóòіâ óä âі÷і áіëüøèé çà іíøèé.

à) 130 àáî 170; á) 120 àáî 135;

â) 140 àáî 145; ã) 180 àáî 128.

10. Îäèí ç êóòіâ ðîìáà äîðіâíþє 120, à ïåðèìåòð 24 ñì. Ìåíøà äіàãî íàëü ðîìáà äîðіâíþє:

à) 2 ñì; á) 3 ñì; â) 4 ñì; ã) 6 ñì.

Êîëî і êðóã

1. Äîâæèíà ÷âåðòі êîëà ðàäіóñà 2ì äîðіâíþє:

à) ² ì; á) 16 ì; â) 2 ì; ã) 4 ì² .

2. Ïëîùà êðóãà äîðіâíþє 100 ñì² . Çíàéäіòü äîâæèíó éîãî êîëà.

à) 100 ñì; á) 50 ñì; â) 20 ñì; ã) 2500 ñì.

3. Êóò ìіæ äâîìà ðàäіóñàìè êîëà äîðіâíþє 125. Çíàéäіòü êóò ìіæ äîòè÷íèìè, ïðîâåäåíèìè ÷åðåç êіíöі öèõ ðàäіóñіâ. à) 125; á) 95; â) 35; ã) 55.

4.

5. Ðàäіóñ êîëà, îïèñàíîãî íàâêîëî ïðàâèëüíîãî øåñòèêóòíèêà ç ïåðèìåòðîì 24 ñì, äîðіâíþє:

à) 12 ñì; á) 3 ñì; â) 6 ñì; ã) 4 ñì.

6. Êîëà ðàäіóñіâ 3 ì і 7 ì ìàþòü âíóòðіøíіé äîòèê. Âіäñòàíü ìіæ їõíіìè öåíòðàìè:

à) 2 ì; á) 10 ì; â) 4 ì; ã) 5 ì.

7. Çíàéäіòü ïëîùó êіëüöÿ, óòâîðåíîãî êîíöåíòðè÷íèìè êîëàìè ðàäіóñіâ 3 ì і 5 ì.

à) 2 ì² ; á) 16 ì² ; â) 2 ì² ; ã) 4 ì² .

8. Ñòîðîíà êâàäðàòà, îïèñàíîãî íàâêîëî êîëà çàâäîâæêè 16 ñì, äîðіâíþє:

à) 16 ñì; á) 8 ñì; â) 4 ñì; ã) 4 ñì.

9. Ïðàâèëüíèé òðèêóòíèê ABC âïèñàíèé ó êîëî. Çíàéäіòü äîâæèíó êîëà, ÿêùî äîâæèíà äóãè ÂÀÑ äîðіâíþє 6 ñì. à) 12 ñì; á) 12 ñì; â) 9 ñì; ã) 4 ñì.

10. Çíàéäіòü ïëîùó ñåêòîðà êðóãà ðàäіóñà 6 ñì ç öåíòðàëüíèì êóòîì 60.

à) 6 ñì² ; á) 3 ñì² ; â) 9 ñì² ; ã) 2 ñì² .

Êîîðäèíàòè íà ïëîùèíі

1. Ñåðåäèíà âіäðіçêà KÐ , äå K (1; –3), Ð (7; 5), ìàє êîîð äèíàòè:

à) (–1; 3); á) (4; 1); â) (2; 1); ã) (3; 4).

2. ßêèé çíàê ñëіä ïîñòàâèòè â çàïèñó ÀÑ * ÂÑ çàìіñòü çіðî÷êè, ÿêùî À (–1; 3),  (5; 6), Ñ (2; 4,5)?

à) >; á) <; â) ; ã) .

3. ßêà ç òî÷îê íå íàëåæèòü ïðÿìіé 2õ + ó  7?

à) (–2; 11); á) (–0,5; 8); â) (2; 5); ã) (0,5; 6).

4. Ïðÿìіé ó  õ + 5 ïàðàëåëüíà ïðÿìà:

à) ó  5; á) 3õ + ó  4; â) 2ó – õ  2; ã) õ + ^[1] ó  6.

5. Ïðÿìà õ + ó  5 óòâîðþє ç äîäàòíèì íàïðÿìîì îñі ÎÕ êóò:

à) 90; á) 45; â) 135; ã) 30.

6. Öåíòð êîëà õ ² + (ó – 2)² – 8  0 ìàє êîîðäèíàòè:

à) (0; 4); á) (1; 2); â) (0; 2); ã) (2; 4).

7. Òî÷êà Ì , ÿêà ëåæèòü íà îñі ÎÕ òà ðіâíîâіääàëåíà âіä òî÷îê À (5; 4) і  (2; 1), ìàє êîîðäèíàòè:

à) (0; 4); á) (1; 0); â) (0; 2); ã) (6; 0).

8. Êîëî ç äіàìåòðîì ÀÂ , äå À (4; 3), Â (–4; –3), ìàє ðіâ íÿííÿ:

à) õ ² + ó ²  5; á) õ ² + ó ²  9;

â) õ ² + ó ²  25; ã) õ ² + ó ²  3.

9. ßêùî äіàìåòð êîëà õ ² + ó ²  25 ïðîõîäèòü ÷åðåç òî÷êó À (3; 4), òî éîãî ðіâíÿííÿ:

à) 3õ + 4ó  25; á) 3ó  4õ ;

â) ó + õ  5; ã) 4õ + 3ó  0.

10. ßêà ç ïðÿìèõ íå є äîòè÷íîþ äî êîëà õ ² + (ó – 2)²  9?

à) õ  ;3 á) ó  3; â) õ  –3; ã) ó  –1.

Âåêòîðè

1. ßêùî À (1; –3) і Â (–7; 12), òî âåêòîð AB ìàє êîîðäèíàòè:

à) (6; –15); á) (–8; 15); â) (–8; 9); ã) (–6; 9).

2. ßêùî âåêòîðè a і b ïåðïåíäèêóëÿðíі, òî:

à) a + b  0; á) a – b  0;

â) a · b  0; ã) a : b  0.

4. Çíàéäіòü äîâæèíó âåêòîðà a  (–2; 4).

à) 2; á) 20; â) 12; ã) 2 .

5. Âåêòîð, êîëіíåàðíèé âåêòîðó a  (–1; 4), ìàє êîîðäèíàòè:

à) (–2; –8); á) (0,5; 2); â) (3; –3); ã) (4; –16).

6. Ñóìîþ âåêòîðіâ BC + AB + DA + CD є âåêòîð:

à) AÂ ; á) AC ; â) 0; ã) AD .

7. ßêùî ñêàëÿðíèé äîáóòîê äâîõ îäèíè÷íèõ âåêòîðіâ äîðіâíþє 0,5, òî êóò ìіæ íèìè:

à) 30; á) 60; â) 120; ã) 45.

8. Ïðè ÿêîìó çíà÷åííі ò âåêòîðè a  (–2; 6) і b  (9; ò ) ïåðïåíäèêóëÿðíі?

à) –3; á) 27; â) 3; ã) –27.

9. Ïðè ÿêîìó çíà÷åííі õ âåêòîðè m  (3; õ ) і n  (–6; 7) êîëіíåàðíі?

à) 14; á) 3,5; â) –3,5; ã) –14.

10. Ïðîåêöії âåêòîðà AB íà îñі õ і ó äîðіâíþþòü âіäïîâіäíî à і b , à ïðîåêöіÿ âåêòîðà BA íà âіñü ó äîðіâíþє: à) –à ; á) –b ; â) b ; ã) à .

МЕТОДИ РОЗВ’ЯЗУВАННЯ

§ 2 ПЛАНІМЕТРИЧНИХ ЗАДАЧ

Ïëàíіìåòðè÷íі çàäà÷і áóâàþòü ðіçíèõ âèäіâ, çäåáіëüøîãî – íà îá÷èñëåííÿ, ïîáóäîâó, äîâåäåííÿ ÷è äîñëіäæåííÿ. Ó çàäà÷àõ íà îá÷èñëåííÿ íàé÷àñòіøå âèìàãàєòüñÿ çíàéòè çíà÷åííÿ ãåîìåòðè÷íîї âåëè÷èíè: âіäñòàíü, äîâæèíó äóãè, ìіðó êóòà, ïåðèìåòð ÷è ïëîùó ôіãóðè.

ÇÀÄÀ×À 1. Çíàéäіòü ñóìó êóòіâ À, Â, Ñ, D, Å çіðêè, çîáðàæåíîї íà ìàëþíêó 24.

ÐÎÇÂ’ßÇÀÍÍß. Çîâíіøíіé êóò òðèêóòíèêà äîðіâíþє ñóìі äâîõ âíóòðіøíіõ êóòіâ, íå ñóìіæíèõ ç íèì. Òîìó, ïîçíà÷èâøè íà ìàëþíêó äâà êóòè öèôðàìè 1 і 2 , ìàєìî:

Â + D  1 , Ñ + Å 2. Îòæå,

C

À + Â + Ñ + D + Å  À +

^B D + 1 +2  180.

ÂІÄÏÎÂІÄÜ. Ñóìà êóòіâ êîæíîї

² 1 òàêîї ï’ÿòèêóòíîї çіðêè äîðіâíþє

180.

^{A E} Ó çàäà÷àõ íà ïîáóäîâó âèìàãà-

_{Ìàë. 24} єòüñÿ ïîáóäóâàòè ôіãóðó çі âêàçàíèìè

ÇÀÄÀ×À 3. Äîâåäіòü, ùî ñóìà âіäñòàíåé âіä äîâіëüíîї òî÷êè Õ âíóòðіøíüîї îáëàñòі ïðàâèëüíîãî òðèêóòíèêà äî éîãî ñòîðіí ñòàëà, òîáòî íå çàëåæèòü âіä ïîëîæåííÿ öієї òî÷êè.

ÐÎÇÂ’ßÇÀÍÍß. Íåõàé ÀÂÑ – ïðàâèëüíèé òðèêóòíèê çі ñòîðîíîþ à і

C âèñîòîþ h , Õ – äîâіëüíà òî÷êà ó éîãî âíóòðіøíіé îáëàñòі, à ÕK , ÕÐ , ÕÒ – ïåðïåíäèêóëÿðè äî À , ÂÑ , ÀÑ (ìàë. 27).

Âèðàçèìî äâîìà ñïîñîáàìè ïëîùó S

Âіäðіçêè ÕÀ , ÕÂ , ÕÑ äàíèé òðèêóòíèê ðîçáèâàþòü íà òðè òðèêóòíèêè ç îñíîâàìè ÀÂ , ÂÑ , ÑÀ і âèñîòàìè ÕK , ÕÐ , ÕÒ . Їõ ïîäâîєíі ïëîùі äîðіâíþþòü à · ÕK , à · ÕÐ , à · ÕÒ , à ïîäâîєíà ïëîùà âñüîãî òðèêóòíèêà à · h . Îòæå, à · ÕK + à · ÕÐ + à · ÕÒ  à · h , çâіäñè ÕK + ÕÐ + ÕÒ  h.

Îòæå, äå á íå áóëà òî÷êà Õ (óñåðåäèíі ABC ), ñóìà âіäñòàíåé âіä íåї äî ñòîðіí íå çìіíþєòüñÿ і äîðіâíþє h .

Ó çàäà÷àõ íà äîñëіäæåííÿ ïðîïîíóєòüñÿ äîñëіäèòè ùî-íåá óäü.

ÇÀÄÀ×À 4. Êîæíà ñòîðîíà ïàðà ëå ëî ãðàìà ïàðàëåëüíà ïðîòè ëåæíіé ñòîðîíі. À ÷è іñíóє ÷îòèðèêóòíèê, êîæíà ñòîð î íà ÿêîãî ïåðïåíäèêóëÿðíà äî ïðî òè ëåæíîї ñòîðîíè?

ÐÎÇÂ’ßÇÀÍÍß. Ïåðøèé ñïîñіá . Ñïðîá óєìî íàêðåñëèòè õî÷à á îäèí ç òàêèõ ÷îòèðèêóòíèêіâ. Íåõàé À і ÑD – éîãî ïðîò èëåæíі ñòîðîíè – ïåðïåíäèêóëÿðíі âіäðіçêè. Ïðîâіâøè âіäðіçêè ÀD і ÂÑ , óòâîðèìî ÷îòèðèêóòíèê ÀÂÑD , ó ÿêîãî À  ÑD (ìàë. 28). Äâі іíøі éîãî ñòîðîíè ÀD і ÂÑ ìîæóòü áóòè íå ïåðïåí äè êóëÿðíі. Àëå ïðîäîâæèâøè àáî âêîð î òèâøè âіä ðі çîê À , ìîæíà äîñÿãòè, ùîá і âîíè ñòàëè ïåðïåíäèêóëÿðíèìè.

ÂІÄÏÎÂІÄÜ. ×îòèðèêóòíèê, êîæíà ñòîðîíà ÿêîãî ïåðïåíäè êóëÿðíà äî ïðî òèëåæíîї ñòîðîíè, іñíóє.

Äðóãèé ñïîñіá. Íåõàé ÀÂÑ – äîâіëüíèé ãîñòðîêóòíèé òðèêóòíèê, à éîãî âèñîòè ïåðåòèíàþòüñÿ â òî÷öі Í (ìàë. 29).

Ìàë. 29

Çàôàðáóєìî íåîïóêëèé ÷îòèðèêóòíèê ÀÂÑÍ . Êîæíà éîãî ñòîðîíà ïåðïåíäèêóëÿðíà äî ïðîòèëåæíîї ñòîðîíè.

Äðóãèé ñïîñіá ïðîäóêòèâíіøèé: âіí äîäàòêîâî ïîêàçóє, ùî â òàêîãî ÷îòèðèêóòíèêà äіàãîíàëі ïåðïåíäèêóëÿðíі. À îòæå, ñåðåäèíè ñòîðіí ÷îòèðèêóòíèêà ÀÂÑÍ – âåðøèíè ïðÿìîêóòíèêà, à ïëîùà ÷îòèðèêóòíèêà ÀÂÑÍ äîðіâíþє ïіâäîáóòêó äіàãîíàëåé òîùî. ßêùî â ðîçâ’ÿçàííі âèêîðèñòîâóþòü òіëüêè ãåîìåòðè÷íі âіäîìîñòі, òàêå ðîçâ’ÿçàííÿ íàçèâàþòü ãåîìåòðè÷íèì . ßêùî æ âèêîðèñòîâóþòü âіäîìîñòі ç àëãåáðè ÷è ìàòåìàòè÷íîãî àíàëіçó, òî êàæóòü ïðî àíàëіòè÷íå ðîçâ’ÿçàííÿ . Íàé÷àñòіøå àíàëіòè÷íå ðîçâ’ÿçàííÿ çàäà÷і çâîäèòüñÿ äî ñêëàäàííÿ çà óìîâîþ ãåîìåòðè÷íîї çàäà÷і âіäïîâіäíèõ ðіâíÿíü ÷è ñèñòåì ðіâíÿíü.

ÇÀÄÀ×À 5. Çíàéäіòü ïëîùó ðîìáà, ÿêùî éîãî âèñîòà і ìåí øà äіàãîíàëü âіäïîâіäíî äîðіâíþþòü 12 ñì і 13 ñì. ÐÎÇÂ’ßÇÀÍÍß. Íåõàé ÀÂÑD – ðîìá

(ìàë. 30), à ÂÍ і ÂD – éîãî âèñîòà і äі à- ãîíàëü. Òîäі ÂÍ  12 ñì, ÂD  13 ñì, à

ÍD  (ñì).

Íåõàé ÀÍ  õ. Òîäі ÀÂ  AD  AH +

+ HD  x + 5.

Ç ÀÂÍ ÀÂ ²  ÂÍ ² + ÀÍ ² . Ìîæåìî Ìàë. 30 ñêëàñòè ðіâíÿííÿ:

(x + 5)²  12² + õ ² , àáî õ ² + 10õ + 25  144 + õ ² , çâіäñè õ  11,9 (ñì).

Ìàєìî ÀÂ  x + 5  11,9 + 5  16,9 (ñì). Çíàéäåìî òåïåð ïëîùó S ðîìáà ÀÂÑD .

S  ÂÍ · AD , òîáòî S  12 · 16,9  202,8 (ñì² ).

ÂІÄÏÎÂІÄÜ. S  202,8 ñì² .

Åôåêòèâíèìè ìåòîäàìè ðîçâ’ÿçóâàííÿ ãåîìåòðè÷íèõ çàäà÷ є êîîðäèíàòíèé і âåêòîðíèé ìåòîäè.

Êîîðäèíàòíèé ìåòîä ïîëÿãàє â òîìó, ùî ðîçâ’ÿçóþ÷è ãåîìåòðè÷íó çàäà÷ó, îïåðóþòü êîîðäèíàòàìè îêðåìèõ òî÷îê, ðіâíÿííÿìè ïðÿìèõ àáî іíøèõ ëіíіé. Ðîçâ’ÿçóþ÷è çàäà÷ó êîîðäèíàòíèì ìåòîäîì, ðîçãëÿäóâàíі ôіãóðè ðîçìіùóþòü íà êîîðäèíàòíіé ïëîùèíі. Ïðèïèñàâøè îêðåìèì òî÷êàì ôіãóð êîîðäèíàòè, à ëіíіÿì — ðіâíÿííÿ, äàëі îá÷èñëþþòü êîîðäèíàòè іíøèõ òî÷îê, âèâîäÿòü ðіâíÿííÿ іíøèõ ëіíіé. Ó ðåçóëüòàòі îòðèìóєìî ïîòðіáíó âіäïîâіäü.

Ðàöіîíàëüíіñòü ðîçâ’ÿçàííÿ çàäà÷і öèì ìåòîäîì çíà÷íîþ ìіðîþ çàëåæèòü âіä òîãî, ÿê ðîçãëÿäóâàíó ôіãóðó ðîçìіñòèòè âіäíîñíî êîîðäèíàòíèõ îñåé. Íàéçðó÷íіøå öèì ìåòîäîì êîðèñòóâàòèñÿ òîäі, êîëè â çàäà÷і ìîâà éäå ïðî ïðÿìі êóòè àáî ñóìè êâàäðàòіâ ÿêèõîñü âіäñòàíåé.

ÇÀÄÀ×À 6. Çíàéäіòü ñóìó êâàäðàòіâ âіäñòàíåé âіä äîâіëüíîї òî÷êè êîëà ðàäіóñà 5 ñì äî âåðøèí îïèñàíîãî íàâêîëî íüîãî êâàäðàòà.

ÐÎÇÂ’ßÇÀÍÍß. Êîëî ðàäіóñà 5 ñì і îïèñàíèé íàâêîëî íüîãî êâàäðàò ðîçìіñòèìî â ñèñòåìі êîîðäèíàò òàê, ùîá її îñі áóëè ñåðåäèííèìè ïåðï åí äè êó ëÿðàìè äëÿ ñòîðіí êâàäðàòà (ìàë. 31). Òîäі êîëó âіäïîâіäàòèìå ðіâíÿííÿ õ ² + + ó ²  25, à âåðøèíè êâàäðàòà ìàòè ìóòü êîîðäèíàòè À (5; –5),  (5; 5), Ñ (–5; 5),

ßêùî Ì (õ ; ó ) – äîâіëüíà òî÷êà êîëà, òî ÌÀ ² + Ì ² + ÌÑ ² + + ÌD  (5 – õ ) + (–5 – ó )² + (5 – õ )² + (5 – ó )² + (–5 – õ )² + + (5 – ó ) + (–5 – õ )² + (–5 – ó )²  2((5 – õ )² + (5 + õ )² + (5 + + ó )² + (5 – ó ) )  200 + 4(õ ² + ó ² )  300 (ñì² ).

2

ßêùî çàäà÷ó ðîçâ’ÿçóþòü, âèêîðèñòîâóþ÷è âëàñòèâîñòі âåêòîðіâ, òî öå – âåêòîðíèé ìåòîä ðîçâ’ÿçóâàííÿ çàäà÷і. Äëÿ åôåêòèâíîãî éîãî çàñòîñóâàííÿ ñëіä óìіòè ãåîìåòðè÷íі ñïіââіäíîøåííÿ (âëàñòèâîñòі ãåîìåòðè÷íèõ ôіãóð) çàïèñóâàòè ó âèãëÿäі âåêòîðíèõ ðіâíîñòåé. Ïðè öüîìó ÷àñòî âèêîðèñòîâóþòü òàêі òâåðäæåííÿ òà âåêòîðíі ðіâíîñòі:

1) OA  OB – òî÷êè À і  çáіãàþòüñÿ;

2) AB  kCD – ïðÿìі ÀÂ і CD ïàðàëåëüíі àáî çáіãàþòüñÿ;

3) AB  kAC – òî÷êè À ,  , Ñ ëåæàòü íà îäíіé ïðÿìіé;

4) AB · CD  0 – ïðÿìі ÀÂ і CD ïåðïåíäèêóëÿðíі;

5) , à ÷èñëà m і n äîäàòíі – òî÷êà Ì äіëèòü

âіä ðіçîê ÀÂ ó âіäíîøåííі ÀÌ : ÌÂ  m : ï ;

6) a · b  |a | · |b | cos – êóò ìіæ ïðÿìèìè, íà ÿêèõ ëåæàòü âåêòîðè a і b , äîðіâíþє ;

– Ì – ñåðåäèíà âіäðіçêà ÀÂ ;

– Ì – òî÷êà ïåðåòèíó ìåäіàí

– òî÷êà Ì äіëèòü âіäðіçîê ÀÂ

Êîðèñòóþ÷èñü öèìè ñïіââіäíîøåííÿìè, ìîæíà ðîçâ’ÿçóâàòè áàãàòî ãåîìåòðè÷íèõ çàäà÷ òà äîâîäèòè òåîðåìè.

Ðîçâ’ÿçóâàííÿ çàäà÷і âåêòîðíèì ìåòîäîì ñêëàäàєòüñÿ ç êіëüêîõ êðîêіâ:

– ïîäàíі â çàäà÷і ñïіââіäíîøåííÿ «ïåðåêëàäàþòü ìîâîþ» âåêòîðіâ, òîáòî çàïèñóþòü їõ âіäïîâіäíèìè âåêòîðíèìè ðіâíîñòÿìè;

– îòðèìàíі âåêòîðíі ðіâíîñòі ïåðåòâîðþþòü, âèêîðèñòîâóþ÷è ïðàâèëà âåêòîðíîї àëãåáðè;

– âіä ìîâè âåêòîðіâ ïåðåõîäÿòü äî ìîâè ãåîìåòðії.

ÇÀÄÀ×À 7. Òî÷êà ïåðåòèíó ïðÿìèõ, ÿêèì íàëåæàòü áі÷íі ñòîðîíè òðàïåöії, òà ñåðåäèíè її îñíîâ ëåæàòü íà îäíіé ïðÿìіé. Äîâåäіòü.

ÐÎÇÂ’ßÇÀÍÍß. Íà ìàëþíêó 32 çîáðàæåíî òðàïåöіþ ÀÂÑD . Òî÷êè Ì і N – ñåðåäèíè її îñíîâ, à Î – òî÷êà ïåðåòèíó ïðÿìèõ À і ÑD . Ùîá äîâåñòè, ùî òî÷êè Ì , N і Î ëåæàòü íà îäíіé ïðÿ ìіé,

ïîêàæåìî, ùî âåêòîðè OM і ON – êî ëіíåàðíі.

Îñêіëüêè Ì – ñåðåäèíà ÂÑ , à N – ñåðåäèíà AD , òî âèêîíóþòüñÿ ðіâíîñòі:

OM  (OB + OC ) і ON  (OA + OD ).

Îñêіëüêè ÎÂÑ ÎÀD , òî OA : OB   OD : OC  k . Çâіäñè

OA  kOB , OD  kOC , ON  (kOB + + kOC )  k (OB + OC )  kOM.

Ìàєìî ON  kOM. Îòæå, òî÷êè Ì , N і

Î ëåæàòü íà îäíіé ïðÿìіé. Ìàë. 32

ЗAДAЧІ І ВПРAВИ

А

1. ×åðåç òî÷êó íà ïëîùèíі ïðîâåäåíî 3 ïðÿìі. Äîâåäіòü, ùî ìіðè ïðèíàéìíі äâîõ ç óòâîðåíèõ êóòіâ ìåíøі çà 61.

2. Óñòàíîâіòü âèä òðèêóòíèêà, ÿêùî éîãî êóòè ïðîïîðöіéíі ÷èñëàì 1, 2 і 3.

3. Âèçíà÷òå íàéáіëüøèé âíóòðіøíіé êóò òðèêóòíèêà, ÿêùî éîãî çîâíіøíі êóòè (âçÿòі ïî îäíîìó ïðè âåðøèíі) ïðîïîðöіéíі ÷èñëàì 2, 3 і 4.

4. Âèñîòà і ìåäіàíà ïðÿìîêóòíîãî òðèêóòíèêà, ïðîâåäåíі ç âåðøèíè ïðÿìîãî êóòà, äіëÿòü êóò íà òðè ðіâíі ÷àñòèíè.

Çíàéäіòü êóò ìіæ âèñîòîþ і áіñåêòðèñîþ, ïðîâåäåíîþ іç öієї âåðøèíè.

5. Òî÷êà Î – ñïіëüíà ñåðåäèíà âіäðіçêіâ AD і BC . Ïðÿìà l , ùî ïðîõîäèòü ÷åðåç òî÷êó Î , ïåðåòèíàє âіäðіçîê À ó òî÷öі Ì , à âіäðіçîê CD ó òî÷öі N . Äîâåäіòü:

à) ÌÎ  NO ; á) AM  DN ; â)DNO  AMO .

6. Ó ðіâíîáåäðåíîìó òðèêóòíèêó ÀÂÑ ïðîâåäåíî ìåäіàíè ÀÌ і BN äî áі÷íèõ ñòîðіí. Äîâåäіòü:

à) ÀÌÂ  BNA ; á) CAM  CBN.

7. Ó ðіâíîáåäðåíîìó òðèêóòíèêó ÀÂÑ ïðîâåäåíî áіñåêòðèñè ÀÌ і BN äî áі÷íèõ ñòîðіí. Äîâåäіòü:

à) ÀÌÂ  BNA ; á) CAM  CBN .

8. Ïîáóäóéòå ðіâíîáåäðåíèé òðèêóòíèê, ó ÿêîãî áі÷íà ñòîðîíà і âèñîòà, ïðîâåäåíà äî îñíîâè, äîðіâíþþòü âіäïîâіäíî 8 ñì і 6 ñì.

9. Ïîáóäóéòå ïðÿìîêóòíèé òðèêóòíèê, ó ÿêîãî îäèí ç êàòåòіâ äîðіâíþє 3 ñì, à ìåäіàíà, ïðîâåäåíà äî іíøîãî êàòåòà, 6 ñì.

10. Ïîäіëіòü çàäàíèé âіäðіçîê íà 7 ðіâíèõ ÷àñòèí.

11. Ñóìà äâîõ ñóñіäíіõ êóòіâ îïóêëîãî ÷îòèðèêóòíèêà äîðіâíþє 100. Çíàéäіòü êóò ìіæ áіñåêòðèñàìè äâîõ іíøèõ éîãî êóòіâ.

12. Çíàéäіòü óñі ìåäіàíè ïðÿìîêóòíîãî òðèêóòíèêà ç êàòåòàìè 3,2 ñì і 4,8 ñì.

13. Áіñåêòðèñà òóïîãî êóòà ïàðàëåëîãðàìà äіëèòü éîãî ñòîðîíó íà âіäðіçêè 5 ñì і 15 ñì, ïî÷èíàþ÷è âіä âåðøèíè ãîñòðîãî êóòà. Îá÷èñëіòü ïåðèìåòð ïàðàëåëîãðàìà.

14. Ïåðïåíäèêóëÿð, ïðîâåäåíèé ç âåðøèíè ïðÿìîãî êóòà äî îäíієї ç äіàãîíàëåé ïðÿìîêóòíèêà, ïîäіëÿє її ó âіäíîøåííі 1 : 3. Äîâåäіòü, ùî îäíà çі ñòîðіí ïðÿìîêóòíèêà äîðіâíþє ïîëîâèíі äіàãîíàëі.

15. Äâі ñòîðîíè òðèêóòíèêà äîðіâíþþòü 6 ñì і 4 ñì, à âèñîòà, ïðîâåäåíà ç їõíüîї ñïіëüíîї âåðøèíè, – 4 ñì. Çíàéäіòü ïëîùó òðèêóòíèêà.

16. Çíàéäіòü îñíîâè òðàïåöії, ÿêùî їõ ðіçíèöÿ і ñåðåäíÿ ëіíіÿ òðàïåöії äîðіâíþþòü 10 ì.

17. Êàòåòè ïðÿìîêóòíîãî òðèêóòíèêà äîðіâíþþòü 5 ñì і 12 ñì. Çíàéäіòü ñèíóñè, êîñèíóñè і òàíãåíñè êóòіâ òðèê óòíèêà.

18. Îá÷èñëіòü êóòè ðіâíîáі÷íîї òðàïåöії, ÿêùî ñèíóñ îäíîãî ç íèõ äîðіâíþє 0,5.

19. Ïîáóäóéòå êóò, êîñèíóñ ÿêîãî äîðіâíþє 0,5. Çíàéäіòü ñèíóñ і òàíãåíñ öüîãî êóòà.

20. Ïîáóäóéòå êóò, òàíãåíñ ÿêîãî äîðіâíþє 5. Çíàéäіòü ñèíóñ і êîñèíóñ öüîãî êóòà.

21. Ïîáóäóéòå ðіâíîáåäðåíèé òðèêóòíèê çà áі÷íîþ ñòîðîíîþ 6 cì і êóòîì ïðè îñíîâі, êîñèíóñ ÿêîãî äîðіâíþє .

22. Êîñèíóñè ãîñòðèõ êóòіâ òðàïåöії äîðіâíþþòü 0,8 і 0,6.

Çíàéäіòü ñèíóñè, êîñèíóñè і òàíãåíñè éîãî òóïèõ êóòіâ.

23. Çíàéäіòü íåâіäîìó ñòîðîíó ÀÂÑ , ÿêùî:

à) ÀÂ  3 ñì, ÂÑ  8 ñì, Â  60;

á) ÀÂ  6 ñì, ÀÑ  4 ñì, À  45.

24. Ñòîðîíè òðèêóòíèêà ïðîïîðöіéíі ÷èñëàì 7, 8 і 13. Çíàéäіòü íàéáіëüøèé êóò òðèêóòíèêà, ÿêùî éîãî ïåðèìåòð 56 ñì.

25. Äіàãîíàëі ïàðàëåëîãðàìà äîðіâíþþòü 12 ñì і 32 ñì, à îäíà çі ñòîðіí 14 ñì. Çíàéäіòü ïåðèìåòð ïàðàëåëîãðàìà і êóò ìіæ éîãî äіàãîíàëÿìè.

26. Äіàãîíàëі ðîìáà äîðіâíþþòü 16 ñì і 12 ñì. Çíàéäіòü ïåðèìåòð і ïëîùó ðîìáà.

27. Ïåðèìåòð ðîìáà äîðіâíþє 6,8 ñì, à îäíà ç äіàãîíàëåé 1,6 ñì. Çíàéäіòü ïëîùó ðîìáà.

28. Ïåðèìåòð ïàðàëåëîãðàìà äîðіâíþє 52 ñì, à éîãî ïëîùà 60 ñì² . Çíàéäіòü ñòîðîíè і âèñîòè ïàðàëåëîãðàìà, ÿêùî éîãî ãîñòðèé êóò 30.

29. Ó ðіâíîáі÷íіé òðàïåöії îñíîâè äîðіâíþþòü 8 ñì і 18 ñì. Çíàéäіòü ðàäіóñ âïèñàíîãî êîëà.

30. Áіñåêòðèñà ïðÿìîãî êóòà òðèêóòíèêà äіëèòü ãіïîòåíóçó íà âіäðіçêè 20 äì і 15 äì. Çíàéäіòü ïëîùó òðèêóòíèêà.

31. Çíàéäіòü äіàãîíàëі ðіâíîáі÷íîї òðàïåöії, îñíîâè ÿêîї äîðіâíþþòü 11 ñì і 21 ñì, à áі÷íà ñòîðîíà 13 ñì.

32. Çíàéäіòü êóòè îïóêëîãî ï’ÿòèêóòíèêà, ÿêùî âîíè ïðîïîðöіéíі ÷èñëàì 3, 4, 5, 7, 8.

33. Öåíòðàëüíèé êóò ïðàâèëüíîãî ï- êóòíèêà ó 4 ðàçè ìåíøèé çà éîãî âíóòðіøíіé êóò. Çíàéäіòü ï .

34. Íàêðåñëіòü êîëî äіàìåòðà 6 ñì. Âïèøіòü ó êîëî é îïèøіòü íàâêîëî íüîãî ïðà âèëüíі ï- êóòíèêè òà îá÷èñëіòü їõ ïåðèìåòðè, ÿêùî: à) ï  3; á) ï  4; â) ï  6; ã) ï  12.

35. Ó êîëî âïèñàíî êâàäðàò і ïðàâèëüíèé øåñòèêóòíèê. Ïåðèìåòð êâàäðàòà 24 ñì. Çíàéäіòü ïåðèìåòð і ïëîùó øåñ òèêóòíèêà.

36. Íàâêîëî êîëà îïèñàíî ïðàâèëüíèé òðèêóòíèê, à â êîëî âïèñàíî ïðàâèëüíèé øåñòèêóòíèê, ïåðèìåòð ÿêîãî 18 ñì. Çíàéäіòü ïåðèìåòð і ïëîùó òðèêóòíèêà.

37. Äàíî ïðàâèëüíèé øåñòèêóòíèê çі ñòîðîíîþ 4 ñì. Çíàéäіòü øèðèíó і ïëîùó êіëüöÿ, óòâîðåíîãî êîëàìè, âïèñàíèì і îïèñàíèì íàâêîëî øåñòèêóòíèêà.

38. Çíàéäіòü ñòîðîíè òà ïëîùó ÀÂÑ , ÿêùî A (3; 4), B (–3; 4), C (–3; –4).

39. Äàíî ÀÂÑ , ó ÿêîãî À (7; 5), Â (4; 1), Ñ (–4; 7). Çíàéäіòü äîâæèíè éîãî ìåäіàí.

40. Âіäðіçîê MN òî÷êàìè K і Ð ïîäіëåíî íà òðè ðіâíі ÷àñòèíè (ÌK  KÐ  PN ). Çíàéäіòü êîîðäèíàòè òî÷êè N , ÿêùî Ì (2; –4), Ð (–6; 2).

41. Íà îñі àáñöèñ çíàéäіòü òî÷êó Ì , ÿêà ðіâíîâіääàëåíà âіä ïî÷àòêó êîîðäèíàò і âіä òî÷êè Ð (2; 3).

42. Íàïèøіòü ðіâíÿííÿ ïðÿìîї, ÿêà ïðîõîäèòü ÷åðåç òî÷êè À (1; 4) і  (–2; 1). Çíàéäіòü ïëîùó òðèêóòíèêà, ÿêèé âіä òèíàє öÿ ïðÿìà âіä îñåé êîîðäèíàò.

43. Äîâåäіòü, ùî òðèêóòíèê ç âåðøèíàìè À (3; 4), Â (6; –2), Ñ (–3; 1) – ðіâíîáåäðåíèé. Çíàéäіòü éîãî ïëîùó.

44. Óñòàíîâіòü âèä ÷îòèðèêóòíèêà ABCD , ÿêùî A (3; 1), B (4; 6), Ñ (9; 7), D (8; 2). Çíàéäіòü éîãî ïåðèìåòð і ïëîùó.

45. Çíàéäіòü êîîðäèíàòè òî÷êè, ÿêà ñèìåòðè÷íà òî÷öі À (3; –5) âіäíîñíî: à) òî÷êè (0; 0); á) îñі àáñöèñ; â) îñі îðäèíàò.

46. Ïîáóäóéòå äâà äîâіëüíі âåêòîðè a і b . Ïîáóäóéòå âåêòîð d òàêèé, ùî:

à) d  a + b ; á) d  a – b ;

â) d  a – 3b ; ã) d  2a + 0,5b .

47.

48. Çíàéäіòü ìîäóëü âåêòîðà p  2a – 3b , ÿêùî a  (1; 3), b   (–2; 0).

49. Ïðè ÿêèõ çíà÷åííÿõ õ âåêòîðè a  (õ ; 2) і b  (4; 2x ) êîëіíåàðíі?

50. Ïðè ÿêèõ çíà÷åííÿõ õ âåêòîðè p  (2; õ ) і s  (õ ; õ + 3) ïåðïåíäèêóëÿðíі?

Б

51. Ïî ðіçíі ñòîðîíè âіä ïðÿìîї MN ïîçíà÷åíî òî÷êè À і  òàê, ùî ÌÀ  Ì і NA  NB . Äîâåäіòü, ùî À  MN .

52. Ó ðіâíîáåäðåíîìó òðèêóòíèêó îñíîâà äîðіâíþє 30 ñì. Âè ñîòà, ïðîâåäåíà äî áі÷íîї ñòîðîíè, ïîäіëÿє її íà âіäðіçêè ó âіäíîøåííі 7 : 18, ïî÷èíàþ÷è âіä âåðøèíè. Çíàéäіòü ïëîùі

÷àñòèí òðèêóòíèêà, íà ÿêі éîãî ïîäіëÿє öÿ âèñîòà.

53. Ñòîðîíà òðèêóòíèêà, ìåäіàíà і âèñîòà, ïðîâåäåíі äî íåї, äîðіâíþþòü âіäïîâіäíî 34, 25 і 24 ñì. Çíàéäіòü ïåðèìåòð òðèêóòíèêà.

54. Îñíîâè òðàïåöії äîðіâíþþòü 6 ñì і 18 ñì. Ó ÿêîìó âіäíîøåííі äіàãîíàëі äіëÿòüñÿ òî÷êîþ ïåðåòèíó?

55. Äîâæèíà êîëà çáіëüøèëàñÿ íà 20 %. Íà ñêіëüêè âіäñîòêіâ çáіëüøèòüñÿ ïëîùà âïèñàíîãî â öå êîëî ïðàâèëüíîãî òðèêóòíèêà?

56. Ãіïîòåíóçà ïðÿìîêóòíîãî òðèêóòíèêà äîðіâíþє 12 ñì, à îäèí ç ãîñòðèõ êóòіâ äîðіâíþє 30. Çíàéäіòü ðàäіóñ êîëà ç öåíòðîì ó âåðøèíі öüîãî êóòà, ÿêå ïîäіëÿє äàíèé òðèêóòíèê íà äâі ðіâíîâåëèêі ÷àñòèíè.

57. Áàòüêî і äî÷êà ñòîÿòü îäíå íàâïðîòè îäíîãî. Їõíі òіíі âіäïîâіäíî äîðіâíþþòü 3 ì і 2,5 ì. ßêèé çðіñò ìàє äî÷êà, ÿêùî çðіñò áàòüêà 183 ñì?

58. Îñíîâè ðіâíîáі÷íîї òðàïåöії, â ÿêó ìîæíà âïèñàòè êîëî, ïðîïîðöіéíі ÷èñëàì 3 і 11. Çíàéäіòü ñèíóñè êóòіâ òðà- ïåöії.

59. Çíàéäіòü íåâіäîìі ñòîðîíè ÀÂÑ , ÿêùî:

à) ÀÂ  5 ñì, ÂÑ  8 ñì, Â  60;

á) ÀÂ  6 ñì, ÀÑ  4 ñì, cos B  ;

â) ÀÑ – ÀÂ  6 ñì, ÂÑ  8 ñì, Â  120;

ã) ÀÑ  6 ñì, ÂÑ  14 ñì, A  60.

60. Ñòîðîíè òðèêóòíèêà äîðіâíþþòü 11 ñì, 23 ñì і 30 ñì. Çíàéäіòü äîâæèíó ìåäіàíè, áіñåêòðèñè і âèñîòè, ïðîâåäåíèõ äî íàéáіëüøîї ñòîðîíè.

61. Ó òðèêóòèêó ÀÂÑ AB  BC  6 ñì, sin A  0,4. Çíàéäіòü âіäñòàíü âіä òî÷êè ïåðåòèíó ìåäіàí òðèêóòíèêà äî öåíòðà êîëà, îïèñàíîãî íàâêîëî òðèêóòíèêà.

62. AL – áіñåêòðèñà ðіâíîáåäðåíîãî ÀÂÑ (ÀÂ  ÂÑ ), BL  à , A  2. Çíàéäіòü ñòîðîíè òðèêóòíèêà і äîâæèíè éîãî áіñåêòðèñ.

63. BM – ìåäіàíà òðèêóòíèêà ÀÂÑ , BM  m , ABM  , CBM   . Çíàéäіòü ÀÂ .

64. Îñíîâè òðàïåöії äîðіâíþþòü 6 ñì і 24 ñì. Çíàéäіòü ðàäіóñè âïèñàíîãî і îïèñàíîãî êіë.

65. Íà ñòîðîíàõ À і ÂÑ òðèêóòíèêà ÀÂÑ âçÿòî òî÷êè K і Ò òàê, ùî À  10 ñì, ÀK  2 ñì, ÂÑ  14 ñì, ÒÑ  9 ñì. Çíàéäіòü ïëîùó ÷îòèðèêóòíèêà ÀKTÑ , ÿêùî S_ÀÂÑ  28 ñì² .

66. Îñíîâè ðіâíîáі÷íîї òðàïåöії ABCD äîðіâíþþòü 11 ñì і 21 ñì, à áі÷íà ñòîðîíà – 13 ñì. Çíàéäіòü ðàäіóñè êіë: à) îïè ñàíîãî íàâêîëî òðàïåöії; á) âïèñàíîãî â ÀÂÑ ; â) âïèñ àíîãî â ACD .

67. Äàíî äâà êðóãè ç ðàäіóñàìè ïî 1 äì, âіäñòàíü ìіæ їõ öåíòðà ìè äîðіâíþє äì. Çíàéäіòü ïëîùó ñïіëüíîї ÷àñòèíè öèõ êðóãіâ.

68. Ñïіëüíà õîðäà äâîõ êðóãіâ ñòÿãóє äóãè 60 і 120. Çíàéäіòü âіäíîøåííÿ ðàäіóñіâ öèõ êðóãіâ.

69. ×îòèðè ñåðïèêè óòâîðåíі êîëîì, îïèñàíèì íàâêîëî êâàäðàòà, і ïіâêîëàìè, ïîáóäîâàíèìè íà ñòîðîíàõ êâàäðàòà ÿê

Ìàë. 33 Ìàë. 34 Ìàë. 35

íà äіàìåòðàõ (ìàë. 33). Äîâåäіòü, ùî ñóìà ïëîù öèõ ÷îòèðüîõ ñåðïèêіâ äîðіâíþє ïëîùі êâàäðàòà.

70. Çíàéäіòü ïëîùó ôіãóðè, çàøòðèõîâàíîї íà ìàëþíêó 34.

71. Íà ìàëþíêó 35 çîáðàæåíî òðè ðіçíі ïîïàðíî äîòè÷íі êîëà і õîðäà, ÿêà äîòèêàєòüñÿ äî äâîõ ìåíøèõ êіë ó їõ ñïіëüíіé òî÷öі. Çíàéäіòü ïëîùó çàøòðèõîâàíîї ÷àñòèíè áіëüøîãî êðóãà, ÿêùî äî âæèíà õîðäè à.

72. Ó êðóãîâèé ñåêòîð ÀÎÂ ðàäіóñà ÎÀ  10 ñì âïèñàíî êîëî. Çíàéäіòü âіäíîøåííÿ ïëîù ñåêòîðà і êðóãà, ÿêùî S_ÀÎÂ   25 ñì² .

73. AK , BL , CM – ìåäіàíè òðèêóòíèêà ÀÂÑ . Çíàéäіòü êîîðäèíàòè òî÷êè L , ÿêùî À (–3; –1),  (–2; 1), K (1; –1).

74. Çíàéäіòü ñòîðîíè òà ïëîùó òðèêóòíèêà ÀÂÑ , ÿêùî A (a ; b ), B (–a ; b ), C (–a ; –b ) і òî÷êà À ëåæèòü ó III êîîðäèíàòíіé ÷âåðòі.

75. Äàíî òðèêóòíèê ÀÂÑ , ó ÿêîãî À (7; 5), Â (4; 1), Ñ (–4; 7). Çíàéäіòü äîâæèíè ìåäіàíè, âèñîòè і áіñåêòðèñè, ïðîâåäåíèõ ç âåðøèíè Â .

76.

77. Òî÷êè À (2; –5) і Ñ (2; –1) є âåðøèíàìè êâàäðàòà ABCD . Íàïèøіòü ðіâíÿííÿ êîëà, âïèñàíîãî â öåé êâàäðàò, òà êîëà, îïè- ñàíîãî íàâêîëî íüîãî. Çíàéäіòü íåâіäîìі âåðøèíè êâàäðàòà.

78. Çàïèøіòü ðіâíÿííÿ ïðÿìîї, ÿêà ïðîõîäèòü ÷åðåç öåíòðè äâîõ êіë: õ ² + ó ² – 4õ + 2ó  0 і õ ² + ó ² + 4õ – 6ó  3.

79. ×è ìàє òðèêóòíèê ÀÂÑ , ó ÿêîãî À (–6; –1),  (–3; 5), Ñ (3; 2), âіñü ñèìåòðії? ßêùî ìàє, òî çàïèøіòü її ðіâíÿííÿ.

80. ÀÑ – äіàãîíàëü êâàäðàòà. Çàïèøіòü ðіâíÿííÿ îñåé ñèìåòðії öüîãî êâàäðàòà, ÿêùî À (1; 2), Ñ (5; 6).

81. Êîëî ðàäіóñà 3 äîòèêàєòüñÿ äî îñåé êîîðäèíàò ó І ÷âåðòі. Çàïèøіòü ðіâíÿííÿ öüîãî êîëà і êîëà, ñèìåòðè÷íîãî äàíîìó âіäíîñíî: à) ïî÷àòêó êîîðäèíàò; á) îñі àáñöèñ; â) îñі îðäèíàò; ã) ïðÿìîї ó  2õ.

82. Î – òî÷êà ïåðåòèíó ìåäіàí ðіâíîñòîðîííüîãî òðèêóòíèêà ÀÂÑ . Ïðè ïàðàëåëüíîìó ïåðåíåñåííі òî÷êà À âіäîáðàçèëàñÿ íà òî÷êó Î . Âèêîíàéòå ïàðàëåëüíå ïåðåíåñåííÿ ÀÂÑ . Çíàé äіòü ïåðèìåòð ïîáóäîâàíîãî òðèêóòíèêà, ÿêùî S_ÀΠ S .

83. Ïðè ãîìîòåòії âіäíîñíî ïî÷àòêó êîîðäèíàò òî÷êà À (1; 2) ïåðåõîäèòü ó òî÷êó À ₁ (3; 6). Ó ÿêó òî÷êó ïðè öіé ãîìîòåòії ïåðåéäå òî÷êà  (3; –2)? Çíàéäіòü êîåôіöієíò ãîìîòåòії.

84. Ðîìáè ABCD і MNPK – ïîäіáíі, ÀÑ : BD  4 : 5. Çíàéäіòü äіàãîíàëі ðîìáà MNPK , ÿêùî éîãî ïëîùà äîðіâíþє 40 ñì² .

85. Ïðÿìà MN , ïàðàëåëüíà îñíîâі ÀÑ òðèêóòíèêà ÀÂÑ , äіëèòü éîãî íà äâі ÷àñòèíè – òðèêóòíèê і òðàïåöіþ. Ïëîùі öèõ ôіãóð ïðîïîðöіéíі ÷èñëàì 1 і 3. Çíàéäіòü ïåðèìåòð ÀÂÑ , ÿêùî ïåðèìåòð MBN äîðіâíþє 7 ñì .

86. Ï îáóäóéòå òðè äîâіëüíі âåêòîðè a , b , c . Ïîáóäóéòå âåêòîð d òàêèé, ùî:

à) d  a + 2b ; á) d  2a – 3b ;

â) d  0,5a – 3b + 2c ; ã) d  a + 0,5b – 2c .

87. Çíàéäіòü ìîäóëü âåêòîðà m  a + 2b , ÿêùî |a |  2, |b |  1,

.

88. Çíàéäіòü êîñèíóñ êóòà À òðèêóòíèêà ÀÂÑ , ÿêùî A (–1; 2), B (3; 5), Ñ (2; –1).

89. Ï ðè ÿêèõ çíà÷åííÿõ à êóò ìіæ âåêò îðàìè m  (6; à ) і b  (–5; à – 1) òóïèé?

90. Çíàéäіòü êóò ìіæ îäèíè÷íèìè âåêòîðàìè a і b , ÿêùî âåê-

òîð 5a – 4b ïåð ïåí äè êóëÿðíèé äî âåêòîðà a – 2b .

91. Äàíî òî÷êè À (4; –2) і B (2; –5). Çàïèøіòü ðіâíÿííÿ ïðÿìîї, ÿêà äîòèêàєòüñÿ äî êîëà äіàìåòðà À ó òî÷öі À .

92. Çàïèøіòü ðіâíÿííÿ äîòè÷íèõ, ïðîâåäåíèõ ç òî÷êè A (5; 0) äî êîëà õ ² + ó ² 9.

93. Íà äіàãðàìі Âîðîíîãî çîáðàæåíî òðè àíòåíè A ,  , C , їõ êîîðä èíàòè òà îáëàñòі îáñëóãîâóâàííÿ (ìàë. 36). Ðåáðà OM , ON , OK êëіòèí íà äіàãðàìі Âîðîíîãî áóäóþòüñÿ ÿê ñåðåäèííі ïåðïåíäèêóëÿðè äî âіäðіçêіâ À , ÂÑ і ÀÑ . Çàïèøіòü ðіâíÿííÿ ðåáåð äіàãðàìè Âîðîíîãî і êîîðäèíàòè òî÷êè Î – âåðøèíè äіàãðàìè Âîðîíîãî.

Ãåîðãіé Ôåîäîñіéîâè÷

Ìàë. 36 ÂÎÐÎÍÈÉ (1868–1908)

94*. Íà ñòîðîíàõ À , ÂÑ і ÑÀ òðè êóòíè êà ÀÂÑ ïîçíà÷åíî òî÷êè À ₁ ,  ₁ , Ñ ₁ òàêі, ùî ÀÑ ₁ : Ñ ₁  ÂÀ ₁ : À ₁ Ñ  Ñ ₁ :  ₁ À  2 (ìàë. 37). ßê âіäíîñÿòüñÿ ïëîùі òðèêóòíèêіâ ÀÂÑ і KÐÒ ?

95*. Íà ñòîðîíàõ äîâіëüíîãî òðèêóòíèêà ÀÂÑ çîâíі íüîãî ïîáóäîâàíî ïðàâèëüíі òðèêóòíèêè (ìàë. 38). Äîâåäіòü, ùî їõ öåíòðè K , Ð , Ò – âåðøèíè ïðàâ èëü íèõ òðèêóòíèêіâ.

96. Íà îñíîâі ÀÑ òðèêóòíèêà ÀÂÑ âçÿòî òî÷êè Ì і Í òàêі, ùî ÀÌ < AH . Ïðÿìі ÂÌ і ÂH äіëÿòü ìåäіàíó ÀK íà òðè ðіâ íі ÷àñòèíè. Çíàéäіòü ÀÑ , ÿêùî ÌÍ  3. 97*. Ïðîòèëåæíі ñòîðîíè îïóêëîãî øåñòèêóòíèêà ïàðàëåëüíі. Äîâåäіòü, ùî ïðÿìі, ÿêі ñïîëó÷àþòü ñåðåäèíè ïðîòèëåæíèõ ñòîðіí, ïåðåòèíàþòüñÿ â îäíіé òî÷öі.

98*. Ïðÿìà Åéëåðà ïðîõîäèòü ÷åðåç öåíòð âïèñàíîãî ó òðèêóòíèê êîëà. Äîâå äіòü, ùî òðèêóòíèê ðіâíîáåäðåíèé.

99*. ßêùî âïèñàíå â òðèêóòíèê êîëî äîòèêàєòüñÿ äî éîãî ñòîðіí À , ÂÑ , ÑÀ â òî÷êàõ À ₁ ,  ₁ , Ñ ₁ , òî ïðÿìі ÀÀ ₁ ,  ₁ , ÑÑ ïåðåòèíàþòüñÿ â îäíіé òî÷öі. Äîâåäіòü.

100*. Íà êàòåòàõ ÀÑ і ÂÑ ïðÿìîêóòíîãî òðèêóòíèêà ÀÂÑ çîâíі íüîãî ïîáóäîâàíî êâàäðàòè ÀÑKÐ і ÑÂÌÒ . Äîâåäіòü, ùî ïðÿìі ÀÌ , ÂÐ і âèñîòà ÑÍ òðèêóòíèêà ïåðåòèíàþòüñÿ â îäíіé òî÷öі.

[1] . Ç íàéäіòü êîîðäèíàòè âåêòîðà m  2p + 3q , ÿêùî p  (–2; 1), q  (4; –3).

à) (8; –7); á) (–14; 0); â) (8; 11); ã) (–2; 3).