| Є. П. Нелін
АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ
Підручник для загальноосвітніх навчальних закладів
Академічний рівень
Харків
«Гімназія»
2010
УДК 373:[512+517]
ББК 22.12я721+2.161я721
H58
Є. П. Нелін
H58 Алгебра і початки аналізу : підруч. для 10 кл. загальноосвіт.
навч. закладів : академ. рівень. — Х. : Гімназія, 2010. — 416 с. : іл.
ISBN 978-966-474-095-8.
УДК 373:[512+517]
ББК 22.12я721+2.161я721
© Є. П. Нелін, 2010
© С. Е. Кулініч, художнє оформлення, 2010
ISBN 978-966-474-095-8 © ТОВ ТО «Гімназія», оригінал-макет, 2010
ПЕРЕДМОВА ДЛЯ УЧНІВ
Ви починаєте вивчати новий предмет «Алгебра і початки аналізу
», який об’єднує матеріал кількох галузей математичної науки. Як і в курсі алгебри, значну увагу буде приділено перетворенням виразів, розв’язуванню рівнянь, нерівностей та їх систем і розгляду властивостей функцій. Поряд із розв’язуванням знайомих задач, пов’язаних з многочленами, раціональними дробами, степенями і коренями, у 10 класі буде розглянуто нові види функцій: степеневі й тригонометричні та відповідні рівняння і нерівності.
Принципово нова частина курсу — початки аналізу — буде розглядатися в 11–12 класах. Математичний аналіз
(або просто аналіз) — галузь математики, сформована у XVIII ст., що відіграла значну роль у розвитку природознавства: з’явився потужний, достатньо універсальний метод дослідження функцій, які виникають під час розв’язування різноманітних прикладних задач.
Кілька зауважень про те, як користуватися підручником.
Система навчального матеріалу підручника з кожної теми представлена на двох рівнях. Основний матеріал
наведено в параграфах, номери яких позначено синім кольором. Додатковий матеріал
(номери параграфів позначено сірим кольором) призначений для оволодіння темою на більш глибокому рівні (наприклад, для виконання складніших завдань з алгебри і початків аналізу зовнішнього незалежного оцінювання з математики). Учень може опановувати його самостійно чи під керівниц твом учителя.
На початку багатьох параграфів наведено довідкові таблиці
, які містять основні означення, властивості та орієнтири
для пошуку плану розв’язування задач з теми. Для ознайомлення з основними ідеями розв’язування задач наводяться приклади, у яких, крім самого розв’язання, міститься також коментар
, що допоможе скласти план розв’язування аналогічного завдання.
З метою закріплення, контролю і самоконтролю засвоєння навчального матеріалу після кожного параграфа запропоновано систему запитань і вправ. Відповіді на ці запитання і приклади розв’язування аналогічних вправ можна знайти в тексті параграфа. Систему вправ до основного матеріалу подана на трьох рівнях. Задачі середнього рівня
позначено символом «°», дещо складніші задачі достатнього рівня
подано без позначень, а задачі високого рівня
складності позначено символом «*». У підручнику для багатьох задач поглибленого рівня також пропонуються спеціальні орієнтири, які дають можливість опанувати методи їх розв’язування. Відповіді і вказівки
до більшості вправ наведено у відповідному розділі. Про походження понять, термінів і символів ви зможете дізнатися, прочитавши «Відомості з історії». У кінці підручника наведено довідковий матеріал.
4 ПЕРЕДМОВА
ПЕРЕДМОВА ДЛЯ ВЧИТЕЛЯ
Пропонований підручник спрямовано на реалізацію основних положень концепції профільного навчання в старшій школі, на організацію особистісно-орієнтованого навчання математики. Підручник підготовлено відповідно до чинної програми з алгебри і початків аналізу академічного рівня з урахуванням програми профільного рівня та програми і змісту зовнішнього незалежного оцінювання з математики.
Відзначимо основні відмінності пропонованого підручника від інших підручників з алгебри і початків аналізу. Це дворівневий підручник
, у кожному розділі якого поряд із параграфами, що призначені для оволодіння учнями стандартом математичної освіти на академічному рівні, є систематичний матеріал для організації індивідуальної роботи з учнями, які цікавляться математикою.
Основний матеріал, який повинні засвоїти учні, структуровано у формі довідкових таблиць
на початку параграфа, які містять систематизацію теоретичного матеріалу та способів діяльності
із цим матеріалом у формі спеціальних орієнтирів для розв’язування завдань
. У першу чергу учні повинні засвоїти матеріал, який міститься в таблицях
.

Тому під час пояснення нового матеріалу доцільно працювати з підручником, використовуючи відповідні таблиці та рисунки. Усі потрібні пояснення й обґрунтування теж наведено в підручнику, але кожен учень може вибирати власний рівень ознайомлення із цими обґрунтуван нями.
Підкреслимо, що будь-який підручник з алгебри і початків аналізу повинен забезпечити не тільки ознайомлення учнів з основними алгебраїчними поняттями та їх властивостями (тобто дати можливість формувати в учнів знання з алгебри і початків аналізу), а й формування способів дій із цими поняттями (тобто дати можливість формувати в учнів уміння з алгебри і початків аналізу). Ту систему умов, на яку реально спирається учень при виконанні дії, психологи називають орієнтовною основою дії. Якщо учням пропонують достатньо загальні орієнтовні основи для розв’язування відповідних завдань у вигляді спеціальних правил та алгоритмів, то кажуть, що їм пропонують орієнтовні основи другого і третього типів. Як правило, у підручниках алгебри і початків аналізу для 10 класів учням пропонуються тільки зразки розв’язувань завдань. Учні приступають до самостійної діяльності, орієнтуючись на ці зразки (тобто учням пропонуються орієнтовні основи першого типу). Таке навчання передбачає, що учень самостійно виконає систематизацію та узагальнення способів дій, орієнтуючись на запропоновані зразки, і виділить для себе орієнтовну основу розв’язування розглянутих завдань. Як правило, у цьому випадку орієнтовна основа, що створюється в учня, неповна, і, крім того, вона часто не усвідомлена ним, бо учень не може пояс-
ПЕРЕДМОВА 5
нити, чому він виконував саме такі перетворення під час розв’язування завдан ня, а не інші.
Із цієї причини одним з принципів побудови нашого підручника було виділення для учнів орієнтовних основ відповідної діяльності з розв’язування алгебраїчних завдань безпосередньо в підручнику.
У кожному розділі розв’язанню вправ передує виділення загальних орієнтирів для розв’язування таких завдань. Тому важливою складовою роботи за пропонованим підручником є обговорення вибору відповідних орієнтирів та планів розв’язування завдань. Пояснення методів розв’язування ведеться за схемою:
| Р о з в ’ я з а н н я
|
К о м е н т а р
|
За умови такої подачі навчального матеріалу коментар, у якому пояснюється розв’язання, не заважає сприйняттю основної ідеї та плану розв’язування завдань певного типу. Це дозволяє учневі, який уже засвоїв спосіб розв’язування, за допомогою наведеного прикладу згадати, як розв’язувати завдання, а учневі, якому потрібна консультація з розв’язування, — отримати детальну консультацію, що міститься в коментарі. За рахунок чіткого виділення загальних орієнтирів роботи з практичними завданнями курсу вдається частину «нестандартних» (з точки зору традиційних підручників) завдань перевести в розряд «стандартних» (наприклад, рівняння, для розв’язування яких доводиться використовувати властивості функцій). Це дозволяє, зокрема, ознайомити учнів з методами розв’язування навіть складних завдань з алгебри і початків аналізу, які пропонуються в зовнішньому незалежному оцінюванні з математики, та з оформленням їх розв’язання.
Умовні позначення
| 
|
головне в навчальному матеріалі
|
| u
|
початок розв’язання задачі
|
| v
|
закінчення розв’язання задачі
|
|
|
початок обґрунтування твердження
|
| -
|
закінчення обґрунтування твердження
|
6 ПЕРЕДМОВА
Позначення, які застосовано в підручнику
множина всіх нату- модуль (абсолютна ве-
N
— | x |
— личина) числа x
ральних чисел множина всіх цілих
Z
— [x
] — ціла частина числа x
чисел
{x
} — дробова частина числа x
множина всіх невід’-
Z
0
— значення функції f
єм них цілих чисел f
(x
) —
у точці x
область визначення D
(f
) —
множина всіх раціо- функції f
Q
—
нальних чисел область значень функ-
E
(f
) — ції f
множина всіх дійсних sin — функція синус
R
—
чисел, числова пряма cos — функція косинус множина всіх додат- tg — функція тангенс
R
+
—

них дійсних чисел ctg — функція котангенс відрізок (замкнений arcsin — функція арксинус
[a
; b
] — проміжок) з кінцями a
і b,
a
< b
arccos — функція арккосинус
інтервал (відкритий arctg — функція арктангенс
(a
; b
) — проміжок) з кінцями a
і b,
a
< b
arcctg — функція арккотангенс напіввідкриті проміж-
(a
; b
],
— ки з кінцями a
і
b,
— арифметичний корінь із
[a
; b
) a
<
b
числа a
арифметичний корінь
(a
; +∞),— 2k-
го степеня із числа a
[a
; +∞), (k
∈ N
)
— нескінченні проміжки
(–∞; b
], арифметичний корінь
(–∞; b
)— 2k-
го степеня із числа a
(k
∈ N
)
 нескінченний промі- 2 1k
+—
корінь (2k
+1)-
го степе- нескінченний промі- 2 1k
+—
корінь (2k
+1)-
го степе-
(–∞; +∞) —
жок, числова пряманя із числа a
(k
∈ N
)
Розділ 1. ФУНКЦІЇ, РІВНЯННЯ І НЕРІВНОСТІ
ОСНОВНИЙ МАТЕРІАЛ
§ 1. Множини
§ 2. Функції
§ 3. Рівняння
§ 4. Нерівності
ДОДАТКОВИЙ МАТЕРІАЛ
§ 5. Графіки рівнянь та нерівностей з двома змінними
§ 6. Метод математичної індукції
§ 7. Многочлени від однієї змінної та дії над ними
§ 8. Рівняння і нерівності, що містять знак модуля
§ 9. Рівняння і нерівності з параметрами
В основній частині
цього розділу ви систематизуєте та узагальните свої знання й уміння, пов’язані з множинами, функціями, рівняннями і нерівностями, уточните, як досліджують і обґрунтовують основні характеристики функцій. Також ви отримаєте рекомендації щодо розв’язування рівнянь та нерівностей різними методами.
У додатковій частині
розділу учні, які бажають узнати більше, зможуть ознайомитися з важливим методом доведення математичних тверджень (методом математичної індукції) та з методами розв’язування деяких складних завдань, що їх пропонують, наприклад, у завданнях зовнішнього незалежного оцінювання чи державної підсумкової атестації з математики (це, у першу чергу, методи розв’язування рівнянь і нерівностей з модулями і параметрами, знаходження цілих коренів многочленів із цілими коефіцієнтами, побудова графіків рівнянь і нерівностей із двома змінними).
Розділ
 Функції, рівняння
1 Функції, рівняння
1
і нерівності
МНОЖИНИ
1.1. Множини та операції над ними
Таблиця 1
| Поняття множини та її елементів
|
| 
|
Множину можна уявити собі як сукупність деяких об’єктів, що об’єднані за якоюсь ознакою. У математиці множини — це одне з основних неозначуваних понять.
Кожний об’єкт, що входить до множини А,
називається елементом
цієї множини
.
Множина, що не містить жодного елемента, називається порожньою
множиною і позначається ∅
|
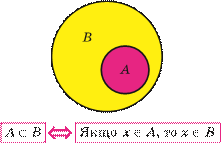
| Підмножина (⊂)
|
| 
|
Якщо кожен елемент однієї множини A
є елементом другої множини B
, то кажуть, що перша множина A
є підмножиною другої множини B
і записують так: A
⊂ B
.
Використовують також запис A
⊆ B
, якщо множина A
або є підмножиною множини B
, або дорівнює множині B
|
| Рівність множин
|
| A B
= ⇔x A
x B
∈ ⇒∈ ⇒x A
x B
∈∈
|
Дві множини називаються рівними
, якщо кожний елемент першої множини є елементом другої множини, і навпаки, кожний елемент другої множини є елементом першої множини
|
§ 1. Множини
Продовження табл. 1
| Переріз множин (Ç)
|
| 
|
Перерізом множин
А
і В
називають їх спільну частину, тобто множину C
всіх елементів, що належать як множині А,
так і множині В
|
| Об’єднання множин (È)
|
| 
|
Об’єднанням множин
А
і В
називають множину C
, складену з усіх елементів, що належать хоча б одній із цих множин (А або
В
)
|
| Різниця множин (\)
|
| 
|
Різницею множин
А
і В
називається множина C
, яка складається з усіх елементів, які належать множині А
і не належать множині В
|
| Доповнення множин
|
| 
|
Якщо всі множини, які ми розглядаємо, є підмножинами якоїсь так званої універсальної
множини U
, то різниця U
\ A
називається доповненням множини A
. Тобто доповненням множини
A
називається множина, яка складається з усіх елементів, які не належать множині А
(але які належать універсальній множині U
)
|
 Пояснення й обґрунтування Пояснення й обґрунтування
1. Поняття множини.
Одним з основних понять, які використовують у математиці, є поняття множини.
Для нього не дають означення. Можна пояснити, що множиною
називають довільну сукупність об’єктів, а самі об’єкти — елементами
даної множини
. Так, можна говорити про множину учнів у класі (елементи — учні), множину днів тижня (елементи — дні тижня), множину натуральних дільників числа 6 (елементи — числа 1, 2, 3, 6) тощо.
У курсах алгебри та алгебри і початків аналізу найчастіше розглядають множини, елементами яких є числа, і тому їх називають числовими множинами
.
Як правило, множини позначають великими літерами латинського алфавіту. Наприклад, якщо множина М
складається із чисел 1; 2; 3, то її позначають так: М
= {1; 2; 3}. Той факт, що число 2 входить до цієї множини (є елементом даної множини М
), записують за допомогою спеціального значка ∈ так: 2 ∈ М
; а те, що число 5 не входить до цієї множини (не є елементом даної множини), записують так: 5 ∉ М
.
Можна розглядати також множину, яка не містить жодного елемента, — порожню множину
.
Наприклад, множина простих дільників числа 1 — порожня множина.
Для деяких множин існують спеціальні позначення. Так, порожню множину позначають символом ∅, множину всіх натуральних чисел — літерою N
, множину всіх цілих чисел — літерою Z
, множину всіх раціональних чисел — літерою Q
, а множину всіх дійсних чисел — літерою R
.
Множини бувають скінченні
і нескінченні
залежно від того, яку кількість елементів вони містять. Так, множини А
= {7}; M
= {1; 2; 3} — скінченні, бо містять скінченне число елементів, а множини N
, Z
, Q
, R
— нескінченні.
Множини задають або за допомогою переліку їх елементів (це можна зробити лише для скінченних множин), або за допомогою опису, коли задається правило — характеристична властивість
, яке дозволяє визначити, належить чи ні даний об’єкт розглядуваній множині. Наприклад, множина А
= {–1; 0; 1} задана переліком елементів, а множина B
парних цілих чисел — характеристичною властивістю елементів множини. Останню множину інколи записують так: B
= {b
| b
— парне ціле число} або так: B
= {b
| b
= 2m
, де m
∈ Z
} — тут після вертикальної риски записана характеристична властивість.
У загальному вигляді запис множини за допомогою характеристичної властивості можна подати так: A
= {x
| P
(x
)}, де P
(x
) — характеристична властивість. Наприклад,{x
| x
2
– 1 = 0} = {–1, 1}, {x
| x
∈ R
і x
2
+ 1 = 0} = ∅.
2.
Рівність множин.
Нехай А
— множина цифр трицифрового числа 312, тобто A
= {3; 1; 2}, а B
— множина натуральних чисел, менших від 4, тобто B
= {1; 2; 3}. Оскільки ці множини складаються з одних і тих самих елементів, то їх вважають рівними. Це записують так: A
= B
. Для нескінченних множин таким способом (порівнюючи всі елементи) установити їх рівність неможливо. Тому в загальному випадку рівність множин означають таким чином.
Дві множини називаються рівними
, якщо кожний елемент першої множини є елементом другої множини і, навпаки, кожний елемент другої множини є елементом першої множини.
З наведеного означення рівності множин випливає, що в множині однакові елементи не розрізняються. Дійсно, наприклад, {1; 2; 2} = {1; 2}, оскільки кожний елемент першої множини (1 або 2) є елементом другої множини і, навпаки, кожний елемент другої множини (1 або 2) є елементом першої. Тому, записуючи множину, найчастіше кожний її елемент записують тільки один раз.
3.
Підмножина
Якщо кожен елемент однієї множини A
є елементом другої множини B
, то кажуть, що перша множина A
є підмножиною
другої множини B
,
і записують так: A
⊂ B
. Наприклад, {1; 2} ⊂ {0; 1; 2; 3}, N
⊂ Z
(оскільки
будь-яке натуральне число — ціле), Z
⊂ Q
(оскільки будь-яке ціле число — раціональне), Q
⊂ R
(оскільки будь-яке раціональне число — дійсне).
Вважають, що завжди ∅ ⊂ A
, тобто порожня множина є підмножиною будь-якої непорожньої множини.
Інколи замість запису A
⊂ B
використовують також запис A
⊆ B
, якщо множина A
або є підмножиною множини B
, або дорівнює множині B
. Наприклад, A
⊆ A
.
Співставимо означення рівності множин з означенням підмножини. Якщо множини А
і В
рівні, то: 1) кожний елемент множини А
є елементом множини B
, отже, А
— підмножина В
(A
⊆ B
); 2) кожний елемент множини В
є елементом множини А
, отже, В
— підмножина А
(B
⊆ A
).
 Таким чином, дві множини рівні, якщо кожна з них є підмножиною іншої. Таким чином, дві множини рівні, якщо кожна з них є підмножиною іншої.
Інколи співвідношення між множинами зручно ілюструвати за допомогою кругів (які часто називають кругами Ейлера—Венна). Наприклад, рисунок 1 ілюструє означення підмножини, а рисунок 2 — співвідношення між множинами N, Z, Q, R.
Рис. 1
 4. Операції над множинами.
Над множинами можна виконувати певні дії: переріз, об’єднання, знаходження різниці множин. Дамо означення цих операцій і проілюструємо їх за допомогою кругів Ейлера—Венна. 4. Операції над множинами.
Над множинами можна виконувати певні дії: переріз, об’єднання, знаходження різниці множин. Дамо означення цих операцій і проілюструємо їх за допомогою кругів Ейлера—Венна.
Перерізом множин
А
і В
називають їхню спільну частину, тобто множину C
усіх елементів, що належать як множині А
, так
Рис. 2 і множині В.
Переріз множин позначають знаком Ç (на рисунку 3 наведено ілюстрацію означення перерізу множин).
Наприклад, якщо A
= {2; 3; 4}, B
= {0; 2; 4; 6}, то A
Ç B
= {2; 4}. Об’єднанням множин
А
і В
називають множину С
, складену з усіх елементів, що належать хоча б одній із цих множин (А або В
).
Об’єднання множин позначають знаком È (на рисунку 4 наведено ілюстрацію означення об’єднання множин).
Наприклад, для множин A
і B
з попереднього прикладу A
È B
= {0; 2; 3; 4; 6}.
Якщо позначити множину ірраціональних чисел через M
, то M
È Q
= R
. Різницею множин
А
і В
називається множина С
, яка складається з усіх елементів, які належать множині А
і не належать множині В.
Різницю множин позначають знаком \ (на рисунку 5 наведено ілстрацію означення різниці множин).

Наприклад, якщо A
= {1; 2; 3}, B
= {2; 3; 4; 5}, то A
\ B
= {1}, а B \
A
= {4; 5}.
Якщо B
— підмножина A
, то різницю A
\ B
називають доповненням множини
B
до множини A
(рис. 6).
Наприклад, якщо знову позначити множину ірраціональних чисел через M
, то R
\ Q
= M
: кажуть, що множина M
ірраціональних чисел доповнює множину Q
раціональних чисел до множини R
усіх дійсних чисел.
Якщо всі множини, які ми розглядаємо, є підмножинами якоїсь так званої універсальної множини
U
(на рисунку її зазвичай зображають у вигляді прямокутника, а всі інші множини зображують кругами всередині цього прямокутника), то різницю U \ A
називають доповненням множини A
(рис. 7). Тобто доповненням множини
A
називається множина, яка складається з усіх елементів, які не належать множині А
,
але які належать універсальній множині U
.
 Доповнення множини А
позначають A
(читають: «А
з рискою» або «доповнення А
»). Доповнення множини А
позначають A
(читають: «А
з рискою» або «доповнення А
»).
Наприклад, якщо U
= R
і A
= [0; 1], то A
= −( ∞;0)Ÿ(1;+∞). (Для цього прикладу зручно використати традиційну ілюстрацію множини дійсних чисел на числовій прямій — рис. 8).

Рис. 6 Рис. 7 Рис. 8
 Запитання для контролю Запитання для контролю
| 1.
|
Наведіть приклади множин, укажіть декілька елементів кожної множини.
|
| 2.
|
Як позначають порожню множину, множини натуральних, цілих, раціональних, дійсних чисел?
|
| 3.
|
Дайте означення рівності множин. Наведіть приклади двох рівних множин.
|
| 4.
|
Дайте означення підмножини. Наведіть приклади. Проілюструйте це поняття за допомогою кругів Ейлера—Венна.
|
| 5.
|
Дайте означення перерізу, об’єднання, різниці двох множин. Наведіть приклади. Проілюструйте за допомогою кругів Ейлера—Венна.
|
| 6.
|
Поясніть, що називають доповненням однієї множини до іншої. Доповненням множини? Наведіть приклади. Проілюструйте ці поняття за допомогою відповідних рисунків.
|
 Вправи Вправи
1°.
Запишіть за допомогою фігурних дужок множину:
1) букв у слові «алгебра»; 2) парних однозначних натуральних чисел; 3) непарних однозначних натуральних чисел; 4) однозначних простих чисел.
2°.
За якою характеристичною властивістю записані такі множини:
1) {понеділок, вівторок, середа, четвер, п’ятниця, субота, неділя};
2) {січень, лютий, березень, квітень, травень, червень, липень, серпень, вересень, жовтень, листопад, грудень};
3) {Австралія, Азія, Америка, Антарктида, Африка, Європа}; 4) {до, ре, мі, фа, соль, ля, сі}; 5) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
3°.
Наведіть приклади порожніх множин.
4°.
А
— множина натуральних чисел, які розміщені між числами 15 і 35. Запишіть множину А
за допомогою фігурних дужок. Які з чисел 18, 28, 36, 40 належать множині А
? Відповідь запишіть за допомогою знаків ∈ і ∉.
5°.
Запишіть за допомогою фігурних дужок і позначте множину:
1) натуральних дільників числа 12;
2) натуральних дільників числа 30;
3) цілих дільників числа 6; 4) простих дільників числа 12.
6°.
Відомо, що M
= {1; 2; 5}, N
= {1; 4; 5; 7; 9}, K
= {4; 7; 9}. Запишіть за допомогою фігурних дужок або знака ∅:
1) переріз M
і N
; 2) переріз M
і K
; 3) переріз N
і K
; 4) об’єднання M
і N
; 5) об’єднання M
і K
; 6) об’єднання N
і K
; 7) різницю M
і N
; 8) різницю M
і K
; 9) різницю N
і K
; 10) доповнення K
до N
.
7°.
Поясніть, чому виконуються такі рівності:
1) А
È ∅ = А
; 2) A
È А
= A
; 3) А
Ç ∅ = ∅; 4) A
Ç А
= A
.
8°.
Запишіть множину всіх двоцифрових чисел, які можна записати за допомогою цифр 0, 1, 3.
9°.
Відомо, що А
— множина натуральних дільників числа 12, а В
— множина цілих дільників числа 6. Запишіть множини:
1) А
È В
; 2) А
Ç В
; 3) А \ В
; 4) В \ А
.
10
*
.
Нехай А
і В
— деякі множини. Доведіть указані рівності та проілюструйте їх за допомогою кругів Ейлера—Венна: 1) А
È В
= В
È А
— переставний закон для об’єднання
; 2) А
Ç В
= В
Ç А
— переставний закон для перерізу
.
11.
В одній множині 40 різних елементів, а в другій — 30. Скільки елементів може бути в їх: 1) перерізі; 2) об’єднанні.
12
*
.
Нехай А
, В
, С
— деякі множини. Доведіть указані рівності та проілюструйте їх за допомогою кругів Ейлера–Венна:
1) (А
È В
) È С
= А
È (В
È С
) — сполучний закон для об’єднання
;
2) (А
Ç В
) Ç С
= А
Ç (В
Ç С
) — сполучний закон для перерізу
;
3) А
Ç (В
È С
) = (А
Ç В
) È (А
Ç С
) 4) А
È (В
Ç С
) = (А
È В
) Ç (А
È С
)
5)  A B
Ÿ =A B A B
Ÿ =A B
— закони де Моргана
.
6) A B
=A B
Ÿ
13.
Кожний учень у класі вивчає англійську або французьку мову. Англійську мову вивчають 25 учнів, французьку — 27 учнів, а обидві мови — 18 учнів. Скільки учнів у класі?
14
*
.
Частина жителів міста вміє розмовляти тільки українською мовою, частина — тільки російською, а частина — обома мовами. Українською мовою розмовляє 95 % жителів, а російською — 85 %. Скільки відсотків жителів міста розмовляє обома мовами?
15
*
.
Доведіть рівності і проілюструйте їх за допомогою кругів Ейлера– Венна:
1) А
\ В
= А
\ (А
Ç В
); 2) A
Ç (В
\ С
) = (А
Ç В
) \ (А
Ç С
).
16
*
.
Запишіть множину всіх правильних дробів a
, де a
∈ A
, b
∈ B
b
і A
= {2; 3; 4; 6}, B
= {1; 3; 4; 5; 6}.
17
*
.
Які трицифрові числа можна записати, якщо: А
= {3; 1; 2} — множина цифр для позначення сотень; В
= {2; 8} — множина цифр для позначення десятків; С
= {5; 7} — множина цифр для позначення одиниць.
Скільки таких чисел одержимо? Спробуйте сформулювати загальне правило підрахунку кількості таких чисел, якщо в множині А
— т
елементів (О
∉ А
), у множині В
— п
елементів, у множині С
— k
елементів.
1.2. Числові множини. Множина дійсних чисел

Продовження табл. 2
| 2. Модуль дійсного числа та його властивості
|
| Означення
|
Геометричний зміст модуля
|
| Модулем
додатного числа називається саме це число, модулем від’ємного числа називається число, йому протилежне, модуль нуля дорівнює нулю.
 a
ïðè a
> 0, a
=
0 ïðè a
= 0, a
ïðè a
> 0, a
=
0 ïðè a
= 0,
−a
ïðè a
< 0
|
 , b OB
= , b OB
=
| a
– b
| = AB
На координатній прямій модуль — це відстань від початку координат до точки, що зображує дане число
Модуль різниці двох чисел a і b — це відстань між точками a і b на координатній прямій.
|
| Властивості
|
| 1. | a
| l 0 Модуль будь-якого числа — невід’ємне число
|
| 2. | –a
| = | a
| Модулі протилежних чисел рівні
|
| 3. a
m | a
| , тобто –| a
| m a
m | a
| Величина числа не перевищує величини його модуля
|
| 4.  При b
> 0 | a
| m b
⇔ –b
m a
m b При b
> 0 | a
| m b
⇔ –b
m a
m b
5. При b
> 0 | a
| l b
⇔ a
m –b
або a
l b
|
| 6. |
a
æ
b
|
=
|
a
|
æ
|
b
|
Модуль добутку дорівнює добутку модулів множників
|
|  Модуль дробу дорівнює модулю чисельника, Модуль дробу дорівнює модулю чисельника,
7.поділеному на модуль знаменника
(якщо
знаменник не дорівнює нулю)
|
| 8. | a
n
| = | a |
n
| a
| 2
= a
2
| a
|2k
= a
2k
|
| | a + b
| m | a
| + | b
| Модуль суми не пере-
9. вищує суми модулів
| a
1
+ a
2
+ ... + a
n
| m | a
1
| + | a
2
| + ... + | a
n
| доданків
|
| 10. || a
| – | b
|| m | a
ä b
| m | a
| + | b
|
|
 Пояснення й обґрунтування Пояснення й обґрунтування
1. Числові множини.
У курсі математики ви зустрічалися з різними числами: натуральними, цілими, раціональними, ірраціональними, дійсними. Уявлення про числа у людства складалися поступово, під впливом вимог практики. Наприклад, натуральні числа
з’явилися у зв’язку з необхідністю підрахунку предметів. Але для того щоб дати відповідь на запитання «Скільки сірників у порожній коробці з-під сірників?», множини натуральних чисел N
= {1; 2; 3; ...} недостатньо — для цього потрібно мати ще й число нуль. Приєднуючи до множини N
натуральних чисел число 0, одержуємо множину невід’ємних цілих чисел
. Її часто позначають Z
0
= {0; 1; 2; 3; ...}. Одних тільки невід’ємних цілих чисел виявилося недостатньо для розв’язування задач практики (а отже, і математичних задач, що відображують задану реальну ситуацію). Так, для того щоб охарактеризувати температуру повітря вище і нижче нуля чи рух тіла в протилежних напрямках, потрібні протилежні до натуральних числа, тобто від’ємні числа
. Для натурального числа n
протилежним вважають число –n
, а для числа –n
протилежним вважають число n
. Нуль вважають числом, протилежним самому собі.
Натуральні числа, числа, протилежні натуральним, і число нуль складають множину Z
цілих чисел
.
Вимірювання величин привело до необхідності розширення множини цілих чисел і введення раціональних чисел
. Наприклад, середня багаторічна температура повітря в січні місяці в м. Харкові складає –7,3 °С, тривалість уроку — 45 хв, або  год. год.
Таким чином, вибираючи якусь одиницю виміру, ми одержуємо числове значення величин, що можна виразити за допомогою різних раціональних чисел — цілих і дробових, додатних і від’ємних.
Цілі і дробові числа складають множину Q
раціональних чисел
.
m
, де Будь-яке раціональне число можна записати у вигляді дробу n m
∈ Z
, n
∈ N
(тобто чисельник m
є цілим числом, а знаменник n
— натуральним).
Раціональне число можна записати різними дробами. Наприклад,
 = = = =  = =  , − = , − =  −
= = −
= = − −
 , 1 2, = = , 1 2, = =  = =  , 5 = = , 5 = =  = =  . .
Як видно з наведених прикладів, серед дробів, що зображують дане раціональне число, завжди є єдиний нескоротний дріб (для цілих чисел — це дріб, знаменник якого дорівнює 1).
Зауважимо, що раціональне число, записане у вигляді дробу m
, де m
∈ Z
, n
∈ N
, можна записати також у вигляді скінченного або
n
нескінченного періодичного десяткового дробу, поділивши чисельник на знаменник. Наприклад,  = 0 75, , = 0 75, ,  = 0,3333.... = 0,3333....
Домовимося, що скінченний десятковий дріб можна зображувати у вигляді нескінченного, у якого після останнього десяткового знака, відмінного від нуля, на місці наступних десяткових знаків записують нулі, наприклад,  = 0 75, = 0,75000.... = 0 75, = 0,75000....
Цілі числа також домовимося записувати у вигляді нескінченного десяткового дробу, у якого справа від коми на місці десяткових знаків стоять нулі, наприклад, 13 = 13,000... . Таким чином, будь-яке раціональне число може бути записане як нескінченний періодичний дріб. Нагадаємо, що у нескінченного періодичного дробу, починаючи з деякого місця, усі десяткові знаки починають повторюватися. Групу цифр, що повторюється, називають періодом дробу
; у записі дробу період наводять у дужках. Наприклад,  = 0,3333...= 0 3,( ), = 0,3333...= 0 3,( ),  = 0 136363636, ...= 0 1 36, ( ). = 0 136363636, ...= 0 1 36, ( ).
Отже, кожне раціональне число може бути записане у вигляді нескінченного періодичного десяткового дробу і, навпаки, кожний нескінченний періодичний десятковий дріб задає раціональне число
.
Зауважимо, що будь-який періодичний десятковий дріб, який має своїм періодом дев’ятку, дорівнює нескінченному десятковому дробу з періодом нуль, у якого десятковий розряд, що передує періоду, збільшений на одиницю порівняно з відповідним розрядом першого дробу. Наприклад, нескінченні періодичні дроби 0,2(9) і 0,3(0) є записом одного й того самого раціонального числа  . Дійсно, ураховуючи, що сума нескінченно спадної геометричної прогресії з першим членом a
1
і знамен- . Дійсно, ураховуючи, що сума нескінченно спадної геометричної прогресії з першим членом a
1
і знамен-
ником q
обчислюється за формулою S
=  a
1
, маємо a
1
, маємо
1−q
0 2, (9) = 0,2999...= 0 2, +  + +  + +  +...= 0 2, + +...= 0 2, +   = 0,2+ = = 0,2+ = 0,3 = 0, (3 0). 0,3 = 0, (3 0).
1−
У подальшому, записуючи раціональні числа за допомогою нескінченних періодичних десяткових дробів, домовимося не розглядати нескінченні періодичні дроби, період яких дорівнює дев’яти.
 Кожне раціональне число можна зобразити точкою на координатній прямій (тобто на прямій, на якій вибрано початок відліку, додатний напрям і одиницю виміру). Наприклад, на рисунку 9 зображено декілька раці- Кожне раціональне число можна зобразити точкою на координатній прямій (тобто на прямій, на якій вибрано початок відліку, додатний напрям і одиницю виміру). Наприклад, на рисунку 9 зображено декілька раці-  ональних чисел (0 1; ;−; ,2 5). ональних чисел (0 1; ;−; ,2 5).
Рис. 9
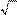  Але на координатній прямій розташовані точки, які зображають числа, що не є раціональними. Наприклад, з курсу алгебри відомо, що число 2 не є раціональним. Це так зване ірраціональне число. Якщо побудувати квадрат із стороною, рівною 1, на координатній прямій х Але на координатній прямій розташовані точки, які зображають числа, що не є раціональними. Наприклад, з курсу алгебри відомо, що число 2 не є раціональним. Це так зване ірраціональне число. Якщо побудувати квадрат із стороною, рівною 1, на координатній прямій х
(рис. 10), то його діагональ дорівнюватиме 2. Тоді, провівши дугу кола із центром
 Рис. 10 у точці O
і радіусом OM
= 2, одержимо Рис. 10 у точці O
і радіусом OM
= 2, одержимо
 точку M
, координата якої дорівнює 2. Крім числа 2, ви також зустрічалися з ірраціональними числами 3, 10 тощо. точку M
, координата якої дорівнює 2. Крім числа 2, ви також зустрічалися з ірраціональними числами 3, 10 тощо.
Раціональні та ірраціональні числа складають множину
дійсних чисел
R
. На координатній прямій кожному дійсному числу відповідає єдина точка, і навпаки, кожній точці координатної прямої відповідає єдине дійсне число (у такому разі кажуть, що між множиною дійсних чисел і множиною точок координатної прямої встановлюється взаємно однозначна відповідність).
Кожне дійсне число можна записати у вигляді нескінченного десяткового дробу: раціональні числа — у вигляді нескінченного періодичного десяткового дробу, а ірраціональні — у вигляді нескінченного неперіодичного десяткового дробу.
 Нагадаємо, що для порівняння дійсних чисел і виконання дій над ними (у випадку, коли хоча б одне з них не є раціональним) використовують наближені значення цих чисел. Зокрема, щоб порівняти два дійсних числа, треба розглянути послідовно їх наближені значення з недостачею з точністю до цілих, десятих, сотих і т. д. до тих пір, поки не одержимо якесь наближене значення одного числа, більше за відповідне наближене значення другого. Тоді те число, у якого наближене значення більше, і вважається більшим
. Наприклад, якщо α= 3 =1 7320508, ..., β=1 Нагадаємо, що для порівняння дійсних чисел і виконання дій над ними (у випадку, коли хоча б одне з них не є раціональним) використовують наближені значення цих чисел. Зокрема, щоб порівняти два дійсних числа, треба розглянути послідовно їх наближені значення з недостачею з точністю до цілих, десятих, сотих і т. д. до тих пір, поки не одержимо якесь наближене значення одного числа, більше за відповідне наближене значення другого. Тоді те число, у якого наближене значення більше, і вважається більшим
. Наприклад, якщо α= 3 =1 7320508, ..., β=1 =1 7500000, ..., то α < β (оскільки =1 7500000, ..., то α < β (оскільки
1,73 < 1,75).
Для того щоб виконати додавання чи множення розглянутих чисел α і β, послідовно записують їх наближені значення з недостачею та з надлишком (з точністю до цілих, десятих, сотих і т. д.) і виконують дії над одержаними раціональними числами. У результаті послідовно отримуємо значення суми чи добутку з потрібною точністю.
| α
|
β
|
α + β
|
αβ
|
| 1 < α < 2
|
1 < β < 2
|
2 < α + β < 4
|
1 < αβ < 4
|
| 1,7 < α < 1,8
|
1,7 < β < 1,8
|
3,4 < α + β < 3,6
|
2,89 < αβ < 3,24
|
| 1,73 < α < 1,74
|
1,75 < β < 1,76
|
3,48 < α + β < 3,50
|
3,0275 < αβ < 3,0624
|
| 1,732 < α < 1,733
|
1,750 < β < 1,751
|
3,482 < α + β < 3,484
|
3,031 < αβ < 3,034483
|
| ...
|
...
|
...
|
...
|
Як бачимо, α + β = 3,48..., αβ = 3,03... .
У курсі математичного аналізу доводиться, що у випадку, коли наближені значення чисел α і β послідовно беруть з точністю до цілих, десятих, сотих і т. д., то значення суми α + β з недостачею і з надлишком прямує до одного і того самого числа, яке і приймають за значення суми α + β (аналогічно означають і добуток αβ).
2. Модуль дійсного числа та його властивості.
Нагадаємо означення модуля.
Модулем
додатного числа називається саме це число, модулем від’ємного числа — число, йому протилежне; модуль нуля дорівнює нулю.
   Це означення можна коротко записати декількома способами. a
ïðè a
> 0, a
=
0− a
ïðè ïðè a
a
=<0,0, або a
=
a
−a
ïðè
ïðè a
a
l
<0
0,
, або r
2
= m
n
22
, або Це означення можна коротко записати декількома способами. a
ïðè a
> 0, a
=
0− a
ïðè ïðè a
a
=<0,0, або a
=
a
−a
ïðè
ïðè a
a
l
<0
0,
, або r
2
= m
n
22
, або
a
ïðè a
l 0,
За потреби ми будемо користуватися будь-яким із −a
ïðè a
m0.
 цих записів означення модуля. Для того щоб знайти | a
|, за означенням необхідно знати знак числа a
і використати відповідну формулу. Наприклад, | 5 | = 5, | –3 | = –(–3) = 3, цих записів означення модуля. Для того щоб знайти | a
|, за означенням необхідно знати знак числа a
і використати відповідну формулу. Наприклад, | 5 | = 5, | –3 | = –(–3) = 3,
На координатній прямій модуль числа — це відстань від початку координат до точки, що зображує це число.
Дійсно, якщо a
> 0 (рис. 11), то відстань
OA
= a
= | a |
. Рис. 11
Якщо b
< 0, то відстань OB
= –b
= | b |
.
 Модуль різниці двох чисел a і b — це відстань між точками a і b на координатній прямій. Модуль різниці двох чисел a і b — це відстань між точками a і b на координатній прямій.
Для доведення можна скористатися тим, що при паралельному перенесенні вздовж осі координат на b
одиниць абсциса відповідної точки змінюється на b
: до абсциси заданої точки додається чис-
 ло b
, тобто при b
> 0 точка переноситься вправо, а при b
< 0 — уліво. Позначимо на координатній прямій числа a
, b
, a –
b
відповідно точками A
, B
, C
. На рисунку 12 ці точки зображено для випадку a
> 0 і b
< 0, хоча наведене далі обґрунту- ло b
, тобто при b
> 0 точка переноситься вправо, а при b
< 0 — уліво. Позначимо на координатній прямій числа a
, b
, a –
b
відповідно точками A
, B
, C
. На рисунку 12 ці точки зображено для випадку a
> 0 і b
< 0, хоча наведене далі обґрунту-
Рис. 12 вання не залежить від знаків a
і b
.
При паралельному перенесенні вздовж
осі Ox
на b
одиниць точка O
перейде в точку B
, а точка C
(з координатою a
– b
) у точку з координатою a
– b
+ b
= a
, тобто в точку A
. Тоді СО
= АВ
. Але відстань CO
— це відстань від точки a
– b
до початку координат, отже, CO
= | a
– b |
, а значить, і AB
= | a
– b
|. -
Використовуючи означення модуля та його геометричний зміст, можна обґрунтувати властивості модуля, наведені в таблиці 2.
Наприклад, ураховуючи, що | a |
— це відстань від точки a
до точки O
, а відстань може виражатися тільки невід’ємним числом, одержуємо
| a |
l 0
,
тобто модуль будь-якого числа є невід’ємне число
.
Ураховуючи, що точки a
і –a
розташовані на однаковій відстані від точки O
, одержуємо
| –a |
= | a |
,
це означає, що модулі протилежних чисел рівні
.
Якщо a
l 0, то | a
| = a
, а якщо a
< 0, то a
< | а |
. Отже, завжди a
m | a |
,
тобто величина числа не перевищує величини його
модуля.
Якщо в останню нерівність замість a
підставити –a
і врахувати, що | –a
| = | a |
, то одержуємо нерівність –a
m | a |
. Звідси a
l –| a |
, що разом із нерівністю a
m | a
| свідчить, що для будь-якого дійсного числа a
виконується подвійна нерівність
– | a |
m a
m | a
|
. (1)
При b
> 0 нерівність | a |
m b
означає, що число a
на координатній прямій розміщене від точки O
на відстані, яка не перевищує b
(рис. 13), тобто в проміжку [–b
; b
]. Навпаки, якщо число a
належить цьому проміжку, тобто –b
m a
m b
, то | a |
m b
. Отже,
при b
> 0 | a |
m b
⇔ –b
m a
m b
. (2)
 Зауважимо, що останнє твердження справедливе і при b
= 0 (тоді обом нерівностям задовольняє тільки одне значення a
= 0). Зауважимо, що останнє твердження справедливе і при b
= 0 (тоді обом нерівностям задовольняє тільки одне значення a
= 0).
Аналогічно при b
> 0 нерівність | a |
l b
означає, що число a
на координатній прямій знаходиться від точки O
на відстані,
яка більша або дорівнює b
(рис. 13), тобто Рис. 13
в цьому випадку a
m –b
або a
l b
. Навпаки, якщо число a
задовольняє одній із цих нерівностей, то | a
| l b
. Отже, при b
> 0 нерівність | a |
l l b
рівносильна сукупності нерівностей a
m –b
або a
l b
, що можна записати так: при b
> 0 | a |
l b
⇔ a
m –b
або a
l b
.
Властивості модуля добутку і модуля дробу фіксують відомі правила дій над числами з однаковими і різними знаками:
модуль добутку дорівнює добутку модулів множників
, тобто
| a
•b
|
= | a
|•| b
|;
 модуль дробу дорівнює модулю чисельника, поділеному на модуль знаменника
(якщо знаменник не дорівнює нулю), тобто a
= a
(b
≠ 0). b b модуль дробу дорівнює модулю чисельника, поділеному на модуль знаменника
(якщо знаменник не дорівнює нулю), тобто a
= a
(b
≠ 0). b b
Формулу для знаходження модуля добутку можна узагальнити для випадку декількох множників:
| a
1
•a
2
•...•a
n
|
= | a
1
|•| a
2
|•...•| a
n
|.
(3)
Якщо у формулі (3) взяти a
1
= a
2
= ... = a
n
= a
, одержуємо формулу
| a
n
| = | a
|
n
.
Застосовуючи останню формулу справа наліво при n
= 2k
і враховуючи, що a
2k
l 0 при всіх значеннях a
, одержуємо | a
|2k
= | a
2k
| = a
2k
.
Отже,
| a
|2k
= a
2k
.
Для обґрунтування нерівності
| a
+ b
| m | a
| + | b
| (4) запишемо нерівність (1) для чисел a
і b
:
–| a
| m a
m | a
|; –| b
| m b
m | b
|.
Додаючи почленно ці нерівності, одержуємо
–(| a
| + | b
|) m a + b
m | a
| + | b
|.
Ураховуючи нерівність (2), маємо
| a
+ b
|
m | a
| + | b
|
,
тобто модуль суми не перевищує суми модулів доданків
.
Якщо в нерівності (4) замінити b
на –b
і врахувати, що | –b
| = | b
|, то одержимо нерівність
| a
– b
| m | a
| + | b
|. (5)
Якщо записати число a
так: a
= b
+ (a – b
) і використати нерівність
(4), то одержимо нерівність | a
| m | b
| + | a
– b
|. Звідси
| a
| – | b
|
m | a
– b
|.
(6)
Якщо в нерівності (6) замінити b
на –b
і врахувати, що | –b
| = | b
|, то одержимо нерівність
| a
| – | b
|
m | a
+ b
|,
(7) тобто модуль суми двох чисел не менше різниці їх модулів.
Міняючи місцями букви a
і b
у нерівностях (6) і (7) та враховуючи, що | a
– b |
= | b
– a
|, маємо також нерівності
| b
| – | a
|
m | a
± b
|.
(8)
Одержані нерівності (4)–(8) можна коротко записати так:
| | a
| – | b | |
m | a
± b
|
m | a
| + | b
|
.
 Приклади розв’язання завдань Приклади розв’язання завдань
Доведіть, що сума, різниця, добуток, натуральний степінь і частка (якщо дільник не дорівнює нулю) двох раціональних чисел завжди є раціональним числом
.
| Розв’язання Коментар
|
|  u Нехай задано два раціональних числа r
1 = mn
11
і r
2 = mn
22 , де m
1 і m
2 — цілі, а n
1
і n
2
— натуральні числа. Оскільки сума, різниця, добуток, натуральний степінь і частка двох звичайних дробів завжди є звичайним дробом, то одержаний результат завжди буде раціональним числом. Наприклад, u Нехай задано два раціональних числа r
1 = mn
11
і r
2 = mn
22 , де m
1 і m
2 — цілі, а n
1
і n
2
— натуральні числа. Оскільки сума, різниця, добуток, натуральний степінь і частка двох звичайних дробів завжди є звичайним дробом, то одержаний результат завжди буде раціональним числом. Наприклад,
m m m n
+n m
 r r
1+ =2 n
11
+ n
22 = 1 2
n n
1 21 2
, r r
1+ =2 n
11
+ n
22 = 1 2
n n
1 21 2
,
де m
1
n
2
+ n
1
m
2
— ціле число, а n
1
n
2
— натуральне.v
|
Будь-яке раціональне число m
можна записати як дріб , де m
— n
ціле, n
— натуральне число. Щоб довести твердження задачі, достатньо довести, що сума, різниця, до-
m
буток і частка двох дробів виду n
буде дробом такого самого виду.
|
 Доведіть, що для будьякого натурального числа n
число
n
або натуральне, або ірраціональне
. Коментар Доведіть, що для будьякого натурального числа n
число
n
або натуральне, або ірраціональне
. Коментар
Для доведення твердження задачі можна використати метод від супротивного: припустити, що задане додатне число є раціональним ненатуральним (тобто дробом), і отримати суперечність з умовою або з якимсь відомим фактом.
 Записуючи n
у вигляді нескоротного дробу, слід ураховувати, що при натуральних значеннях n
це число завжди буде невід’ємним. Розв’язання Записуючи n
у вигляді нескоротного дробу, слід ураховувати, що при натуральних значеннях n
це число завжди буде невід’ємним. Розв’язання
  u Припустимо, що n
не є ірраціональним числом (тоді це число раціональне) і не є натуральним числом. Отже, це число може бути тільки раціональним нескоротним дробом n
= p
, де p
і q
— натуральні числа u Припустимо, що n
не є ірраціональним числом (тоді це число раціональне) і не є натуральним числом. Отже, це число може бути тільки раціональним нескоротним дробом n
= p
, де p
і q
— натуральні числа
q
(q
≠ 1). За означенням кореня m
-го степеня маємо n
= q
p
2
2
, тобто n
=
 q q
p p
i
i
. q q
p p
i
i
.
Ураховуючи, що q
≠ 1, одержуємо, що дріб  p p
i
, який дорівнює натуq q
i p p
i
, який дорівнює натуq q
i
ральному числу n
, повинен бути скоротним. Отже, у натуральних множників, що стоять у чисельнику і знаменнику цього дробу, повинен бути спільний натуральний дільник, який відрізняється від 1. Але в чисельнику стоять тільки множники p
, а в знаменнику — тільки множники q
. Тоді числа p
і q
мають натуральний дільник, який відрізняється від 1,
тобто дріб p
є скоротним дробом, що суперечить умові. Таким чином, q
наше припущення неправильне, і для будь-якого натурального числа n
число n
або натуральне, або ірраціональне.v
  Наприклад, оскільки числа 3 і 10 не є натуральними числами (1< 3 < 2 3, < 10 < 4), то 3 і 10 — ірраціональні числа. Наприклад, оскільки числа 3 і 10 не є натуральними числами (1< 3 < 2 3, < 10 < 4), то 3 і 10 — ірраціональні числа.
  Приклад 3*.
Доведіть, що сума 3 + 5 — число ірраціональне. Приклад 3*.
Доведіть, що сума 3 + 5 — число ірраціональне.
| Розв’язання
|
Коментар
|
| u Припустимо, що число
 3 + 5 =r
— раціональне. Тоді 5 = −r
3. Піднісши обидві частини останньої рівності до квадрата, маємо 5 = −r
2
2r
3 +3. Звідси 3 + 5 =r
— раціональне. Тоді 5 = −r
3. Піднісши обидві частини останньої рівності до квадрата, маємо 5 = −r
2
2r
3 +3. Звідси
2
  2r
3 = −r
2
2. Отже, 3 = r
−
2
. Але 2r
3 = −r
2
2. Отже, 3 = r
−
2
. Але
2r
права частина цієї рівності — раціональне число (оскільки за припущенням r
— раціональне число), а ліва — ірраціональне. Одержана суперечність означає, що наше припущення неправильне і число
 3 + 5 — ірраціональне. v 3 + 5 — ірраціональне. v
|
 Для доведення твердження задачі можна використати метод «від супротивного» припустити, що задане число є раціональним і отримати суперечність з якимсь відомим фактом, наприклад, з тим, що 3 — ірраціональне число. Для доведення твердження задачі можна використати метод «від супротивного» припустити, що задане число є раціональним і отримати суперечність з якимсь відомим фактом, наприклад, з тим, що 3 — ірраціональне число.
Аналізуючи одержані вирази, використовуємо результат прикладу 1: якщо число r — раціональне, то числа r
2
– 2 і 2r та їх частка теж будуть раціональними
.
 Зазначимо, що знаменник отриманого дробу 2r
= 2( 3 + 5) ≠ 0. Зазначимо, що знаменник отриманого дробу 2r
= 2( 3 + 5) ≠ 0.
|
Розв’яжіть рівняння[1]
| 2х
+ 5 | = 7.
u 2х
+ 5 = 7 або 2х
+ 5= –7,
2х
= 2 або 2х
= –12, х
= 1 або х
= –6.
Відповідь:
1; –6. v
 І спосіб І спосіб
Задане рівняння має вигляд
| t
| = 7 (у дано му випадку t
= 2х
+ 5). Його зручно розв’язувати, використовуючи геометричний зміст модуля: | 2х
+ 5 | — це відстань від точки
u 2х
– (–5) | = 7,

2х
= 2 або 2х
= –12, х
= 1 або х
= –6.
Відповідь:
1; –6. v
0 до точки 2х
+ 5. Але відстань 7 може бути відкладена від 0 як праворуч (одержуємо число 7), так і ліворуч (одержуємо число –7). Отже, рівність | 2х
+ 5 | = 7 можлива тоді і тільки тоді, коли 2х
+ 5 = 7 або 2х
+ 5 = –7.
ІІ спосіб
З геометричної точки зору | a
– – b
| — це відстань між точками a
і b
на координатній прямій. Запишемо задане рівняння так: | 2х
– (–5) | = 7. Тоді рівність | 2х
– (–5) | = 7 означає, що відстань від точки 2х
до точки –5 дорівнює 7. На відстані 7 від точки –5 знаходяться точки 2 і –12. Отже, задана рівність виконується тоді і тільки тоді, коли 2х
= 2 або 2х
= –12, тобто задане рівняння рівносильне цій сукупності рівнянь.
Розв’яжіть нерівність | х
2
– 5х
| m 6.
| Розв’язання
|
Коментар
|
| u –6
m х
2
– 5х
m 6,
x
2
−5x
m 6, x
2
−5x
− 6 m0, 2 x
2 −5x
+ 6 l0,
x
−5x
l−6,
(x
+1)(x
−6) m 0,
(x
−2)(x
−6)l 0,
|
Задана нерівність має вигляд
| t
| m 6 (у даному випадку t
= х
2
– 5х
), і її можна розв’язувати, використовуючи геометричний зміст модуля. З геометричної точки зору, | t
| — це відстань від точки 0 до точки t
. На відстані 6 від 0 знаходяться числа 6 і –6.
|
  Тоді нерівності | t
| m 6 задовольняють усі ті і тільки ті точки, які знаходяться в проміжку [–6; 6], тобто 6 m t
m 6. Для розв’язування одержаної подвійної нерівності її зручно Розв’язуючи ці нерівності, отримаємо Тоді нерівності | t
| m 6 задовольняють усі ті і тільки ті точки, які знаходяться в проміжку [–6; 6], тобто 6 m t
m 6. Для розв’язування одержаної подвійної нерівності її зручно Розв’язуючи ці нерівності, отримаємо
−1m x
m6,замінити відповідною системою.
x
m2 àáîx
l3.
Отже, –1 m х
m 2 або 3 m х
m 6. Відповідь:
[–1; 2] È [3; 6] . v
 Запитання для контролю Запитання для контролю
| 1.
|
Поясніть, які числа входять до множин цілих, раціональних та дійсних чисел. Наведіть приклади. Зобразіть відповідні точки на координатній прямій.
|
| 2.
|
Поясніть, чим відрізняються записи у вигляді нескінченного десяткового дробу раціонального та ірраціонального чисел.
|
| 3.
|
Поясніть, як порівнюють дійсні числа.
|
| 4.
|
Дайте означення модуля дійсного числа. а) Сформулюйте властивості модуля. б*
) Обґрунтуйте властивості модуля дійсного числа.
|
 Вправи Вправи
1.
Поясніть, чому задане дійсне число не може бути раціональним:
  1) 1+ 2; 2) 3 −5; 1) 1+ 2; 2) 3 −5;
 3) 10; 4) 7 +3; 5) 2− 5. 3) 10; 4) 7 +3; 5) 2− 5.
2
*
.
Доведіть, що сума (різниця, добуток і частка) раціонального та ірраціонального чисел завжди є число ірраціональне (добуток і частка тільки у випадку, коли задане раціональне число не дорівнює нулю).
3
*
.
Доведіть, що задані дійсні числа є ірраціональними:
  1) 2 + 3; 2) 5 + 2; 1) 2 + 3; 2) 5 + 2;
3) 7 − 3; 4) 7 − 2.
4.
Користуючись геометричним змістом модуля, зобразіть на координатній прямій множину чисел, які задовольняють нерівності:
1°) | х
| m 2; 2°) | х
| > 5; 3) | х
– 3 | m 0,5; 4) | х
+ 1 | < 0,3.
5.
Розв’яжіть рівняння:
1) | 3х
+ 1 | = 4; 2) | 4х
– 2 | = 6;
3*
) | | х
– 1 | – 2 | = 1; 4*
) | | 2х
+ 3 | – 5 | = 3.
6.
Розв’яжіть нерівність:
1) | 2х
– 7 | m 1; 2) | 3х
+ 5 | > 7;
3*
) || 2х
– 1 | + 3 | l 5; 4*
) || 4х
+ 7 | –11 | < 4.
ФУНКЦІЇ
2.1. Поняття числової функції.
Найпростіші властивості числових функцій
Таблиця 3
| 1. Поняття числової функції
|
| 
D E
|
Числовою функцією з областю визначення D
називається залежність, при якій кожному числу x
із множини D
(області визначення) ставиться у відповідність єдине число y
.
Записують цю відповідність так: y
= f
(x
).
Позначення і терміни в
(f
) — область визначення E
(f
) — область значень
x
— аргумент (незалежна змінна) y
— функція (залежна змінна) f
— функція
f
(x
0
) — значення функції f
у точці x
0
|
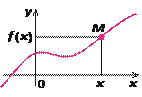
| 2. Графік функції
|
| 
|
Графіком функції f
називається множина всіх точок координатної площини з координатами (x
; f
(x
)),
де перша координата x
«пробігає» всю область визначення функції, а друга координата — це відповідне значення функції f
у точці x
|
| 3. Зростаючі та спадні функції
|
| 
|
Функція f
(x
) зростаюча на множині P
: якщо x
2
> x
1
, то f
(x
2
) > f
(x
1
)
для всіх x
∈ P
(при збільшенні аргументу відповідні точки графіка піднімаються)
|
§ 2. Функції
Продовження табл. 3
| 
|
Функція f
(x
) спадна на множині P
:
якщо x
2
> x
1
, то f
(x
2
) < f
(x
1
)
для всіх x
∈ P
(при збільшенні аргументу відповідні точки графіка опускаються)
|
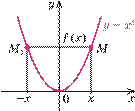
| 4. Парні та непарні функції
|
| 
|
Функція f
(x
) парна:
f
(–x
) = f
(x
)
для всіх x
з області визначення. Графік парної функції симетричний відносно осі Oy
|
| 
|
Функція f
(x
) непарна:
f
(–x
) = –f
(x
)
для всіх x
із області визначення.
Графік непарної функції симетричний відносно початку координат — точки О
|
 Пояснення й обґрунтування Пояснення й обґрунтування
1. Поняття функції.
З поняттям функції ви ознайомилися в курсі алгебри. Нагадаємо, що залежність змінної y
від змінної x
називається функцією
, якщо кожному значенню x
відповідає єдине значення y.
У курсі алгебри і початків аналізу ми будемо користуватися таким означенням числової функції.
Числовою функцією
з областю визначення
D
називається залежність, при якій кожному числу x
із множини D
ставиться у відповідність єдине число y
.
Функції позначають латинськими (інколи грецькими) буквами. Розглянемо довільну функцію f
. Число y
, яке відповідає числу x
(на рисунку 16 це показано стрілкою), називають значенням функції f
у точці x
і позначають f
(x
).
Область визначення функції
f
— це множина тих значень, яких може набувати аргумент x
. Вона позначається D
(f
).
Область значень
функції
f
— це множина, яка складається з усіх чисел f
(x
), де x
належить області визначення. Її позначають E
(f
). Найчастіше функцію задають за допомогою формули. Якщо немає додаткових обмежень, то областю визначення функції, заданої формулою, вважають множину всіх значень змінної, при яких ця формула має зміст
.
 Наприклад, якщо функція задана формулою y
= x
+1, то її область визначення — x
l 0, тобто D
(y
) = [0; +∞), а область значень — y
l 1, тобто E
(y
) = [1; +∞). Наприклад, якщо функція задана формулою y
= x
+1, то її область визначення — x
l 0, тобто D
(y
) = [0; +∞), а область значень — y
l 1, тобто E
(y
) = [1; +∞).
 Іноді функція може задаватися різними формулами на різних множинах значень аргументу. Наприклад, y x
==x
−x
ïðè
ïðèxx
l
<0
0,
. Іноді функція може задаватися різними формулами на різних множинах значень аргументу. Наприклад, y x
==x
−x
ïðè
ïðèxx
l
<0
0,
.
Функцію можна задати не тільки за допомогою формули, а й за допомогою таблиці, графіка чи словесного опису. Наприклад, на рисунку 17 графічно задана функція y
= f
(x
) з областю визначення D
(f
) = [–1; 3] і множиною значень E
(f
) = [1; 4].

Рис. 16 Рис. 17
2.
Графік функції.
Нагадаємо, що графіком функції
y
= f
(x
) називається множина всіх точок координатної площини з координатами (x
; f
(x
)), де перша координата x
«пробігає» всю область визначення функції, а друга координата — це відповідне значення функції f
у точці x
.
На рисунках до пункту 4 таблиці 3 наведено графіки функцій y
= x
2
та y
=1
, а на рисунку 18 — графік функції y
= | x
|.
x
Наведемо також графік функції y
= [x
], де [x
] — позначення цілої частини
числа x
, тобто найбільшого цілого числа, яке не перевищує x
(рис. 19). Область визначення цієї функції D
(y
) = R
— множина всіх дійсних чисел, а область значень E
(y
) = Z
— множина всіх цілих чисел.
§ 2. Функції
  Рис. 18 Рис. 18
На рисунку 20 наведено графік ще однієї числової функції y
= {x
}, де {x
} — позначення дробової частини
числа x
(за означенням {x
} = x
– [x
]).
3.
Зростаючі та спадні функції.
Важ-
ливими характеристиками функцій є їх
зростання та спадання. Рис. 20
Функція f
(x
) називається зростаючою
на множині Р
, якщо більшому значенню аргументу із цієї множини відповідає більше значення функції.
Тобто для будь-яких двох значень x
1
і x
2
з множини Р
, якщо x
2
> x
1
, то f
(x
2
) > f
(x
1
).
Наприклад, функція f
(x
) = 2x
зростаюча (на всій області визначення, тобто на множині R
), оскільки, якщо x
2
> x
1
, то 2x
2
> 2x
1
, отже, f
(x
2
) > f
(x
1
).
Відповідні точки графіка зростаючої функції при збільшенні аргументу піднімаються (рис. 21).

Рис. 21 Рис. 22
На рисунку 22 наведено графік ще однієї зростаючої функції у
= х
3
.
Дійсно, при x
2
> x
1
маємо x
2
3
>x
1
3
, тобто f
(x
2
) > f
(x
1
).
Функція f
(x
) називається спадною на множині
Р
, якщо більшому значенню аргументу із цієї множини відповідає менше значення функції.
Тобто для будь-яких двох значень x
1
і x
2
з множини Р
, якщо x
2
> x
1
, то f
(x
2
) < f
(x
1
).
Наприклад, функція f
(x
) = –2x
спадна (на всій області визначення, тобто на множині R
), оскільки, якщо x
2
> x
1
, то –2x
2
<
–2x
1
, отже, f
(x
2
) < f
(x
1
). Відповідні точки графіка спадної функції при збільшенні аргументу опускаються (рис. 23).

Рис. 23 Рис. 24
Розглядаючи графік функції y
= x
2
(рис. 24), бачимо, що на всій області визначення ця функція не є ні зростаючою, ні спадною. Але можна виділити проміжки області визначення, де ця функція зростає і де спадає. Так, на проміжку [0; +∞) функція y
= x
2
зростає, а на проміжку (–∞; 0] — спадає.
 Зазначимо, що для зростаючих і спадних функцій виконуються властивості, обернені до тверджень, що містяться в означеннях. Якщо функція зростає, то більшому значенню функції відповідає більше значення аргументу. Зазначимо, що для зростаючих і спадних функцій виконуються властивості, обернені до тверджень, що містяться в означеннях. Якщо функція зростає, то більшому значенню функції відповідає більше значення аргументу.
Якщо функція спадає, то більшому значенню функції відповідає менше значення аргументу.
Обґрунтуємо першу із цих властивостей методом від супротивного. Нехай функція f
(x
) зростає і f
(x
2
) > f
(x
1
). Припустимо, що аргумент x
2
не більше аргументу x
1
, тобто x
2
m x
1
. Із цього припущення одержуємо:
якщо x
2
m x
1
і f
(x
) зростає, то f
(x
2
) m f
(x
1
), що суперечить умові f
(x
2
) > f
(x
1
). Отже, наше припущення неправильне і, якщо f
(x
2
) > f
(x
1
), то x
2
> x
1
, що і потрібно було довести.
Аналогічно можна обґрунтувати і другу властивість. -
Наприклад, якщо x
3
> 8, тобто x
3
> 23
, то, ураховуючи зростання функції f
(x
) = x
3
, одержуємо x
> 2.
[1]
Детальніше розв’язування рівнянь і нерівностей з модулями розглянуто у §
8.
|