| Зошит номер Міністерство освіти і науки України
Український центр оцінювання якості освіти
| МАТЕМАТИКА
ЗОВНІШНЄ ОЦІНЮВАННЯ
Час виконання – 135 хвилин
|
Екзаменаційний тест складається з трьох частин, у яких представлено 38 завдань різної форми. Відповіді на завдання Частини 1 та Частини 2 Ви повинні перенести в бланк А
. Розв’язання завдань Частини 3 необхідно записати у бланку Б
. Правила виконання завдань вказано на початку кожної форми завдань.
Інструкція щодо роботи в тестовому зошиті
1.
Відповідайте тільки після того, як Ви уважно прочитали та зрозуміли завдання й правила його виконання.
2.
Використовуйте як чернетку місця, відведені у тестовому зошиті.
3.
Намагайтеся відповісти на всі тестові завдання.
Інструкція щодо заповнення бланків відповідей А і Б
1.
До бланків записуйте лише правильні, на Вашу думку, відповіді.
2.
Відповіді вписуйте чітко, відповідно до інструкцій щодо кожної форми завдань.
3.
Подвійні, неправильно записані, закреслені, підчищені та виправлені відповіді у бланку А
– це ПОМИЛКА!
4.
Якщо Ви записали відповідь неправильно, можете її виправити у відведеному місці на бланку А
.
5.
Виконавши завдання Частини 3, запишіть їх на бланку Б
.
6.
Ваш результат залежатиме від загальної кількості правильних відповідей, записаних до бланка А
, та розв’язання завдань Частини 3.
7.
Перш ніж виконувати завдання, позначте номер Вашого зошита у відповідному місці бланка А
.
Ознайомившись з інструкцією, перевірте якість друку зошита й кількість сторінок. Їх має бути 24.
Зичимо Вам успіху!
|
Частина 1
Завдання 1
–
20 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Виберіть правильну, на Вашу думку, відповідь і позначте її у бланку А.
1.
 Обчисліть 1255
32 −5 Обчисліть 1255
32 −5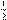 . .
| 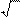 А
11 5 А
11 5
|
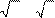 Б
10 2 − 5 Б
10 2 − 5
|
В
9
|
 Г
9 5 Г
9 5
|
 Д
10
4000 − Д
10
4000 −
|

5
|
2.
 Якщо 1
= 1
−1
, то c
= a b c Якщо 1
= 1
−1
, то c
= a b c
| ab
А
 a
−b a
−b
|
ab
Б
 b
−a b
−a
|
В
a
−b
|
1 1
 Г
− a b Г
− a b
|
a
−b
Д

ab
|
| 3.
Знайдіть вираз, тотожно рівний даному виразу
|
x
4
+ x
|
3
− x
−1.
|
| А
|
Б
|
В
|
Г
|
Д
|
| (x
+1)2
(x
2
+ x
+1)
|
(x
2
− x
+1)(x
−1)2
|
(x
−1)3
(x
+1)
|
(x
−1)(x
+1)3
|
(x
2
−1)(x
2
+ x
+1)
|
| 4.
Розв’яжіть нерівність a
2
> a
.
|
| А
(1;+∞)
|
Б
(0; 1)
|
В
(−∞; 0)
|
Г
(−∞; 0)Υ(1;+∞)
|
Д
(−∞; 1)
|
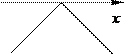
5.
З-поміж наведених графіків укажіть графік функції y
=−  x
+ 3 x
+ 3  . .
| А
|
Б
|
В
|
Г
|
Д
|
| 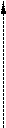 y
3 y
3
|

|
x
|
–3
|

|
3 x
|

|
3
x
|
 –3 –3
|
 y y
x
–3
|
–3
|
y
|
3
|

6.
Товар подешевшав на 20%. На скільки відсотків більше можна купити товару за ту ж саму суму грошей?
| 1
А
 % %
5
|
1
Б
 % %
4
|
В
10%
|
Г
20%
|
Д
25%
|
7.
Обчисліть значення виразу log5
49 + 2log5
 5
. 5
.
7
8.
Розв’яжіть рівняння sin (3x
) =  1
. 1
.
2
| А
|
Б
|
В
|
Г
|
Д
|
| 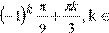 Z Z
|
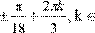 Z Z
|
(−1)k
|
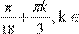 Z Z
|
 Z Z
|
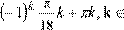 Z Z
|
9.
Знайдіть множину значень функції f
(x
) = (sin x
+ cos x
)2
.
| А
[1; 2]
|
Б
[0; 2]
|
В
[− 
|
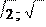 2 ] 2 ]
|
Г
[0; 1]
|
Д
інша відповідь
|
10.
Задано рівняння:
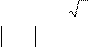 log2
x
− log2
(x
− 2)=1, (1) cos x
=1− 3, (2) x
+ 2 =−3, (3) log2
x
− log2
(x
− 2)=1, (1) cos x
=1− 3, (2) x
+ 2 =−3, (3)
sin(x
+ ) = −π. (4) ) = −π. (4)
Укажіть рівняння, яке НЕ МАЄ коренів на множині дійсних чисел.
| А
(1) і (4)
|
Б
(2) і (3)
|
В
(1) і (2)
|
Г
(3) і (4)
|
Д
інша відповідь
|
11.
 На рисунку зображено графік функції y
= f
( )x
і дотичну до нього в точці з абсцисою x
0
. На рисунку зображено графік функції y
= f
( )x
і дотичну до нього в точці з абсцисою x
0
.
Знайдіть значення f
′(x
0
).

12.
Обчисліть значення виразу sinα+sinβ, якщо α−β=180ο
.
| А
1
|
1
Б
 2 2
|
В
0
|
1
Г –

2
|
Д
інша відповідь
|
13.
Розв’яжіть нерівність log1
3⋅log4
x
> 0.

4
| А
(1;+∞)
|
Б
(0; 4)
|
В
(0; 1)
|
Г
(4;+∞)
|
Д
(−∞; 1)
|
14.
Укажіть непарну функцію.
| А
y
= x
2
−4
|
Б
y
= −x
2
|
В
y
=x
3
−1
|
Г
y
=
|
 x
−2 x
−2
|
Д
y
= x
3
−x
|
15.
 Знайдіть область визначення функції y
= x
x
+
2
. Знайдіть область визначення функції y
= x
x
+
2
.
2 −1
| А
[− 2; 0) (Υ 0; +∞)
|
Б
[− 2; +∞)
|
В
(− 2; 0)Υ(0;+∞)
|
Г
(−∞; − 2]
|
Д
x
≠1
|
16.
Власник банкоматної картки забув останні дві цифри свого PIN-коду, але пам’ятає, що вони різні. Знайдіть імовірність того, що з першої спроби він отримає доступ до системи.
| 1
А

2
|
1
Б

25
|
1
В

50
|
1
Г
 90 90
|
1
Д

100
|

17.
 Прямі m
і n
паралельні. Обчисліть величину кута х
, зображеного на рисунку. Прямі m
і n
паралельні. Обчисліть величину кута х
, зображеного на рисунку.
| А
40º
|
Б
45º
|
В
50º
|
Г
80º
|
Д
140º
|
 A 18.
У прямокутнику ABCD
прямі m
і n
проходять через точку перетину діагоналей. Площа фігури, що складається з трьох зафарбованих трикутників, дорівнює 12 см2
. Обчисліть площу прямокутника ABCD
. A 18.
У прямокутнику ABCD
прямі m
і n
проходять через точку перетину діагоналей. Площа фігури, що складається з трьох зафарбованих трикутників, дорівнює 12 см2
. Обчисліть площу прямокутника ABCD
.
D
| А
24 см2
|
Б
30 см2
|
В
36 см2
|
Г
42 см2
|
Д
48 см2
|
19.
Ортогональною проекцією відрізка з кінцями у точках А
(−1; 0; 5) і В
(−1; 0; 8) на координатну площину xy
є:
| А
|
Б
|
В
|
Г
|
Д
|
| пряма
|
промінь
|
відрізок
|
точка
|
фігура, що відрізняється від перелічених
|
20.
Знайдіть об’єм тіла, утвореного обертанням куба навколо свого ребра, довжина якого а
.
| А
4а
3
|
Б
πа
3
|
В
2πа
3
|
Г
4πа
3
|
 Д
(2 + 2 2 ) πа
2 Д
(2 + 2 2 ) πа
2
|

Частина 2
Розв’яжіть завдання 21
–
36. Запишіть відповідь у зошит і перенесіть її до бланка А.
x
2
+ 2x
− 3
21.
 Укажіть найменше ціле число, яке є розв’язком нерівності < 0 . x
+ 2 Укажіть найменше ціле число, яке є розв’язком нерівності < 0 . x
+ 2
Відповідь: _
-1
_________________
22.
Обчисліть суму перших 20 членів арифметичної прогресії, якщо її перший член дорівнює 2, а сьомий – 20.
Відповідь: _610
_________________
23.
Обчисліть значення виразу 53
+ 2
− 9
.
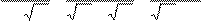 8− 11 13 + 11 13 + 2 8− 11 13 + 11 13 + 2
Відповідь: _10
_________________

24.
(Задача Л.Пізанського, XII-XIII ст.)
Дві вежі, одна з яких 40 футів, а друга – 30 футів заввишки, розташовано на відстані 50 футів одна від одної. До криниці, що знаходиться між ними, одночасно з обох веж злетіло по пташці. Рухаючись з однаковою швидкістю, вони прилетіли до криниці одночасно. Знайдіть відстань від криниці до найближчої вежі (у футах)
.
Відповідь: _18
___________ футів
.
25.
Обчисліть значення виразу sin 2α, якщо ctgα= − . .
Відповідь запишіть ДЕСЯТКОВИМ ДРОБОМ.
Відповідь: _-0,8
_________________
26.
 Розв’яжіть рівняння x
2
−x
− 6 = − 2x
. Розв’яжіть рівняння x
2
−x
− 6 = − 2x
.
Якщо рівняння має один корінь, запишіть його у відповідь. Якщо рівняння має кілька коренів, запишіть у відповідь їх добуток.
Відповідь: _-3
_________________

⎧⎪2x
⋅3y
= 24,
27.
Розв’яжіть систему рівнянь ⎨ y x
Запишіть у відповідь СУМУ x
0
+ y
0
, ⎪⎩
2
⋅
3
=
54.
якщо пара (x
0
; y
0
) є розв’язком системи рівнянь.
Відповідь: _4
_________________
28.
 Обчисліть Обчисліть  1 ⋅9log
3
14 + 0,5 . 1 ⋅9log
3
14 + 0,5 .
25
Відповідь запишіть ДЕСЯТКОВИМ ДРОБОМ.
Відповідь: _1,68
_________________
29.
Відрізок 12 см завдовжки поділили на дві частини так, що сума площ квадратів, побудованих на цих частинах, стала найменшою. Обчисліть суму площ квадратів.
Відповідь: _72
_________________

30.
Річка тече лугом і двічі перетинає шосе, утворюючи криву y
= 3x
− x
2
. Яка площа лугу між шосе та річкою, якщо вважати, що лінія шосе збігається з віссю OX
(див. рис.)? Одиниця довжини – 1 км.
Відповідь: _4,5
______________ км
2
річка
⎧⎪x
2
+ y
2
= a
2
,
31.
 Знайдіть НАЙМЕНШЕ значення параметра а
, при якому система ⎨ 2 2 ⎪⎩(x
− 7) + y
=1 Знайдіть НАЙМЕНШЕ значення параметра а
, при якому система ⎨ 2 2 ⎪⎩(x
− 7) + y
=1
має єдиний розв’язок.
Відповідь: _-8
_________________
32.
На рисунку зображено графік функції f
(x
) = x
4
− x
2
+ bx
+ c
.
Визначте знаки параметрів b
і c
.
У відповіді вкажіть номер правильного варіанта з наведених нижче.
⎧b
> 0, ⎧b
> 0, ⎧b
< 0, ⎧b
< 0,
1. ⎨ 2. ⎨ 3. ⎨ 4. ⎨
⎩c
> 0. ⎩c
< 0. ⎩c
> 0. ⎩c
< 0.
Відповідь: _3
_________________

⎧ ⎛π ⎞ 8

33.
Розв’яжіть систему рівнянь ⎪⎪
⎨cos⎜⎝
2
(2x
+ 5)⎠
⎟=1+(y
−1) ,
⎪
4sinπ
 y
= 4x
2
+ 4x
+ 5. y
= 4x
2
+ 4x
+ 5.
⎪⎩ 2
Запишіть у відповідь ДОБУТОК x
0
y
0
, якщо пара (x
0
; y
0
) є розв’язком системи рівнянь.
Відповідь: _-0,5
_________________
34.
 Обчисліть скалярний добуток векторів, зображених на рисунку. Обчисліть скалярний добуток векторів, зображених на рисунку.
Відповідь: _18
_________________
35.
Укажіть номер фужера, у який можна налити НАЙБІЛЬШЕ рідини.
Відповідь: _3
_________________
36.
Висота правильної чотирикутної піраміди дорівнює 3 см. Апофема утворює з площиною основи кут 60º. Обчисліть площу бічної поверхні піраміди (у см2
).
Відповідь: _24
____________ см2

Частина 3
Розв’язання завдань 37
–
38 повинно мати обґрунтування. Запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання завдань схемами, графіками, таблицями.
УВАГА! Розв’язання завдань 37
–
38 запишіть у бланку Б.
37.
Основою прямого паралелепіпеда є квадрат ABCD
зі стороною 3 см. Бічне ребро AA
1
дорівнює 4 см. Знайдіть площу перерізу паралелепіпеда площиною, що проходить через вершину А
перпендикулярно до прямої BA
1
(у см
2
).
ЧЕРНЕТКА

ЧЕРНЕТКА

38.
Розв’яжіть рівняння 2 (tg2
x
+ ctg2
x
+ 2)+ a
2
= 3a
(tgx
+ ctgx
), якщо x
 π
n
, де n
∈Z
. π
n
, де n
∈Z
.
ЧЕРНЕТКА

ЧЕРНЕТКА

ЧЕРНЕТКА

УВАГА! Розв’язання завдань 37
–
38 запишіть у бланку Б.
Кінець тестового зошита
|