ВІДПОВІДІ НА ЗАВДАННЯ ТЕСТУ З МАТЕМАТИКИ

ЗОВНІШНЬОГО НЕЗАЛЕЖНОГО ОЦІНЮВАННЯ 2010 РОКУ ОСНОВНА СЕСІЯ № 2

1. Обчисліть 1001² −999² .

Відповідь : 4000.

2. 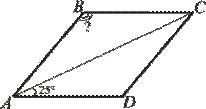На рисунку зображено ромб АВСD . Знайдіть градусну міру кута АBС , якщо ∠CAD =25° .

Відповідь : 130°.

3. Перед Новим роком у магазині побутової техніки на всі товари було знижено ціни на 15%. Скільки коштуватиме після знижки телевізор вартістю 1800 грн ?

Відповідь : 1530 грн .

4. Обчисліть .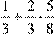

Відповідь : .

5. Спростіть вираз (_a ⁶ )⁴ :_a ² , де a ≠ 0.

Відповідь : a ²² .

6. На рисунку зображено розгортку многогранника. Визначте кількість його ребер.

Відповідь : 12.

7. Обчисліть sin 210^o .

Відповідь : − .

8. Осьовим перерізом циліндра є прямокутник, діагональ якого дорівнює 10 см . Знайдіть радіус основи циліндра, якщо його висота дорівнює 8 см .

Відповідь : 3 см .

⎧3x − 2y = 9,

9. Розв’яжіть систему ⎨ Для одержаного розв’язку (x ₀ ; y ₀ ) обчисліть суму _⎩ x + 2y =−5.

x 0 + y 0.

Відповідь : – 2.

10. 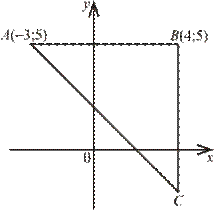У прямокутній системі координат зображено прямокутний рівнобедрений трикутник АВС , в якому А (−3; 5) і В (4; 5) (див. рисунок). Знайдіть координати точки С .

Відповідь : (4; − 2).

11. Серед чисел а = 5 − 2 , b = 2 3 −3 2 , с = ³ 3 − ³ 2 укажіть усі додатні.

Відповідь : a ; с .

12. До кола з центром у точці О проведено дотичну АВ (В – точка дотику). ВС – хорда, що утворює з радіусом кола кут 35° (див. рисунок). Знайдіть градусну міру кута АВС .

Відповідь : 55°.

13. У скільки разів збільшиться об’єм кулі, якщо її радіус збільшити у 2 рази?

Відповідь : у 8 разів.

14. Діаграма, зображена на рисунку, містить інформацію про кількість опадів (у мм ), що випали упродовж року в місті N . Користуючись діаграмою, установіть, які з наведених тверджень є правильними.

І. Улітку опадів випало менше, ніж навесні.

ІІ. У вересні опадів випало у 1,5 рази більше, ніж у жовтні.

ІІІ. Середня місячна кількість опадів за рік становить 19 мм .

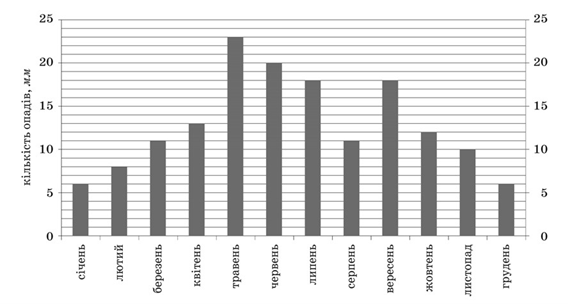
Відповідь : лише ІІ.

15. На папері у клітинку зображено паралелограм ABCD , вершини якого збігаються з вершинами клітинок (див. рисунок). Знайдіть площу паралелограма ABCD , якщо кожна клітинка є квадратом зі стороною завдовжки 1 см .

Відповідь : 18 см ² .

16. Якому з наведених проміжків належить корінь рівняння log x = 2?

3 Відповідь : (8;11].

r r

17. Обчисліть скалярний добуток векторів a (−3; 2; −1) і b (− −1; 4; 5).

Відповідь : – 10.

18. На полиці знаходяться 18 однакових скляних банок із джемом. Серед них 6 банок з абрикосовим джемом, 12 – з яблучним. За кольором джеми не відрізняються один від одного. Господиня навмання взяла одну банку. Яка ймовірність того, що вона буде з абрикосовим джемом?

Відповідь : .

19. Знайдіть значення похідної функції f x ( )= 2x ³ −5 у точці x ₀ =−1.

Відповідь : 6.

20. На одному з рисунків зображено ескіз графіка функції y =−log₄ x . Укажіть цей рисунок.

Відповідь :

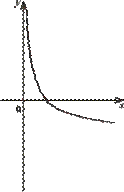
21. Кодовий замок на дверях має десять кнопок, на яких нанесено десять різних цифр (див. рисунок). Щоб відчинити двері, потрібно одночасно натиснути дві кнопки, цифри на яких складають код замка. Скільки всього існує різних варіантів коду замка? Уважайте, що коди, утворені перестановкою цифр (наприклад, 1-2 і 2-1), є однаковими.

Відповідь : 45.

22. 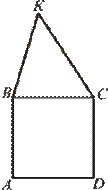На рисунку зображено квадрат ABCD і трикутник BKС , периметри яких відповідно дорівнюють 24 см і 20 см . Знайдіть периметр п’ятикутника ABKCD .

Відповідь : 32 см .

23. 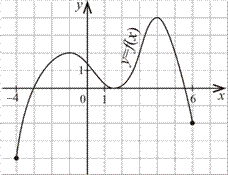На рисунку зображено графік функції y = f x ( ), яка визначена на відрізку [− 4; 6]. Укажіть усі значення х , для яких виконується нерівність f x ( )≥ 2?

Відповідь : { }−1 U[3; 5].

24. Дерев’яний брусок має форму прямокутного паралелепіпеда з вимірами 10 см , 20 см , 80 см . Скільки лаку потрібно для того, щоб один раз покрити ним усю поверхню цього бруска, якщо на 1 м ² витрачається 100 г лаку?

Відповідь : 52 г .

25. 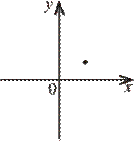У прямокутній системі координат зображено точку, що є вершиною параболи y = + +x ² bx c (див. рисунок). Укажіть правильне твердження щодо коефіцієнтів b і c .

⎧b < 0, Відповідь : ⎨⎩c > 0.

26. Установіть відповідність між числом (1 – 4) та множиною, до якої воно належить (А –Д).

Число Множина

1 3,4 А множина натуральних чисел

2 8 Б множина складених чисел

В множина цілих чисел, що не є натуральними

3 числами

4 – 13 Г множина дробових чисел

Д множина ірраціональних чисел

Відповідь : 1 – Г, 2 – Д, 3 – А, 4 – В.

27. Установіть відповідність між функціями, заданими формулами (1 – 4), та їхніми властивостями (А – Д).

Функція Властивість функції

1 y = cos x А областю визначення функції є інтервал

(0; +∞)

2 y = ctg x Б областю значень функції є відрізок [−1;1]

3 y = 4 В функція спадає на інтервалі (−∞; +∞)

⎛1⎞x ⎝3⎠

4 y =⎜ ⎟ Г непарна функція

Д періодична функція, що не має найменшого

додатного періоду

Відповідь : 1 – Б, 2 – Г, 3 – Д, 4 – В.

28. Установіть відповідність між перерізами геометричних тіл (1 – 4) та їхніми назвами (А – Д).

Відпов ді ь : 1 – Г, 2 – А, 3 – Д, 4 – Б.

29. Знайдіть значення виразу 6^{2log 6 9 −log 6 4} .

Відповідь : 20,25.

2log 7 log− 4 Знайдіть значення виразу 5 ^{5 5} .

Відповідь : 12,25.

2log 6 log− 5 Знайдіть значення виразу 7 ^{7 7} .

Відповідь : 7,2.

30. Робітники отримали замовлення викопати криницю. За перший викопаний у глибину метр криниці їм платять 50 грн , а за кожний наступний – на 20 грн більше, ніж за попередній. Скільки грошей (у грн ) сплатять робітникам за викопану криницю завглибшки 12 м ?

Відповідь : 1920.

Робітники отримали замовлення викопати криницю. За перший викопаний у глибину метр криниці їм платять 60 грн , а за кожний наступний – на 20 грн більше, ніж за попередній. Скільки грошей (у грн ) сплатять робітникам за викопану криницю завглибшки 12 м ?

Відповідь : 2040.

Робітники отримали замовлення викопати криницю. За перший викопаний у глибину метр криниці їм платять 50 грн , а за кожний наступний – на 25 грн більше, ніж за попередній. Скільки грошей (у грн ) сплатять робітникам за викопану криницю завглибшки 11 м ?

Відповідь : 1925.

x x ² −

31. Розв’яжіть нерівність ^⎛ ⎜ ^{1 ⎞} ⎟ > 8^{x −5} . У відповідь запишіть суму всіх цілих розв’язків

⎝ 2⎠

цієї нерівності. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100.

Відповідь : – 7.

x ² −2x

⎛ 1⎞ ^{x − 6} ⎝ 2⎠

Розв’яжіть нерівність ⎜ ⎟ >16 . У відповідь запишіть суму всіх цілих розв’язків

цієї нерівності. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100.

Відповідь : – 9.

x ² −3x

⎛ 1⎞ ^{x − 7} ⎝ 2⎠

Розв’яжіть нерівність ⎜ ⎟ > 32 . У відповідь запишіть суму всіх цілих розв’язків

цієї нерівності. Якщо нерівність має безліч цілих розв’язків, то у відповідь запишіть число 100.

Відповідь : – 11.

32. Тарас може доїхати на велосипеді від села до станції за 3 год , а пішки дійти за 7 год . Його швидкість пішки на 8 км /год менша, ніж на велосипеді. Знайдіть відстань від села до станції (у км ).

Відповідь : 42.

Тарас може доїхати на велосипеді від села до станції за 2 год , а пішки дійти за 6 год . Його швидкість пішки на 10 км /год менша, ніж на велосипеді. Знайдіть відстань від села до станції (у км ).

Відповідь : 30.

Тарас може доїхати на велосипеді від села до станції за 3 год , а пішки дійти за 9 год .

Його швидкість пішки на 8 км /год менша, ніж на велосипеді. Знайдіть відстань від села до станції (у км ).

Відповідь : 36.

33. Два кола, довжини яких дорівнюють 9π см і 36π см , мають внутрішній дотик. Знайдіть відстань між центрами цих кіл (у см ).

Відповідь : 13,5.

Два кола, довжини яких дорівнюють 4π см і 25π см , мають внутрішній дотик. Знайдіть відстань між центрами цих кіл (у см ).

Відповідь : 10,5.

Два кола, довжини яких дорівнюють 4π см і 16π см , мають внутрішній дотик. Знайдіть відстань між центрами цих кіл (у см ).

Відповідь : 6.

34. Обчисліть площу фігури, обмеженої лініями: y = 2sin x , y = cos x , x = , x =π.

Відповідь : 3.

Обчисліть площу фігури, обмеженої лініями: y = sin x , y = 3cos x , x = , x =π.

Відповідь : 4.

Обчисліть площу фігури, обмеженої лініями: y = 4sin x , y =cosx , x = , x =π.

Відповідь : 5.

35. Основою піраміди є прямокутний трикутник, гіпотенуза якого дорівнює 4 3 см , гострий кут – 30o . Усі бічні ребра піраміди нахилені до площини її основи під кутом 45o .

Знайдіть об’єм піраміди (у см ³ ).

Відповідь : 12.

Основою піраміди є прямокутний трикутник, гіпотенуза якого дорівнює 2 3 см , гострий кут – 30o . Усі бічні ребра піраміди нахилені до площини її основи під кутом 45o .

Знайдіть об’єм піраміди (у см ³ ).

Відповідь : 1,5.

Основою піраміди є прямокутний трикутник, гіпотенуза якого дорівнює 6 3 см , гострий кут – 30o . Усі бічні ребра піраміди нахилені до площини її основи під кутом 45o .

Знайдіть об’єм піраміди (у см ³ ).

Відповідь : 40,5.

36. Розв’яжіть рівняння 2x ² + 7x − +9 sin(π + =x ) 10. Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше, ніж один корінь, то у відповідь запишіть суму всіх коренів.

Відповідь : – 4,5.

Розв’яжіть рівняння 2x ² +13x − +7 cos(π + =x ) 10. Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше, ніж один корінь, то у відповідь запишіть суму всіх коренів.

Відповідь : – 7.

Розв’яжіть рівняння 2x ² + 3x −14 + sin(π − =x ) 10 . Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше одного кореня, то у відповідь запишіть суму всіх коренів.

Відповідь : – 3,5.