Ìèíèñòåðñòâî îáðàçîâàíèÿ è êóëüòóðû Êûðãûçñêîé Ðåñïóáëèêè
Êûðãûçñêèé Íàöèîíàëüíûé Óíèâåðñèòåò èì. Æ.Áàëàñàãûíà Ôàêóëüòåò õèìèè è õèìè÷åñêîé òåõíîëîãèè
Êàôåäðà íåîðãàíè÷åñêîé õèìèè è õèìè÷åñêîé òåõíîëîãèè
Ïîÿñíèòåëüíàÿ çàïèñêà ê êóðñîâîìó ïðîåêòó
ïî ïðèêëàäíîé ìåõàíèêå
Äèñöèïëèíà ïðèêëàäíàÿ ìåõàíèêà
Ñòóäåíò ___________________Äæåíëîäà Ð.Õ.
Ãðóïïà ÕÒ-01
Íàïðàâëåíèå (ñïåöèàëüíîñòü) Ò-08
Ðóêîâîäèòåëü ___________________Öîé Ó.À.
Äàòà çàùèòû __________________________
Îöåíêà __________________________
Áèøêåê-2004
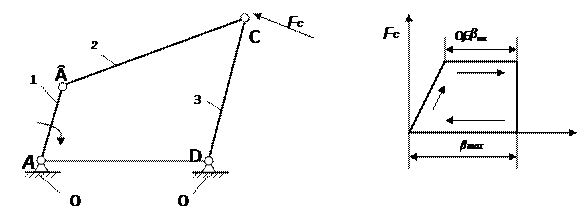
Èñõîäíûå äàííûå:
lAB
, ì=0,05
l, ì=0,14
BC
lDC
, ì=0,16 lAD
, ì=0,10

|
| ÊÍÓ.ÕÒ.000 ÏÇ |
| Çàäàíèå |
Ëèò. |
Ìàññà |
Ìàñøòàá |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
| Ðàçðàá. |
Äæåíëîäà Ð.Õ. |
| Ïðîâ. |
Öîé Ó.À. |
| Ò. êîíòð. |
Ëèñò 2 |
Ëèñòîâ 37 |
| ÊÍÓ ãðóïïà ÕÒ –
01 |
| Í. Êîíòð. |
| Óòâ. |
1, ÑÒÐÓÊÒÓÐÍÛÉ ÀÍÀËÈÇ ÊÐÈÂÎØÈÏÍÎ-ÏÎËÇÓÍÍÎÃÎ ÌÅÕÀÍÈÇÌÀ
 1
 1
Â
0 0
Íàçíà÷åíèå äàííîãî ìåõàíèçìà –
ýòî ïðåîáðàçîâàíèå âðàùàòåëüíîãî äâèæåíèÿ çâåíà 1, â âîçâðàòíî-
ïîñòóïàòåëüíîå äâèæåíèå çâåíà 3. Çâåíî 1, îáðàçóþùåå ñî ñòîéêîé 4 âðàùàòåëüíóþ êèíåìàòè÷åñêóþ ïàðó, íàçûâàþò êðèâîøèïîì; çâåíî 3, îáðàçóþùàÿ ñî ñòîéêîé 0 ïîñòóïàòåëüíóþ êèíåìàòè÷åñêóþ ïàðó, -ïîëçóíîì. Òàêîé ìåõàíèçì íàçûâàåòñÿ êðèâîøèïíî-ïîëçóííûì.
Ðàññìàòðèâàåìûé ìåõàíèçì ñîñòîèò èç òðåõ ïîäâèæíûõ çâåíüåâ (n=3), è ñîäåðæèò ÷åòûðå îäíîïîäâèæíûå êèíåìàòè÷åñêèå ïàðû ïÿòîãî êëàññà (ð5
=4), èç êîòîðûõ îäíà ÿâëÿåòñÿ ïîñòóïàòåëüíîé (Ï30
) - ñîåäèíÿåò ïîëçóí ñî ñòîéêîé 0, è òðè âðàùàòåëüíûìè (Â01
,Â12
,Â23
) -ñîåäèíÿåò ñîîòâåòñòâåííî, ñòîéêó 0 ñ êðèâîøèïîì 1, êðèâîøèï 1 ñ øàòóíîì 2 è øàòóí 2 ñ ïîëçóíîì 3. Êèíåìàòè÷åñêèõ ïàð ÷åòâåðòîãî êëàññà â ìåõàíèçìå íåò, ò.å.
ð4
=0. Ñòåïåíü ïîäâèæíîñòè ìåõàíèçìà îïðåäåëÿåòñÿ ïî ôîðìóëå ×åáûøåâà:
W
= 3n
−2p
5
− p
4
= 3⋅3− 2⋅4−0 =1.
Ìåõàíèçì ñîñòîèò èç îäíîé ãðóïïû Àññóðà, ñîäåðæàùåé øàòóí 2, ïîëçóí 3 è òðè êèíåìàòè÷åñêèå ïàðû (ðèñ.1), è íà÷àëüíîãî ìåõàíèçìà, ñîäåðæàùåãî êðèâîøèï 1, ñòîéêó 0 è îäíó êèíåìàòè÷åñêóþ ïàðó (ðèñ.2).
Çâåíüÿ 2 è 3, ñ òðåìÿ êèíåìàòè÷åñêèìè ïàðàìè ïðåäñòàâëÿþò ñîáîé ãðóïïó Àññóðà II êëàññà âòîðîãî ïîðÿäêà âòîðîé ìîäèôèêàöèè. Êðèâîøèï 1 è ñòîéêà 6, ïðåäñòâëÿþò ñîáîé íà÷àëüíûé ìåõàíèçì.
Ñòåïåíü ïîäâèæíîñòè ãðóïïû Àññóðà:
Wçâ.2,3
= 3n⋅2p5
= 3⋅2 −2⋅3 = 0
  Â Â Â Â
À 3
0
Ðèñ.1 Ãðóïïà Àññóðà Ðèñ.2 Íà÷àëüíûé ìåõàíèçì Ôîðìóëà ñòðîåíèÿ ìåõàíèçìà:
Â01
→
[Â12
→
Â23
→
Ï30
]
Èç ñòðóêòóðíîãî àíàëèçà ìåõàíèçìà ñëåäóåò, ÷òî äëÿ ïîëó÷åíèÿ âïîëíå îïðåäåëåííûõ äâèæåíèé çâåíüåâ, äîñòàòî÷íî ïåðâîíà÷àëüíî çàäàòü îíîìó èç çâåíüåâ îïðåäåëåííîå äâèæåíèå. Ýòî è ïîäòâåðæäàåòñÿ ïðèíöèïîì îáðàçîâàíèÿ ìåõàíèçìîâ ïî Àññóðó. Ïî ôîðìóëå ñòðîåíèÿ ìåõàíèçìà ìîæíîïîñòðîèòü åãî ñòðóêòóðíóþ ñõåìó.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 3 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
1.2 ÑÒÐÓÊÒÓÐÍÛÉ ÀÍÀËÈÇ ÌÅÕÀÍÈÇÌÀ ÏÎÄÀÒ×ÈÊÀ ÕËÅÁÎÐÅÇÀÒÅËÜÍÎÉ ÌÀØÈÍÛ ÌÐÕ-200
Ðàññìàòðèâàåìûé ìåõàíèçì ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ –
200 ñîñòîèò èç ñëåäóþùèõ çâåíüåâ:
íåïîäâèæíûõ äåòàëåé ìåõàíèçìà –
ñòîåê 0; çâåíà 1 îáðàçóþùåãî ñî ñòîéêîé 0 âðàùàòåëüíî êèíåìàòè÷åñêóþ
ïàðó - êðèâîøèïîì; êà÷àþùåãîñÿ çâåíà 3 - êîðîìûñëà; çâåíà 2 -øàòóíà.
Ìåõàíèçì ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ –
200, ñëóæèò äëÿ ïðåîáðàçîâàíèÿ âðàùàòåëüíîãî äâèæåíèÿ êðèâîøèïà 1 â âîçâðàòíî-âðàùàòåëüíîå äâèæåíèå çâåíà 3.
Ò.ê. çâåíî 1 –
êðèâîøèï (ñîâåðøàåò ïîëíûé îáîðîò), à çâåíî 3 –
êîðîìûñëî (ñîâåðøàåò íåïîëíûé îáîðîò, òî ìåõàíèçì äàííîé ìàøèíû ÌÐÕ –
200, ÿâëÿåòñÿ êðèâîøèïíî-êîðîìûñëîâûì.
Òðè ïîäâèæíûå çâåíà (n=3) è ñòîéêà 0 ìåõàíèçìà ïîäàò÷èêè õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ –
200 îáðàçóþò ÷åòûðå êèíåìàòè÷åñêèå ïàðû V êëàññà. Âðàùàòåëüíûå ïàðû (p5
=4) îáðàçîâàíû çâåíüÿìè 0 è 1, 1 è 2, 2 è 3, 3 è 0 (B01
, B12
, B23
, B30
). Ñòåïåíü ïîäâèæíîñòè ìåõàíèçìà îïðåäåëÿåòñÿ ïî ôîðìóëå ×åáûøåâà:
W =3n−2p5
−p4
=3⋅3−2⋅4−0 =1
ò.å. ìåõàíèçì èìååò îäíî âåäóùåå çâåíî.
Ìåõàíèçì õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ –
200 ñîñòîèò èç îäíîé ãðóïïû Àññóðà, ñîäåðæàùåé øàòóí 2 è
êîðîìûñëî 3, è èç íà÷àëüíîãî ìåõàíèçìà, âêëþ÷àþùåãî êðèâîøèï 1 è ñòîéêó 0 (ðèñ 1,2). Ãðóïïîé Àññóðà íàçûâàþò
êèíåìàòè÷åñêóþ öåïü, ïîëó÷àþùàÿ íóëåâóþ ïîäâèæíîñòü ïîñëå ïðèñîåäèíåíèÿ åå ê ñòîéêå.
Wãð2,3
=3n−2p5
=3⋅2−2⋅3=0
Çâåíî 2 è 3 ñ òðåìÿ êèíåìàòè÷åñêèìè ïàðàìè B, C, в îáðàçóþò ãðóïïó Àññóðà II êëàññà âòîðîãî ïîðÿäêà
ïåðâîé ìîäèôèêàöèè. Êðèâîøèï 1 è ñòîéêà 0, ïðåäñòàâëÿþò ñîáîé íà÷àëüíûé ìåõàíèçì.
  C B C B
1
ðèñ.1. Ãðóïïà Àññóðà ðèñ.2. Íà÷àëüíûé ìåõàíèçì
Ôîðìóëà ñòðîåíèÿ ìåõàíèçìà:
B01 → [B12 →B23 →B30]
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 4 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
2.ÊÈÍÅÌÀÒÈ×ÅÑÊÈÉ ÀÍÀËÈÇ ÌÅÕÀÍÈÇÌÀ ÏÎÄÀÒ×ÈÊÀ ÕËÅÁÎÐÅÇÀÒÅËÜÍÎÉ ÌÀØÈÍÛ ÌÐÕ-200
2.1 Ïîñòðîåíèå ïëàíîâ ïîëîæåíèé ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû
ÌÐÕ-200
Ïðèíèìàþ ïðîèçâîëüíóþ äèíó êðèâîøèïà íà ÷åðòåæå AB=50 ìì. Ìàñøòàá äëèíû:
l 0,05
µ
l
= AB
=  =0,001ì/ìì =0,001ì/ìì
AB 50
Ìàñøòàá äëèíû çâåíüåâ:
l 0,14
BC = BC
=  =140 ìì µl
0,001 l 0,16 =140 ìì µl
0,001 l 0,16
CD = CD
=  =160ìì =160ìì
µ
l
0,001 l 0,1
AD = AD
=  =100ìì =100ìì
µ
l
0,001
Ïî ïîëó÷åííûì äàííûì ñòðîèì ñõåìó ìåõàíèçìà â 12 ïîëîæåíèÿõ. Äëÿ ýòîãî ïðîâîäèì îêðóæíîñòü ðàäèóñîì À è äåëèì åå íà 12 ðàâíûõ ÷àñòåé, íà÷èíàÿñ íóëåâîãî.  êà÷åñòâå íóëåâîãî ïîëîæåíèÿ âûáèðàåì òî, ïðè êîòîðîì êîðîìûñëî îêàçûâàåòñÿ â ëåâîì êðàéíåì ïîëîæåíèè, äëÿ ÷åãî íà ðàññòîÿíèè AD íàìå÷àåì òî÷êó в è èç íåå êàê èç öåíòðà îïèøåì äóãó ðàäèóñîì CD. Èç òî÷êè À êàê èç öåíòðà ñäåëàåì íà ýòîé äóãå äâå çàñå÷êè –
îäíó ðàäèóñîì CB-AB –
ýòî áóäåò íóëåâîå ïîëîæåíèå òî÷êè Ñ, ò.å. Ñ0
, äðóãóþ –
ðàäèóñîì CB+AB –
ýòî áóäåò òî÷êà C8
, ñîîòâåòñòâóþùàÿ êðàéíåìó ïðàâîìó ïîëîæåíèþ êîðîìûñëà CD. Òî÷êè äåëåíèÿ îêðóæíîñòåé ðàäèóñà AB ñîåäèíÿåì ïðÿìûìè ëèíèÿìè ñ òî÷íîé A, îáîçíà÷àåì B0
, B1
,…, B11
èç íèõ ðàäèóñîì BC ïðîâîäèì çàñå÷êè íà äóãå ðàäèóñà DC. Ïîëó÷åííûå òî÷êè C0
, C1
,…, C11
ñîåäèíÿåì ïðÿìûìè ëèíèÿìè ñîîòâåòñòâåííî ñ òî÷êàìè B0
, B1
,…, B11
è ñ òî÷êîé D. Òàêèì îáðàçîì, ÿ ïîëó÷èë 12 ïëàíîâ ìåõàíèçìà, ïîñòðîåííûõ â ìàñøòàáå µ
l
=0,001 ì/ìì.
2.2 Ïîñòðîåíèå ïëàíîâ ñêîðîñòåé òî÷åê çâåíüåâ ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ-200 Îïðåäåëÿåì ñêîðîñòü òî÷êè Â:
VB
= ω1
•lAB
=22•0,05 =1,1 ì/ñ.
Äëÿ îïðåäåëåíèÿ ñêîðîñòè òî÷êè Ñ ñîñòàâëÿåì äâà âåêòîðíûõ óðàâíåíèÿ:

VC =VB +VCB, VC =VD +VCD .
Ðåøàÿ ýòè óðàâíåíèÿ ãðàôè÷åñêè, ïîëó÷àåì ïëàíû ñêîðîñòåé. Ïîñòðîåíèå ïëàíà ñêîðîñòåé ïðîèçâîäèòüñÿ ñëåäóþùèì îáðàçîì:
Èç ïðîèçâîëüíî âûáðàííîãî ïîëþñà ð îòêëàäûâàåì îòðåçîê ïðîèçâîëüíî âçÿòîé äëèíû ðb=44 ììâ íàïðàâëåíèè, ïåðïåíäèêóëÿðíîì çâåíó ÀÂ â 1-îì ïîëîæåíèè, â ñòîðîíó íàïðàâëåíèÿ óãëîâîé ñêîðîñòè ω
1
. Ìàñøòàáíûé êîýôôèöèåíò ïëàíà ñêîðîñòåé áóäåò:
V 1,1
µ
V
= B
=  =0,025,ì/ñ⋅ìì. pb 44 =0,025,ì/ñ⋅ìì. pb 44
 ×åðåç òî÷êó b ïðîâîäèì ëèíèþ âåêòîðà V
Cb
ïåðïåíäèêóëÿðíî çâåíó BC, à ÷åðåç ïîëþñ p –
ëèíèþ âåêòîðà ×åðåç òî÷êó b ïðîâîäèì ëèíèþ âåêòîðà V
Cb
ïåðïåíäèêóëÿðíî çâåíó BC, à ÷åðåç ïîëþñ p –
ëèíèþ âåêòîðà
 V
CD
ïåðïåíäèêóëÿðíî çâåíó CD. Òî÷êà ïåðåñå÷åíèÿ ýòèõ âåêòîðîâ îïðåäåëÿåò êîíåö âåêòîðà pc
, êîòîðûé â ìàñøòàáå µ
V
èçîáðàæàåò ñêîðîñòü òî÷êè C. Ÿ âåëè÷èíà îïðåäåëèòñÿ: V
CD
ïåðïåíäèêóëÿðíî çâåíó CD. Òî÷êà ïåðåñå÷åíèÿ ýòèõ âåêòîðîâ îïðåäåëÿåò êîíåö âåêòîðà pc
, êîòîðûé â ìàñøòàáå µ
V
èçîáðàæàåò ñêîðîñòü òî÷êè C. Ÿ âåëè÷èíà îïðåäåëèòñÿ:
VC
= pc• µV
=3•0,025 =0,075ì/ñ
 Îòíîñèòåëüíàÿ ñêîðîñòü V
Cb
îïðåäåëÿåòñÿ: Îòíîñèòåëüíàÿ ñêîðîñòü V
Cb
îïðåäåëÿåòñÿ:
VCD
=cb• µV
=41 •0,025 =1,025ì/ñ
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 5 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Óãëîâàÿ ñêîðîñòü êîðîìûñëà îïðåäåëÿåòñÿ ïî ôîðìóëå:
V 0,075 ω
CD
= CD
=  =0,47 1/ñ, lCD
0,16 =0,47 1/ñ, lCD
0,16
 (îòíîñèòåëüíàÿ ñêîðîñòü V
CD
ðàâíà àáñîëþòíîé), óãëîâàÿ ñêîðîñòü øàòóíà: (îòíîñèòåëüíàÿ ñêîðîñòü V
CD
ðàâíà àáñîëþòíîé), óãëîâàÿ ñêîðîñòü øàòóíà:
V 1,025
ω
CB
= CB
=  =7,32 1/ñ. =7,32 1/ñ.
lCB
0,14
Ðåçóëüòàòû âû÷èñëåíèé ñêîðîñòåé ñâåäåíû â òàáëèöó 1.
2.3 Ïîñòðîåíèå ãðàôèêà èçìåíåíèÿ ñèëû ïîëåçíîãî ñîïðîòèâëåíèÿ
Ïî óñëîâèþ çàäàíèÿ ïëàí óñêîðåíèé è ñèëîâîé àíàëèçìåõàíèçìà ñëåäóåò âûïîëíèòü äëÿ ïîëîæåíèÿ ìåõàíèçìà, êîãäà òî÷êà Ñ ðàçâèâàåò ìàêñèìàëüíóþ ìîùíîñòü Nmax
=FC
⋅VC
. Äëÿ îïðåäåëåíèÿ Nmax
íåîáõîäèìî çíàòü çíà÷åíèå ñèëû FC
âî âñåõ ïîëîæåíèÿõ ìåõàíèçìà, ñ òåì ÷òî áû ïîòîì èç ïðîèçâåäåíèé FC
⋅VC
âûáðàòü íàèáîëüøåå. Ïîýòîìó ñëåäóåò ïîñòðîèòü ãðàôèê FC
= (β
max
). Äëÿ ýòîãî ïðîâîæó ëèíèþ ÷åðåç äâà êðàéíèõ ïîëîæåíèÿ â òî÷êàõ Ñ0
è Ñ8
. Çàòåì ïðîâîæó ëèíèþ íàä Ñ0
Ñ8
ïàðàëëåëüíóþ åé –
ïîëó÷àåì îñü àáñöèññ, (ñì. ñõåìó), ïðîâåäÿ ê íåé ïåðïåíäèêóëÿð èç òî÷êè Ñ0
, ïîëó÷àåì òî÷êó à –
íà÷àëî êîîðäèíàò, à ïðîâåäÿ ïåðïåíäèêóëÿð èç òî÷êè Ñ8
, ïîëó÷àåì òî÷êó d, îãðàíè÷èâàþùóþ õîä òî÷êè Ñ. Èç òî÷êè à ïðîâîäèì îñü îðäèíàò. Èç òî÷êè в ïî îñè àáñöèññ îòëîæó îòðåçîê 0,6β
max,
âîññòàíàâëèâàåì èç ïîëó÷åííîé òî÷êè F0
îðäèíàòó F0
Fmax
ïðîèçâîëüíîé äëèíû (â ìîåì ñëó÷àå F0
Fmax
=36 ìì). Ýòà îðäèíàòà âûðàæàåòñÿ â ìàñøòàáå µF
ìàêñèìàëüíóþ ñèëó ïîëåçíîãî ñîïðîòèâëåíèÿ FCmax
.
Âåëè÷èíó ìàñøòàáíîãî êîýôôèöèåíòà íàéäó èç âûðàæåíèÿ:
F 1,8
 µ
F
= C
= =5⋅10−
2
,êÍ/ìì. µ
F
= C
= =5⋅10−
2
,êÍ/ìì.
ymax
36
Ñîåäèíèâ ïðÿìîé ëèíèåé òî÷êè a è Fm
è ïðîâåäÿ èõ òî÷êè Fm
ãîðèçîíòàëüíóþ ëèíèþ íà ðàññòîÿíèå 0,6β
max
îò îñè îðäèíàò, ïîëó÷àåì èñêîìûé ãðàôèê FC
(β
max
). Ïðè äâèæåíèè òî÷êè Ñ â ïðàâî ñèëà FC
óâåëè÷èâàåòñÿ ïî ëèíåéíîìó çàêîíó äî ìàêñèìàëüíîãî çíà÷åíèÿ (òî÷êà Fm
), à ïðè äâèæåíèè âëåâî ñèëû FC
ðàâíà íóëþ. Ïðîâåäÿ èç òî÷åê C1
,C2
,C3
,C4
,C5
,C6
,C7
,C8
âåðòèêàëüíûå ëèíèè äî ïåðåñå÷åíèÿ èõ ñ ãðàôèêîì FC
(β
max
), ïîëó÷àåì ñîîòâåòñòâóþùèå êîîðäèíàòû y
1
, y
2
,..., y
8
, ïî êîòîðûì ìîæíî ñóäèòü îâåëè÷èíå ñèëû ñîïðîòèâëåíèÿ â ëþáîì ïîëîæåíèè ìåõàíèçìà. Ðåçóëüòàòû âû÷èñëåíèé ñâåäåíû â òàáëèöó 1.
Àíàëèç äàííûõ òàáëèöû 1 ïîêàçûâàåò, ÷òî íàèáîëüøóþ ìîùíîñòü ìåõàíèçì ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ðàçâèâàåò â ÷åòâåðòîì ïîëîæåíèè, ò.å. Nmax
=1800⋅1,3=2,34êÂò, òàê êàê ìîùíîñòü Nîïðåäåëÿåòñÿ ïðîèçâåäåíèåì FC
⋅VC
, à ýòè ïàðàìåòðû äàþò ìàêñèìàëüíîå ïðîèçâåäåíèå èìåííî â ïÿòîì ïîëîæåíèè.
Ñëåäîâàòåëüíî, ïëàí óñêîðåíèé íåîáõîäèìî ñòðîèòü äëÿ ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû, êîãäà îí íàõîäèòñÿ â ïÿòîì ïîëîæåíèè.  ýòîì æå ïîëîæåíèè ìåõàíèçìà îïðåäåëÿþòñÿ ðåàêöèè â êèíåìàòè÷åñêèõ ïàðàõ çâåíüåâ è óðàâíîâåøèâàþùàÿ ñèëà Fy
.
2.4 Ïîñòðîåíèå ïëàíà óñêîðåíèé
Èç àíàëèçà ïëàíîâ ñêîðîñòåé âèäíî, ÷òî íàèáîëüøåé ìîùíîñòüþ òî÷êà Ñ áóäåò îáëàäàòü â 5–
îì ïîëîæåíèè, ò.ê. ïðè ïîñòîÿííîé ñèëå ìîùíîñòü çàâèñèò îò ñêîðîñòè, à ñêîðîñòü òî÷êè Ñ ìàêñèìàëüíà â 5 –
îì ïîëîæåíèè.
Ïîýòîìó ïëàí óñêîðåíèé ñòîèì äëÿ 5 - ãî ïîëîæåíèÿ. Îïðåäåëÿåì óñêîðåíèå òî÷êè Â:
 aB
=aB
n
= ω2
AB
•lAB
=222
•0,05 =24,2ì/ñ2 aB
=aB
n
= ω2
AB
•lAB
=222
•0,05 =24,2ì/ñ2
Äëÿ îïðåäåëåíèÿ óñêîðåíèÿ òî÷êè Ñ ñîñòàâëÿåì äâà âåêòîðíûõ óðàâíåíèÿ:
~ ~
n l n laC =aB +aCB +aCB, aC =aD +aCD +aCD.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 6 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
n n
Íîðìàëüíûå óñêîðåíèÿ a è CB
a îïðåäåëÿþòñÿ: CD
n VCB
2 0,72 2
cCB
= =  =3,5ì/ñ =3,5ì/ñ
lCB
0,14 2 2
V
cCDn = C
=1 ,3 =10,56ì/ñ2 lCD
0,16 ,3 =10,56ì/ñ2 lCD
0,16
Âûáèðàåì ïðîèçâîëüíî ïîëþñ Π
è èç íåãî ïàðàëëåëüíî êðèâîøèïó ÀÂ â íàïðàâëåíèè îò À ê Â ïðîâîäèì ïðÿìóþ Ïb ïðîèçâîëüíîé äëèíû (ïðèìåì Ïb=96,8 ìì). Ìàñøòàá ïëàíà óñêîðåíèé áóäåò:
 a 24,2 a 24,2
µa
 =0,25ì/ñ2
Ĥìì =0,25ì/ñ2
Ĥìì
Èç ïîëþñà Ï ïðîâîäèì ïðÿìóþ ïàðàëëåëüíî CD â íàïðàâëåíèè îò C ê в è íà íåé îòêëàäûâàåì îòðåçîê:
aCD
n
10,56
∏Cn
= =  =42,24ìì =42,24ìì
µa
0,25
Èç òî÷êè b ïðîâîäèì ïðÿìóþ ïàðàëëåëüíî BC â íàïðàâëåíèè îò C ê B è íà íåé îòêëàäûâàåì îòðåçîê:
aCB
n 3,5
bbn
= =  =14ìì =14ìì
µa
0,25
Èç òî÷åê ñn
è bn
ïðîâîäèì ïðÿìûå ëèíèè ïåðïåíäèêóëÿðíî Ïñï
è bbn
äî ïåðåñå÷åíèÿ èõ â òî÷êå Ñ. Îòðåçêè ññï
è bn
c èçîáðàæàþò â ìàñøòàáå µ
à
òàíãåíöèàëüíûå óñêîðåíèÿ òî÷êè Ñ îòíîñèòåëüíî òî÷åê в è B. Îòðåçîê ñîåäèíÿþùèé ïîëþñ Ï ñ òî÷êîé Ñ, èçîáðàæàåò ïîëíîå óñêîðåíèå òî÷êè Ñìåõàíèçìà, à îòðåçêè, ñîåäèíÿþùèå ïîëþñ ñ ñåðåäèíàìè îòðåçêîâ Ïb, bc è Ïñ –
ïîëíûå óñêîðåíèÿ öåíòðîâ ìàññ çâåíüåâ ìåõàíèçìà. Çíà÷åíèÿ óñêîðåíèé:
~
aCB
l
=bn
c• µa
=55•0,25 =13,75ìì/ñ2
~
aCD
l
=cn
c• µa
=10•0,25 =5 ìì/ñ2
a =bc•µ =57 •0,25 =14,25 ìì/ñ2
CB a aCD
=aC
= Πc•µa
=44•0,25 =11ìì/ñ2
aS
1
= ΠS1
• µa
=48,4•0,25 =12,1 ìì/ñ2
aS
2
= ΠS2
• µa
=69•0,25 =17,25ìì/ñ2
aS
3
= ΠS3
• µa
=22•0,25 =5,5 ìì/ñ2
~ l
a 13,75
ε
CB
= CB
=  =98,2 1/ñ2
. =98,2 1/ñ2
.
lCB
0,14
~
aCD
l 5 2 ε
CD
= =  =31,2 1/ñ. =31,2 1/ñ.
lCD
0,16
Òàíãåíöèàëüíûå óñêîðåíèÿ íàïðàâëåíû ïî ÷àñîâîé ñòðåëêå.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 7 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
3.ÄÈÍÀÌÈ×ÅÑÊÈÉ ÀÍÀËÈÇ ÌÅÕÀÍÈÇÌÀ
3.1 Îïðåäåëåíèå èíåðöèîííûõ íàãðóçîê
Ïðèíÿâ êîýôôèöèåíò (ïîãîííàÿ ìàññà) q=20 êã/ì, îïðåäåëÿåì ìàññû çâåíüåâ è èõ ñèëû âåñà:
m1
=q•lAB
=20•0,05 =1êã; G1
=m1
g=1 •9,8=9,8Í; m2
=q•lBC
=20•014, =2,8êã; G2
=m2
g=2,8•9,8=27,44Í;m3
=q•lCD
=20•016, =3,2êã; G3
=m3
g=3,2•9,8=31,36Í;
Ñèëû èíåðöèè:
FU
1
=m1
•aS
1
=1•12,1 =12,1 Í
FU
2
=m2
•aS
2
=2,8•17,25 =48,3Í
FU
3
=m3
•aS
13
=3,2•5,5 =17,6 Í
Ìîìåíòû èíåðöèè çâåíüåâ:
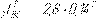 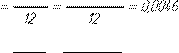 m m
I
S2
 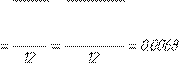 m m
I
S3 Ìîìåíòû ñèë èíåðöèè:
MU
2
=IS
2
•ξCB
=0,0046•98,2 =0,45Í/ì
MU
3
=IS
3
•ξCD
=0,0068•31,2 =0,21Í/ì
3.2 Îïðåäåëåíèå ðåàêöèé â êèíåìàòè÷åñêèõ ïàðàõ
Äëÿ îïðåäåëåíèÿ ðåàêöèé â êèíåìàòè÷åñêèõ ïàðàõ âîñïîëüçóþñü ïðèíöèïàìè Äàëàìáåðà è ñòàòè÷åñêîé îïðåäåëèìîñòüþ ãðóïïû Àññóðà. Âû÷åð÷èâàþ ãðóïïó Àñóðà (çâåíüÿ 2-3) â íàòóðàëüíóþ âåëè÷èíó (ìîæíî òàêæå èñïîëüçîâàòü óæå âû÷èñëåííûé ìàñøòàáíûé êîýôôèöèåíò µ
l
) â ïîëîæåíèè 5 (ñì.ñõåìó) è ïðèêëàäûâàþ ê íåé â ñîîòâåòñòâóþùèõ òî÷êàõ âñå äåéñòâóþùèå ñèëû âåñà çâåíüåâ G2
, G3
; ñèëû èíåðöèè â øàðíèðàõ Â è в ðàñêëàäûâàþ íà íîðìàëüíûå è òàíãåíöèàëüíûå ñîñòàâëåíèÿ; ñèëó ïîëåçíîãî ñîïðîòèâëåíèÿ FC
. Ñèëû èíåðöèè Fu2
è Fu3
íàïðàâëåíû ïðîòèâîïîëîæíî óñêîðåíèÿì as2
è as3
, à ìîìåíòû ñèë èíåðöèè Mu2
è Mu3
, íàïðàâëåíû ïðîòèâîïîëîæíî óãëîâûì óñêîðåíèÿì ξ
CD
è ξ
CB
.
Îïðåäåëÿþ ðåàêöèè R è 12
τ
R , äëÿ ÷åãî ñîñòàâèë óðàâíåíèÿ ðàâíîâåñèÿ êàæäîãî èç çâåíüåâ: 03
τ
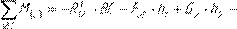 Mu2
=0; Mu2
=0;
 Mu3
=0. Mu3
=0.
Èç ýòèõ óðàâíåíèé ïîëó÷àåì:
Fh -Gh +M
R12τ = u2 1 2 2 u2
=48 ,3•70-27,44•38+0,45 =16,7Í ,3•70-27,44•38+0,45 =16,7Í
BC 140
Gh -Fh +M
R03τ = 3 4 u3 3 u3
=31 ,36•34-17,6•19+0,21 =4,57Í ,36•34-17,6•19+0,21 =4,57Í
DC 160
Äëÿ îïðåäåëåíèÿ íîðìàëüíûõ ñîñòàâëÿþùèõ R è 12
τ
R ñîñòàâëÿåì óðàâíåíèÿ ðàâíîâåñèÿ ãðóïïû Àññóðà: 03
τ
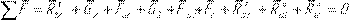
Äëÿ îïðåäåëåíèÿ ìàñøòàáà ñèë µ
F
ïðèìó, ÷òî íàèáîëüøàÿ ñèëà, âõîäÿùàÿ â ýòî óðàâíåíèå –
FC
èçîáðàæàåòñÿ îòðåçêîì fk äëèíîé â 60ìì. Òîãäà ìàñøòàá ïëàíà ñèë áóäåò:
F 1800
µF
= C
=  =30Í/ìì fk 60 =30Í/ìì fk 60
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 8 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Îñòàëüíûå ñèëû îïðåäåëÿþòñÿ íà ÷åðòåæå îòðåçêàìè:
 R R
ab= 12
==0,56 ìì
µF
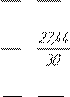 G G
bc= 2
==0,91ìì
µF
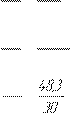 F F
cd = u2
==1,61 ìì
µF
G 31,36
de= 3
=  =1,05ìì =1,05ìì
µF
30
F 17,6
ef = u3
=  =0,58 ìì =0,58 ìì
µF
30
R 4,57
kl= 03
=  =0,15ìì =0,15ìì
µF
30
Äàííûå äëÿ ïîñòðîåíèÿ ïëàíà ñèë ãðóïïû Àññóðà ñâåäåíû â òàáëèöó 2.
Ïðè ýòèì îòðåçêàì ñòðîèì ïëàí ñèë, íà÷èíàÿ ñ òî÷êè à; èç òî÷êè l ïðîâîæó ïðÿìóþ ïàðàëëåëüíóþ R03
n
, à èç òî÷êè a –
ïðÿìóþ, ïàðàëëåëüíóþ R Ýòè ïðÿìûå ïåðåñåêàþòñÿ â òî÷êå t (ñì. ïðèëîæåíèå). Îòðåçêè at è ltâ 12
n
.
ìàñøòàáå µF
èçîáðàæàþò òàíãåíöèàëüíûå ñîñòàâëÿþùèå ðåàêöèé R è 12
n
R , âåëè÷èíû êîòîðûõ îïðåäåëÿþòñÿ: 03
n
R12
n
=at⋅µ
F
=72⋅30 =2160H;
R03
n
=lt⋅µ
F
=38⋅30 =1140H.
Äëÿ îïðåäåëåíèÿ âåëè÷èíû óðàâíîâåøèâàþùåé ñèëû Fó
, äëÿ ÷åãî ñîñòàâëþ óðàâíåíèÿ ðàâíîâåñèÿ âåäóùåãî çâåíà:
∑M(A)
=Fy
⋅AB−R12
⋅h1
−G1
⋅h2
=0,
çâ.1
îòêóäà íàõîæó
 R ⋅h +G ⋅h 2160⋅50+9,8⋅22 R ⋅h +G ⋅h 2160⋅50+9,8⋅22
F
y
12 1 1 2 .
Äëÿ îïðåäåëåíèÿ ðåàêöèé â øàðíèðå À (R01
) çàïèøó óðàâíåíèå âåêòîðíîé ñóììû ñèë, äåéñòâóþùèõ íà êðèâîøèï:

∑F =Fy
+R21
+G1
+Fu1
+R01
=0.
çâ.1
Ïðè îïðåäåëåíèè ìàñøòàáà ïëàíà ñèë µF
ÿ ïðèíÿë, ÷òî íàèáîëüøàÿ ñèëà âõîäÿùàÿ â óðàâíåíèå –
Fy
, èçîáðàæåííàÿ îòðåçêîì ab äëèíîé 108ìì. Èç ýòîãî îïðåäåëþ ìàñøòàá ïëàíà ñèë:
Fy
2164,312
 µF
= = =20Í/ìì ab 108 µF
= = =20Í/ìì ab 108
Äàííûå äëÿ ïîñòðîåíèÿ ïëàíà ñèë âåäóùåãî çâåíà ñâåäåíû â òàáëèöó 3; (ñì.ñõåìó). Èç ïëàíà ñèë âåäóùåãî çâåíà îïðåäåëèòüñÿ R01
:
R01
=ea⋅µ
F
=1⋅20 =20Í.
Òàêèì îáðàçîì, ìåòîäîì êèíåòîñòàòèêè îïðåäåëåíû ðåàêöèè âî âñåõ êèíåìàòè÷åñêèõ ïàðàõ è âåëè÷èíà óðàâíîâåøèâàþùåé ñèëû; óêàçàííûå çàäà÷è ðåøåíû äëÿ ìåõàíèçìà â 5-îì ïîëîæåíèè, êîãäà òî÷êà ïðèëîæåíèÿ ñèëû ïîëåçíîãî ñîïðîòèâëåíèÿ ðàçâèâàåò íàèáîëüøóþ ìîùíîñòü.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 9 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
3.3 Ïîñòðîåíèå ãðàôèêà ïðèâåäåííûõ ìîìåíòîâ ñèë ñîïðîòèâëåíèÿ
Ñèëà F îïðåäåëèòñÿ èç óðàâíåíèÿ ðàâíîâåñèÿ ðû÷àãà Æóêîâñêîãî: y
Fy
⋅pb=Fc
⋅pc,
îòêóäà
F pc
Fy
=  C
. C
.
pb
 Ïðèâåäåííûé ìîìåíò ñèë ñîïðîòèâëåíèÿ îïðåäåëÿåòñÿ êàê TC
=Fn
⋅lAB
,ãäå Fn
= Fy
. Ðåçóëüòàòû âû÷èñëåíèé ñâåäåíû â òàáëèöó 4. Ïðèâåäåííûé ìîìåíò ñèë ñîïðîòèâëåíèÿ îïðåäåëÿåòñÿ êàê TC
=Fn
⋅lAB
,ãäå Fn
= Fy
. Ðåçóëüòàòû âû÷èñëåíèé ñâåäåíû â òàáëèöó 4.
Ïðèíÿâ ìàêñèìàëüíóþ îðäèíàòó y
max
=53 ìì, îïðåäåëÿþ ìàñøòàá äèàãðàììû TC
(ϕ):
T 106,36
µ
T
= Cmax
=  =2Íì/ìì. =2Íì/ìì.
ymax
53
T
Íàõîæó îðäèíàòû y=  (ðåçóëüòàòû â òàáëèöå 4) è ïî ïîëó÷åííûì çíà÷åíèÿì ñòðîþ ãðàôèê TC
(ϕ). (ðåçóëüòàòû â òàáëèöå 4) è ïî ïîëó÷åííûì çíà÷åíèÿì ñòðîþ ãðàôèê TC
(ϕ).
µ
T
Èíòåãðèðóÿ ãðàôè÷åñêè ýòó äèàãðàììó, ïîëó÷àþ äèàãðàììó ðàáîòû ñèë ñîïðîòèâëåíèÿ.
ÎÊ =30ìì –
ïðèíÿòîå ìíîþ ïîëþñíîå ðàññòîÿíèå.
Ñîåäèíèâ ïðÿìîé ëèíèåé íà÷àëî è êîíåö ãðàôèêà AC
(ϕ), ïîëó÷àþ ãðàôèê ðàáîò äâèæóùèõñÿ ñèë AD
(ϕ).
Äèôôåðåíöèðóÿ åãî, ïîëó÷àþ ãðàôèê ìîìåíòîâ äâèæóùèõñÿ ñèë –
îí ïðåäñòàâëÿåò ñîáîé ïðÿìóþ ëèíèþ, ïàðàëëåëüíóþ àáñöèññå. Âåëè÷èíà ìîìåíòà äâèæóùèõ ñèë îïðåäåëÿåòñÿ:
TD
= yD
•µT
=21•2 =42Íì,
ãäå óD
- îðäèíàòà ãðàôèêà TD
( )ϕ.
Ìîùíîñòü íà âàëó êðèâîøèïà îïðåäåëèòüñÿ ïî ôîðìóëå
:
P =TD
⋅ω
1
=42⋅22 =924Âò= 0,924ÊÂò.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 10 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Òàáëèöà 1
| Ïàðàìåòðû |
Ïîëîæåíèÿ |
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| ðñ,ìì |
3 |
18 |
30 |
40 |
47 |
52 |
51 |
37 |
0 |
89 |
134 |
49 |
| VC
, ì/ñ |
0,075 |
0,45 |
0,75 |
1 |
1,175 |
1,3 |
1,275 |
0,925 |
0 |
2,225 |
3,35 |
1,225 |
| cb,ìì |
41 |
55 |
55 |
50 |
40 |
28 |
14 |
8 |
43 |
111 |
112 |
5 |
| Vcb
, ì/ñ |
1,025 |
1,375 |
1,375 |
1,25 |
1 |
0,7 |
0,35 |
0,2 |
1,075 |
2,775 |
2,8 |
0,125 |
| ω
ÑÂ
,1/ñ |
7,32 |
9,82 |
9,82 |
8,93 |
7,14 |
5 |
2,5 |
1,43 |
7,68 |
19,8 |
20 |
0,89 |
| ω
ÑD
,1/ñ |
0,47 |
2,81 |
4,69 |
6,25 |
7,34 |
8,125
|
7,97 |
5,78 |
0 |
13,9 |
20,94 |
7,66 |
| yi, ìì
|
0 |
3 |
10 |
20,5 |
34,5 |
36 |
36 |
36 |
36 |
0 |
0 |
0 |
| FC,
êÍ |
0 |
0,15 |
0,5 |
1,025 |
1,725 |
1,8
|
1,8 |
1,8 |
1,8 |
0 |
0 |
0 |
Òàáëèöà 2
| R
12τ |
G
2
|
F
u
2 |
G
3
|
F
u
3 |
F
C
|
R
τ03 |
| 16,7 |
24,44 |
48,3 |
31,36 |
17,6 |
1800 |
4,57 |
| ab |
bc |
cd |
de |
ef |
fk |
kl |
| 0,56 |
0,91 |
1,61 |
1,05 |
0,58 |
60 |
0,15 |
Òàáëèöà 2
| F
y
|
R
21
|
G
1
|
F
u
1 |
| 2164,31 |
2160 |
9,8 |
12,1 |
| ab |
bc |
cd |
de |
| 108 |
108 |
0,49 |
0,6 |
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 11 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Òàáëèöà 3
| Ïàðàìåòðû |
Ïîëîæåíèÿ |
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| ðñ,ìì |
3 |
18 |
30 |
40 |
47 |
52 |
51 |
37 |
0 |
89 |
134 |
49 |
| Fy
, Í |
0 |
61,36 |
375 |
931,81 |
1843 |
2127 |
2086,4 |
1513,6 |
0 |
0 |
0 |
0 |
| TC
, Íì |
0 |
3,068 |
18,75 |
46,59 |
92,13 |
106,4 |
104,32 |
75,18 |
0 |
0 |
0 |
0 |
| ó, ìì |
0 |
1,5 |
9,37 |
23,29 |
46,06 |
53 |
52,16 |
37,84 |
0 |
0 |
0 |
0 |
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 12 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
4.ÊÈÍÅÌÅÒÈ×ÅÑÊÈÉ ÐÀÑ×ÅÒ ÏÐÈÂÎÄÀ
Èñõîäíûå äàííûå
:
N=0.924 êÂò ω
=12ñ−
1
Ïîäáîð ýëåêòðîäâèãàòåëÿ:
4.1 ×àñòîòà âðàùåíèÿ âàëà èñïîëíèòåëüíîãî ìåõàíèçìà: n îá/ìèí; îá/ìèí;
i =iðì
⋅içï
= (2÷5) (⋅ 8÷40) = (16÷200);nîá
=114,59⋅(16÷200) (= 1834÷22929);
4.2 Îáùèé êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ ïðèâîäà η
= η
çï
⋅η
ïê
2
⋅η
ðï
=0,85⋅0,992
⋅0,95 =0,791;
ηïê
=0.99 –
ê.ï.ä. ïàðû ïîäøèïíèêîâ êà÷åíèÿ; η÷ï
=0.85 –
ê.ï.ä. ÷åðâÿ÷íîé ïåðåäà÷è; ηïñ
=0.95 –
ê.ï.ä. ðåìåííîé ïåðåäà÷è.
4.3 Ïîòðåáíàÿ ìîùíîñòü ýëåêòðîäâèãàòåëÿ
 Näâ. = N = 0,924=1,167êÂò; η
0,791 Näâ. = N = 0,924=1,167êÂò; η
0,791
4.4 Ïåðåäàòî÷íîå ÷èñëî ïðèâîäà
 Uîáù. = níîì. = 2880 =25,13; Uîáù. = níîì. = 2880 =25,13;
n3
114,59
4.5 Ïåðåäàòî÷íîå ÷èñëî ðåìåííîé ïåðåäà÷è i
 iðì = îáù. = 25,13 =2,513 iðì = îáù. = 25,13 =2,513
içï
10
Z=4, òî U÷åðâ
=10
Òàáëèöà 4.1
Ñèíõðàíèç.
×àñòîòà âðàùåíèÿ
|
n ïðè N=1,5
|
n
U =  ýë.äâ ýë.äâ
nïð.
|
Uðåì
|
U÷åðâ
|
| 3000 |
2880 |
 =25,13 =25,13 |
2,513 |
10 |
Îïðåäåëåíèå êèíåìàòè÷åñêèõ è ñèëîâûõ ïàðàìåòðîâ ïðèâîäà.
4.6 Ïåðåäàòî÷íûå ÷èñëà ñòóïåíåé ïåðåäà÷ ïðèâîäà
Uðåì
=2.513
U÷åðâ
=10
Uîáù
=Uðåì
⋅U÷åðâ
=2,513⋅10 =25,13
4.7 ×àñòîòà âðàùåíèÿ âàëîâ ïðèâîäà:
n1
=nýë.äâ
=2880 n2
=n1
/Uðåì
=2880/2,513=1145,9 n3
=n2
/U÷åðâ
=1145,9/10=114,59
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 13 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Ìîùíîñòè.
4.8 Ìîùíîñòè íà âàëàõ: P3
=Pïð.â
=0,924 êÂò
P2
=P3
/η÷ï
=0,924/0,85=1,087 êÂò
P1
=P2
/ηðï
=1,087/0,95=1,144 êÂò
Âðàùàþùèå ìîìåíòû íà âàëàõ 4.9 Ìîìåíòû íà âàëàõ:
P 1,144
T1
=9550 1
=9550  =3,794Íì =3,794Íì
n1
2880
T2
=T1
⋅Uðåì
⋅η
ðåì
=3,794⋅2,513⋅0,95 =7,689Íì
T3
=T2
⋅U÷åð
⋅η
÷åð
=7,689⋅10⋅0,85 =65,356 Íì
Òàáëèöà 4.2
Ðåçóëüòàòû êèíåìàòè÷åñêîãî ðàñ÷åòà
| ÂÀËÛ |
1 |
2 |
3 |
| Ïåðåäà÷à |
Ðåìåííàÿ |
×åðâÿ÷íàÿ |
| ÊÏÄ |
0,95 |
0,85 |
| Ïåðåäàòî÷íîå ÷èñëî U |
2,513 |
10 |
| ×àñòîòà âðàùåíèÿ n |
2880 |
1145,9 |
114,59 |
| Ìîùíîñòü N |
0,924 |
1,087 |
1,144 |
| Ìîìåíò Ò |
3,794 |
7,689 |
65,356 |
| d ÂÀËÀ |
22 |
 |
 |
Òàáëèöà 4.3
Òåõíè÷åñêèå õàðàêòåðèñòèêè äâèãàòåëÿ
| Òèï ýëåêòðîäâèãàòåëÿ |
Ìîùíîñòü
N, êÂò
|
Àñèíõðîííàÿ
÷àñòîòà âðàùåíèÿ
|
Tïóñê

Tíîì
|
Tmax
Tíîì
|
| 4A80A2Ó3 |
1,5 |
2880 |
2 |
2,2 |
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 14 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
5.ÐÀÑ×ÅÒ ×ÅÐÂß×ÍÎÉ ÏÅÐÅÄÀ×È
5.1 Èñõîäíûå äàííûå T2
=65,356 Íì - ìîìåíò íà âàëó ÷åðâÿ÷íîãî êîëåñà. n1
=1145,9 îá/ìèí - ÷àñòîòà âðàùåíèÿ âàëà ÷åðâÿêà. n2
=114,59 îá/ìèí - ÷àñòîòà âðàùåíèÿ âàëà êîëåñà.
U=10 –
ïåðåäàòî÷íîå ÷èñëî ÷åðâÿ÷íîé ïåðåäà÷è.
Ðàñïîëîæåíèå ÷åðâÿêà –
íèæíåå.
5.2 Óñòàíîâëåíèå îñíîâíûõ äàííûõ
5.2.1 ×èñëî âèòêîâ ÷åðâÿêà ïðè U=10 ïðèíèìàåì Z1
=10
5.2.2 ×èñëî çóáüåâ ÷åðâÿ÷íîãî êîëåñà ñ îêðóãëåíèåì äî öåëîãî ÷èñëà Z2
=Z1
⋅U =4⋅10 =40
5.2.3 Óòî÷íåííîå ïðèäàòî÷íîå ÷èñëî
r 40
U = 2
=  =10 =10
r1
4
5.2.4 ×àñòîòà âðàùåíèÿ âàëà ÷åðâÿ÷íîãî êîëåñà.
n 1145,9
 n2
= 1
= =114,59îá/ìèí n2
= 1
= =114,59îá/ìèí
u 10
5.2.5 Îðèåíòèðîâî÷íàÿ ñêîðîñòü ñêîëüæåíèÿ â çàöåïëåíèè.
Vñê
 ì/ñ ì/ñ
5.2.6 Âûáîð ïðîôèëÿ ÷åðâÿêà è ìàòåðèàëîâ ÷åðâÿ÷íîé ïàðû.
Ïðèíèìàåì àðõèìåäîâ ÷åðâÿê ZA èç ñòàëè 20 ñ öåìåíòàöèåé è çàêàëêîé äî òâåðäîñòè 56 … 63 HRC, âèòêè øëèôîâàííûå è ïîëèðîâàííûå. Ó÷èòûâàÿ, ÷òî Vck
< 4ì/ñ, ïî òàáëèöå ïðèíèìàåì â êà÷åñòâå ìàòåðèàëà ÷åðâÿ÷íîãî êîëåñà áåçîëîâÿííóþ áðîíçó ÁðÀ9ÆÇË ñ õàðàêòåðèñòèêàìè: E2
=(0.88...1.14)·105
ÌÏà; v2
=0.35ì/ñ; σT2
=196...343 ÌÏà; σâ2
=490...588 ÌÏà.
5.2.7  ñîîòâåòñòâèè ñ òàáëè÷íûìè äàííûìè ïðè V=2,077 ì/ñ ïðèíèìàåì 8 ñòåïåíü òî÷íîñòè (nT
=8)
5.2.8 Îðèåíòèðîâî÷íûé ÊÏÄ ïåðåäà÷è.
0,98 0,98
 η
= = =0,873 η
= = =0,873
1 +0,25f⋅u 1 +0,25⋅0,049⋅10
ãäå f=tgϕ=tg2°49’
39,17”
=0,049–
ïðèâåäåííûé êîýôôèöèåíò òðåíèÿ â çàöåïëåíèè;
φ
=3,5-0,92·ln(Vñê
)=3,5-0,92·ln(2,077)=20
49’
39,18”
–
ïðèâåäåííûé óãîë òðåíèÿ.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 15 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
5.2.9 Ìîùíîñòü íà âàëó ÷åðâÿêà.
T ⋅n 65,356⋅114,59
 P1
= 2 2
= =0,898êÂò P1
= 2 2
= =0,898êÂò
9550⋅0,901 9550⋅0,873
5.2.10 Êîýôôèöèåíò äèàìåòðà ÷åðâÿêà. q=0,25z2
=0,25⋅40 =10 ïî ÃÎÑÒ 19672-74
5.2.11 Êîýôôèöèåíò íàãðóçêè.
K=Kβ
·Kv
=1,02·1,14=1,163
Kβ
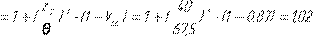   - êîýôôèöèåíò íåðàâíîìåðíîñòè - êîýôôèöèåíò íåðàâíîìåðíîñòè
ðàñïðåäåëåíèÿ íàãðóçêè ïî äëèíå ëèíèè êîíòàêòà â ñëåäñòâèå äåôîðìàöèè ÷åðâÿêà;
⎛ 1 ⎞ ⎛ 1 ⎞
θ
=9⋅(q−4)⋅⎜⎜
1 + z
 1 ⎟⎟⎠
=9⋅(10−4)⋅⎜⎝
1 +4 1 ⎟⎟⎠
=9⋅(10−4)⋅⎜⎝
1 +4
 ⎟⎠
=67,5–
êîýôôèöèåíò äåôîðìàöèè ÷åðâÿêà. ⎝ ⎟⎠
=67,5–
êîýôôèöèåíò äåôîðìàöèè ÷åðâÿêà. ⎝
T t
vcp
=
∑
T
 maxi
⋅
t
Σ
i
=1⋅0,3+0,8⋅0,7 =0,87 - ñðåäíÿÿ îòíîñèòåëüíàÿ íàãðóçêà; maxi
⋅
t
Σ
i
=1⋅0,3+0,8⋅0,7 =0,87 - ñðåäíÿÿ îòíîñèòåëüíàÿ íàãðóçêà;
Kv
=0,3+0,1⋅nT
+0,02⋅Vñê
=0,3+0,1⋅8+0,02⋅2,077 =1,14 - êîýôôèöèåíò, ó÷èòûâàþùèé äèíàìè÷åñêóþ íàãðóçêó.
5.6 Äîïóñêàåìûå êîíòàêòíûå íàïðÿæåíèÿ.
5.6.1 Äëÿ áåçîëîâÿííîé áðîíçû
[σ]H
= [σ]H
0
⋅C
V
′ = 300⋅0,823 = 246,9
ãäå [σ]H
0
= 300 ÌÏà –
èñõîäíîå äîïóñêàåìîå íàïðÿæåíèå ìàòåðèàëà ÷åðâÿ÷íîãî êîëåñà ïðè øëèôîâàííûõ è ïîëèðîâàííûõ ñ òâåðäîñòüþ HRCý
≥
45;
CV
′ =1 −0.085⋅Vñê
=1 −0,085⋅2,077 =0,823 - êîýôôèöèåíò, ó÷èòûâàþùèé âëèÿíèå ñêîðîñòè ñêîëüæåíèÿ íà çàåäàíèå.
5.7 Îïðåäåëåíèå îñíîâíûõ ðàçìåðîâ.
5.7.1 Ìåæîñåâîå ðàññòîÿíèå:
  K⋅T 1,163⋅65,356 aw
= 625⋅3 2
2
=625⋅3
2
=68ìì K⋅T 1,163⋅65,356 aw
= 625⋅3 2
2
=625⋅3
2
=68ìì
[σ]H
247
5.7.2 Ðàñ÷åòíûé ìîäóëü:
2⋅a 2⋅68
 m= w
= =2,72ìì. z2
+q 40+10 m= w
= =2,72ìì. z2
+q 40+10
Ïî ÃÎÑÒ 2144-76 ïðèíèìàåì m = 3,15ìì.
5.7.3 Ìåæîñåâîå ðàññòîÿíèå ïðè ñòàíäàðòíûõ çíà÷åíèÿõ m è q:
 m(q+z ) 3,15⋅(10+40) m(q+z ) 3,15⋅(10+40)
aw
ìì
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 16 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
5.7.4 Êîýôôèöèåíò ñìåùåíèÿ
x ìì ìì
5.7.5 Ãåîìåòðè÷åñêèå ïàðàìåòðû ïåðåäà÷è:
×åðâÿê
Äåëèòåëüíûé äèàìåòð: d1
=m⋅q =3,15⋅10 =31,5ìì.
Äèàìåòð âåðøèí âèòêîâ: da1
=d1
+2m=31,5+2⋅3,15 =37,8ìì.
Äèàìåòð âïàäèí âèòêîâ: df1
=d1
−2,4m=31,5−2,4⋅3,15 =23,94ìì.
z 4
Äåëèòåëüíûé óãîë ïîäú¸ìà âèòêà: γ
=arctg 1
=arctg  =21°48'5,07'' =21°48'5,07''
q 10
⎛ z ⎞
Íà÷àëüíûé óãîë ïîäúåìà âèòêà: γ
w
=arctg⎜⎜
q
 +
2
1
⋅
x
⎟⎟
⎠
=arctg⎜⎝
⎛
10 +
2
1
⋅
x
⎟⎟
⎠
=arctg⎜⎝
⎛
10
 +
4
2
⋅
0
⎠
⎞
⎟ =21°48'5,07'' ⎝ +
4
2
⋅
0
⎠
⎞
⎟ =21°48'5,07'' ⎝
Óãîë ïðîôèëÿ âèòêà â íîðìàëüíîì ñå÷åíèè ÷åðâÿêà íà íà÷àëüíîì öèëèíäðå: α
nw
=arctg(tg20°⋅cosγo
=arctg(tg20°⋅cos21ο
48'5,07'') =18°40'19,41''
Äëèíà íàðåçíîé ÷àñòè ÷åðâÿêà: b1
≥(12,5 +0,09⋅z2
)⋅m=(12,5 +0,09⋅40)⋅3,15 =50,71ìì.
×åðâÿ÷íîå êîëåñî
Øèðèíà çóá÷àòîãî âåíöà: z1
=4; b2
≤0,67⋅da1
=0,67⋅37,8=25,32ìì.
Íà÷àëüíûé è äåëèòåëüíûå äèàìåòðû: d2
=dw2
=m⋅z2
=3,15⋅40 =126ìì.
Äèàìåòð âåðøèí çóáüåâ: da2
=d2
+2⋅m=126+2⋅3,15 =132,3ìì.
Äèàìåòð âïàäèí çóáüåâ: df2
=d2
−2,4m=126−2,4⋅3,15 =118.44ìì.
6⋅m 6⋅3,15
Íàèáîëüøèé äèàìåòð: daM2
≤da2
+  =132,3+ =132,3+  =135,45ìì. =135,45ìì.
z1
+2 4+2
b 25,32
Óñëîâíûé óãîë îáõâàòà: 2δ
=2⋅arcsin  2
=2⋅arcsin 2
=2⋅arcsin  =88°42'52,42''. da1
−0.5⋅m 37,8−0,5⋅3,15 =88°42'52,42''. da1
−0.5⋅m 37,8−0,5⋅3,15
5.8 Îêðóæíûå ñêîðîñòè.
π
⋅d ⋅n π
⋅31,5⋅1145,9
 Íà ÷åðâÿêå: V1
= w1 1
= =1,889ì/ñ. 60000 60000 Íà ÷åðâÿêå: V1
= w1 1
= =1,889ì/ñ. 60000 60000
π
⋅d ⋅n π
⋅126⋅114,59
 Íà êîëåñå: V2
= w2 2
= =0,756ì/ñ. Íà êîëåñå: V2
= w2 2
= =0,756ì/ñ.
60000 60000
5.9 Ñêîðîñòü ñêîëüæåíèÿ.
V 1,889
 Vñê
= 1
= =2,034ì/ñ Vñê
= 1
= =2,034ì/ñ
cosγ
w
cos21°48'5,07''
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 17 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
5.10 Óòî÷íåíèå ÊÏÄ ïåðåäà÷è, êðóòÿùåãî ìîìåíòà è ìîùíîñòè íà ÷åðâÿêå.
5.10.1 ÊÏÄ ÷åðâÿ÷íîãî çàöåïëåíèÿ:
tgγ tg21°48'5,07"
 ηçàö
= w
= =0,871 ηçàö
= w
= =0,871
tg(γw
+ϕ) tg(21°48'5,07"+2°50'48,47'')
ϕ=3,5−0,92⋅ln(Vck
) =3,5−0,92⋅ln(2,034) =2°50'48,47''- óòî÷í¸ííûé ïðèâåä¸ííûé óãîë òðåíèÿ
5.10.2 Îáùèé ÊÏÄ ÷åðâÿ÷íîãî ðåäóêòîðà
η
= η
çàö
⋅η
ð
=0,871⋅0,98=0,854
ãäå ηр
= 0,98 –
ÊÏÄ ó÷èòûâàþùèé ïîòåðè íà ðàçáðûçãèâàíèå è ïåðåìåøèâàíèÿ ìàñëà.
T 65,356
5.10.3 Êðóòÿùèé ìîìåíò íà âàëó ÷åðâÿêà:T1
= 2
=  =7,65Íì. u⋅η
10⋅0,854 =7,65Íì. u⋅η
10⋅0,854
5.10.4 Ìîùíîñòü íà âàëó ÷åðâÿêà:P1
 êÂò. êÂò.
5.11 Ñèëû â çàöåïëåíèè.
5.11.1 Îêðóæíàÿ ñèëà íà êîëåñå (îñåâàÿ íà ÷åðâÿêå):
2000⋅T 2000⋅65,356
 Ft2
=Fx1
= 2
= =1037,39Í. Ft2
=Fx1
= 2
= =1037,39Í.
dw2
126
5.11.2 Îêðóæíàÿ ñèëà íà ÷åðâÿêå (îñåâàÿ íà êîëåñå):
2000⋅T 2000⋅7,65
 Ft1
=Fx2
= 1
= =485,71Í. Ft1
=Fx2
= 1
= =485,71Í.
dw1
31,5
5.11.3 Ðàäèàëüíàÿ ñèëà: F
r
=Ft2
⋅tgα
=1037,39⋅tg20° =377,57Í.
5.12 Ïðîâåðî÷íûé ðàñ÷åò ïî êîíòàêòíûì íàïðÿæåíèÿì.
5.12.1 Êîýôôèöèåíò, ó÷èòûâàþùèé ìåõàíè÷åñêèå ñâîéñòâà ìàòåðèàëîâ:
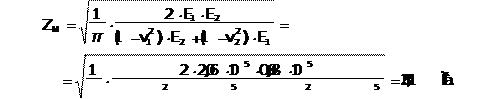 π
(1 −0,35 )⋅0,88⋅10 +(1 −0,49)⋅2,06⋅10 π
(1 −0,35 )⋅0,88⋅10 +(1 −0,49)⋅2,06⋅10
Çäåñü Å1
è Å2
–
ìîäóëè óïðóãîñòè ìàòåðèàëîâ ÷åðâÿêà è âåíöà êîëåñà â ÌÏà
v1
è v3
–
êîýôôèöèåíòû Ïóàññîíà ìàòåðèàëîâ ÷åðâÿêà è âåíöà ÷åðâÿ÷íîãî êîëåñà
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 18 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
5.12.2 Êîýôôèöèåíò, ó÷èòûâàþùèé ôîðìó ïîâåðõíîñòåé:
2⋅cos2
γ
w
2⋅cos2
21°48'5,07''
 ZH
= = =1,82 ZH
= = =1,82
sin2⋅α
nw
sin2⋅18°40'19,41''
5.12.3 Êîýôôèöèåíò, ó÷èòûâàþùèé ñóììàðíóþ äëèíó êîíòàêòíûõ ëèíèé:
1 1
 Zε
= = =0,848, ãäå Zε
= = =0,848, ãäå
ε
α
⋅Kε
1,85⋅0,75
3,9 3,9
ε
α
=1,95− =1,95− =1,852 - êîýôôèöèåíò òîðöåâîãî ïåðåêðûòèÿ,
z2
40
Kε
=0,75 - êîýôôèöèåíò èçìåíåíèÿ ñóììàðíîé äëèíû êîíòàêòíûõ ëèíèé.
5.12.4 Êîýôôèöèåíò, ó÷èòûâàþùèé óñëîâíûé óãîë îáõâàòà:
360° 360°
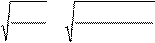 Zδ
= = =2,01. Zδ
= = =2,01.
2⋅δ
88°42'52,42''
5.12.5 Óòî÷íåíèå êîýôôèöèåíòà íàãðóçêè
K =Kβ
⋅Kv
=1,02⋅1,14=1,162 ãäåK
β
= 1,02 –
êîýôôèöèåíò íåðàâíîìåðíîñòè ðàñïðåäåëåíèÿ íàãðóçêè ïî äëèíå ëèíèè êîíòàêòà,
âñëåäñòâèå äåôîðìàöèè ÷åðâÿêà, îñòàëñÿ ïðåæíèì, òàê êàê íå èçìåíèëèñü q è θ
,
Kv
=0,3+0,1⋅nT
+0,02⋅Vñê
=0,3+0,1⋅8+0,02⋅2,034=1,14 - èçìåíèëàñü ñêîðîñòü ñêîëüæåíèÿ.
5.12.6 Óòî÷íåíèå äîïóñêàåìîãî êîíòàêòíîãî íàïðÿæåíèÿ: [δ]H
= [δ]H
0
⋅CV
′ =300⋅0,827 =248,13ÌÏà , ãäå CV
′ =1 −0,085⋅2,034=0,827
5.12.7 Äåéñòâèòåëüíûå êîíòàêòíûå íàïðÿæåíèÿ:
25,2 K⋅T 25.2 1,162⋅65,356
 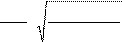 δ
H
=ZM
⋅ZH
⋅Zτ
⋅Zδ
⋅ ⋅ 2
=203,01⋅1,82⋅0,848⋅2,01⋅ ⋅ =195,56 ÌÏà δ
H
=ZM
⋅ZH
⋅Zτ
⋅Zδ
⋅ ⋅ 2
=203,01⋅1,82⋅0,848⋅2,01⋅ ⋅ =195,56 ÌÏà
d2
ddw
1 126 31,5
Óñëîâèå ïðî÷íîñòè ïî êîíòàêòíûì íàïðÿæåíèÿì âûïîëíåíî, ò.ê. σH
π [δ]H
= 246ÌÏà
5.12.8 Ïðîâåðêà íà ñòàòè÷åñêóþ ïðî÷íîñòü:
T
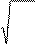 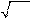 δ
Íïèê
= δ
H
⋅ max
=195,56⋅ 2.2 =290ÌÏà –
äåéñòâèòåëüíîå ïèêîâîå íàïðÿæåíèå δ
Íïèê
= δ
H
⋅ max
=195,56⋅ 2.2 =290ÌÏà –
äåéñòâèòåëüíîå ïèêîâîå íàïðÿæåíèå
Tíîì
[δ]ст
=2⋅δ
T2
=2⋅270 =540ÌÏà –
ïðåäåëüíî äîïóñòèìîå êîíòàêòíîå íàïðÿæåíèå.
Ñòàòè÷åñêàÿ ïðî÷íîñòü îáåñïå÷åíà, ò.ê. σНпик
< [δ]ст
= 540ÌÏà.
Óñëîâèÿ ïðî÷íîñòè 5.12.7 è 5.12.8 âûïîëíÿþòñÿ. Ìàòåðèàë êîëåñà îñòàâëÿåì ïðåæíèì.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 19 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
5.13 Ïðîâåðî÷íûé ðàñ÷åò çóáüåâ êîëåñà íà ïðî÷íîñòü ïðè èçãèáå
5.13.1 Êîýôôèöèåíò, ó÷èòûâàþùèé ñóììàðíóþ äëèíó êîíòàêòíûõ ëèíèé:
 cosγ
cos21°48'5,07'' cosγ
cos21°48'5,07''
Y 
α ε
5.13.2 Êîýôôèöèåíò, ó÷èòûâàþùèé óñëîâíûé óãîë îáõâàòà:
360° 360°
 Yδ
= = =4,058 Yδ
= = =4,058
2⋅δ
88°42'52,42''
5.13.3 Êîýôôèöèåíò, ó÷èòûâàþùèé íàêëîí çóáà êîëåñà:
λ
21°48'5,07''
 Yγ
=1 − =1− =0,844 Yγ
=1 − =1− =0,844
140° 140°
5.13.4 Êîýôôèöèåíò ôîðìû çóáà:
z 40
 Ïðè x
=0 è zV
= 2
3
=
3
=50 Ïðè x
=0 è zV
= 2
3
=
3
=50
cosγ
cos21°48'5,07''
êîýôôèöèåíò ôîðìû çóáà áóäåò YF
=2,19.
5.13.5 Óñëîâíûé áàçîâûé ïðåäåë èçãèáíîé âûíîñëèâîñòè çóáüåâ êîëåñà äëÿ áðîíç ïðè íåðåâåðñèâíîé íàãðóçêå:
δ
F0
=0,14⋅δ
â2
+0,44⋅δ
T2
=0,14⋅540+0,44⋅270 =194,4ÌÏà.
5.13.6 Êîýôôèöèåíò ðåæèìà:
 µ
= µ
=
 9 ∑
t
t
Σ
i
⎛
⎜⎜⎝
T
T
maxi
⎞
⎟⎟⎠
=0,35⋅( )1 +0,65⋅(0.8) =0,437 9 ∑
t
t
Σ
i
⎛
⎜⎜⎝
T
T
maxi
⎞
⎟⎟⎠
=0,35⋅( )1 +0,65⋅(0.8) =0,437
5.13.7 Ýêâèâàëåíòíîå ÷èñëî öèêëîâ:
NFE
=25⋅107
5.13.7 Êîýôôèöèåíò äîëãîâå÷íîñòè:
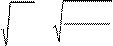 NF0
9 106 7 =0,543 KFL
=9 = NF0
9 106 7 =0,543 KFL
=9 =
NFE
25⋅10
5.13.8 Äîïóñêàåìîå íàïðÿæåíèå èçãèáà:
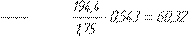 δ δ
[δ]F
=  F0
⋅KFL
= ÌÏà F0
⋅KFL
= ÌÏà
SF
ãäå S
F
=1,75- êîýôôèöèåíò áåçîïàñíîñòè.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 20 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
5.13.9 Íàïðÿæåíèå èçãèáà â çóáüÿõ:
F ⋅K 1037⋅1,73
δ
F
=Yε
⋅Yδ
⋅Yγ
⋅YF
⋅  t2
=0,668⋅4,058⋅0,844⋅2,193⋅ t2
=0,668⋅4,058⋅0,844⋅2,193⋅  =28,87ÌÏà =28,87ÌÏà
π
⋅dw1
⋅m π
⋅31,5⋅3,15
σF
< [δ]F
0
= 60,32ÌÏà.
5.13.10 Ïðîâåðî÷íûé ðàñ÷åò çóáüåâ êîëåñà íà ñòàòè÷åñêóþ ïðî÷íîñòü ïðè èçãèáå:
T
δ
Fïïè
= δ
F
⋅ max
=28,87⋅2,2 =63,52 ÌÏà –
äåéñòâèòåëüíîå ïèêîâîå íàïðÿæåíèå
Tíîì
[δ]Нст
= 0,8⋅δT
2
=0.8⋅270 =216ÌÏà –
ïðåäåëüíî äîïóñòèìîå íàïðÿæåíèå èçãèáà.
σFппи
π [ ]σ Fсста
= 216ÌÏà
Óñëîâèÿ ïðî÷íîñòè 5.13.10 è 5.13.11 âûïîëíÿþòñÿ. Ìàòåðèàë êîëåñà îñòàâëÿåì ïðåæíèì.
5.14 Òåïëîâîé ðàñ÷åò
5.14.1 Òåìïåðàòóðà ìàñëà ïðè óñòàíîâèâøåìñÿ ðåæèìå:
1000⋅P ⋅(1 − η)
1000⋅1,087⋅(1 −0,854) tóñò
=t0
+  2
=20+ 2
=20+  =65,1°Ñ < [t] =70°Ñ =65,1°Ñ < [t] =70°Ñ
k⋅A⋅(1 + ψ)
15⋅0,125⋅(1 +0,3)
t0
=20°Ñ - òåìïåðàòóðà îêðóæàþùåé ñðåäû; k=15Âò/(ì2
ãðàäóñ) –
êîýôôèöèåíò òåïëîîòäà÷è;
A≈20⋅aw
2
=20⋅0,0792
=0,125ì2
–
ñâîáîäíàÿ ïîâåðõíîñòü îõëàæäåíèÿ êîðïóñà ðåäóêòîðà; ψ
=0.3- êîýôôèöèåíò, ó÷èòûâàþùèé òåïëîîòâîä â ôóíäàìåíòàëüíóþ ïëèòó èëè ðàìó ìàøèíû.
Òåìïåðàòóðíûé ðåæèì óäîâëåòâîðèòåëüíûé.
5.15 Ðàñ÷åò ÷åðâÿêà íà æåñòêîñòü.
Ðàññòîÿíèå ìåæäó ñåðåäèíàìè îïîð âàëà ÷åðâÿêà ïðè ïðèáëèæåííîì ðàñ÷åòå ìîæíî ïðèíèìàòü ðàâíûì:
L = 0.95⋅d2
= 0.95⋅126 = 119,7 ìì
Ïðàâèëüíîñòü çàöåïëåíèÿ ÷åðâÿ÷íîé ïàðû ìîæåò áûòü îáåñïå÷åíà ëèøü ïðè äîñòàòî÷íîé æåñòêîñòè ÷åðâÿêà. Ñðåäíÿÿ äîïóñêàåìàÿ ñòðåëà ïðîãèáà [f] ÷åðâÿêà ìîæåò áûòü ïðèíÿòà:
 f =(0,005...0,01)m=(0,005...0,01)•315, =0,015....0,031ìì f =(0,005...0,01)m=(0,005...0,01)•315, =0,015....0,031ìì
Ñòðåëà ïðîãèáà ÷åðâÿêà, âàë êîòîðîãî îïèðàåòñÿ íà äâà ðàäèàëüíî-óïîðíûõ ïîäøèïíèêà îïðåäåëÿåòñÿ ïî ôîðìóëå:
 L3 (Fr1)2 +(Ft2)2 f = L3 (Fr1)2 +(Ft2)2 f =
48EJïð
ãäå E = 2.1 10.
5
МПа
L –
ðàññòîÿíèå ìåæäó ñåðåäèíàìè îïîð;
Jïð –
ïðèâåäåííûé ìîìåíò èíåðöèè ñå÷åíèÿ ÷åðâÿêà, îïðåäåëÿåìûé ïî ýìïèðè÷åñêîé ôîðìóëå:
πdf
4
1
da1
π•23,944
37,8 4
  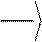 Jïð
= 0,375+0,625 = 0,375+0,625=21958,02ìì 64 df1
64 23,94 Jïð
= 0,375+0,625 = 0,375+0,625=21958,02ìì 64 df1
64 23,94
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 21 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Íàéäåì ðåàëüíóþ ñòðåëó ïðîãèáà:
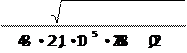 f =1197, 3 • (377,57)2 + 485( 75, )2 =0,0047ìì f =1197, 3 • (377,57)2 + 485( 75, )2 =0,0047ìì
f < [f], ñëåäîâàòåëüíî, óñëîâèå æåñòêîñòè âûïîëíÿåòñÿ.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 22 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
6.ÏÐÎÅÊÒÍÛÉ ÐÀÑ×ÅÒ ÂÀËΠÐÅÄÓÊÒÎÐÀ È ÏÎÄÁÎÐ ÏÎÄØÈÏÍÈÊÎÂ.
Ðàññ÷èòàåì âõîäíîé è âûõîäíîé âàëû. Èç ïðåäûäóùèõ ðàñ÷åòîâ ðåäóêòîðà èçâåñòíî:
à) ìîìåíòû ïåðåäàâàåìûå âàëàìè ÒI
= 7.689 Í⋅ì è ÒII
= 65.356 Í⋅ì;
á) äèàìåòðû d1
= 31,5 ìì è d2
= 126 ìì;
6.1. Âõîäíîé âàë ÷åðâÿ÷íîãî ðåäóêòîðà.
6.1.1. Âûáîð ìàòåðèàëà âàëà.
Íàçíà÷àåì ìàòåðèàë âàëà –
ÁðÀ9Æ3Ë: σÂ
= 500 ÌÏà, σÒ
= 230 ÌÏà.
6.1.2. Ïðîåêòíûé ðàñ÷åò âàëà.
Ïðèáëèæåííî îöåíèì äèàìåòð êîíñîëüíîãî ó÷àñòêà âàëà ïðè [τ]=20 ÌÏà.
T 7,689•1000
 dâ
= 3 = 3
=12 ìì dâ
= 3 = 3
=12 ìì
0,2[ ]τk
0.2•20
Ïî ñòàíäàðòíîìó ðÿäó ïðèíèìàåì dâ
=12 ìì, òîãäà t =2 ìì, r = 1.6 ìì, f =1.
6.1.3. Îïðåäåëèì äèàìåòðû ó÷àñòêîâ âàëà.
Äèàìåòðû ïîäøèïíèêîâûõ øååê:
dï1
= dâ
+2⋅t = 12 +2⋅2 = 16 ìì; ïðèíèìàåì dï1
= 17 ìì
6.2. Âûõîäíîé âàë.
6.2.1. Âûáîð ìàòåðèàëà âàëà.
Âûáåðåì ñòàëü 40Õ
6.2.2. Ïðèáëèæåííî îöåíèì äèàìåòð âûõîäíîãî êîíöà âàëà ïðè [τ] = 30 ÌÏà.
Ò 65.356•1000
 dâ
= 3 = 3 = 20 ìì dâ
= 3 = 3 = 20 ìì
0,2• [ ]τ 0,2•30
Ïî ñòàíäàðòíîìó ðÿäó ïðèíèìàåì dâ
=20 ìì
6.2.3. Îïðåäåëèì äèàìåòðû ó÷àñòêîâ âàëà. Äèàìåòðû ïîäøèïíèêîâûõ øååê:
dï2
= dâ
+2⋅t = 20+2⋅2 = 24 ìì;
Çíà÷åíèÿ dï
äîëæíû áûòü êðàòíû 5, ïîýòîìó ïðèíèìàåì dï2
= 25 ìì
dáï2
= dï2
+3,2⋅r = 24+3,2⋅1,6 = 29ìì
Ïî ñòàíäàðòíîìó ðÿäó ïðèíèìàåì dáï2
= 30 ìì
Çäåñü t = 2 ìì, r = 1,6 ìì, f = 1
Äèàìåòð ñòóïèöû ÷åðâÿ÷íîãî êîëåñà:
dñò2
= (1.6…1.8)dáï2
= (1.6…1.8)⋅30 = 48…54 (ìì) Ïðèíèìàåì dñò2
= 50ìì.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 23 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Äëèíà ñòóïèöû ÷åðâÿ÷íîãî êîëåñà:
lñò2
= (1.2…1.8)dáï2
= (1.2…1.8)⋅30 = 36…54 (ìì) Ïðèíèìàåì lñò2
= 40 ìì.
6.3. Ïîäáîð ïîäøèïíèêîâ.
6.3.1.Ïîäáîð ïîäøèïíèêîâ äëÿ ÷åðâÿêà.
Äëÿ ÷åðâÿêà ïðèìåì ïðåäâàðèòåëüíî ïîäøèïíèêè ðîëèêîâûå êîíè÷åñêèå 7205 ëåãêîé ñåðèè. Ñõåìà óñòàíîâêè ïîäøèïíèêîâ –
âðàñïîð. Èç òàáëèöû âûïèñûâàåì:
d = 25 ìì, в = 52 ìì, Ò = 16,5 ìì, e = 0.36.
Ñìåùåíèå òî÷êè ïðèëîæåíèÿ ðàäèàëüíîé ðåàêöèè îò òîðöà ïîäøèïíèêà:
T (d +D)e 16,5 (25+52)•0,36
 a2
= + = + = 13 ìì a2
= + = + = 13 ìì
2 6 2 6
6.3.2.Ïîäáîð ïîäøèïíèêîâ äëÿ âàëà ÷åðâÿ÷íîãî êîëåñà.
Äëÿ âàëà ÷åðâÿ÷íîãî êîëåñà ïðèìåì øàðèêîïîäøèïíèêè ðàäèàëüíî-óïîðíûå 46303 ñðåäíåé ñåðèè. Èç òàáëèöû âûïèñûâàåì:
d = 17 ìì, в = 47 ìì,
 = 14 ìì,
α
= 260
Ñìåùåíèå òî÷êè ïðèëîæåíèÿ ðàäèàëüíîé ðåàêöèè îò òîðöà ïîäøèïíèêà:
a1
=0,5{B+0,5(D+d)tgα} =0,5{14+0,5•(47 +17)tg200
) = 15 ìì
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 24 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
7.ÊÎÍÑÒÐÓÊÒÈÂÍÛÅ ÐÀÇÌÅÐÛ ×ÅÐÂßÊÀ È ×ÅÐÂß×ÍÎÃÎ ÊÎËÅÑÀ.
7.1.Ðàçìåðû ÷åðâÿêà.
×åðâÿê âûïîëíÿåì çà îäíî öåëîå ñ âàëîì. Ðàçìåðû âàëà è ÷åðâÿêà áûëè îïðåäåëåíû ðàíåå, ïîýòîìó òîëüêî âûïèøåì èõ äëÿ óäîáíîãî äàëüíåéøåãî èñïîëüçîâàíèÿ:
- äèàìåòð äåëèòåëüíîé îêðóæíîñòè d1
= 31,5 ìì;
- äèàìåòð âåðøèí da1
= 37,8 ìì;
- äèàìåòð âïàäèí df1
= 23,9 ìì;
- äëèíà íàðåçàííîé ÷àñòè ÷åðâÿêà b1
= 50,7 ìì;
- äèàìåòð âàëà dáï1
= 17 ìì.
7.2.Ðàñ÷åò êîíñòðóêòèâíûõ ðàçìåðîâ ÷åðâÿ÷íîãî êîëåñà.
Îñíîâíûå ãåîìåòðè÷åñêèå ðàçìåðû ÷åðâÿ÷íîãî êîëåñà áûëè íàìè îïðåäåëåíû ðàíåå. Äëÿ óäîáñòâà äàëüíåéøåãî èñïîëüçîâàíèÿ âûïèøåì èõ:
- äèàìåòð äåëèòåëüíîé îêðóæíîñòè d2
= 126 ìì;
- äèàìåòð âåðøèí da2
= 132,3 ìì;
- äèàìåòð âïàäèí df2
= 118,4 ìì;
- øèðèíà âåíöà ÷åðâÿ÷íîãî êîëåñà b2
= 25,3 ìì;
- äèàìåòð îòâåðñòèÿ ïîä âàë в = 30 ìì;
- äèàìåòð ñòóïèöû ÷åðâÿ÷íîãî êîëåñà dñò2
= 50 ìì; -äëèíà ñòóïèöû ÷åðâÿ÷íîãî êîëåñà lñò2
= 40 ìì.
Êîëåñî êîíñòðóèðóåì îòäåëüíî îò âàëà. Èçãîòîâèì ÷åðâÿ÷íîå êîëåñî ñîñòàâíûì): öåíòð êîëåñà èç ñåðîãî ÷óãóíà, çóá÷àòûé âåíåö –
èç áðîíçû ÁðÀ9ÆÇË. Ñîåäèíèì çóá÷àòûé âåíåö ñ öåíòðîì ïîñàäêîé ñ íàòÿãîì. Òàê êàê ó íàñ íàïðàâëåíèå âðàùåíèÿ ïîñòîÿííîå, òî íà íàðóæíîé ïîâåðõíîñòè öåíòðà ñäåëàåì áóðòèê. Òàêàÿ ôîðìà öåíòðà ÿâëÿåòñÿ òðàäèöèîííîé. Îäíàêî íàëè÷èå áóðòèêà óñëîæíèò èçãîòîâëåíèå è öåíòðà, è âåíöà.
×åðâÿ÷íîå êîëåñî âðàùàåòñÿ ñ íåáîëüøîé ñêîðîñòüþ, ïîýòîìó íåðàáî÷èå ïîâåðõíîñòè îáîäà, äèñêà, ñòóïèöû êîëåñà îñòàâëÿåì íåîáðàáîòàííûìè è äåëàåì êîíóñíûìè ñ áîëüøèìè ðàäèóñàìè çàêðóãëåíèé.
Îñòðûå êðîìêè íà òîðöàõ âåíöà ïðèòóïëÿåì ôàñêàìè f ≈ 0.5m, ãäå m –
ìîäóëü çàöåïëåíèÿ.
f = 0,5⋅3,15 = 1,6 ìì
Ðàññ÷èòàåì îñíîâíûå êîíñòðóêòèâíûå ýëåìåíòû êîëåñà: Ñ = 0,25b2
= 0,25⋅25,3 = 6 ìì; δ
1
= δ
2
= 2m = 2⋅3,15 = 6,3 ìì;
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 25 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
8.ÐÀÑ×ÅÒ ÝËÅÌÅÍÒΠÊÎÐÏÓÑÀ ÐÅÄÓÊÒÎÐÀ.
8.1. Òîëùèíà ñòåíêè êîðïóñà è êðûøêè ÷åðâÿ÷íîãî ðåäóêòîðà:
δ
=0,04a + 2 = 0,04 · 79 + 2 = 5,16 ìì
ïðèíèìàåì δ
= 8 ìì; δ
1
= 0,032à + 2 = 0,032 · 79 + 2 = 4,53 ìì,
ïðèíèìàåì δ
= 8 ìì.
8.2. Òîëùèíà ôëàíöåâ êîðïóñà è êðûøêè:
b = b1
= 1,5δ
= 1,5 · 8 = 12 ìì
8.3.Òîëùèíà íèæíåãî ïîÿñà êîðïóñà ïðè íàëè÷èè áîáûøåê:
ð1
= 1,5δ
= 1,5 · 8 = 12 ìì;
ð2
= (2,25 ÷ 2,75)δ
= (2,25 ÷ 2,75) · 8 = 18…22 ìì; ïðèíèìàåì ð2
= 20 ìì;
8.4.Òîëùèíà ðåáåð îñíîâàíèÿ êîðïóñà è êðûøêè:
m = m1
= (0,85 ÷ 1)δ
= 6,8…8 ìì
8.5.Äèàìåòð ôóíäàìåíòíûõ áîëòîâ:
d1
= (0,03 ÷ 0,036)a + 12 = (0,03 ÷ 0,036) · 79 + 12 = 14,4…15 ìì, ïðèíèìàåì áîëòû ñ ðåçüáîé Ì16;
8.6.Äèàìåòð áîëòîâ:
ó ïîäøèïíèêîâ: d2
= (0,7 ÷ 0,75)d1
= (0,7 ÷ 0,75) · 16 = 11,2…12 ìì ïðèíèìàåì áîëòû ñ ðåçüáîé Ì8
ñîåäèíÿþùèõ îñíîâàíèå êîðïóñà ñ êðûøêîé: d3
= (0,5 ÷ 0,6)d1
= (0,5 ÷ 0,6) · 16 = 8…10 ìì ïðèíèìàåì áîëòû ñ ðåçüáîé Ì10;
8.7.Ðàçìåð øòèôòà: äèàìåòð: dø
= d3
ïðèíèìàåì dø
= 8 ìì
äëèíà: lø
= b + b1
+ 5 ìì = 12 + 12 + 5 = 29 ìì ïðèíèìàåì äëèíó øòèôòà l = 30 ìì
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 26 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
9.Ïðîâåðêà äîëãîâå÷íîñòè ïîäøèïíèêîâ
Âåäîìûé âàë
Ðàññòîÿíèå ìåæäó îïîðàìè (òî÷íåå, ìåæäó òî÷êàìè ïðèëîæåíèÿ ðàäèàëüíûõ ðåàêöèé R3
è R4
) l2
= 70 ìì; äèàìåòð d2
= 126 ìì.

9.1 Îïîðíûå ðåàêöèè â ïëîñêîñòè xz:
1038
 R3x
= R4x
= Ft
/ 2 = = 519 H. R3x
= R4x
= Ft
/ 2 = = 519 H.
2
9.2 Îïîðíûé ðåàêöèè â ïëîñêîñòè yz:
R4yl2 + Frl2
- Fad2
= 0; 2 2
l d
-F
r 2
+
F
a 2
-377,57•35+485,71•63
 R4y
= 2 2
= =248,35 H l2
70 R4y
= 2 2
= =248,35 H l2
70
R3yl2 –
Frl2
- Fad2
= 0; 2 2
l d
F
r 2
+
F
a 2
377,57•35+48571, •63
R3y
= 2 2
=  =625,92 H l2
70 =625,92 H l2
70
Ïðîâåðêà: ∑Fy
= - R3y
–
Fr
–
R4y
= - 625,92 + 377,57 + 248,35 = 0
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 27 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
9.3 Ñóììàðíûå ðåàêöèè:
Fr3
= R3
= R3
2
x
+R3
2
y
= 5192
+6252
= 813 H
 Fr4
= R4
= R4
2
x
+R4
2
y
= 5192
+2482
= 575 H Fr4
= R4
= R4
2
x
+R4
2
y
= 5192
+2482
= 575 H
9.4 Îñåâûå ñîñòàâëÿþùèå ðàäèàëüíûõ ðåàêöèé êîíè÷åñêèõ ïîäøèïíèêîâ: S3
= 0,83eFr3
= 0,83 · 0,360 · 813 = 243 H
S4
= 0,83eFr3
= 0,83 · 0,360 · 575 = 172 H
e = 0,360 –
êîýôôèöèåíò âëèÿíèÿ îñåâîãî íàãðóæåíèÿ
9.5 Îñåâûå íàãðóçêè ïîäøèïíèêîâ:
S3
≥ S4
; Fa
= 0; S3
< S4
; Fa
> S4
–
S3
Fa3
= S3
= 243 H;
Fa4
= S3
+ Fa
= 243 + 486 = 729 H.
«3» ïîäøèïíèê:
 F
a3
= 243
= 0,298 < å, F
a3
= 243
= 0,298 < å,
Fr3
813
Ýêâèâàëåíòíàÿ íàãðóçêà:
Pý3
= Fr3
VKá
KT
= 813 · 1 · 1,2 · 1 = 975,6 H.
ãäå, V –
êèíåìàòè÷åñêèé êîýôôèöèåíò;
Ká
–
êîýôôèöèåíò äèíàìè÷íîñòè íàãðóçêè èëè êîýôôèöèåíò áåçîïàñíîñòè;
KT
–
êîýôôèöèåíò âëèÿíèÿ òåìïåðàòóðû ïîäøèïíèêà íà åãî äîëãîâå÷íîñòü.
«4» ïîäøèïíèê:
 F
a4
= 729
= 1,268 > å, F
a4
= 729
= 1,268 > å,
Fr4
575
Pý4
= (XVFr3
+ YFa
) · Ká
KT
= (0,4 · 1 · 575 + 1,666 · 729) · 1,2 · 1 = 1,73 êÍ.
Ká
= 1,2 –
êîýôôèöèåíò áåçîïàñíîñòè;
KÒ
= 1,0 –
òåìïåðàòóðíûé êîýôôèöèåíò;
Õ –
êîýôôèöèåíò ðàäèàëüíîé íàãðóçêè;
V –
êîýôôèöèåíò âðàùåíèÿ îòíîñèòåëüíîãî âåêòîðà íàãðóçêè âíóòðåííåãî êîëüöà ïîäøèïíèêà.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 28 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Äîëãîâå÷íîñòü îïðåäåëÿþ äëÿ «4» ïîäøèïíèêà, ò.å. äëÿ ïîäøèïíèêà ó êîòîðîãî ýêâèâàëåíòíàÿ íàãðóçêà çíà÷èòåëüíî áîëüøå.
9.6 Ðåñóðñ ïîäøèïíèêà:
L = (C/Pý4
)m
= (23,4/1,733)3,33
= 5811 ìëí. îá.
m =3.33 –
ïîêàçàòåëü êðèâîé âûíîñëèâîñòè.
L•106
5811•106
 Lh
= = = 0,84·106
÷. Lh
= = = 0,84·106
÷.
60•n 60•114,59
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 29 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
10. ÏÐÎÂÅÐÊÀ ÏÐÎ×ÍÎÑÒÈ ØÏÎÍÎ×ÍÎÃÎ ÑÎÅÄÈÍÅÍÈß È ÏÎÑÀÄÊÈ ÂÅÍÖÀ ×ÅÐÂß×ÍÎÃÎ ÊÎËÅÑÀ.
10.1. Ðàññ÷èòàåì øïîíî÷íîå ñîåäèíåíèå äëÿ âõîäíîãî âàëà ñ øêèâîì. Øïîíêó âûáèðàåì ïðèçìàòè÷åñêóþ ïî ÃÎÑÒ 23360-78. Ðàçìåðû øïîíêè:
- ñå÷åíèå b × h = 5 × 5 ìì;
- ãëóáèíà ïàçà âàëà t1
= 3 ìì;
- ãëóáèíà ïàçà ñòóïèöû t2
= 2,3 ìì;
- äëèíà l = 32 ìì.
Øïîíêà ïðèçìàòè÷åñêàÿ ñî ñêðóãëåííûìè òîðöàìè. Ìàòåðèàë øïîíêè –
ñòàëü 45 íîðìàëèçîâàííàÿ. Íàïðÿæåíèÿ ñìÿòèÿ è óñëîâèÿ ïðî÷íîñòè îïðåäåëÿåì ïî ôîðìóëå:
2Т
σсм =  ≤ [σ]см ≤ [σ]см
d(h − t1)⋅l
Ïðè ÷óãóííîé ñòóïèöå [σ]ñì
= 70…100 ÌÏà.
Ïåðåäàâàåìûé ìîìåíò Ò = 7,689 Í⋅ì.
2Ò 2• 7.689 •1000
 σñì = = =23.73ÌÏà d(h- t1
)(l - b) 12•(5 - 3)(32 -5) σñì = = =23.73ÌÏà d(h- t1
)(l - b) 12•(5 - 3)(32 -5)
σñì
< [σ]ñì
, ñëåäîâàòåëüíî, äîïóñòèìî óñòàíîâèòü øêèâ èç ÷óãóíà Ñ×32
10.2.Ðàññ÷èòàåì øïîíî÷íûå ñîåäèíåíèÿ äëÿ âûõîäíîãî âàëà.
10.2.1.Ñîåäèíåíèå âàë-êîëåñî.
Øïîíêó âûáèðàåì ïðèçìàòè÷åñêóþ ïî ÃÎÑÒ 23360-78. Ðàçìåðû øïîíêè:
- ñå÷åíèå b × h = 10 × 8 ìì;
- ãëóáèíà ïàçà âàëà t1
= 5 ìì;
- ãëóáèíà ïàçà ñòóïèöû t2
= 3,3 ìì;
- äëèíà l = 32 ìì.
Øïîíêà ïðèçìàòè÷åñêàÿ ñî ñêðóãëåííûìè òîðöàìè. Ìàòåðèàë øïîíêè –
ñòàëü 45 íîðìàëèçîâàííàÿ. Íàïðÿæåíèÿ ñìÿòèÿ è óñëîâèÿ ïðî÷íîñòè îïðåäåëÿåì ïî ôîðìóëå:
2Т
 σ = σ =  ≤ [σ]см l ≤ [σ]см l
Ïðè ÷óãóííîì öåíòðå êîëåñà [σ]ñì
= 70…100 ÌÏà.
Ïåðåäàâàåìûé ìîìåíò Ò = 65,356 Í⋅ì.
2Ò 2• 65.356 •1000
 σñì = = =66ÌÏà d(h-t1)(l- b) 30 •(8-5)(32-10) σñì = = =66ÌÏà d(h-t1)(l- b) 30 •(8-5)(32-10)
σñì
< [σ]ñì
, ñëåäîâàòåëüíî, äîïóñòèìî öåíòð ÷åðâÿ÷íîãî êîëåñà èçãîòîâèòü èç ñåðîãî ÷óãóíà Ñ×20
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 30 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
10.2.2.Ñîåäèíåíèå âàëà ñ èñïîëíèòåëüíûì ìåõàíèçìîì:
10.2.3. Øïîíêó âûáèðàåì ïðèçìàòè÷åñêóþ ïî ÃÎÑÒ 23360-78. Ðàçìåðû øïîíêè:
2Ò 2• 65.356 •1000
 σñì = = =67ÌÏà σñì = = =67ÌÏà
d(h-t1)(l- b) 20(6-3.5)(45 - 6)
- ñå÷åíèå b × h = 6 × 6 ìì;
- ãëóáèíà ïàçà âàëà t1
= 3,5 ìì;
- ãëóáèíà ïàçà t2
= 2,8 ìì;
2Т
σсм =  ≤ [σ]см ≤ [σ]см
d(h − t1)⋅l
- äëèíà l = 45 ìì.
Øïîíêà ïðèçìàòè÷åñêàÿ ñî ñêðóãëåííûìè òîðöàìè. Ìàòåðèàë øïîíêè –
ñòàëü 45 íîðìàëèçîâàííàÿ. Íàïðÿæåíèÿ ñìÿòèÿ è óñëîâèÿ ïðî÷íîñòè îïðåäåëÿåì ïî ôîðìóëå:
Ïðè ÷óãóííîé ñòóïèöå [σ]ñì
= 70…100 ÌÏà.
Ïåðåäàâàåìûé ìîìåíò Ò = 65,356 Í⋅ì.
σñì
< [σ]ñì
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 31 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
11. ÂÛÁÎÐ ÑÌÀÇÊÈ ÐÅÄÓÊÒÎÐÀ È ÓÏËÎÒÍÈÒÅËÜÍÛÕ ÓÑÒÐÎÉÑÒÂ.
11.1 Âûáîð ñèñòåìû è âèäà ñìàçêè.
Ïðè ñêîðîñòè ñêîëüæåíèÿ â çàöåïëåíèè VS
=2,034 ì/ñ, ðåêîìåíäóåìàÿ âÿçêîñòü ν
50
= 266 ñÑò. Ïî ÃÎÑÒó íåôòåïðîäóêòîâ ïðèíèìàþ ìàñëî òðàíñìèññèîííîå ÒÀÄ-17è(ÃÎÑÒ 23652-79).
Èñïîëüçóåì êàðòåðíóþ ñèñòåìó ñìàçûâàíèÿ.  êîðïóñ ðåäóêòîðà çàëèâàåì ìàñëî, íà âûñîòó âèòêà, íî íå âûøå öåíòðà òåëà êà÷åíèÿ ïîäøèïíèêà. Ïðè âðàùåíèè êîëåñà ìàñëî áóäåò óâëåêàòüñÿ åãî çóáüÿìè, ðàçáðûçãèâàòüñÿ, ïîïàäàòü íà âíóòðåííèå ñòåíêè êîðïóñà, îòêóäà ñòåêàòü â íèæíþþ åãî ÷àñòü. Âíóòðè êîðïóñà îáðàçóåòñÿ âçâåñü ÷àñòèö ìàñëà â âîçäóõå, êîòîðûì ïîêðûâàþòñÿ ïîâåðõíîñòè ðàñïîëîæåííûõ âíóòðè êîðïóñà
äåòàëåé, â òîì ÷èñëå è ïîäøèïíèêè.
Îáúåì ìàñëÿíîé âàííû V = 0,75 ë.
11.2 Âûáîð óïëîòíåíèé.
È äëÿ ÷åðâÿêà, è äëÿ ÷åðâÿ÷íîãî êîëåñà âûáåðåì ìàíæåòíûå óïëîòíåíèÿ ïî ÃÎÑÒ 8752-79. Óñòàíîâèì èõ ðàáî÷åé êðîìêîé âíóòðü êîðïóñà òàê, ÷òîáû îáåñïå÷èòü ê íåé õîðîøèé äîñòóï ìàñëà.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 32 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
12. Ñáîðêà ðåäóêòîðà
Ïåðåä ñáîðêîé âíóòðåííþþ ïîëîñòü êîðïóñà òùàòåëüíî î÷èùàþò è ïîêðûâàþò ìàñëîñòîéêîé êðàñêîé. Ñáîðêó ðåäóêòîðà ïðîèçâîäÿò â ñîîòâåòñòâèè ñ ÷åðòåæîì îáùåãî âèäà. Íà÷èíàþò ñáîðêó ñ òîãî, ÷òî íà ÷åðâÿ÷íûé âàë 0 íàäåâàþò êðûëü÷àòêè è ðàäèàëüíî-óïîðíûå ïîäøèïíèêè, ïðåäâàðèòåëüíî íàãðåâ èõ â ìàñëå äî 80-100Ñ. Ñîáðàííûé ÷åðâÿ÷íûé âàë âñòàâëÿþò â êîðïóñ.
âàëà; çàòåì íàäåâàþò ðàñïîðíóþ âòóëêó è óñòàíàâëèâàþ Âíà÷àëå ñáîðêè âàëà ÷åðâÿ÷íîãî êîëåñà çàêëàäûâàþò øïîíêó è íàïðåññîâûâàþò êîëåñî äî óïîðà â áóðò ò ðîëèêîâûå êîíè÷åñêèå ïîäøèïíèêè, íàãðåòûå â ìàñëå. ïîâåðõíîñòè ñòûêà ôëàíöåâ ñïèðòîâûì ëàêîì. Äëÿ öÑîáðàííûé âàë óêëàäûâàþò â îñíîâàíèå êîðïóñà è íàäåâàþåíòðîâêè êðûøêó óñòàíàâëèâàþò íà êîðïóñ ñ ïîìîùüþ äâóõ ò êðûøêó êîðïóñà, ïîêðûâàÿ ïðåäâàðèòåëüíî êîíè÷åñêèõ øòèôòîâ è çàòÿãèâàþò áîëòû. Çàêëàäûâàþò â ïîäøèïíèêîâûå ñêâîçíûå êðûøêè ðåçèíîâûå ìàíæåòû è óñòàíàâëèâàþò êðûøêè ñ ïðîêëàäêàìè.
Ââåðòûâàþò ïðîáêó ìàñëîñïóñêíîãî îòâåðñòèÿ ñ ïðîêëàäêîé è ìàñëîóêàçàòåëü. Çàëèâàþò â ðåäóêòîð ìàñëî è çàêðûâàþò ñìîòðîâîå îòâåðñòèå êðûøêîé.
Ñîáðàííûé ðåäóêòîð îáêàòûâàþò è èñïûòûâàþò íà ñòåíäå â ñîîòâåòñòâèè ñ òåõíè÷åñêèìè óñëîâèÿìè.
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 33 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
Ïðèëîæåíèå
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 34 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
 |
 |
 |
Îáîçíà÷åíèå |
Íàèìåíîâàíèå |
Êîë. |
Ïðèìå-
÷àíèå
|
| Äîêóìåíòàöèÿ
|
| ÊÍÓ.ÕÒ.000 Ñ |
Á |
Ñáîðî÷íûé ÷åðòåæ |
| ÊÍÓ.ÕÒ.000 Ï |
Ç |
Ïîÿñíèòåëüíàÿ çàïèñêà |
| Ñáîðî÷íûå åäèíèöû
|
| 1 |
ÊÍÓ.ÕÒ.101 |
Êîëåñî ÷åðâÿ÷íîå |
1 |
| 2 |
ÊÍÓ.ÕÒ.102 |
Ìàñëîóêàçàòåëü |
1 |
| Äåòàëè
|
| 3 |
ÊÍÓ.ÕÒ.103 |
Êîðïóñ |
1 |
| 4 |
ÊÍÓ.ÕÒ.104 |
Êðûøêà êîðïóñà |
1 |
| 5 |
ÊÍÓ.ÕÒ.105 |
Âàë |
1 |
| 6 |
ÊÍÓ.ÕÒ.106 |
×åðâÿê |
1 |
| 7 |
ÊÍÓ.ÕÒ.107 |
Âòóëêà |
1 |
| 8 |
ÊÍÓ.ÕÒ.108 |
Êîëüöî |
1 |
| 9 |
ÊÍÓ.ÕÒ.109 |
Êðûøêà ëþêà |
1 |
| 10 |
ÊÍÓ.ÕÒ.110 |
Êðûøêà ïîäøèïíèêà |
1 |
| 11 |
ÊÍÓ.ÕÒ.111 |
Êðûøêà ïîäøèïíèêà |
1 |
| 12 |
ÊÍÓ.ÕÒ.112 |
Ïðîêëàäêà ðåãóëèðîâî÷íàÿ |
6 |
| 13 |
ÊÍÓ.ÕÒ.113 |
Ïðîêëàäêà ðåãóëèðîâî÷íàÿ |
5 |
| 14 |
ÊÍÓ.ÕÒ.114 |
Ïðîêëàäêà óïëîòíèòåëüíàÿ |
1 |
| 15 |
ÊÍÓ.ÕÒ.115 |
Ïðîêëàäêà óïëîòíèòåëüíàÿ |
1 |
| 16 |
ÊÍÓ.ÕÒ.116 |
Ñòàêàí |
1 |
| 17 |
ÊÍÓ.ÕÒ.117 |
Ñòàêàí |
1 |
| 18 |
ÊÍÓ.ÕÒ.118 |
Ïðîáêà |
1 |
| ÊÍÓ.ÕÒ.000 ÑÏ |
| Èçì |
Ëèñò |
¹ äîêóìåíòà |
Ïîäïèñü |
Äàòà |
| Ðàçðàá. |
Äæåíëîäà Ð.Õ. |
Ðåäóêòîð ÷åðâÿ÷íûé |
Ëèò. |
Ëèñò |
Ëèñòîâ |
| Ïðîâ. |
Öîé Ó.À. |
ó |
1 |
2 |
ÊÍÓ
ãðóïïà ÕÒ –
01
|
| Í. êîíòð. |
| Óòâ |
 |
 |
 |
Îáîçíà÷åíèå |
Íàèìåíîâàíèå |
Êîë. |
Ïðèìå-
÷àíèå
|
| Ñòàíäàðòíûå èçäåëèÿ
|
| Ïîäøèïíèêè: |
| 19 |
Ðîëèêîâûé êîíè÷åñêèé |
2 |
| 7205 ÃÎÑÒ 333-79 |
| 20 |
Øàðèêîâûé ðàäèàëüíî-óïîðíûé |
2 |
| 46303 ÃÎÑÒ 831-75 |
| Êðåïåæíûå èçäåëèÿ: |
| 21 |
Âèíò Ì8õ25.36 ÃÎÑÒ 11738-84 |
16 |
| 22 |
Âèíò Ì5õ30.36 ÃÎÑÒ 1491-80 |
4 |
| 23 |
Áîëò Ì10õ90.36 ÃÎÑÒ 7798-70 |
4 |
| 24 |
Áîëò Ì10õ40.36 ÃÎÑÒ 7798-70 |
4 |
| 25 |
Ãàéêà Ì12.4 ÃÎÑÒ 5915-70 |
8 |
| 26 |
Øàéáà 8 65Ã ÃÎÑÒ 6402-70 |
16 |
| 27 |
Øàéáà 10 65Ã ÃÎÑÒ 6402-70 |
8 |
| 28 |
Øòèôò 5õ30 ÃÎÑÒ 3129-70 |
2 |
| 29 |
Ìàíæåòà 32õ52 ÃÎÑÒ 8752-79 |
1 |
| 30 |
Ìàíæåòà 28õ47 ÃÎÑÒ 8752-79 |
1 |
| 31 |
Øïîíêà 10õ8 ÃÎÑÒ 23360-78 |
1 |
| Ìàòåðèàëû
: |
| 32 |
Ìàñëî ÒÀÄ-17èÃÎÑÒ 23652-79 |
0,7ë |
| ÊÍÓ.ÕÒ.000 ÑÏ |
Ëèñò |
| 2 |
| Èçì |
. Ëèñò |
¹ äîêóìåíòà |
Ïîäïèñü |
Äàòà |
Ëèòåðàòóðà
1. Àðêóøà À.È. Òåõíè÷åñêàÿ ìåõàíèêà. Òåîðåòè÷åñêàÿ ìåõàíèêà è ñîïðîòèâëåíèå ìàòåðèàëîâ. Ì., «Âûñøàÿ øêîëà», 1989.
2. Àðòîáîëåâñêèé È.È. Òåîðèÿ ìàøèí è ìåõàíèçìîâ. Ì., «Íàóêà», 1975.
3. Áàáóëèí Í.À. Ïîñòðîåíèå è ÷òåíèå ìàøèíîñòðîèòåëüíûõ ÷åðòåæåé. Ì.: «Âûñøàÿ øêîëà», 1987.
4. Äåòàëè ìàøèí, àòëàñ êîíñòðóêöèé / Ïîä ðåä. Ðåøåòîâà Ä.Í. Ì.: Ìàøèíîñòðîåíèå, 1979
5. Äóíàåâ Ï.Ô., Ëåëèêîâ Î.Ï. Äåòàëè ìàøèí. Êóðñîâîå ïðîåêòèðîâàíèå. Ì.: «Âûñøàÿ øêîëà», 1990.
6. Èöêîâè÷ Ã.Ì., Êèñåëåâ Â.À. è äð. Êóðñîâîå ïðîåêòèðîâàíèå äåòàëåé ìàøèí. Ì., «Ìàøèíîñòðîåíèå», 1965.
7. Êóêëèí Í.Ã., Êóêëèíà Ã.Ñ. Äåòàëè ìàøèí. Ì., «Ìàøèíîñòðîåíèå», 1987.
8. Ìåòîäè÷åñêèå óêàçàíèÿ è âàðèàíòû ê çàäàíèÿì äëÿ ñòóäåíòîâ íåìåõàíè÷åñêèõ ñïåöèàëüíîñòåé. Áèøêåê, «Êûðãûçñêèé Òåõíè÷åñêèé Óíèâåðñèòåò»; ñîñò. Ïàíîâà Ë.Ò., Öîé Ó.À., 1996.
9. Ìåòîäè÷åñêèé óêàçàíèÿ ê âûïîëíåíèþ êóðñîâîãî ïðîåêòèðîâàíèÿ äëÿ ñòóäåíòîâ íåìåõàíè÷åñêèõ ñïåöèàëüíîñòåé. Ôðóíçå, «Ôðóíçåíñêèé Ïîëèòåõíè÷åñêèé Èíñòèòóò»; ñîñò. Ôðåéç Â.Í., Óñóáàëèåâ Æ.Ó.
10.×åðíàâñêèé Ñ.À., Èöêîâè÷ Ã.Ì. è äð. Êóðñîâîå ïðîåêòèðîâàíèå äåòàëåé ìàøèí. Ì., «Ìàøèíîñòðîåíèå», 1979.
11.×åðíàâñêèé Ñ.À., Ñíåñàðåâ Ã.À. Ïðîåêòèðîâàíèå ìåõàíè÷åñêèõ ïåðåäà÷. Ì., «Ìàøèíîñòðîåíèå», 1984.
12.Øåéíáëèò À.Å. Êóðñîâîå ïðîåêòèðîâàíèå äåòàëåé ìàøèí. Ì., «Âûñøàÿ øêîëà», 1991.
|
| ÊÍÓ.ÕÒ.000 ÑÏ |
Ëèñò |
| 37 |
| Èçì. |
Ëèñò |
¹ äîêóìåíòà |
Ïîäïèñü |
Äàòà |
Ñîäåðæàíèå
Çàäàíèå……………………………………………………………………………………………………………………………………………………………………………2
1. Ñòðóêòóðíûé àíàëèç ìåõàíèçìà…………………………………………………………………………………………………………………………..3
2. Êèíåìàòè÷åñêèé àíàëèç ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ –
200………5
3. Äèíàìè÷åñêèé àíàëèç ìåõàíèçìà………………………………………………………………………………………………………………………….8
4. Êèíåìàòè÷åñêèé ðàñ÷åò ïðèâîäà……………………………………………………………………………………………………………………...…13
5. Ðàñ÷åò ÷åðâÿ÷íîé ïåðåäà÷è…………………………………………………………………………………………………………………………….........15
6. Ïðîåêòíûé ðàñ÷åò âàëîâ ðåäóêòîðà è ïîäøèïíèêîâ………………………………………………………………………...……..23
7. Êîíñòðóêòèâíûå ðàçìåðû ÷åðâÿêà è ÷åðâÿ÷íîãî êîëåñà………………………………………………………………………..25
8. Ðàñ÷åò ýëåìåíòîâ êîðïóñà ðåäóêòîðà…………………………………………………………………………………………………………….26
9. Ïðîâåðêà äîëãîâå÷íîñòè ïîäøèïíèêîâ…………………………………………………………………………………………………………..…27
10. Ïðîâåðêà ïðî÷íîñòè øïîíî÷íîãî ñîåäèíåíèÿ è ïîñàäêè âåíöà ÷åðâÿ÷íîãî êîëåñà………………...30
11. Âûáîð ñìàçêè è óïëîòíèòåëüíûõ óñòðîéñòâ………………………………………………………………………………………………..32
12. Ñáîðêà ðåäóêòîðà………………………………………………………………………………………………………………………………………………………...33
Ïðèëîæåíèå………………………………………………………………………………………………………………………………………………………………..34
Ëèòåðàòóðà………………………………………………………………………………………………………………………………………………………………37
|
| ÊÍÓ.ÕÒ.000 ÏÇ |
Ëèñò |
| 38 |
| Èçì. |
Ëèñò |
¹ äîêóì. |
Ïîäïèñü |
Äàòà |
|


 1
Â
1
   Â
  
 C B
C B  aB
=aB
n
= ω2
AB
•lAB
=222
•0,05 =24,2ì/ñ2
aB
=aB
n
= ω2
AB
•lAB
=222
•0,05 =24,2ì/ñ2
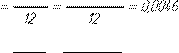 m
m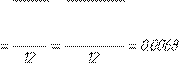 m
m R
R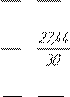 G
G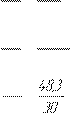 F
F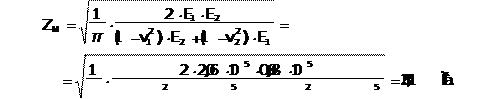 π
(1 −0,35 )⋅0,88⋅10 +(1 −0,49)⋅2,06⋅10
π
(1 −0,35 )⋅0,88⋅10 +(1 −0,49)⋅2,06⋅10 Zε
= = =0,848, ãäå
Zε
= = =0,848, ãäå 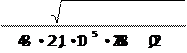 f =1197, 3 • (377,57)2 + 485( 75, )2 =0,0047ìì
f =1197, 3 • (377,57)2 + 485( 75, )2 =0,0047ìì